Analysis of the Sign of the Solution for Certain Second-Order Periodic Boundary Value Problems with Piecewise Constant Arguments
Abstract
1. Introduction
- Theorems 1–3 give sufficient conditions for the unique solution to problem (2) with or to have a constant sign. The technical Lemmas A2–A6 allow to interpret two of the sufficient conditions directly in terms of the coefficients of the linear problem (see Remarks 1 and 2). The other condition is algebraically manipulated in Lemma 1, Remark 3, Lemma 2, and Remark 4;
- An analogous study can be made for with , see Theorem 4, Lemma 3, Theorem 5, and Remark 5;
- To improve significantly these first results, it is important to determine what planar regions of the type:for a certain , are such that their elements are mapped into the interval when scalar multiplied by a certain vector , which will be defined in relation with the differential problem. Lemma 4 is helpful to give an answer, therefore, some of the results are extended in the sense that the conditions required are reduced to some properties on the sign of functions and , and the fact that certain iterates remain in (see Theorems 6 and 7);
- Finally, Theorems 9 and 10 provide sufficient conditions for the unique solution to problem (1) to have a constant sign on J.
2. Main Results
- (i)
- y continuous for ,
- (ii)
- continuous for , and there exist , ,
- (iii)
- exists and is continuous for , , and there exist , , , .
- (i)
- , on ;
- (ii)
- , on ;
- (iii)
- The elements in the second column of the matrix are non-negative.
- The elements in the second column of the matrix are non-positive,
- If , :and one of the following hypotheses are satisfied:
- *
- ; or
- *
- , ; or
- *
- , , ;
- If :and ;
- If :, and ;
- If , :, and ;
- If , :One of the following conditions holds:
- *
- ; or
- *
- and ,
and one of the following conditions holds:- *
- and ; or
- *
- and ; or
- *
- , and
- , .
- ; or
- and ,
- and ; or
- and ; or
- , and ; or
- , and , provided that ; or
- , and , provided that .
- The elements in the second column of the matrix:are non-negative.
- Conditions (i), (ii) in Theorem 1, that is, , , and are non-negative on ; or more generally
- Condition (i) in Theorem 1, and , , , .
- (iv)
- The elements in , the second column of the matrix:are non-positive, and the elements of are non-positive.
- If , by the properties of and , by the definition of ;
- On the other hand, for , and, since ,thus the non-negativity of is derived;
- Finally, if , we have and we distinguish two cases. If , it is reduced to , which is non-negative, and if , then, by the continuity of and ,and we conclude. □
- (I)
- , and on ;
- (II)
- The vector given by:satisfies that for every .
- (I)
- , and on ;
- (II*)
- The vector given by (8) satisfies that for every .
- (I)
- , and on ;
- (III)
- The function g given by (3) is non-negative on ;
- (IV)
- The vector given, for , by:and, for , bysatisfies that , for every ;
- (V)
- If , assume also that the vector:satisfies that , for every .
- , , and one of the following conditions hold:
- *
- ; or
- *
- , and ; or
- *
- , , and ; or
- *
- , , , and .
- , , and one of the following conditions hold:
- *
- ; or
- *
- , and .
- , , and one of the following conditions hold:
- *
- ; or
- *
- , and .
- , , and one of the following conditions hold:
- *
- ; or
- *
- , and .
- , , where , and one of the following conditions hold:
- *
- and ; or
- *
- , and ; or
- *
- , and ; or
- *
- , and one of the following restrictions hold:
- ⋆
- and ; or
- ⋆
- and ; or
- ⋆
- , and ; or
- ⋆
- , and ; or
- ⋆
- , and ; or
- ⋆
- , and
- *
- and one of the following restrictions hold:
- ⋆
- , and ; or
- ⋆
- , and .
- *
- , and .
- ;
- ;
- , and .
3. Examples
- ; or
- , ; or
- , , .
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Some Preliminary Results
Appendix B. Technical Results Concerning the Properties of Functions h1 and h2
- If , then on .
- If , then on . In this case, if , then on .
- If , then on .
- If , then on .
- on , if one of the following conditions hold:
- *
- ; or
- *
- , and ; or
- *
- , , and .
In any case, on . - If , and , then on and on . In this case, if , then on .
- If , then , and, using that , we deduce that and on .
- If , then , so that is decreasing on . Since and we get on if .Suppose that:then if ,which is contradiction. Hence and has a change of sign at the point such that , that is, . In these hypotheses, . Indeed, if , condition (A9) implies , thus , and . Besides, , and , which implies that . If , condition (A9) implies . Thus and . On the other hand, , which implies , and , obtaining .This joint to and proves that is increasing on and decreasing on , and takes values between:andNote that, even in this case, on if . □
- If , then on .
- If , then on .
- If , then on .
- If , then on .
- If , , then on .
- If , then on , and on .
- If , then in and on . In this case, on if .
- If , then on .
- If , then on . In this case, if , then on .
- If , then on .
- If , then on .
- If , then on , and on .
- If , then in , and in . In this case, if , then on .
- If , then on .
- If , then on . In this case, if , then on .
- If , then on .
- If , then on .
- If , then on , and on .
- If , then in and on , whereIn these conditions, if , then on .
- If and , then on .
- If and , then on . In this case, ifthen on .
- If , then on .
- If ; or [ and ], then on .
- Suppose that one of the following conditions holds:
- *
- and ; or
- *
- and ; or
- *
- , and
then on , and on . - If one of the following conditions holds:
- *
- and ; or
- *
- and ; or
- *
- , and ,
- *
- , and ,
then on , and on , where:Under these hypotheses, if , then on . - If one of the following conditions hold:
- *
- , and ; or
- *
- , and
then on and on , where:Under these hypotheses, if , then on . - If one of the following conditions hold:
- *
- , and ; or
- *
- , and ,
then on , on , and on . Moreover, if , then on , and if , then on . - If , then in the interval , for even, and in that interval for odd. In consequence, if , and , then on .
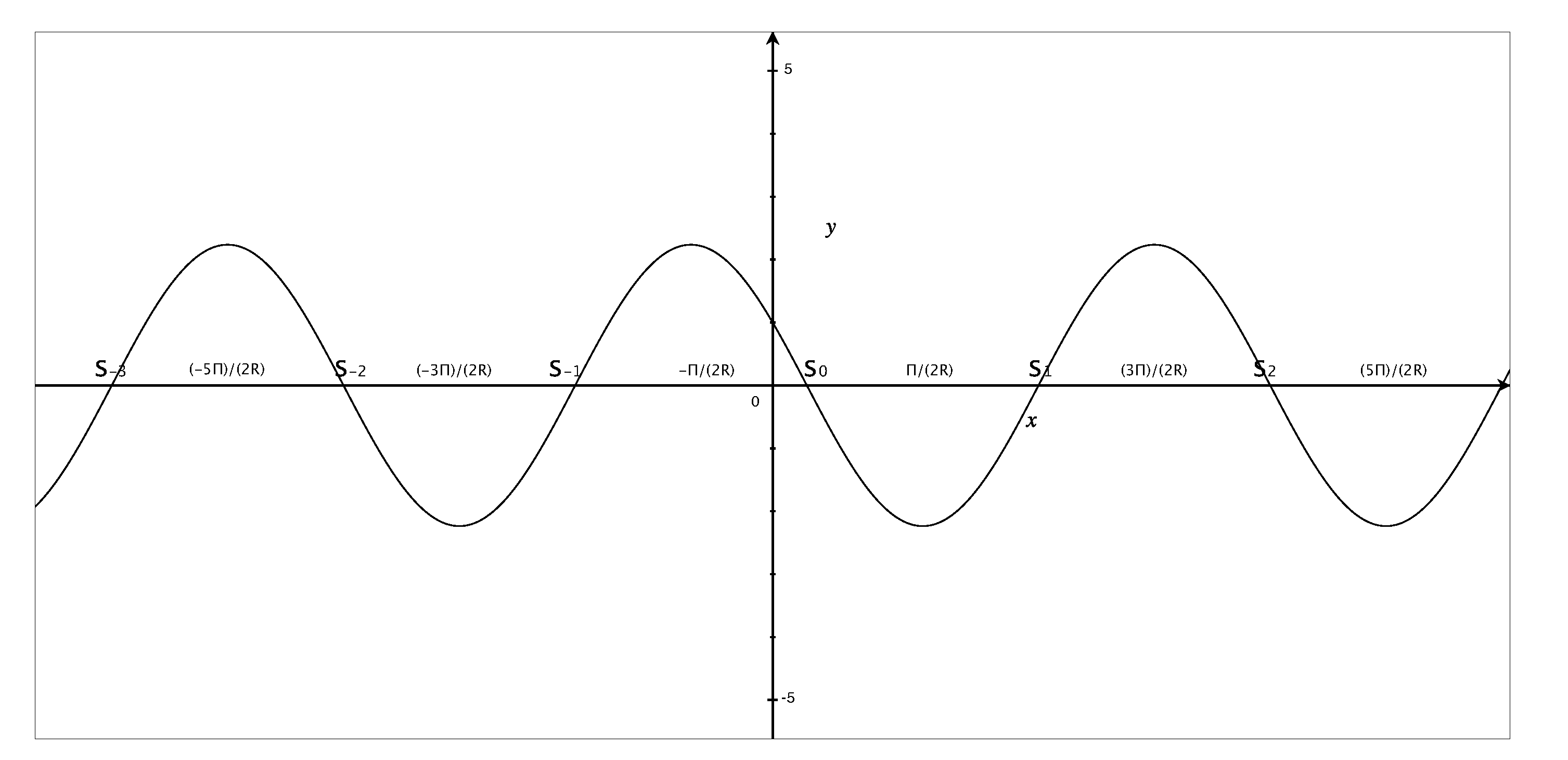
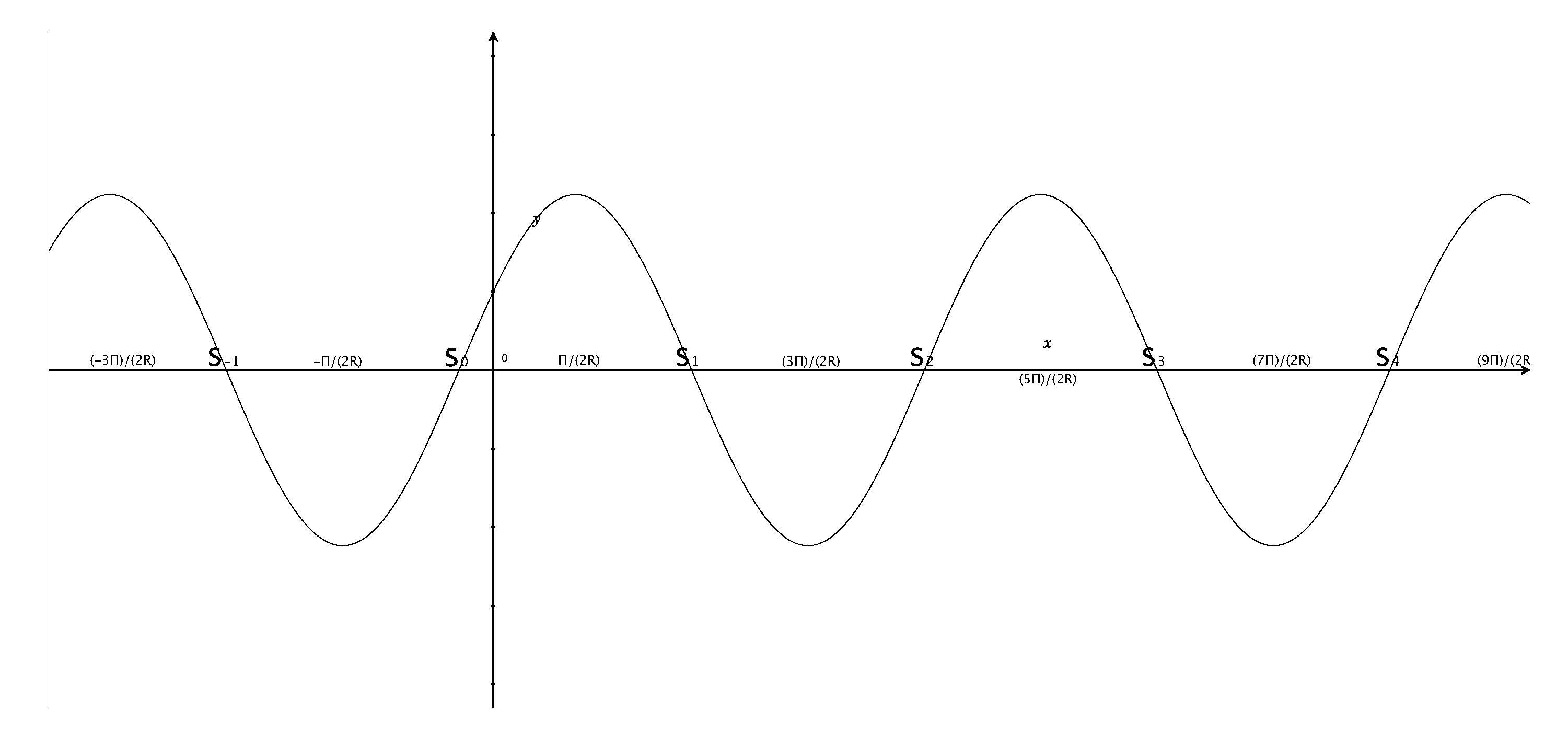
- 1.
- and ; or
- 2.
- and .
- 1.
- ; or
- 2.
- , , that is, , provided that .

Appendix C. Technical Results Concerning the Properties of Function g
- If one of the following properties holds:
- *
- ,
- *
- , and ,
- *
- , and ,
- *
- , , and , that is,
then on . - On the other hand, if , , and , that is,then on and on , where .
- If one of the following conditions holds:
- *
- and ,
- *
- , and ,
- *
- , and ,
then on , and, thus, on . - If one of the following conditions holds:
- *
- and ; or
- *
- and ; or
- *
- , and ; or
- *
- , and ,
then on , and on , where - If one of the following conditions hold:
- *
- , and ; or
- *
- , and
then on and on , where - If one of the following conditions hold:
- *
- , and ; or
- *
- , and ,
then on , on , and on . - If , then the zeros of in areIn consequence, if , , then on .
- If , then in the interval , for even, and in that interval for odd. In consequence, if and , then on .
- *
- If , then on , for , and on , for .
- *
- If , then on , for , and on , for .
- , and ; or
- , and
- If :
- *
- k odd with ; and
- *
- if , odd with , that is, with odd.
- If :
- *
- k even with ; and
- *
- if , even with , that is, , with even.
References
- Halanay, A.; Safta, C.A. A critical case for stability of equilibria of delay differential equations and the study of a model for an electrohydraulic servomechanism. Syst. Control Lett. 2020, 142, 104722. [Google Scholar] [CrossRef]
- Karatza, E.; Karalis, V. Delay differential equations for the description of Irbesartan pharmacokinetics: A population approach to model absorption complexities leading to dual peaks. Eur. J. Pharm. Sci. 2020, 153, 105498. [Google Scholar] [CrossRef] [PubMed]
- Rameh, R.B.; Cherry, E.M.; dos Santos, R.W. Single-variable delay-differential equation approximations of the Fitzhugh-Nagumo and Hodgkin-Huxley models. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105066. [Google Scholar] [CrossRef]
- Shu, H.; Xu, W.; Wang, X.-S.; Wu, J. Complex dynamics in a delay differential equation with two delays in tick growth with diapause. J. Differ. Equ. 2020, 269, 10937–10963. [Google Scholar] [CrossRef]
- Wurm, J.; Bachler, S.; Woittennek, F. On delay partial differential and delay differential thermal models for variable pipe flow. Int. J. Heat Mass Transf. 2020, 152, 119403. [Google Scholar] [CrossRef]
- Győri, I.; Horváth, L. Explicit estimates and limit formulae for the solutions of linear delay functional differential systems with non-negative Volterra type operators. Appl. Math. Comput. 2020, 385, 125451. [Google Scholar]
- Bodnar, M. The nonnegativity of solutions of delay differential equations. Appl. Math. Lett. 2000, 13, 91–95. [Google Scholar] [CrossRef]
- Pituk, M. Existence of Nonnegative Solutions of Linear Autonomous Functional Differential Equations. Mathematics 2020, 8, 1098. [Google Scholar] [CrossRef]
- Kunisch, K.; Schappacher, W. Order preserving evolution operators of functional differential equations. Boll. Unione Mat. Ital. B 1979, 16, 480–500. [Google Scholar]
- Aruğaslan Çinçin, D.; Cengiz, N. Qualitative behavior of a Liénard-type differential equation with piecewise constant delays. Iran. J. Sci. Technol. Trans. Sci. 2020, 44, 1439–1446. [Google Scholar] [CrossRef]
- Seifert, G. Second order scalar functional differential equations with piecewise constant arguments. J. Differ. Equ. Appl. 2002, 8, 427–445. [Google Scholar] [CrossRef]
- Seifert, G. Second-order neutral delay-differential equations with piecewise constant time dependence. J. Math. Anal. Appl. 2003, 281, 1–9. [Google Scholar] [CrossRef]
- Yuan, R. Pseudo-almost periodic solutions of second-order neutral delay differential equations with piecewise constant argument. Nonlinear Anal. 2000, 41, 871–890. [Google Scholar] [CrossRef]
- Yuan, R. On the second-order differential equation with piecewise constant argument and almost periodic coefficients. Nonlinear Anal. 2003, 52, 1411–1440. [Google Scholar] [CrossRef]
- Zhang, F.Q. Boundary value problems for second order differential equations with piecewise constant arguments. Ann. Differ. Equ. 1993, 9, 369–374. [Google Scholar]
- Jankowski, T.; Szatanik, W. Second-order differential equations with deviating arguments. Bound. Value Probl. 2006, 2006, 23092. [Google Scholar] [CrossRef][Green Version]
- Mukhigulashvili, S. On a periodic boundary value problem for second-order linear functional differential equations. Bound. Value Probl. 2005, 2005, 960698. [Google Scholar] [CrossRef][Green Version]
- Cabada, A.; Ferreiro, J.B.; Nieto, J.J. Green’s function and comparison principles for first order periodic differential equations with piecewise constant arguments. J. Math. Anal. Appl. 2004, 291, 690–697. [Google Scholar] [CrossRef]
- Nieto, J.J. A comparison result for a linear differential equation with piecewise constant delay. Glas. Mat. Ser. III 2004, 39, 73–76. [Google Scholar] [CrossRef]
- Nieto, J.J.; Rodríguez-López, R. Green’s function for second-order periodic boundary value problems with piecewise constant arguments. J. Math. Anal. Appl. 2005, 304, 33–57. [Google Scholar] [CrossRef]
- Akhmet, M.U.; Büyükadalı, C.; Ergenç, T. Periodic solutions of the hybrid system with small parameter. Nonlinear Anal. Hybrid Syst. 2008, 2, 532–543. [Google Scholar] [CrossRef]
- Akhmet, M.U. On the reduction principle for differential equations with piecewise constant argument of generalized type. J. Math. Anal. Appl. 2007, 336, 646–663. [Google Scholar] [CrossRef]
- Yang, P.; Liu, Y.; Ge, W. Green’s function for second order differential equations with piecewise constant arguments. Nonlinear Anal. 2006, 64, 1812–1830. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buedo-Fernández, S.; Cao Labora, D.; Rodríguez-López, R.; Tersian, S.A. Analysis of the Sign of the Solution for Certain Second-Order Periodic Boundary Value Problems with Piecewise Constant Arguments. Mathematics 2020, 8, 1953. https://doi.org/10.3390/math8111953
Buedo-Fernández S, Cao Labora D, Rodríguez-López R, Tersian SA. Analysis of the Sign of the Solution for Certain Second-Order Periodic Boundary Value Problems with Piecewise Constant Arguments. Mathematics. 2020; 8(11):1953. https://doi.org/10.3390/math8111953
Chicago/Turabian StyleBuedo-Fernández, Sebastián, Daniel Cao Labora, Rosana Rodríguez-López, and Stepan A. Tersian. 2020. "Analysis of the Sign of the Solution for Certain Second-Order Periodic Boundary Value Problems with Piecewise Constant Arguments" Mathematics 8, no. 11: 1953. https://doi.org/10.3390/math8111953
APA StyleBuedo-Fernández, S., Cao Labora, D., Rodríguez-López, R., & Tersian, S. A. (2020). Analysis of the Sign of the Solution for Certain Second-Order Periodic Boundary Value Problems with Piecewise Constant Arguments. Mathematics, 8(11), 1953. https://doi.org/10.3390/math8111953





