A Memetic Decomposition-Based Multi-Objective Evolutionary Algorithm Applied to a Constrained Menu Planning Problem

Abstract

Encouraging healthy and balanced diet plans is one of the most important action points for governments around the world. Generating healthy, balanced and inexpensive menu plans that fulfil all the recommendations given by nutritionists is a complex and time-consuming task; because of this, computer science has an important role in this area. This paper deals with a novel constrained multi-objective formulation of the menu planning problem specially designed for school canteens that considers the minimisation of the cost and the minimisation of the level of repetition of the specific courses and food groups contained in the plans. Particularly, this paper proposes a multi-objective memetic approach based on the well-known multi-objective evolutionary algorithm based on decomposition (MOEA/D). A crossover operator specifically designed for this problem is included in the approach. Moreover, an ad-hoc iterated local search (ILS) is considered for the improvement phase. As a result, our proposal is referred to as ILS-MOEA/D. A wide experimental comparison against a recently proposed single-objective memetic scheme, which includes explicit mechanisms to promote diversity in the decision variable space, is provided. The experimental assessment shows that, even though the single-objective approach yields menu plans with lower costs, our multi-objective proposal offers menu plans with a significantly lower level of repetition of courses and food groups, with only a minor increase in cost. Furthermore, our studies demonstrate that the application of multi-objective optimisers can be used to implicitly promote diversity not only in the objective function space, but also in the decision variable space. Consequently, in contrast to the single-objective optimiser, there was no need to include an explicit strategy to manage the diversity in the decision space in the case of the multi-objective approach.

1. Introduction

Nowadays, due to unhealthy and sedentary lifestyles, a high percentage of the human population suffers from various diseases such as high cholesterol, diabetes and other conditions related to those habits which can cause other serious illnesses, including several types of cancer [1]. As a result, promoting healthy and active habits for young people is becoming a significant duty for governments around the world. Since it is impossible for governments to control what children and teenagers consume in their homes, having a healthy and balanced meal plan for school cafeterias is essential to help mitigate the effects of the remaining meals. The Government of the Canary Islands wants to promote healthy habits in children and teenagers. Generating healthy and balanced menu plans is key to this effort. This is precisely the main goal of this research, which is part of the “Programa de Eco-comedores Escolares de Canarias” programme, which seeks to generate healthy, balanced and affordable menu plans for regional school cafeterias.

This work presents a novel constrained multi-objective formulation of the well-known menu planning problem (MPP) [2]. Specifically, the version of the MPP considered herein is a multi-objective formulation that includes a set of daily and n-days constraints for several nutrients, as introduced in [3], as well as the two objective functions related to the cost of the menu and the level of repetition of courses and food groups proposed in [4].

Planning and scheduling problems have been successfully solved with meta-heuristics. Particularly, many of the best-known solutions for problems in this area have been achieved with memetic algorithms (MAs) [5,6,7,8]. In [3], an MA was proposed to deal with a single-objective constrained formulation of the MPP where the cost of the menu had to be minimised. To do so, a specific iterated local search (ILS) was designed, as well as an ad-hoc crossover operator. Additionally, the MA included an explicit mechanism to promote diversity in the decision variable space in order to avoid premature convergence. The above allowed high-quality solutions to be attained. The working hypothesis herein is that by using our novel multi-objective constrained formulation of the MPP, which considers the cost of the plan and at the same time the level of repetition of the specific courses and food groups contained in the plan, it is possible to find solutions that are similar in terms of the cost to those provided by the aforementioned single-objective MA, but significantly better regarding the level of repetition.

Taking these findings into account, this work presents a novel multi-objective approach based on the well-known multi-objective evolutionary algorithm based on decomposition (MOEA/D) [9]. MOEA/D was applied to the menu planning problem in a previous work carried out by the authors [10]. It was compared to the well-known Non-dominated Sorting Genetic Algorithm II (NSGA-II) [11] and Strength Pareto Evolutionary Algorithm 2 (SPEA2) [12]. Since knowledge about the menu planning problem was not considered, ad-hoc variation operators, as well as an improvement operator, were not incorporated into MOEA/D. Results showed that MOEA/D was outperformed by NSGA-II and SPEA2. In order to improve the performance of MOEA/D when dealing with the menu planning problem, in the current work, an extension of the ILS applied by the single-objective MA proposed in [3] was considered as the improvement operator of MOEA/D. We should note that, in opposition to other approaches, MOEA/D facilitates the incorporation of an improvement operator, which is an important component to quickly yield feasible solutions. Finally, the ad-hoc crossover operator proposed by the same authors was also integrated into MOEA/D.

As a result, our proposal is referred to as ILS-MOEA/D, and in contrast to the single-objective optimiser presented in [3], it does not include an explicit strategy to manage diversity in the decision variable space. The reason is that, as in other problems [13], the promotion of diversity in the objective function space, imposed by the use of different weights in ILS-MOEA/D to decompose the problem, causes an implicit preservation of diversity in the decision variable space. A wide experimental evaluation is carried out herein, where the novel ILS-MOEA/D is compared against the single-objective MA proposed in [3], in terms of the quality of the solutions attained by both optimisers.

Bearing all the above in mind, the main contributions of this work are the following:

• A novel constrained multi-objective formulation of the MPP.
• A novel adaptation of MOEA/D, ILS-MOEA/D, that integrates an ILS as the improvement step of the approach, as well as an ad-hoc crossover operator to speed up the achievement of high-quality solutions for the multi-objective constrained version of the MPP.
• In comparison to the single-objective MA, ILS-MOEA/D yields menu plans with a similar cost, but with a significantly better level of repetition.
• The promotion of diversity in the objective function space through the application of a multi-objective algorithm helps avoid premature convergence, since diversity is also implicitly kept in the decision variable space.

The rest of this paper is structured as follows. Section 2 provides a review of related works and presents our new formulation of the MPP. Afterwards, the novel ILS-MOEA/D is detailed in Section 3. Then, the experimental evaluation performed to validate our proposals is presented in Section 4. The results obtained from the experiments are discussed in Section 5. Finally, the conclusions are exposed in Section 6, together with some lines of further research.

2. Menu Planning Problem

2.1. Background

Menu planing has been solved by using computers since early 1960 [2,14]. Many of the proposed formulations are NP-complete, meaning it is quite a complex task [15]. In essence, the classical MPP aims to find a combination of dishes which satisfies certain restrictions involving budget, variety and nutritional requirements for an n-day sequence. Even though there is no consensus on the specific objectives that an MPP formulation should consider, in almost every formulation, it is common for the cost of the menu plan to be considered one of the main objectives to optimise [2,3,4,10,16,17]. Other options for defining the objective functions are the users’ preferences for certain foods, the level of adequacy or the level of acceptance [18,19,20,21].

The constraints considered in menu planning problems are usually based on the nutritional requirements that meal plans have to satisfy. As a result a set of constraints is defined that models the recommended minimum and maximum amounts of different nutrients [21,22,23,24,25,26]. Other constraints consider the variety of the meals, their predominant colour, their consistency, the time required to prepare them and food that cannot be consumed, among others [19,22,25,27]. Two of the most frequently used techniques to handle constraints are based on the application of repairing methods [4,10,19,26,28,29] or penalisation functions [16,30,31]. In the first case, operators are applied to an infeasible solution until it becomes feasible. In the second case, the fitness function is penalised somehow depending on the degree of infeasibility of the corresponding solution. Hence, the higher the degree of infeasibility of the solution, the larger the probability to be discarded.

Both single-objective [3,16,19,32] and multi-objective optimisers [4,10,17,28] have been devised for the MPP. In the single-objective case, most of the formulations consider the cost as the only objective to optimise, while the nutritional requirements are used as constraints. In the case of multi-objective formulations, the cost is always considered as one of the objective functions to optimise [29,30,31]. Additionally, the seasonal quality, food flavour and food temperature [29], food preferences [30] and the nutritional error [31] are considered as other objective functions. In almost all cases, the nutritional requirements, as well as the users’ personal preferences, model the constraints of the multi-objective formulations.

Although there exist many different types of algorithms for solving this problem, a high percentage of published papers use evolutionary algorithms (EAs) or other types of meta-heuristics due to the benefits they offer, such as robustness, reliability, global-search ability and simplicity [16,20,21,26,28]. EAs are approximated methods based on the concept in natural evolution of survival of the fittest individual [33]. Given a population of individuals in some environment with limited resources, the competition for survival causes natural selection, with the fittest individuals more likely to survive and reproduce. In addition, being approximated methods means that although there is no guarantee of obtaining the optimal solution to a problem, high-quality solutions can be found in a reasonable period of time. The classical genetic algorithm (GA) is the most common approach for solving single-objective formulations of the MPP [16,34], while previous multi-objective formulations of the MPP have been frequently addressed by applying the state-of-art NSGA-II, such as the work proposed in [28,30,31].

The lack of ad-hoc operators for the MPP could possibly yield sub-optimal solutions due to the problem of premature convergence. In order to avoid this, problem-specific operators or procedures, such as intensification mechanisms, have been included into EAs, resulting in memetic algorithms (MAs) [35,36]. MAs can be seen as the combination of an EA with an intensification mechanism in order to improve the general performance of the optimiser [37]. An example of a single-objective MA successfully applied to the MPP is that proposed in [3].

Additionally, a software named schoolthy was proposed in [4], which allows menus to be planned automatically. The tool uses an MPP formulation similar to the one proposed in this work to generate not only affordable plans, but also varied from a nutritional standpoint. Although it was designed for school cafeterias, it could be adapted to other environments, such as hospitals, prisons and retirement homes, among others.

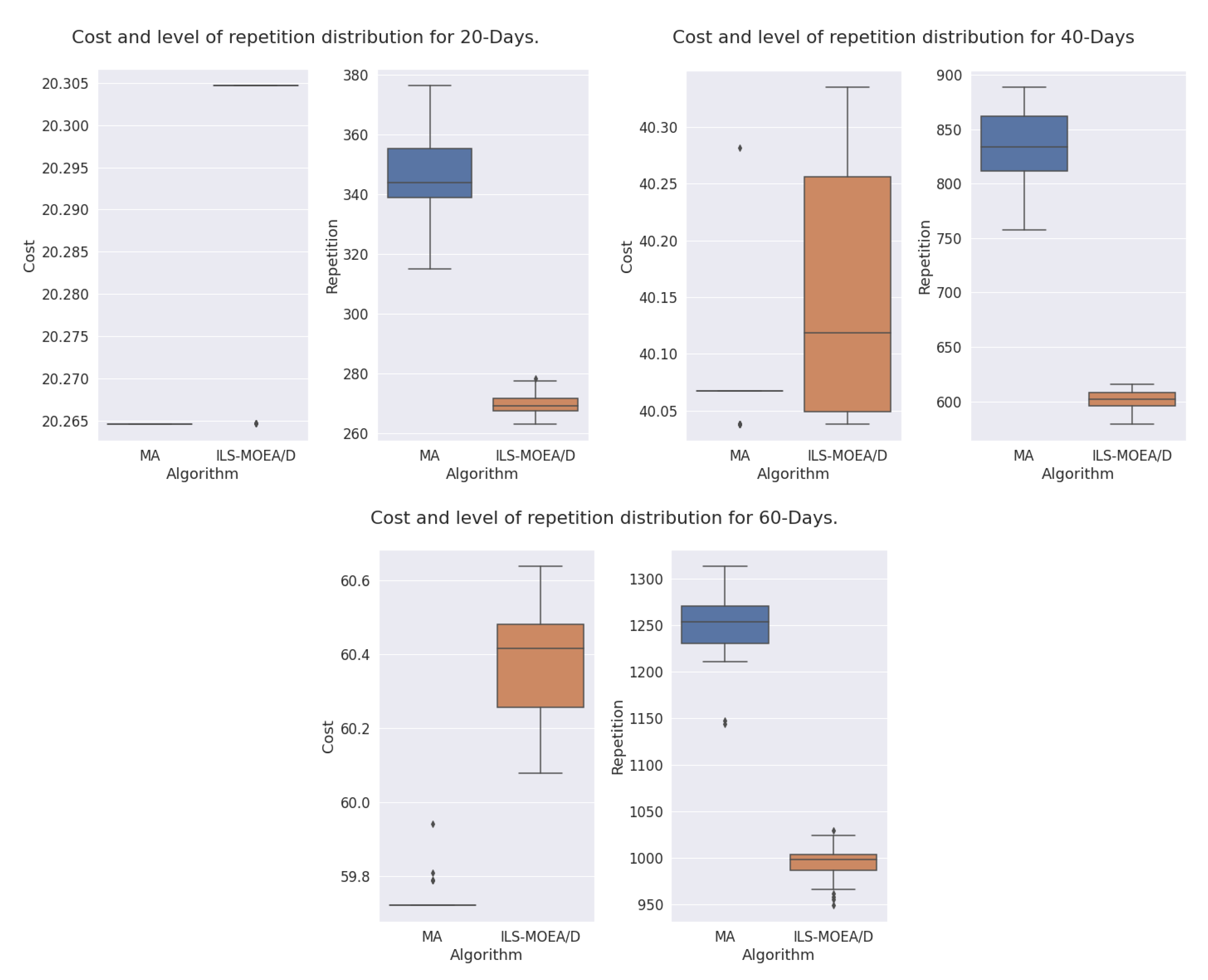
As we previously mentioned in Section 1, in the current work, we present a novel constrained multi-objective formulation of the MPP. It consists of the same set of nutritional daily and n-days (global) constraints presented in [3]. At the same time, the two objective functions proposed in [4], i.e., the cost of the meal plan and its level of repetition of courses and food groups, are also considered. As far as we know, this is the first time that an objective function modelling the level of repetition of specific courses and food groups is optimised together with the cost under a multi-objective formulation of the menu planning problem, which in addition considers the management of daily and global nutritional constraints. Those constraints are successfully managed by considering the infeasibility degree of a particular solution, thus giving preference to those solutions with, first, a lower infeasibility degree, and second, a lower fitness in terms of both aforementioned objective functions. Furthermore, the application of a multi-objective memetic approach based on decomposition that includes knowledge about the menu planning problem in the form of a tailored improvement operator and an ad-hoc crossover operator had never been carried out before. The above allows feasible solutions of the multi-objective constrained formulation that we are presenting herein to be attained quickly.

2.2. Formulation

In this work, a novel multi-objective constrained formulation of the MPP focused on school cafeterias is proposed. Due to the above, only lunch is planned for n days, including a starter, a main course and a dessert per day. The different courses are selected from a database containing their cost and nutritional facts. Courses in the database are grouped into three different categories: starters, main courses and desserts. The particular objective functions are, on the one hand, the cost of the whole plan, which has to be minimised, and on the other hand, the level of repetition of specific courses and food groups that the plan consists of, which has to be minimised as well. The motivation behind the second objective function is to promote a varied plan from a nutritional point of view.

Additionally, the set of daily and global constraints applied in [3] are also taken into account in this new formulation. Those constraints are modelled on the recommendations on intakes of macro-nutrients and micro-nutrients following the guidelines given in the White Book on Child Nutrition. Furthermore, other reference documents regarding school diets and allergens were also consulted, specifically, those endorsed by the Spanish Government Ministry of Education, Culture and Sports and the Ministry of Health, Social Services and Equality (These consensus documents are available at http://www.aecosan.msssi.gob.es/AECOSAN/docs/documentos/nutricion/educanaos/documento_consenso.pdf and https://www.aepnaa.org/).

As we said, the cost is an objective to be minimised and is calculated as the sum of the costs of the courses included in the plan. Note that the cost of each course is calculated as the sum of the costs of all the ingredients required to prepare that course. Formally, the cost is defined as follows:

$$C=\sum _{j=1}^n\left(c_{f{c}_j}+c_{s{c}_j}+c_{d{s}_j}\right)$$

(1)

where C is the total cost of the menu plan and $c_{f{c}_j},c_{s{c}_j},c_{d{s}_j}$ represent the cost of the starter, main course and dessert, respectively, for day j, and n is the number of days for which the menu plan is being designed.

An assorted menu plan is particularly important when it is intended for children. As a result of this, the level of repetition of courses and food groups was defined as the second objective function to be minimised. The level of repetition represents the percentage of courses and food groups repeated throughout the meal plan. The following equation defines how it is calculated:

$$L_{Rep}=\sum _{j=1}^n\left(v_{{MC}_j}+\frac{p_{fc}}{d_{f{c}_j}}+\frac{p_{sc}}{d_{s{c}_j}}+\frac{p_{ds}}{d_{d{s}_j}}+v_{F{G}_j}\right)$$

(2)

where $L_{Rep}$ is the level of repetition, $v_{{MC}_j}$ represents the compatibility, in terms of food groups, among courses $f{c}_j,s{c}_j,d{s}_j$ for day j; p is a penalty constant for every kind of course and d stands for the number of days since a specific course was repeated. Finally, $v_{F{G}_j}$ is the penalty value for repeating particular food groups in the last five days.

Equation (3) allows the value of $v_{{MC}_j}$ to be calculated, where $\left|G\right|$ is the number of food groups, $x_g\in \{0,1,2,3\}$ is the number of times a particular food group is contained in the three courses (starter, main course and dessert) of the menu for day j and $p_g$ is the corresponding penalty value for repeating the food group g. The food groups considered in this work are as follows: meat, cereal, fruit, dairy, legume, shellfish, pasta, fish, vegetable and other.

$$v_{{MC}_j}=\sum _{g=1}^{\left|G\right|}\left(x_{g_j}·p_g\right)$$

(3)

$$v_{{FG}_j}=\sum _{i=1}^{min(j-1,T)}\left((\sum _{g=1}^{\left|G\right|}{x}_{g_i}·p_g)+(y_i·p_{\left|G\right|+i})\right)$$

(4)

Equation (4) is used to compute $v_{{FG}_j}$, where $T=5$ days is the number of previous days considered, $\left|G\right|$ is the number of food groups, $x_{g_i}\in \{0,1\}$ indicates whether the food group g is repeated on day $j-i$ ($x_{g_i}=1$) or not ($x_{g_i}=0$) with respect to day j, $y_i\in \{0,1\}$ indicates whether any food group was repeated i day(s) before the current day j ($y_i=1$) or not ($y_i=0$), and $p_g$ and $p_{\left|G\right|+i}$ are the corresponding penalty values.

The types of penalties and their values used to compute $v_{{MC}_j}$ and $v_{{FG}_j}$ are shown in

Table 1. Types of penalties defined to calculate the level of repetition objective.

Penalty	Description	Value
$p_1$	penalty for repeating other food group	0.1
$p_2$	penalty for repeating meat food group	3
$p_3$	penalty for repeating cereal food group	0.3
$p_4$	penalty for repeating fruit food group	0.1
$p_5$	penalty for repeating dairy food group	0.3
$p_6$	penalty for repeating legume food group	0.3
$p_7$	penalty for repeating shellfish food group	2
$p_8$	penalty for repeating pasta food group	1.5
$p_9$	penalty for repeating fish food group	0.5
$p_{10}$	penalty for repeating vegetable food group	0.1
$p_{11}$	penalty for repeating the same food group one day earlier	3
$p_{12}$	penalty for repeating the same food group two days earlier	2.5
$p_{13}$	penalty for repeating the same food group three days earlier	1.8
$p_{14}$	penalty for repeating the same food group four days earlier	1
$p_{15}$	penalty for repeating the same food group five days earlier	0.2
$p_{16}=p_{fc}$	penalty for repeating a starter	8
$p_{17}=p_{sc}$	penalty for repeating a main course	10
$p_{18}=p_{ds}$	penalty for repeating a dessert	2

. Furthermore, penalties are determined by the repetition of food groups ($p_1$–$p_{10}$), the repetition of the same food group from one to five days prior to the current day ($p_{11}$–$p_{15}$), and the repetition of specific courses ($p_{16}=p_{fc}$, $p_{17}=p_{sc}$, and $p_{18}=p_{ds}$). In the case of penalties for repeating food groups ($p_1$–$p_{10}$), if the penalty value of a given food group is very large in comparison to the remaining food group penalty values, then a plan with a lower number of courses belonging to that food group will be provided. For instance, we have given preference to those courses consisting primarily of vegetables ($p_{10}=0.1$) over courses composed primarily of meat ($p_2=3$).

Additionally, as stated earlier, in order to consider a menu plan as feasible, it must fulfil some constraints related to a set of nutritional requirements, such as having each nutrient intake be within a given range. Besides, the set of constraints of this MPP formulation is modelled by two sub-sets of constraints: global constraints and daily constraints. For instance, energy (kcal), fats and proteins are evaluated both daily and globally. At this point, we note that, since only lunch is considered in the meal plans, the recommended nutritional intakes were adapted. For each nutrient h considered, $r_h$ denotes the recommended amount to ingest every day at lunch. Based on the recommended amount, a range of acceptable intake is generated for each nutrient.

Table 2. Minimum and maximum ranges for nutrient intakes

Nutrient	${\mathit{r}}_{\mathbf{min}}$	${\mathit{r}}_{\mathbf{max}}$
Energy (per day)	0.85	1.15
Fats (per day)	0.75	1.25
Proteins (per day)	0.75	1.25
Energy (n days)	0.90	1.10
Fats (n days)	0.90	1.10
Proteins (n days)	0.90	1.10
Micro-nutrients	0.70	1.30

defines a set R of pairs $(r_{min},r_{max})$ with the minimum and maximum amount allowed for each nutrient h, respectively (The set of micro-nutrients is as follows: Folic acid, Phosphorus, Magnesium, Selenium, Sodium, Vitamins A, B1, B2, B6, B12, C, D, E, Iodine, Zinc).

Formally, an individual S would be considered feasible if and only if it satisfies the following set of global constraints:

$$\forall h\in HG:n\times r_{{min}_h}\times r_h\le in(S,h)\le n\times r_{ma{x}_h}\times r_h$$

(5)

where $in(S,h)$ is the global intake of nutrient h in the plan S, and $HG$ denotes the set of nutrients considered for the global constraints.

In the case of energy, fats and proteins, their intakes for every single day d, i.e., $in(S,h,d)$ are also checked to be in the established daily ranges:

$$\forall h\in HD:r_{{min}_h}\times r_h\le in(S,h,d)\le r_{ma{x}_h}\times r_h$$

(6)

where $HD$ is the set of nutrients considered for the daily constraints.

In order to properly compare solutions, a definition of an infeasibility degree $id$ is required. As previously defined in [3], the infeasibility degree of a solution S is calculated as shown in Equation (7). Note that an individual S that satisfies Equations (5) and (6) would have an infeasibility degree $id\left(S\right)=0$, and it would be considered a feasible solution.

$$id\left(S\right)=gid\left(S\right)+did\left(S\right)$$

(7)

The infeasibility degree $id$ is calculated as the sum of the global infeasibility degree $gid\left(S\right)$ and the daily infeasibility degree $did\left(S\right)$. Equations (8) and (9) show the calculation of $gid\left(S\right)$ and $did\left(S\right)$, respectively.

$$\begin{array}{cc}\hfill gid\left(S\right)=& \sum _{h\in HG}{\left(max\left(in(S,h),r_{ma{x}_h}\right)-r_{ma{x}_h}\right)}^2\times {10}^6+\hfill \\ \hfill & \sum _{h\in HG}{\left(r_{mi{n}_h}-min\left(in(S,h),r_{mi{n}_h}\right)\right)}^2\times {10}^6\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill did\left(S\right)=& \sum _{h\in HD}\sum _{d=1}^n{\left(max\left(in(S,h,d),r_{ma{x}_h}\right)-r_{ma{x}_h}\right)}^2+\hfill \\ \hfill & \sum _{h\in HD}\sum _{d=1}^n{\left(r_{mi{n}_h}-min\left(in(S,h,d),r_{mi{n}_h}\right)\right)}^2\hfill \end{array}$$

(9)

3. Algorithms

The method that we are presenting herein (ILS-MOEA/D) is a particularisation of MOEA/D that has been specifically designed to deal with the multi-objective constrained MPP proposed in the previous section. MOEA/D is an EA for multi-objective optimisation proposed in [9], where the underlying idea is to decompose a Multi-objective Optimisation Problem (MOP) into a number of scalar optimisation sub-problems and optimise them simultaneously.

MOEA/D is a population-based EA that maintains N candidate solutions in the population. The decomposition approach is applied to generate N sub-problems that are simultaneously optimised. Specifically, each individual is associated to one of the generated sub-problems (a one-to-one mapping is performed). Furthermore, it establishes some relationships between sub-problems and organises them into neighbourhoods. These neighbourhoods are defined in terms of the weight vectors used to decompose the problem. The optimisation of each sub-problem is influenced by information of its neighbouring sub-problems. The principle for organising the optimisation process in this way is that the optimal solution for two neighbouring sub-problems is expected to be similar [9]. Furthermore, the process of decomposing an MOP into N scalar optimisation sub-problems can be done by applying different approaches.

In this paper, our strategy relies on the Tchebycheff decomposition approach [38]. Let $\lambda =\{{\lambda }^1,\dots ,{\lambda }^N\}$ be a set of even spread weight vectors. In this approach, the scalar objective function associated to the j-th sub-problem, with $j=1,\dots ,N$, is defined as follows:

$$g^{te}\left(x\right|{\lambda }^j,z^{*})=ma{x}_{i=1}^m\{{\lambda }_i^j|f_i\left(x\right)-z_i^{*}\left|\right\}$$

(10)

where $x\in \Omega$ is a solution to a multi-objective problem with m original objectives; $z^{*}=(z_1^{*},\dots ,z_m^{*})$ is the reference point with the best solution found so far for each of the $i=1,\dots ,m$ original objectives and ${\lambda }^j=({\lambda }_1^j,\dots ,{\lambda }_m^j)$. We note that MOEA/D minimises all those N scalar optimisation sub-problems simultaneously.

Since the MPP formulation considered in this work implies handling the feasibility constraints, the replacement of any individual from the population must satisfy certain criteria. For example, given two individuals $S_1$ and $S_2$:

• If their infeasibility degrees are different, the one with a lower infeasibility degree is better.
• Otherwise, if two individuals have the same infeasibility degree, i.e., $id\left(S_1\right)=id\left(S_2\right)$, the individual with better fitness is preferred. The fitness of an individual is computed using Equation (10).

Moreover, our novel ILS-MOEA/D includes two main improvements to speed up the achievement of high-quality solutions. First, the Similarity-based Crossover (SX) proposed in [3] is used as the only genetic operator that produces new individuals. Second, an adapted version of the ILS (Algorithm 1), which was also proposed in [3], was integrated as the intensification phase of ILS-MOEA/D. This ILS is based on the well-known First-Improvement Hill Climbing approach (line 3). It explores the neighbourhood of a solution in a random way by accepting any movement that improves the current solution, and stopping after reaching a local optimum. The key difference of the ILS applied herein in comparison to the one proposed in [3] is that the procedure evaluates each improvement by using the Tchebycheff decomposition approach (Equation (10)) in a similar way as MOEA/D. Furthermore, the reference point $z^{*}$ is also updated if any objective improves the current reference point In addition, for any solution, instead of using the neighbourhood structure of MOEA/D, the neighbours are generated by modifying a single course of the menu plan. As a result, the number of neighbours of any solution is $n\times (l_{fc}+l_{sc}+l_{ds}-3)$, where $l_{fc}$, $l_{sc}$ and $l_{ds}$ are the number of options for starters, main courses and desserts, respectively. Finally, the procedure Perturb makes use of problem-dependent information of the MPP, since it identifies the potential problems in a menu plan in order to mitigate them. However, this procedure does not guarantee that the algorithm will not stagnate in local optima solutions. Additionally, since this MPP formulation has not been solved with any exact method, there is not any certainty that the solutions found by either ILS-MOEA/D or MA are global optima. The  Perturb (line 7) procedure is the same as the one applied in [3]. The above steps are repeated $Iterations$ times.

Algorithm 1: Iterated Local Search — ILS

The proposed ILS-MOEA/D outlined in Algorithm 2 involves similar steps as the standard MOEA/D [9]:

• The algorithm receives the population size N, the neighbourhood size L and a set of uniform sparse weight vectors $\lambda$, as the parameters to set up the run.
• In line 1, an external population, $EP$, is created to store the non-dominated individuals found during the search. Since the population size parameter was set to a small value in this work, the external population is used to keep additional solutions to those maintained in the current population. An unbounded $EP$ that maintains feasible non-dominated individuals is used.
• Then, a set of neighbourhoods B is created in line 2. For each individual j in the population, its corresponding neighbourhood $B_j$ is created, considering the L closest weight vectors to ${\lambda }^j$. The above is performed by computing the Euclidean distance between any two weight vectors.
• After that, in line 3, the reference point $z^{*}$ is initialised using the opposite largest value to the corresponding objective function direction, i.e., the maximum floating point number allowed for an objective function that has to be minimised and vice-versa.
• The last step before starting the MOEA/D updating phase is to initialise the population (line 4). This procedure creates N new individuals randomly and then applies the aforementioned ILS to improve the quality of the initial solutions. Additionally, the reference point z is updated if required.

Algorithm 2: ILS-MOEA/D

Afterwards, the main loop of the MOEA/D performs the updating phase of the algorithm by carrying out the following steps until the stopping criterion is met:

• For each individual j in the population (line 6), a new offspring is created by applying the $SX$ crossover operator to two neighbours of individual j (line 7), which are selected at random from its neighbourhood $B_j$. Afterwards, the ILS is applied to the new offspring (line 8).
• Then, in line 9, the reference point $z^{*}$ is updated if better objective values were found.
• Next, in line 10, the offspring created is considered to replace individual j in the population by following the aforementioned replacement criteria. Note that each offspring at most replaces one individual in the population.
• Finally, in line 11, the offspring is considered for insertion into the $EP$ if its infeasibility degree is equal to zero and there is no individual in $EP$ that dominates it.

4. Experimental Assessment

Due to the fact that the same constraints and courses database used in [3] is applied in this work, the results obtained by ILS-MOEA/D were compared, in terms of the meal plan cost, with those attained by the single-objective MA proposed in [3], which will be referred to as MA in the rest of the paper. Moreover, the level of repetition of the solutions provided by MA was also computed to properly evaluate the difference between the two approaches.

Regarding the courses database, a total of 64 different courses were available, grouped into three different categories: $l_{fc}$: 18 starters, $l_{sc}$: 33 main courses, $l_{ds}$: 13 desserts. Moreover, for every course available, the following information was obtained: name of the course, cost of the course, amount of nutrients in the course and the particular food groups the course belongs to.

Standard configurations for MA and ILS-MOEA/D were applied to different instances of the MPP. Specifically, plans for $n=20$, $n=40$ and $n=60$ days were considered. All the experiments were performed using the elapsed time as the stopping criterion, which was different depending on the instance size. For $n=20$ days, the stopping criterion was set to one hour, and it was increased to two and a half hours and five hours for $n=40$ and $n=60$ days, respectively.

Regarding the parameterisation of ILS-MOEA/D, the population size was set to $N=15$ individuals, the neighbourhood size was fixed to $L=5$ individuals and the crossover rate was set to $CR=1.0$. The set of weight vectors $\lambda$ was generated using the method described in [9]. We note that the same parameterisation was used to apply the single-objective MA, which means that the population size was set to $N=15$ individuals and the crossover rate $CR=1.0$. None of the algorithms applied a mutation operator. Finally, the number of iterations of the ILS was set to 100 in both cases.

The Metaheuristic-based Extensible Tool for Cooperative Optimisation (METCO) (Available at: https://github.com/PAL-ULL/software-metco), described in [39], was used to implement ILS-MOEA/D and the multi-objective constrained formulation of the MPP discussed here, as well as to perform the entire experimental assessment.Experiments were run on a server belonging to the “Laboratorio de Supercómputo del Bajío”, which is maintained by the “Centro de Investigación en Matemáticas” (CIMAT), Mexico. The server provides two Intel Xeon E5-2620 v2 processors with 6 cores each at 2.1 GHz with 32 GB RAM. Since we are dealing with stochastic approaches, every execution was repeated 30 times. In order to statistically support the conclusions, the following statistical testing procedure, which was formerly used in previous work by the authors [40], was applied to conduct comparisons between experiments. First, a Shapiro–Wilk test was performed to check whether the values of the results followed a normal (Gaussian) distribution. If so, the Levene test checked for the homogeneity of the variances. If the samples had equal variances, an anova test was done; if not, a Welch test was performed. For non-Gaussian distributions, the non-parametric Kruskal–Wallis test was used. For every test, a significance level $\alpha =0.05$ was considered.

The hypervolume ($HV$) [41], normalised in the range $[0,1]$, was selected as the metric to measure the performance of ILS-MOEA/D. To compute the normalised $HV$, the resulting Pareto Fronts of ILS-MOEA/D were normalised using the worst and best values achieved for each objective function, which defines the lower and upper bounds among all the executions performed. We should note that since the $HV$ metric has to be maximised, the higher its value, the better the performance.

5. Discussion

In this section, the results from the experimental assessment introduced previously are discussed (The results, plots and source code are available at https://github.com/Tomas-Morph/MenuPlanning_MOEAD_Mathematics). As mentioned earlier, the results attained by ILS-MOEA/D were compared to the results achieved by MA. The reader should recall that the working hypothesis behind this comparison is that by applying ILS-MOEA/D to a multi-objective formulation of the MPP, which considers not only the cost of the plan but also the level of repetition, it is possible to find solutions that are similar in terms of the cost to those provided by MA, but significantly better with respect to the level of repetition of specific courses and food groups contained in the menu plan.

First of all, MA seeks to obtain the cheapest menu plan that satisfies all the constraints defined in Section 2. Consequently, the menu plans generated by MA had a higher level of repetition in comparison to those provided by ILS-MOEA/D, as shown in Figure 1. The statistical procedure introduced previously shows that there were significant statistical differences in the results of ILS-MOEA/D and MA. Although an explicit diversity management strategy was implemented in MA, not considering the level of repetition in the single-objective formulation of the MPP led to more affordable but less varied menu plans. In fact, in terms of the cost, the results obtained by MA were statistically better than those achieved by ILS-MOEA/D for the three instances considered.

Since ILS-MOEA/D considers the level of repetition as one of the objective functions to be optimised, the menu plans generated by this algorithm had a better ratio between the cost and the level of repetition. Considering the level of repetition, ILS-MOEA/D provided statistically significant better results than MA for the three instances. Furthermore, as Figure 1 shows, although the results of ILS-MOEA/D in terms of the cost were noticeably more scattered than those attained by MA, in a few executions, ILS-MOEA/D yielded the best menu plan cost obtained by MA with a significantly lower level of repetition, in the case of $n=20$ and $n=40$ days. As the results in

Table 3. Statistics for the cost and level of repetition achieved by ILS-MOEA/D and MA, considering menu plans for $n=20$, $n=40$ and $n=60$ days.

n	Algorithm	Cost				Level of Repetition
		Mean	Std	Min	Max	Mean	Std	Min	Max
20	ILS-MOEA/D	20.299	1.384 $\times {10}^{-2}$	20.264	20.304	269.800	3.695	263.166	278.222
	MA	20.264	7.226 $\times {10}^{-15}$	20.264	20.264	346.074	14.508	314.943	376.298
40	ILS-MOEA/D	40.153	0.102	40.038	40.335	601.309	8.616	579.400	615.871
	MA	40.067	0.042	40.038	40.281	833.067	33.055	757.831	888.489
60	ILS-MOEA/D	60.368	0.154	60.076	60.636	994.252	19.886	949.750	1029.680
	MA	59.738	0.045	59.721	59.940	1247.270	36.995	1143.820	1312.760

show, for $n=20$ days, the mean cost of the solutions provided by ILS-MOEA/D was only $0.17\%$ higher in comparison to the mean cost of the solutions attained by MA. However, the mean level of repetition of the solutions obtained by MA was $28.3\%$ higher when compared to the mean level of repetition of the solutions given by ILS-MOEA/D.

Something similar happened for the menu plans for $n=40$ days. In this case, the mean cost of the solutions provided by ILS-MOEA/D was only $0.21\%$ higher in comparison to the mean cost of the solutions attained by MA. The mean level of repetition of the solutions obtained by MA, however, was $38.5\%$ higher when compared to the mean level of repetition of the solutions given by ILS-MOEA/D. Finally, for $n=60$ days, the mean cost provided by ILS-MOEA/D was only $1.05\%$ higher in comparison to the mean cost attained by MA. Still, the mean level of repetition of MA was considerably larger than that obtained by ILS-MOEA/D, specifically, $25.4\%$. Bearing the above discussion in mind, it is clear that the slight difference obtained by ILS-MOEA/D, in terms of the cost, is much lower when compared to the difference between the two approaches in terms of the level of repetition. As a result, ILS-MOEA/D clearly outperforms MA in this regard, which confirms our hypothesis.

In order to graphically confirm the above conclusions, the best solution found by MA, i.e., that with the lowest cost, was compared to the first of the thirty Pareto Fronts obtained by ILS-MOEA/D for each instance considered. To do this, the level of repetition of the solutions obtained by MA had to be calculated independently by considering the same source code implemented in the case of the multi-objective constrained formulation of the MPP. Figure 2 undoubtedly shows how MA obtains the best results in terms of the menu plan cost, for every instance. Nevertheless, the level of repetition of said solutions is significantly higher when compared to the level of repetition of the solutions belonging to the Pareto Fronts provided by ILS-MOEA/D. Note also how ILS-MOEA/D yielded different Pareto Front shapes, depending on the instance size. Bearing the above in mind, it is difficult to apply a priori methods to focus the search on a certain region of the Pareto Front. Finally, we note that one of the main advantages of applying a multi-objective optimiser, such as ILS-MOEA/D, is that a diverse set of solutions, regarding the objective function space, is provided. All of these solutions are trade-offs between cost and level of repetition, and the above allows the decision maker to select one of those solutions depending on their particular requirements, something that is not possible when solving a single-objective formulation of the MPP.

In the previous experiment, ILS-MOEA/D was unable to achieve the lowest cost provided by MA for a menu plan of $n=60$ days in any execution. In order to determine if ILS-MOEA/D could yield the results attained by MA in large instances, such as $n=60$, executions using a stopping criterion equal to ten hours were also performed. As in the previous experiment, 30 repetitions were also run by applying the same parameterisation of ILS-MOEA/D. The results obtained are shown in

Table 4. Statistics for the cost and level of repetition achieved by ILS-MOEA/D, considering menu plans for $n=60$ days, after ten hours of execution.

Cost				Repetition
Mean	Std	Min	Max	Mean	Std	Min	Max
60.368	0.154	60.076	60.636	994.252	19.886	949.750	1029.680

. We note that even though ILS-MOEA/D could not replicate the best menu plan cost obtained by MA after a five-hour execution (see Table 3), its results were improved in terms of both cost and level of repetition. As a result, devoting more effort to the development of ILS-MOEA/D could improve its performance when dealing with large instances.

Single-objective techniques that do not include any explicit diversity management mechanism may fall into premature convergence. This means that solutions only improve for a short period of time before stagnating at local optima. At the same time, multi-objective optimisers may also converge to sub-optimal regions of the decision variable space of some MOPs, yielding effects that are similar to premature convergence [42]. Although our proposal ILS-MOEA/D does not include any explicit technique for properly managing diversity in the decision variable space, it would be interesting to analyse if the above could be possible implicitly as a consequence of promoting diversity in the objective function space.

Figure 3 shows, in the case of MA and ILS-MOEA/D, how the mean diversity in the population, considering the decision variable space, evolves during the runs for each instance considered. Diversity was computed by applying a distance-like function specifically created for the MPP formulations considered herein. This function determines distances among the courses assigned to the different days of the plan. Further details about the distance-like function can be found in the reference work [3]. Now how the mean diversity gradually decreases throughout the executions for both MA and ILS-MOEA/D, starting from a more diverse population and finishing with one that is less diverse. Figure 4 shows the evolution of the mean $HV$ over the course of the ILS-MOEA/D executions. Not only does the mean diversity gradually decrease throughout the executions for every instance in the case of ILS-MOEA/D, but the mean $HV$ also increases, which means that the effectiveness of ILS-MOEA/D is suitable. Since ILS-MOEA/D implicitly promotes diversity in the objective function space, diversity is also properly managed in the decision variable space. At this point, we should note, however, that MA preserves, in a smarter and more explicit way, a larger diversity in the decision variable space during the whole execution in comparison to ILS-MOEA/D, which results in better cost solutions, something that we had already stated in previous experiments.

Consequently, we note that not considering explicit diversity management schemes in the decision variable space in the case of a multi-objective algorithm, like ILS-MOEA/D, seems to impact the performance less than not considering them in the case of a single-objective optimiser. Even so, it would be interesting to check in the future whether explicitly managing diversity in the decision variable space helps ILS-MOEA/D to improve its performance in terms of the cost of the resulting menu plans.

Lastly, regarding the time complexity of the proposed algorithm, the average elapsed time and generations performed by ILS-MOEA/D are presented in

Table 5. Running time of ILS-MOEA/D.

Days	Avg. ILS Time (s)	Avg. Total Time (s)	Avg. Number of Generations
20	3591.6 (99.47%)	3610.7	187.2
40	8979.2 (99.31%)	9041.3	112.5
60	17962.1 (99.29%)	18089.7	110.1

. As it can be observed, ILS is the most computationally expensive step of ILS-MOEA/D, since it involves the majority of the total computational work. In particular, more than $99\%$ of the total elapsed time of the algorithm is performed by ILS.

6. Conclusions

This paper proposes a memetic multi-objective algorithm based on the well-known MOEA/D, which applies an ILS as the improvement phase, i.e., ILS-MOEA/D, to solve a novel multi-objective constrained formulation of the MPP. The experimental assessment conducted to contrast the diversity in the decision variable space of ILS-MOEA/D in comparison to a single-objective MA yielded interesting conclusions and possible future lines of work.

Firstly, depending on the problem size evaluated, ILS-MOEA/D obtained different Pareto Front shapes. This hinders the application of a priori methods to guide the search in a certain region of the space. Second, the results show that for reduced problem sizes, i.e., $n=20$, ILS-MOEA/D and MA yield practically the same results in terms of the menu plan cost. However, as the problem size increases, such as $n=40,60$, the results provided by ILS-MOEA/D are slightly worse than those of MA in terms of the cost. Third, in the case of ILS-MOEA/D, diversity management in the decision variable space is not as crucial when compared to MA. Considering the results, both techniques gradually decrease the level of diversity; however, ILS-MOEA/D preserves lower levels of diversity in the same time even though MA includes an explicit diversity management technique. This is due to the fact that ILS-MOEA/D properly manages diversity in the decision variable space implicitly, since it also promotes diversity in the objective function space. Last but not least, the working hypothesis of this work is confirmed by the results provided in Section 5. Even though MA and ILS-MOEA/D yielded similar results in terms of the menu plan cost for the different instances assessed, the latter provided a much lower level of repetition of specific courses and food groups in comparison to the former. As a consequence, the application of ILS-MOEA/D to solve the multi-objective constrained formulation of the MPP presented here, which considers the cost and the level of repetition as the objectives to be optimised, produces not only affordable, but also considerably more balanced, menu plans when compared to the plans obtained by MA when solving the single-objective formulation of the MPP, which only considers the cost.

As we previously mentioned, note that the single-objective MA incorporates a mechanism to explicitly promote diversity in the decision variable space, something that has not been included into ILS-MOEA/D. The above could be the main reason why ILS-MOEA/D obtained slightly worse meal plans in terms of their cost in comparison to the single-objective MA, particularly, for larger instances. Consequently, including techniques in ILS-MOEA/D to explicitly manage the diversity in the decision variable space could improve its performance in terms of the cost of the menu plans provided. Moreover, even though proposing a deep comparison of evolutionary algorithms is not aligned with our working hypothesis, further research may include a comparison with other multi-objective evolutionary algorithms and state-of-art metaheuristics. For example, it would be interesting to compare ILS-MOEA/D to differential evolution or particle swarm optimisation, even though major design changes would have to be considered to apply those algorithms to a combinatorial optimisation problem. As an alternative line of further research, it would be interesting to consider a comparison between ILS-MOEA/D and a single-objective MA intended to optimise the level of repetition of courses and food groups, rather than optimising the menu plan cost. Finally, we should note that our method could be applied to constrained multi-objective problems in other domains by performing a few modifications. First, the perturbation step of the ILS, as well as how neighbours are obtained, should be adapted by considering information of the particular problem at hand. Moreover, other problem-dependent variation operators should be incorporated into ILS-MOEA/D as well.