A Fuzzy Graph Based Chemometrics Method for Gelatin Authentication

Abstract

Graph theory is a well-established concept that is widely used in numerous applications such as in biology, chemistry and network analysis. The advancement in the theory of graph has led to the development of a new concept called fuzzy autocatalytic set. In this paper, a fuzzy graph-based chemometrics method, namely, chemometrics fuzzy autocatalytic set (c-FACS) is developed and applied for gelatin authentication. The issue on authenticity of gelatin has become a sensitive issue among some religious communities. Due to the matter, Fourier transform infrared (FTIR) spectra of bovine, porcine and fish gelatins are analyzed using c-FACS to identify their signatures and differences and presented in this paper. The results from the c-FACS analysis showed distinct features of each gelatin, particularly porcine. Furthermore, the new method is faster than principal component analysis (PCA) in identifying the gelatin sources.

1. Introduction

Leonhard Euler first introduced graph theory in 1736 [1]. Euler’s idea in solving the Konigsberg bridge problem in form of nodes and edges has contributed towards the development of a concept called graph. Since then, graph has been widely used in many areas such as chemistry [2,3], biology [4], and social network analysis [5]. Jain and Krishna [2] applied graph to represent catalytic interaction between molecules while Imran et al. [3] studied chemical graph of an oxide network. Falcon et al. [4] and Kostić et al. [5] implemented graph on cell cycle and social network analysis in telecommunications, respectively. The founder of fuzzy set theory, Zadeh [6] pointed out that some real application problems may involve imprecise description or fuzziness; hence, fuzzy set is suitable for such challenges. The advancement in fuzzy set theory has led to the development of a new concept in graph, namely, fuzzy graph [7]. Akram et al. [8] presented different notions and applications of fuzzy graph. Furthermore, Jan et al. [9] studied the concept of interval-valued fuzzy graph and neutrosophic graphs, and Mathew et al. [10] introduced vertex rough graphs. In addition, fuzzy graph concept, introduced first by Rosenfeld [7], was further explored by Ahmad et al. [11] later. Ahmad et al. [11] introduced fuzzy autocatalytic set (FACS) as a result of a merger between fuzzy graph and autocatalytic set (ACS). In short, fuzzy graph is a graph that incorporates fuzziness [7], and ACS is a graph representation of chemically interacting molecules [2]. Ahmad et al. [11] introduced FACS to model a clinical waste incineration process. The process occurring in the system was represented in the form of a FACS graph, whereby the vertices represent variables that play important roles during the process while the edges represent their connections. The FACS method was able to identify the sequence of the depleted variables as well as products of the system. Since then, FACS has been further studied and applied in other systems such as the pressurized water reactor (PWR) [12]. On the other hand, Bakar et al. [13] studied the mathematical properties of FACS and its coordinated transformation form. However, in this paper, FACS and coordinated FACS are composed together to form a new algorithm in solving large and complex chemical data.

Chemometrics is a field of chemistry that applies mathematical methods in analyzing chemical data [14]. The chemometrics technique is commonly used in authentication analysis involving gelatin. Gelatin is a protein substance that is usually used as an ingredient in foods such as jelly, dairy product and various desserts as well as pharmaceutical capsule-based products. However, the issue of authenticity of the sources of the gelatins has become a concern, particularly for the Muslim community due to the possible presence of non-halal porcine gelatin in some products. Numerous methods have been developed and reported on authentication of gelatins [14]. Nemati et al. [15] and Widyaninggar et al. [16] applied high performance liquid chromatography (HPLC) in combination with principal component analysis (PCA) to differentiate bovine and porcine gelatins. Their results showed distinct classification of the gelatins. Hashim et al. [17] and Zilhadia [18] also utilized PCA in combination with Fourier transform infrared (FTIR) spectroscopy to analyze bovine and porcine gelatins, while Cebi et al. [19] included fish gelatin in their study. The FTIR method was proven to be efficient in analyzing food adulteration analysis [17]. However, further analysis using mathematical or chemometrics methods are required to differentiate the gelatins due to large similarities of their protein structure. Thus, Hashim et al. [17], Cebi et al. [19] and Zilhadia [18] used PCA to analyze the gelatin spectra and their PCA results showed that the gelatins clusters were well separated. The PCA is widely used in multivariate data analysis to extract information from data with multiple variables [20]. It decomposes the data to principal components (PCs) that describe the variations in the data set and the scores of the PCs are plotted as output. The PCA is widely used for gelatin authentication due to its capability in classifying the sources of gelatin into their groups in the score plot. However, it requires pre-processing of data, which is often time-consuming and tedious. Hence, a faster yet effective chemometrics method is needed, particularly for gelatin and food authentication analysis [21].

In this paper, an advanced form of FACS, namely, chemometrics FACS (c-FACS) is developed and applied for authentication of gelatin sources. Chemometrics analysis using PCA is commonly used in food authentication; however, graph and fuzzy graph-based techniques have never been reported in the literature. In this study, the fuzzy graph approach is integrated with FTIR spectroscopy for authentication of bovine, porcine and fish gelatins whereby the FTIR spectra of the gelatins are represented in a form of FACS graph and dominant wavenumbers for each gelatin are identified. In addition, coordinated FACS is applied to further investigate the spectra of the gelatin. The FACS graph of FTIR spectra of bovine, porcine and fish gelatin is transformed into coordinated FACS to visualize and identify the patterns of the gelatin spectra. The FACS graph, its matrix and its transformation as a coordinated form of FACS are coded into an algorithm, namely, the c-FACS algorithm for the purpose.

2. Materials and Methods

2.1. Fourier Transform Infrared (FTIR) Spectroscopy of Gelatin

In this study, the FTIR method is applied on three types of gelatin. They are bovine (Sigma-Aldrich, St. Louis, MO, USA), porcine (Sigma-Aldrich, St. Louis, MO, USA) and fish (Sigma-Aldrich, St. Louis, MO, USA) with a total of 81 samples. The gelatin solutions are prepared at concentrations between 4% (w/v) and 20% (w/v) and analyzed using Spectrum Two FTIR spectrometer (Perkin Elmer, MA, USA).

2.2. Fuzzy Autocatalytic Set (FACS)

Generally, a graph $G=(V,E)$ consists of a set of vertices, $V=\{v_1,v_2,v_3,v_4,\dots ,v_{n-1},v_n\}$, and a set of edges, $E=\{e_1,e_2,e_3,e_4,\dots ,e_{n-1},e_n\}$ [22]. The fuzzy graph introduced by Rosenfeld [7] is a graph that incorporates fuzziness. Later, Jain and Krishna [2] developed autocatalytic set (ACS) to describe catalytic interaction between chemical compounds in the form of a graph. The ACS graph signifies that every catalytic interaction takes place in the system. The formal definition of ACS by Jain and Krishna [2] is as follows:

Definition 1

([2]). An autocatalytic set is a subgraph, each of whose nodes has at least one incoming link from a node belonging to the same subgraph.

In 2010, Ahmad et al. [11] introduced the concept of fuzziness into ACS. They formed a new concept called fuzzy autocatalytic set (FACS) to model a waste incineration process, whereby the edges of the graph have fuzzy membership values. The formal definition of FACS by Ahmad et al. [11] is given as follows:

Definition 2

([11]). Fuzzy autocatalytic set (FACS) is a sub graph each of whose nodes has at least one incoming link with membership value $\mu (e_i)\in \left(0,1\right],\forall e_i\in E$

The FACS graph can be presented in the form of a matrix $n\times n$ called adjacency matrix, $A=[a_{ij}]$, whereby the entries of the matrix are fuzzy membership values. Since then, further properties on FACS were studied and reported in [12,13,23,24]. Ahmad et al. [23] also showed that any FACS graph could be induced and transformed to coordinated FACS. Mathematical structures that related to the transformation involve the formation of transition and Laplacian matrices of FACS. The formal definition and the procedure with respect to the transition matrix of FACS by Bakar et al. [24] are given as follow:

Definition 3

([24]). The transition matrix of FACS of fuzzy graph is $P^{*}$, with the entries, $P^{*}(u,v)$, such that:

$$P^{*}(u,v)=\{\begin{array}{l}\frac{\mu (u,v)}{d_{out}(u)}\mathrm{if}(u,v)\in E\\ 0\mathrm{otherwise}\end{array}$$

(1)

The out-degree of u is $d_{out}(u)={\displaystyle \sum \mu (u,t)}$ and $\mu (u,v)$ is the fuzzy value of its edge.

According to Bakar et al. [24], the transition matrix is used in identifying the steady state vector of a system. Bakar et al. [24] constructed the steady state vector through iteration on $P^{*(n)}$ until it generates a steady-state matrix. The rows in the steady-state matrix converge towards a fixed number and the elements in the row represent the steady state vector or Perron vector. The Perron vector is used to compute the Laplacian matrix of FACS [13] as follows:

Definition 4

([13]). Suppose $P^{*}$ is the transition matrix for fuzzy graph of FACS with fuzzy value $P^{*}(u,v)$. If the graph is strongly connected and aperiodic, then based on Perron Frobenius, there exists a unique (row) vector, φ for which $\phi P^{*}=\phi$ with $\phi (v)>0$ for all v and ${\displaystyle \sum \phi (v)}=1$ which is called Perron vector of $P^{*}$ . Let $\Phi$ be the diagonal matrix with $\Phi (v,v)=\phi (v)$, then the directed Laplacian of FACS is $L=I-\frac{1}{2}({\Phi }^{1/2}{P}^{*}{\Phi }^{-1/2}+{\Phi }^{-1/2}{(P^{*})}^t{\Phi }^{1/2})$ and the combinatorial directed Laplacian of FACS is defined as:

$$L=\Phi -\frac{1}{2}(\Phi P^{*}+{(P^{*})}^t\Phi )$$

(2)

where ${\left(P^{*}\right)}^t$ denotes the transpose of $P^{*}$ and $\Phi$ is the diagonal matrix with $\Phi (v,v)=\phi (v)$.

Further procedure to transform the FACS graph to coordinated FACS in Euclidean space involves the modified method from Carmel et al. [25] that is based on combinatorial Laplacian matrix and followed by solving optimization problem. The definitions of balanced vector and optimal arrangement for directed graph by Carmel et al. [25] are as follow:

Definition 5

([25]). Let $G(V,E)$ be a digraph. The balance of node i is $b_i={\displaystyle \sum _{j=1}^n{w}_{ij}{\delta }_{ij}}$, where w is the weight of the edges and ${\delta }_{ij}$ is target height differences.

Proposition 1

([25]). Let $G(V,E)$ be a digraph, with Laplacian, L and balance, b. An optimal arrangement y* is a solution of Ly = b.

The y-coordinates for a directed graph are obtained by solving the optimal arrangement y* [25]. The definitions were then modified by Bakar et al. [13] for FACS graph:

Definition 6

([13]). Let $G_{FT3}(V,E)$ be a graph of FACS with Laplacian, L and balance, b. Its optimal arrangement, y^*, is the solution of Ly = b, subject to the constraint $y^t{.1}_n=0$ where balance vector $b={(b_1,\dots ,b_n)}^t$ is the balance of ith node such that $b_i={\displaystyle \sum _{j=1}^n{\mu }_{ij}}-{\displaystyle \sum _{j=1}^n{\mu }_{ji}}$.

The y-coordinates of FACS are obtained by solving the optimal arrangement y^* using conjugate gradient method while x-coordinates are obtained by finding the Fiedler vector of combinatorial directed Laplacian. All the computational aspects of the procedure are performed using MATLAB.

3. Results and Discussion

3.1. Fourier Transform Infrared (FTIR) Spectra of Gelatin

The FTIR spectra of bovine, porcine and fish gelatins are depicted in Figure 1. The spectra of the gelatins exhibit very similar patterns at 3600–3200 cm⁻¹ (Amide A), 1700–1600 cm⁻¹ (Amide I), 1560–1335 cm⁻¹ (Amide II) and 1330–670 cm⁻¹ (Amide III) regions.

Similar spectra patterns were also reported in [17,18]. The absorption bands in each Amide region contain the details and information of various features present in the substances. However, due to the large similarities of protein structures of the gelatin substances, the FTIR method is unable to identify the differences between the gelatin spectra clearly. Hence further analysis using a chemometrics method is required to identify the differences between them.

3.2. C-FACS

A chemometrics FACS (c-FACS) method is developed and applied to differentiate between bovine, porcine and fish gelatin spectra. The method involves the representation of the FTIR spectra in the form of a FACS graph and its adjacency matrix for further analysis to identify the dominant output.

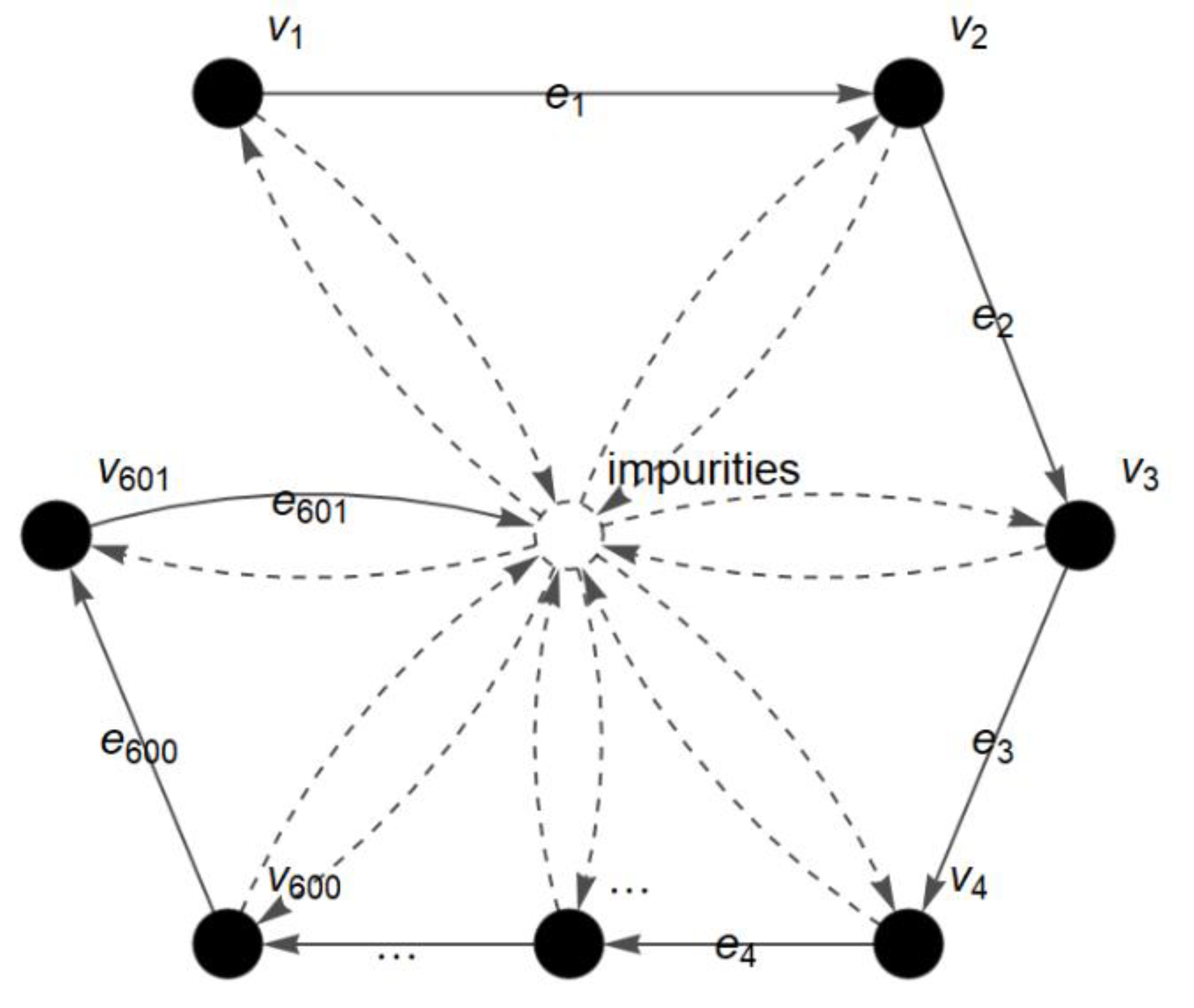
The process of infrared absorption by the gelatin molecule during FTIR analysis is represented in the form of vertices and edges. Each vertex in $V=\{v_1,v_2,v_3,v_4,\dots ,v_{n-1},v_n\}$ represents the wavenumber (cm⁻¹) and an edge in $E=\{e_1,e_2,e_3,e_4,\dots ,e_{n-1},e_n\}$ is the transitional path of a given molecule throughout the FTIR analysis (see Figure 2).

In short, the FACS graph describes the flow process and movement of a molecule from one wavenumber of light to the next wavenumber during the FTIR analysis. The detected amount of infrared radiation absorbed by the molecule at each wavenumber (cm⁻¹) is represented as the absorbance value (A) and plotted in the FTIR spectrum [26]. In addition, the presence of impurities during the analysis is also considered in the FACS graph. The obtained graph is then converted into a matrix for further analysis. The entries of the matrix are the membership values, $\mu \left(v_i\right)$ of the absorbance readings ($Q_i$) at each wavenumber. The $\mu \left(v_i\right)$ is called fuzzy absorbance value and defined by:

$$\mu \left(v_i\right)=\{\begin{array}{ll}0& \mathrm{if}{Q}_i<0\\ 1& \mathrm{if}\max (Q_i)\\ Q_i/\max (Q_i)& \mathrm{others}\end{array}\mathrm{for}i=1,2,3,\dots ,n,$$

(3)

The fuzzy absorbance value $\mu \left(v_i\right)$ is substituted as an entry for the FTIR matrix. Further descriptions of the FTIR matrix are provided by the following definitions.

Definition 7.

A square matrix$A=[a_{ij}]$is called a FTIR matrix such that$a_{ij}=\mu (v_t)$is the membership value of the absorbance reading,$Q_i$for$t=1,2,\dots ,n$and the dimension of matrix A is defined as follows:

$$A=\{\begin{array}{ll}{[a_{ij}]}_k& \mathrm{if}n=k^2\mathrm{for}\mathrm{some}k\in \mathrm{N}\\ {[a_{ij}]}_{k+p}& \mathrm{if}n\ne k^2\mathrm{and}n+m={(k+p)}^2\mathrm{with}p<k\mathrm{and}m\in \mathrm{N}\end{array}$$

In other words, whenever$n=k^2$, then

$$A={\left[\begin{array}{ccc}\mu (v_1)& \mu (v_2)& \dots \\ \dots & \dots & \dots \\ \dots & \mu (v_{n-1})& \mu (v_n)\end{array}\right]}_k$$

and whenever$n\ne k^2$, then

$$A={\left[\begin{array}{ccccc}\mu (v_1)& \mu (v_2)& \mu (v_3)& \dots & \dots \\ \dots & \dots & \dots & \dots & \dots \\ \dots & \dots & \dots & \dots & \dots \\ \dots & \dots & \dots & \dots & \dots \\ \dots & \mu (v_{n+1})& \dots & \mu \left(v_{{(k+p)}^2-1}\right)& \mu \left(v_{{(k+p)}^2}\right)\end{array}\right]}_{k+p}$$

Definition 8.

If the number of data is$n$and$A$is not a square matrix ($n\ne k^2$and$n+m={(k+p)}^2$with$p<k$and$m\in \mathrm{N}$), then the entries$\mu (v_{n+1})=\mu (v_{n+2})=\dots =\mu (v_{n+m-1})=\mu (v_{n+m})=0$and they are named as the ghost entries.

The FTIR matrices are further analyzed using graph dynamic procedures by Ahmad et al. [11] to determine their dominances. The procedure then computes the eigenvalues and Perron Frobenius eigenvectors. Several new definitions and theorems are introduced to formalize the procedure. A reverse transformation matrix is defined since the FTIR spectra are conventionally presented in descending order of wavenumbers. Thus, the reverse transformation matrix of FACS is needed to show the equivalence of adjacency matrix and its reverse matrix. The new definitions and theorems for the transformation matrix are introduced as follows.

Definition 9.

The row swap,$R_s$is an operation whereby two rows in the matrix together with their entries are exchanged in their positions such that

$$\left[\begin{array}{c}{r}_1\\ r_2\\ r_3\\ ⋮\\ r_{n-2}\\ r_{n-1}\\ r_n\end{array}\right]\stackrel{R_s}{\to }\left[\begin{array}{c}{r}_n\\ r_{n-1}\\ r_{n-2}\\ ⋮\\ r_3\\ r_2\\ r_1\end{array}\right]$$

In short,

$r_1\to r_n$  Replace row 1 with row n,

$r_2\to r_{n-1}$ Replace row 2 with row n−1,

$r_3\to r_{n-2}$ Replace row 3 with row n−2,

$⋮$

$r_{n-1}\to r_2$ Replace row n−1 with row 2,

$r_n\to r_1$  Replace row n with row 1.

Definition 10.

The column swap,$C_s$, is an operation whereby two columns in the matrix together with their entries are exchanged in their positions such that

$$\left[\begin{array}{ccccccc}{c}_1& c_2& c_3& \dots & c_{n-2}& c_{n-1}& c_n\end{array}\right]\stackrel{C_s}{\to }\left[\begin{array}{ccccccc}{c}_n& c_{n-1}& c_{n-2}& \dots & c_3& c_2& c_1\end{array}\right]$$

In short,

$c_1\to c_n$  Replace column 1 with column n,

$c_2\to c_{n-1}$ Replace column 2 with column n−1,

$c_3\to c_{n-2}$ Replace column 3 with column n−2,

$⋮$

$c_{n-1}\to c_2$ Replace column n−1 with column 2,

$c_n\to c_1$  Replace column n with column 1.

Definition 11.

The$C_s{R}_s$transformation of matrix$A$to$A_{CR}$is a composition of two operations.

$$A\stackrel{R_s}{\to }{A}_R\stackrel{C_s}{\to }{A}_{CR}$$

whereby$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \dots & a_{nn}\end{array}\right]$is transformed to$A_{CR}=\left[\begin{array}{cccc}{a}_{nn}& \dots & a_{n2}& a_{n1}\\ ⋮& \ddots & ⋮& ⋮\\ a_{2n}& ⋮& a_{22}& a_{21}\\ a_{1n}& \dots & a_{12}& a_{11}\end{array}\right]$. In short, the$C_s{R}_s$transformation is an operation to switch position of rows to columns simultaneously.

The row swap, $R_s$, and column swap, $C_s$, operations are stated as mappings in the following two lemmas without proofs, respectively.

Lemma 1.

Let$M_n$be a square matrix. The$f_1:M_n\to M_n$is a mapping such that$f_1(A)=I_{R}A=A_R$and

$$I_R=\left[\begin{array}{cccccc}0& 0& \dots & 0& 0& 1\\ ⋮& ⋮& \dots & ⋮& 1& ⋮\\ 0& 0& \dots & 1& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& ⋰& \dots & 0& 0& 0\\ 1& 0& \dots & 0& 0& 0\end{array}\right]$$

(4)

The mapping$f_1$is called row swapping; i.e.,$R_s=f_1$.

Further properties on the row swapping are listed in the following theorems. Their proofs are also omitted since trivial.

Theorem 1.

The row swapping$f_1:M_n\to M_n$is a function.

Theorem 2.

The row swapping$f_1:M_n\to M_n$is linear.

Lemma 2.

Let$M_n$be a square matrix.$f_2:M_n\to M_n$is a mapping such that$f_2(A)=A{I}_R=A_C$and

$$I_R=\left[\begin{array}{cccccc}0& 0& \dots & 0& 0& 1\\ ⋮& ⋮& \dots & ⋮& 1& ⋮\\ 0& 0& \dots & 1& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& ⋰& \dots & 0& 0& 0\\ 1& 0& \dots & 0& 0& 0\end{array}\right]$$

(5)

The mapping$f_2$is called column swapping; i.e.,$C_s=f_2$.

Further properties on the column swapping are presented without proofs as follows.

Theorem 3.

The column swapping$f_2:M_n\to M_n$is a function.

Theorem 4.

The column swapping$f_2:M_n\to M_n$is linear.

Theorems 2 and 4 lead to the following result.

Theorem 5.

The$C_s{R}_s$transformation is linear.

Next, based on Definition 11, Lemmas 1 and 2, transformation of FACS to its reverse is stated in the following corollary.

Corollary 1.

Let$A$be square$n\times n$FACS matrix. The composition of linear transformations$f_2\circ f_1$yields the transformation of$A$to its reverse matrix,$A_{CR}$, such that$I_{R}A{I}_R=A_{CR}$.

The transformation of the FACS matrix, $A$ yields the reverse FACS matrix, $A_{CR}$. The relation for both matrices is presented in the following theorem.

Theorem 6.

The eigenvalues of the FACS matrix are the same as the eigenvalues of its reverse.

Proof. 

By Corollary 1, the reverse of matrix FACS $A$ is $A_{CR}=I_{R}A{I}_R$.

Notice,

$$\det (I_R{I}_R)=\det (I_R^2)=\det (I)=1$$

since $I_R^2=I$

Then, the characteristic equation of $A_{CR}$, $f(\lambda )$ is

$f(\lambda )=\det (A_{CR}-\lambda I)$

$=\det (I_{R}A{I}_R-\lambda I_R^2)$         by Corollary 1 and $I_R^2=I$

$=\det (I_{R}A{I}_R-\lambda I_R{I}_R)$

$=\det (I_{R}A{I}_R-I_R\lambda I_R)$          by scalar multiplication of a matrix

$=\det [I_R(A-\lambda I)I_R]$         by distributive property of matrices

$=\det (I_R)\det (A-\lambda I)\det (I_R)$     by property of determinant, $\det (AB)=\det (A)\det (B)$

$=\det (I_R)\det (I_R)\det (A-\lambda I)$     commutativity for scalar multiplication

$=\det (I_R{I}_R)\det (A-\lambda I)$          by property of determinant, $\det (AB)=\det (A)\det (B)$

$=\det (I_R^2)\det (A-\lambda I)$

$=\det (I)\det (A-\lambda I)$         since $I_R^2=I$

$=\det (A-\lambda I)$             since $\det (I)=1$.

Hence, characteristic equation for $A_{CR}$ is identical to $A$. In other words, the eigenvalues of matrix FACS and its reverse matrix are identical. □

Since $A_{CR}=I_{R}A{I}_R=I_R^{-1}A{I}_R$, then $A$ is equivalent to $A_{CR}$. By Theorem 6, the matrix of FACS and its reverse produce the same characteristic equation; hence, its respective eigenvalues and eigenvectors are similar. Consequently, using the FACS graph dynamic procedure, it surely will produce the same output. In this paper, the reverse matrix is denoted as FTIR matrix, otherwise stated, and is solved using the modified FACS graphing dynamic procedure.

A new algorithm involving the FTIR matrix is constructed to identify the dominant matrix. The algorithm contains the FACS graph dynamic and coordinated FACS procedures. The algorithm is specifically designed in order to facilitate the chemometrics analysis involving FTIR spectroscopy and is called the chemometrics FACS (c-FACS) algorithm. The c-FACS algorithm is presented in Algorithm 1.

Algorithm 1: The c-FACS algorithm

Select the preferred variables from a system as inputs. Build FACS graph by representing the variables as vertices, $V=\{v_1,v_2,v_3,v_4,\dots ,v_{n-1},v_n\}$ and their links as edges, $E=\{e_1,e_2,e_3,e_4,\dots ,e_{n-1},e_n\}$. Describe the membership value of the FACS graph. Determine the $n\times n$ adjacency matrix of the graph with the membership values as the entries. For FTIR matrix, the entries or membership values $\mu (e_i)$ are described by the fuzzy absorbance values at each wavenumber. Identify the Perron Frobenius eigenvectors (PFE) of the matrix. The smallest PFE and its corresponding vertices and edges are removed from the system to form $(n-1)\times (n-1)$ matrix. Display the dominant output matrix together with its corresponding dominant variables, until $2\times 2$ matrix is obtained. Calculate the transition and Laplacian matrices to obtain the xy-coordinates. The y-coordinates of FACS are obtained by solving Ly = b using conjugate gradient method and the x-coordinates are determined using the Fiedler vector of Laplacian. Plot the obtained coordinates in the Euclidean space. Repeat step 1 to 9 to analyze another sample or system.

Step 2 and 9 have complexity of O(n). Step 4 has complexity of O(n²) and for Step 8, the overall computation takes O(n³). The others have O(1) complexities. The algorithm is used to analyze the FACS matrix of the FTIR gelatin spectra for selected regions to determine the dominant wavenumbers of each gelatin and the patterns of their nodes in Euclidean space. The implementation and analysis on gelatin using c-FACS are presented in the next subsection.

3.3. C-FACS Implementation and Results

The FTIR spectra of bovine, porcine and fish gelatins are analyzed using the c-FACS algorithm to identify their dominant wavenumbers and signatures. The gelatin spectra at Amide and 1600–1000 cm⁻¹ (fingerprint) wavenumber regions are represented in the form of a FACS graph and analyzed as described in the c-FACS algorithm. The FACS graph for spectra at fingerprint region that contains 601 wavenumbers (1600–1000 cm⁻¹) is shown in Figure 3 with the set of vertices $V=\{v_1,v_2,v_3,v_4,\dots ,v_{600},v_{601}\}$ and the set of edges $E=\{e_1,e_2,e_3,e_4,\dots ,e_{600},e_{601}\}$. The vertices in the graph represent the wavenumbers and the absorbance at each of the wavenumbers is the membership value of the vertex.

The graph is then converted into the FTIR matrix with dimension of $25\times 25$ to illustrate all 601 entries or absorbance data in the fingerprint region and further analyzed to obtain the dominant matrix. The differences between the gelatins are observed based on their dominant obtained output matrices. The dominant output matrix represents the dominant wavenumbers of each gelatin at Amide II, Amide III and fingerprint regions. The dominant matrices of each gelatin at the fingerprint region are listed in

Table 1. Dominant matrices and their respective wavenumbers for bovine, porcine and fish gelatins.

Gelatins	Output Matrix	Wavenumber Region (cm−1)
Bovine	$\left[\begin{array}{l}1.00000.97690.95620.93540.8965\\ 0.71860.71620.71500.71380.7113\\ 0.66870.66380.65770.65410.6468\\ 0.48600.47870.47140.46160.4385\\ 0.30090.30450.30820.30940.3106\end{array}\right]$	$\left[\begin{array}{l}16001599159815971595\\ 15751574157315721570\\ 15501549154815471545\\ 15251524152315221520\\ 14751474147314721470\end{array}\right]$
Porcine	$\left[\begin{array}{l}1.00000.97590.95300.93240.8721\\ 0.69600.69360.69240.69240.6924\\ 0.65860.65140.64170.63210.5935\\ 0.45720.44870.44030.42940.4186\\ 0.29920.29550.29190.28830.2786\end{array}\right]$	$\left[\begin{array}{l}16001599159815971594\\ 15751574157315721569\\ 15501549154815471544\\ 15251524152315221519\\ 14501449144814471444\end{array}\right]$
Fish	$\left[\begin{array}{l}1.00000.97770.95670.93560.9146\\ 0.69680.69550.69430.69310.6931\\ 0.66710.66210.65720.65220.6485\\ 0.49260.48390.47520.46410.4517\\ 0.30450.29950.29460.28960.2847\end{array}\right]$	$\left[\begin{array}{l}16001599159815971596\\ 15751574157315721571\\ 15501549154815471546\\ 15251524152315221521\\ 15001499149814971496\end{array}\right]$

and the overall results are presented in

Table 2. Summary of dominant wavenumbers.

Region	Gelatin	Dominant Wavenumbers (cm−1)
Fingerprint	Bovine	1475–1470
	Porcine	1450–1444
	Fish	1500–1496
Amide II	Bovine	1480–1473
	Porcine	1448–1441
	Fish	1496–1490
Amide III	Bovine	810–786, 1232–1228, 1252–1249
	Porcine	680–678, 1077–1071, 1096–1087
	Fish	844–837, 862–853, 1303–1280

.

At the fingerprint region, the differences between the gelatins are observed from the output matrix ($5\times 5$) such that the dominant wavenumbers for bovine, porcine and fish gelatins are identified at 1475–1470 cm⁻¹, 1450–1444 cm⁻¹ and 1500–1496 cm⁻¹, respectively. At the Amide II region, the dominant wavenumbers for bovine gelatin are in the range of 1480–1473 cm⁻¹, while dominant wavenumbers for porcine and fish gelatins are detected at 1448–1441 cm⁻¹ and 1496–1490 cm⁻¹, respectively. Dominant wavenumbers for the gelatins at the Amide III region are observed at 810–786 cm⁻¹, 1232–1228 cm⁻¹ and 1252–1249 cm⁻¹ for bovine, 680–678 cm⁻¹, 1077–1071 cm⁻¹ and 1096–1087 cm⁻¹ for porcine, and 844–837 cm⁻¹, 862–853 cm⁻¹ and 1303–1280 cm⁻¹ for fish gelatin. These results showed that each gelatin possesses distinct and unique dominant wavenumbers, particularly at the fingerprint and Amide II regions. Further analysis using coordinated FACS is performed to examine the pattern and signature of bovine, porcine and fish gelatins at the fingerprint region and displayed in Euclidean space. The transformation procedure involves the construction of transition and combinatorial Laplacian matrices based on Equations (1) and (2) to determine the x-coordinates followed by solving the optimal arrangement y^* using conjugate gradient method to compute for y-coordinates. The x-coordinates of the nodes of FACS are determined by identifying the Fiedler vector that is the eigenvector associated with the smallest positive eigenvalue of the Laplacian matrix. The Fiedler vector is obtained by solving the eigenvalue problem and the optimal arrangement y^* representing the y-coordinates are determined using the conjugate gradient method. All computations are performed using MATLAB. The coordinated FACS of the gelatins exhibits distinct patterns for bovine, porcine and fish (see Figure 4).

Based on the figure, distinct patterns for bovine, porcine and fish gelatin are observed, particularly on the right area. The nodes of each gelatin are dispersed at different locations; particularly nodes for porcine gelatin are clearly separated and located a distance away from nodes of bovine and fish gelatins. The result indicates that porcine gelatin has a unique feature as compared to other gelatins since it is at farthest distance, while bovine and fish are closer to each other. The information indicates that the distance signifies the relationship and characteristic between the variables. The c-FACS method has successfully identified the differences between the gelatins, particularly non-halal porcine, based on the dominant wavenumbers’ identification and location of their nodes in the Euclidean space. The unique and different dominant wavenumbers signify the feature for each gelatin. The performance of c-FACS is then compared against principal component analysis (PCA). The PCA is a well-established method in chemometrics analysis. It is usually implemented with the aid of MATLAB and Minitab software [17,18], and the results are displayed in the form of score and loading plots. The clusters of bovine, porcine and fish gelatins are observed in the score plot. However, significant wavenumbers for porcine and fish gelatins failed to be identified in the loading plot (see Figure 5).

The performances of c-FACS and PCA are summarized in

Table 3. Comparison of c-FACS and PCA performances.

	c-FACS	PCA
Computing time	7.86 s	12.86 s
Observations	Significant and unique signature wavenumbers for bovine, porcine and fish gelatins.	Significant wavenumbers for bovine gelatin only.
Pattern Classification	Distinct classification of gelatins, particularly porcine.	Distinct classification of gelatins.

. The c-FACS is found to be faster, with elapsed time of 7.86 s than PCA (12.86 s) for analysis involving bovine, porcine and fish gelatin samples at the fingerprint region. Furthermore, the c-FACS was able to identify a particular range of wavenumbers as signature for each gelatin, while PCA failed to identify the corresponding wavenumbers for porcine and fish. Nevertheless, distinct classifications for the gelatins were observed using both methods, particularly porcine gelatin by c-FACS.

C-FACS on Published Data

The c-FACS method is applied on some published data to demonstrate its capability and efficiency. Several published data involving food products are analyzed using c-FACS and compared against PCA used by the respective researchers.

The first analysis involves a dataset of coffee products that is adopted from Briandet et al. [27]. The two types of their coffee products are Arabica and Robusta. The researchers [27] differentiated the two types of coffee products using FTIR and PCA. The FTIR spectra of 29 samples of Arabica and 27 samples of Robusta were obtained and further analyzed using PCA in their study. However, in this paper, the spectra of Arabica and Robusta at the 1600–1000 cm⁻¹ region are analyzed using c-FACS. The FACS graph of the coffee at the 1600–1000 cm⁻¹ region is shown in Figure 6. The vertices $V=\{v_1,v_2,v_3,v_4,\dots ,v_{600},v_{601}\}$ represent the position of wavenumbers for 1600 to 1000 cm⁻¹ and the edges $E=\{e_1,e_2,e_3,e_4,\dots ,e_{600},e_{601}\}$ are the light that travels and passes through molecules during the FTIR analysis.

The graph is then converted into a matrix to determine its dominance and pattern in the Euclidean space. As a result, the dominant wavenumbers for Arabica and Robusta are identified and presented in

Table 4. Dominant wavenumbers for Arabica and Robusta.

Updated Matrix Size	Dominant Wavenumbers (cm−1)
	Arabica	Robusta
$4\times 4$	$\left[\begin{array}{l}1598158615831559\\ 1447143614321409\\ 1397138613821359\\ 1096108510811058\end{array}\right]$	$\left[\begin{array}{l}1598158315751559\\ 1397138213741359\\ 1297128212741258\\ 1096108110731058\end{array}\right]$
$3\times 3$	$\left[\begin{array}{l}159815831559\\ 139713821359\\ 109610811058\end{array}\right]$	$\left[\begin{array}{l}159815751559\\ 129712741258\\ 109610731058\end{array}\right]$
$2\times 2$	$\left[\begin{array}{l}15981559\\ 10961058\end{array}\right]$	$\left[\begin{array}{l}15981575\\ 12971274\end{array}\right]$

.

The dominant wavenumbers for Arabica are identified at 1447–1409 cm⁻¹ and 1096–1058 cm⁻¹. On the other hand, the dominant wavenumbers for Robusta are detected at 1297–1258 cm⁻¹. These results indicate that each type of coffee bean has distinct and unique dominant wavenumbers. Furthermore, coordinated FACS shows that the nodes for Arabica are mainly clustered in the right area while Robusta’s nodes are mainly observed in the left area of the plane (see Figure 7).

The results of the c-FACS are compared against PCA. The PCA score plot of the coffee shows that Arabica is clustered mainly in the upper right area, while Robusta is clustered in the left area (see Figure 8).

The PCA results by Briandet et al. [27] also showed distinct clusters of Arabica and Robusta coffee beans with respect to second and third component scores. However, their PCA method failed to determine their significant wavenumbers. According to Briandet et al. [27], Robusta coffee has higher content of caffeine and chlorogenic acid as compared to Arabica, and the bands that associated with caffeine and chlorogenic acid are in the range of 1750–1550 cm⁻¹ and 1300–1150 cm⁻¹ regions, respectively. Thus, the dominant wavenumber results obtained from c-FACS for Robusta at 1297–1258 cm⁻¹ were in agreement with the range of chlorogenic acid at 1300–1150 cm⁻¹.

The c-FACS method is also applied on a dataset of meat, which is obtained from Al–Jowder et al. [28]. Three different types of meats, namely, chicken, pork and turkey, were used in their study. The spectra of the meats were obtained and PCA was used by the researchers [28]. In this paper, the spectra of the samples at 1600–1000 cm⁻¹ region are analyzed using c-FACS. Its graph is shown in Figure 9.

The vertices, $V=\{v_1,v_2,v_3,v_4,\dots ,v_{600},v_{601}\}$, are the wavenumbers and the edges, $E=\{e_1,e_2,e_3,e_4,\dots ,e_{600},e_{601}\}$, are the light that travels and passes through the molecules. The graph is then converted into a matrix to identify its dominance and pattern in the Euclidean space. As a result, the dominant wavenumbers for chicken, pork and turkey are identified and presented in

Table 5. Dominant wavenumbers for chicken, pork and turkey.

Meat	Dominant Wavenumbers (cm−1)
Chicken	$\left[\begin{array}{l}1409141414161418\\ 1513151915211523\\ 1548155315551557\\ 1582158815901592\end{array}\right]$
Pork	$\left[\begin{array}{l}1042106710691071\\ 1494151915211523\\ 1528155315551557\\ 1563158815901592\end{array}\right]$
Turkey	$\left[\begin{array}{l}1409141414161418\\ 1513151915211523\\ 1548155315551557\\ 1582158815901592\end{array}\right]$

.

The dominant wavenumbers for pork are clearly identified at 1042–1071 cm⁻¹, and dominant wavenumbers for both chicken and turkey are identified at 1409–1418 cm⁻¹. In addition, the dominant wavenumbers for pork are also detected at 1005–1036 cm⁻¹, and turkey showed dominance at 1216–1245 cm⁻¹ in $9\times 9$ dominant matrix.

Furthermore, coordinated FACS showed distinct locations of nodes for each meat, particularly pork (see Figure 10).

The results of the c-FACS are compared against PCA. The PCA score plot shows that the meats are clustered at different locations (see Figure 11), which are in agreement with the report published by Al-Jowder et al. [28].

However, their PCA method failed to determine the significant wavenumbers for the meats. In addition, the samples for chicken and turkey are often grouped in the same area and overlapped with each other in PCA score plot [28,29], hence justify the similarity in dominant wavenumbers obtained for the two meats when analyzed using c-FACS. Furthermore, the dominant wavenumbers for pork at 1005–1071 cm⁻¹ obtained using c-FACS is in agreement to the dominant wavenumbers of porcine gelatin listed in Table 2 earlier. Therefore, it provides some sort of signature for pig derivative in related food products.

The c-FACS and PCA are two different chemometrics methods that have different approaches in dealing with the dataset. The c-FACS is a fuzzy graph-based method that converts a system to a graph with fuzzy vertices and edges, and PCA is a statistical method that transforms variables to components called principal components. The results for c-FACS are presented in the form of dominant matrices and coordinated nodes, while PCA displayed its result in the form of a score plot. The PCA method has been around for chemometrics analyses, particularly in food authentication. In this paper, a novel fuzzy graph-based chemometrics method is introduced and applied for gelatin authentication and the results show superior performance compared to PCA, with respect to computing time and identification of significant features. Every sample or system possesses some differences [30]. The c-FACS is efficient in determining the signature and feature of samples via their dominant wavenumbers and nodes pattern in Euclidean space. The unique feature of the sample with respect to the dominant wavenumbers signifies the identity of the sample. The c-FACS method is able to extract the most dominant and signature features of each sample through graph representation and eigen-analysis of its matrix. Thus, c-FACS holds promise as the superior method for authentication purposes.

4. Conclusions

The signatures of bovine, porcine and fish gelatin spectra were successfully identified using c-FACS. The differences between the gelatins were determined based on the unique wavenumbers observed for each source of gelatin. The identified wavenumbers indicate that each gelatin has its own unique signature and feature. Furthermore, coordinated FACS showed that the non-halal porcine gelatin has a very distinct characteristic and clustered far away from bovine and fish nodes. In this study, the c-FACS was constructed and applied on system involving Fourier transform infrared (FTIR) spectrum only. In the future, the c-FACS can be enhanced and applied to different types of fuzziness in graph in other chemical system. The capability of c-FACS in identifying the significant characteristics of variables in a dataset was shown and its possibilities for other applications are endless. The differences between bovine, porcine and fish gelatins were successfully detected and the c-FACS executed faster than PCA. Furthermore, the consistency of c-FACS is proven when published data were used and compared against PCA. On top of that, the c-FACS is able to identify the dominant wavenumbers unlike PCA. Thus, the c-FACS offers another robust method for halal authentication in food and related products.