An Integral Equation Approach to the Irreversible Investment Problem with a Finite Horizon
Abstract
:1. Introduction
2. Literature Review
3. The Model
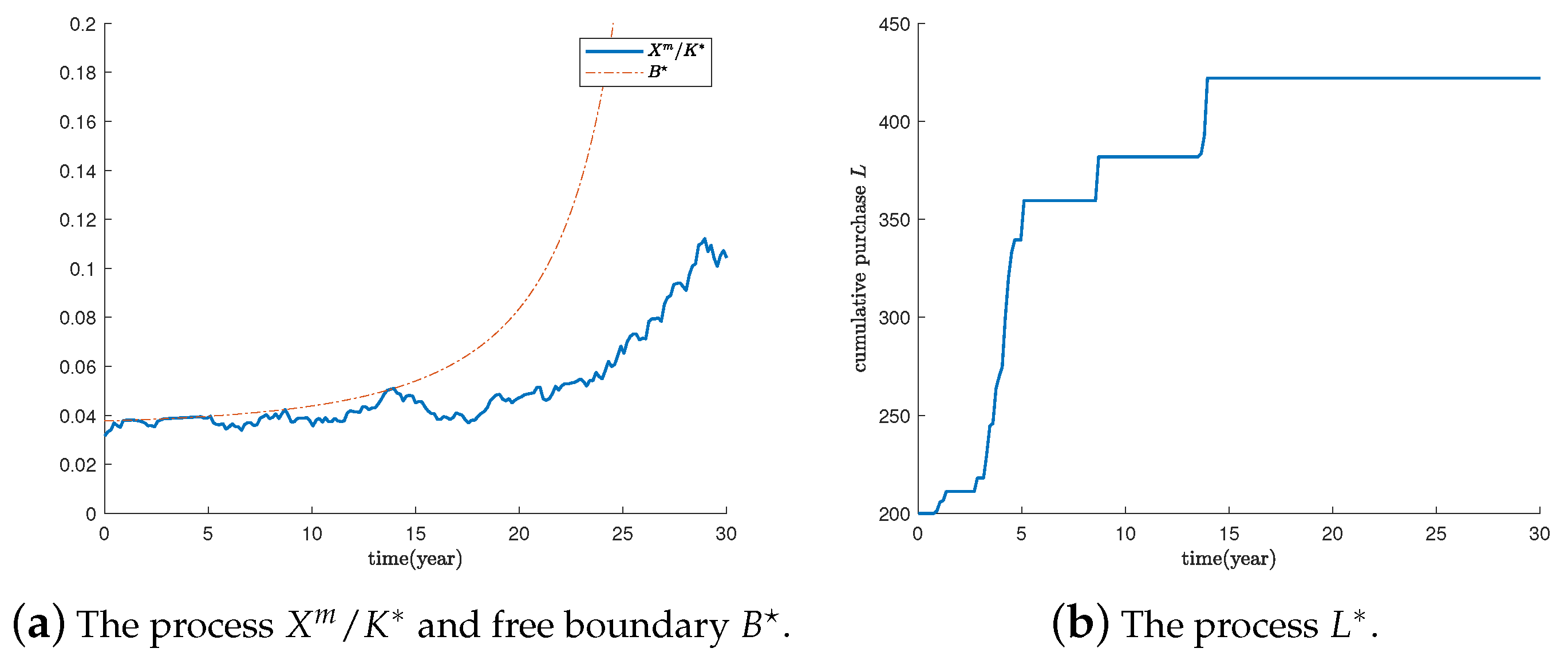
4. Free Boundary Problem
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A. Supplement of Proposition 1
References
- Abel, A.B.; Eberly, J.C. Optimal investment with costly reversibility. Rev. Econ. Stud. 1996, 63, 581–593. [Google Scholar] [CrossRef] [Green Version]
- Eberly, J.C.; Mieghem, J.A.V. Multi-factor Dynamic Investment under Uncertainty. J. Econ. Theory 1997, 75, 345–387. [Google Scholar] [CrossRef] [Green Version]
- Bertola, G. Irreversible investment. Res. Econ. 1998, 52, 3–37. [Google Scholar] [CrossRef] [Green Version]
- Dangl, T. Investment and capacity choice under uncertain demand. Eur. J. Oper. Res. 1999, 117, 415–428. [Google Scholar] [CrossRef] [Green Version]
- Frontczak, R.; Schöbel, R. On modified Mellin transforms, Gauss-Laguerre quadrature, and the valuation of American call options. J. Comput. Appl. Math. 2010, 234, 1559–1571. [Google Scholar] [CrossRef] [Green Version]
- Yoon, J.H. Mellin transform method for European option pricing with Hull-White stochastic interest rate. J. Appl. Math. 2017, 2017, 759562. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.; Han, H.; Kim, H.U.; Kang, M. An integral equation representation approach for Russian options with finite time horizon. Commun. Nonlinear Sci. 2016, 36, 496–516. [Google Scholar] [CrossRef]
- Jeon, J.; Yoon, J.H. Pricing external-chained barrier options with exponential barriers. Bull. Korean Math. Soc. 2016, 53, 1497–1530. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.; Han, H.; Kang, M. Valuing American floating strike lookback option and Neumann problem for inhomogeneous Black-scholes equation. J. Comput. Appl. Math. 2017, 313, 218–234. [Google Scholar] [CrossRef]
- Yoon, J.H.; Kim, J.-H. The pricing of vulnerable options with double Mellin transforms. J. Math. Anal. Appl. 2015, 422, 838–857. [Google Scholar] [CrossRef]
- Jeon, J.; Yoon, J.H.; Kang, M. Valuing vulnerable geometric Asian options. Comput. Math. Appl. 2016, 71, 676–691. [Google Scholar] [CrossRef]
- Kim, G.; Koo, E. Closed-form pricing formula for exchange option with credit risk. Chaos Soliton Fract. 2016, 91, 221–227. [Google Scholar] [CrossRef]
- Jeon, J.; Yoon, J.H.; Kang, M. Pricing vulnerable path-dependent options using integral transforms. J. Comput. Appl. Math. 2017, 313, 259–272. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, G. Pricing of vulnerable options with early counterparty credit risk. N. Am. J. Econ. Financ. 2019, 47, 645–656. [Google Scholar] [CrossRef]
- Jeon, J.; Choi, S.Y.; Yoon, J.H. Analytic valuation of European continuous-installment barrier options. J. Comput. Appl. Math. 2020, 363, 392–412. [Google Scholar] [CrossRef]
- Chiarolla, M.B.; Haussmann, U.G. On a Stochastic, Irreversible Investment Problem. SIAM J. Control Optim. 2009, 48, 438–462. [Google Scholar] [CrossRef] [Green Version]
- Ewald, C.-O.; Wang, W.-K. Irreversible investment with Cox-Ingersoll-Ross type mean reversion. Math. Soc. Sci. 2010, 59, 314–318. [Google Scholar] [CrossRef]
- Riedel, F.; Su, X. On irreversible investment. Financ. Stoch. 2011, 15, 607–633. [Google Scholar] [CrossRef] [Green Version]
- Chiarolla, M.; Ferrari, G.; Riedel, F. Generalized Kuhn–Tucker conditions for n-firm stochastic irreversible investment under limited resources. SIAM J. Control Optim. 2013, 51, 3863–3885. [Google Scholar] [CrossRef] [Green Version]
- Chiarolla, M.; Ferrari, G. Identifying the free boundary of a stochastic, irreversible investment problem via the BankEl Karoui representation theorem. SIAM J. Control Optim. 2014, 52, 1048–1070. [Google Scholar] [CrossRef]
- Ferrari, G. On an integral equation for the free-boundary of stochastic, irreversible investment problems. Ann. Appl. Probab. 2015, 25, 150–176. [Google Scholar] [CrossRef]
- Ferrari, G.; Salminen, P. Irreversible investment under Lévy uncertainty: An equation for the optimal boundary. Adv. Appl. Probab. 2016, 48, 298–314. [Google Scholar] [CrossRef] [Green Version]
- Angelis, T.D.; Federico, S.; Ferrari, G. Optimal Boundary Surface for Irreversible Investment with Stochastic Costs. Math. Oper. Res. 2017, 42, 1135–1161. [Google Scholar] [CrossRef]
- Christensen, S.; Salminen, P. Multidimensional investment problem. Math. Financ. Econ. 2018, 12, 75–95. [Google Scholar] [CrossRef]
- Federico, S.; Rosestolato, M.; Tacconi, E. Irreversible investment with fixed adjustment costs: A stochastic impulse control approach. Math. Financ. Econ. 2019, 13, 579–616. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.; Kim, G. An integral equation approach for optimal investment policies with partial reversibility. Chaos Soliton Fract. 2019, 125, 73–78. [Google Scholar] [CrossRef]
- Fleming, W.H.; Soner, H.M. Controlled Markov Processes and Viscosity Solutions; Springer: New York, NY, USA, 2006. [Google Scholar]
- Guo, X.; Miao, J.; Morellec, E. Irreversible investment with regime shifts. J. Econ. Theory 2005, 122, 37–59. [Google Scholar] [CrossRef]
- Huang, J.; Subrahmanyam, M.; Yu, G. Pricing and hedging American options: A recursive integration method. Rev. Financ. Stud. 1996, 9, 277–300. [Google Scholar] [CrossRef]
- Lions, P.L.; Snitaman, A.S. Stochastic differential equations with reflecting boundary conditions. Commun. Pure Appl. Math. 1984, 37, 511–537. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, J.; Kim, G. An Integral Equation Approach to the Irreversible Investment Problem with a Finite Horizon. Mathematics 2020, 8, 2084. https://doi.org/10.3390/math8112084
Jeon J, Kim G. An Integral Equation Approach to the Irreversible Investment Problem with a Finite Horizon. Mathematics. 2020; 8(11):2084. https://doi.org/10.3390/math8112084
Chicago/Turabian StyleJeon, Junkee, and Geonwoo Kim. 2020. "An Integral Equation Approach to the Irreversible Investment Problem with a Finite Horizon" Mathematics 8, no. 11: 2084. https://doi.org/10.3390/math8112084



