A Simple-FSDT-Based Isogeometric Method for Piezoelectric Functionally Graded Plates
Abstract
1. Introduction
2. Mathematical Model
2.1. Functionally Graded Materials
2.2. Mechanical Displacement and Strain Based on S-FSDT
2.3. Constitutive Relationship
2.4. Nurbs-Based Isogeometric Analysis
2.4.1. Basis Functions
2.4.2. Approximation of Mechanical Displacement
2.4.3. Approximation of the Electric Potential Field
2.4.4. Isogeometric Finite Element Motion Equations
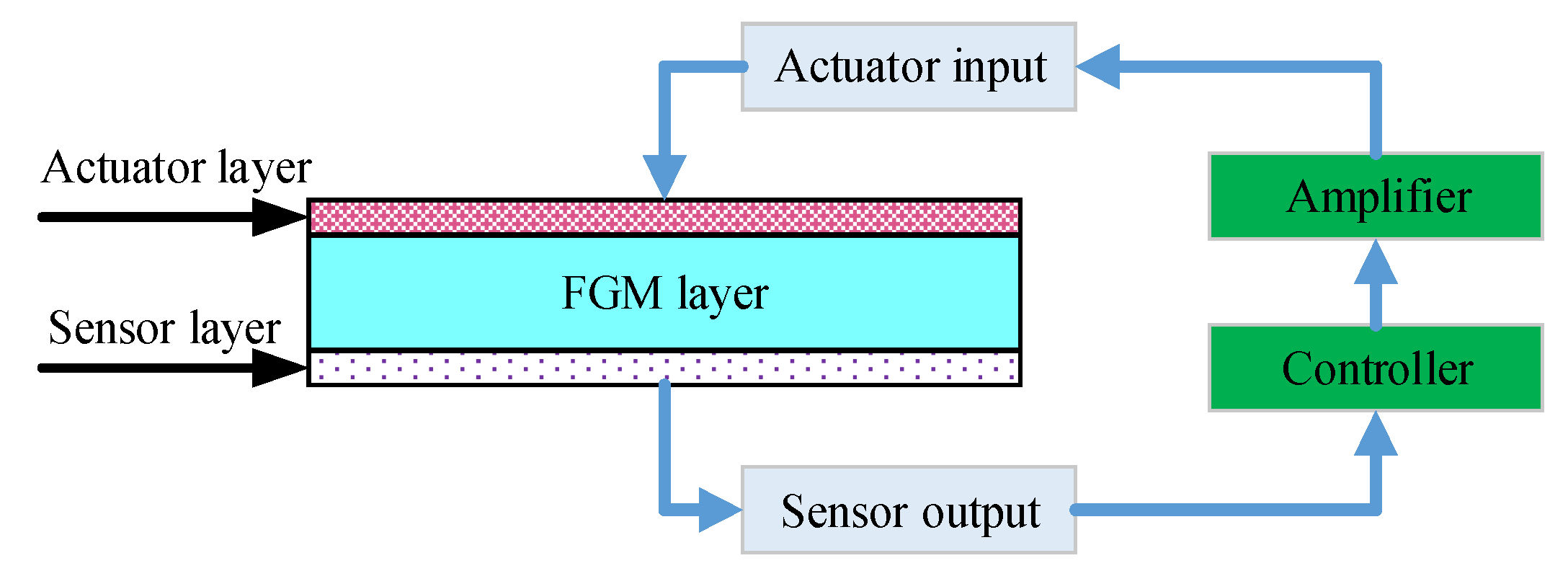
3. Closed-Loop Control
4. Numerical Results
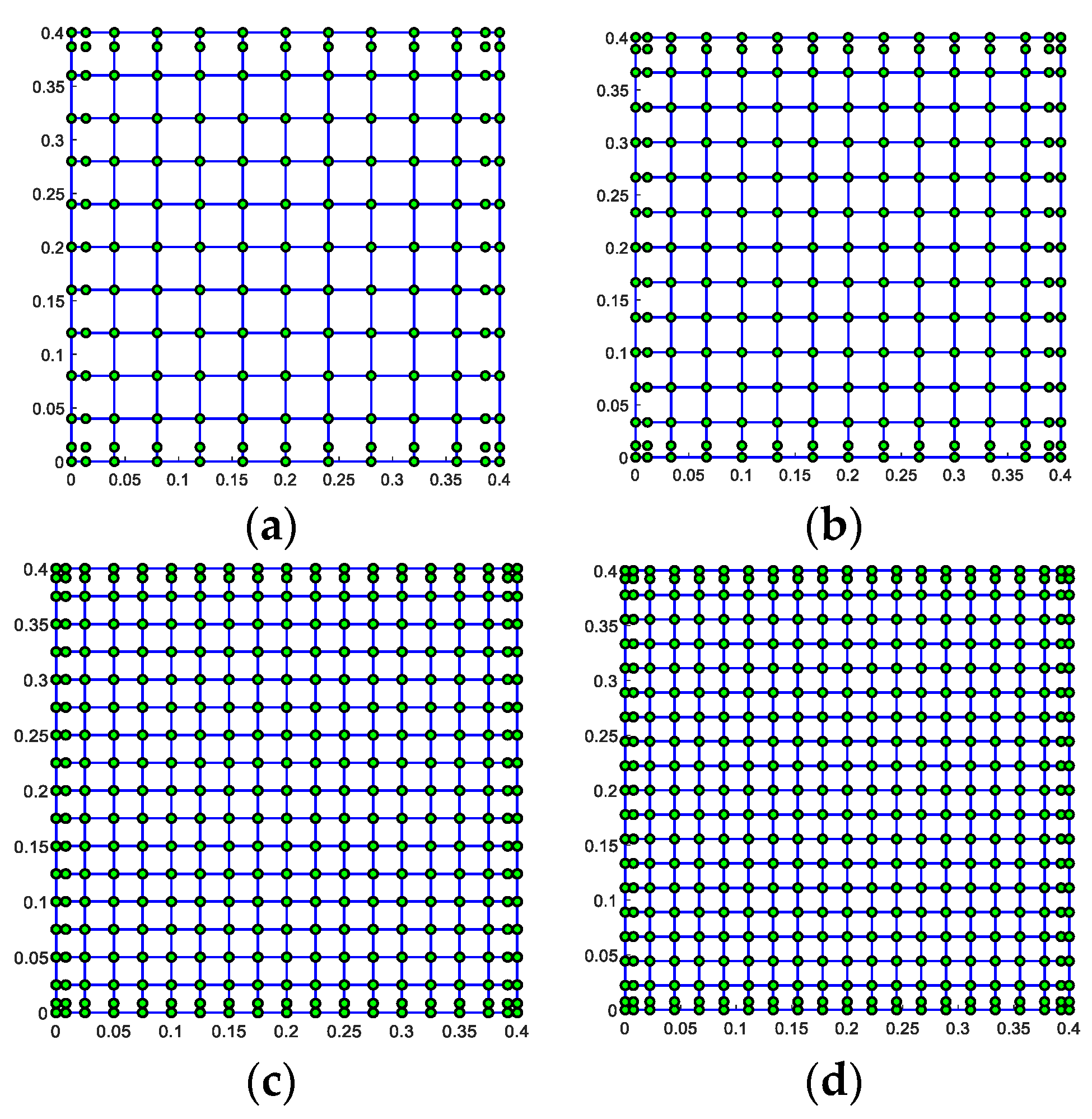
4.1. Convergence and Verification Studies
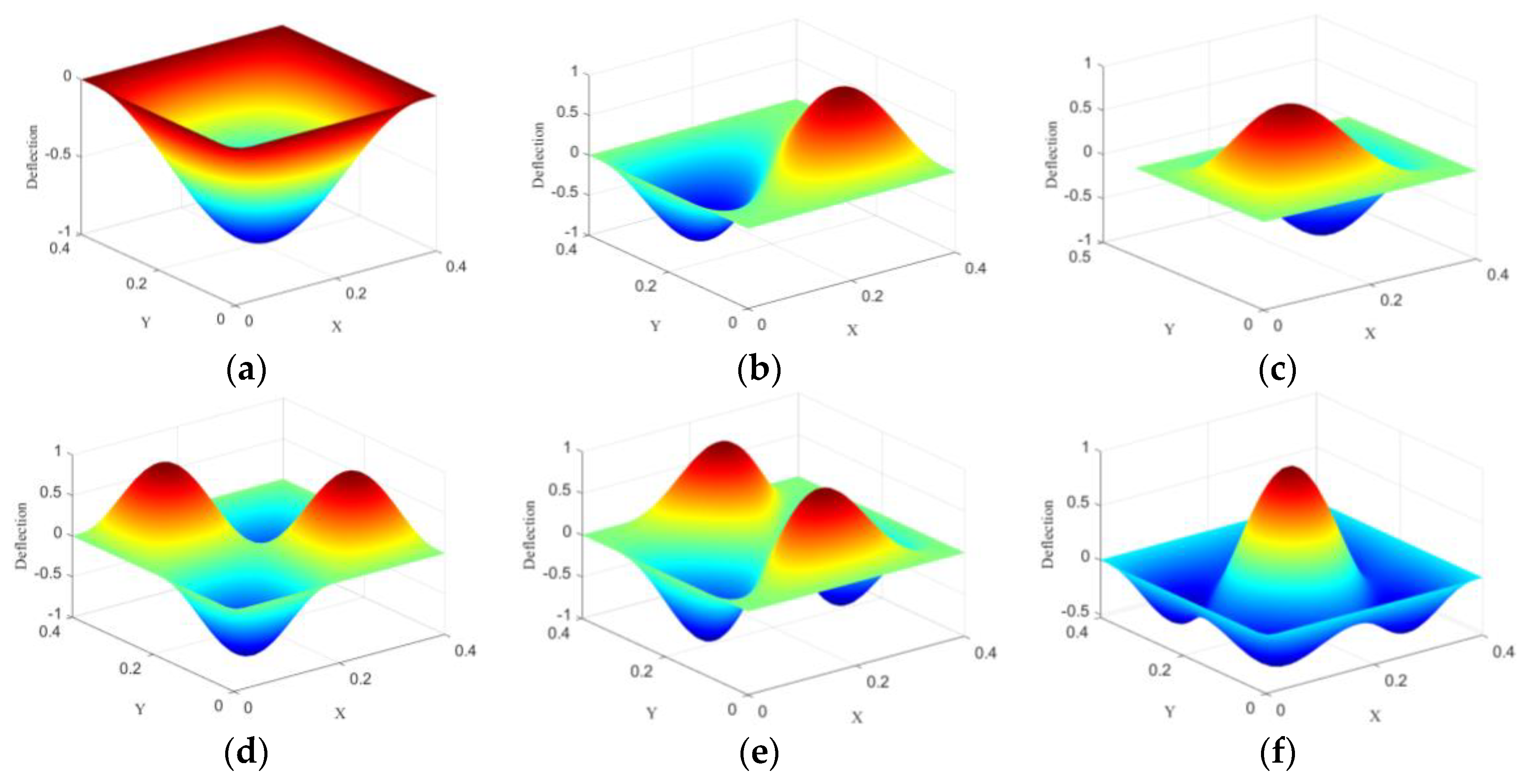
4.2. Free Vibration Analysis
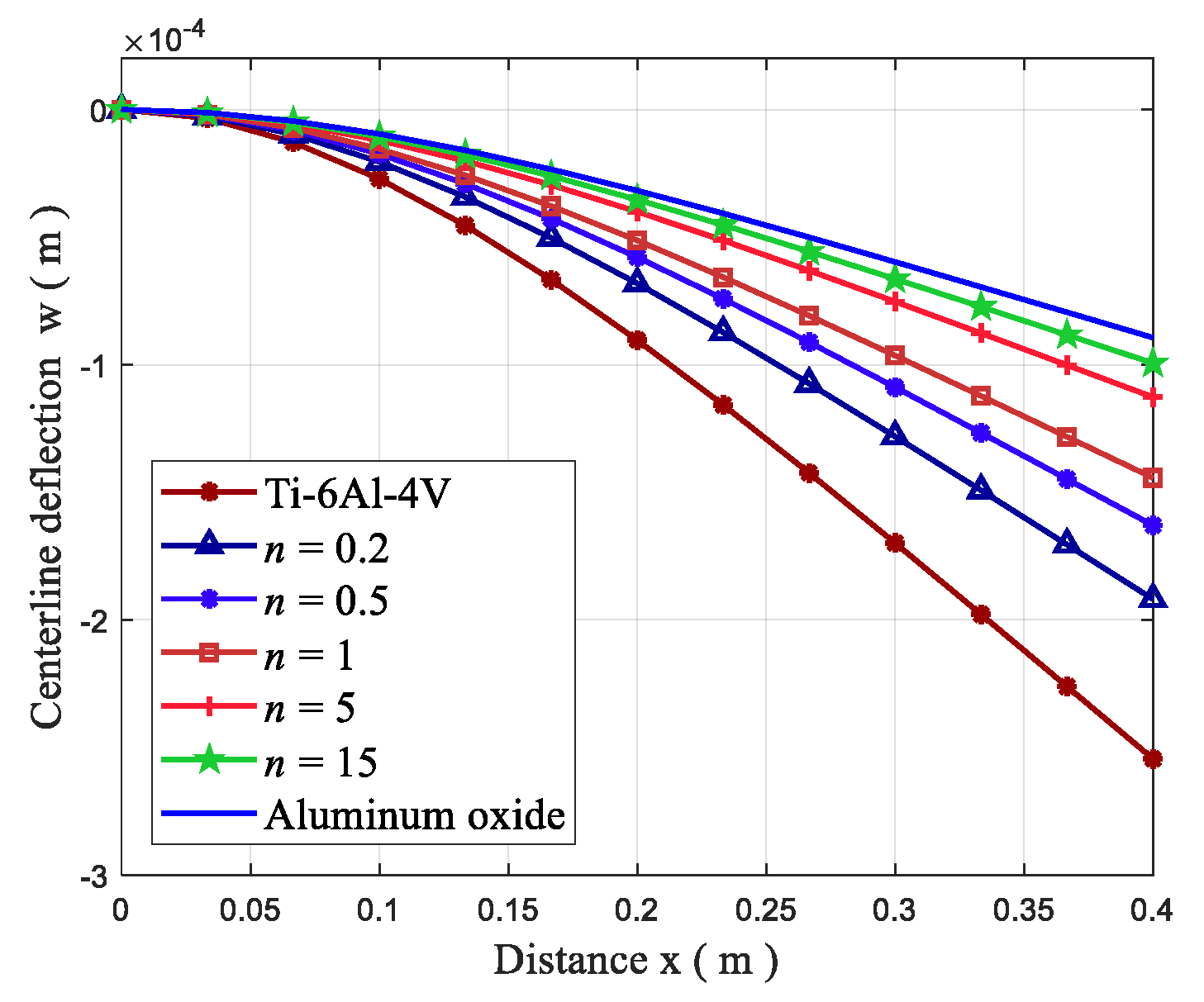
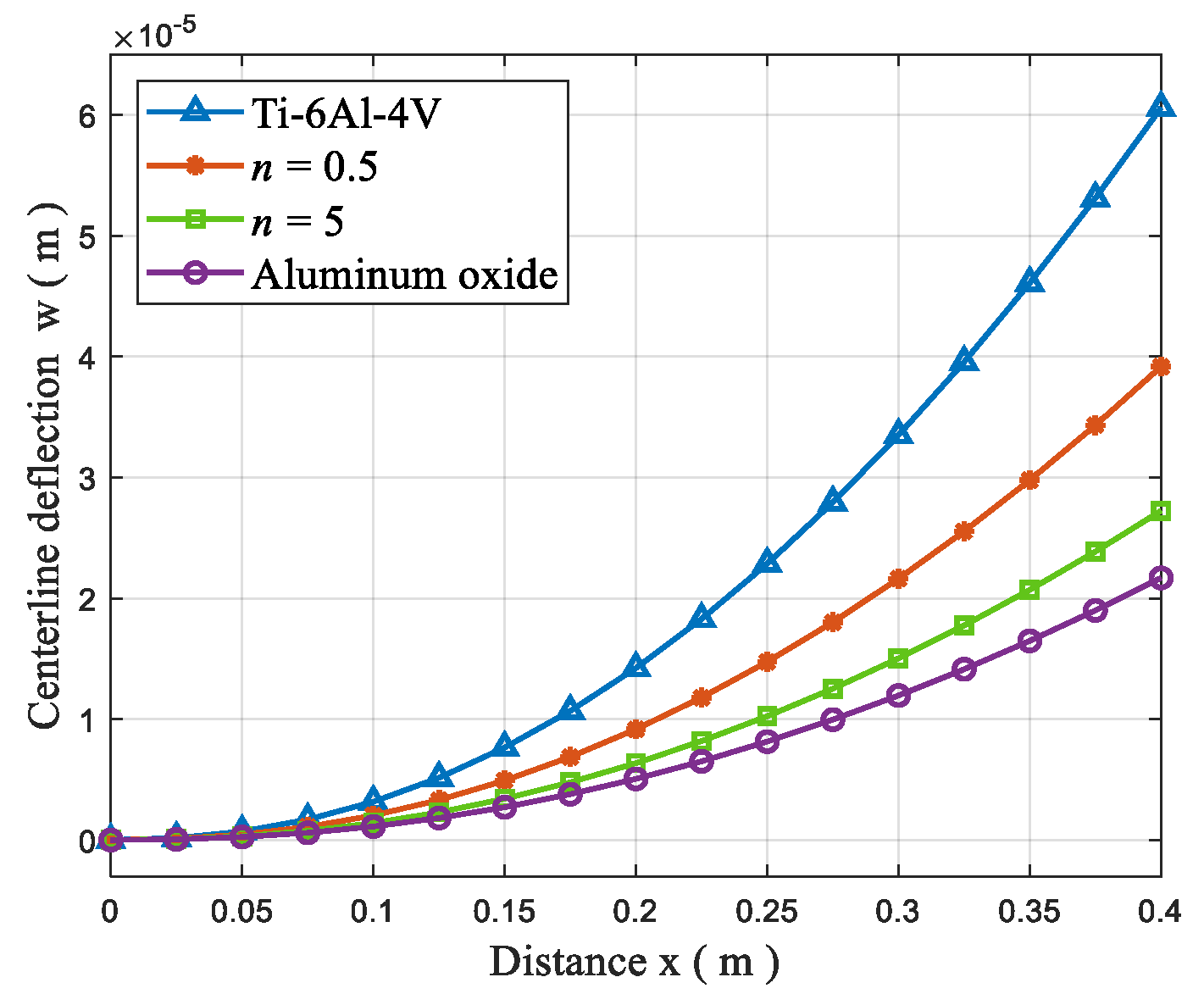
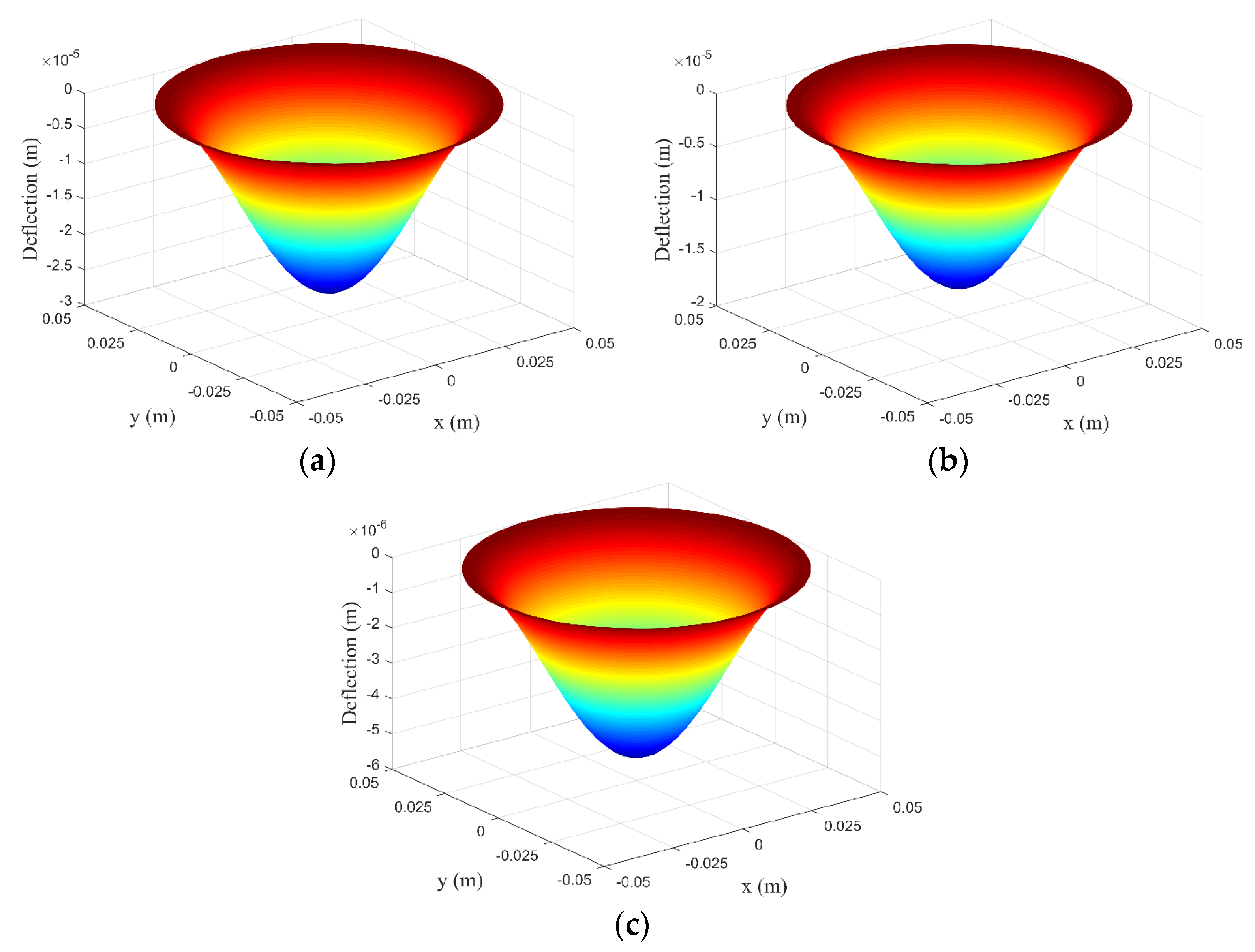
4.3. Static Bending Analysis
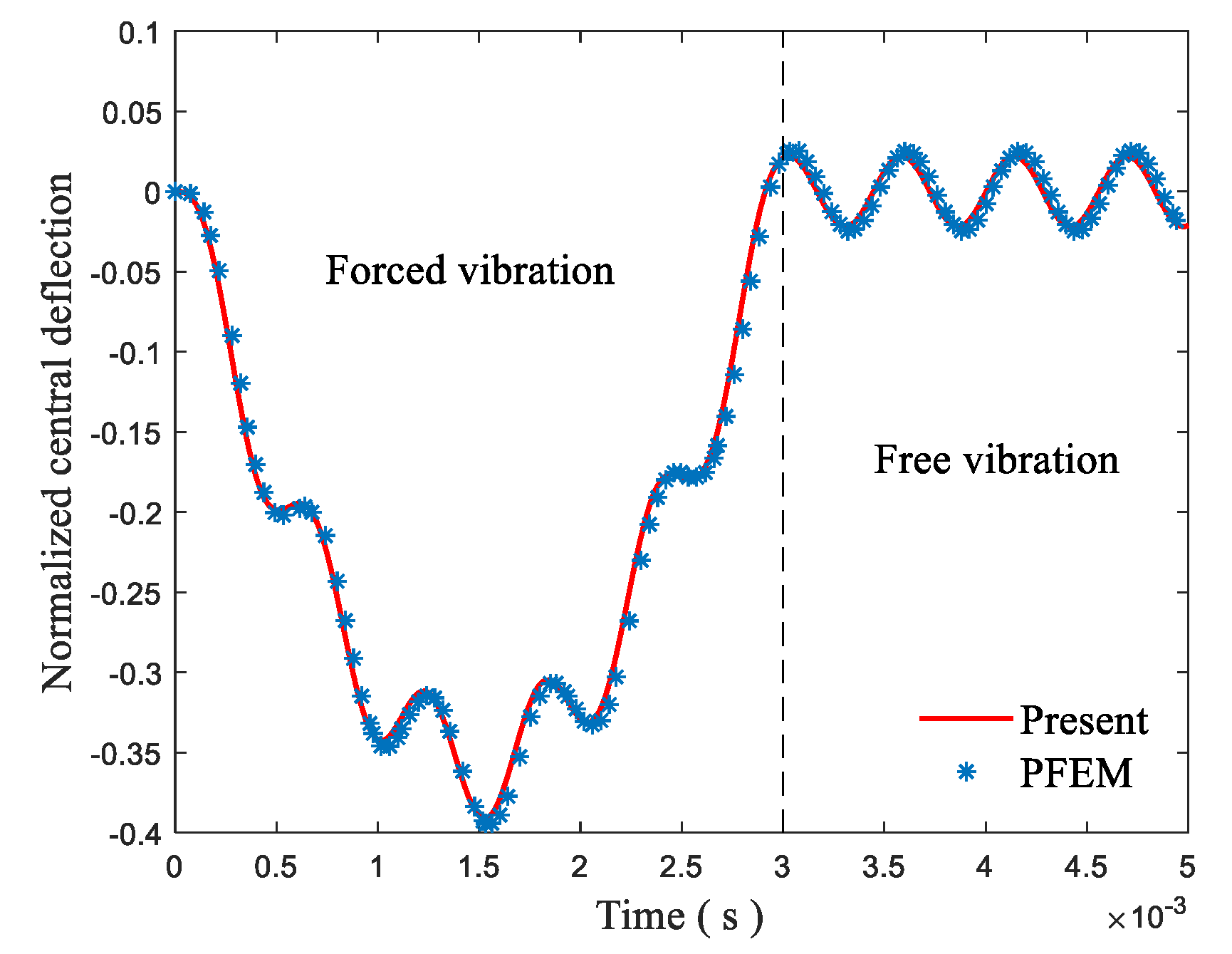
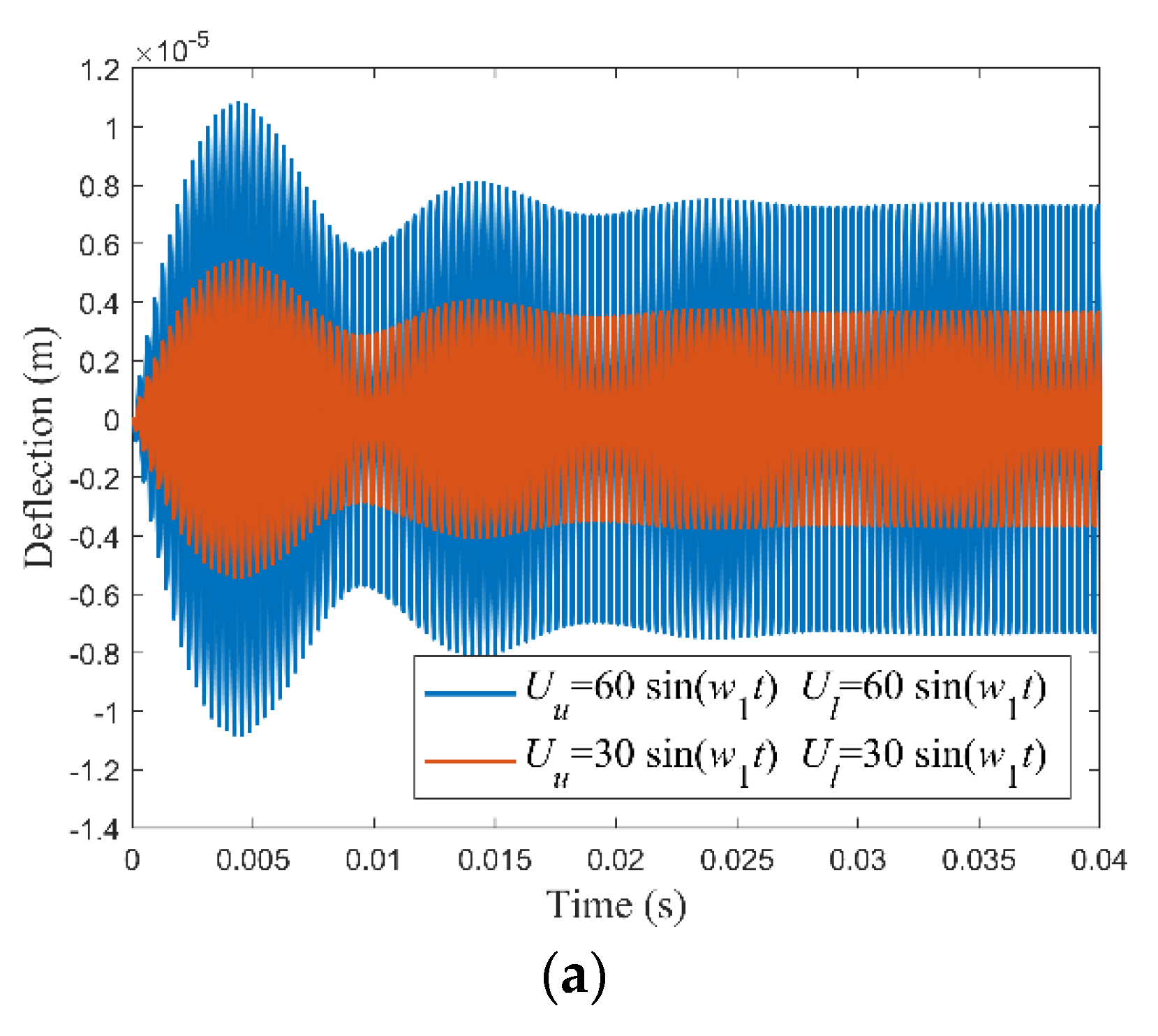
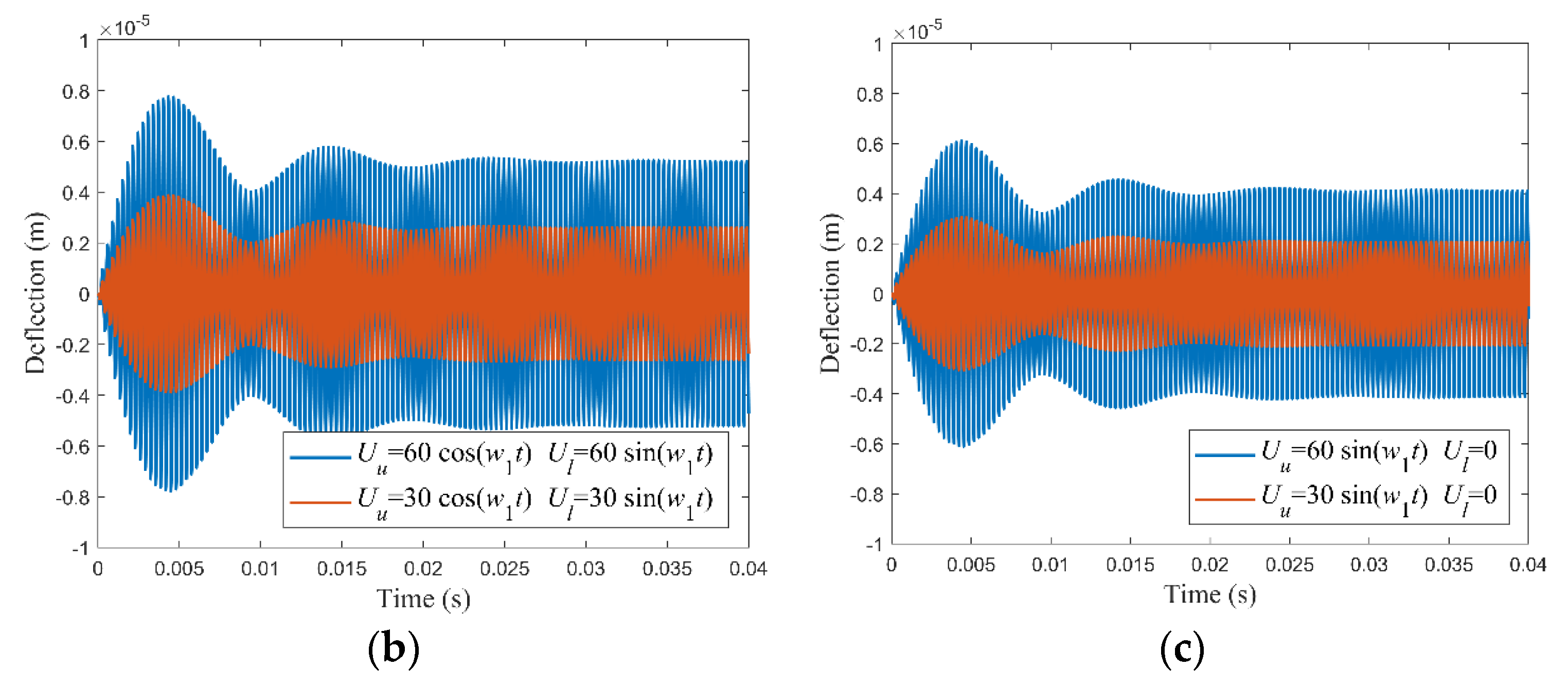
4.4. Dynamic analysis
4.5. Active Control Analysis
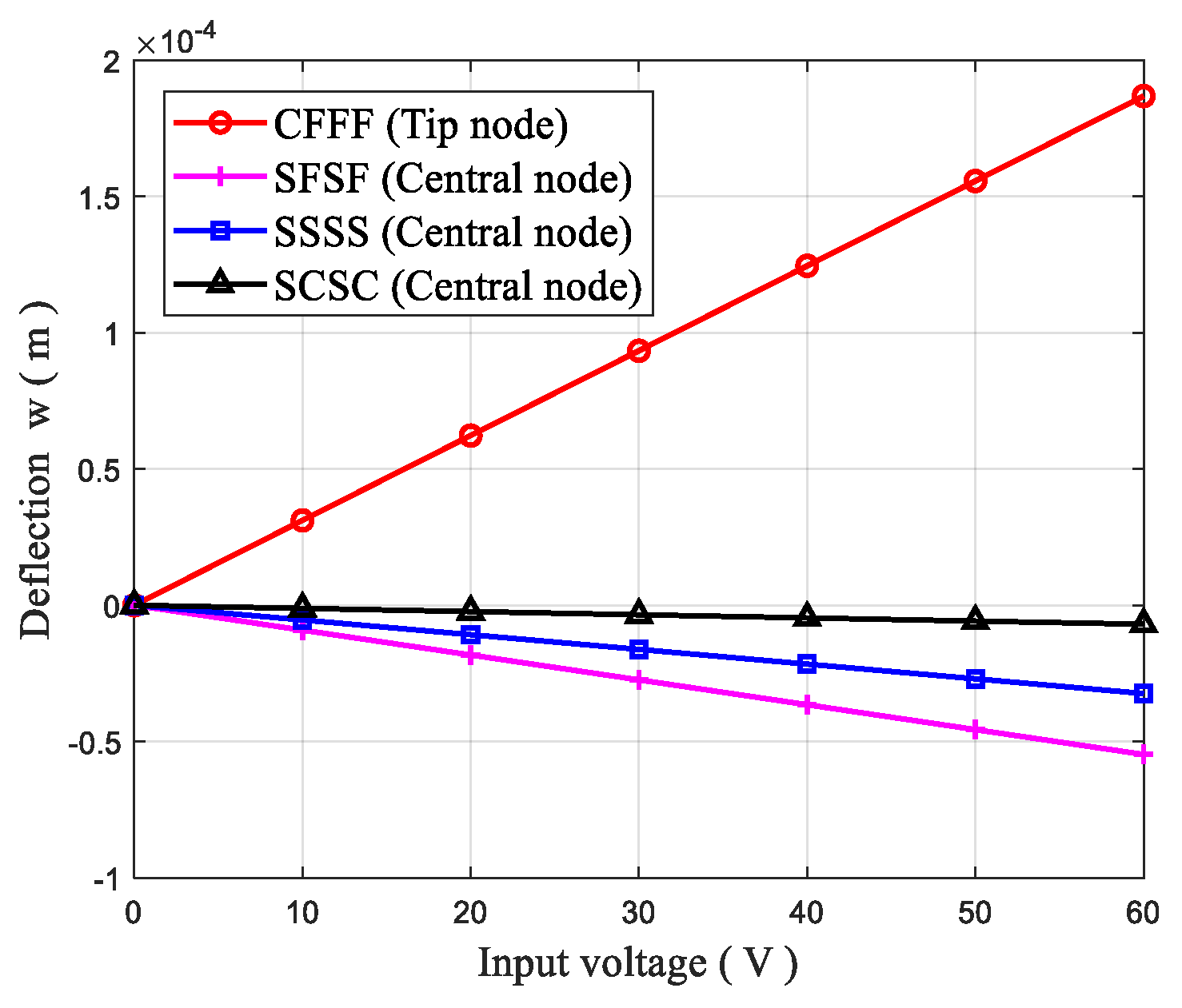
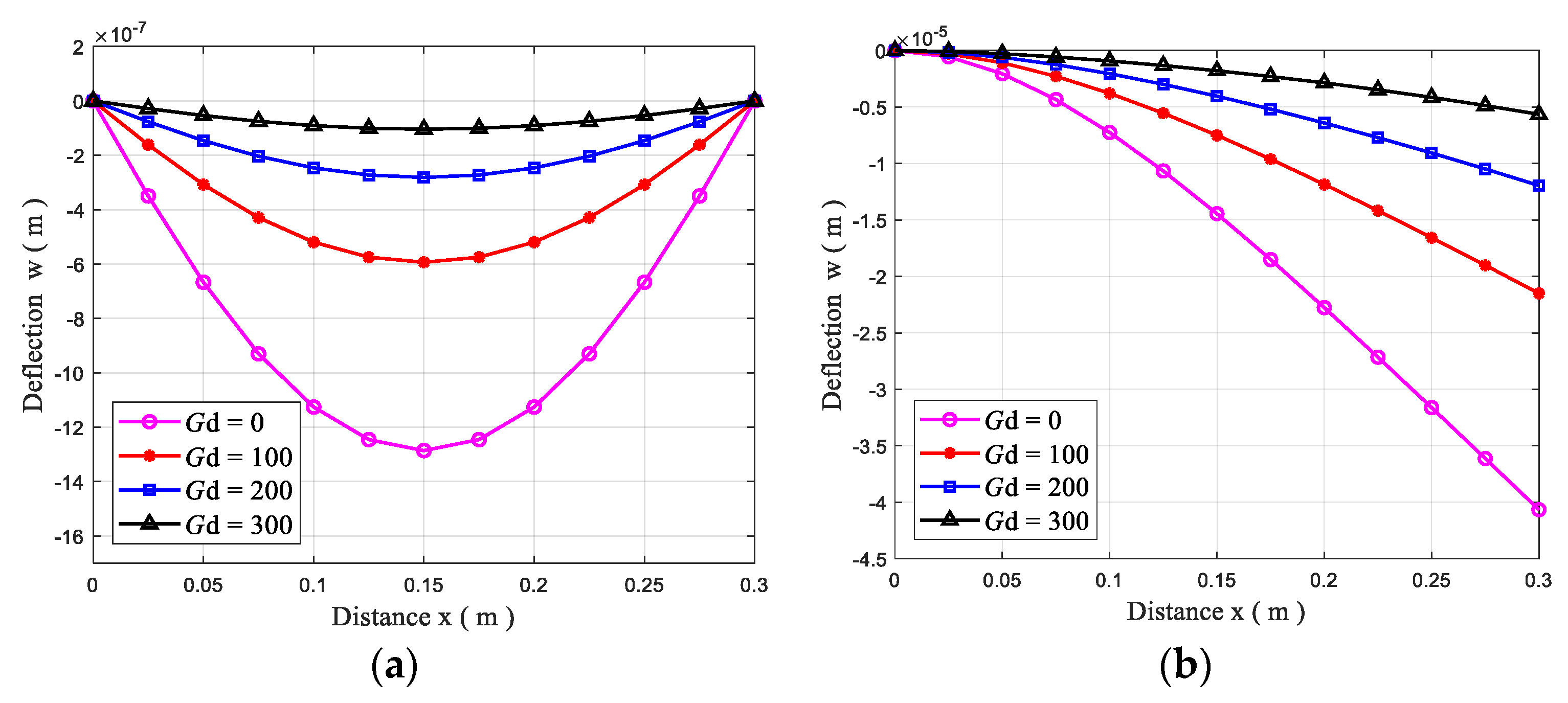
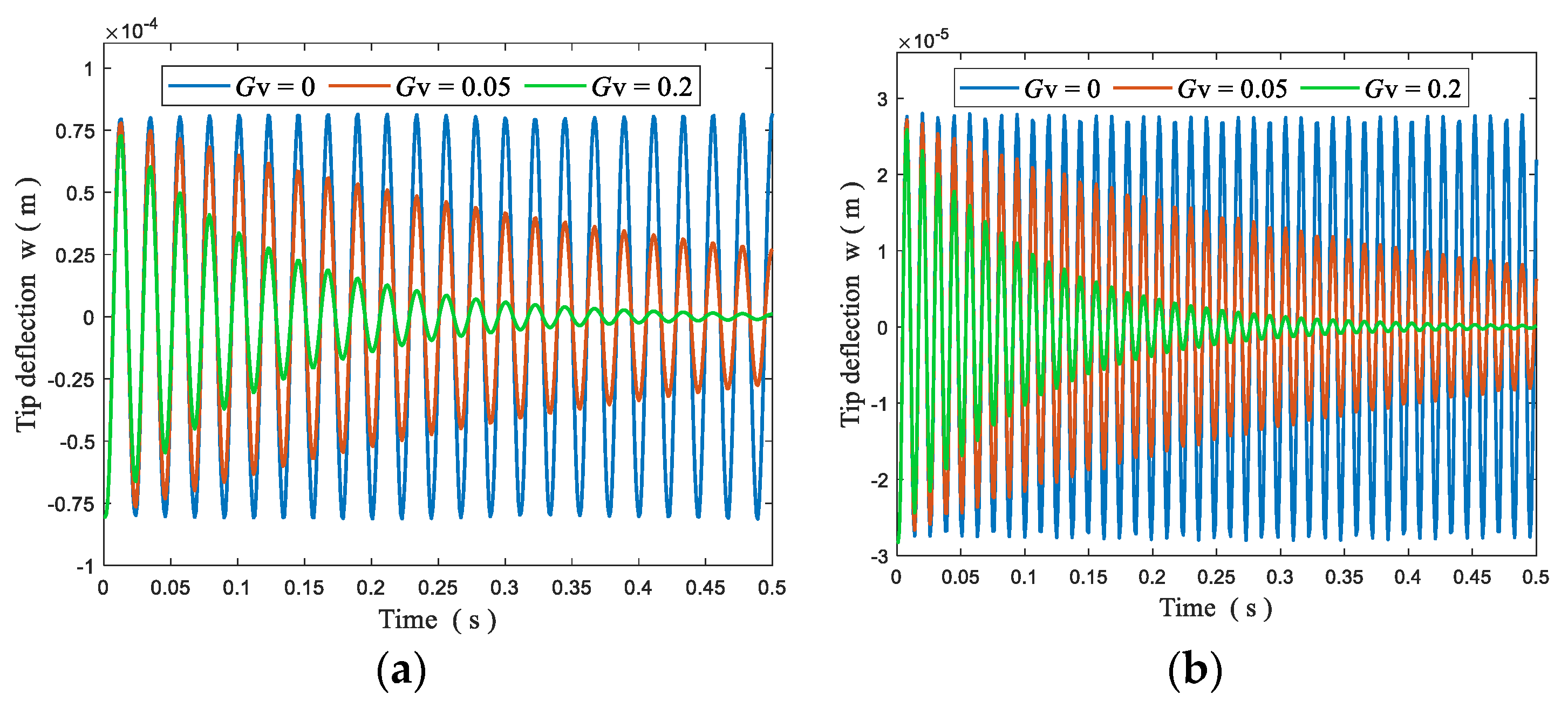
4.5.1. Static Bending Control
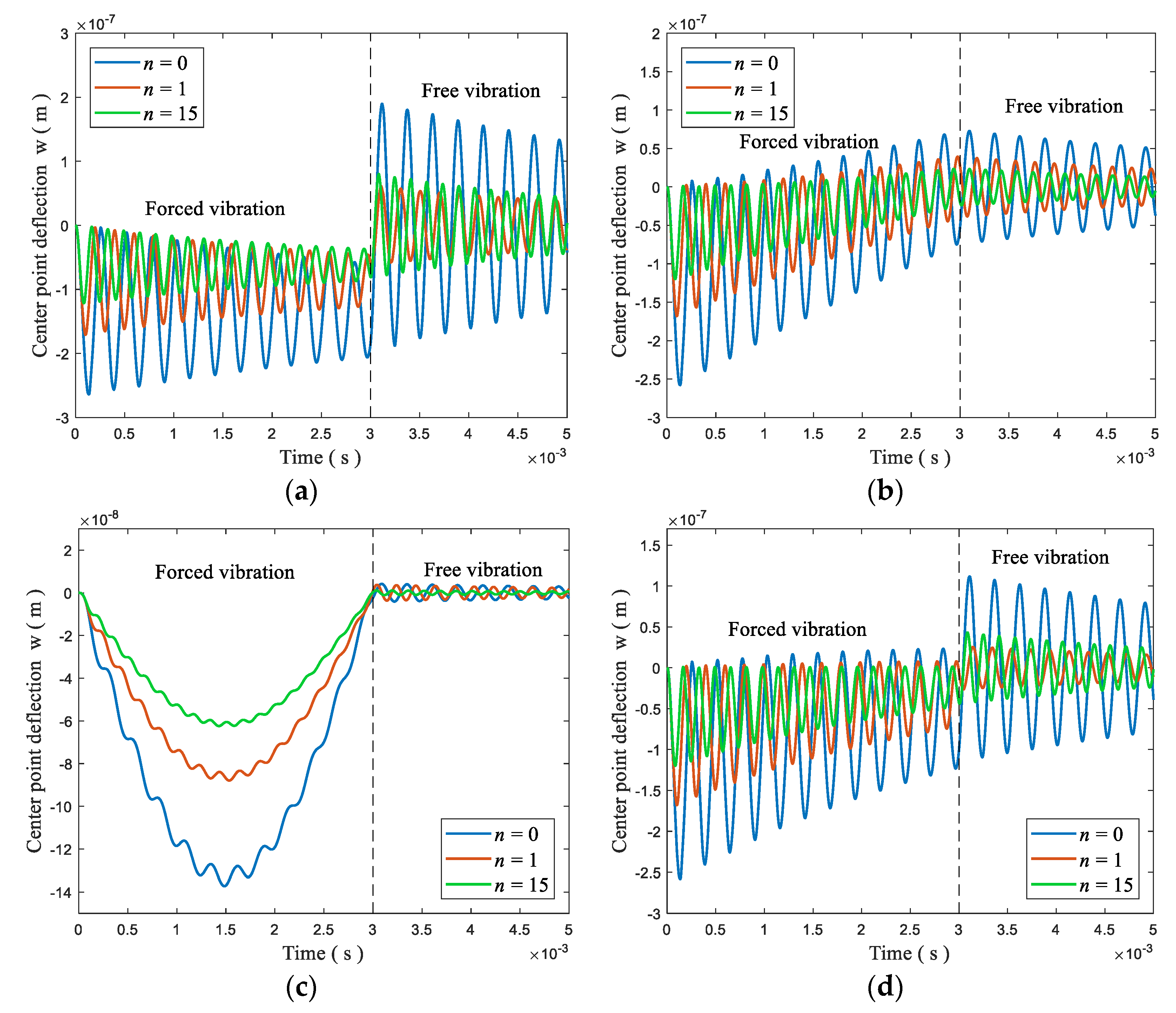
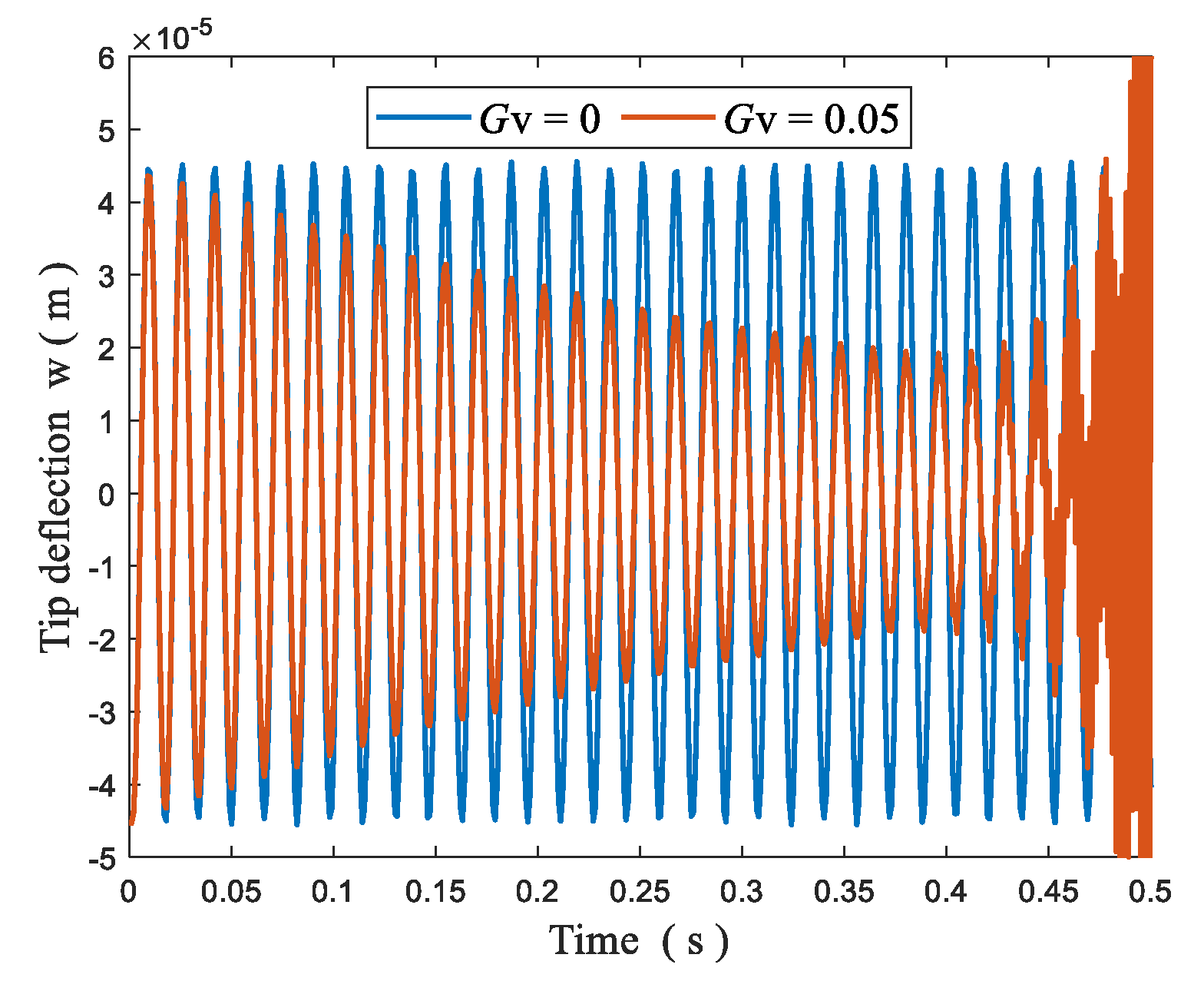
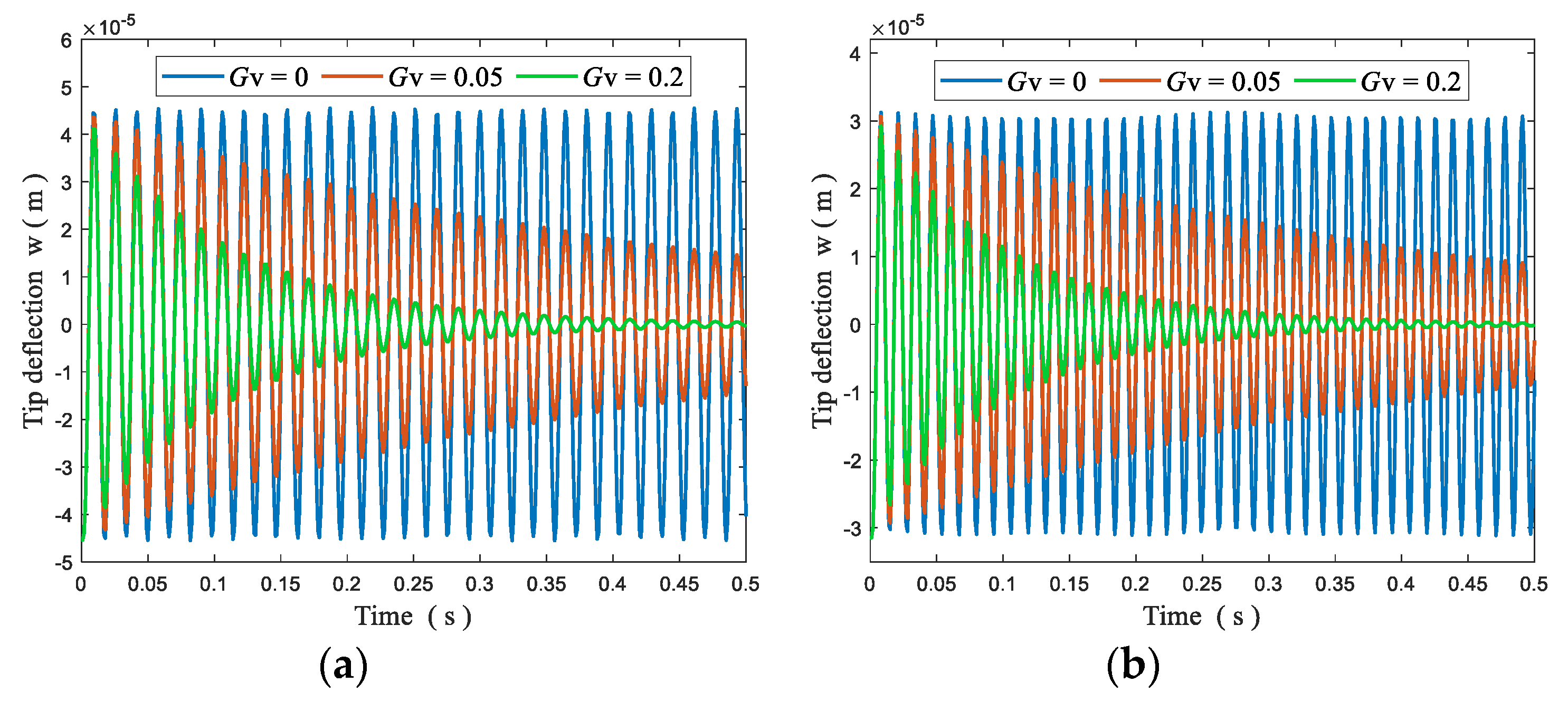
4.5.2. Dynamic Vibration Control
5. Conclusions
- ♦
- The isogeometric finite element motion equations of piezoelectric functionally graded plates (PFGPs) based on the simple first-order shear deformation theory can be derived easily, due to one unknown saved in S-FSDT.
- ♦
- From some comparison studied of free vibration and static bending analyses of piezoelectric functionally graded plates, it can be obtained that although one unknown is saved in simple first-order shear deformation theory, the S-FSDT-based IGA method is still effective and accurate.
- ♦
- Due to the electromechanical coupling effect, the natural frequencies of the piezoelectric functionally graded plates in open-circuit state are greater than those in closed-circuit state.
- ♦
- The vibration amplitude tends to be stable after a period of time when the plate is subjected to time-varying electric loads; the greater the amplitude of the voltage, the greater the amplitude of the vibration.
- ♦
- For closed-loop control analysis of the plates, the static bending response can be altered by adjusting the displacement feedback control gain , and the dynamic vibration and vibration time can be controlled through the velocity feedback control gain .
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Plate length | In-plane forces | ||
| Plate width | Moments | ||
| Total thickness of the plate | Shear forces | ||
| Thickness of the FGM layer | Transverse mechanical surface load | ||
| Thickness of each piezoelectric layer | Moments generated by electric field | ||
| Material properties of FGM | Relation matrix between electric field and electric potential | ||
| Material properties of metal constituent | Displacement vector after assembling the elements | ||
| Material properties of ceramic constituent | Displacement vector | ||
| Volume fraction of metal | First time derivative of | ||
| Gradient index | Surface charge | ||
| Electrical displacement | Surface loads | ||
| Permittivity constant matrix | Mass matrix | ||
| Distance between the mid and neutral surfaces | Second time derivative of | ||
| Geometric strain | First time derivative of | ||
| In-plane strains | Electric field | ||
| Shear strains | Electric stiffness matrix | ||
| Rotations of a transverse normal about the y axis | In-plane forces generated by electric field | ||
| Rotations of a transverse normal about the x axis | Charge density on the surface of piezoelectric layer | ||
| Piezoelectric stress constant matrix | Active damping matrix | ||
| Elastic constant of piezoelectric materials | Rayleigh damping | ||
| Elastic constant of FGM | , | Rayleigh damping factors | |
| Shear correction factor | Displacement feedback control gain | ||
| Weight | Velocity feedback control gain | ||
| , | B-spline basis functions | , | Displacement-electric stiffness matrices |
| , | Orders of B-spline basis functions | Nodal electric potential vector | |
| Displacement vector of control point k | Stiffness matrix |
References
- Zenkour, A.; Hafed, Z.S.; Radwan, A.F. Bending Analysis of Functionally Graded Nanoscale Plates by Using Nonlocal Mixed Variational Formula. Mathematics 2020, 8, 1162. [Google Scholar] [CrossRef]
- Sobczak, J.J.; Drenchev, L. Metallic Functionally Graded Materials: A Specific Class of Advanced Composites. J. Mater. Sci. Technol. 2013, 29, 297–316. [Google Scholar] [CrossRef]
- Li, Y.-D.; Tang, Z.-C.; Fu, Z.-J. Generalized Finite Difference Method for Plate Bending Analysis of Functionally Graded Materials. Mathematics 2020, 8, 1940. [Google Scholar] [CrossRef]
- Tran, L.V.; Thai, C.H.; Nguyen-Xuan, H. An isogeometric finite element formulation for thermal buckling analysis of functionally graded plates. Finite Elem. Anal. Des. 2013, 73, 65–76. [Google Scholar] [CrossRef]
- He, X.-T.; Yang, Z.-X.; Li, Y.-H.; Li, X.; Sun, J.-Y. Application of Multi-Parameter Perturbation Method to Functionally-Graded, Thin, Circular Piezoelectric Plates. Mathematics 2020, 8, 342. [Google Scholar] [CrossRef]
- Milazzo, A.; Orlando, C. An equivalent single-layer approach for free vibration analysis of smart laminated thick composite plates. Smart Mater. Struct. 2012, 21, 75031. [Google Scholar] [CrossRef]
- Yiqi, M.; Yiming, F. Nonlinear dynamic response and active vibration control for piezoelectric functionally graded plate. J. Sound Vib. 2010, 329, 2015–2028. [Google Scholar] [CrossRef]
- Jadhav, P.A.; Bajoria, K.M. Buckling of piezoelectric functionally graded plate subjected to electro-mechanical loading. Smart Mater. Struct. 2012, 21, 105005. [Google Scholar] [CrossRef]
- Ray, M.; Sachade, H. Finite element analysis of smart functionally graded plates. Int. J. Solids Struct. 2006, 43, 5468–5484. [Google Scholar] [CrossRef][Green Version]
- Loja, M.A.R.; Soares, C.M.M.; Barbosa, J. Analysis of functionally graded sandwich plate structures with piezoelectric skins, using B-spline finite strip method. Compos. Struct. 2013, 96, 606–615. [Google Scholar] [CrossRef]
- He, X.; Ng, T.; Sivashanker, S.; Liew, K. Active control of FGM plates with integrated piezoelectric sensors and actuators. Int. J. Solids Struct. 2001, 38, 1641–1655. [Google Scholar] [CrossRef]
- Liew, K.; He, X.Q.; Ng, T.Y.; Sivashanker, S. Active control of FGM plates subjected to a temperature gradient: Modelling via finite element method based on FSDT. Int. J. Numer. Methods Eng. 2001, 52, 1253–1271. [Google Scholar] [CrossRef]
- Liew, K.; Sivashanker, S.; He, X.Q.; Ng, T.Y. The modelling and design of smart structures using functionally graded materials and piezoelectrical sensor/actuator patches. Smart Mater. Struct. 2003, 12, 647–655. [Google Scholar] [CrossRef]
- Aryana, F.; Bahai, H.; Mirzaeifar, R.; Yeilaghi, A. Modification of dynamic characteristics of FGM plates with integrated piezoelectric layers using first- and second-order approximations. Int. J. Numer. Methods Eng. 2007, 70, 1409–1429. [Google Scholar] [CrossRef]
- Nguyen-Quang, K.; Dang-Trung, H.; Ho-Huu, V.; Luong-Van, H.; Nguyen-Thoi, T. Analysis and control of FGM plates integrated with piezoelectric sensors and actuators using cell-based smoothed discrete shear gap method (CS-DSG3). Compos. Struct. 2017, 165, 115–129. [Google Scholar] [CrossRef]
- Nguyen-Thoi, T.; Phung-Van, P.; Nguyen-Xuan, H.; Thai-Hoang, C. A cell-based smoothed discrete shear gap method using triangular elements for static and free vibration analyses of Reissner-Mindlin plates. Int. J. Numer. Methods Eng. 2012, 91, 705–741. [Google Scholar] [CrossRef]
- Fakhari, V.; Ohadi, A.; Yousefian, P. Nonlinear free and forced vibration behavior of functionally graded plate with piezoelectric layers in thermal environment. Compos. Struct. 2011, 93, 2310–2321. [Google Scholar] [CrossRef]
- Fakhari, V.; Ohadi, A. Nonlinear vibration control of functionally graded plate with piezoelectric layers in thermal environment. J. Vib. Control. 2010, 17, 449–469. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Lee, J.; Nguyen-Xuan, H. Active vibration control of GPLs-reinforced FG metal foam plates with piezoelectric sensor and actuator layers. Compos. Part B Eng. 2019, 172, 769–784. [Google Scholar] [CrossRef]
- Belinha, J.; Araújo, A.; Ferreira, A.J.M.; Dinis, L.; Natal, R.M. The analysis of laminated plates using distinct advanced discretization meshless techniques. Compos. Struct. 2016, 143, 165–179. [Google Scholar] [CrossRef]
- Sladek, J.; Stanak, P.; Han, Z.D.; Sladek, V.; Atluri, S.N. Applications of the MLPG method in engineering & sciences: A review. Comput. Model Eng. 2013, 92, 423–475. [Google Scholar]
- Dai, K.; Liu, G.; Han, X.; Lim, K.-M. Thermomechanical analysis of functionally graded material (FGM) plates using element-free Galerkin method. Comput. Struct. 2005, 83, 1487–1502. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, Z.; Liew, K. Stability of piezoelectric FGM rectangular plates subjected to non-uniformly distributed load, heat and voltage. Adv. Eng. Softw. 2008, 39, 121–131. [Google Scholar] [CrossRef]
- Nourmohammadi, H.; Behjat, B. Geometrically nonlinear analysis of functionally graded piezoelectric plate using mesh-free RPIM. Eng. Anal. Bound. Elem. 2019, 99, 131–141. [Google Scholar] [CrossRef]
- Selim, B.; Zhang, L.; Liew, K. Active vibration control of FGM plates with piezoelectric layers based on Reddy’s higher-order shear deformation theory. Compos. Struct. 2016, 155, 118–134. [Google Scholar] [CrossRef]
- Hughes, T.; Cottrell, J.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Phung-Van, P.; Tran, L.V.; Ferreira, A.J.M.; Nguyen-Xuan, H.; Wahab, M.A. Nonlinear transient isogeometric analysis of smart piezoelectric functionally graded material plates based on generalized shear deformation theory under thermo-electro-mechanical loads. Nonlinear Dyn. 2017, 87, 879–894. [Google Scholar] [CrossRef]
- Van, P.P.; De Lorenzis, L.; Thai, C.H.; Wahab, M.A.; Nguyen-Xuan, H. Analysis of laminated composite plates integrated with piezoelectric sensors and actuators using higher-order shear deformation theory and isogeometric finite elements. Comput. Mater. Sci. 2015, 96, 495–505. [Google Scholar] [CrossRef]
- Van, P.P.; Nguyen, L.B.; Tran, L.V.; Dinh, T.D.; Thai, C.H.; Bordas, S.; Wahab, M.A.; Nguyen-Xuan, H. An efficient computational approach for control of nonlinear transient responses of smart piezoelectric composite plates. Int. J. Non-Linear Mech. 2015, 76, 190–202. [Google Scholar] [CrossRef]
- Nguyen, L.B.; Nguyen, N.V.; Thai, C.H.; Ferreira, A.; Nguyen-Xuan, H. An isogeometric Bézier finite element analysis for piezoelectric FG porous plates reinforced by graphene platelets. Compos. Struct. 2019, 214, 227–245. [Google Scholar] [CrossRef]
- Nguyen-Quang, K.; Vo-Duy, T.; Dang-Trung, H.; Nguyen-Thoi, T. An isogeometric approach for dynamic response of laminated FG-CNT reinforced composite plates integrated with piezoelectric layers. Comput. Methods Appl. Mech. Eng. 2018, 332, 25–46. [Google Scholar] [CrossRef]
- Lv, Q.; Yao, Z.; Li, X. Contact analysis and experimental investigation of a linear ultrasonic motor. Ultrasonics 2017, 81, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Li, C.; Yuan, T. Design and experiment of a small-scale walking robot employing stick-slip motion principle. Rev. Sci. Instrum. 2017, 88, 115001. [Google Scholar] [CrossRef]
- Trabelsi, S.; Frikha, A.; Zghal, S.; Dammak, F. A modified FSDT-based four nodes finite shell element for thermal buckling analysis of functionally graded plates and cylindrical shells. Eng. Struct. 2019, 178, 444–459. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 96, 165–173. [Google Scholar] [CrossRef]
- Thai, H.-T.; Choi, D.-H. A simple first-order shear deformation theory for laminated composite plates. Compos. Struct. 2013, 106, 754–763. [Google Scholar] [CrossRef]
- Yin, S.; Hale, J.S.; Yu, T.; Bui, T.Q.; Bordas, S.P. Isogeometric locking-free plate element: A simple first order shear deformation theory for functionally graded plates. Compos. Struct. 2014, 118, 121–138. [Google Scholar] [CrossRef]
- Yu, T.T.; Yin, S.; Bui, T.Q.; Hirose, S. A simple FSDT-based isogeometric analysis for geometrically nonlinear analysis of functionally graded plates. Finite Elem. Anal. Des. 2015, 96, 1–10. [Google Scholar] [CrossRef]
- Zhang, D.-G.; Zhou, H.-M. Nonlinear bending analysis of FGM circular plates based on physical neutral surface and higher-order shear deformation theory. Aerosp. Sci. Technol. 2015, 41, 90–98. [Google Scholar] [CrossRef]
- Wang, C.; Koh, J.M.; Yu, T.; Xie, N.-G.; Cheong, K.H. Material and shape optimization of bi-directional functionally graded plates by GIGA and an improved multi-objective particle swarm optimization algorithm. Comput. Methods Appl. Mech. Eng. 2020, 366, 113017. [Google Scholar] [CrossRef]
- Wang, S. A finite element model for the static and dynamic analysis of a piezoelectric bimorph. Int. J. Solids Struct. 2004, 41, 4075–4096. [Google Scholar] [CrossRef]
- Chowdhury, I.; Dasgupta, S.P. Computation of Rayleigh damping coefficients for large systems. Electron. J. Geotech. Eng. 2013, 8, 1–11. [Google Scholar] [CrossRef]
- Liu, G.R.; Dai, K.Y.; Lim, K.M. Static and vibration control of composite laminates integrated with piezoelectric sensors and actuators using the radial point interpolation method. Smart Mater. Struct. 2004, 13, 1438–1447. [Google Scholar] [CrossRef]
- Tran, L.V.; Ferreira, A.; Nguyen-Xuan, H. Isogeometric analysis of functionally graded plates using higher-order shear deformation theory. Compos. Part B Eng. 2013, 51, 368–383. [Google Scholar] [CrossRef]
- Farsangi, M.A.A.; Saidi, A.R. Levy type solution for free vibration analysis of functionally graded rectangular plates with piezoelectric layers. Smart Mater. Struct. 2012, 21, 94017. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Nguyen, H.X.; Lee, S.; Nguyen-Xuan, H. Geometrically nonlinear polygonal finite element analysis of functionally graded porous plates. Adv. Eng. Softw. 2018, 126, 110–126. [Google Scholar] [CrossRef]
- Wang, S.; Quek, S.; Ang, K. Dynamic stability analysis of finite element modeling of piezoelectric composite plates. Int. J. Solids Struct. 2004, 41, 745–764. [Google Scholar] [CrossRef]





| Parameters | FGMs | Piezoelectric Materials | |||
|---|---|---|---|---|---|
| Ti-6Al-4V | Aluminum Oxide | Al | Al2O3 | PZT-G1195N | |
| Young’s modulus (Gpa) | |||||
| E11 | 105.70 | 320.24 | 70 | 380 | 63.0 |
| E22 | 105.70 | 320.24 | 70 | 380 | 63.0 |
| E33 | 105.70 | 320.24 | 70 | 380 | 63.0 |
| G12 | - | - | - | - | 24.2 |
| G13 | - | - | - | - | 24.2 |
| G23 | - | - | - | - | 24.2 |
| Poisson’s ratio | |||||
| v12 | 0.2981 | 0.26 | 0.3 | 0.3 | 0.3 |
| v13 | 0.2981 | 0.26 | 0.3 | 0.3 | 0.3 |
| v23 | 0.2981 | 0.26 | 0.3 | 0.3 | 0.3 |
| Density (kg/m3) | |||||
| 𝜌 | 4429 | 3750 | 2707 | 3800 | 7600 |
| Piezoelectric coefficients (m/V) | |||||
| d31 | - | - | - | - | 254 × 10−12 |
| d32 | - | - | - | - | 254 × 10−12 |
| Dielectric constant (F/m) | |||||
| k11 | - | - | - | - | 15.3 × 10−9 |
| k22 | - | - | - | - | 15.3 × 10−9 |
| k33 | - | - | -- | 15.0 × 10−9 | |
| Mode | Method | n | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 5 | 15 | 100 | 1000 | ||
| 1 | IGA (10 × 10) | 145.355 | 186.550 | 200.615 | 232.411 | 249.284 | 261.318 | 263.696 |
| IGA (12 × 12) | 145.355 | 186.550 | 200.615 | 232.411 | 249.283 | 261.317 | 263.695 | |
| IGA (16 × 16) | 145.355 | 186.550 | 200.614 | 232.410 | 249.283 | 261.317 | 263.695 | |
| IGA (18 × 18) | 145.355 | 186.550 | 200.614 | 232.410 | 249.283 | 261.317 | 263.695 | |
| [45] | 145.350 | 186.254 | 200.569 | 233.036 | 250.327 | 262.674 | 265.114 | |
| 2/3 | IGA (10 × 10) | 363.085 | 466.002 | 501.155 | 580.604 | 622.741 | 652.785 | 658.721 |
| IGA (12 × 12) | 363.070 | 465.982 | 501.133 | 580.581 | 622.716 | 652.759 | 658.695 | |
| IGA (16 × 16) | 363.061 | 465.970 | 501.119 | 580.566 | 622.701 | 652.743 | 658.678 | |
| IGA (18 × 18) | 363.060 | 465.968 | 501.117 | 580.563 | 622.698 | 652.740 | 658.676 | |
| [45] | 363.050 | 465.223 | 500.994 | 582.112 | 625.288 | 656.108 | 662.201 | |
| 4 | IGA (10 × 10) | 580.400 | 744.936 | 801.160 | 928.208 | 995.551 | 1043.553 | 1053.035 |
| IGA (12 × 12) | 580.382 | 744.911 | 801.132 | 928.178 | 995.520 | 1043.520 | 1053.001 | |
| IGA (16 × 16) | 580.371 | 744.895 | 801.115 | 928.160 | 995.500 | 1043.500 | 1052.981 | |
| IGA (18 × 18) | 580.369 | 744.893 | 801.112 | 928.160 | 995.497 | 1043.496 | 1052.977 | |
| [45] | 580.350 | 743.699 | 800.911 | 930.617 | 999.616 | 1048.857 | 1058.589 | |
| 5/6 | IGA (10 × 10) | 725.405 | 931.104 | 1001.409 | 1160.205 | 1244.348 | 1304.318 | 1316.163 |
| IGA (12 × 12) | 725.196 | 930.812 | 1001.091 | 1159.861 | 1243.988 | 1303.943 | 1315.785 | |
| IGA (16 × 16) | 725.073 | 930.640 | 1000.904 | 1159.658 | 1243.766 | 1303.721 | 1315.561 | |
| IGA (18 × 18) | 725.052 | 930.612 | 1000.873 | 1159.624 | 1243.741 | 1303.685 | 1315.524 | |
| [45] | 725.000 | 929.078 | 1000.571 | 1162.638 | 1248.819 | 1310.310 | 1322.461 | |
| 7/8 | IGA (10 × 10) | 941.987 | 1209.114 | 1300.455 | 1506.753 | 1616.004 | 1693.840 | 1709.211 |
| IGA (12 × 12) | 941.818 | 1208.877 | 1300.197 | 1506.741 | 1615.712 | 1693.536 | 1708.904 | |
| IGA (16 × 16) | 941.718 | 1208.738 | 1300.047 | 1506.310 | 1615.540 | 1693.357 | 1708.723 | |
| IGA (18 × 18) | 941.702 | 1208.716 | 1300.022 | 1506.283 | 1615.512 | 1693.327 | 1708.694 | |
| [45] | 941.640 | 1206.740 | 1299.640 | 1510.197 | 1622.102 | 1701.923 | 1717.694 | |
| 9/10 | IGA (10 × 10) | 1232.501 | 1582.351 | 1702.018 | 1971.842 | 2114.649 | 2216.399 | 2236.490 |
| IGA (12 × 12) | 1231.079 | 1580.332 | 1699.815 | 1969.482 | 2112.191 | 2213.838 | 2233.907 | |
| IGA (16 × 16) | 1230.273 | 1579.200 | 1698.580 | 1968.149 | 2110.799 | 2212.388 | 2232.444 | |
| IGA (18 × 18) | 1230.145 | 1579.021 | 1698.386 | 1967.938 | 2110.579 | 2212.158 | 2232.212 | |
| [45] | 1229.880 | 1576.201 | 1697.617 | 1972.734 | 2118.843 | 2223.021 | 2243.603 | |
| Electrical Condition | Mode | n = 0 | n = 0.5 | n = 1 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Present | [45] | Present | [45] | Present | [45] | ||||
| 0.05 | 0.1 | Closed | 1 | 426.704 | 426.662 | 369.050 | 369.015 | 339.888 | 339.859 |
| 2 | 1049.687 | 1049.356 | 908.204 | 907.918 | 836.293 | 836.020 | |||
| Open | 1 | 433.793 | 433.747 | 377.971 | 377.934 | 350.126 | 350.092 | ||
| 2 | 1066.743 | 1066.390 | 929.708 | 929.406 | 860.967 | 860.669 | |||
| 0.2 | Closed | 1 | 408.435 | 408.475 | 362.207 | 362.269 | 340.242 | 340.311 | |
| 2 | 1001.350 | 1001.133 | 887.808 | 887.637 | 833.442 | 833.266 | |||
| Open | 1 | 421.961 | 421.983 | 378.417 | 378.460 | 358.168 | 358.212 | ||
| 2 | 1033.682 | 1033.381 | 926.547 | 926.311 | 876.222 | 875.953 | |||
| 0.1 | 0.1 | Closed | 1 | 826.873 | 826.463 | 715.679 | 715.319 | 658.905 | 658.555 |
| 2 | 1954.769 | 1952.530 | 1694.005 | 1691.992 | 1558.808 | 1556.838 | |||
| Open | 1 | 840.030 | 839.595 | 732.294 | 731.920 | 677.970 | 677.597 | ||
| 2 | 1983.671 | 1981.321 | 1730.703 | 1728.702 | 1600.948 | 1598.821 | |||
| 0.2 | Closed | 1 | 786.393 | 786.011 | 697.081 | 696.730 | 654.023 | 653.652 | |
| 2 | 1841.071 | 1838.475 | 1630.952 | 1628.388 | 1527.467 | 1524.747 | |||
| Open | 1 | 811.198 | 810.723 | 726.796 | 726.393 | 686.798 | 686.343 | ||
| 2 | 1894.719 | 1891.714 | 1695.063 | 1692.715 | 1598.083 | 1595.292 | |||
| n | Mode | Boundary Conditions | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SSSC | SCSC | ||||||||
| Open Circuit | Closed Circuit | Open Circuit | Closed Circuit | ||||||
| Present | [25] | Present | [25] | Present | [25] | Present | [25] | ||
| 0 | 1 | 209.750 | 208.651 | 206.281 | 205.550 | 256.565 | 254.251 | 252.330 | 251.120 |
| 2 | 457.219 | 454.822 | 449.683 | 448.463 | 484.164 | 480.640 | 476.190 | 474.440 | |
| 3 | 518.331 | 513.724 | 509.805 | 507.453 | 611.731 | 602.687 | 601.699 | 596.858 | |
| 4 | 759.533 | 751.930 | 747.075 | 743.357 | 833.053 | 821.085 | 819.420 | 813.141 | |
| 5 | 883.305 | 876.924 | 868.834 | 866.929 | 900.225 | 892.760 | 885.483 | 882.944 | |
| 6 | 995.360 | 982.452 | 979.117 | 973.305 | 1131.713 | 1109.422 | 1113.343 | 1101.578 | |
| 1 | 1 | 169.301 | 168.200 | 164.296 | 163.727 | 207.096 | 204.560 | 200.984 | 200.041 |
| 2 | 369.044 | 366.401 | 358.167 | 357.223 | 390.797 | 386.889 | 379.288 | 377.936 | |
| 3 | 418.385 | 413.303 | 406.077 | 404.247 | 493.802 | 483.968 | 493.318 | 475.541 | |
| 4 | 613.063 | 604.586 | 595.075 | 592.200 | 672.432 | 659.364 | 652.744 | 647.876 | |
| 5 | 712.952 | 705.039 | 692.056 | 690.600 | 726.615 | 717.565 | 705.327 | 703.381 | |
| 6 | 803.453 | 788.691 | 779.993 | 775.467 | 913.608 | 889.211 | 887.063 | 877.852 | |
| 15 | 1 | 147.106 | 145.798 | 140.782 | 140.155 | 179.859 | 176.792 | 172.147 | 171.103 |
| 2 | 320.364 | 317.022 | 306.656 | 305.467 | 339.173 | 334.267 | 324.677 | 323.006 | |
| 3 | 362.992 | 356.745 | 347.506 | 345.368 | 428.071 | 416.219 | 409.888 | 405.664 | |
| 4 | 531.147 | 520.850 | 508.885 | 505.316 | 582.586 | 566.509 | 557.909 | 552.131 | |
| 5 | 617.872 | 607.441 | 591.657 | 589.345 | 629.633 | 617.822 | 602.937 | 600.054 | |
| 6 | 695.567 | 677.205 | 666.222 | 660.679 | 789.825 | 760.509 | 756.752 | 746.359 | |
| 1000 | 1 | 132.128 | 130.883 | 125.082 | 124.591 | 161.553 | 158.500 | 152.959 | 152.151 |
| 2 | 287.775 | 284.556 | 272.499 | 271.659 | 304.677 | 299.892 | 288.521 | 287.316 | |
| 3 | 326.083 | 319.956 | 308.822 | 307.247 | 384.572 | 372.904 | 364.300 | 361.092 | |
| 4 | 477.475 | 467.118 | 452.296 | 449.750 | 523.425 | 507.747 | 495.908 | 491.650 | |
| 5 | 555.120 | 544.766 | 525.892 | 524.530 | 565.693 | 554.003 | 535.927 | 534.127 | |
| 6 | 624.981 | 606.883 | 592.251 | 588.375 | 709.757 | 681.066 | 672.853 | 665.183 | |
| n | Method | Input Electric Voltages (V) | ||
|---|---|---|---|---|
| 0 | 20 | 40 | ||
| n = 0 | [15] | −2.5460 | −1.3346 | −0.1232 |
| Present | −2.5433 | −1.3323 | −0.1212 | |
| n = 0.5 | [15] | −1.6199 | −0.8440 | −0.0681 |
| Present | −1.6167 | −0.8421 | −0.0675 | |
| n = 5 | [15] | −1.1266 | −0.5820 | −0.0375 |
| Present | −1.1253 | −0.5811 | −0.0369 | |
| n = ∞ | [15] | −0.8947 | −0.4609 | −0.0271 |
| Present | −0.8939 | −0.4602 | −0.0265 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Li, C.; Wang, C.; Lai, J.W.; Cheong, K.H. A Simple-FSDT-Based Isogeometric Method for Piezoelectric Functionally Graded Plates. Mathematics 2020, 8, 2177. https://doi.org/10.3390/math8122177
Liu T, Li C, Wang C, Lai JW, Cheong KH. A Simple-FSDT-Based Isogeometric Method for Piezoelectric Functionally Graded Plates. Mathematics. 2020; 8(12):2177. https://doi.org/10.3390/math8122177
Chicago/Turabian StyleLiu, Tao, Chaodong Li, Chao Wang, Joel Weijia Lai, and Kang Hao Cheong. 2020. "A Simple-FSDT-Based Isogeometric Method for Piezoelectric Functionally Graded Plates" Mathematics 8, no. 12: 2177. https://doi.org/10.3390/math8122177
APA StyleLiu, T., Li, C., Wang, C., Lai, J. W., & Cheong, K. H. (2020). A Simple-FSDT-Based Isogeometric Method for Piezoelectric Functionally Graded Plates. Mathematics, 8(12), 2177. https://doi.org/10.3390/math8122177







