Relating Hydraulic Conductivity Curve to Soil-Water Retention Curve Using a Fractal Model
Abstract
:1. Introduction
2. Materials and Methods
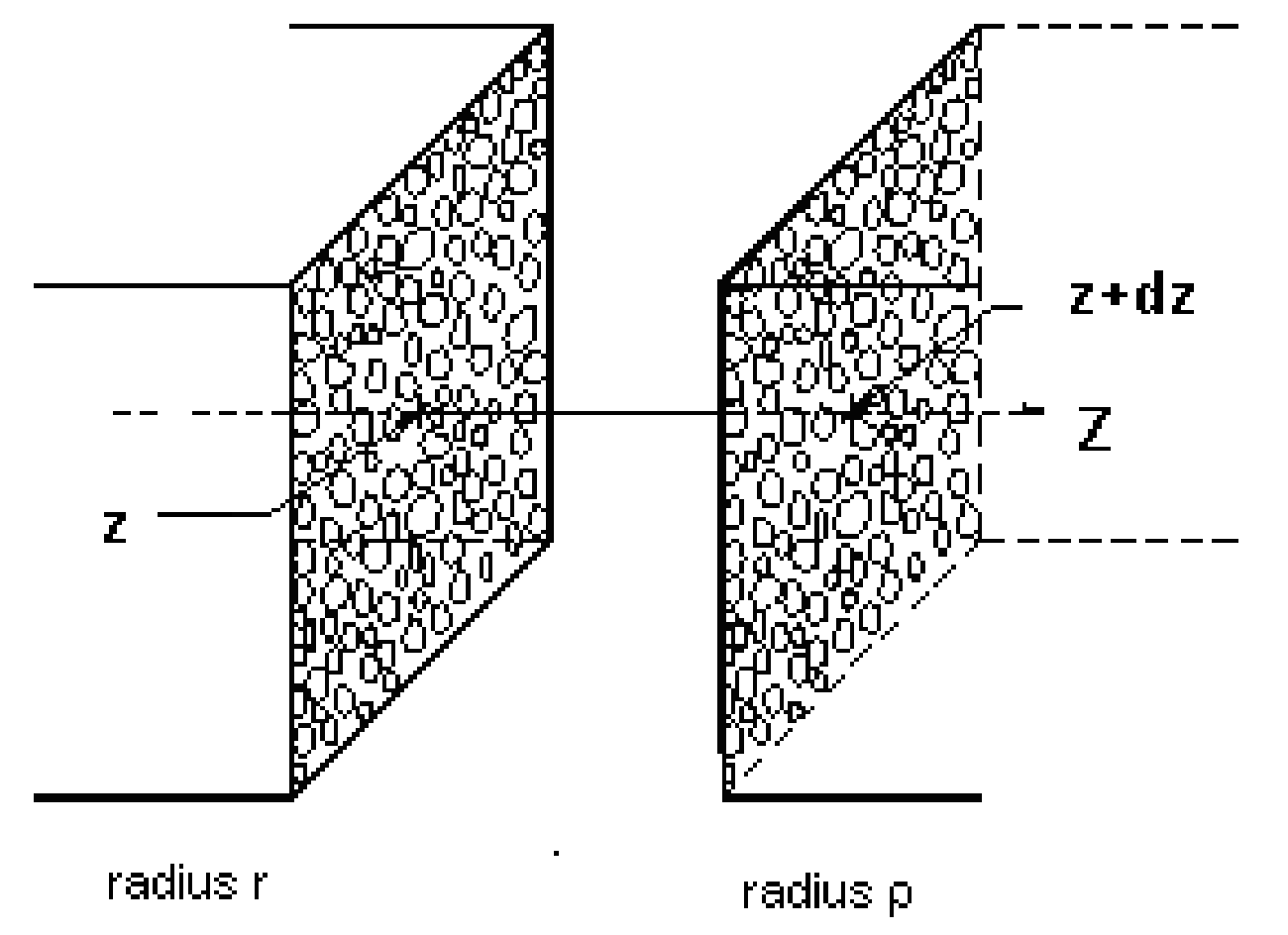
2.1. A General Model of Hydraulic Conductivity
2.2. Classical Models of Hydraulic Conductivity
3. Results and Discussion
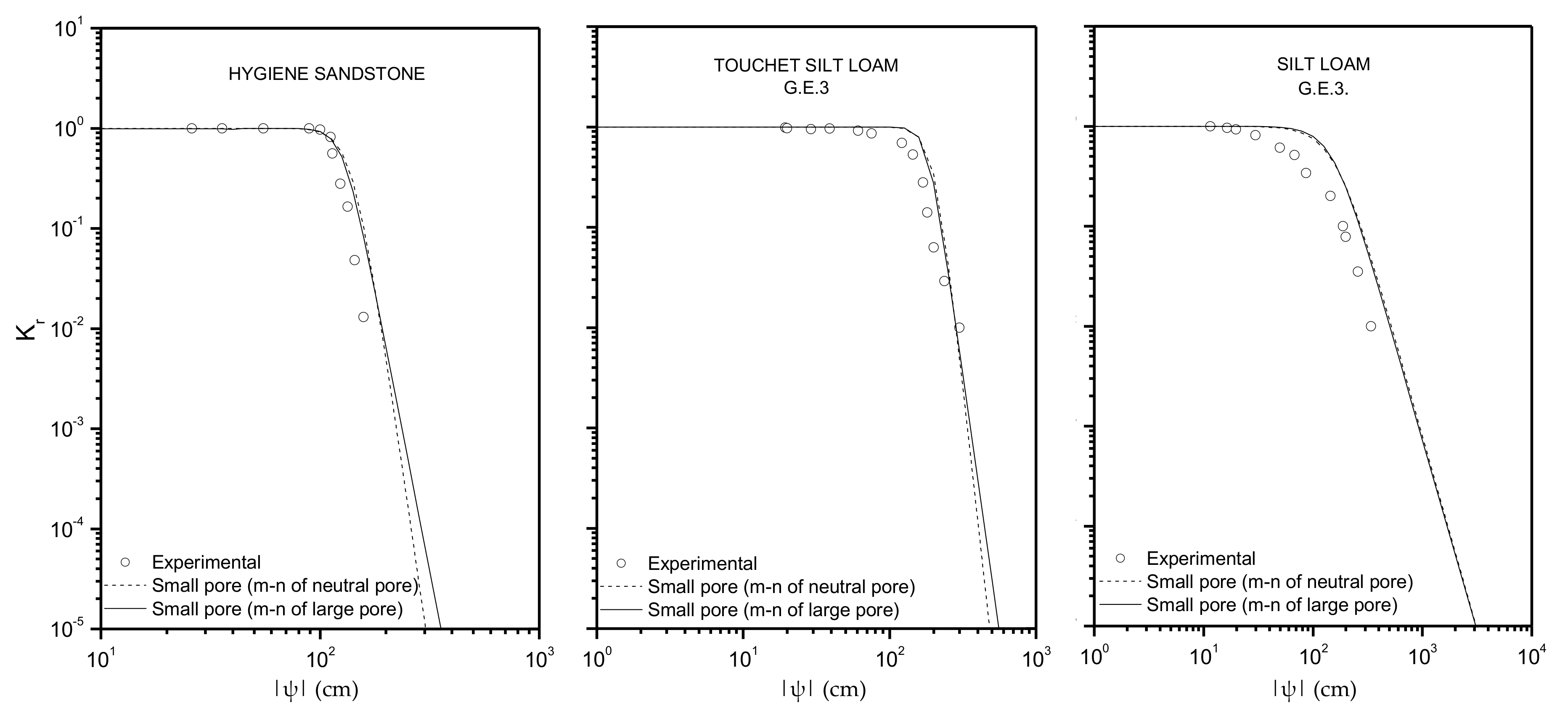
3.1. Some New Models of Hydraulic Conductivity
3.2. Applications
3.2.1. Brooks and Corey Equation
3.2.2. Generalized Power Function
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Darcy, H. Dètermination des lois d’ècoulement de l’eau à travers le sable. In Les Fontaines Publiques de la Ville de Dijon; Dalmont, V., Ed.; Victor Dalmont: Paris, France, 1856; pp. 590–594. [Google Scholar]
- Buckingham, E. Studies on the Movement of Soil Moisture; Bulletin 38; U.S. Department of Agriculture Bureau of Soils: Washington, DC, USA, 1907.
- Fuentes, S.; Trejo-Alonso, J.; Quevedo, A.; Fuentes, C.; Chávez, C. Modeling Soil Water Redistribution under Gravity Irrigation with the Richards Equation. Mathematics 2020, 8, 1581. [Google Scholar] [CrossRef]
- Fu, Q.; Hou, R.; Li, T.; Li, Y.; Liu, D.; Li, M. A new infiltration model for simulating soil water movement in canal irrigation under laboratory conditions. Agric. Water Manag. 2019, 213, 433–444. [Google Scholar]
- Mahallati, S.; Pazira, E.; Abbasi, F.; Babazadeh, H. Estimation of soil water retention curve using fractal dimension. J. Appl. Sci. Environ. Manag. 2018, 22, 173–178. [Google Scholar] [CrossRef] [Green Version]
- Hossein, B.; Golnaz, E.Z. Estimation of the soil water retention curve using penetration resistance curve models. Comput. Electron. Agric. 2018, 144, 329–343. [Google Scholar]
- Zhang, J.; Wang, Z.; Luo, X. Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm. Water 2018, 10, 815. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Huang, C.; Huang, L. Parameter Estimation of the Soil Water Retention Curve Model with Jaya Algorithm. Comput. Electron. Agric. 2018, 151, 349–353. [Google Scholar] [CrossRef]
- Fuentes, C.; Chávez, C.; Quevedo, A.; Trejo-Alonso, J.; Fuentes, S. Modeling of Artificial Groundwater Recharge by Wells: A Model Stratified Porous Medium. Mathematics 2020, 8, 1764. [Google Scholar] [CrossRef]
- Fuentes, C.; Chávez, C. Analytic Representation of the Optimal Flow for Gravity Irrigation. Water 2020, 12, 2710. [Google Scholar] [CrossRef]
- Ket, P.; Oeurng, C.; Degré, A. Estimating Soil Water Retention Curve by Inverse Modelling from Combination of in Situ Dynamic Soil Water Content and Soil Potential Data. Soil Syst. 2018, 2, 55. [Google Scholar] [CrossRef] [Green Version]
- Baiamonte, G. Analytical solution of the Richards equation under gravity-driven infiltration and constant rainfall intensity. J. Hydrol. Eng. 2020, 25, 04020031. [Google Scholar] [CrossRef]
- Mualem, Y.; Dagan, G. Hydraulic conductivity of soils: Unified approach to the statistical models. Soil Sci. Soc. Am. J. 1978, 42, 392–395. [Google Scholar] [CrossRef]
- Fuentes, C. Approche Fractale des Transferts Hydriques dans les sols non Saturès. Ph.D. Thesis, Université Joseph Fourier de Grenoble, Grenoble, France, 1992; p. 267. [Google Scholar]
- Fuentes, C.; Vauclin, M.; Parlange, J.-Y.; Haverkamp, R. A note on the soil-water conductivity of a fractal soil. Transp. Porous Media 1996, 23, 31–36. [Google Scholar] [CrossRef]
- Fuentes, C.; Vauclin, M.; Parlange, J.-Y.; Haverkamp, R. Soil-water conductivity of a fractal soil. In Fractals in Soil Science; Baveye, P.H., Parlange, J.-Y., Stewart, B.A., Eds.; CRC Press: Boca Raton, FL, USA, 1998; pp. 333–340. [Google Scholar]
- Fuentes, C.; Brambila, F.; Vauclin, M.; Parlange, J.-Y.; Haverkamp, R. Modelación fractal de la conductividad hidráulica de los suelos no saturados. Ing. Hidraul. Mex. 2001, 16, 119–137. [Google Scholar]
- Fuentes, C.; Antonino, A.C.D.; Sepúlveda, J.; Zataráin, F.; De León, B. Predicción de la conductividad hidráulica relativa con modelos fractales. Ing. Hidraul. Mex. 2003, 18, 31–40. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications, Inc.: New York, NY, USA, 1972; p. 764. [Google Scholar]
- Dullien, F.A.L. Porous Media, Fluid Transport and Pore Structure; Academic Press: New York, NY, USA, 1979; p. 574. [Google Scholar]
- Childs, E.C.; Collis-George, N. The permeability of porous materials. Proc. R. Soc. Ser. A 1950, 201, 392–405. [Google Scholar]
- Purcell, W.R. Capillary pressures- their measurement using mercury and the calculation of permeability thereform. Pet. Trans. Am. Inst. Min. Metall. Eng. 1949, 186, 39–48. [Google Scholar]
- Millington, R.J.; Quirk, J.P. Permeability of porous solids. Trans. Faraday Soc. 1961, 57, 1200–1206. [Google Scholar] [CrossRef]
- Rieu, M.; Sposito, G. Fractal fragmentation, soil porosity, and soil-water properties: I. Theory. Soil Sci. Soc. Am. J. 1991, 55, 1231–1238. [Google Scholar] [CrossRef] [Green Version]
- Rieu, M.; Sposito, G. Fractal fragmentation, soil porosity, and soil-water properties: II. Applications. Soil Sci. Soc. Am. J. 1991, 55, 1239–1244. [Google Scholar] [CrossRef]
- Oleschko, K.; Fuentes, C.; Brambila, F.; Álvarez, R. Linear fractal analysis of three mexican soils in different management systems. Soil Technol. 1997, 10, 185–206. [Google Scholar] [CrossRef]
- Huang, G.H.; Zhang, R.D.; Huang, Q.Z. Modeling Soil Water Retention Curve with a Fractal Method. Pedosphere 2006, 16, 137–146. [Google Scholar] [CrossRef]
- Ding, D.; Zhao, Y.; Feng, H. A user-friendly modified pore-solid fractal model. Sci. Rep. 2016, 6, 39029. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1983; p. 460. [Google Scholar]
- Falconer, K. Fractal Geometry, Mathematical Foundations and Applications; John Wiley & Sons: England, UK, 1990; p. 288. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W. Some methods of calculating unsaturated permeability. Trans. ASAE 1967, 10, 400–404. [Google Scholar] [CrossRef]
- Burdine, N.T. Relative permeability calculation from size distribution data. Trans. AIME 1953, 198, 71–78. [Google Scholar] [CrossRef]
- Landau, L.; Lifchitz, E. Physique Théorique. Tome 6: Mécanique des Fluids, 2nd ed.; Editions Mir: Moscow, Russia, 1989; p. 748. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media. In Hydrology Papers; Colorado State University: Colorado, CO, USA, 1964; Volume 3. [Google Scholar]
- Braddock, R.D.; Parlange, J.-Y.; Lee, H. Application of a soil water hysteresis model to simple water retention curves. Trans. Porous Media 2001, 44, 407–420. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Haverkamp, R.; Zammit, C.; Bouraoui, F.; Rajkai, K.; Arrúe, J.L.; Heckmann, N. GRIZZLY, Grenoble Catalogue of Soils: Survey of Soil Field Data and Description of Particle-Size, Soil Water Retention and Hydraulic Conductivity Functions; Laboratoire d’Etude des Transferts en Hydrologie et Environnement (LTHE): Grenoble, France, 1998. [Google Scholar]
| ϕ | S = D/3 | p1 | p2 | p = p1 + p2 |
|---|---|---|---|---|
| 0 | 1/2 | −1 | 0 | −1 |
| 0.3671 | 2/3 | −2/3 | 2/3 | 0 |
| ½ | 0.6942 | −0.6115 | 0.8470 | 0.2355 |
| 0.6180 | 0.7202 | −0.5596 | 1.0494 | 0.4898 |
| 1 | 1 | 0 |
| Soil Name | θs (cm3/cm3) | θr (cm3/cm3) | Ks (cm/day) | s |
|---|---|---|---|---|
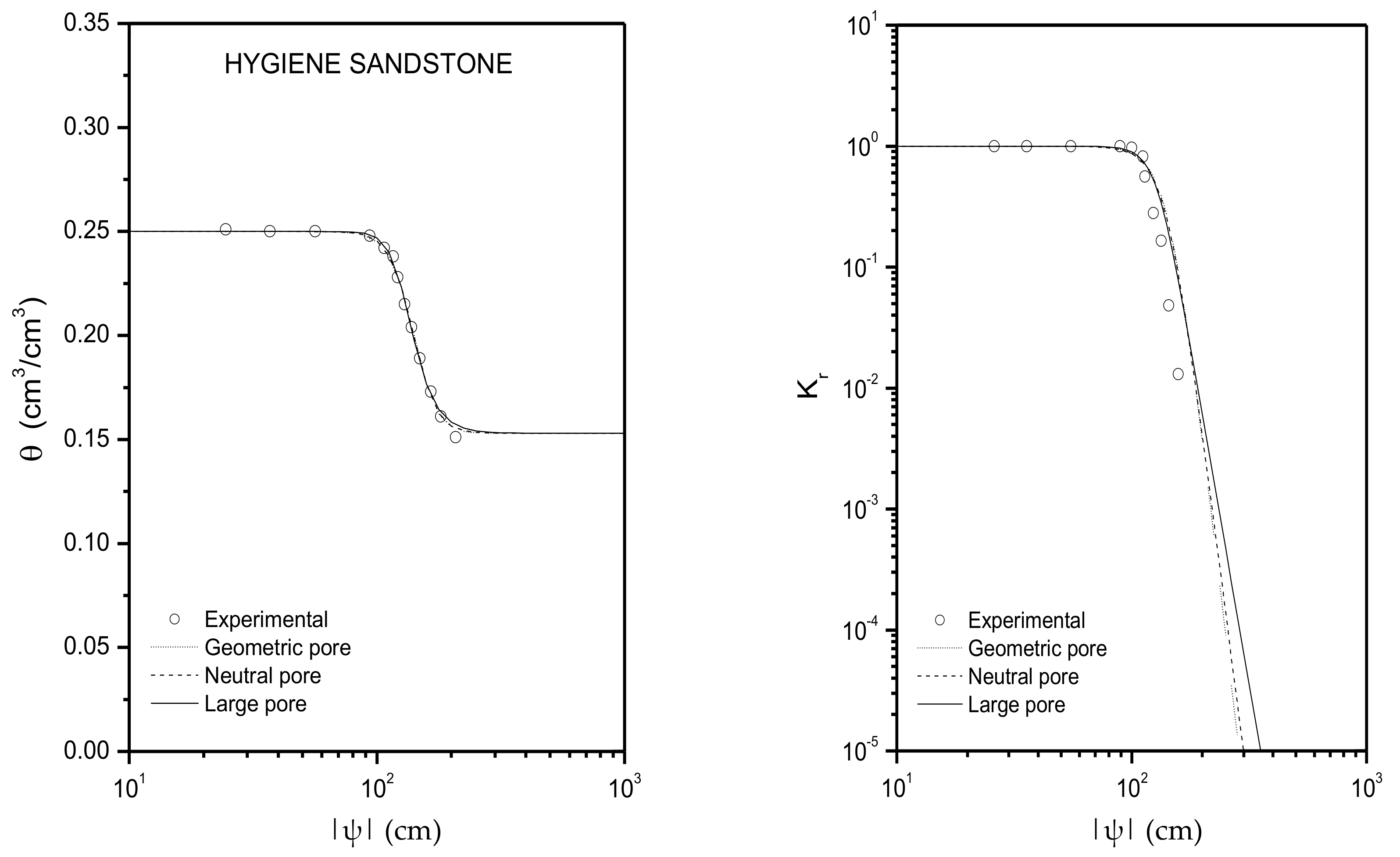
| Hygiene sandstone | 0.250 | 0.153 | 108.0 | 0.642 |
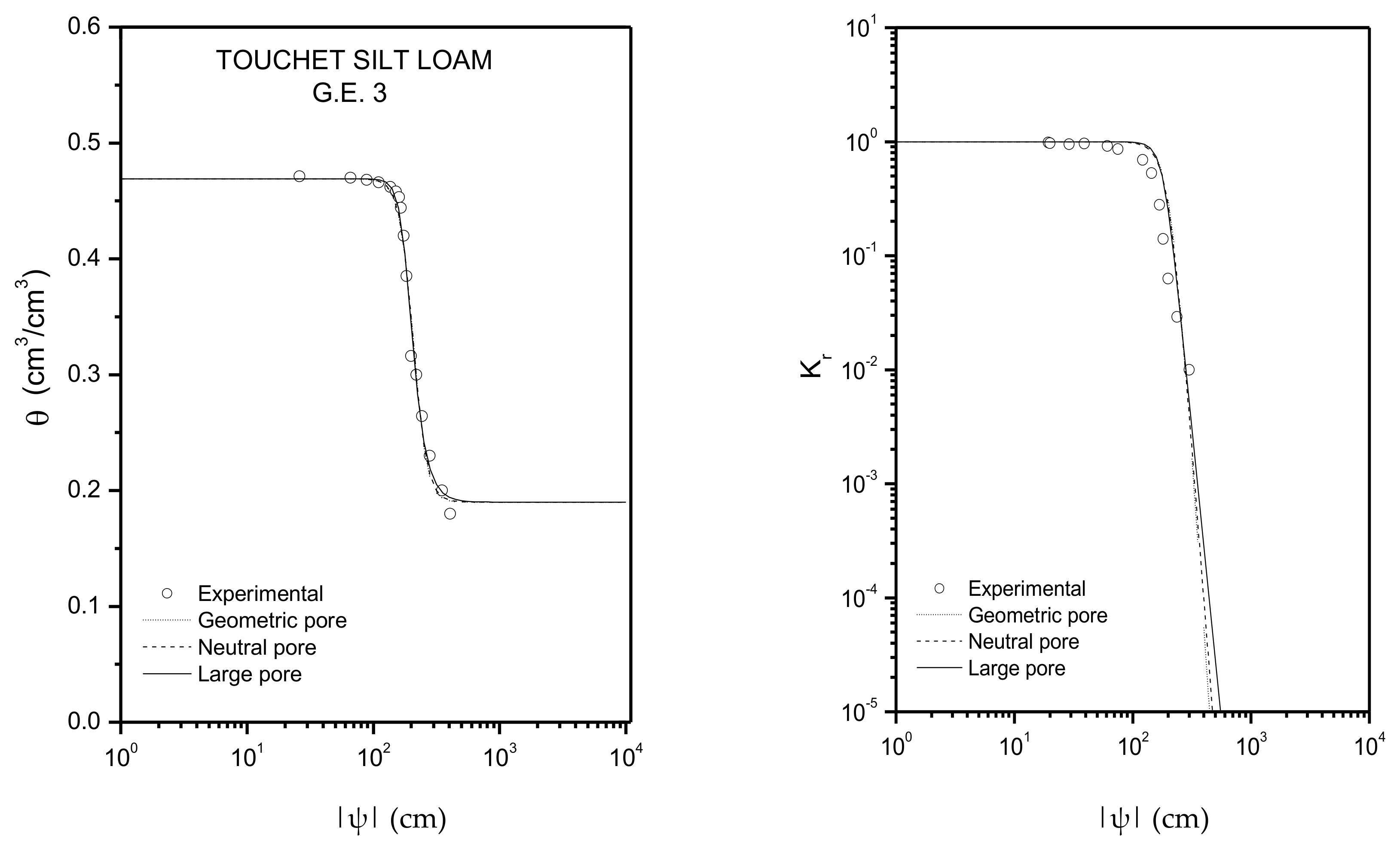
| Touchet Silt Loam G.E.3 | 0.469 | 0.190 | 303.0 | 0.688 |
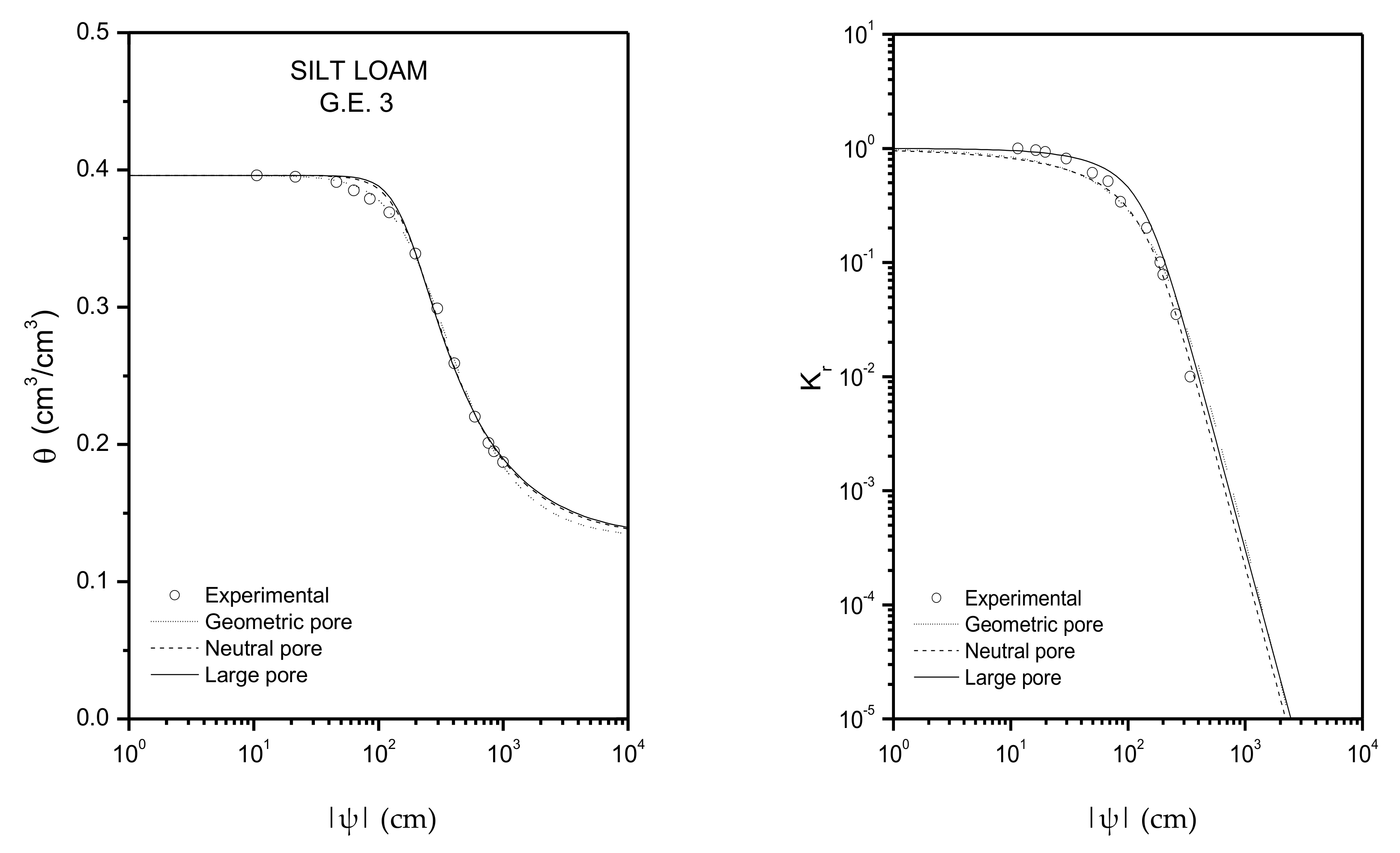
| Silt Loam G.E.3 | 0.396 | 0.131 | 4.96 | 0.673 |
| Soil Name | Geometric Pore | Neutral Pore | Large Pore | |||
|---|---|---|---|---|---|---|
| −ψd (cm) | m | −ψd (cm) | m | −ψd (cm) | m | |
| Hygiene sandstone | 146.71 | 1.3176 | 142.23 | 1.1020 | 129.61 | 0.6000 |
| Touchet Silt Loam G.E.3 | 213.94 | 1.1896 | 205.17 | 0.9554 | 185.86 | 0.5329 |
| Silt Loam G.E.3 | 253.28 | 0.5421 | 176.75 | 0.2687 | 165.63 | 0.2197 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuentes, C.; Chávez, C.; Brambila, F. Relating Hydraulic Conductivity Curve to Soil-Water Retention Curve Using a Fractal Model. Mathematics 2020, 8, 2201. https://doi.org/10.3390/math8122201
Fuentes C, Chávez C, Brambila F. Relating Hydraulic Conductivity Curve to Soil-Water Retention Curve Using a Fractal Model. Mathematics. 2020; 8(12):2201. https://doi.org/10.3390/math8122201
Chicago/Turabian StyleFuentes, Carlos, Carlos Chávez, and Fernando Brambila. 2020. "Relating Hydraulic Conductivity Curve to Soil-Water Retention Curve Using a Fractal Model" Mathematics 8, no. 12: 2201. https://doi.org/10.3390/math8122201
APA StyleFuentes, C., Chávez, C., & Brambila, F. (2020). Relating Hydraulic Conductivity Curve to Soil-Water Retention Curve Using a Fractal Model. Mathematics, 8(12), 2201. https://doi.org/10.3390/math8122201






