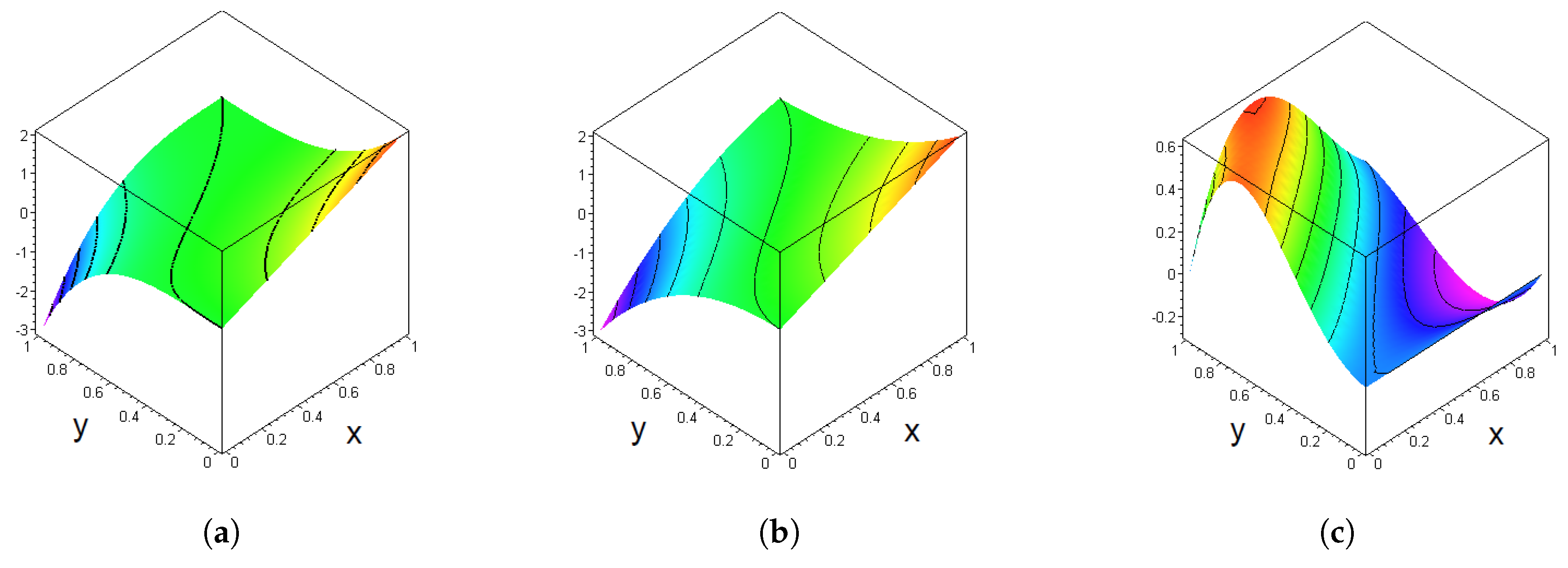
Figure 1.
Plots of the functions in Example 1. (a) Plot of f(x,y). (b) Plot of Bnf(x,y). (c) Plot of f(x,y) − Bnf(x,y).
Figure 1.
Plots of the functions in Example 1. (a) Plot of f(x,y). (b) Plot of Bnf(x,y). (c) Plot of f(x,y) − Bnf(x,y).
Figure 2.
Plots of the functions in Example 2, n1 = 3 and n2 = 5. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
Figure 2.
Plots of the functions in Example 2, n1 = 3 and n2 = 5. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
Figure 3.
Plots of the functions in Example 2, n1 = 11 and n2 = 7. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
Figure 3.
Plots of the functions in Example 2, n1 = 11 and n2 = 7. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
Figure 4.
Plots of the functions in Example 2, n1 = 50 and n2 = 50. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
Figure 4.
Plots of the functions in Example 2, n1 = 50 and n2 = 50. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
Figure 5.
Plots for the empirical Bernstein copula in Example 3. (a) Support points of scaled skeleton. (b) Empirical Bernstein copula density contour plot. (c) Simulation of 5000 empirical Bernstein copula pairs.
Figure 5.
Plots for the empirical Bernstein copula in Example 3. (a) Support points of scaled skeleton. (b) Empirical Bernstein copula density contour plot. (c) Simulation of 5000 empirical Bernstein copula pairs.
Figure 6.
Plots for the Gaussian copula in Example 3. (a) Support points of scaled skeleton. (b) Gaussian copula density contour plot. (c) Simulation of 5000 Gaussian copula pairs.
Figure 6.
Plots for the Gaussian copula in Example 3. (a) Support points of scaled skeleton. (b) Gaussian copula density contour plot. (c) Simulation of 5000 Gaussian copula pairs.
Figure 7.
Plots of the copula densities in Example 4. (a) Copula density . (b) Copula density
Figure 7.
Plots of the copula densities in Example 4. (a) Copula density . (b) Copula density
Figure 8.
Contour plots for the Bernstein copula densities in Example 3. (a) Bernstein copula density . (b) Bernstein copula density
Figure 8.
Contour plots for the Bernstein copula densities in Example 3. (a) Bernstein copula density . (b) Bernstein copula density
Figure 9.
Contour plots for the adaptive Bernstein copula densities in Example 3. (a) Adaptive Bernstein copula density . (b) Adaptive Bernstein copula density
Figure 9.
Contour plots for the adaptive Bernstein copula densities in Example 3. (a) Adaptive Bernstein copula density . (b) Adaptive Bernstein copula density
Figure 10.
Plots related to the adaptive Bernstein copulas in Example 3. (a) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 10. (b) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 10. (c) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 5. (d) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 5. (e) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 5. (f) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 5.
Figure 10.
Plots related to the adaptive Bernstein copulas in Example 3. (a) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 10. (b) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 10. (c) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 5. (d) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 5. (e) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 5. (f) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 5.
Figure 11.
Empirical histograms for the densities of the aggregated risk in Example 3. (a) Bernstein copula, grid type 34 × 34. (b) Bernstein copula, grid type 10 × 10. (c) Bernstein copula, grid type 5 × 5. (d) Bernstein copula, grid type 4 × 4. (e) Gaussian copula. (f) Independence copula. (g) Comonotonicity copula. (h) Countermonotonicity copula.
Figure 11.
Empirical histograms for the densities of the aggregated risk in Example 3. (a) Bernstein copula, grid type 34 × 34. (b) Bernstein copula, grid type 10 × 10. (c) Bernstein copula, grid type 5 × 5. (d) Bernstein copula, grid type 4 × 4. (e) Gaussian copula. (f) Independence copula. (g) Comonotonicity copula. (h) Countermonotonicity copula.
Figure 12.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 100. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 12.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 100. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 13.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 20. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 13.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 20. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 14.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 17. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 14.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 17. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 15.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 13. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 15.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 13. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 16.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 7. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Figure 16.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 7. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
Table 1.
Values of for the polynomial in Example 1.
Table 1.
Values of for the polynomial in Example 1.
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 2 | 2 |
| | | | | | |
Table 2.
Values of for the modified polynomial .
Table 2.
Values of for the modified polynomial .
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 2 | 2 |
| | | | | | |
Table 3.
Distribution of the vector in Example 2.
Table 3.
Distribution of the vector in Example 2.
| | |
|---|
| 0.3 | 0.2 |
| 0.2 | 0.3 |
Table 4.
Ranks for observed insurance data from windstorm () and flooding () losses in Example 3.
Table 4.
Ranks for observed insurance data from windstorm () and flooding () losses in Example 3.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 2 | 12 | 5 | 31 | 7 | 24 | 18 | 17 | 3 | 2 | 19 | 10 | 9 | 21 | 15 | 14 | 4 | 6 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
| 1 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
| 2 | 34 | 1 | 23 | 11 | 29 | 33 | 13 | 8 | 20 | 32 | 28 | 22 | 16 | 26 | 25 | 30 | 27 |
Table 5.
Ranks and probabilities in Example 4.
Table 5.
Ranks and probabilities in Example 4.
| 1 | 2 | |
|---|
| 1 | 1 | 3 | 0.2 |
| 2 | 2 | 4 | 0.2 |
| 3 | 3 | 1 | 0.2 |
| 4 | 4 | 2 | 0.2 |
| 5 | 5 | 5 | 0.2 |
Table 6.
Resulting pseudo-ranks and probabilities in Example 4.
Table 6.
Resulting pseudo-ranks and probabilities in Example 4.
| 1 | 2 | |
|---|
| 1 | 12 | 36 | |
| 2 | 11 | 35 | |
| 3 | 10 | 34 | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 13 | 24 | 48 | |
| 14 | 23 | 47 | |
| 15 | 22 | 46 | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 25 | 36 | 12 | |
| 26 | 35 | 11 | |
| 27 | 34 | 10 | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 58 | 51 | 51 | |
| 59 | 50 | 50 | |
| 60 | 49 | 49 | |
Table 7.
Final ranks and probabilities in Example 4.
Table 7.
Final ranks and probabilities in Example 4.
| 1 | 2 | |
|---|
| 1 | 1 | 2 | |
| 2 | 1 | 3 | |
| 3 | 2 | 1 | |
| 4 | 2 | 2 | |
| 5 | 2 | 3 | |
| 6 | 2 | 4 | |
| 7 | 3 | 2 | |
| 8 | 3 | 4 | |
Table 8.
Probabilities in the resulting optimal discrete skeleton in Example 3.
Table 8.
Probabilities in the resulting optimal discrete skeleton in Example 3.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| 9 | 0.0032 | 0.0000 | 0.0022 | 0.0000 | 0.0032 | 0.0266 | 0.0320 | 0.0274 | 0.0028 | 0.0028 |
| 8 | 0.0318 | 0.0000 | 0.0014 | 0.0000 | 0.0024 | 0.0000 | 0.0312 | 0.0000 | 0.0020 | 0.0314 |
| 7 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0204 | 0.0251 | 0.0545 |
| 6 | 0.0032 | 0.0275 | 0.0022 | 0.0000 | 0.0032 | 0.0265 | 0.0026 | 0.0000 | 0.0322 | 0.0028 |
| 5 | 0.0003 | 0.0246 | 0.0287 | 0.0215 | 0.0003 | 0.0000 | 0.0000 | 0.0246 | 0.0000 | 0.0000 |
| 4 | 0.0034 | 0.0278 | 0.0024 | 0.0246 | 0.0034 | 0.0000 | 0.0029 | 0.0000 | 0.0324 | 0.0030 |
| 3 | 0.0266 | 0.0000 | 0.0000 | 0.0000 | 0.0266 | 0.0206 | 0.0261 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 0.0034 | 0.0000 | 0.0025 | 0.0540 | 0.0034 | 0.0000 | 0.0029 | 0.0277 | 0.0031 | 0.0031 |
| 1 | 0.0252 | 0.0201 | 0.0000 | 0.0000 | 0.0546 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0 | 0.0029 | 0.0000 | 0.0607 | 0.0000 | 0.0029 | 0.0263 | 0.0023 | 0.0000 | 0.0025 | 0.0025 |
Table 9.
Probabilities after application of the adaptive strategy in Example 3.
Table 9.
Probabilities after application of the adaptive strategy in Example 3.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| 9 | 0.0118 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0294 | 0.0294 | 0.0294 | 0.0000 | 0.0000 |
| 8 | 0.0176 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0294 | 0.0000 | 0.0235 | 0.0294 |
| 7 | 0.0000 | 0.0059 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0059 | 0.0176 | 0.0706 |
| 6 | 0.0000 | 0.0235 | 0.0000 | 0.0176 | 0.0000 | 0.0294 | 0.0000 | 0.0000 | 0.0294 | 0.0000 |
| 5 | 0.0000 | 0.0294 | 0.0294 | 0.0118 | 0.0000 | 0.0000 | 0.0000 | 0.0294 | 0.0000 | 0.0000 |
| 4 | 0.0000 | 0.0235 | 0.0059 | 0.0176 | 0.0235 | 0.0000 | 0.0000 | 0.0000 | 0.0294 | 0.0000 |
| 3 | 0.0294 | 0.0000 | 0.0000 | 0.0000 | 0.0176 | 0.0059 | 0.0412 | 0.0059 | 0.0000 | 0.0000 |
| 2 | 0.0000 | 0.0059 | 0.0059 | 0.0529 | 0.0000 | 0.0059 | 0.0000 | 0.0294 | 0.0000 | 0.0000 |
| 1 | 0.0412 | 0.0118 | 0.0000 | 0.0000 | 0.0471 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0 | 0.0000 | 0.0000 | 0.0588 | 0.0000 | 0.0118 | 0.0294 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Table 10.
Estimated values of for different grid types in Example 3.
Table 10.
Estimated values of for different grid types in Example 3.
| Grid Type | | | | | Gaussian | Independence | Comonotonic | Countermonotonic |
|---|
| 1348 | 1334 | 1356 | 1369 | 1386 | 1349 | 1500 | 1327 |
Table 11.
Insurance losses in Example 5, part I.
Table 11.
Insurance losses in Example 5, part I.
| Year | Area 1 | Area 2 | Area 3 | Area 4 | Area 5 | Area 6 | Area 7 | Area 8 | Area 9 | Area 10 |
|---|
| 1 | 23.664 | 154.664 | 40.569 | 14.504 | 10.468 | 7.464 | 22.202 | 17.682 | 12.395 | 18.551 |
| 2 | 1.080 | 59.545 | 3.297 | 1.344 | 1.859 | 0.477 | 6.107 | 7.196 | 1.436 | 3.720 |
| 3 | 21.731 | 31.049 | 55.973 | 5.816 | 14.869 | 20.771 | 3.580 | 14.509 | 17.175 | 87.307 |
| 4 | 28.990 | 31.052 | 30.328 | 4.709 | 0.717 | 3.530 | 6.032 | 6.512 | 0.682 | 3.115 |
| 5 | 53.616 | 62.027 | 57.639 | 1.804 | 2.073 | 4.361 | 46.018 | 22.612 | 1.581 | 11.179 |
| 6 | 29.950 | 41.722 | 12.964 | 1.127 | 1.063 | 4.873 | 6.571 | 11.966 | 15.676 | 24.263 |
| 7 | 3.474 | 14.429 | 10.869 | 0.945 | 2.198 | 1.484 | 4.547 | 2.556 | 0.456 | 1.137 |
| 8 | 10.020 | 31.283 | 21.116 | 1.663 | 2.153 | 0.932 | 25.163 | 3.222 | 1.581 | 5.477 |
| 9 | 5.816 | 14.804 | 128.072 | 0.523 | 0.324 | 0.477 | 3.049 | 7.791 | 4.079 | 7.002 |
| 10 | 170.725 | 576.767 | 108.361 | 41.599 | 20.253 | 35.412 | 126.698 | 71.079 | 21.762 | 64.582 |
| 11 | 21.423 | 50.595 | 4.360 | 0.327 | 1.566 | 64.621 | 5.650 | 1.258 | 0.626 | 3.556 |
| 12 | 6.380 | 28.316 | 3.740 | 0.442 | 0.736 | 0.470 | 3.406 | 7.859 | 0.894 | 3.591 |
| 13 | 124.665 | 33.359 | 14.712 | 0.321 | 0.975 | 2.005 | 3.981 | 4.769 | 2.006 | 1.973 |
| 14 | 20.165 | 49.948 | 17.658 | 0.595 | 0.548 | 29.350 | 6.782 | 4.873 | 2.921 | 6.394 |
| 15 | 78.106 | 41.681 | 13.753 | 0.585 | 0.259 | 0.765 | 7.013 | 9.426 | 2.180 | 3.769 |
| 16 | 11.067 | 444.712 | 365.351 | 99.366 | 8.856 | 28.654 | 10.589 | 13.621 | 9.589 | 19.485 |
| 17 | 6.704 | 81.895 | 14.266 | 0.972 | 0.519 | 0.644 | 8.057 | 18.071 | 5.515 | 13.163 |
| 18 | 15.550 | 277.643 | 26.564 | 0.788 | 0.225 | 1.230 | 26.800 | 64.538 | 2.637 | 80.711 |
| 19 | 10.099 | 18.815 | 9.352 | 2.051 | 1.089 | 6.102 | 2.678 | 4.064 | 2.373 | 2.057 |
| 20 | 8.492 | 138.708 | 46.708 | 3.680 | 1.132 | 1.698 | 165.600 | 7.926 | 2.972 | 5.237 |
Table 12.
Insurance losses in Example 5, part II.
Table 12.
Insurance losses in Example 5, part II.
| Year | Area 11 | Area 12 | Area 13 | Area 14 | Area 15 | Area 16 | Area 17 | Area 18 | Area 19 |
|---|
| 1 | 1.842 | 4.100 | 46.135 | 14.698 | 44.441 | 7.981 | 35.833 | 10.689 | 7.299 |
| 2 | 0.429 | 1.026 | 7.469 | 7.058 | 4.512 | 0.762 | 14.474 | 9.337 | 0.740 |
| 3 | 0.209 | 2.344 | 22.651 | 4.117 | 26.586 | 3.920 | 13.804 | 2.683 | 3.026 |
| 4 | 0.521 | 0.696 | 31.126 | 1.878 | 29.423 | 6.394 | 18.064 | 1.201 | 0.894 |
| 5 | 2.715 | 1.327 | 40.156 | 4.655 | 104.691 | 28.579 | 17.832 | 1.618 | 3.402 |
| 6 | 4.832 | 0.701 | 16.712 | 11.852 | 29.234 | 7.098 | 17.866 | 5.206 | 5.664 |
| 7 | 0.268 | 0.580 | 11.851 | 2.057 | 11.605 | 0.282 | 16.925 | 2.082 | 1.008 |
| 8 | 0.741 | 0.369 | 3.814 | 1.869 | 8.126 | 1.032 | 14.985 | 1.390 | 1.703 |
| 9 | 0.524 | 6.554 | 5.459 | 3.007 | 8.528 | 1.920 | 5.638 | 2.149 | 2.908 |
| 10 | 9.882 | 6.401 | 106.197 | 44.912 | 191.809 | 90.559 | 154.492 | 36.626 | 36.276 |
| 11 | 1.052 | 8.277 | 22.564 | 8.961 | 19.817 | 16.437 | 25.990 | 2.364 | 6.434 |
| 12 | 0.136 | 0.364 | 28.000 | 7.574 | 3.213 | 1.749 | 12.735 | 1.744 | 0.558 |
| 13 | 1.990 | 15.176 | 57.235 | 23.686 | 110.035 | 17.373 | 7.276 | 2.494 | 0.525 |
| 14 | 0.630 | 0.762 | 25.897 | 3.439 | 8.161 | 3.327 | 24.733 | 2.807 | 1.618 |
| 15 | 0.770 | 15.024 | 36.068 | 1.613 | 6.127 | 8.103 | 12.596 | 4.894 | 0.822 |
| 16 | 0.287 | 0.464 | 24.211 | 38.616 | 51.889 | 1.316 | 173.080 | 3.557 | 11.627 |
| 17 | 0.590 | 2.745 | 16.124 | 2.398 | 20.997 | 2.515 | 5.161 | 2.840 | 3.002 |
| 18 | 0.245 | 0.217 | 12.416 | 4.972 | 59.417 | 3.762 | 24.603 | 7.404 | 19.107 |
| 19 | 0.415 | 0.351 | 10.707 | 2.468 | 10.673 | 1.743 | 27.266 | 1.368 | 0.644 |
| 20 | 0.566 | 0.708 | 22.646 | 6.652 | 14.437 | 63.692 | 113.231 | 7.218 | 2.548 |
Table 13.
Values of the parameters and estimated from the log data in Example 5, part I.
Table 13.
Values of the parameters and estimated from the log data in Example 5, part I.
| Parameter | Area 1 | Area 2 | Area 3 | Area 4 | Area 5 | Area 6 | Area 7 | Area 8 | Area 9 | Area 10 |
|---|
| 2.8063 | 4.0717 | 3.1407 | 0.6375 | 0.3984 | 1.2227 | 2.3210 | 2.2123 | 1.0783 | 2.1055 |
| 1.2161 | 1.0521 | 1.2110 | 1.5685 | 1.2998 | 1.5987 | 1.1980 | 0.9882 | 1.1445 | 1.2531 |
Table 14.
Values of the parameters and estimated from the log data in Example 5, part II.
Table 14.
Values of the parameters and estimated from the log data in Example 5, part II.
| Parameter | Area 11 | Area 12 | Area 13 | Area 14 | Area 15 | Area 16 | Area 17 | Area 18 | Area 19 |
|---|
| −0.3231 | 0.3815 | 3.0198 | 1.7488 | 3.0409 | 1.5501 | 3.0700 | 1.2444 | 0.9378 |
| 1.0881 | 1.3353 | 0.8027 | 1.0033 | 1.1221 | 1.4765 | 0.9622 | 0.8577 | 1.2141 |
Table 15.
Correlations between original losses in adjacent areas in Example 5.
Table 15.
Correlations between original losses in adjacent areas in Example 5.
| Area | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | A17 | A18 | A19 |
|---|
| A1 | 1 | 0.46 | 0.03 | 0.16 | 0.47 | 0.20 | 0.35 | 0.49 | 0.41 | 0.24 | 0.78 | 0.64 | 0.91 | 0.63 | 0.85 | 0.66 | 0.30 | 0.67 | 0.56 |
| A2 | 0.46 | 1 | 0.64 | 0.78 | 0.67 | 0.36 | 0.51 | 0.76 | 0.57 | 0.51 | 0.58 | −0.04 | 0.59 | 0.84 | 0.68 | 0.58 | 0.87 | 0.77 | 0.90 |
| A3 | 0.03 | 0.64 | 1 | 0.93 | 0.41 | 0.26 | 0.11 | 0.16 | 0.33 | 0.16 | 0.08 | −0.09 | 0.13 | 0.64 | 0.25 | 0.10 | 0.74 | 0.14 | 0.35 |
| A4 | 0.16 | 0.78 | 0.93 | 1 | 0.54 | 0.36 | 0.16 | 0.25 | 0.43 | 0.19 | 0.22 | −0.10 | 0.30 | 0.79 | 0.36 | 0.19 | 0.84 | 0.32 | 0.49 |
| A5 | 0.47 | 0.67 | 0.41 | 0.54 | 1 | 0.41 | 0.35 | 0.51 | 0.84 | 0.63 | 0.59 | 0.02 | 0.64 | 0.67 | 0.59 | 0.50 | 0.58 | 0.71 | 0.67 |
| A6 | 0.20 | 0.36 | 0.26 | 0.36 | 0.41 | 1 | 0.07 | 0.11 | 0.28 | 0.19 | 0.28 | 0.14 | 0.31 | 0.42 | 0.24 | 0.27 | 0.39 | 0.27 | 0.40 |
| A7 | 0.35 | 0.51 | 0.11 | 0.16 | 0.35 | 0.07 | 1 | 0.44 | 0.27 | 0.19 | 0.48 | −0.07 | 0.46 | 0.35 | 0.45 | 0.91 | 0.64 | 0.61 | 0.49 |
| A8 | 0.49 | 0.76 | 0.16 | 0.25 | 0.51 | 0.11 | 0.44 | 1 | 0.50 | 0.75 | 0.61 | −0.03 | 0.54 | 0.47 | 0.71 | 0.53 | 0.40 | 0.75 | 0.90 |
| A9 | 0.41 | 0.57 | 0.33 | 0.43 | 0.84 | 0.28 | 0.27 | 0.50 | 1 | 0.66 | 0.68 | −0.01 | 0.52 | 0.60 | 0.50 | 0.41 | 0.46 | 0.65 | 0.63 |
| A10 | 0.24 | 0.51 | 0.16 | 0.19 | 0.63 | 0.19 | 0.19 | 0.75 | 0.66 | 1 | 0.33 | −0.12 | 0.27 | 0.28 | 0.43 | 0.24 | 0.23 | 0.45 | 0.65 |
| A11 | 0.78 | 0.58 | 0.08 | 0.22 | 0.59 | 0.28 | 0.48 | 0.61 | 0.68 | 0.33 | 1 | 0.19 | 0.79 | 0.65 | 0.80 | 0.73 | 0.43 | 0.84 | 0.74 |
| A12 | 0.64 | −0.04 | −0.09 | −0.10 | 0.02 | 0.14 | −0.07 | −0.03 | −0.01 | −0.12 | 0.19 | 1 | 0.44 | 0.21 | 0.28 | 0.17 | −0.12 | 0.13 | 0.03 |
| A13 | 0.91 | 0.59 | 0.13 | 0.30 | 0.64 | 0.31 | 0.46 | 0.54 | 0.52 | 0.27 | 0.79 | 0.44 | 1 | 0.71 | 0.86 | 0.74 | 0.47 | 0.76 | 0.65 |
| A14 | 0.63 | 0.84 | 0.64 | 0.79 | 0.67 | 0.42 | 0.35 | 0.47 | 0.60 | 0.28 | 0.65 | 0.21 | 0.71 | 1 | 0.74 | 0.54 | 0.79 | 0.68 | 0.72 |
| A15 | 0.85 | 0.68 | 0.25 | 0.36 | 0.59 | 0.24 | 0.45 | 0.71 | 0.50 | 0.43 | 0.80 | 0.28 | 0.86 | 0.74 | 1 | 0.69 | 0.47 | 0.71 | 0.75 |
| A16 | 0.66 | 0.58 | 0.10 | 0.19 | 0.50 | 0.27 | 0.91 | 0.53 | 0.41 | 0.24 | 0.73 | 0.17 | 0.74 | 0.54 | 0.69 | 1 | 0.63 | 0.77 | 0.64 |
| A17 | 0.30 | 0.87 | 0.74 | 0.84 | 0.58 | 0.39 | 0.64 | 0.40 | 0.46 | 0.23 | 0.43 | −0.12 | 0.47 | 0.79 | 0.47 | 0.63 | 1 | 0.59 | 0.64 |
| A18 | 0.67 | 0.77 | 0.14 | 0.32 | 0.71 | 0.27 | 0.61 | 0.75 | 0.65 | 0.45 | 0.84 | 0.13 | 0.76 | 0.68 | 0.71 | 0.77 | 0.59 | 1 | 0.86 |
| A19 | 0.56 | 0.90 | 0.35 | 0.49 | 0.67 | 0.40 | 0.49 | 0.90 | 0.63 | 0.65 | 0.74 | 0.03 | 0.65 | 0.72 | 0.75 | 0.64 | 0.64 | 0.86 | 1 |
Table 16.
Correlations between log losses in adjacent areas in Example 5.
Table 16.
Correlations between log losses in adjacent areas in Example 5.
| Area | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | A17 | A18 | A19 |
|---|
| A1 | 1 | 0.27 | 0.30 | 0.16 | 0.17 | 0.45 | 0.28 | 0.32 | 0.32 | 0.29 | 0.67 | 0.51 | 0.76 | 0.34 | 0.67 | 0.74 | 0.18 | 0.21 | 0.29 |
| A2 | 0.27 | 1 | 0.48 | 0.66 | 0.39 | 0.37 | 0.71 | 0.69 | 0.52 | 0.64 | 0.30 | −0.02 | 0.45 | 0.66 | 0.58 | 0.45 | 0.73 | 0.74 | 0.78 |
| A3 | 0.30 | 0.48 | 1 | 0.70 | 0.40 | 0.31 | 0.42 | 0.51 | 0.58 | 0.53 | 0.18 | 0.07 | 0.21 | 0.32 | 0.54 | 0.26 | 0.47 | 0.21 | 0.57 |
| A4 | 0.16 | 0.66 | 0.70 | 1 | 0.77 | 0.47 | 0.46 | 0.47 | 0.59 | 0.49 | 0.18 | −0.13 | 0.33 | 0.50 | 0.47 | 0.18 | 0.76 | 0.43 | 0.54 |
| A5 | 0.17 | 0.39 | 0.40 | 0.77 | 1 | 0.59 | 0.30 | 0.20 | 0.49 | 0.39 | 0.28 | 0.08 | 0.35 | 0.56 | 0.44 | 0.16 | 0.55 | 0.36 | 0.41 |
| A6 | 0.45 | 0.37 | 0.31 | 0.47 | 0.59 | 1 | 0.14 | 0.01 | 0.36 | 0.34 | 0.33 | 0.12 | 0.48 | 0.46 | 0.48 | 0.37 | 0.59 | 0.17 | 0.50 |
| A7 | 0.28 | 0.71 | 0.42 | 0.46 | 0.30 | 0.14 | 1 | 0.52 | 0.27 | 0.40 | 0.45 | −0.07 | 0.31 | 0.31 | 0.46 | 0.62 | 0.63 | 0.58 | 0.57 |
| A8 | 0.32 | 0.69 | 0.51 | 0.47 | 0.20 | 0.01 | 0.52 | 1 | 0.64 | 0.81 | 0.27 | −0.02 | 0.38 | 0.35 | 0.56 | 0.35 | 0.28 | 0.62 | 0.63 |
| A9 | 0.32 | 0.52 | 0.58 | 0.59 | 0.49 | 0.36 | 0.27 | 0.64 | 1 | 0.78 | 0.40 | 0.19 | 0.27 | 0.50 | 0.44 | 0.30 | 0.33 | 0.57 | 0.61 |
| A10 | 0.29 | 0.64 | 0.53 | 0.49 | 0.39 | 0.34 | 0.40 | 0.81 | 0.78 | 1 | 0.21 | −0.02 | 0.21 | 0.37 | 0.52 | 0.30 | 0.31 | 0.53 | 0.81 |
| A11 | 0.67 | 0.30 | 0.18 | 0.18 | 0.28 | 0.33 | 0.45 | 0.27 | 0.40 | 0.21 | 1 | 0.47 | 0.49 | 0.45 | 0.60 | 0.67 | 0.20 | 0.45 | 0.39 |
| A12 | 0.51 | −0.02 | 0.07 | −0.13 | 0.08 | 0.12 | −0.07 | −0.02 | 0.19 | −0.02 | 0.47 | 1 | 0.44 | 0.21 | 0.24 | 0.46 | −0.23 | 0.25 | 0.05 |
| A13 | 0.76 | 0.45 | 0.21 | 0.33 | 0.35 | 0.48 | 0.31 | 0.38 | 0.27 | 0.21 | 0.49 | 0.44 | 1 | 0.55 | 0.60 | 0.71 | 0.37 | 0.39 | 0.24 |
| A14 | 0.34 | 0.66 | 0.32 | 0.50 | 0.56 | 0.46 | 0.31 | 0.35 | 0.50 | 0.37 | 0.45 | 0.21 | 0.55 | 1 | 0.59 | 0.43 | 0.57 | 0.58 | 0.53 |
| A15 | 0.67 | 0.58 | 0.54 | 0.47 | 0.44 | 0.48 | 0.46 | 0.56 | 0.44 | 0.52 | 0.60 | 0.24 | 0.60 | 0.59 | 1 | 0.59 | 0.36 | 0.35 | 0.63 |
| A16 | 0.74 | 0.45 | 0.26 | 0.18 | 0.16 | 0.37 | 0.62 | 0.35 | 0.30 | 0.30 | 0.67 | 0.46 | 0.71 | 0.43 | 0.59 | 1 | 0.38 | 0.43 | 0.39 |
| A17 | 0.18 | 0.73 | 0.47 | 0.76 | 0.55 | 0.59 | 0.63 | 0.28 | 0.33 | 0.31 | 0.20 | −0.23 | 0.37 | 0.57 | 0.36 | 0.38 | 1 | 0.52 | 0.56 |
| A18 | 0.21 | 0.74 | 0.21 | 0.43 | 0.36 | 0.17 | 0.58 | 0.62 | 0.57 | 0.53 | 0.45 | 0.25 | 0.39 | 0.58 | 0.35 | 0.43 | 0.52 | 1 | 0.60 |
| A19 | 0.29 | 0.78 | 0.57 | 0.54 | 0.41 | 0.50 | 0.57 | 0.63 | 0.61 | 0.81 | 0.39 | 0.05 | 0.24 | 0.53 | 0.63 | 0.39 | 0.56 | 0.60 | 1 |
Table 17.
-estimates for different values of m in Example 5.
Table 17.
-estimates for different values of m in Example 5.
| m | 100 | 20 | 17 | 13 | 7 |
|---|
| 2842 | 2247 | 2204 | 2105 | 1878 |