Fuzzy Simheuristics: Solving Optimization Problems under Stochastic and Uncertainty Scenarios

Abstract

Simheuristics combine metaheuristics with simulation in order to solve the optimization problems with stochastic elements. This paper introduces the concept of fuzzy simheuristics, which extends the simheuristics approach by making use of fuzzy techniques, thus allowing us to tackle optimization problems under a more general scenario, which includes uncertainty elements of both stochastic and non-stochastic nature. After reviewing the related work, the paper discusses, in detail, how the optimization, simulation, and fuzzy components can be efficiently integrated. In order to illustrate the potential of fuzzy simheuristics, we consider the team orienteering problem (TOP) under an uncertainty scenario, and perform a series of computational experiments. The obtained results show that our proposed approach is not only able to generate competitive solutions for the deterministic version of the TOP, but, more importantly, it can effectively solve more realistic TOP versions, including stochastic and other uncertainty elements.

1. Introduction

Optimization models play an essential role in many business and industrial sectors, including: logistics and transportation, manufacturing and production, telecommunication and computer networks, finance and insurance, energy, smart cities, bioinformatics, etc. With the goal of finding an optimal solution to a well-defined objective function, one can use mathematical models, combined with either exact or approximate methods (e.g., heuristics). Many real-life optimization problems contain a large number of variables and/or constraints, while, at the same time, they are NP-hard [1]. Hence, the use of heuristic-based approaches is usually a good choice to find near-optimal solutions that satisfy all the problem requirements [2]. By adding random variables, mathematical models allow for us to consider stochastic conditions, which are quite frequent in real-life applications. Thus, for instance, travel times, processing times, customers’ demands, and asset returns in a portfolio are better modeled as random variables than as constant values. Whenever these random variables are considered (either in the objective function or in the constraints), the problem becomes stochastic in nature, and the process of solving it might require the use of advanced mathematical/computational tools, such as stochastic programming or simulation. Precisely, simheuristic algorithms [3], which combine heuristics with simulation techniques, constitute a powerful tool for tackling real-life optimization problems under stochastic conditions. However, as described in Chica et al. [4], simheuristics are specifically designed to deal with scenarios, in which the non-deterministic behavior can be modeled as a set of random variables following certain probability distributions (stochastic uncertainty). When dealing with other types of uncertainty scenarios, fuzzy systems can become an excellent option. The fuzzy logic is the base of a fuzzy system. These systems take the inputs and transform them into fuzzy outputs, which are computed according to some ad hoc rules that are created by a human expert [5]. Fuzzy systems allow for generating outputs that consider different degrees of membership for different groups. In this way, these fuzzy techniques allows us to have solutions that combine information from different sources. Hence, fuzzy systems can handle decisions that are based on a non-binary logic, where the outputs consider a certain degree of ‘true’ and certain degree of ‘false’.

One of the main contributions of this paper is the analysis of how simheuristics can be extended by employing fuzzy systems. As discussed in this paper, these ‘fuzzy simheuristics’ become a powerful tool when solving complex and large-scale optimization problems under different degrees of uncertainty (of both stochastic and fuzzy nature). In other words, by extending simheuristics with fuzzy logic, the new methodology can benefit from both historical data to model random variables as well as from experts’ opinions in order to model non-stochastic uncertainty. Figure 1 illustrates, in a web chart, the typical advantages and pitfalls of different solving approaches in each of the following dimensions: ’optimality’, ’stochasticity’, ’uncertainty’, and ’large scale’. In this figure, a value of 0 represents a low performance in the associated dimension, while a value of 2 represents a high performance.

Hence, for instance, exact methods can provide optimal solutions in many optimization problems; however, they are not the best alternative when dealing with large-scale NP-hard problems and with problems under uncertainty scenarios. Similarly, heuristics can efficiently solve large-scale instances, but they do not guarantee optimality and, moreover, they are not well-designed to tackle uncertainty scenarios. Simulation allows for us to consider stochastic scenarios in a natural way, but it typically does not provide optimal or near-optimal solutions, and it can only consider stochastic uncertainty. Fuzzy techniques are well-designed to deal with non-stochastic uncertainty, but they are limited when considering stochastic uncertainty and they do not guarantee optimality either. Finally, simheuristics provide some of the combined benefits of simulation and heuristics, but they still have severe limitations when dealing with uncertainty of non-stochastic nature. Notice that none of the methodologies achieves a ‘perfect’ performance in all of the considered dimensions. Still, as it will be discussed in this paper, the proposed fuzzy simheuristics methodology has the potential to reach the maximum score in at least three out of the four dimensions (stochasticity, uncertainty, and large scale), while keeping a reasonably good score in the remaining one (optimality). In addition to the introduction of the new fuzzy simheuristic methodology, a second contribution of our paper is the solving of a rich and realistic version of the team orienteering problem (TOP) [6]. In the classical (deterministic) version of the TOP, a fixed fleet of vehicles has to visit a number of candidate nodes while going from an origin depot to a destination depot. Visiting each node for the first time raises a reward, and the goal is to maximize the total accumulated reward without exceeding the maximum distance/time allowed per vehicle route. While both deterministic and stochastic versions of the TOP have been analyzed in the existing literature [7], our work is the first one that considers the TOP with dual stochastic and fuzzy rewards.

The remaining sections of this paper are distributed, as follows. In Section 2, basic concepts on fuzzy systems are reported, while Section 3 provides an overview of simheuristics. Section 4 includes a literature review on hybrid approaches combining heuristics with simulation and fuzzy techniques. In Section 5, we describe the principles of fuzzy simheuristics. In order to illustrate the previous concepts, Section 6 introduces the TOP with dual stochastic and fuzzy rewards, and a series of numerical experiments are carried out in Section 7. Section 8 discuses the challenges and open research lines. Finally, Section 9 highlights the main contributions and results of this work.

2. Overview of Fuzzy Concepts

Fuzzy logic emerges as an extension of the classical set logic to model uncertainty in sets. Fuzzy logic allows for us to quantify and understand data with uncertainty. In a practical sense, fuzzy logic cannot state with total certainty whether something is true or false. Instead, fuzzy logic assigns a degree of membership to the linguistic concept of true or false. From this idea, it is possible to design fuzzy inference systems (FIS) in order to transform input values to an output space, where the internal mapping only uses linguistic rules. FIS allows for representing the knowledge of an expert in a simple yet powerful manner. In general, fuzzy inference systems share a five-element structure, as depicted in Figure 2.

In the context of this article, the FIS will estimate the rewards that were collected by the vehicle from those nodes with an uncertain behavior that cannot be modeled while using probability distributions. Next, the five-element structure is described in more detail:

• Fuzzification: the first element in a FIS is fuzzification, which transforms the inputs that are expressed in crisp values into their corresponding fuzzified variable [5]. A fuzzified variable is associated with a linguistic concept that usually describes labels [8]. In the case of the considered TOP, for instance, historical reward data that are related to similar nodes might be used as an input criterion to assign labels to each node. The input values (crisp) will then be transformed into a fuzzy value while using the associated membership functions.
• Membership functions: the second element is a database containing membership or belonging functions, which defines a fuzzy set that is associated with a linguistic label [9,10]. The membership function must be standardized, convex, and distinct (i.e., it has a limited overlap with other functions) [5]. Following the TOP example, the reward input variables might have three membership functions: low, medium, and high.
• Inference rules: the third element is composed of the inference rules. The rules are usually designed by experts in the field while using ‘if … then’ expressions [11]. In this context, simple rules, such as the following, can be employed: “if a given percentage of similar nodes have offered a low reward in the last n visits, then the reward of this node is likely to be low”.
• Decision unit: the fourth element is the decision unit, which is dedicated to performing the inference operations on the rules in order to obtain a fuzzy result [12]. Operators, such as union, intersection, and complement are commonly used to combine fuzzy sets through a t-norm operator, which multiplies or determines the minimum in the input fuzzy set in order to generate a fuzzy output set [13]. In the TOP context, all of the input variables in the form of membership functions are combined to produce an output distribution following the inference rules and a union operation.
• Defuzzification: the fifth and last element is defuzzification, which transforms the fuzzy results into a crisp equivalent. In general terms, the resulting distribution of the decision unit is reduced to a numeric value. It is possible to use operators such as the weighted mean, the center of gravity method, the mean of maximums, etc. The last two are used to provide good results in many applications [14]. In this article, the defuzzification step is conducted after the inference step by considering each membership function’s contribution with the union operation on a Mamdani-type system. Subsequently, the fuzzy representation of the problem is transformed into a crisp value while using the center-of-gravity method.

Fuzzy approaches have been extensively used in different fields. In particular, many practical applications of fuzzy systems appear in the context of logistics, transportation, and supply networks, including production management, quality, and cost-benefit analysis. In the aforementioned networks, it is common to suffer from incomplete information, imprecise references, or unreliable data, which incentives the use of fuzzy logic in many practical applications. Finally, the common methods that are used to solve the drawbacks in decision making are handled while using the structured approach of scoring methods [15]. However, such techniques are not effective in supplier evaluation decisions [16]. In this sense, the fuzzy inference systems might constitute an effective approach.

3. Overview of Simheuristics

Modeling and simulation techniques allow for us to study the behavior, performance, and reliability of complex systems with random elements [17]. Despite simulation being an excellent tool for analyzing systems under stochastic uncertainty conditions, it is not an optimization methodology. Hence, in order to efficiently solve stochastic optimization problems, the simulation must be hybridized with optimization methods [18]. Many articles have been devoted to analyzing different ways of building simulation-optimization approaches. Among these, recent reviews on simulation-optimization can be found in Figueira and Almada-Lobo [18], Amaran et al. [19], and de Sousa Junior et al. [20].

The simheuristics concept, which can be seen as one particular case of simulation-optimization, is based on the combination of simulation with metaheuristics. To the best of our knowledge, Glover et al. were the first authors proposing such a combination for dealing with stochastic optimization problems [21]. Hence, a typical simheuristic algorithm integrates a simulation component into a metaheuristic framework, so that the latter drives the searching process in the solution space, while the former is employed in order to manage the random elements of the stochastic optimization problem [22]. Simheuristics are specially designed to tackle optimization problems that, in its mathematical formulation, contain random components in the objective function and/or probabilistic constraints (i.e., constraints that need to be satisfied with a certain probability). Equally important, because they are based on simulation, simheuristics can not only provide estimates of one single statistic (e.g., the expected cost in a cost-minimization problem), but many other dispersion measures (e.g., variance, quartiles, etc.), which allow for us to consider the risk or reliability aspects of a proposed solution. Some recent articles using this methodology are shortly introduced next in order to illustrate the potential applications of simheuristics in many different fields.

In the area of logistics and transportation, different authors have used simheuristics in order to solve stochastic and rich versions of the vehicle routing problem [23,24,25], the arc routing problem [26], the team orienteering problem [27], the facility location problem [28], the inventory routing problem [29,30,31], the waste collection problem [32,33], and the location routing problem [34]. Thus, for instance, Latorre-Biel et al. [35] study a vehicle routing problem with stochastic and correlated demands by extending the simheuristic algorithm with a Petri net component that allows for predicting correlations among customers’ demands. Likewise, Gruler et al. [36] provide a case study, in which the goal is to optimize a waste collection problem with random travel times that also depend upon the period of the day that we are considering. In the area of manufacturing and production, simheuristics have been used to solve flow shop scheduling problems [37]. A nice example is the paper by Villarinho et al. [38], where a rich flow shop scheduling problem, including delivery dates and cumulative payoffs, is modeled and solved when considering random processing times. In the area of computational finance, simheuristics have been employed in order to optimize a project portfolio selection problem with stochastic elements [39]. Finally, in the area of Internet computing, simheuristics have been utilized to analyze the reliability of services that were deployed over distributed networks of computers [40].

This review shows that simheuristics have successfully been applied to solve different stochastic optimization problems in a wide range of application areas. Still, in order to deal with non-stochastic uncertainty, simheuristics need to be combined with fuzzy techniques, as discussed in this paper.

4. Literature Review on Hybrid Heur-Sim-Fuzzy Approaches

In most academic papers, combinatorial optimization problems are modeled while assuming deterministic conditions. This allows for reducing the difficulty of the optimization problems and also working on methodologies that are capable of generating optimal or near-optimal solution under deterministic scenarios. Unfortunately, many real-life problems contain different levels of uncertainty, i.e.,: stochastic and non-stochastic or fuzzy uncertainty. Dealing with uncertainty typically introduces additional challenges during the solving process. Still, the solutions that are found might be more realistic and directly applicable to the original problem. It is not common to find papers hybridizing heuristics and simulation in order to solve optimization problems with inputs of three different nature: deterministic, stochastic, and fuzzy [41]. It is easier to find approaches that deal with just deterministic and stochastic inputs or just deterministic and fuzzy inputs [42]. In the control engineering literature, it is possible to find works that present fuzzy-heuristic-based methodologies [43,44]. Nevertheless, these papers rarely consider combinatorial optimization problems, as the one discussed in our work.

In the areas of simulation and optimization, we find similar approaches to different problems: multiple versions of the location routing problem (LRP) are faced by means of hybrid heuristics and simulation. For instance, Ghaffari-Nasab et al. [45] solve the LRP with fuzzy demands, designing a hybrid approach combining simulated annealing (SA) with stochastic simulation. In Nadizadeh and Nasab [46], the authors combine stochastic simulation with heuristics in order to solve the dynamic LRP with fuzzy demands. Another approach to a similar problem is that proposed in Zhang et al. [47]. In this case, the authors solve a multi-depot LRP with uncertainty elements by combining a simulation with a genetic algorithm (GA).

Another commonly studied problem with a number of variants is the vehicle routing problem (VRP). Expósito et al. [48] defines a fuzzy GRASP metaheuristic in order to solve an optimization problem in which a tourist has to maximize the total added value that is gathered by visiting different points of interest (POI). The proposed fuzzy GRASP differs from the standard GRASP, since it considers the set of promising POIs with fuzzy scores to be included in the solution. In Yan et al. [49], a fuzzy evolutionary algorithm (EA) is used in order to tackle a two-echelon VRP. With the goal of minimizing total cost, these authors combine a fuzzy assignment method with an iterative evolutionary learning process. Additionally, a graph-based fuzzy operator is employed in order to filter out non-promising solutions. Another work on routing optimization is that of Zhang et al. [50], who propose an adaptive large neighborhood search (LNS) algorithm, enhanced with a fuzzy simulation, in order to solve the fuzzy electric VRP with time windows and recharging stations. The authors use fuzzy variables to model different uncertain elements, such as: service/travel times and energy consumption of the batteries. In addition, they also consider the possibility of completing partial recharges. Another work, as presented in Brito et al. [51], introduces a new hybrid metaheuristic, which combines ant colony optimization (ACO), GRASP, and variable neighborhood search with fuzzy sets in order to solve the VRP with time windows (VRPTW). These authors consider soft time windows and, hence, they are modeled as fuzzy constraints.

The flow shop scheduling problem (FSP) has also received attention by the fuzzy-optimization community. The study presented in Ladj et al. [52] focuses on the permutation FSP under availability constraints with makespan and maintenance cost optimization criteria. According to the authors, values, such as the remaining useful life or the degradation level, are difficult to predict. Hence, fuzzy logic is employed to model this variables. In order to solve this problem, they propose a hybrid heuristic method that combines a variable neighborhood search algorithm with fuzzy logic. In a similar work, Ladj et al. [53] propose a differnt approach: a GA to solve the FSP under availability constraints with makespan criterion. Due to the several sources of uncertainty in the prognosis process of maintenance interventions scheduled, they model the prognostics and health management of machines while using fuzzy logic. A flow shop scheduling problem, with fuzzy processing times, is studied by Shao et al. [54]. In this paper, several factories are considered, with each factory being modeled as a flow shop without buffers between machines. With the goal of minimizing the (fuzzy) makespan among factories, the authors propose two fuzzy-based heuristics. Similarly, He et al. [55] propose a discrete multi-objective fireworks algorithm, which is based on fuzzy logic, in order to solve the multi-objective FSP. The defined objective is to minimize, simultaneously, the total cost, makespan, mean flow-time, and mean idle time of machines.

The portfolio optimization problem (POP) is yet another family of optimization problems where fuzzy variables are usually found. Ferreira et al. [56] present a hybrid integrated framework for solving the POP in private banking. These authors consider investors’ preferences as well as legal aspects, which are modeled as fuzzy variables. Chen and Xu [57] present a hybrid metaheuristic method that combines features of the bat algorithm and differential evolution for solving the POP with fuzzy returns. Their approach aims at simultaneously optimizing different dimensions, i.e.,: the portfolio’s risk, return, and diversification. They also consider other realistic features, such as cardinality constraints, transaction costs, etc. Another approach to the aforementioned problem can be found in Saborido et al. [58], where a risk model is proposed. These authors consider the investor’s requirements, as well as other desirable characteristics of the portfolio. Hence, while assuming the cardinality constraints and others, they try to optimize the portofolio’s expected return, downside risk, and skewness. In order to solve this problem, the authors propose an evolutionary multi-objective optimization algorithm, which is combined with fuzzy logic to model the uncertain future return on given portfolios. Finally, Dutta et al. [59] propose a fuzzy GA to solve the POP. For that, they use a fuzzy price scenario that is based on a ratio factor. The factor that is associated with each stock is a fuzzy variable, where the value is estimated from historical data. Once estimated, this factor allows for forecasting future stock prices and returns.

Table 1. A summary of different works combining heuristics, simulation, and fuzzy-related techniques.

Article Ref.	Problem Type	Fuzzy Elements	Solving Methodology
[43]	LRP	Demands	SA + stochastic simulation
[44]	Dynamic capacitated LRP	Demands	Local search + stochastic simulation
[45]	Uncertain multidepot LRP	Travel time, emergency relief costs, CO2 emissions	GA + stochastic simulation
[46]	VRP—Tourist trip design problem with clustered POI	POIs	Fuzzy GRASP
[47]	Two-echelon VRP	Assignment schema	Fuzzy EA
[48]	Fuzzy electric VRPTW with recharging stations	Service time, battery energy consumption, and travel time	Adaptive LNS + fuzzy simulation
[49]	VRPTW	Soft time windows	ACO + GRASP + VNS with fuzzy sets
[50]	Permutation FSP	Useful life and degradation values	VNS + Fuzzy logic
[51]	FSP	Prognostics and machines’ health management	GA
[52]	Distributed FSP	Processing time	Fuzzy heuristics
[53]	Multi-objective FSP	Makespan	Fireworks algorithm
[54]	POP	Legal aspects, investor’s preferences	Fuzzy multiatribute
[55]	POP	Returns	Bat algorithm + differential evolution
[56]	POP	Returns	Evolutionary multi-objective optimization algorithm + Fuzzy logic
[57]	POP	Stocks’ ratio factors	Fuzzy GA

summarizes how some of the aforementioned authors have been working in optimization problems when considering different uncertainty sources. The methodologies in these papers make use of different strategies, but they always combine heuristics, simulation, and fuzzy-related modeling techniques.

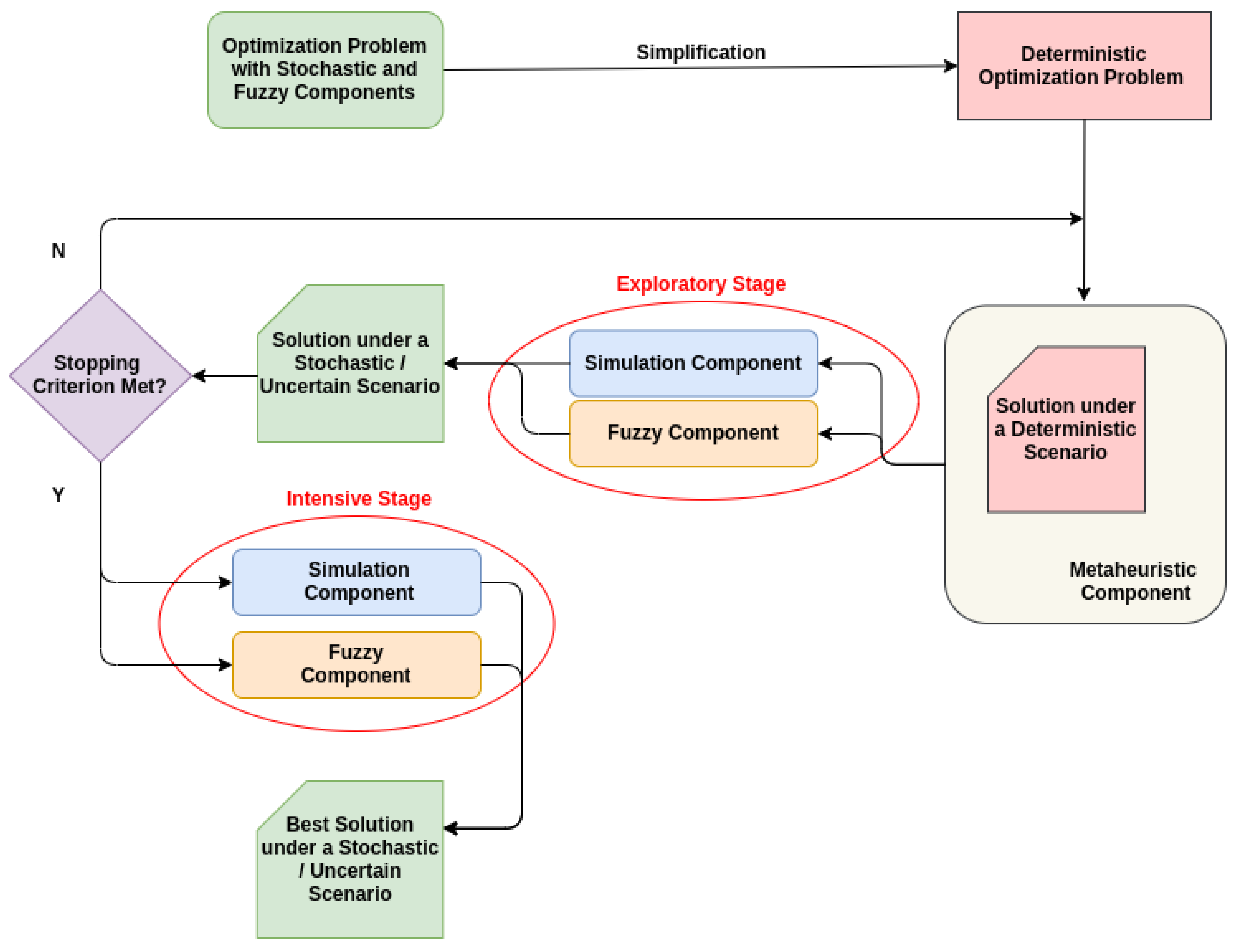
5. Extending the Simheuristic Framework with Fuzzy Techniques

We propose extending the simheuristic framework [4] by including a fuzzy component in order to deal with combinatorial optimization problems with uncertainty components of both stochastic and non-stochastic nature, as described in Figure 3.

Thus, given an optimization problem with both stochastic and uncertainty elements, the methodology combines a heuristic-based component, a simulation component, and a fuzzy component, as follows:

• Stochastic and other uncertainty elements (random variables, uncertain inputs, etc.) are substituted by their expected or most likely values, which provides a deterministic version of the original optimization problem.
• Until a stopping criterion is met (e.g., a maximum time allowed to do computations), a metaheuristic framework is employed in order to iteratively generate feasible solutions of ’good’ quality to the deterministic version of the problem.
• Whenever a solution that is generated by the optimization component is considered as a ’promising’ one—in terms of the deterministic objective function—, it is processed by the simulation and the fuzzy components, i.e.,: (i) for a relative low number of runs, each a new value is assigned to each random or fuzzy element based on its probability distribution or fuzzy function, respectively; (ii) the objective function and the constraints are evaluated under the randomly/fuzzy generated values; and, (ii) summary statistics (mean, variance, quantiles, percentiles, etc.) and risk/reliability values (whenever probabilistic constraints are considered) are obtained for the promising solution being considered.
• The summary statistics and risk/reliability values gathered are employed in order to guide the heuristic search during the next iteration. This can be achieved, for instance, by updating the ’base’ or reference solution in a single-solution metaheuristic algorithm, such as an iterated local search [60], or by updating the current population of parents in a multi-population metaheuristic, such as a genetic algorithm.
• Once the stopping criterion is met, a small subset of ’elite’ solutions is collected. A final and more intensive simulation is executed for each elite solution in order to obtain more accurate estimates of summary statistics and risk/reliability values. As before, in this simulation, both probability distributions and fuzzy functions are employed, depending on whether the element has a stochastic or fuzzy nature.
• Finally, the ’best’ solution (or pull of best alternative solutions) is returned, while taking into account that the decision maker might be not only interested in the average value that is associated with a solution, but also in its variance and reliability level.

6. The Team Orienteering Problem with Stochastic and Fuzzy Rewards

We have selected a rich and realistic variant of the TOP in order to illustrate the use of fuzzy simheuristics for solving combinatorial optimization problems with different levels of uncertainty [6]. As can be seen in Figure 4, a number of candidate nodes can be visited using a given fleet of vehicles. The first time a node is visited, a reward is collected. Because each vehicle has a maximum driving range and the number of vehicles is limited, not all of the nodes can typically be visited. Thus, the goal is to find the routes (one per vehicle) that maximize the collected reward without exceeding the driving range threshold in any route.

Using a more formal description, we consider a limited number of vehicles, m, and a maximum time, $t_0$, in which each route has to be completed. A graph $G=(N,A)$ describes the candidate nodes, with $N=\{0,1,\dots ,n+1\}$ being the set of nodes—which includes n customer nodes, an origin, 0, and a destination $n+1$—and  $A=\left\{\right(i,j)/i,j\in N,i<j\}$ being the set of edges connecting these nodes. A traverse time, $t_{ij}$, is given for each edge. Additionally, a first-visit reward, $u_i\ge 0$, is associated with each customer node. In this paper, we consider a more realistic scenario in which the reward $u_i$ at any customer node $i\in N$ can be given by a deterministic value, a random variable following a probability distribution, or a fuzzy function. A set M, including m open routes will be a solution to the TOP. Here, each route can be represented by a vector of sorted nodes from the origin to the destination. In this stochastic-fuzzy version of the TOP, one natural goal will be to maximize the total expected reward, i.e.,

$$max\sum _{m\in M}E\left[U_m\right],$$

(1)

where $U_m$ represents the total reward that is associated with route $m\in M$. Regarding the constraints, the first one is that each node is visited at most once by any route:

$$\sum _{m\in M}\sum _{i\in N}{x}_{ijm}\le 1,\forall j\in N\backslash \left\{0,n+1\right\}$$

(2)

The next equation limits the maximum time that is required to complete a tour:

$$\sum _{(i,j)\in A}{x}_{ijm}·t_{ij}\le t_0,\forall m\in M$$

(3)

Node 0 is always the starting node of any route, while node $n+1$ is always the ending node:

$$\sum _{j\in N}{x}_{0jm}=1,\forall m\in M$$

(4)

$$\sum _{i\in N}{x}_{i(n+1)m}=1,\forall m\in M$$

(5)

Lastly, except in the case of the origin and destination nodes, every vehicle will always leave any node it visits:

$$\sum _{i\in N}{x}_{ihm}-\sum _{j\in N}{x}_{hjm}=0,\forall h\in N\backslash \{0,n+1\},\forall m\in M$$

(6)

Although the deterministic version of the TOP has been widely studied in the literature, the high degree of uncertainty in real-life applications of the TOP make it a good candidate for our purpose. In this work, both stochastic and fuzzy rewards are introduced in the TOP. Hence, we will consider that the reward of some nodes can be modeled as random variables following a theoretical probability distribution. Likewise, we will consider that other nodes have an uncertain demand that has to be modeled while using fuzzy functions. As far as we know, no other authors have addressed this realistic version of the TOP in the past.

7. Computational Experiments

Because there are not benchmark instances in the literature for the stochastic-and-fuzzy TOP described above, we have extended the ones that were proposed for the deterministic TOP by Chao et al. [6]. In order to extend this deterministic benchmark, which is available from https://www.mech.kuleuven.be/en/cib/op/instances, we have substituted some deterministic-reward nodes by others with stochastic or fuzzy rewards. In particular, we will assume that half of the nodes show uncertain or stochastic rewards, whilst the remaining nodes maintain their original deterministic reward. The deterministic benchmark contains a total of 320 instances that are distributed in seven subsets. From each subset, we have randomly selected 10 instances. Given an instance “p$a.b.c$”, a represents the subset, b defines the number of available vehicles, and c helps to identify the specific instance being considered.

With the aim of generating the fuzzy inference system, we have considered the case of electric vehicles and used their battery levels as well as the weather conditions at each node as input variables. The output of the system consists in a single variable, which represents the reward collected from the node. The range of possible values that can handle the battery and reward variables depends upon the specific instance, and they are set between 0 and the maximum driving-range value that is given in the deterministic instance. Similarly, the weather input variable is set between 0 and 100 for all instances. The input variables and the output variables are both characterized by three fuzzy-sets: low, medium, and high (Figure 5).

Finally, we have established a total of nine fuzzy rules, which describe the knowledge that is necessary to compute the collected reward. These rules can be visualized in Figure 6, where each cell in the grid defines a rule. In order to transform the collected reward from a fuzzy representation to a crisp value, the contribution of each membership function is combined on the inference while using a union operator to determine the output distribution. Subsequently, the center-of-gravity method is applied in order to obtain a crisp output value that corresponds to the reward.

Concerning to the parameters of the fuzzy-simheuristic approach, we have executed the exploratory phase during 100 seconds. In this phase, we have set the number of Monte-Carlo simulation (MCS) runs to 100, and we have restricted the number of solutions in the ‘elite’ set to 3. These elite solutions have been further analyzed in a second stage, where a larger number of MCS runs, 2000 has been used in order to obtain more accurate estimations. After this process, the solution with the highest expected reward has been chosen. In regard to technical specifications, the fuzzy-simheuristic algorithm has been implemented while using Python $3.7$. It has been run using a standard PC with an Intel $i7$ CPU at $2.20$ GHz and 16 GB RAM. With the aim of verifying the viability of the proposed approach and evaluating its behavior, we carried out an experimental study, where four different uncertainty scenarios were considered:

• Deterministic scenario: here, all of the information is available. Thus, we have perfect information regarding the collected reward at each node. This scenario corresponds to the classical TOP version without uncertainty. For solving this deterministic scenario, we have employed the heuristic algorithm proposed by Panadero et al. [27]. Algorithm 1 depicts its main components. Firstly, an initial dummy solution is computed. This dummy solution contains one route per node, i.e.,: for each customer node, a vehicle departs from the origin depot, visits the node, and then goes to the destination depot. Notice that all of these single-customer routes should satisfy the driving-range constraint—otherwise, the problem is trivially unfeasible. Subsequently, the benefits that are associated with each edge connecting two different nodes are generated, i.e., the savings in driving time (or distance), as well as the reward increase in reward collected in that route. Notice that each edge has two different savings, one per direction or arc. Next, the arcs that are associated with each edge are sorted in a list in descending order—from the highest saving to the lowest saving. This sorted list of arcs is traversed in a descending order, trying to merge the two routes that are connected by the corresponding arc–i.e., routes linked by high-savings arcs are merged as far as the resulting route does not exceed the driving-range constraint. This merging process is iterated until all of the savings are considered. Finally, the m routes (one per vehicle) that are providing the highest reward constitute the solution proposed by the heuristic. Additional details regarding how to improve this solution by employing biased-randomization techniques are described in the aforementioned reference.
• Stochastic scenario: here, we assume that the rewards of a subset of nodes (nodes with even id) are random variables following a Log-Normal probability distribution. The Log-Normal distribution allows for us to model stochastic rewards, since these are always non-negative values. In practice, historical observations on each node’s rewards can be used to determine the specific parameters of the associated probability distribution.
  In our experiments, the variance of the reward associated to a node i, $U_i$, has been set, as follows: $Var\left[U_i\right]=c·E\left[U_i\right]=c·u_i$, where $u_i$ is the deterministic reward, while $c\ge 0$ represents an experimental parameter that can be employed in order to analyze scenarios with different degrees of variability. In our case, we have set $c=40$.
• Stochastic-fuzzy scenario: to evaluate this scenario, we have divided the subset of non-deterministic nodes into stochastic and fuzzy nodes. Thus, we consider three different types of nodes: deterministic, stochastic, and fuzzy.
• Completely fuzzy scenario: this is the scenario with the highest uncertainty degree, since all of the rewards that are associated with non-deterministic nodes are modeled as fuzzy variables. Therefore, two types of nodes are considered: deterministic and fuzzy.

Algorithm 1 Heuristic algorithm for the deterministic TOP.

1: Sol ← genDummySol (Inputs) 2: Savings ← genSortedSavingList (Inputs) 3: while (Savings $\ne \varnothing$) do % Starts the route-merging process 4:   Arc ← selectNext (Savings) 5:   Route${}_i\leftarrow$ getStartingRoute (Arc) 6:   Route${}_j\leftarrow$ getClosingRoute (Arc) 7:   Route${}^{*}\leftarrow$ mergeRoutes (Route${}_i$, Route${}_j$) 8:   timeRoute${}^{*}$← calcRouteTime (Route${}^{*}$) 9:   acceptMerge ← checkMergeConditions (timeRoute${}^{*}$) 10:   if (acceptMerge) then 11:    Sol ← removeRoute (Route${}_i$, Sol) 12:    Sol ← removeRoute (Route${}_j$, Sol) 13:    Sol ← updateSolution (Route${}^{*}$, Sol) 14:   end if 15:   Savings ← remove (Savings, Arc) 16: end while 17: Sol ← sortRoutesByProfit (Sol) 18: Sol ← deleteRoutesByProfit (Sol, maxVehicles) 19: return Sol

Table 2. The results of the deterministic, stochastic, and fuzzy TOP.

	Deterministic Scenario			Stochastic Scenario		Uncertainty Scenario
Instance	BKS	Deterministic	GAP(%)	Deterministic	Stochastic	Stoch-Fuzzy	Fuzzy
	(1)	Sol (2)	(1–2)	Sol. (3)	Sol. (4)	Sol. (5)	Sol. (6)
p1.4.j	75	75	0.0	59.3	63.3	51.3	45.1
p1.4.k	100	100	0.0	78.5	78.5	66.2	62.6
p1.4.l	120	120	0.0	93.8	93.8	84.3	77.1
p1.4.m	130	125	4.0	98.2	102.9	91.5	86.3
p1.4.n	155	150	3.3	99.9	104.0	107.5	98.2
p1.4.o	165	165	0.0	122.1	131.1	123.7	103.3
p1.4.p	175	175	0.0	124.9	128.8	126.7	114.8
p2.2.d	160	160	0.0	80.2	142.1	83.1	74.0
p3.2.q	760	760	0.0	755.0	758.2	584.9	441.8
p3.2.r	790	790	0.0	767.0	774.7	577.5	384.3
p5.2.d	80	80	0.0	57.2	64.6	63.4	63.4
p5.2.p	1150	1150	0.0	1049.6	1139.3	1075.9	1021.1
p5.2.k	670	670	0.0	563.0	628.1	470.7	297.5
p6.2.d	192	192	0.0	170.4	175.2	147.1	103.0
p6.2.g	660	660	0.0	584.6	587.3	301.2	285.6
Average:	359	358	0.5	313.6	331.5	263.7	217.2

presents the results for some selected instances with different characteristics. The first column of the table identifies the instances. We have divided the remaining columns into three different parts. In the first part, we validate our approach in a deterministic scenario, i.e., without considering the fuzzy or stochastic variables. In particular, we measure the performance of our deterministic solution (column 2) with respect to the current best-known solution (BKS), as reported by [61] (column 1). Notice that, even when the goal of this paper is not to solve the deterministic version of the TOP, our approach obtains an average gap of $0.5\%$ with respect to BKS for this version. This result contributes to validate the quality of our base algorithm, which constitutes the optimization component in our fuzzy simheuristic. In the second part of the table, we present the obtained solutions for the stochastic scenario. Column 3 offers the expected cost that is associated with the best solution to the deterministic TOP (best deterministic solution), when it is execcuted under a stochastic scenario. Similarly, the next column shows the expected cost that was obtained while using our simheuristic approach. The last part of the table shows the results for the fuzzy scenarios. Column 5 shows the results that were gathered for the stochastic-fuzzy scenario, while the last column shows the solutions for the completely fuzzy scenario. Several considerations need to be made here in order to correctly interpret these results: (i) as discussed above, the optimization component of our hybrid methodology provides competitive solutions when used to solve the deterministic version of the TOP, which validates its potential for being used in the uncertainty version; (ii) our simheuristic approach provides better solutions than the ones that can be obtained by simply using the near-optimal solutions to the deterministic TOP in the stochastic scenario; and, (iii) our fuzzy simheuristic can also be employed in order to solve the TOP version with fuzzy rewards—in this case, however, the results have to be considered with caution, since they strongly depend on the design of the fuzzy function and, therefore, they are not directly comparable with the previous ones.

Figure 7 depicts an overview of Table 2, where the vertical axis of the box-plot represents the gap that was obtained in the stochastic and fuzzy scenarios with respect to the deterministic scenario. The latter can be considered as an ideal scenario with perfect information on the rewards, which is not the case when introducing nodes with stochastic and/or fuzzy rewards. Regarding the stochastic solutions, the results show that employing the best deterministic solution into a scenario under uncertainty usually leads to sub-optimal solutions, i.e., our fuzzy-simheuristic approach is able to generate solutions that outperform the optimal (or near-optimal) ones for the deterministic TOP when the latter are employed in a scenario under stochastic and/or fuzzy conditions. This justifies the importance of integrating hybrid simulation-fuzzy methods during the searching process when dealing with optimization problems under uncertainty conditions.

8. Challenges and Open Research Lines

This article analyzes the combination of simheuristics with fuzzy systems for solving complex problems under stochastic and uncertainty scenarios. The results in the computational experiments that are presented in Section 7 establish the fuzzy simheuristics concept as a promising tool when solving complex and large scale optimization problems under different degrees of uncertainty. However, this novel methodology needs to be explored in-depth, and it raises a number of challenges and open research branches. For the convenience of the reader, we discuss three possible research directions:

• Modifications in the Simheuristic Component: a promising line of work is the analysis of different simheuristic algorithms coupled with the fuzzy system. It is expected that some of these algorithms benefit more from the modeling of uncertainty with a fuzzy inference system in various instances.
• Variations in the Applications: on the one hand, most applications of simheuristics can benefit from the incorporation of an uncertainty-management mechanism, especially whenever the input information is limited. For instance, scheduling and facility location problems, waste collection management, and, of course, vehicle routing problems. On the other hand, the use of the fuzzy-simheuristic methodology can also be extended to different domains. A good idea could be to test it with different instances and over real problems. For example, applications in the fields of Internet of things and fog computing seem to be promising—partly because of the large amount of information that is available and the need to distribute the tasks among different devices. Implementing the proposed approach for solving smart-logistics problems is a natural open area, e.g., in smart mobility or healthcare logistics under uncertainty.
• Modification on the Uncertainty-Handling Mechanism: The fuzzy inference system has a significant impact on the overall results, since its configuration decides how to handle the uncertainty. Further analysis should be carried out in order to establish guidelines in order to select membership functions or inference rules for a specific instance of a problem. In this direction, the type-2 fuzzy logic could help to choose the parameters of the fuzzy system [62]. In the same context, rough sets [63] are another exciting tool far less explored than fuzzy systems for handling the uncertainty. All such mechanisms can be extended to the simheuristic domain, as an alternative to fuzzy systems, in order to manage uncertainty.

9. Conclusions

This paper presents a novel methodology that combines metaheuristic optimization algorithms with simulation and fuzzy techniques. The resulting fuzzy simheuristic approach constitutes a flexible and efficient methodology for solving large-scale NP-hard optimization problems that include uncertainty elements of both probabilistic and non-probabilistic nature. Hence, while the metaheuristic component leads the searching process (typically in a vast solution space), the simulation component allows for us to manage stochastic inputs and probabilistic constraints, while the fuzzy component takes care of those elements showing a non-stochastic uncertainty.

The proposed methodology is employed in order to efficiently solve a stochastic and fuzzy version of the team orienteering problem. In the deterministic version of the problem, a group of vehicles need to serve a selection of costumers without exceeding a maximum driving range. In the deterministic version, all of the information is known (i.e., we have constant inputs and no probabilistic constraints). However, in many real-life scenarios, different degrees of uncertainty will occur. Thus, we employ our fuzzy simheuristic methodology to solve the team orienteering problem with stochastic and uncertainty conditions. The experiments allow for us to illustrate the potential of our hybrid methodology, but they also provide some conclusions that need to be accounted for: (i) the optimal (or near-optimal) solution in a deterministic environment might be a sub-optimal solution in a scenario with uncertainty, especially as the degree of uncertainty increases; and, (ii) the results from the uncertainty scenario should be analyzed with caution, since they might be quite sensitive to the specific fuzzy functions being employed—i.e., to the expert’s opinion. All in all, we consider that the hybrid methodology that is proposed in this paper has tremendous potential in addressing complex optimization problems in realistic scenarios with different degrees of uncertainty, of both probabilistic and non-probabilistic nature. To the best of our knowledge, no other individual approach can simultaneously deal with optimization of NP-hard problems under stochastic and uncertainty scenarios. The team orienteering problem that is solved in this paper is a good example of such a stochastic and fuzzy optimization problem. Hence, we foresee multiple applications of fuzzy-simheuristic algorithms in fields, such as logistics and transportation, manufacturing and production, finance and insurance, telecommunication networks, energy, smart cities, etc.