Interference among Multiple Vibronic Modes in Two-Dimensional Electronic Spectroscopy
Abstract
:1. Introduction
2. Results and Discussion
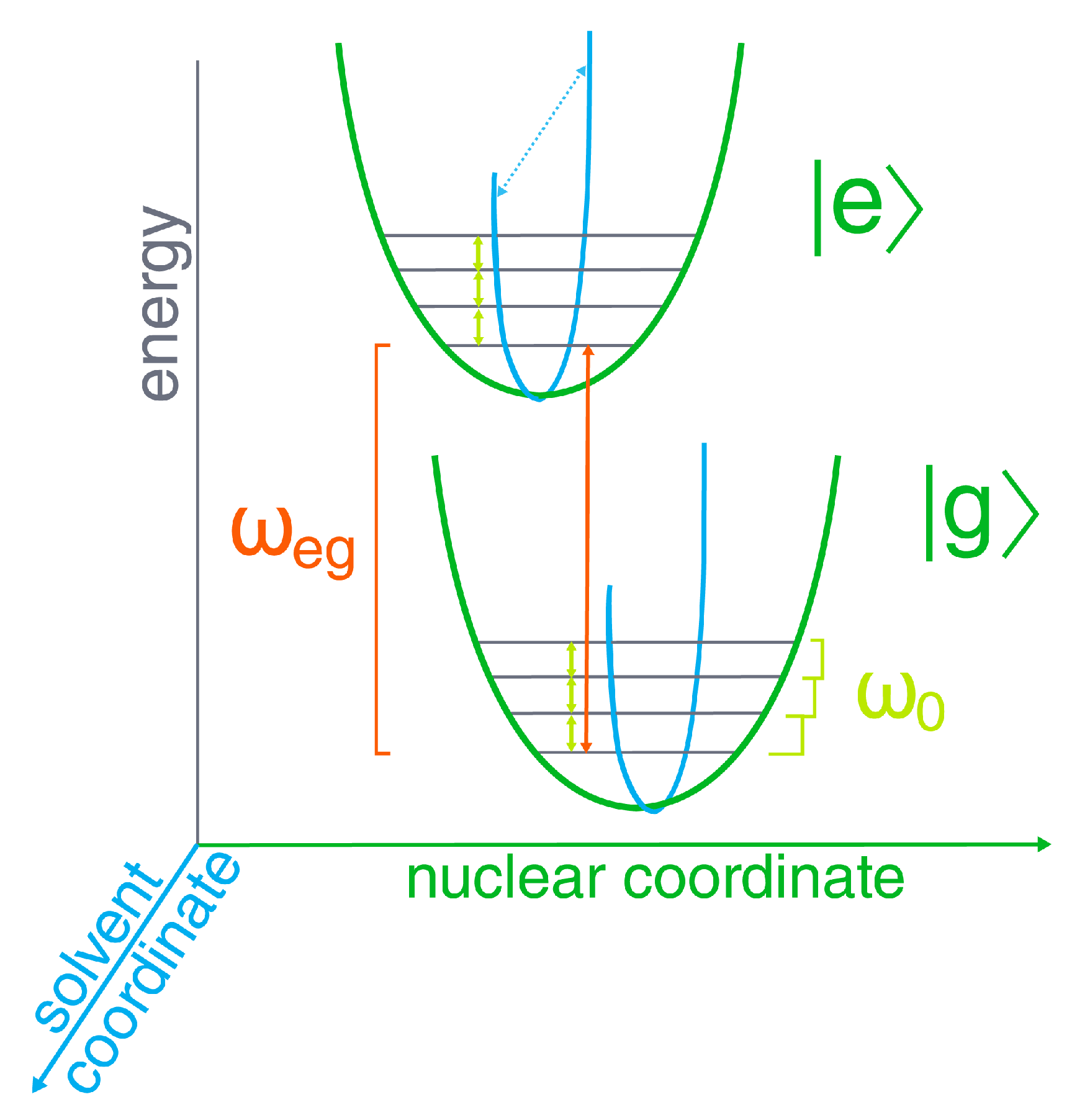
2.1. Theory: 2D ES Simulations
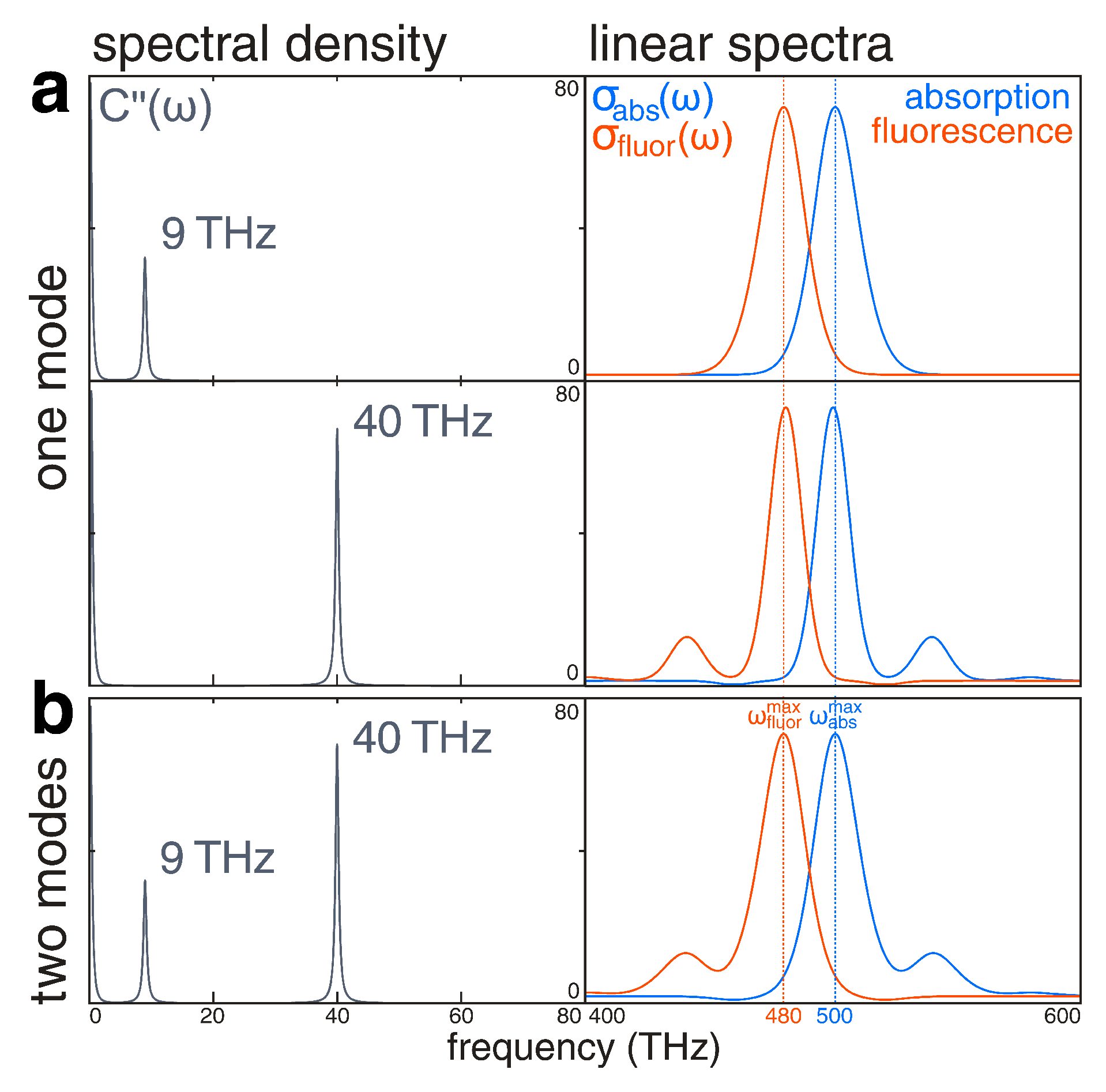
2.2. Linear Response: Spectral Density and Absorption and Fluorescence Spectra
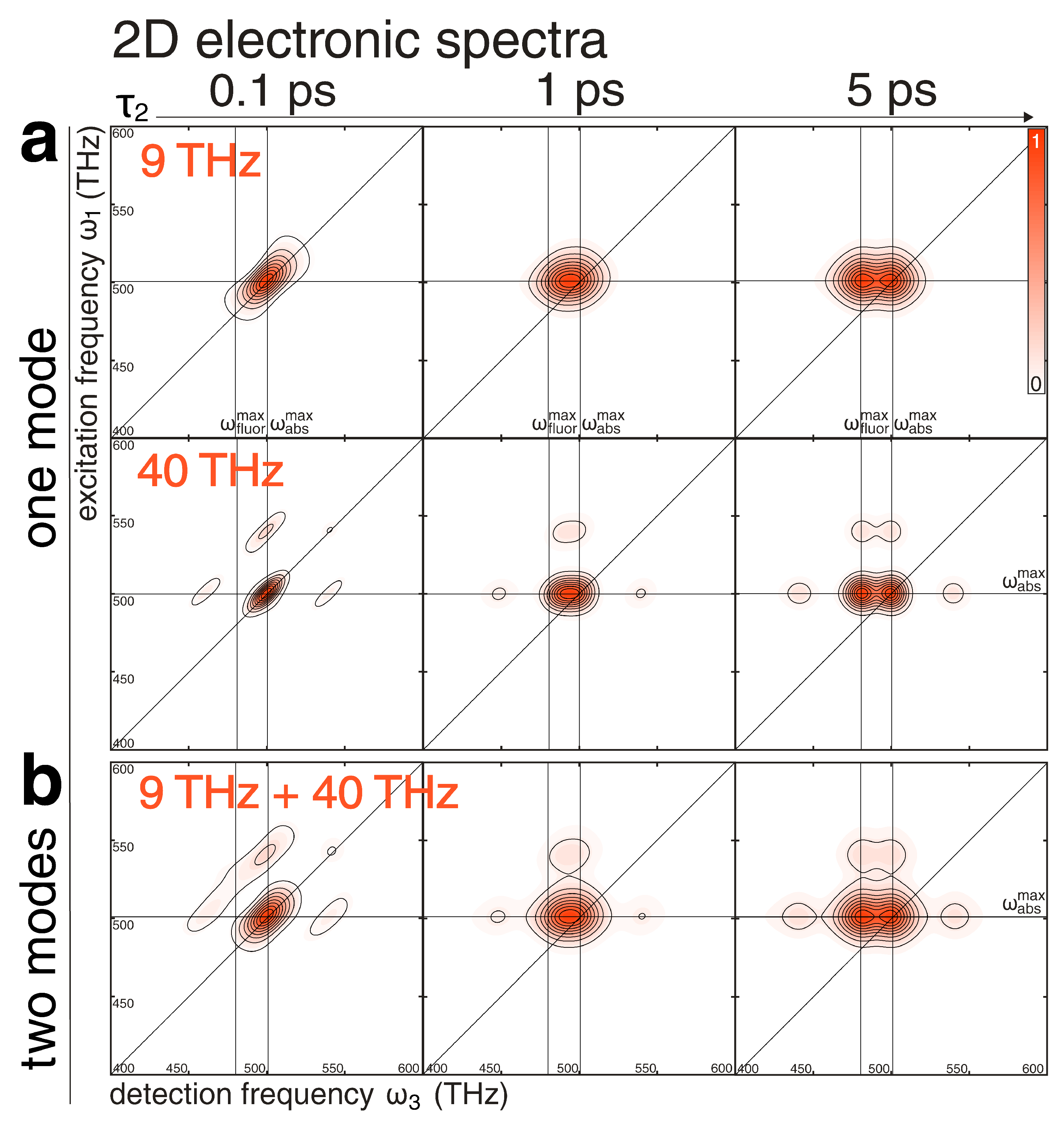
2.3. Nonlinear Response: 2D Electronic Spectra
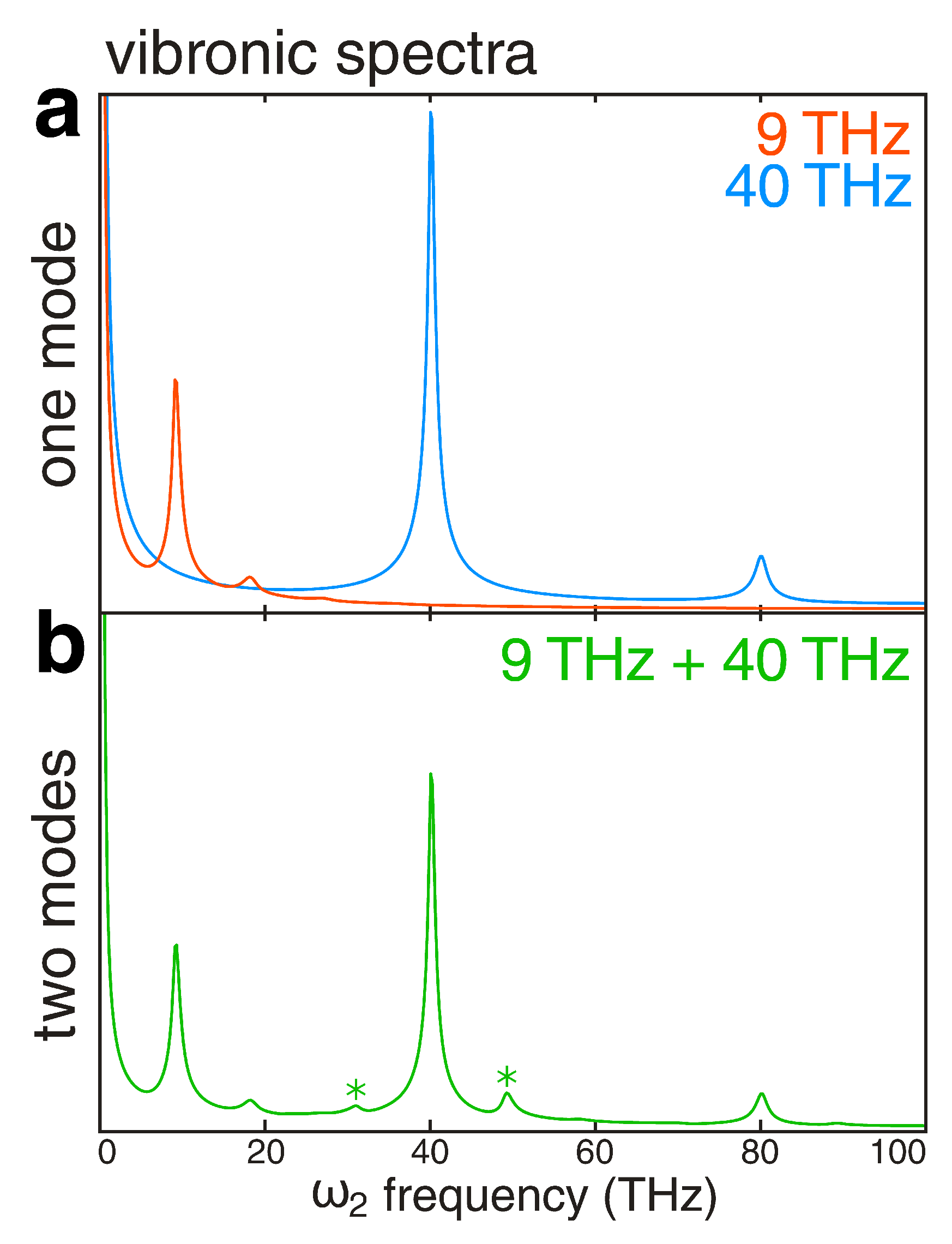
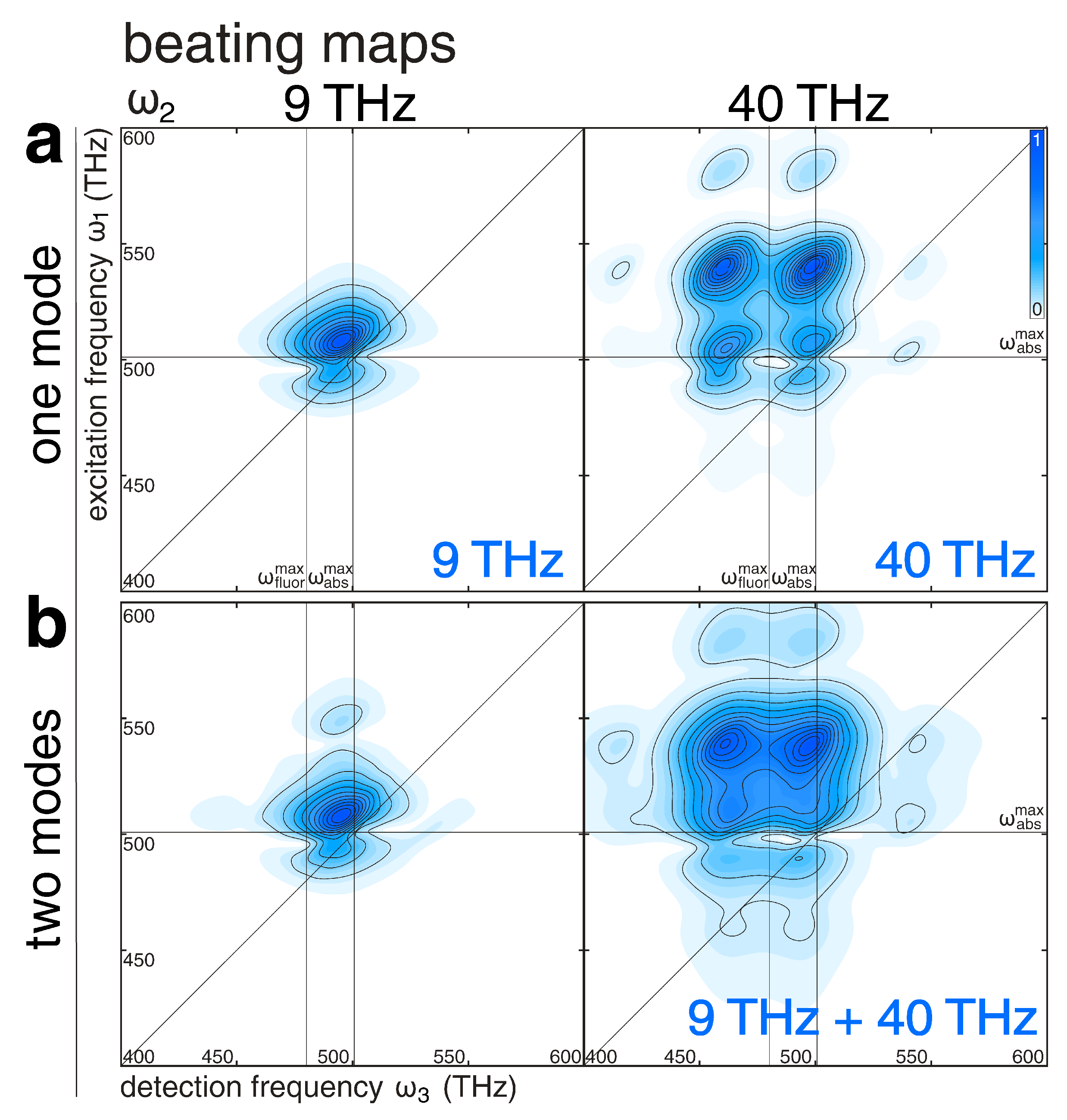
2.4. Vibronic Spectra and Beating Maps from 3D Electronic Spectra
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 2D ES—Two-dimensional electronic spectroscopy |
References
- Fulton, R.L. Vibronic Interactions. The Adiabatic Approximation. J. Chem. Phys. 1972, 56, 1210–1218. [Google Scholar] [CrossRef]
- Azumi, T.; Matsuzaki, K. What Does the Term “Vibronic Coupling” Mean? Photochem. Photobiol. 1977, 25, 315–326. [Google Scholar] [CrossRef]
- McQuarrie, D.A.; Simon, J.D. Physical Chemistry: A Molecular Approach; University Science Books: Mill Valley, CA, USA, 1997. [Google Scholar]
- McHale, J.L. Molecular Spectroscopy, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Bakulin, A.A.; Morgan, S.E.; Kehoe, T.B.; Wilson, M.W.B.; Chin, A.W.; Zigmantas, D.; Egorova, D.; Rao, A. Real-time observation of multiexcitonic states in ultrafast singlet fission using coherent 2D electronic spectroscopy. Nat. Chem. 2015, 8, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Breen, I.; Tempelaar, R.; Bizimana, L.A.; Kloss, B.; Reichman, D.R.; Turner, D.B. Triplet separation drives singlet fission after femtosecond correlated triplet pair production in rubrene. J. Am. Chem. Soc. 2017, 139, 11745–11751. [Google Scholar] [CrossRef] [PubMed]
- Fuller, F.D.; Pan, J.; Gelzinis, A.; Butkus, V.; Senlik, S.S.; Wilcox, D.E.; Yocum, C.F.; Valkunas, L.; Abramavicius, D.; Ogilvie, J.P. Vibronic coherence in oxygenic photosynthesis. Nat. Chem. 2014, 6, 706–711. [Google Scholar] [CrossRef] [PubMed]
- Womick, J.M.; Moran, A.M. Vibronic Enhancement of Exciton Sizes and Energy Transport in Photosynthetic Complexes. J. Phys. Chem. B 2011, 115, 1347–1356. [Google Scholar] [CrossRef] [PubMed]
- Womick, J.M.; West, B.A.; Scherer, N.F.; Moran, A.M. Vibronic effects in the spectroscopy and dynamics of C-phycocyanin. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 154016. [Google Scholar] [CrossRef]
- Richards, G.H.; Wilk, K.E.; Curmi, P.M.G.; Quiney, H.M.; Davis, J.A. Coherent Vibronic Coupling in Light-Harvesting Complexes from Photosynthetic Marine Algae. J. Phys. Chem. Lett. 2012, 3, 272–277. [Google Scholar] [CrossRef]
- Singh, V.P.; Westberg, M.; Wang, C.; Dahlberg, P.D.; Gellen, T.; Gardiner, A.T.; Cogdell, R.J.; Engel, G.S. Towards quantification of vibronic coupling in photosynthetic antenna complexes. J. Chem. Phys. 2015, 142, 212446. [Google Scholar] [CrossRef] [Green Version]
- Thyrhaug, E.; Tempelaar, R.; Alcocer, M.J.P.; Zidek, K.; Bina, D.; Knoester, J.; Jansen, T.L.C.; Zigmantas, D. Identification and characterization of diverse coherences in the Fenna–Matthews–Olson complex. Nat. Chem. 2018, 10, 780–786. [Google Scholar] [CrossRef]
- Song, Y.; Clafton, S.N.; Pensack, R.D.; Kee, T.W.; Scholes, G.D. Vibrational coherence probes the mechanism of ultrafast electron transfer in polymer–fullerene blends. Nat. Commun. 2014, 5, 4933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lenngren, N.; Abdellah, M.A.; Zheng, K.; Al-Marri, M.J.; Zigmantas, D.; Zidek, K.; Pullerits, T. Hot electron and hole dynamics in thiol-capped CdSe quantum dots revealed by 2D electronic spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 26199–26204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Sio, A.; Lienau, C. Vibronic coupling in organic semiconductors for photovoltaics. Phys. Chem. Chem. Phys. 2017, 19, 18813. [Google Scholar] [CrossRef] [PubMed]
- Meyer, H.D. A classical model of vibronic coupling: The ultrafast non-radiative decay via a conical intersection. Chem. Phys. 1983, 82, 199–205. [Google Scholar] [CrossRef]
- Vos, M.H.; Rappaport, F.; Lambry, J.C.; Breton, J.; Martin, J.L. Visualization of Coherent Nuclear Motion in a Membrane Protein by Femtosecond Spectroscopy. Nature 1993, 363, 320–325. [Google Scholar] [CrossRef]
- Peters, W.K.; Smith, E.R.; Jonas, D.M. Femtosecond Pump-Probe Polarization Spectroscopy of Vibronic Dynamics at Conical Intersections and Funnels. In Conical Intersections: Theory, Computation and Experiment; Advanced Series in Physical Chemistry; Domcke, W., Yarkony, D.R., Köppel, H., Eds.; World Scientific: Singapore, 2011; Volume 17. [Google Scholar]
- Johnson, P.J.M.; Halpin, A.; Morizumi, T.; Prokhorenko, V.I.; Ernst, O.P.; Miller, R.J.D. Local Vibrational Coherences Drive the Primary Photochemistry of Vision. Nat. Chem. 2015, 7, 980–986. [Google Scholar] [CrossRef]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Hamm, P.; Zanni, M.T. Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Brańczyk, A.M.; Turner, D.B.; Scholes, G.D. Crossing disciplines—A view on two-dimensional optical spectroscopy. Ann. Phys. 2013, 526, 31–49. [Google Scholar] [CrossRef] [Green Version]
- Wright, J.C. Analytical chemistry, multidimensional spectral signatures, and the future of coherent multidimensional spectroscopy. Chem. Phys. Lett. 2016, 662, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Fuller, F.D.; Ogilvie, J.P. Experimental Implementations of Two-Dimensional Fourier Transform Electronic Spectroscopy. Ann. Rev. Phys. Chem. 2015, 66, 667–690. [Google Scholar] [CrossRef]
- Lepetit, L.; Cheriaux, G.; Joffre, M. Linear Techniques of Phase Measurement by Femtosecond Spectral Interferometry for Application in Spectroscopy. J. Opt. Soc. Am. B 1995, 12, 2467–2474. [Google Scholar] [CrossRef]
- Jonas, D.M. Optical Analogs of 2D NMR. Science 2003, 300, 1515–1517. [Google Scholar] [CrossRef] [PubMed]
- Lewis, K.L.M.; Ogilvie, J.P. Probing Photosynthetic Energy and Charge Transfer with Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. Lett. 2012, 3, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Hybl, J.D.; Albrecht, A.W.; Gallagher Faeder, S.M.; Jonas, D.M. Two-Dimensional Electronic Spectroscopy. Chem. Phys. Lett. 1998, 297, 307–313. [Google Scholar] [CrossRef] [Green Version]
- Gallagher Faeder, S.M.; Jonas, D.M. Two-Dimensional Electronic Correlation and Relaxation Spectra: Theory and Model Calculations. J. Phys. Chem. A 1999, 103, 10489–10505. [Google Scholar] [CrossRef]
- Hybl, J.D.; Albrecht Ferro, A.; Jonas, D.M. Two-Dimensional Fourier Transform Electronic Spectroscopy. J. Chem. Phys. 2001, 115, 6606–6622. [Google Scholar] [CrossRef]
- Hybl, J.D.; Yannick, C.; Jonas, D.M. Peak Shapes in Femtosecond 2D Correlation Spectroscopy. Chem. Phys. 2001, 266, 295–309. [Google Scholar] [CrossRef]
- Nemeth, A.; Milota, F.; Mancal, T.; Lukes, V.; Kauffmann, H.F.; Sperling, J. Vibronic modulation of lineshapes in two-dimensional electronic spectra. Chem. Phys. Lett. 2008, 459, 94–99. [Google Scholar] [CrossRef]
- Milota, F.; Sperling, J.; Nemeth, A.; Mancal, T.; Kauffmann, H.F. Two-dimensional electronic spectroscopy of molecular excitons. Acc. Chem. Res. 2009, 42, 1364–1374. [Google Scholar] [CrossRef]
- Turner, D.B.; Dinshaw, R.; Lee, K.K.; Belsley, M.S.; Wilk, K.E.; Curmi, P.M.G.; Scholes, G.D. Quantitative investigations of quantum coherence for a light-harvesting protein at conditions simulating photosynthesis. Phys. Chem. Chem. Phys. 2012, 14, 4857–4874. [Google Scholar] [CrossRef] [Green Version]
- Chenu, A.; Christensson, N.; Kauffmann, H.F.; Mancal, T. Enhancement of Vibronic and Ground-State Vibrational Coherences in 2D Spectra of Photosynthetic Complexes. Sci. Rep. 2013, 3, 2029. [Google Scholar] [CrossRef] [Green Version]
- Egorova, D. Oscillations in two-dimensional photo-echo signals of excitonic and vibronic systems: Stick-spectrum analysis and its computational verification. J. Chem. Phys. 2014, 140, 034314. [Google Scholar] [CrossRef] [PubMed]
- Halpin, A.; Johnson, P.J.M.; Tempelaar, R.; Murphy, R.S.; Knoester, J.; Jansen, T.L.C.; Miller, R. Two-dimensional spectroscopy of a molecular dimer unveils the effects of vibronic coupling on exciton coherences. Nat. Chem. 2014, 6, 196–201. [Google Scholar] [CrossRef] [PubMed]
- Spokoyny, B.; Harel, E. Mapping the Vibronic Structure of a Molecule by Few-Cycle Continuum Two-Dimensional Spectroscopy in a Single Pulse. J. Phys. Chem. Lett. 2014, 5, 2808–2814. [Google Scholar] [CrossRef] [PubMed]
- Albert, J.; Falge, M.; Gomez, S.; Sola, I.R.; Hildenbrand, H.; Engel, V. Communication: Vibrational and vibronic coherences in the two dimensional spectroscopy of coupled electron-nuclear motion. J. Chem. Phys. 2015, 143, 041102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bizimana, L.A.; Brazard, J.; Carbery, W.P.; Gellen, T.; Turner, D.B. Resolving Molecular Vibronic Structure using High-Sensitivity Two-Dimensional Electronic Spectroscopy. J. Chem. Phys. 2015, 143, 164203. [Google Scholar] [CrossRef] [PubMed]
- Carbery, W.P.; Pinto-Pacheco, B.; Buccella, D.; Turner, D.B. Resolving the Fluorescence Quenching Mechanism of an Oxazine Dye Using Ultrabroadband Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. A 2019, 123, 5072–5080. [Google Scholar] [CrossRef] [PubMed]
- Ohta, K.; Larsen, D.S.; Yang, M.; Fleming, G.R. Influence of intramolecular vibrations in third-order, time-domain resonant spectroscopies. II. Numerical calculations. J. Chem. Phys. 2001, 114, 8020–8039. [Google Scholar] [CrossRef]
- Nemeth, A.; Milota, F.; Mancal, T.; Lukes, V.; Hauer, J.; Kauffmann, H.F.; Sperling, J. Vibrational wave packet induced oscillations in two-dimensional electronic spectra. I. Experiments. J. Chem. Phys. 2010, 132, 184514. [Google Scholar] [CrossRef] [Green Version]
- Fidler, A.F.; Harel, E.; Engel, G.S. Dissecting Hidden Couplings Using Fifth-Order Three-Dimensional Electronic Spectroscopy. J. Phys. Chem. Lett. 2010, 1, 2876–2880. [Google Scholar] [CrossRef]
- Bizimana, L.A.; Carbery, W.P.; Gellen, T.; Turner, D.B. Signatures of Herzberg–Teller coupling in three-dimensional electronic spectroscopy. J. Chem. Phys. 2017, 146, 084311. [Google Scholar] [CrossRef]
- Bizimana, L.A.; Epstein, J.; Brazard, J.; Turner, D.B. Conformational Homogeneity in the Pr Isomer of Phytochrome Cph1. J. Phys. Chem. B 2017, 121, 2622–2630. [Google Scholar] [CrossRef] [PubMed]
- Milota, F.; Prokhorenko, V.I.; Mancal, T.; von Berlepsch, H.; Bixner, O.; Kauffmann, H.F.; Hauer, J. Vibronic and Vibrational Coherences in Two-Dimensional Electronic Spectra of Supramolecular J-Aggregates. J. Phys. Chem. A 2013, 117, 6007–6014. [Google Scholar] [CrossRef] [PubMed]
- Tempelaar, R.; Jansen, T.L.C.; Knoester, J. Vibrational Beatings Conceal Evidence of Electronic Coherence in the FMO Light-Harvesting Complex. J. Phys. Chem. B 2014, 118, 12865–12872. [Google Scholar] [CrossRef] [PubMed]
- Policht, V.R.; Niedringhaus, A.; Ogilvie, J.P. Characterization of Vibrational Coherence in Monomeric Bacteriochlorophyll a by Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 6631–6637. [Google Scholar] [CrossRef] [PubMed]
- Butkus, V.; Valkunas, L.; Abramavicius, D. Molecular Vibrations-Induced Quantum Beats in Two-Dimensional Electronic Spectroscopy. J. Chem. Phys. 2012, 137, 044513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mancal, T.; Nemeth, A.; Milota, F.; Lukes, V.; Hauer, J.; Kauffmann, H.F.; Sperling, J. Vibrational wave packet induced oscillations in two-dimensional electronic spectra. II. Theory. J. Chem. Phys. 2010, 132, 184515. [Google Scholar] [CrossRef] [Green Version]
- Gallagher Faeder, S.M. A Two-Dimensional Fourier Transform Spectroscopic Study of the Non-Equilibrium Solvation Dynamics of IR144 in Methanol. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1999. [Google Scholar]
- Turner, D.B.; Stone, K.W.; Gundogdu, K.; Nelson, K.A. Three-Dimensional Electronic Spectroscopy of Excitons in GaAs Quantum Wells. J. Chem. Phys. 2009, 131, 144510. [Google Scholar] [CrossRef]
- Bašinskaitė, E.; Butkus, V.; Abramavicius, D.; Valkunas, L. Vibronic models for nonlinear spectroscopy simulations. Photosynth. Res. 2014, 121, 95–106. [Google Scholar] [CrossRef]
- Gellen, T.A.; Lem, J.; Turner, D.B. Probing Homogeneous Line Broadening in CdSe Nanocrystals using Multidimensional Electronic Spectroscopy. Nano Lett. 2017, 17, 2809–2815. [Google Scholar] [CrossRef]
- Bizimana, L.A.; Farfan, C.A.; Brazard, J.; Turner, D.B. E to Z Photoisomerization of Phytochrome Cph1Δ Exceeds the Born–Oppenheimer Adiabatic Limit. J. Phys. Chem. Lett. 2019, 10, 3550–3556. [Google Scholar] [CrossRef]
- Butkus, V.; Valkunas, L.; Abramavicius, D. Vibronic phenomena and exciton-vibrational interference in two-dimensional spectra of molecular aggregates. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberts, S.T.; Loparo, J.J.; Tokmakoff, A. Characterization of Spectral Diffusion from Two-Dimensional Line Shapes. J. Chem. Phys. 2006, 125, 084502. [Google Scholar] [CrossRef] [PubMed]
- Efremov, E.V.; Ariese, F.; Mank, A.J.G.; Gooijer, C. Strong Overtones and Combination Bands in Ultraviolet Resonance Raman Spectroscopy. Anal. Chem. 2006, 78, 3152–3157. [Google Scholar] [CrossRef] [PubMed]
- De Souza, B.; Farias, G.; Neese, F.; Izsák, R. Efficient simulation of overtones and combination bands in resonant Raman spectra. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef] [PubMed]
- Khalil, M.; Tokmakoff, A. Signatures of vibrational interactions in coherent two-dimensional infrared spectroscopy. Chem. Phys. 2001, 266, 213–230. [Google Scholar] [CrossRef]
- Nee, M.J.; Baiz, C.R.; Anna, J.M.; McCanne, R.; Kubarych, K.J. Multilevel vibrational coherence transfer and wavepacket dynamics probed with multidimensional IR spectroscopy. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef]
- Liang, K.K.; Villaeys, A.A. Anharmonicity and mode-mode coupling effects analyzed by four-wave-mixing photon-echo spectroscopy. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Gaynor, J.D.; Khalil, M. Signatures of vibronic coupling in two-dimensional electronic-vibrational and vibrational-electronic spectroscopies. J. Chem. Phys. 2017, 147. [Google Scholar] [CrossRef]
- Santoro, F.; Improta, R.; Lami, A.; Bloino, J.; Barone, V. Effective method to compute Franck–Condon integrals for optical spectra of large molecules in solution. J. Chem. Phys. 2007, 126. [Google Scholar] [CrossRef]
- Niu, Y.; Peng, Q.; Deng, C.; Gao, X.; Shuai, Z. Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules. J. Phys. Chem. A 2010, 114, 7817–7831. [Google Scholar] [CrossRef]
- Duschinsky, F.Z.D. Der Elektronenspektren mehratomiger Moleküle. Acta Physicochim. URSS 1937, 7, 551–566. [Google Scholar]
- Fuji, T.; Saito, T.; Kobayashi, T. Dynamical observation of Duschinksy rotation by sub-5-fs real-time spectroscopy. Chem. Phys. Lett. 2000, 332, 324–330. [Google Scholar] [CrossRef]
- Tanimura, Y.; Mukamel, S. Real-time path-integral approach to quantum coherence and dephasing in nonadiabatic transitions and nonlinear optical response. Phys. Rev. E 1993, 47, 118–136. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farfan, C.A.; Turner, D.B. Interference among Multiple Vibronic Modes in Two-Dimensional Electronic Spectroscopy. Mathematics 2020, 8, 157. https://doi.org/10.3390/math8020157
Farfan CA, Turner DB. Interference among Multiple Vibronic Modes in Two-Dimensional Electronic Spectroscopy. Mathematics. 2020; 8(2):157. https://doi.org/10.3390/math8020157
Chicago/Turabian StyleFarfan, Camille A., and Daniel B. Turner. 2020. "Interference among Multiple Vibronic Modes in Two-Dimensional Electronic Spectroscopy" Mathematics 8, no. 2: 157. https://doi.org/10.3390/math8020157




