Chaotic Synchronization Using a Self-Evolving Recurrent Interval Type-2 Petri Cerebellar Model Articulation Controller †
Abstract
:1. Introduction
2. System Description
3. Architecture of SRIT2PC
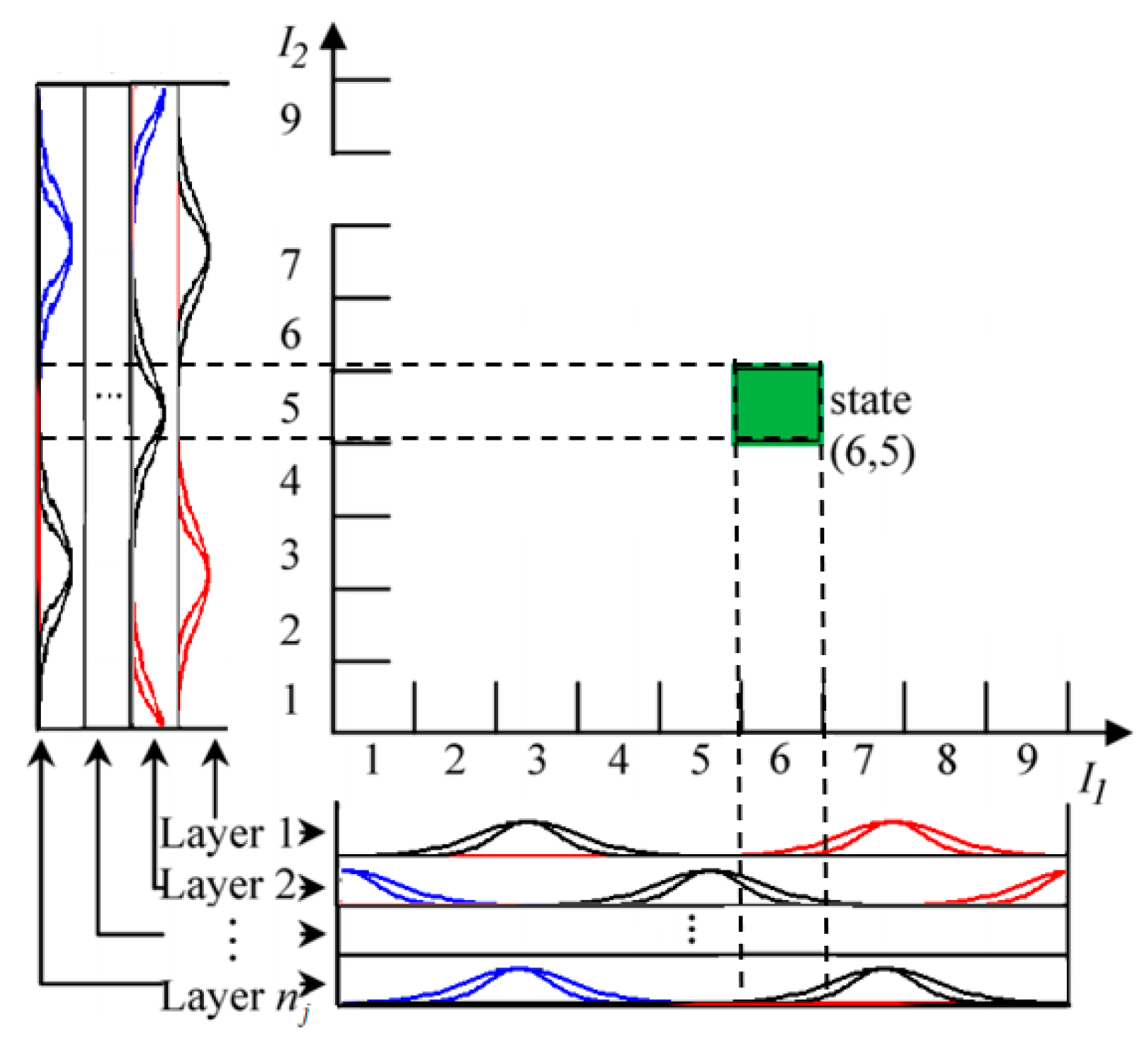
3.1. Recurrent Interval Type-2 Petri CMAC
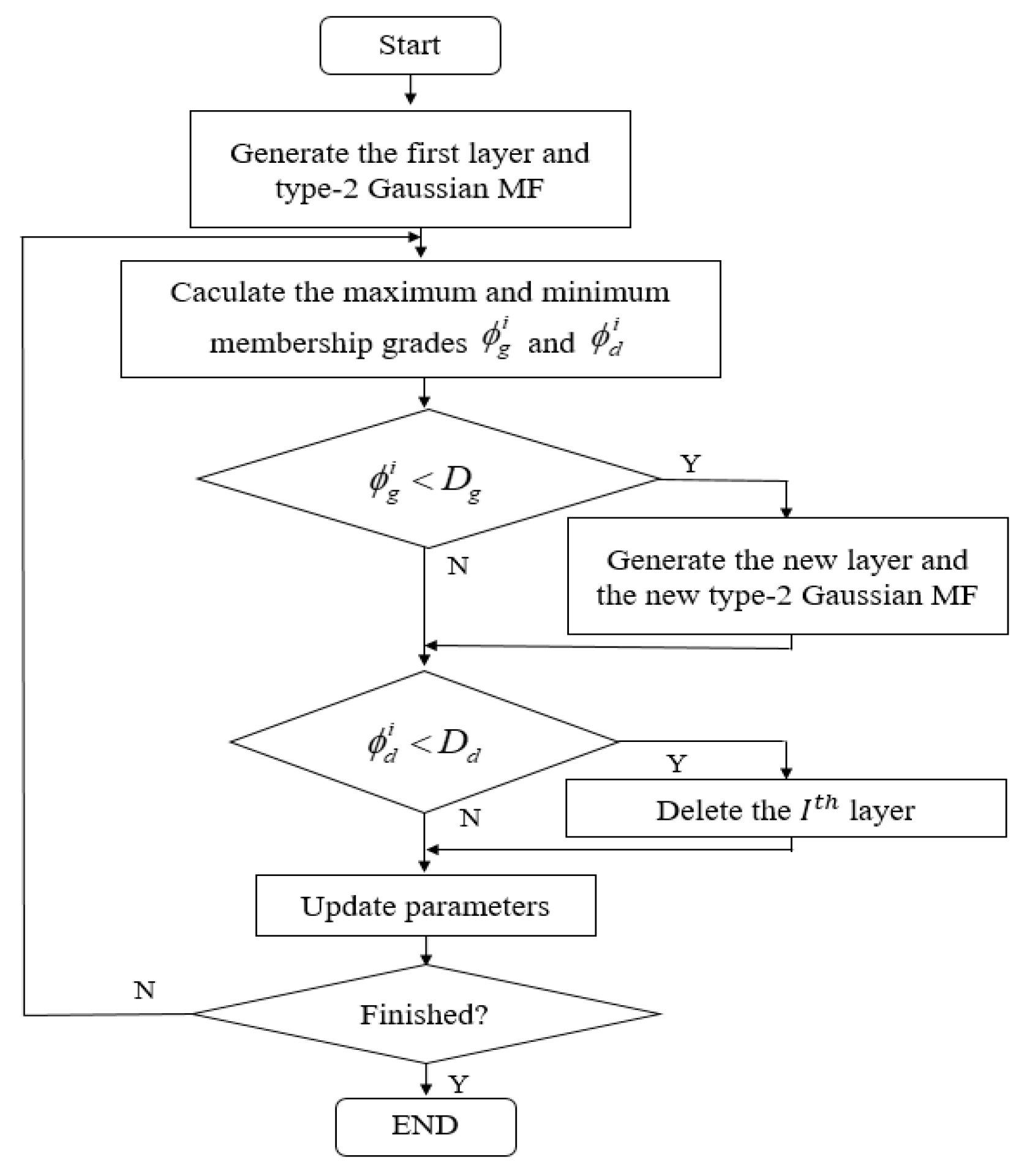
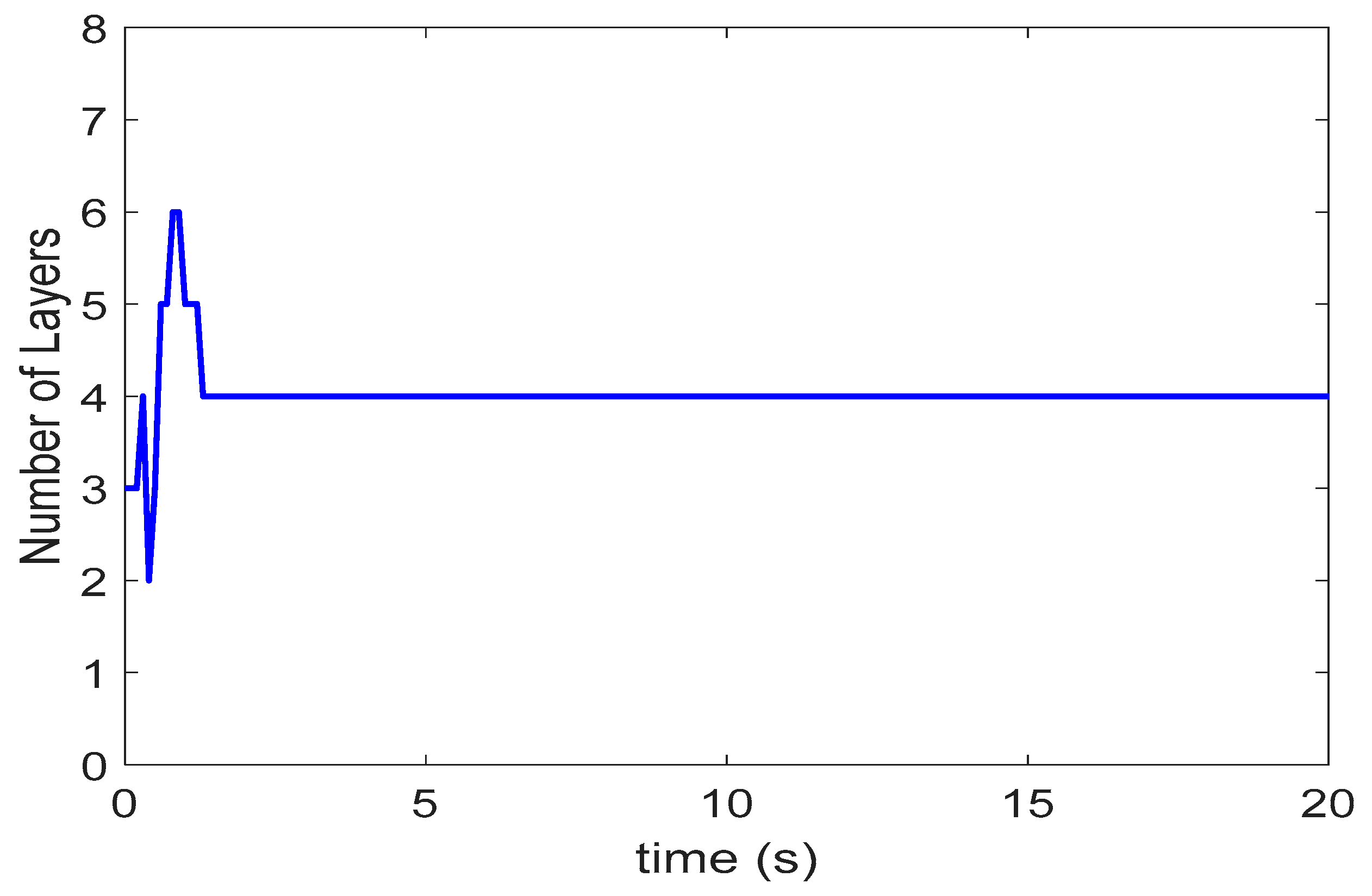
3.2. Self-Evolving Algorithm
3.3. Parameter Learning For SRIT2PC
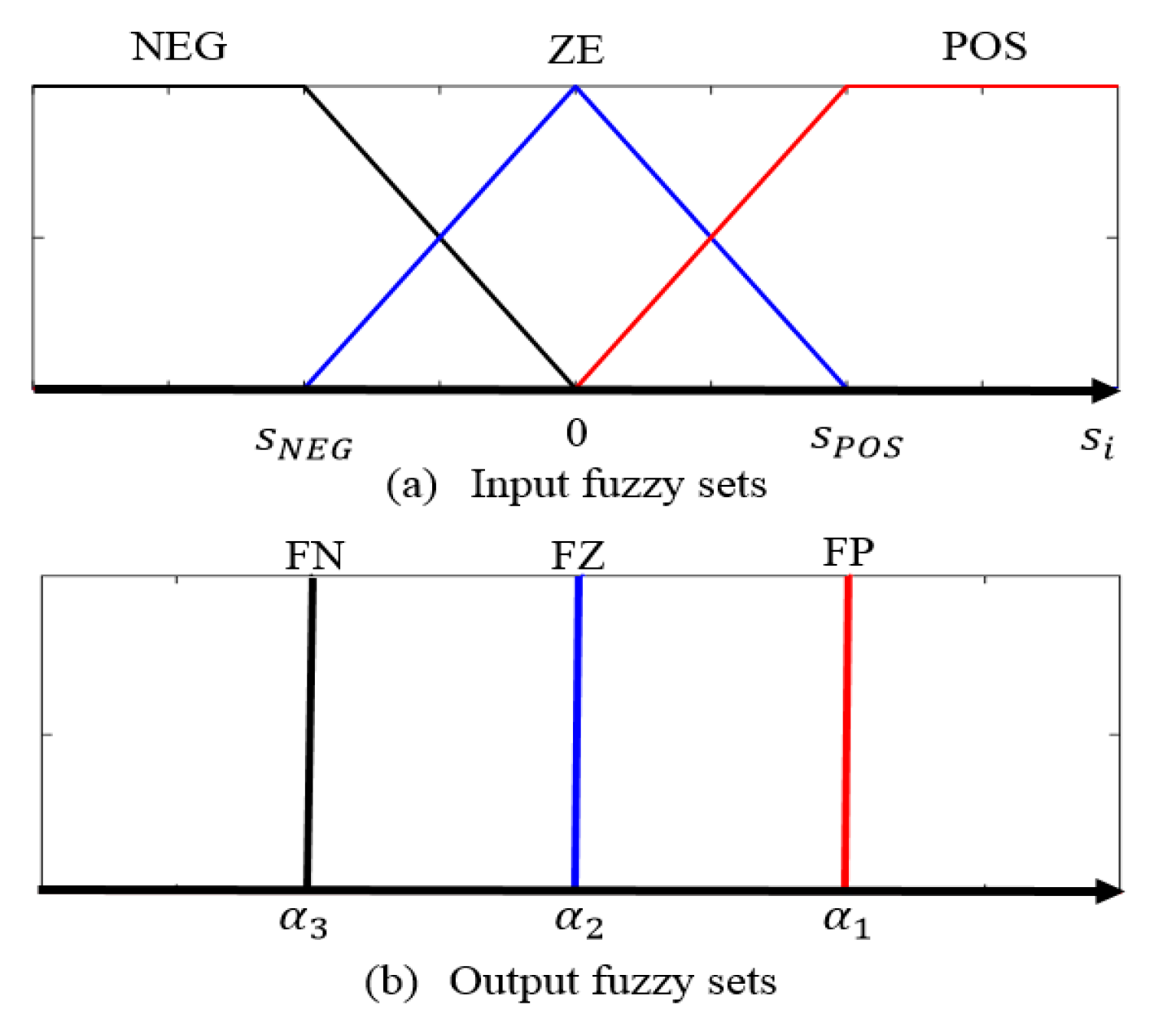
3.4. Compensator Controller
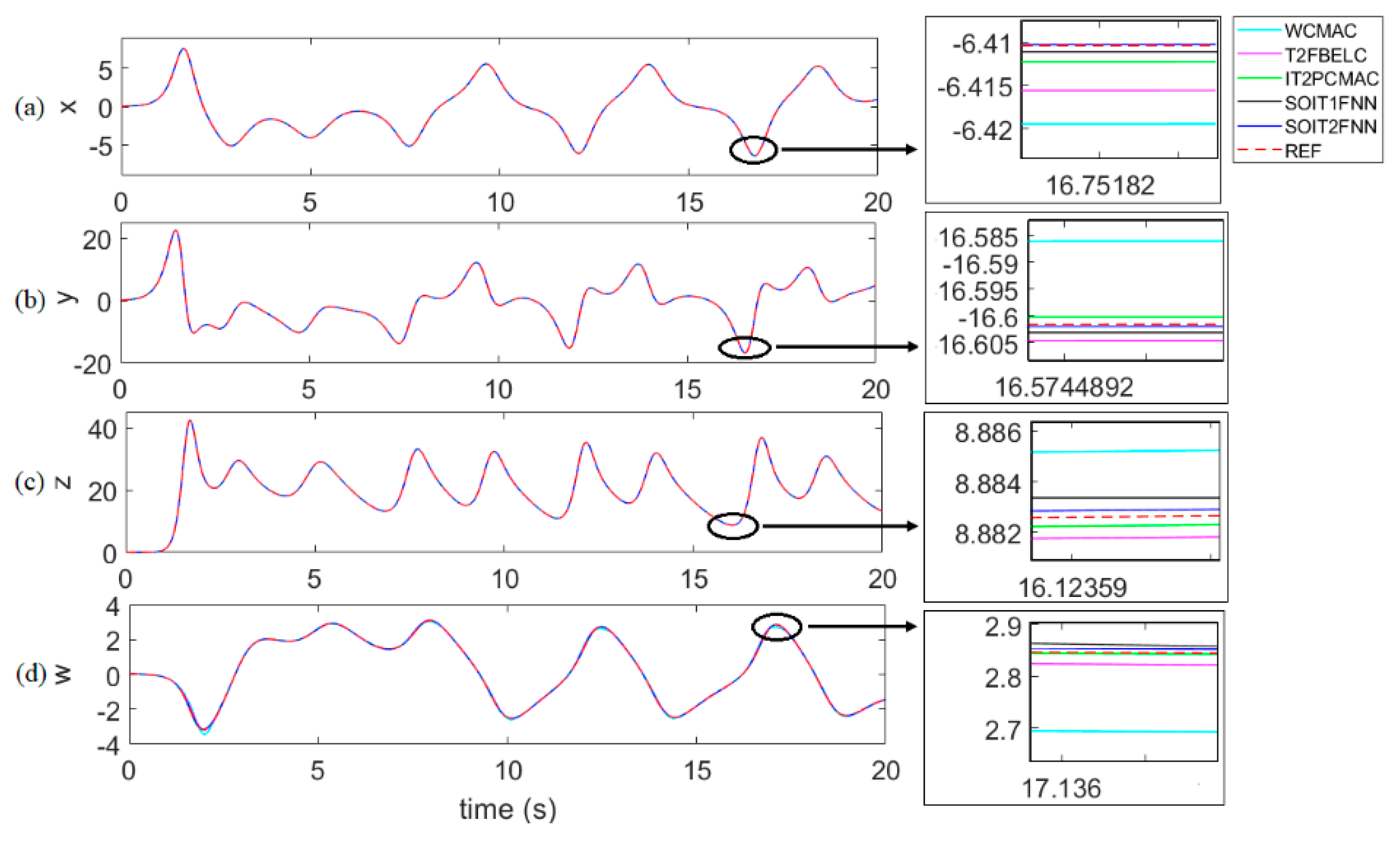
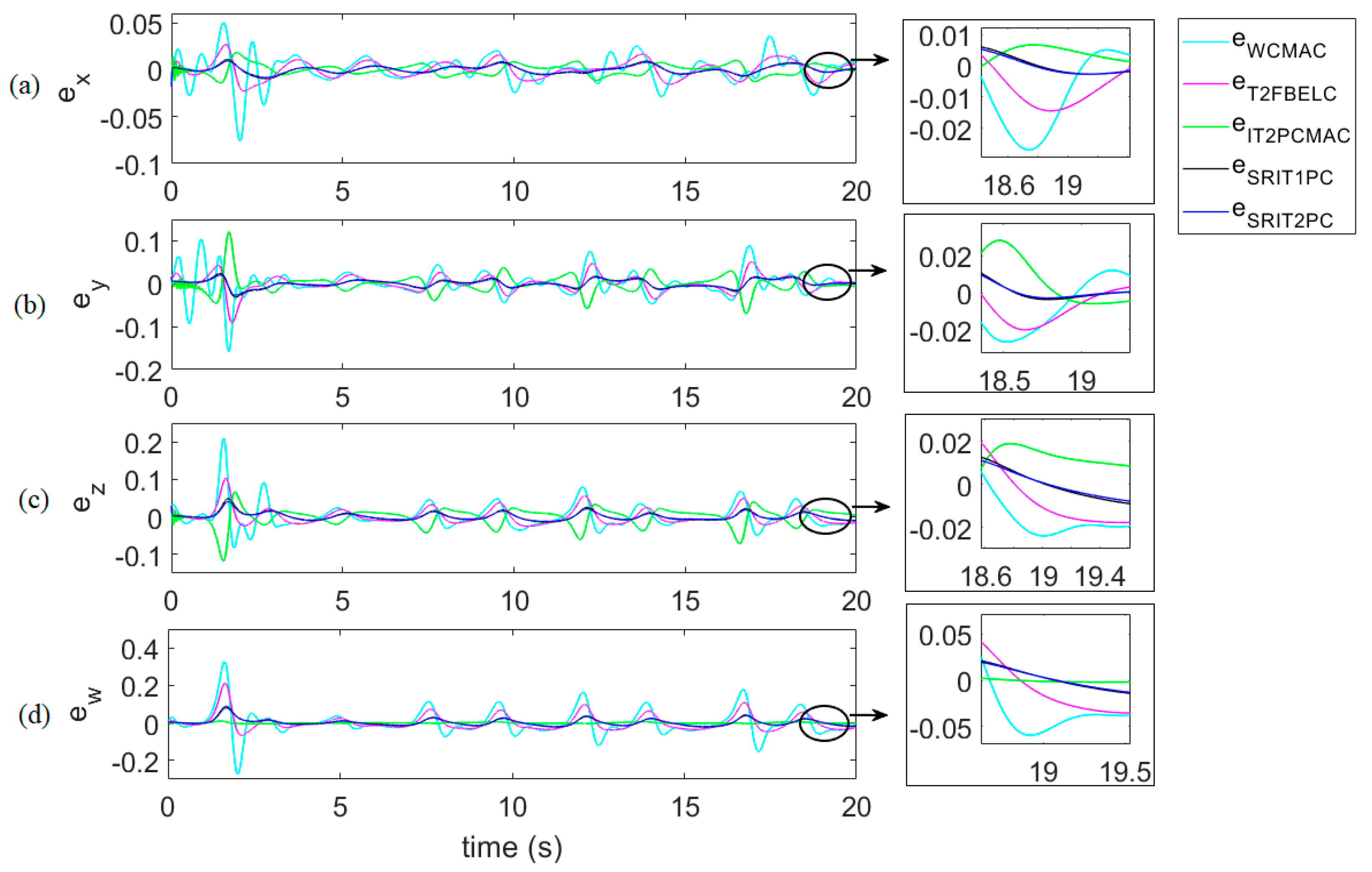
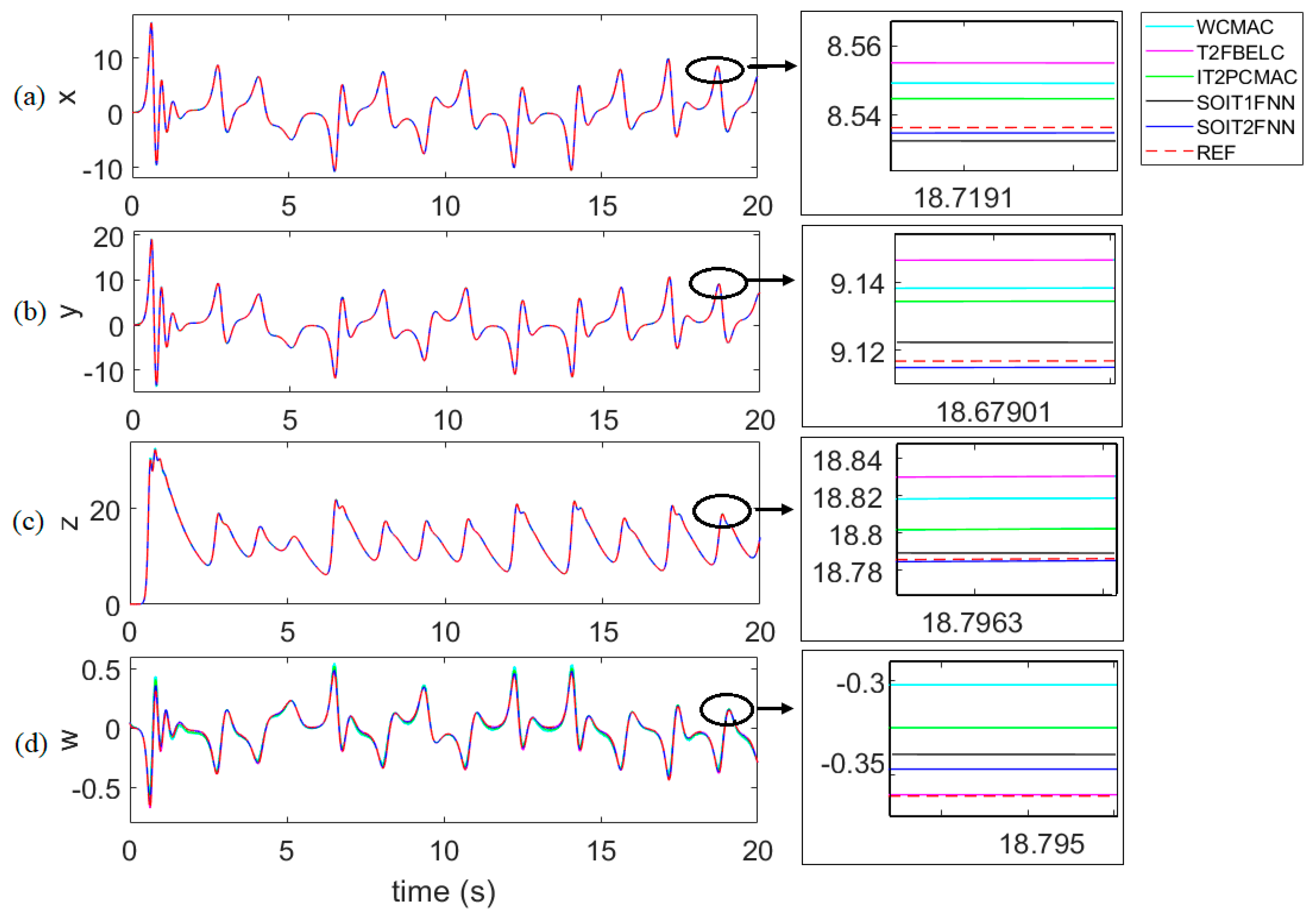
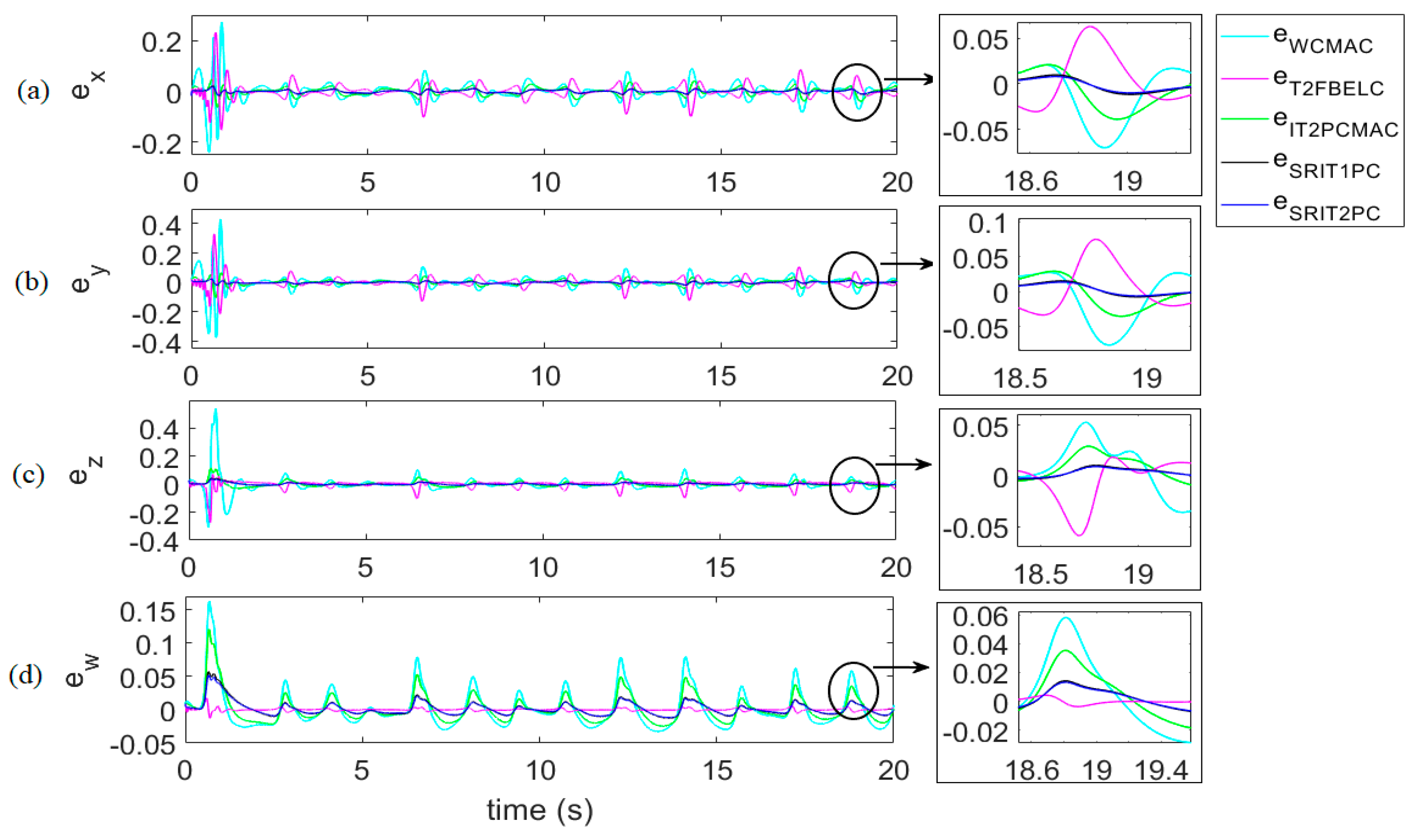
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sadaoui, D.; Boukabou, A.; Merabtine, N.; Benslama, M. Predictive synchronization of chaotic satellites systems. Expert Syst. Appl. 2011, 38, 9041–9045. [Google Scholar] [CrossRef]
- Naderi, B.; Kheiri, H. Exponential synchronization of chaotic system and application in secure communication. Opt. Int. J. Light Electron Opt. 2016, 127, 2407–2412. [Google Scholar] [CrossRef]
- Pappu, C.S.; Flores, B.C.; Debroux, P.S.; Boehm, J.E. An electronic implementation of lorenz chaotic oscillator synchronization for bistatic radar applications. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2001–2013. [Google Scholar] [CrossRef]
- Jayaprasath, E.; Wu, Z.M.; Sivaprakasam, S.; Hou, Y.S.; Tang, X.; Lin, X.D.; Deng, T.; Xia, G.Q. Investigation of the Effect of Intra-Cavity Propagation Delay in Secure Optical Communication Using Chaotic Semiconductor Lasers. Photonics 2019, 6, 49. [Google Scholar] [CrossRef] [Green Version]
- Mandal, M.K.; Das, A.K. Chaos-Based Colour Image Encryption Using Microcontroller ATMEGA 32. In Nanoelectronics, Circuits and Communication Systems; Lecture Notes in Electrical Engineering; Nath, V., Mandal, J., Eds.; Springer: Singapore, 2019; Volume 2019, p. 511. [Google Scholar]
- Ohtsubo, J. Chaos Synchronization in Semiconductor Lasers. In Semiconductor Lasers; Springer Series in Optical Sciences; Springer: Cham, Switzerland, 2017; p. 111. [Google Scholar]
- Xu, L.; Ma, H.; Xiao, S. Exponential Synchronization of Chaotic Lur’e Systems Using an Adaptive Event-Triggered Mechanism. IEEE Access 2018, 6, 61295–61304. [Google Scholar] [CrossRef]
- Boulkroune, A.; Bouzeriba, A.; Bouden, T. Fuzzy generalized projective synchronization of incommensurate fractional-order chaotic systems. Neurocomputing 2016, 173, 606–614. [Google Scholar] [CrossRef]
- Zhou, Q.; Chao, F.; Lin, C.M. A functional-link-based fuzzy brain emotional learning network for breast tumor classification and chaotic system synchronization. Int. J. Fuzzy Syst. 2018, 20, 349–365. [Google Scholar] [CrossRef]
- Mufti, M.R.; Afzal, H.; Rehman, F.U.; Butt, Q.R.; Qureshi, M.I. Synchronization and antisynchronization between two non-identical Chua oscillators via sliding mode control. IEEE Access 2018, 6, 45270–45280. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Ghaemi, S. Optimal synchronization of fractional-order chaotic systems subject to unknown fractional order, input nonlinearities and uncertain dynamic using type-2 fuzzy CMAC. Nonlinear Dyn. 2017, 88, 2993–3002. [Google Scholar] [CrossRef]
- Albus, J.S. A new approach to manipulator control: The cerebellar model articulation controller (CMAC). J. Dyn. Syst. Meas. Control 1975, 97, 220–227. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.M.; Le, T.L. WCMAC-based control system design for nonlinear systems using PSO. J. Intell. Fuzzy Syst. 2017, 33, 807–818. [Google Scholar] [CrossRef]
- Lu, H.C.; Chuang, C.Y. Robust parametric CMAC with self-generating design for uncertain nonlinear systems. Neurocomputing 2011, 74, 549–562. [Google Scholar] [CrossRef]
- Lin, C.M.; Li, H.Y. Self-organizing adaptive wavelet CMAC backstepping control system design for nonlinear chaotic systems. Nonlinear Anal. Real World Appl. 2013, 14, 206–223. [Google Scholar] [CrossRef]
- Lin, C.M.; Huynh, T.T.; Le, T.L. Adaptive TOPSIS fuzzy CMAC back-stepping control system design for nonlinear systems. Soft Comput. 2019, 23, 6947–6966. [Google Scholar] [CrossRef]
- Fang, W.; Chao, F.; Yang, L.; Lin, C.M.; Shang, C.; Zhou, C.; Shen, Q. A recurrent emotional CMAC neural network controller for vision-based mobile robots. Neurocomputing 2019, 334, 227–238. [Google Scholar] [CrossRef]
- Wang, J.G.; Tai, S.C.; Lin, C.J. Medical diagnosis applications using a novel interactively recurrent self-evolving fuzzy CMAC model. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 4092–4098. [Google Scholar]
- Chung, C.C.; Chen, T.S.; Lin, L.H.; Lin, Y.C.; Lin, C.M. Bankruptcy prediction using cerebellar model neural networks. Int. J. Fuzzy Syst. 2016, 18, 160–167. [Google Scholar] [CrossRef]
- Guan, J.S.; Lin, L.Y.; Ji, G.L.; Lin, C.M.; Le, T.L.; Rudas, I.J. Breast tumor computer-aided diagnosis using self-validating cerebellar model neural networks. Acta Polytech. Hung. 2016, 13, 39–52. [Google Scholar]
- Tsao, Y.; Chu, H.C.; Fang, S.H.; Lee, J.; Lin, C.M. Adaptive noise cancellation using deep cerebellar model articulation controller. IEEE Access 2018, 6, 37395–37402. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, C.M. Wavelet-TSK-type fuzzy cerebellar model neural network for uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2018, 27, 549–558. [Google Scholar] [CrossRef]
- Lin, C.M.; Yang, M.S.; Chao, F.; Hu, X.M.; Zhang, J. Adaptive filter design using type-2 fuzzy cerebellar model articulation controller. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2084–2094. [Google Scholar] [CrossRef]
- Wang, J.G.; Tai, S.C.; Lin, C.J. The application of an interactively recurrent self-evolving fuzzy CMAC classifier on face detection in color images. Neural Comput. Appl. 2018, 29, 201–213. [Google Scholar] [CrossRef]
- Lin, C.M.; Hou, Y.L.; Chen, T.Y.; Chen, K.H. Breast nodules computer-aided diagnostic system design using fuzzy cerebellar model neural networks. IEEE Trans. Fuzzy Syst. 2013, 22, 693–699. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Yang, G.H. Observer-based fuzzy adaptive sensor fault compensation for uncertain nonlinear strict-feedback systems. IEEE Trans. Fuzzy Syst. 2017, 26, 2301–2310. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, G.H. Low-computation Adaptive Fuzzy Tracking Control for Nonlinear Systems via Switching-Type Adaptive Laws. IEEE Trans. Fuzzy Syst. 2019, 27, 1931–1942. [Google Scholar] [CrossRef]
- Wang, H.; Liu, P.X.; Zhao, X.; Liu, X. Adaptive Fuzzy Finite-Time Control of Nonlinear Systems with Actuator Faults. Available online: https://ieeexplore.ieee.org/abstract/document/8709959 (accessed on 2 November 2019).
- Zhao, X.; Wang, X.; Zhang, S.; Zong, G. Adaptive neural backstepping control design for a class of nonsmooth nonlinear systems. IEEE Trans. Syst. Man Cybern. 2019, 49, 178–183. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wang, Y.C.; Chen, T.C.T.; Lin, H.F. Evaluating the Suitability of a Smart Technology Application for Fall Detection Using a Fuzzy Collaborative Intelligence Approach. Mathematics 2019, 7, 1097. [Google Scholar] [CrossRef] [Green Version]
- Djeddi, A.; Dib, D.; Azar, A.T.; Abdelmalek, S. Fractional Order Unknown Inputs Fuzzy Observer for Takagi–Sugeno Systems with Unmeasurable Premise Variables. Mathematics 2019, 7, 984. [Google Scholar] [CrossRef] [Green Version]
- Salamat, N.; Mustahsan, M.; Missen, M.M.S. Switching Point Solution of Second-Order Fuzzy Differential Equations Using Differential Transformation Method. Mathematics 2019, 7, 231. [Google Scholar] [CrossRef] [Green Version]
- Shiev, K.; Ahmed, S.; Shakev, N.; Topalov, A.V. Trajectory control of manipulators using an adaptive parametric type-2 fuzzy cmac friction and disturbance compensator. In Novel Applications of Intelligent Systems; Springer: Berlin, Germany, 2016; pp. 63–82. [Google Scholar]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mendel, J.M. Type-2 fuzzy sets. In Uncertain Rule-Based Fuzzy Systems; Springer: Berlin, Germany, 2017; pp. 259–306. [Google Scholar]
- Oh, S.K.; Jang, H.J.; Pedrycz, W. A comparative experimental study of type-1/type-2 fuzzy cascade controller based on genetic algorithms and particle swarm optimization. Expert Syst. Appl. 2011, 38, 11217–11229. [Google Scholar] [CrossRef]
- Castillo, O.; Marroquín, R.M.; Melin, P.; Valdez, F.; Soria, J. Comparative study of bio-inspired algorithms applied to the optimization of type-1 and type-2 fuzzy controllers for an autonomous mobile robot. Inf. Sci. 2012, 192, 19–38. [Google Scholar] [CrossRef]
- Liang, Q.; Mendel, J.M. Interval type-2 fuzzy logic systems: Theory and design. IEEE Trans. Fuzzy Syst. 2000, 8, 535–550. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.H.; Chang, F.Y.; Lin, C.M. An efficient interval type-2 fuzzy CMAC for chaos time-series prediction and synchronization. IEEE Trans. Cybern. 2014, 44, 329–341. [Google Scholar] [CrossRef]
- Chang, C.W.; Xiao, W.R.; Hsiao, C.C.; Chen, S.S.; Tao, C.W. A simplified interval type-2 fuzzy CMAC. In Proceedings of the Joint 17th World Congress of International Fuzzy Systems Association and 9th International Conference on Soft Computing and Intelligent Systems (IFSA-SCIS), Otsu, Japan, 27–30 June 2017; pp. 1–4. [Google Scholar]
- Lin, C.M.; La, V.H.; Le, T.L. DC–DC converters design using a type-2 wavelet fuzzy cerebellar model articulation controller. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Zhao, T.; Ping, L.; Cao, J. Self-organising interval type-2 fuzzy neural network with asymmetric membership functions and its application. Soft Comput. 2019, 23, 7215–7228. [Google Scholar] [CrossRef]
- Peterson, J.L. Petri Net Theory and the Modeling of Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1981. [Google Scholar]
- Looney, C.G. Fuzzy Petri nets for rule-based decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 178–183. [Google Scholar] [CrossRef]
- Rosdi, F.S.; Salim, S.; Mustafa, M.B. An FPN-based classification method for speech intelligibility detection of children with speech impairments. Soft Comput. 2019, 23, 2391–2408. [Google Scholar] [CrossRef]
- Zhu, G.; Li, Z.; Wu, N. Model-based fault identification of discrete event systems using partially observed Petri nets. Automatica 2018, 96, 201–212. [Google Scholar] [CrossRef]
- Lin, C.M.; Li, H.Y. Dynamic petri fuzzy cerebellar model articulation controller design for a magnetic levitation system and a two-axis linear piezoelectric ceramic motor drive system. IEEE Trans. Control Syst. Technol. 2015, 23, 693–699. [Google Scholar] [CrossRef]
- Bibi, Y.; Bouhali, O.; Bouktir, T. Petri type 2 fuzzy neural networks approximator for adaptive control of uncertain non-linear systems. IET Control Theory Appl. 2017, 11, 3130–3136. [Google Scholar] [CrossRef]
- Hansen, P.; Franco, P.; Kim, S.Y. Soccer ball recognition and distance prediction using fuzzy petri nets. In Proceedings of the IEEE International Conference on Information Reuse and Integration (IRI), Salt Lake City, UT, USA, 7–9 July 2018; pp. 315–322. [Google Scholar]
- Mejía, G.; Niño, K.; Montoya, C.; Sánchez, M.A.; Palacios, J.; Amodeo, L. A Petri Net-based framework for realistic project management and scheduling: An application in animation and videogames. Comput. Oper. Res. 2016, 66, 190–198. [Google Scholar] [CrossRef]
- Juang, C.F.; Lin, C.T. A recurrent self-organizing neural fuzzy inference network. IEEE Trans. Neural Netw. 1999, 10, 828–845. [Google Scholar] [CrossRef]
- Hsu, C.F.; Cheng, K.H. Recurrent fuzzy-neural approach for nonlinear control using dynamic structure learning scheme. Neurocomputing 2008, 71, 3447–3459. [Google Scholar] [CrossRef]
- Yen, V.T.; Nan, W.Y.; Cuong, P.V. Recurrent fuzzy wavelet neural networks based on robust adaptive sliding mode control for industrial robot manipulators. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Lin, F.J.; Lee, S.Y.; Chou, P.H. Intelligent integral backstepping sliding-mode control using recurrent neural network for piezo-flexural nanopositioning stage. Asian J. Control 2016, 18, 456–472. [Google Scholar] [CrossRef]
- Sharma, R.; Kumar, V.; Gaur, P.; Mittal, A. An adaptive PID like controller using mix locally recurrent neural network for robotic manipulator with variable payload. Isa Trans. 2016, 62, 258–267. [Google Scholar] [CrossRef]
- Wang, S.Y.; Liu, F.Y.; Chou, J.H. Applications on adaptive recurrent cerebellar model articulation controller for switched reluctance motor drive systems. In Proceedings of the International Symposium on Computer, Consumer and Control (IS3C), Xi’an, China, 4–6 July 2016; pp. 6–9. [Google Scholar]
- Le, T.L.; Lin, C.M.; Huynh, T.T. Interval Type-2 Petri CMAC Design for 4D Chaotic System. Available online: https://ieeexplore.ieee.org/abstract/document/8823251 (accessed on 2 November 2019).
- Le, T.L.; Lin, C.M.; Huynh, T.T. Self-evolving type-2 fuzzy brain emotional learning control design for chaotic systems using PSO. Appl. Soft Comput. 2018, 73, 418–433. [Google Scholar] [CrossRef]
- Lin, C.M.; Le, T.L.; Huynh, T.T. Self-evolving function-link interval type-2 fuzzy neural network for nonlinear system identification and control. Neurocomputing 2018, 275, 2239–2250. [Google Scholar] [CrossRef]
- Le, T.L. Self-organizing recurrent interval type-2 Petri fuzzy design for time-varying delay systems. IEEE Access 2018, 7, 10505–10514. [Google Scholar] [CrossRef]
- Lin, C.M.; Le, T.L. PSO-self-organizing interval type-2 fuzzy neural network for antilock braking systems. Int. J. Fuzzy Syst. 2017, 19, 1362–1374. [Google Scholar] [CrossRef]
- Rong, H.J.; Yang, Z.X.; Wong, P.K.; Vong, C.M.; Zhao, G.S. Self-evolving fuzzy model-based controller with online structure and parameter learning for hypersonic vehicle. Aerosp. Sci. Technol. 2017, 64, 1–15. [Google Scholar] [CrossRef]
- Ge, D.; Zeng, X.J. A self-evolving fuzzy system which learns dynamic threshold parameter by itself. Ieee Trans. Fuzzy Syst. 2018, 27, 1625–1637. [Google Scholar] [CrossRef] [Green Version]
- Le, T.L. Intelligent fuzzy controller design for antilock braking systems. J. Intell. Fuzzy Syst. 2019, 36, 3303–3315. [Google Scholar] [CrossRef]
- Vincent, U. Synchronization of identical and non-identical 4-D chaotic systems using active control. Chaossolitons Fractals 2008, 37, 1065–1075. [Google Scholar] [CrossRef]














| Control Method | Computation Time (s) | Case 1 | Case 2 | Case 3 | Case 4 Time-Varying θ |
|---|---|---|---|---|---|
| WCMAC | 0.0147 | 0.1481 | 0.1804 | 0.1498 | 0.1379 |
| T2FBELC | 0.0183 | 0.0902 | 0.0955 | 0.0602 | 0.0797 |
| IT2PCMAC | 0.0172 | 0.0524 | 0.0716 | 0.0486 | 0.0704 |
| SRIT1PC | 0.0145 | 0.0507 | 0.0422 | 0.0347 | 0.0431 |
| SRIT2PC (proposed controller) | 0.0196 | 0.0476 | 0.0366 | 0.0299 | 0.0322 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.-L.; Huynh, T.-T.; Nguyen, V.-Q.; Lin, C.-M.; Hong, S.-K. Chaotic Synchronization Using a Self-Evolving Recurrent Interval Type-2 Petri Cerebellar Model Articulation Controller. Mathematics 2020, 8, 219. https://doi.org/10.3390/math8020219
Le T-L, Huynh T-T, Nguyen V-Q, Lin C-M, Hong S-K. Chaotic Synchronization Using a Self-Evolving Recurrent Interval Type-2 Petri Cerebellar Model Articulation Controller. Mathematics. 2020; 8(2):219. https://doi.org/10.3390/math8020219
Chicago/Turabian StyleLe, Tien-Loc, Tuan-Tu Huynh, Vu-Quynh Nguyen, Chih-Min Lin, and Sung-Kyung Hong. 2020. "Chaotic Synchronization Using a Self-Evolving Recurrent Interval Type-2 Petri Cerebellar Model Articulation Controller" Mathematics 8, no. 2: 219. https://doi.org/10.3390/math8020219
APA StyleLe, T.-L., Huynh, T.-T., Nguyen, V.-Q., Lin, C.-M., & Hong, S.-K. (2020). Chaotic Synchronization Using a Self-Evolving Recurrent Interval Type-2 Petri Cerebellar Model Articulation Controller. Mathematics, 8(2), 219. https://doi.org/10.3390/math8020219








