A Novel Meshfree Approach with a Radial Polynomial for Solving Nonhomogeneous Partial Differential Equations
Abstract
:1. Introduction
2. Formulation of the Meshfree Approach with a Radial Polynomial
3. Numerical Examples
3.1. Modeling of a Two-Dimensional Laplace Equation
3.2. Modeling of a Two-Dimensional Modified Helmholtz Equation
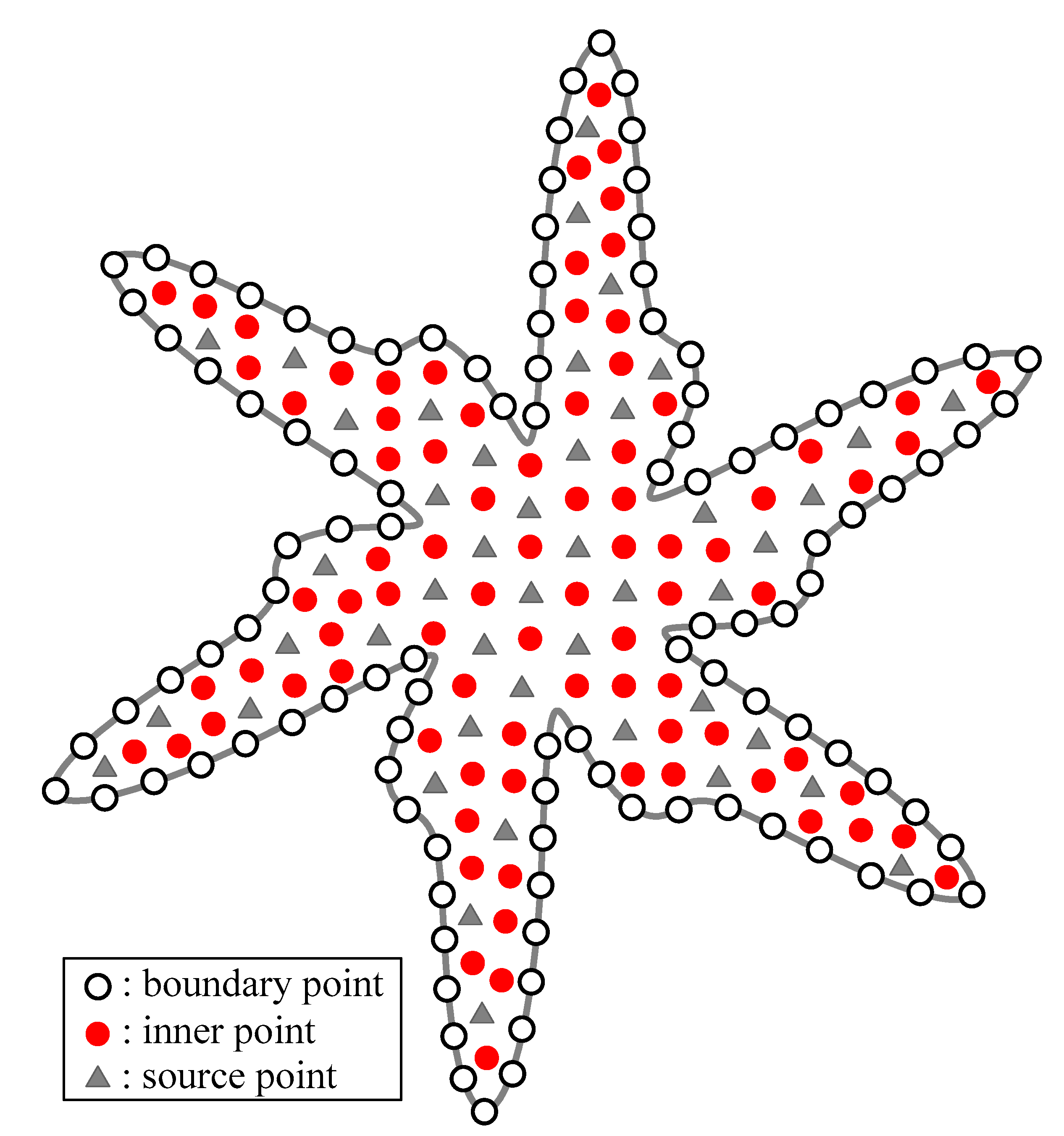
3.3. Modeling of a Two-Dimensional Poisson Equation
3.4. Modeling of a Two-Dimensional Nonhomogeneous Modified Helmholtz Equation
3.5. Modeling of a Nonhomogeneous Modified Helmholtz Equation in a Doubly Connected Region
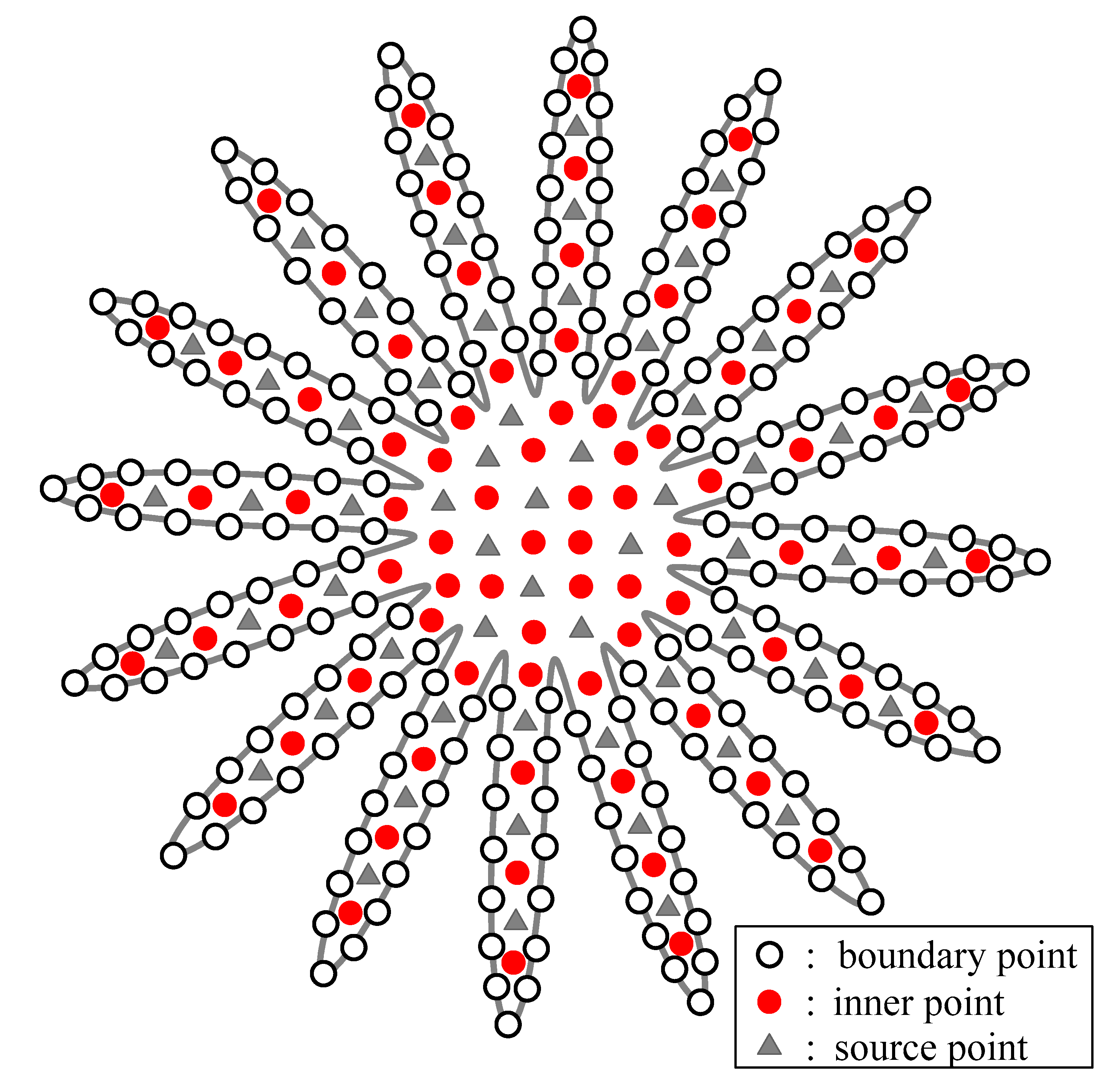
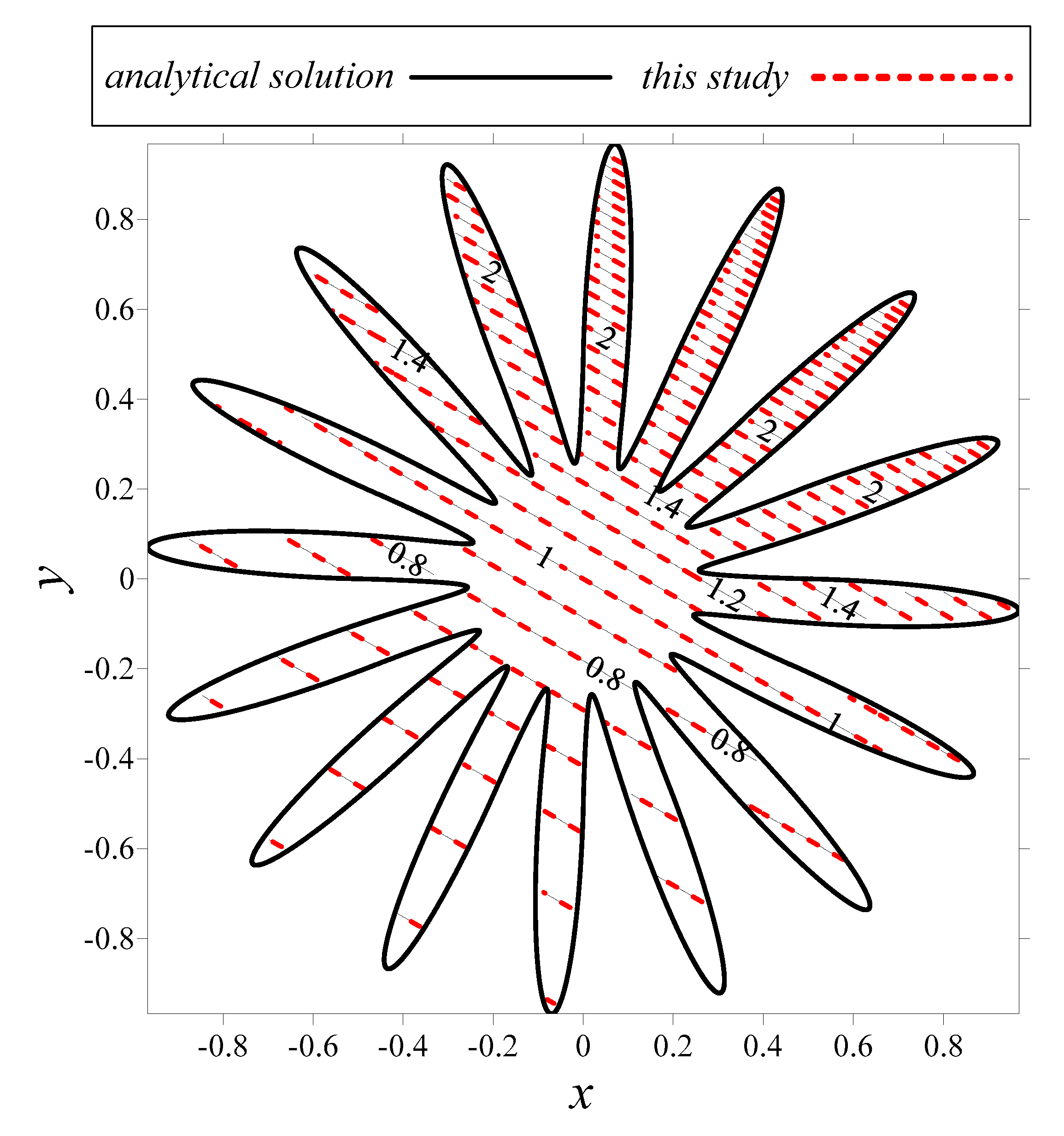
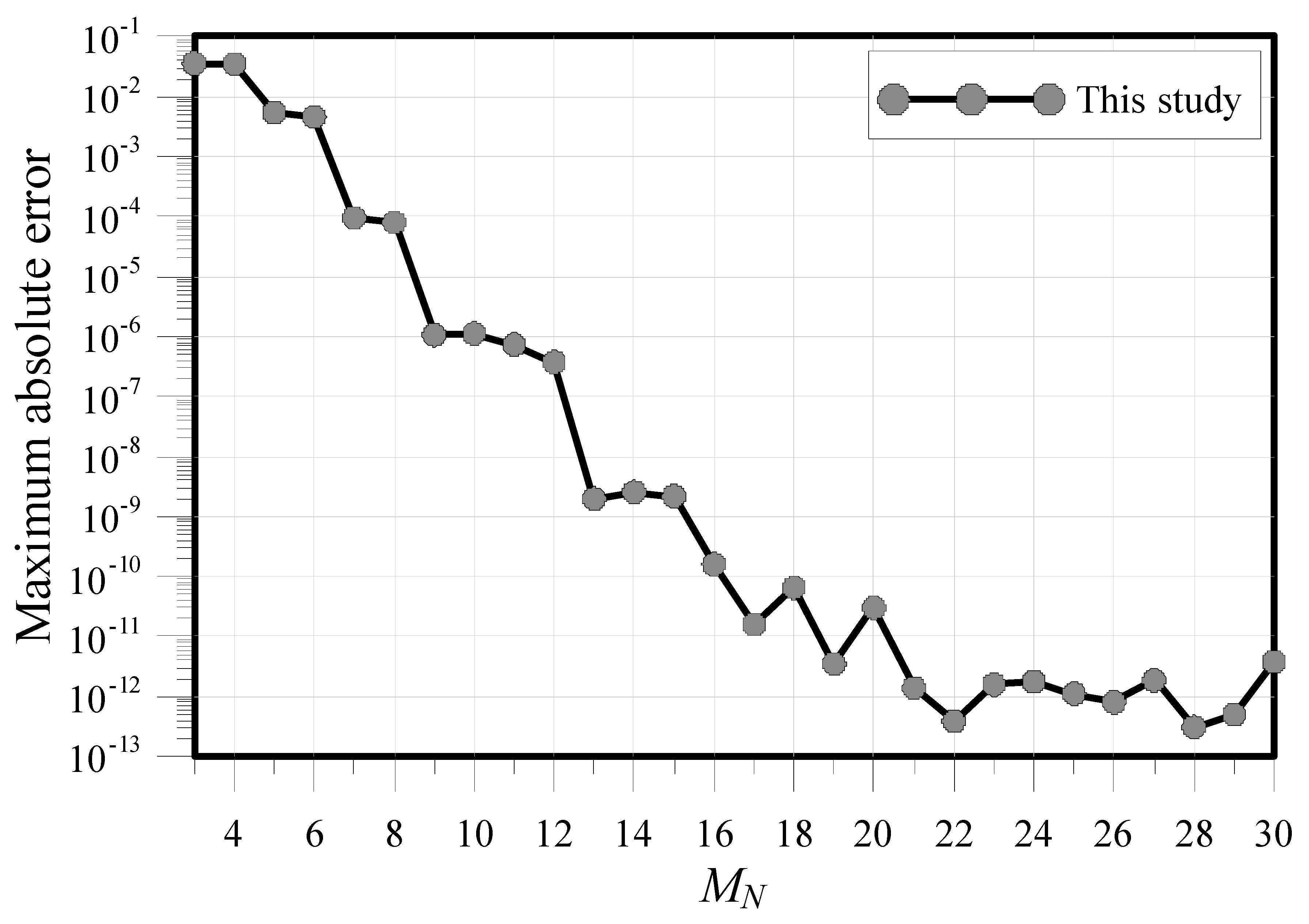
3.6. Modeling of the General Elliptic Partial Differential Equation
4. Discussion
5. Conclusions
- In this study, the meshfree approach using RPBF as the basis function is proposed. We resolve a major issue in the RBFCM using the MQ function for finding a satisfactory value for the shape parameter.
- The proposed method may obtain highly accurate numerical solutions with the use of higher order radial polynomial terms. Numerical examples show that the proposed RPBF is much more accurate than the MQ RBF, even when the optimal shape parameter for the MQ RBF is adopted. Additionally, the comparison results between the proposed RPBF and the PS RBF demonstrate that the accuracy of the proposed method is better than the PS RBF with the same number of collocation points.
- In this paper, a novel, meshfree approach using the RPBF is first presented. We conduct a pioneering work for solving the nonhomogeneous PDEs bounded by simply and doubly connected domains. The proposed novel method provides a promising solution in which the advantages of the conventional RBFCM are still remained, such as the domain collocation only. Moreover, the ease of use for solving nonhomogeneous PDEs is revealed, and the tedious procedure to determine the shape parameter is no longer required.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, Y.; Gao, X.; Xiao, M.Q. A high-order finite difference method for 1D nonhomogeneous heat equations. Numer. Meth. Part D 2009, 25, 327–346. [Google Scholar] [CrossRef]
- Park, Y.S.; Ang, W.T. A complex variable boundary element method for an elliptic partial differential equation with variable coefficients. Commun. Numer. Meth. Eng. 2000, 16, 697–703. [Google Scholar] [CrossRef]
- Fix, G.J.; Gunzburger, M.D.; Peterson, J.S. On finite element approximations of problems having inhomogeneous essential boundary conditions. Comput. Math. Appl. 1983, 9, 687–700. [Google Scholar] [CrossRef] [Green Version]
- Song, R.; Chen, W. An investigation on the regularized meshless method for irregular domain problems. CMES Comp. Model. Eng. 2009, 42, 59–70. [Google Scholar]
- Lin, J.; Chen, C.S.; Liu, C.S. Fast solution of three-dimensional modified Helmholtz equations by the method of fundamental solutions. Commun. Comput. Phy. 2016, 20, 512–533. [Google Scholar] [CrossRef]
- Kuo, L.H.; Gu, M.H.; Young, D.L.; Lin, C.Y. Domain type kernel-based meshless methods for solving wave equations. CMC Comput. Mater. Contin. 2013, 33, 213–228. [Google Scholar]
- Bourantas, G.C.; Skouras, E.D.; Loukopoulos, V.C.; Nikiforidisa, G.C. An accurate, stable and efficient domain-type meshless method for the solution of MHD flow problems. J. Comput. Phys. 2009, 228, 8135–8160. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.Z.; Li, X.L. Numerical analysis of the meshless element-free Galerkin method for hyperbolic initial-boundary value problems. Appl. Math. 2017, 62, 477–492. [Google Scholar] [CrossRef]
- Sun, F.X.; Liu, C.; Cheng, Y.M. An improved interpolating element-free Galerkin method based on nonsingular weight functions. Math. Probl. Eng. 2014, 2014, 323945. [Google Scholar] [CrossRef]
- Mirzaei, D.; Schaback, R. Direct meshless local Petrov–Galerkin (DMLPG) method: A generalized MLS approximation. Appl. Numer. Math. 2013, 68, 73–82. [Google Scholar] [CrossRef] [Green Version]
- Mirzaei, D.; Hasanpour, K. Direct meshless local Petrov–Galerkin method for elastodynamic analysis. Acta Mech. 2016, 227, 619–632. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Chen, Y.; Guo, C.X.; Fu, Z.H. Application of radial basis function method for solving nonlinear integral equations. J. Appl. Math. 2014, 2014, 381908. [Google Scholar] [CrossRef] [Green Version]
- Seydaoglu, M. A meshless method for Burgers’ equation using multiquadric radial basis functions with a Lie-group integrator. Mathematics 2019, 7, 113. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Dong, J.L.; Yao, L.Q. A modification of the moving least-squares approximation in the element-free Galerkin method. J. Appl. Math. 2014, 2014, 528082. [Google Scholar] [CrossRef]
- Assari, P.; Adibi, H.; Dehghan, M. A meshless method based on the moving least squares (MLS) approximation for the numerical solution of two-dimensional nonlinear integral equations of the second kind on non-rectangular domains. Numer. Algorithms 2014, 67, 423–455. [Google Scholar] [CrossRef]
- Fan, C.M.; Li, P.W. Generalized finite difference method for solving two-dimensional Burgers’ equations. Procedia Eng. 2014, 79, 55–60. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.M.; Li, P.W.; Yeih, W.C. Generalized finite difference method for solving two-dimensional inverse Cauchy problems. Inverse Probl. Sci. Eng. 2015, 23, 737–759. [Google Scholar] [CrossRef]
- Gu, Y.; Qu, W.Z.; Chen, W.; Song, L.; Zhang, C.Z. The generalized finite difference method for long-time dynamic modeling of three-dimensional coupled thermoelasticity problems. J. Comput. Phys. 2019, 384, 42–59. [Google Scholar] [CrossRef]
- Fornberg, B.; Larsson, E.; Flyer, N. Stable computations with Gaussian radial basis functions. SIAM. J. Sci. Comput. 2011, 33, 869–892. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Faul, A.C.; Powell, M.J.D. Proof of convergence of an iterative technique for thin plate spline interpolation in two dimensions. Adv. Comput. Math. 1999, 11, 183–192. [Google Scholar] [CrossRef]
- Powell, M.J.D. The uniform convergence of thin plate spline interpolation in two dimensions. Numer. Math. 1994, 68, 107–128. [Google Scholar] [CrossRef]
- Assari, P.; Dehghan, M. Application of thin plate splines for solving a class of boundary integral equations arisen from Laplace’s equations with nonlinear boundary conditions. Int. J. Comput. Math. 2019, 96, 170–198. [Google Scholar] [CrossRef]
- Bouhamidi, A.; Jbilou, K. Meshless thin plate spline methods for the modified Helmholtz equation. Comput. Methods Appl. Mech. Engrgy 2008, 197, 3733–3741. [Google Scholar] [CrossRef]
- Chen, W.; Tanaka, M. A meshless, integration-free, and boundary-only RBF technique. Comput. Math. Appl. 2002, 43, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Kołodziej, J.A.; Grabski, J.K. Application of the method of fundamental solutions and the radial basis functions for viscous laminar flow in wavy channel. Eng. Anal. Bound. Elem. 2015, 57, 58–65. [Google Scholar] [CrossRef]
- Ben-Ahmed, E.; Sadik, M.; Wakrim, M. Radial basis function partition of unity method for modelling water flow in porous media. Comput. Math. Appl. 2018, 75, 2925–2941. [Google Scholar] [CrossRef]
- Sarler, B. A radial basis function collocation approach in computational fluid dynamics. CMES Comp. Model. Eng. 2005, 7, 185–193. [Google Scholar]
- Li, Y.; Hon, Y.C. Finite integration method with radial basis function for solving stiff problems. Eng. Anal. Bound. Elem. 2017, 82, 32–42. [Google Scholar] [CrossRef]
- Liu, C.S.; Chang, C.W. An energy regularization of the MQ-RBF method for solving the Cauchy problems of diffusion-convection-reaction equations. Commun. Nonlinear Sci. 2019, 67, 375–390. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, G.R. On the optimal shape parameters of radial basis functions used for 2-D meshless methods. Comput. Method Appl. Mech. Eng. 2002, 191, 2611–2630. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Rocha, H. On the selection of the most adequate radial basis function. Appl. Math. Model. 2009, 33, 1573–1583. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Ferreira, A.J.M. Numerical experiments on optimal shape parameters for radial basis functions. Numer. Meth. Part. D 2010, 26, 675–689. [Google Scholar] [CrossRef]
- Afiatdoust, F.; Esmaeilbeigi, M. Optimal variable shape parameters using genetic algorithm for radial basis function approximation. Ain. Shams Eng. J. 2015, 6, 639–647. [Google Scholar] [CrossRef]
- Biazar, J.; Hosami, M. An interval for the shape parameter in radial basis function approximation. Appl. Math. Comput. 2017, 315, 131–149. [Google Scholar] [CrossRef]
- Chen, W.; Hong, Y.X.; Lin, J. The sample solution approach for determination of the optimal shape parameter in the Multiquadric function of the Kansa method. Comput. Math. Appl. 2018, 75, 2942–2954. [Google Scholar] [CrossRef]
- Fallah, A.; Jabbari, E.; Babaee, R. Development of the Kansa method for solving seepage problems using a new algorithm for the shape parameter optimization. Comput. Math. Appl. 2019, 77, 815–829. [Google Scholar] [CrossRef]
- Chen, C.S.; Lee, S.W.; Huang, C.S. Derivation of particular solutions using Chebyshev polynomial based functions. Int. J. Comp. Meth. 2011, 4, 15–32. [Google Scholar] [CrossRef]
- Tsai, C.C. Particular solutions of Chebyshev polynomials for polyharmonic and poly-Helmholtz equations. CMES-Comp. Model. Eng. 2008, 27, 151–162. [Google Scholar]
- Dangal, T.; Chen, C.S.; Lin, J. Polynomial particular solutions for solving elliptic partial differential equations. Comput. Math. Appl. 2017, 73, 60–70. [Google Scholar] [CrossRef]
- Lin, J.; Chen, C.S.; Wang, F.J.; Dangal, T. A new backward node interpolation method using polynomial basis functions for plane bending vibrations. Appl. Math. Model. 2017, 49, 452–469. [Google Scholar] [CrossRef]
- Ahmed, S.G. A collocation method using new combined radial basis functions of thin plate and multiquadraic types plate. Eng. Anal. Bound. Elem. 2006, 30, 697–701. [Google Scholar] [CrossRef]
- Xiang, S.; Bi, Z.Y.; Jiang, S.X.; Jin, Y.X.; Yang, M.S. Thin plate spline radial basis function for the free vibration analysis of laminated composite shells. Compos. Struct. 2011, 93, 611–615. [Google Scholar] [CrossRef]
- Muleshkov, A.S.; Golberg, M.A.; Chen, C.S. Particular solutions of Helmholtz-type operators using higher order polyhrmonic splines. Comput. Mech. 1999, 23, 411–419. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.S.; Liu, D.J. Optimal shape parameter in the MQ-RBF by minimizing an energy gap functional. Appl. Math. Lett. 2018, 86, 157–165. [Google Scholar] [CrossRef]
- Liu, C.S. Improving the ill-conditioning of the method of fundamental solutions for 2D Laplace equation. CMES-Comp. Model. Eng. 2009, 851, 1–17. [Google Scholar]
- Chen, C.S.; Fan, C.M.; Wen, P.H. The method of particular solutions for solving certain partial differential equations. Numer. Meth. Part. D 2012, 28, 506–522. [Google Scholar] [CrossRef]








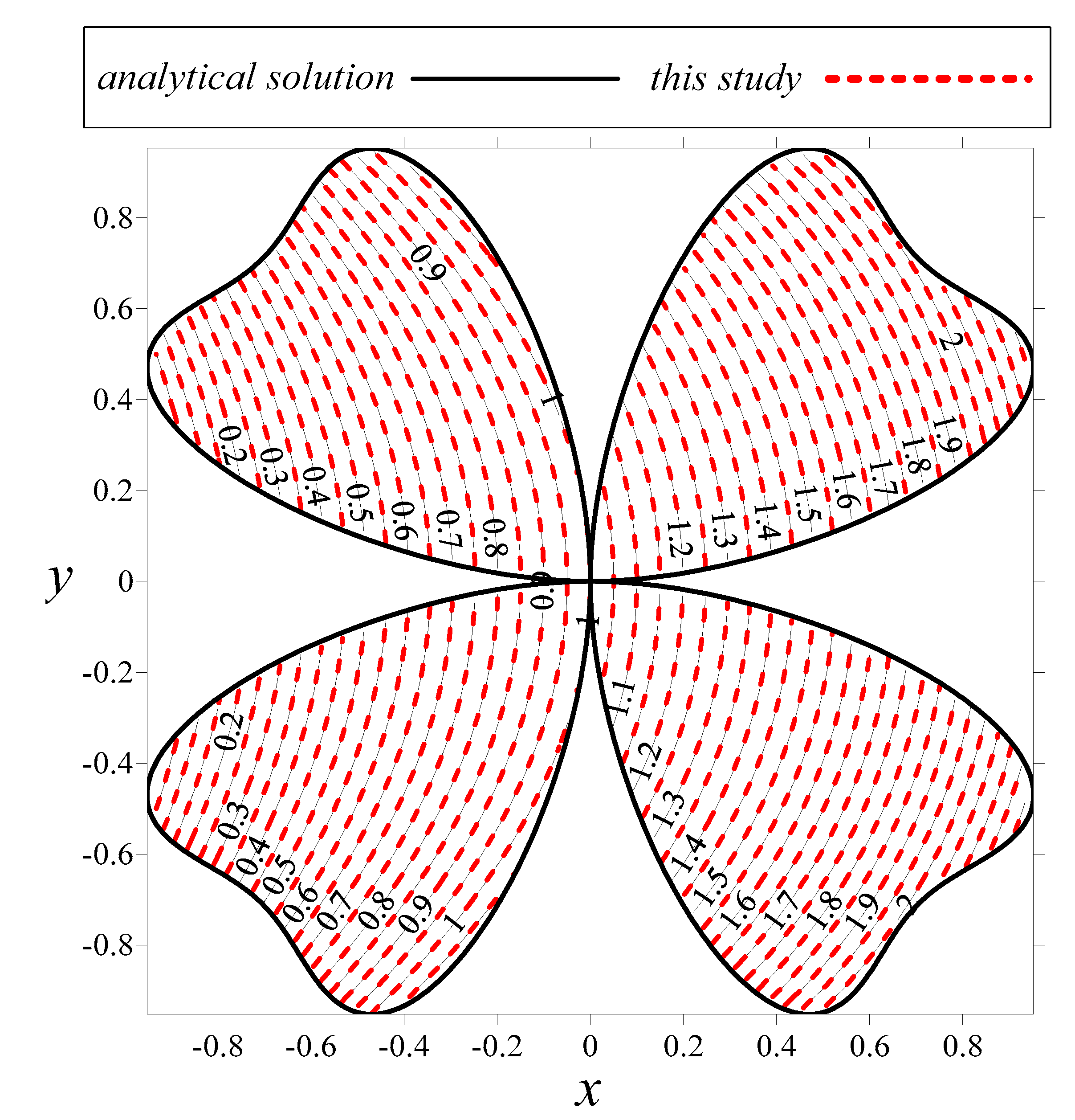



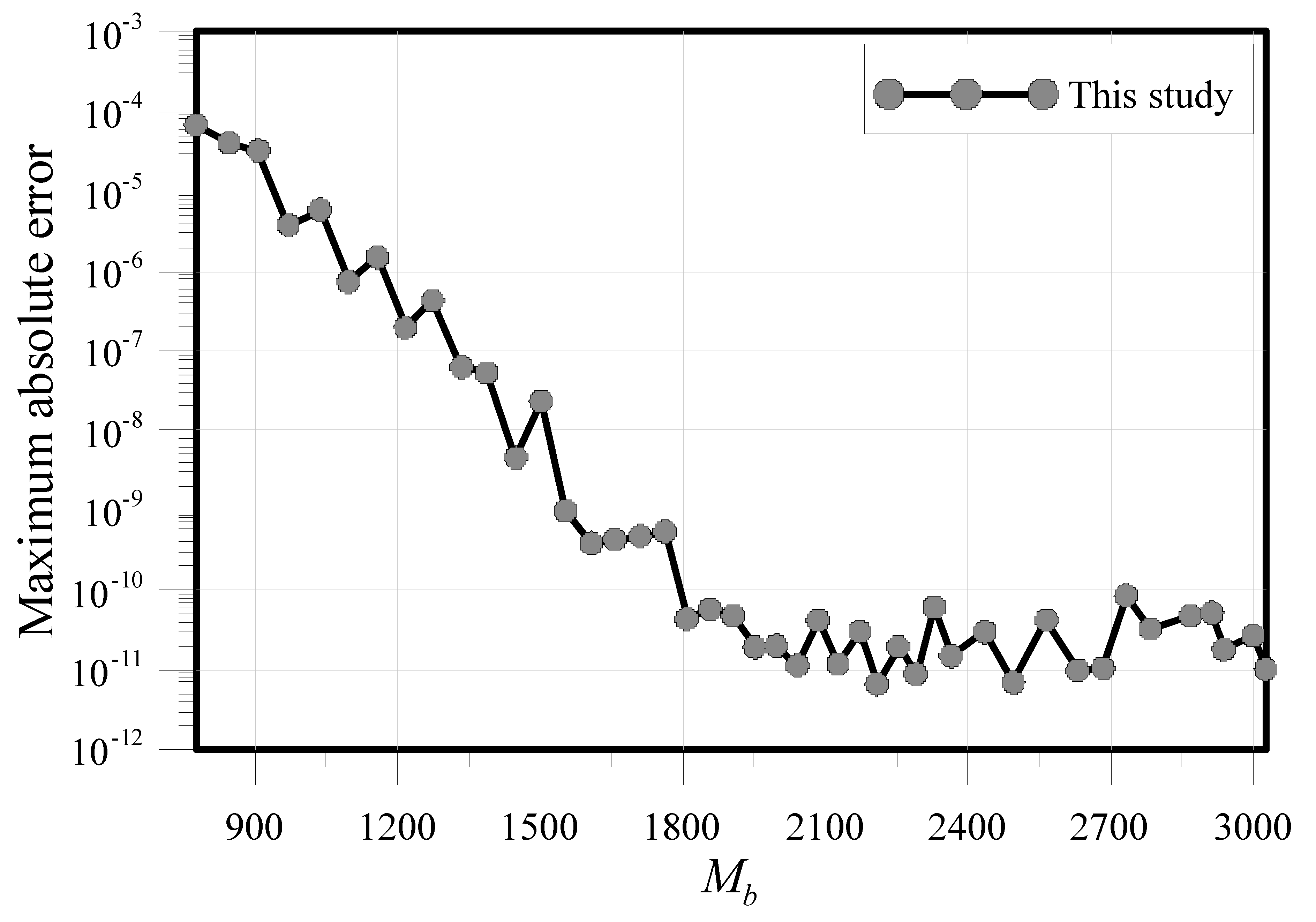


| Condition Number | MAE | CPU Time (s) | ||||
|---|---|---|---|---|---|---|
| This Study | This Study | MQ RBF | This Study | MQ RBF | ||
| 471 | 357 | 0.79 | 1.25 | |||
| 812 | 556 | 3.78 | 6.06 | |||
| 1471 | 1265 | 12.68 | 39.58 | |||
| 2486 | 2176 | 58.60 | 188.81 | |||
| 4056 | 3612 | 248.43 | 834.01 | |||
| 5808 | 5334 | 730.76 | 2532.95 | |||
| MAE | |||
|---|---|---|---|
| This Study | MQ RBF | ||
| 537 | 211 | () | |
| 840 | 486 | () | |
| 1579 | 1192 | () | |
| 2056 | 1548 | () | |
| 4351 | 3418 | () | |
| 6224 | 5234 | () | |
| Collocation Point Number | RMSE | |
|---|---|---|
| PS RBF49 | ||
| , | ||
| , | ||
| , | ||
| , | NA | |
| MAE | |
|---|---|
| 16 | |
| 25 | |
| 36 | |
| 100 | |
| 2000 | |
| 4000 | |
| 6000 | |
| 8000 | |
| 10,000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Xiao, J.-E.; Liu, C.-Y. A Novel Meshfree Approach with a Radial Polynomial for Solving Nonhomogeneous Partial Differential Equations. Mathematics 2020, 8, 270. https://doi.org/10.3390/math8020270
Ku C-Y, Xiao J-E, Liu C-Y. A Novel Meshfree Approach with a Radial Polynomial for Solving Nonhomogeneous Partial Differential Equations. Mathematics. 2020; 8(2):270. https://doi.org/10.3390/math8020270
Chicago/Turabian StyleKu, Cheng-Yu, Jing-En Xiao, and Chih-Yu Liu. 2020. "A Novel Meshfree Approach with a Radial Polynomial for Solving Nonhomogeneous Partial Differential Equations" Mathematics 8, no. 2: 270. https://doi.org/10.3390/math8020270
APA StyleKu, C.-Y., Xiao, J.-E., & Liu, C.-Y. (2020). A Novel Meshfree Approach with a Radial Polynomial for Solving Nonhomogeneous Partial Differential Equations. Mathematics, 8(2), 270. https://doi.org/10.3390/math8020270







