Derived Hyperstructures from Hyperconics
Abstract
:1. Introduction
2. Preliminaries
2.1. Conics
2.2. Krasner’s Hyperrings and Hyperfields
- (i)
- At least H has one identity e;
- (ii)
- every element x of H has one inverse, that is ;
- (iii)
- implies that and , where and .
- (i)
- for every
- (ii)
- for every
- (iii)
- there exists such that for every ,
- (iv)
- for every there exists a unique element such that ; (we shall write for and we call it the opposite of x.)
- (v)
- implies and ;
- (1)
- is a canonical hypergroup,
- (2)
- is a semigroup having zero as a bilaterally absorbing element, i.e., .
- (3)
- The multiplication is distributive with respect to the hyperoperation +.
- (i)
- and
- (ii)
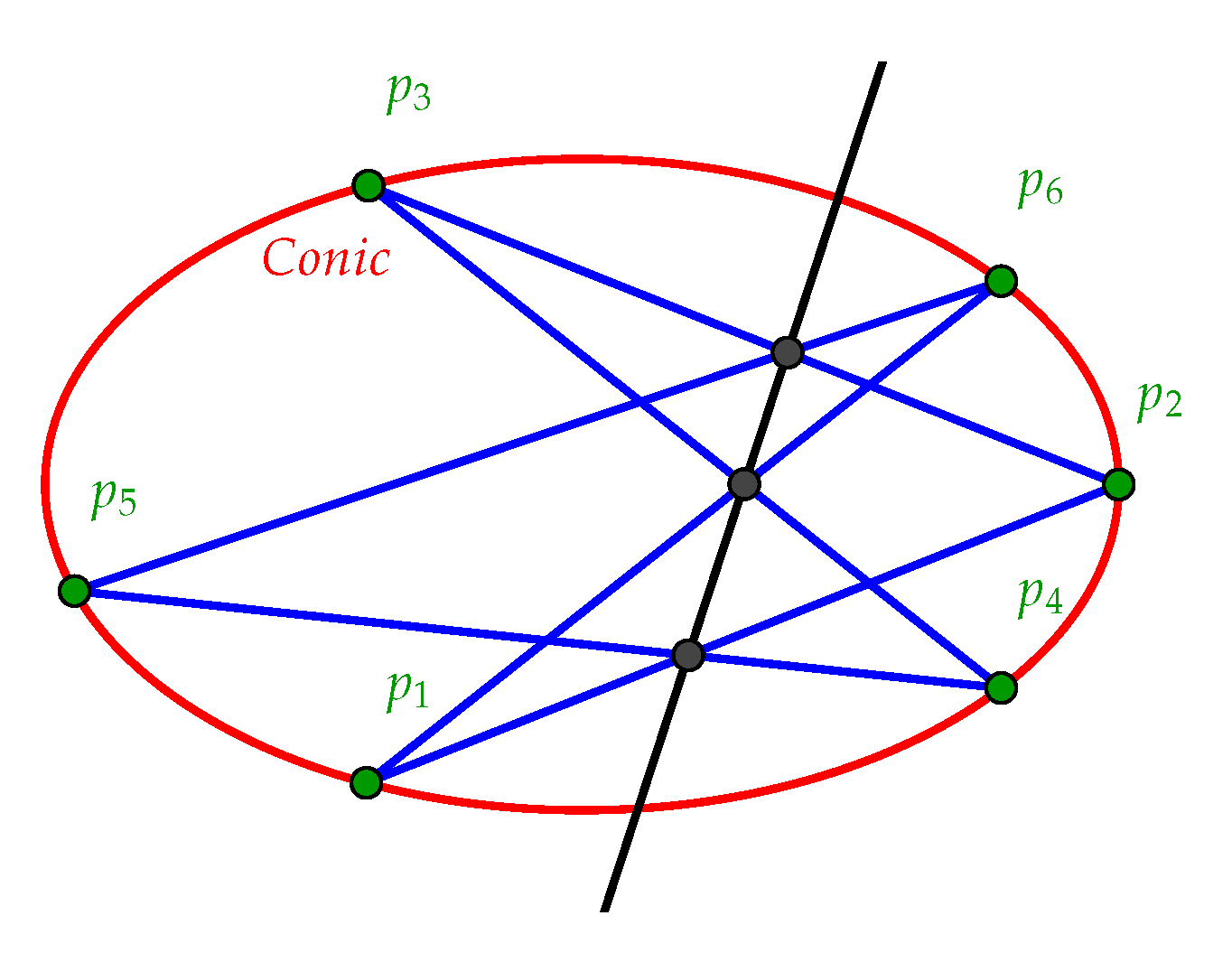
3. Hyperconic
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Marty, F. Sur Une Generalization de Group. In Proceedings of the 8th Congres Des Mathematiciens Scandinaves, Stockholm, Sweden, 14–18 August 1934; pp. 45–49. [Google Scholar]
- Corsini, P. Prolegomena of Hypergroup Theory; Aviani Editore: Tricesimo, Italy, 1993. [Google Scholar]
- Davvaz, B.; Leoreanu-Fotea, V. Hyperring Theory and Applications; International Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Corsini, P.; Leoreanu-Fotea, V. Applications of Hyperstructure Theory; Kluwer Academical Publications: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Vougiouklis, T. Hyperstructures and Their Representations; Hadronic Press: Palm Harbor, FL, USA, 1994. [Google Scholar]
- Hoskova, S.; Chvalina, J. A survey of investigations of the Brno research group in the hyperstructure theory since the last AHA Congress. In Proceedings of the AHA 2008: 10th International Congress-Algebraic Hyperstructures and Applications, University of Defence, Brno, Czech Republic, 3–9 September 2008; pp. 71–83, ISBN 78-80-7231-688-5. [Google Scholar]
- Antampoufis, N.; Hoskova-Mayerova, S. A Brief Survey on the two Different Approaches of Fundamental Equivalence Relations on Hyperstructures. Ratio Math. 2017, 33, 47–60. [Google Scholar] [CrossRef]
- Connes, A.; Consani, C. From monoids to hyperstructures: In search of an absolute arithmetic. In Casimir Force, Casimir Operators and the Riemann Hypothesis: Mathematics for Innovation in Industry and Science; van Dijk, G., Wakayama, M., Eds.; De Gruyter: Berlin, Germany, 2010; pp. 147–198. [Google Scholar]
- Connes, A.; Consani, C. The hyperring of adele classes. J. Number Theory 2011, 131, 159–194. [Google Scholar] [CrossRef] [Green Version]
- Connes, A.; Consani, C. The universal thickening of the field of real numbers. In Proceedings of the Thirteenth Conference of the Canadian Number Theory Association, Ottawa, ON, Canada, 16–20 June 2014. [Google Scholar]
- Viro, O. On basic concepts of tropical geometry. Proc. Steklov Inst. Math. 2011, 273, 252–282. [Google Scholar] [CrossRef]
- Gladki, P.; Marshall, M. Orderings and signatures of higher level on multirings and hyperfields. J.-Theory-Theory Appl. Algebr. Geom. Topol. 2012, 10, 489–518. [Google Scholar]
- Vahedi, V.; Jafarpour, M.; Aghabozorgi, H.; Cristea, I. Extension of elliptic curves on Krasner hyperfields. Comm. Algebra 2019, 47, 4806–4823. [Google Scholar] [CrossRef]
- Vahedi, V.; Jafarpour, M.; Cristea, I. Hyperhomographies on Krasner Hyperfields. Symmetry Class. Fuzzy Algebr. Hypercompos. Struct. 2019, 11, 1442. [Google Scholar] [CrossRef] [Green Version]
- Freni, D. Strongly Transitive Geometric Spaces: Applications to Hypergroups and Semigroups Theory. Comm. Algebra 2004, 32, 969–988. [Google Scholar] [CrossRef]
- Izhakian, Z.; Knebusch, M.; Rowen, L. Layered tropical mathematics. J. Algebra 2014, 416, 200–273. [Google Scholar] [CrossRef]
- Izhakian, Z.; Rowen, L. Supertropical algebra. Adv. Math. 2010, 225, 2222–2286. [Google Scholar] [CrossRef] [Green Version]
- Lorscheid, O. The geometry of blueprints: Part i: Algebraic background and scheme theory. Adv. Math. 2012, 229, 1804–1846. [Google Scholar] [CrossRef] [Green Version]
- Lorscheid, O. Scheme theoretic tropicalization. arXiv 2015, arXiv:1508.07949. [Google Scholar]
- Krasner, M. A class of hyperrings and hyperfields. Int. J. Math. Math. Sci. 1983, 6, 307–311. [Google Scholar] [CrossRef]
- Krasner, M. Approximation des corps value complets de caracteristique p10 par ceux de caracteristique 0. In Colloque d Algebre Superieure, Tenu a Bruxelles du 19 au 22 Decembre 1956; Centre Belge de Recherches Mathematiques Etablissements Ceuterick: Louvain, Belgium; Gauthier-Villars: Paris, France, 1957; pp. 129–206. [Google Scholar]
- Ameri, R.; Eyvazi, M.; Hoskova-Mayerova, S. Superring of Polynomials over a Hyperring. Mathematics 2019, 7, 902. [Google Scholar] [CrossRef] [Green Version]
- Mittas, J.D. Hypergroupes canoniques. Math. Balk. 1972, 2, 165–179. [Google Scholar]
- Massouros, C.G. A field theory problem relating to questions in hyperfield theory. In Proceedings of the International Conference on Numerical Analysis and Applied Mathematics, Halkidiki, Greece, 19–25 September 2011; Volume 1389, pp. 1852–1855. [Google Scholar]
- Dakic, J.; Jancic-Rasovic, S.; Cristea, I. Weak Embeddable Hypernear-Rings. Symmetry 2019, 11, 964. [Google Scholar] [CrossRef] [Green Version]
- Massouros, C.G.; Massouros, G.G. On Join Hyperrings. In Proceedings of the 10th International Congress on Algebraic Hyperstructures and Applications, University of Defence, Brno, Czech Republic, 3–9 September 2008; pp. 203–215. [Google Scholar]
- Massouros, C.G. On the theory of hyperrings and hyperfields. Algebra Log. 1985, 24, 728–742. [Google Scholar] [CrossRef]
- Massouros, G.G.; Massouros, C.G. Homomorphic Relations on Hyperringoids and Join Hyperrings. Ratio Math. 1999, 13, 61–70. [Google Scholar]
- Ameri, R.; Kordi, A.; Sarka-Mayerova, S. Multiplicative hyperring of fractions and coprime hyperideals. An. Stiintifice Univ. Ovidius Constanta Ser. Mat. 2017, 25, 5–23. [Google Scholar] [CrossRef] [Green Version]
- Jancic-Rasovic, S. About the hyperring of polynomials. Ital. J. Pure Appl. Math. 2007, 21, 223–234. [Google Scholar]
- Cristea, I.; Jancic-Rasovic, S. Operations on fuzzy relations: A tool to construct new hyperrings. J. Mult-Val. Logic Soft Comput. 2013, 21, 183–200. [Google Scholar]
- Jancic-Rasovic, S.; Dasic, V. Some new classes of (m,n)-hyperrings. Filomat 2012, 26, 585–596. [Google Scholar] [CrossRef]
- Cristea, I.; Jancic-Rasovic, S. Composition Hyperrings. An. Stiintifice Univ. Ovidius Constanta Ser. Mat. 2013, 21, 81–94. [Google Scholar] [CrossRef] [Green Version]
- Flaut, C.; Flaut, D.; Hoskova-Mayerova, S.; Vasile, R. From Old Ciphers to Modern Communications. Adv. Mil. Technol. 2019, 14, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Saeid, A.B.; Flaut, C.; Hoskova-Mayerova, S. Some connections between BCK-algebras and n-ary block codes. Soft Comput. 2017. [Google Scholar] [CrossRef] [Green Version]
- Hankerson, D.; Menezes, A.; Vanstone, S.A. Guide to Elliptic Curve Cryptography; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Koblitz, N. Introduction to elliptic curves and modular forms. In Volume 97 of Graduate Texts in Mathematics; Springer: New York, NY, USA, 1984. [Google Scholar]
- Silverman, J.H.; Tate, I.T. Rational Points on Elliptic Curves; Springer: New York, NY, USA, 1992; p. 289. [Google Scholar]
- Vougiouklis, T. The fundamental relation in hyperrings, The general hyperfield. In Proceedings of the 4th International Congress on AHA, Xanthi, Greece, 27–30 June 1990; World Scientific: Singapore, 1991; pp. 209–217. [Google Scholar]
- Berardi, L.; Eugeni, F.; Innamorati, S. Remarks on Hypergroupoids and Cryptography. J. Combin. Inform. Syst Sci. 1992, 17, 217–231. [Google Scholar]
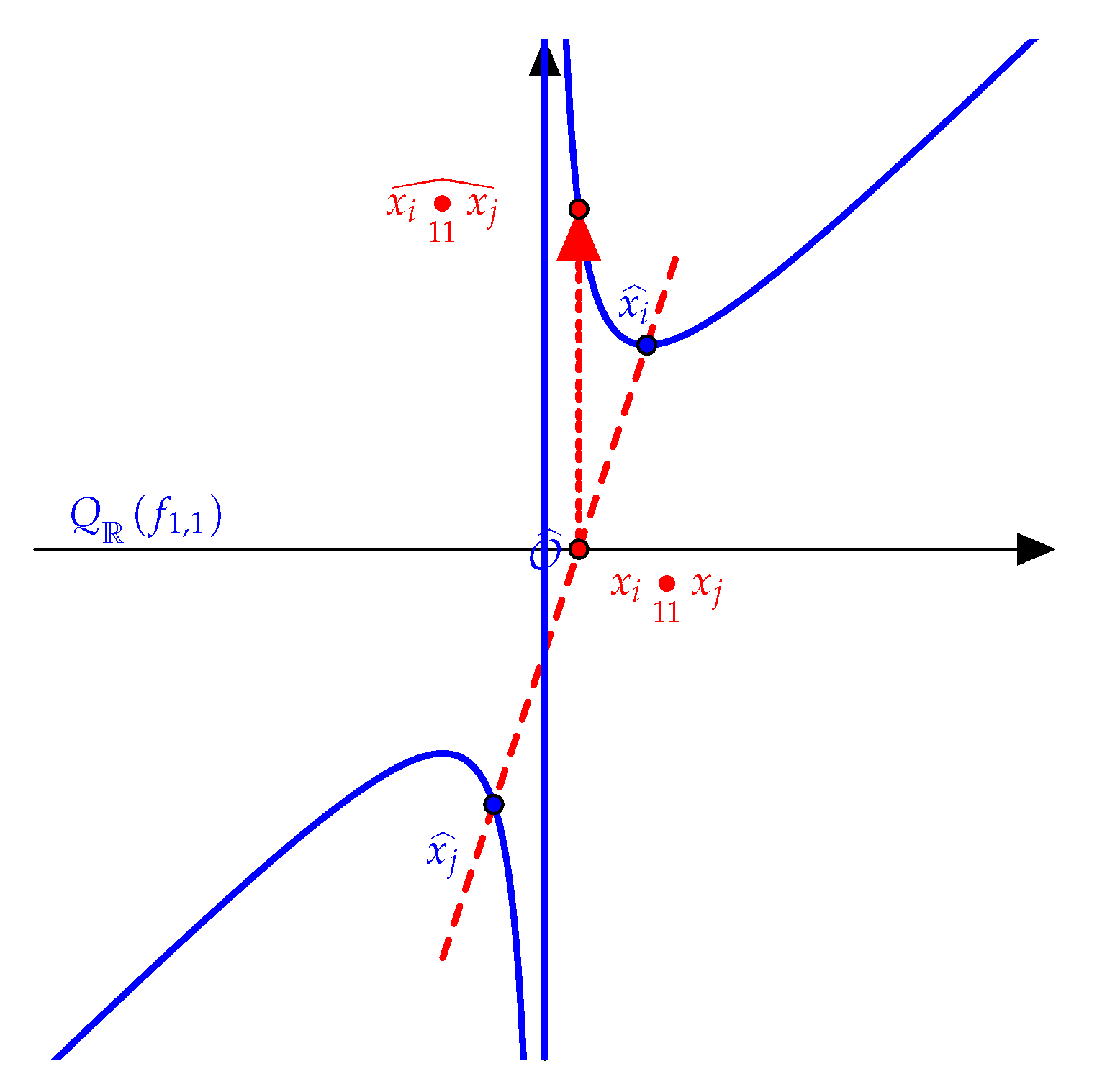

| •11 | (0, ∞) | (1, 2) | (2, −1) | (3, 1) | (−3, −1) | (−2, 1) | (−1, −2) | (∞, ∞) |
|---|---|---|---|---|---|---|---|---|
| ∘ | |||||
|---|---|---|---|---|---|
| ∘ | |||||
|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vahedi, V.; Jafarpour, M.; Hoskova-Mayerova, S.; Aghabozorgi, H.; Leoreanu-Fotea, V.; Bekesiene, S. Derived Hyperstructures from Hyperconics. Mathematics 2020, 8, 429. https://doi.org/10.3390/math8030429
Vahedi V, Jafarpour M, Hoskova-Mayerova S, Aghabozorgi H, Leoreanu-Fotea V, Bekesiene S. Derived Hyperstructures from Hyperconics. Mathematics. 2020; 8(3):429. https://doi.org/10.3390/math8030429
Chicago/Turabian StyleVahedi, Vahid, Morteza Jafarpour, Sarka Hoskova-Mayerova, Hossein Aghabozorgi, Violeta Leoreanu-Fotea, and Svajone Bekesiene. 2020. "Derived Hyperstructures from Hyperconics" Mathematics 8, no. 3: 429. https://doi.org/10.3390/math8030429
APA StyleVahedi, V., Jafarpour, M., Hoskova-Mayerova, S., Aghabozorgi, H., Leoreanu-Fotea, V., & Bekesiene, S. (2020). Derived Hyperstructures from Hyperconics. Mathematics, 8(3), 429. https://doi.org/10.3390/math8030429







