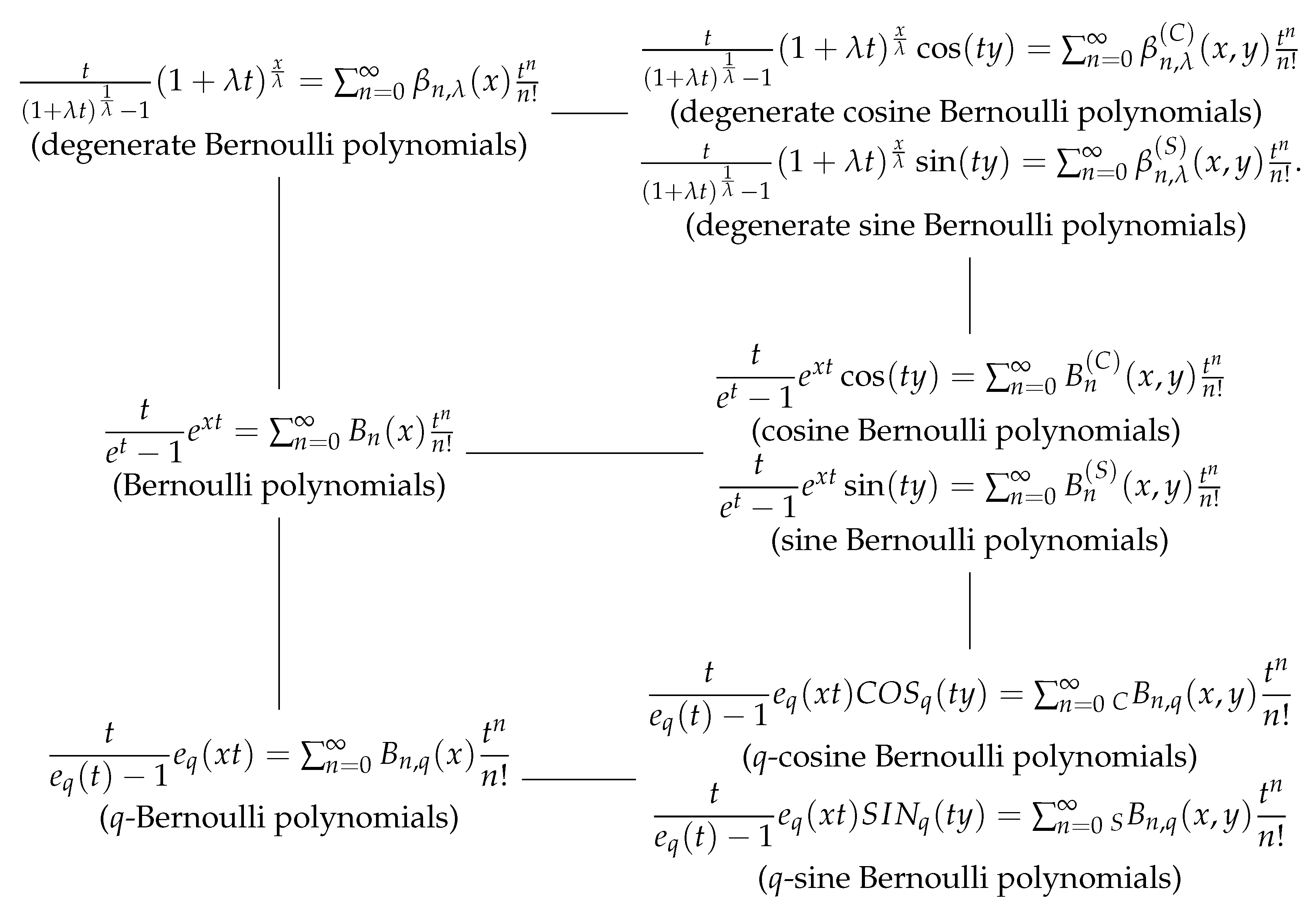Various Structures of the Roots and Explicit Properties of q-cosine Bernoulli Polynomials and q-sine Bernoulli Polynomials

Abstract

In this paper, we define cosine Bernoulli polynomials and sine Bernoulli polynomials related to the q-number. Furthermore, we intend to find the properties of these polynomials and check the structure of the roots. Through numerical experimentation, we look for various assumptions about the polynomials above.

1. Introduction

In the last three decades, the area of q-calculus has acted as a bridge between applied mathematics and engineering sciences. Many mathematicians studied the various fields of mathematics such as q-differential equations, q-integrals and differentials, q-series, q-trigonometric functions, q-hypergeometric functions, q-gamma and q-beta functions, and many properties, which are based on the discovery of q-numbers by Jackson (see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]). This q-calculus plays important roles in many different areas of mathematics such as number theory, combinatorics, special functions and analysis, differential equations, and numerous interesting properties of them (see [1,2]).

The following diagram shows the variations of the different types of degenerate Bernoulli polynomials, Bernoulli polynomials, and q-Bernoulli polynomials. Those polynomials in the first row and the second row of the diagram were studied by Carlitz [5] and Kim and Ryoo [13,14], respectively. The study of these has produced beneficial results in combinatorics and number theory. The motivation of this paper is to investigate some explicit identities for q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials in the third row of the diagram.

Properties of certain q-orthogonal polynomials are connected to the q-oscillator algebra. The Wall and q-Laguerre polynomials are shown to arise as matrix elements of q-exponentials of the generators in a representation of this algebra (see [21]). Throughout this paper, the symbols $\mathbb{N},\mathbb{Z},\mathbb{R}$ and $\mathbb{C}$ denote the set of natural numbers, the set of integers, the set of real numbers, and the set of complex numbers, respectively.

We would like to begin by introducing several definitions related to q-numbers used in this paper (see [3,4,7,9,10,17,19,21,25,26,27]). For any $n\in \mathbb{N}$, the q-number can be defined as follows.

$${\left[n\right]}_q=\frac{1-q^n}{1-q}=\sum _{0\le i\le n}{q}^i=1+q+q^2+\cdots +q^{n-1},\mathrm{where}q\ne 1.$$

(1)

We would like to begin by introducing several definitions related to q-numbers used in this paper.

Definition 1.

The Gaussian binomial coefficients are defined by:

$${\left[\begin{array}{c}m\\ r\end{array}\right]}_q=\left\{\begin{array}{cc}0& if r>m\\ \frac{(1-q^m)(1-q^{m-1})\cdots (1-q^{m-r+1})}{(1-q)(1-q^2)\cdots (1-q^r)}& if r\le m\end{array}\right.,$$

(2)

where m and r are non-negative integers. For $r=0$, the value is one since the numerator and the denominator are both empty products. Like the classical binomial coefficients, the Gaussian binomial coefficients are center-symmetric. There are analogues of the binomial formula, and this definition has a number of properties (see [3,4,6,7,8,9,11,12,19,22]).

Definition 2.

The q-analogues of ${(x-a)}^n$ and ${(x+a)}^n$ are defined by:

$$\begin{array}{c}\left(i\right){(x\ominus a)}_q^n=\left\{\begin{array}{cc}1& if n=0\\ (x-a)(x-qa)\cdots (x-q^{n-1}a)& if n\ge 1\end{array}\right.,\hfill \\ \left(ii\right){(x\oplus a)}_q^n=\left\{\begin{array}{cc}1& if n=0\\ (x+a)(x+qa)\cdots (x+q^{n-1}a)& if n\ge 1\end{array}\right.,\mathrm{respectively}.\hfill \end{array}$$

(3)

Definition 3.

Let z be any complex numbers with $\left|z\right|<1$. Two forms of q-exponential functions can be expressed as:

$$e_q\left(z\right)={\displaystyle \sum _{n=0}^{\infty }}\frac{z^n}{{\left[n\right]}_q!},E_q\left(z\right)={\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}\frac{z^n}{{\left[n\right]}_q!}.$$

(4)

From Definition 3, we note that (1) $e_q\left(x\right)e_q\left(y\right)=e_q(x+y)$ if $yx=qxy$, (2) $e_q\left(x\right)E_q(-x)=1$, and (3) $e_{q^{-1}}\left(x\right)=E_q\left(x\right)$.

Definition 4.

The definition of the q-derivative operator of any function f follows:

$$D_{q}f\left(x\right)=\frac{f\left(x\right)-f\left(qx\right)}{(1-q)x},x\ne 0,$$

(5)

and $D_{q}f\left(0\right)=f^{\prime }\left(0\right)$.

We can prove that f is differentiable at zero, and it is clear that $D_q{x}^n={\left[n\right]}_q{x}^{n-1}$.

Definition 5.

We define the q-integral as:

$${\int }_0^{b}f\left(x\right)d_{q}x=(1-q)b{\displaystyle \sum _{j=0}^{\infty }}{q}^{j}f\left(q^{j}b\right).$$

(6)

If this function, $f\left(x\right)$ is differentiable on the point x, and the q-derivative in Definition 4 goes to the ordinary derivative in the classical analysis when $q\to 1$.

Definition 6.

The q-trigonometric functions are:

$$\begin{array}{ll}{sin}_q\left(x\right)=\frac{e_q\left(ix\right)-e_q(-ix)}{2i},& {SIN}_q\left(x\right)=\frac{E_q\left(ix\right)-E_q(-ix)}{2i}\\ {cos}_q\left(x\right)=\frac{e_q\left(ix\right)+e_q(-ix)}{2},& {COS}_q\left(x\right)=\frac{E_q\left(ix\right)+E_q(-ix)}{2},\end{array}$$

(7)

where ${SIN}_q\left(x\right)={sin}_{q^{-1}}\left(x\right),{COS}_q\left(x\right)={cos}_{q^{-1}}\left(x\right)$.

In various mathematics applications, which include number theory, finite difference calculus, combinatorial analysis, p-adic analytic number theory, and other fields, the Bernoulli, Euler, and Genocchi polynomials are widely studied. Acknowledging their significance, many mathematicians are familiar with these numbers and polynomials, and they have been studied for a long time. The previous definitions and theorems are also applied to polynomials, and their properties are studied in various ways in combination with Bernoulli, Euler, and Genocchi polynomials, which are considered important (see [1,5,13,14,15,16,17,18,20,21,22,23,24,25,26,28]). The definition of q-Bernoulli polynomials is as follows:

Definition 7.

q-Bernoulli numbers, $B_{n,q}$, and polynomials, $B_{n,q}\left(z\right)$, can be expressed as(see [17]):

$${\displaystyle \sum _{n=0}^{\infty }}{B}_{n,q}\frac{t^n}{n!}=\frac{t}{e_q\left(t\right)-1},{\displaystyle \sum _{n=0}^{\infty }}{B}_{n,q}\left(z\right)\frac{t^n}{n!}=\frac{t}{e_q\left(t\right)-1}{e}^{tz}.$$

(8)

Recently, in [13], we confirmed the properties of cosine Bernoulli polynomials and sine Bernoulli polynomials. The definitions and representative properties of cosine Bernoulli polynomials and sine Bernoulli polynomials are the following.

Definition 8.

Cosine Bernoulli polynomials $B_n^{\left(C\right)}(x,y)$ and sine Bernoulli polynomials $B_n^{\left(S\right)}(x,y)$ are defined by means of the generating functions:

$${\displaystyle \sum _{n=0}^{\infty }}{B}_n^{\left(C\right)}(x,y)\frac{t^n}{n!}=\frac{t}{e^t-1}{e}^{tx}cos\left(ty\right),{\displaystyle \sum _{n=0}^{\infty }}{B}_n^{\left(S\right)}(x,y)\frac{t^n}{n!}=\frac{t}{e^t-1}{e}^{tx}sin\left(ty\right).$$

(9)

Theorem 1.

For $n\ge 1$, we have:

$$\begin{array}{l}\left(i\right)B_n^{\left(C\right)}(x+1,y)-B_n^{\left(C\right)}(x,y)=n{C}_{n-1}(x,y),\\ \left(ii\right)B_n^{\left(S\right)}(x+1,y)-B_n^{\left(S\right)}(x,y)=n{S}_{n-1}(x,y).\end{array}$$

(10)

Based on the above, many studies can confirm various polynomials and their properties (see [28]).

The main aim of this paper is to identify the property of q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials. In Section 2, we introduce cosine Bernoulli polynomials and sine Bernoulli polynomials combined with the q-number and confirm various properties and identities of polynomials. Here, we use the properties and exponential functions associated with the q-number. In Section 3, we can affirm the structure of the approximation roots of q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials. By changing the q-numbers, we can find interesting properties and speculations.

2. Some Properties of $\mathit{q}$-cosine Bernoulli Polynomials and $\mathit{q}$-sine Bernoulli Polynomials

In this section, we introduce q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials. By using the q-exponential function and q-trigonometric function, we can find various properties and identities.

Lemma 1.

Let $y\in \mathbb{R}$ and $i=\sqrt{-1}\in \mathbb{C}$. Then, we have:

$$\begin{array}{l}\left(i\right)E_q\left(ity\right)=CO{S}_q\left(ty\right)+iSI{N}_q\left(ty\right)\\ \left(ii\right)E_q(-ity)=CO{S}_q\left(ty\right)-iSI{N}_q\left(ty\right),\end{array}$$

(11)

where $SI{N}_q\left(x\right)=si{n}_{q^{-1}}\left(x\right)$, $CO{S}_q\left(x\right)=co{s}_{q^{-1}}\left(x\right).$

Proof. 

To find a relation between the q-exponential function, $E_q$, and the q-trigonometric function, in particular q-sine and q-cosine functions, we can make the following equation:

$$\begin{array}{cc}\hfill \left(i\right)E_q\left(ity\right)& =\frac{E_q\left(ity\right)+E_q(-ity)+E_q\left(ity\right)-E_q(-ity)}{2}\hfill \\ & =\frac{E_q\left(ity\right)+E_q(-ity)}{2}+i\frac{E_q\left(ity\right)-E_q(-ity)}{2i}\hfill \\ & =CO{S}_q\left(ty\right)+iSI{N}_q\left(ty\right),\hfill \end{array}$$

(12)

and:

$$\begin{array}{cc}\hfill \left(ii\right)E_q(-ity)& =\frac{E_q\left(ity\right)+E_q(-ity)-E_q\left(ity\right)+E_q(-ity)}{2}\hfill \\ & =\frac{E_q\left(ity\right)+E_q(-ity)}{2}-i\frac{E_q\left(ity\right)-E_q(-ity)}{2i}\hfill \\ & =CO{S}_q\left(ty\right)-iSI{N}_q\left(ty\right).\hfill \end{array}$$

(13)

Therefore, we obtain the required results, Lemma 1. □

Lemma 2.

Let $x,y\in \mathbb{R}$ and $i=\sqrt{-1}\in \mathbb{C}$. Then, we have:

$$\begin{array}{c}\left(i\right)e_q\left(tx\right)E_q\left(ity\right)=e_q\left(t{(x\oplus iy)}_q\right)\hfill \\ \left(ii\right)e_q\left(tx\right)E_q(-ity)=e_q\left(t{(x\ominus iy)}_q\right).\hfill \end{array}$$

(14)

Proof. 

$\left(i\right)$ Using the property of two q-exponential functions, we can find:

$$\begin{array}{cc}\hfill e_q\left(tx\right)E_q\left(ity\right)& ={\displaystyle \sum _{n=0}^{\infty }}{x}^n\frac{t^n}{{\left[n\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}{\left(iy\right)}^n\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{k}{2}\right)}{x}^{n-k}{\left(iy\right)}^k\right)\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}{(x\oplus iy)}_q^n\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & =e_q\left(t{(x\oplus iy)}_q\right),\hfill \end{array}$$

(15)

which is the required result.

$\left(ii\right)$ By substituting $-ity$ in $\left(i\right)$, we can find the result $\left(ii\right)$ in the same manner, so we omit this proof. □

Theorem 2.

For $\left|q\right|<1$, we obtain:

$$\begin{array}{c}\left(i\right){\displaystyle \sum _{n=0}^{\infty }}\left(B_{n,q}\left({(x\oplus iy)}_q\right)+B_{n,q}\left({(x\ominus iy)}_q\right)\right)\frac{t^n}{{\left[n\right]}_q!}=\frac{2t}{e_q\left(t\right)-1}{e}_q\left(tx\right)CO{S}_q\left(ty\right)\hfill \\ \left(ii\right){\displaystyle \sum _{n=0}^{\infty }}\left(B_{n,q}\left({(x\oplus iy)}_q\right)-B_{n,q}\left({(x\ominus iy)}_q\right)\right)\frac{t^n}{{\left[n\right]}_q!}=\frac{2it}{e_q\left(t\right)-1}{e}_q\left(tx\right)SI{N}_q\left(ty\right).\hfill \end{array}$$

(16)

Proof. 

$\left(i\right)$ By taking ${(x\oplus iy)}_q$ instead of z in q-Bernoulli polynomials and applying Lemmas 1 and 2, we obtain:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{B}_{n,q}\left({(x\oplus iy)}_q\right)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}{e}_q\left(t{(x\oplus iy)}_q\right)\hfill \\ & =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)E_q\left(ity\right)\hfill \\ & =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)(CO{S}_q\left(ty\right)+iSI{N}_q\left(ty\right)).\hfill \end{array}$$

(17)

In a similar way, we can find the following equation,

$${\displaystyle \sum _{n=0}^{\infty }}{B}_{n,q}\left({(x\ominus iy)}_q\right)\frac{t^n}{{\left[n\right]}_q!}=\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)(CO{S}_q\left(ty\right)-iSI{N}_q\left(ty\right)).$$

(18)

From (17) and (18), we can find:

$${\displaystyle \sum _{n=0}^{\infty }}(B_{n,q}\left({(x\oplus iy)}_q\right)+B_{n,q}\left({(x\ominus iy)}_q\right))\frac{t^n}{{\left[n\right]}_q!}=\frac{2t}{e_q\left(t\right)-1}{e}_q\left(tx\right)CO{S}_q\left(ty\right),$$

(19)

and:

$${\displaystyle \sum _{n=0}^{\infty }}(B_{n,q}\left({(x\oplus iy)}_q\right)-B_{n,q}\left({(x\ominus iy)}_q\right))\frac{t^n}{{\left[n\right]}_q!}=\frac{2it}{e_q\left(t\right)-1}{e}_q\left(tx\right)SI{N}_q\left(ty\right),$$

(20)

which is the required result shown of Theorem 2. □

From Lemmas 1 and 2 and Theorem 2, we need to find some properties of $e_q\left(tx\right)CO{S}_q\left(ty\right)$ and $e_q\left(tx\right)SI{N}_q\left(ty\right)$ in order to investigate some identities of special polynomials (see Definition 9).

Let:

$$e_q\left(tx\right)CO{S}_q\left(ty\right)={\displaystyle \sum _{n=0}^{\infty }}{C}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!},e_q\left(tx\right)SI{N}_q\left(ty\right)={\displaystyle \sum _{n=0}^{\infty }}{S}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}.$$

(21)

Then, we can find Lemma 3.

Lemma 3.

Let k be a nonnegative integer. Then, we derive:

$$\begin{array}{c}\left(i\right)C_{n,q}(x,y)={\displaystyle \sum _{k=0}^{\left[\frac{n}{2}\right]}}{\left[\begin{array}{c}n\\ 2k\end{array}\right]}_q{(-1)}^k{q}^{(2k-1)k}{x}^{n-2k}{y}^{2k}\hfill \\ \left(ii\right)S_{n,q}(x,y)={\displaystyle \sum _{k=0}^{\left[\frac{n-1}{2}\right]}}{\left[\begin{array}{c}n\\ 2k+1\end{array}\right]}_q{(-1)}^k{q}^{(2k+1)k}{x}^{n-(2k+1)}{y}^{2k+1},\hfill \end{array}$$

(22)

where $\left[x\right]$ is the greatest integer not exceeding x.

Proof. 

$\left(i\right)$ We also know that the cosine functions consist of even terms in power series. In the same manner on quantum-calculus, we note that $CO{S}_q\left(x\right)={\sum }_{n=0}^{\infty }\frac{{(-1)}^n}{{\left[2n\right]}_q!}{q}^{(2n-1)n}{x}^{2n}$ (see [12]). Multiplying $CO{S}_q\left(ty\right)$ in the q-exponential function, we have:

$$\begin{array}{cc}\hfill e_q\left(tx\right)CO{S}_q\left(ty\right)& ={\displaystyle \sum _{n=0}^{\infty }}{x}^n\frac{t^n}{{\left[n\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{(-1)}^n{q}^{(2n-1)n}{y}^{2n}\frac{t^{2n}}{{\left[2n\right]}_q!}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{(-1)}^k{q}^{(2k-1)k}{x}^{n-k}{y}^{2k}\frac{t^{n+k}}{{[n-k]}_q!{\left[2k\right]}_q!}\right)\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n+k\\ 2k\end{array}\right]}_q{(-1)}^k{q}^{(2k-1)k}{x}^{n-k}{y}^{2k}\right)\frac{t^{n+k}}{{[n+k]}_q!}.\hfill \end{array}$$

(23)

From Equation (21), it holds:

$${\displaystyle \sum _{n=0}^{\infty }}{C}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^{\left[\frac{n}{2}\right]}}{\left[\begin{array}{c}n\\ 2k\end{array}\right]}_q{(-1)}^k{q}^{(2k-1)k}{x}^{n-2k}{y}^{2k}\right)\frac{t^n}{{\left[n\right]}_q!}.$$

(24)

By comparing the coefficients of both sides, we complete the proof of Lemma 3$\left(i\right)$. $\left(ii\right)$ We also note that $SI{N}_q\left(x\right)={\sum }_{n=0}^{\infty }\frac{{(-1)}^n}{{[2n+1]}_q!}{q}^{(2n+1)n}{x}^{2n+1}$ in quantum calculus (see [12]), and we can derive:

$$\begin{array}{cc}\hfill e_q\left(tx\right)SI{N}_q\left(ty\right)& ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{x}^{n-k}\frac{t^{n-k}}{{[n-k]}_q!}{(-1)}^k{q}^{(2k+1)k}{y}^{2k+1}\frac{t^{2k+1}}{{[2k+1]}_q!}\right)\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n+1+k\\ 2k+1\end{array}\right]}_q{(-1)}^k{q}^{(2k+1)k}{x}^{n-k}{y}^{2k+1}\right)\frac{t^{n+k+1}}{{[n+k+1]}_q!}.\hfill \end{array}$$

(25)

By applying (21), we can change Equation (25) as follows:

$${\displaystyle \sum _{n=0}^{\infty }}{S}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^{\left[\frac{n-1}{2}\right]}}{\left[\begin{array}{c}n\\ 2k+1\end{array}\right]}_q{(-1)}^k{q}^{(2k+1)k}{x}^{n-(2k+1)}{y}^{2k+1}\right)\frac{t^n}{{\left[n\right]}_q!}.$$

(26)

From the equation above, we can find the required result of Lemma 3(ii). □

Now, we will introduce the q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials considered in the previous lemmas and theorem.

Definition 9.

Let x, y be real numbers. Then, q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials are defined by:

$${\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}=\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)CO{S}_q\left(ty\right),$$

(27)

and:

$${\displaystyle \sum _{n=0}^{\infty }}{}_S{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}=\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)SI{N}_q\left(ty\right),$$

(28)

respectively.

Corollary 1.

From Theorem 2 and Definition 9, it holds:

$$\begin{array}{c}\left(i\right)2{}_C{B}_{n,q}(x,y)=B_{n,q}\left({(x\oplus iy)}_q\right)+B_{n,q}\left({(x\ominus iy)}_q\right)\hfill \\ \left(ii\right)2i{}_S{B}_{n,q}(x,y)=B_{n,q}\left({(x\oplus iy)}_q\right)+B_{n,q}\left({(x\ominus iy)}_q\right).\hfill \end{array}$$

(29)

Theorem 3.

Let $x,y\in \mathbb{R}$. Then, we have:

$$\begin{array}{c}\left(i\right){}_C{B}_{n,q}(x,y)={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{B}_{k,q}{C}_{n-k,q}(x,y)\hfill \\ \left(ii\right){}_S{B}_{n,q}(x,y)={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{B}_{k,q}{S}_{n-k,q}(x,y),\hfill \end{array}$$

(30)

where $B_{n,q}$ is the q-Bernoulli numbers.

Proof. 

$\left(i\right)$ Here, we will show a relation between q-cosine Bernoulli polynomials and q-Bernoulli numbers. From the generating function of q-cosine Bernoulli polynomials, we can find the following Equation (31).

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)CO{S}_q\left(ty\right)\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}{B}_{n,q}\frac{t^n}{{\left[n\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{C}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{B}_{k,q}{C}_{n-k,q}(x,y)\right)\frac{t^n}{{\left[n\right]}_q!}.\hfill \end{array}$$

(31)

From (31), we can clearly obtain the required result of Theorem 3$\left(i\right)$.

$\left(ii\right)$ We omit the proof of Theorem 3$\left(ii\right)$ because we can derive the required result if we use a similar proof method as the proof in Theorem 3$\left(i\right)$. □

Theorem 4.

Let $n\in \mathbb{Z}$ and $x,y\in \mathbb{R}$. Then, we derive:

$$\begin{array}{c}\left(i\right)C_{n-1,q}(x,y)=\frac{1}{{\left[n\right]}_q}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{}_C{B}_{k,q}(x,y)-{}_C{B}_{n,q}(x,y)\right)\hfill \\ \left(ii\right)S_{n-1,q}(x,y)=\frac{1}{{\left[n\right]}_q}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{}_S{B}_{k,q}(x,y)-{}_S{B}_{n,q}(x,y)\right).\hfill \end{array}$$

(32)

Proof. 

$\left(i\right)$ We can transform the generating function of the q-cosine Bernoulli polynomials as follows when $e_q\left(t\right)\ne 1$.

$${\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}(e_q\left(t\right)-1)=t{e}_q\left(tx\right)CO{S}_q\left(ty\right).$$

(33)

The left-hand side of Equation (33) can be transformed to:

$${\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}(e_q\left(t\right)-1)={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{}_C{B}_{k,q}(x,y)-{}_C{B}_{n,q}(x,y)\right)\frac{t^n}{{\left[n\right]}_q!},$$

(34)

and the right-hand side of Equation (33) is transformed as:

$${\displaystyle \sum _{n=0}^{\infty }}{C}_{n,q}(x,y)\frac{t^{n+1}}{{\left[n\right]}_q!}={\displaystyle \sum _{n=0}^{\infty }}{\left[n\right]}_q{C}_{n-1,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}.$$

(35)

From (34) and (35), we complete the proof of Theorem 4$\left(i\right)$.

$\left(ii\right)$ Since we can find the required result from the same method $\left(i\right)$, we omit the proof of Theorem 4$\left(ii\right)$. □

Theorem 5.

Let a be a real number. Then, we investigate:

$$\begin{array}{c}\left(i\right){}_C{B}_{n,q}(1,y)={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{(-1)}^{n-k}{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}({\left[k\right]}_q{C}_{k-1,q}(a,y)+{}_C{B}_{k,q}(a,y))a^{n-k}\hfill \\ \left(ii\right){}_S{B}_{n,q}(1,y)={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{(-1)}^{n-k}{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}({\left[k\right]}_q{S}_{k-1,q}(a,y)+{}_S{B}_{k,q}(a,y))a^{n-k}.\hfill \end{array}$$

(36)

Proof. 

$\left(i\right)$ In the Introduction, we referred to the two kinds of q-exponential functions and noted that $e_q\left(x\right)E_q(-x)=1$. Using this property of q-exponential functions in q-cosine Bernoulli polynomials, we have:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(1,y)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}(e_q\left(t\right)-1+1)CO{S}_q\left(ty\right)\hfill \\ & =t{e}_q\left(ta\right)CO{S}_q\left(ty\right)E_q(-ta)+\frac{t}{e_q\left(t\right)-1}{e}_q\left(ta\right)CO{S}_q\left(ty\right)E_q(-ta)\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}{\left[n\right]}_q{C}_{n-1,q}(a,y)\frac{t^n}{{\left[n\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}{(-a)}^n\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & +{\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(a,y)\frac{t^n}{{\left[n\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}{(-a)}^n\frac{t^n}{{\left[n\right]}_q!}.\hfill \end{array}$$

(37)

Applying Cauchy’s product in Equation (37), we obtain:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(1,y)\frac{t^n}{{\left[n\right]}_q!}& ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{\left[k\right]}_q{C}_{k-1,q}(a,y)q^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{(-a)}^{n-k}\right)\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & +{\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{}_C{B}_{k,q}(a,y)q^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{(-a)}^{n-k}\right)\frac{t^n}{{\left[n\right]}_q!},\hfill \end{array}$$

(38)

where the required result $\left(i\right)$ is completed instantly.

$\left(ii\right)$ From the q-sine Bernoulli polynomials, we can consider the following equation in a similar way to $\left(i\right)$.

$$\begin{array}{c}{\displaystyle \sum _{n=0}^{\infty }}{}_S{B}_{n,q}(1,y)\frac{t^n}{{\left[n\right]}_q!}\hfill \\ =\frac{t}{e_q\left(t\right)-1}(e_q\left(t\right)-1+1)SI{N}_q\left(ty\right)\hfill \\ =t{e}_q\left(ta\right)SI{N}_q\left(ty\right)E_q(-ta)+\frac{t}{e_q\left(t\right)-1}{e}_q\left(ta\right)SI{N}_q\left(ty\right)E_q(-ta).\hfill \end{array}$$

(39)

Using the same method $\left(i\right)$, we are able to find the required result $\left(ii\right)$. □

Corollary 2.

From Theorem 5, it holds:

$$\begin{array}{cc}\left(i\right)\hfill & {}_C{B}_n(1,y)={\displaystyle \sum _{k=0}^n}\left(\genfrac{}{}{0pt}{}{n}{k}\right){(-1)}^{n-k}(k{C}_{k-1}(a,y)+{}_C{B}_k(a,y))a^{n-k}\hfill \\ \left(ii\right)\hfill & {}_S{B}_n(1,y)={\displaystyle \sum _{k=0}^n}\left(\genfrac{}{}{0pt}{}{n}{k}\right){(-1)}^{n-k}(k{S}_{k-1}(a,y)+{}_S{B}_k(a,y))a^{n-k}\hfill \\ \left(iii\right)\hfill & {\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{(-1)}^{n-k}{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{\left[k\right]}_q{C}_{k-1,q}(1,y)\hfill \\ & ={}_C{B}_{n,q}(1,y)-{\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{(-1)}^{n-k}{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{}_C{B}_{k,q}(1,y)\hfill \\ \left(iv\right)\hfill & {\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{(-1)}^{n-k}{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{\left[k\right]}_q{S}_{k-1,q}(1,y)\hfill \\ & ={}_S{B}_{n,q}(1,y)-{\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{(-1)}^{n-k}{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{}_S{B}_{k,q}(1,y).\hfill \end{array}$$

(40)

Theorem 6.

Let $x,y$, and r be any real numbers. Then, we investigate:

$$\begin{array}{c}\left(i\right){}_C{B}_{n,q}({(x\oplus r)}_q,y)+{}_S{B}_{n,q}({(x\ominus r)}_q,y)\hfill \\ ={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{r}^{n-k}\left({}_C{B}_{k,q}(x,y)+{(-1)}^{n-k}{}_S{B}_{k,q}(x,y)\right)\hfill \\ \left(ii\right){}_S{B}_{n,q}({(x\oplus r)}_q,y)+{}_C{B}_{n,q}({(x\ominus r)}_q,y)\hfill \\ ={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{r}^{n-k}\left({}_S{B}_{k,q}(x,y)+{(-1)}^{n-k}{}_C{B}_{k,q}(x,y)\right).\hfill \end{array}$$

(41)

Proof. 

$\left(i\right)$ By substituting ${(x\oplus r)}_q$ into x in the generating function of q-cosine Bernoulli polynomials, we can see the following equation.

$${\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}({(x\oplus r)}_q,y)\frac{t^n}{{\left[n\right]}_q!}=\frac{t}{e_q\left(t\right)-1}{e}_q\left(t{(x\oplus r)}_q\right)CO{S}_q\left(ty\right).$$

(42)

Using Lemma 2$\left(i\right)$ in Equation (42), we have:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}({(x\oplus r)}_q,y)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)CO{S}_q\left(ty\right)E_q\left(tr\right)\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}{r}^n\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{}_C{B}_{n,q}(x,y)r^{n-k}\right)\frac{t^n}{{\left[n\right]}_q!}.\hfill \end{array}$$

(43)

In a similar method, we can find the following equation.

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_S{B}_{n,q}({(x\ominus r)}_q,y)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)SI{N}_q\left(ty\right)E_q(-tr)\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{(-1)}^{n-k}{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{}_S{B}_{k,q}(x,y)r^{n-k}\right)\frac{t^n}{{\left[n\right]}_q!}.\hfill \end{array}$$

(44)

By adding (43) with (44), we can derive the result $\left(i\right)$ of Theorem 6.

$\left(ii\right)$ We also can find the following equations,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_S{B}_{n,q}({(x\oplus r)}_q,y)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}{e}_q\left(t{(x\oplus r)}_q\right)SI{N}_q\left(ty\right)\hfill \\ & =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)SI{N}_q\left(ty\right)E_q\left(tr\right),\hfill \\ \hfill {\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}({(x\ominus r)}_q,y)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}{e}_q\left(t{(x\ominus r)}_q\right)CO{S}_q\left(ty\right)\hfill \\ & =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)CO{S}_q\left(ty\right)E_q(-tr).\hfill \end{array}$$

(45)

Using Equation (45) appropriately, we can obtain the required result $\left(ii\right)$ of Theorem 6. □

Corollary 3.

From Theorem 6, it holds:

$$\begin{array}{c}\left(i\right){}_C{B}_{n,q}({(x\oplus r)}_q,y)+{}_C{B}_{n,q}({(x\ominus r)}_q,y)\hfill \\ ={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{r}^{n-k}\left({}_C{B}_{k,q}(x,y)+{(-1)}^{n-k}{}_C{B}_{k,q}(x,y)\right)\hfill \\ \left(ii\right){}_S{B}_{n,q}({(x\oplus r)}_q,y)+{}_S{B}_{n,q}({(x\ominus r)}_q,y)\hfill \\ ={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}{r}^{n-k}\left({}_S{B}_{k,q}(x,y)+{(-1)}^{n-k}{}_S{B}_{k,q}(x,y)\right).\hfill \end{array}$$

(46)

Corollary 4.

Setting $r=1$ in Theorem 6, it holds:

$$\begin{array}{c}\left(i\right){}_C{B}_{n,q}({(x\oplus 1)}_q,y)+{}_S{B}_{n,q}({(x\ominus 1)}_q,y)\hfill \\ ={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}\left({}_C{B}_{k,q}(x,y)+{(-1)}^{n-k}{}_S{B}_{k,q}(x,y)\right)\hfill \\ \left(ii\right){}_S{B}_{n,q}({(x\oplus 1)}_q,y)+{}_C{B}_{n,q}({(x\ominus 1)}_q,y)\hfill \\ ={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{q}^{\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)}\left({}_S{B}_{k,q}(x,y)+{(-1)}^{n-k}{}_C{B}_{k,q}(x,y)\right).\hfill \end{array}$$

(47)

Theorem 7.

For $x,y\in \mathbb{R}$, we derive:

$$\begin{array}{c}\left(i\right)\frac{\partial }{\partial x}{}_C{B}_{n,q}(x,y)={\left[n\right]}_q{}_C{B}_{n-1,q}(x,y),\frac{\partial }{\partial y}{}_C{B}_{n,q}(x,y)=-{\left[n\right]}_q{}_S{B}_{n-1,q}(x,qy).\hfill \\ \left(ii\right)\frac{\partial }{\partial x}{}_S{B}_{n,q}(x,y)={\left[n\right]}_q{}_S{B}_{n-1,q}(x,y),\frac{\partial }{\partial y}{}_S{B}_{n,q}(x,y)={\left[n\right]}_q{}_C{B}_{n-1,q}(x,qy).\hfill \end{array}$$

(48)

Proof. 

$\left(i\right)$ Considering the q-partial derivative for x in the q-cosine Bernoulli polynomials, we have:

$${\displaystyle \sum _{n=0}^{\infty }}\frac{\partial }{\partial x}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}=\frac{t}{e_q\left(t\right)-1}\frac{\partial }{\partial x}\left(e_q\left(tx\right)\right)CO{S}_q\left(ty\right).$$

(49)

Here, we note that:

$$D_q{e}_q\left(tx\right)={\displaystyle \sum _{n=1}^{\infty }}{x}^{n-1}\frac{t^n}{{[n-1]}_q!}=t{\displaystyle \sum _{n=0}^{\infty }}\frac{{\left(tx\right)}^n}{{\left[n\right]}_q!}=t{e}_q\left(tx\right).$$

(50)

Therefore, we obtain:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}\frac{\partial }{\partial x}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}& =t\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)CO{S}_q\left(ty\right)\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^{n+1}}{{\left[n\right]}_q!}={\displaystyle \sum _{n=0}^{\infty }}{\left[n\right]}_q{}_C{B}_{n-1,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}.\hfill \end{array}$$

(51)

For q-exponential function $E_q\left(tx\right)$, we note that:

$$D_q{E}_q\left(tx\right)=t{\displaystyle \sum _{n=1}^{\infty }}{q}^{\frac{n(n-1)}{2}}\frac{{\left(xt\right)}^{n-1}}{{[n-1]}_q!}=t{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}\frac{{\left(qtx\right)}^n}{{\left[n\right]}_q!}=t{E}_q\left(qtx\right),$$

(52)

and the q-derivative of q-trigonometric functions is:

$$D_{q}SI{N}_q\left(x\right)=CO{S}_q\left(qx\right),D_{q}CO{S}_q\left(x\right)=-SI{N}_q\left(qx\right).$$

(53)

To find the required result, we derive:

$$\begin{array}{cc}\hfill D_{q}CO{S}_q\left(ty\right)& =\frac{1}{2}{D}_q\left(E_q\left(ity\right)+E_q(-ity)\right)\hfill \\ & =\frac{1}{2}{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}{D}_q\left(y^n+{(-1)}^n{y}^n\right)\frac{{\left(it\right)}^n}{{\left[n\right]}_q!}\hfill \\ & =\frac{1}{2}\left(it{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}\frac{{\left(iqty\right)}^n}{{\left[n\right]}_q!}-it{\displaystyle \sum _{n=0}^{\infty }}{q}^{\left(\genfrac{}{}{0pt}{}{n}{2}\right)}\frac{{(-iqty)}^n}{{\left[n\right]}_q}\right)\hfill \\ & =\frac{it(E_q\left(iqty\right)-E_q(-iqty))}{2}\hfill \\ & =-\frac{t(E_q\left(iqty\right)-E_q(-iqty))}{2i}.\hfill \end{array}$$

(54)

Since $SI{N}_q\left(x\right)=\frac{E_q\left(ix\right)-E_q(-ix)}{2i}$, we can find:

$$D_{q}CO{S}_q\left(ty\right)=-tSI{N}_q\left(qty\right).$$

(55)

Hence, we investigate:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}& =\frac{t}{e_q\left(t\right)-1}{e}_q\left(tx\right)\frac{\partial }{\partial y}CO{S}_q\left(ty\right)\hfill \\ & =-\frac{t^2}{e_q\left(t\right)-1}{e}_q\left(tx\right)SI{N}_q\left(qty\right)\hfill \\ & =-{\displaystyle \sum _{n=0}^{\infty }}{}_S{B}_{n,q}(x,qy)\frac{t^{n+1}}{{\left[n\right]}_q!}=-{\displaystyle \sum _{n=0}^{\infty }}{\left[n\right]}_q{}_S{B}_{n-1,q}(x,qy)\frac{t^n}{{\left[n\right]}_q!},\hfill \end{array}$$

(56)

and complete the proof of Theorem 7$\left(i\right)$.

$\left(ii\right)$ We note that:

$$D_{q}SI{N}_q\left(ty\right)=\frac{1}{2i}{D}_q\left(E_q\left(ity\right)-E_q(-ity)\right)=tCO{S}_q\left(qty\right).$$

(57)

By using Equation (57) and applying a similar proof method as $\left(i\right)$, we can find the required result, so we omit the proof of Theorem 7$\left(ii\right)$. □

Based on the content above, we introduce the new type of q-Bernoulli polynomials, which are polynomials of q-cosine Bernoulli polynomials when $x=0$.

Definition 10.

For $y\in \mathbb{R}$, we define the new type of q-Bernoulli polynomials as:

$${\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}\left(y\right)\frac{t^n}{{\left[n\right]}_q!}=\frac{t}{e_q\left(t\right)-1}CO{S}_q\left(ty\right),{\displaystyle \sum _{n=0}^{\infty }}{}_S{B}_{n,q}\left(y\right)\frac{t^n}{{\left[n\right]}_q!}=\frac{t}{e_q\left(t\right)-1}SI{N}_q\left(ty\right).$$

(58)

Theorem 8.

Let $x,y$ be real numbers. Then, we have:

$$\begin{array}{c}\left(i\right){}_C{B}_{n,q}(x,y)={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{}_C{B}_{k,q}\left(y\right)x^{n-k}\hfill \\ \left(ii\right){}_S{B}_{n,q}(x,y)={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{}_S{B}_{k,q}\left(y\right)x^{n-k}.\hfill \end{array}$$

(59)

Proof. 

$\left(i\right)$ From the q-cosine Bernoulli polynomials, we find:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}(x,y)\frac{t^n}{{\left[n\right]}_q!}& ={\displaystyle \sum _{n=0}^{\infty }}{}_C{B}_{n,q}\left(y\right)\frac{t^n}{{\left[n\right]}_q!}{\displaystyle \sum _{n=0}^{\infty }}{x}^n\frac{t^n}{{\left[n\right]}_q!}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q{}_C{B}_{k,q}\left(y\right)x^{n-k}\right)\frac{t^n}{{\left[n\right]}_q!},\hfill \end{array}$$

(60)

and we obtain the required result $\left(i\right)$.

$\left(ii\right)$ We omit the proof of Theorem 8$\left(ii\right)$ because the proof is very similar to $\left(i\right)$. □

Corollary 5.

Putting $x=1$ in Theorem 8, it holds:

$${}_C{B}_{n,q}(1,y)+{}_S{B}_{n,q}(1,y)={\displaystyle \sum _{k=0}^n}{\left[\begin{array}{c}n\\ k\end{array}\right]}_q\left({}_C{B}_{k,q}\left(y\right)+{}_S{B}_{k,q}\left(y\right)\right).$$

(61)

3. The Structures, Experiments, and Speculations of Specific Approximations of ${}_{\mathit{C}}{\mathit{B}}_{\mathit{n},\mathit{q}}(\mathit{x},\mathit{y})$ and ${}_{\mathit{S}}{\mathit{B}}_{\mathit{n},\mathit{q}}(\mathit{x},\mathit{y})$

In this section, we would like to confirm the specific polynomial of q-cosine Bernoulli polynomials and q-sine Bernoulli polynomials. Mathematica can be used to identify the structure and build-up of the roots of polynomials to think bout a number of assumptions.

Example 1.

The specific polynomials of $C_{n,q}$ defined in Section 2 are shown below:

$$\begin{array}{c}{C}_{0,q}(x,y)=1\hfill \\ C_{1,q}(x,y)=x\hfill \\ C_{2,q}(x,y)=x^2-q{y}^2\hfill \\ C_{3,q}(x,y)=x^3-q(1+q+q^2)x{y}^2\hfill \\ C_{4,q}(x,y)=x^4-q(1+q^2)(1+q+q^2)x^2{y}^2+q^6{y}^4\hfill \\ C_{5,q}(x,y)=x^5-q(1+q^2)(1+q+q^2+q^3+q^4)x^3{y}^2+q^6(1+q+q^2+q^3+q^4)x{y}^4\hfill \end{array}$$

Let us take a look at the specific shape and structure of the roots for the q-cosine Bernoulli polynomials defined in Definition 9, which are related to $C_{n,q}$.

Example 2.

By using the q-cosine Bernoulli polynomials from the theorems obtained in Section 2, we can discover the following:

$$\begin{array}{c}{}_C{B}_{0,q}(x,y)=0\hfill \\ {}_C{B}_{1,q}(x,y)=1\hfill \\ {}_C{B}_{2,q}(x,y)=(1+q)(1+x)\hfill \\ {}_C{B}_{3,q}(x,y)=(1+q+q^2)(2+x+x^2+q(1+x-y^2))\hfill \\ {}_C{B}_{4,q}(x,y)=\frac{((1-q^4)(1+x^3+(1+q+q^2)(1+x)-q(1+q+q^2)x{y}^2}{1-q}+\cdots .\hfill \end{array}$$

Let us check the structure of the roots of these q-cosine Bernoulli polynomials. First, assume that $y=5$. Let us change q and n in these circumstances. Then, the following Figure 1 can be obtained. First, when q is fixed at $0.9$, the figure on the left is when $n=10$, the center is when $n=20$, and the right is when $n=30$. Then, the following Figure 1 can be obtained.

Figure 1. Approximate root of ${}_C{B}_{n,0.9}(x,5)$ for $n=10,20,30$.

Based on Figure 1, we can assume that the larger the value of n, the more elliptical the structure becomes, excluding the three real roots. Figure 2 is the structure of approximation roots when $n=50$.

Figure 2. Approximate roots for ${}_C{B}_{50,0.9}(x,5)$.

From the Figure above, we can make the following assumption.

Conjecture 3.

The greater the value of n is in ${}_C{B}_{n,0.9}(x,5)$, the greater the distribution of approximate roots leaving out the three real roots shows an elliptical structure leaving out the three real roots.

Now, we are going to leave y at five and change the value of q. The following Figure 3 shows the distribution of the roots at $q=0.5$. The figure on the left is the distribution of approximation roots at $n=10$, and the figure on the right is at $n=30$. In Figure 3, we can see that as n increases, the roots excluding three real roots become closer to a circle.

Figure 3. Approximate roots of ${}_C{B}_{n,0.5}(x,5)$ for $n=10,20,30$.

Here, we can make the following assumption through Mathematica and also by observing Figure 1, Figure 2 and Figure 3.

Conjecture 4.

${}_C{B}_{(}n,q)(x,5)$ always contains only three real roots in the range of $0.5\le q<1$.

Let us look at the structure of the roots that supports the assumption above. Figure 4 is when y is fixed at five. In Figure 4, the left figure shows the structure of approximations at $q=0.9$, and the right figure shows when $q=0.5$.

Figure 4. Stacking structure in 3D of ${}_C{B}_{n,q}(x,5)$ for $2\le n\le 30,0.5\le q\le 0.9$.

Let us check Figure 5 by observing the last picture of ${}_C{B}_{n,0.1}(x,5)$. As before, fix the value of y at five. The left figure in Figure 5 shows the location of the approximations at $n=10$, while the middle one shows when $n=20$, and finally, the right one shows when $n=30$. Most importantly, in Figure 5, we can see that as the value of q approaches zero and as n increases, the structure changes from an ellipse to a circular structure.

Figure 5. Approximate roots of ${}_C{B}_{n,0.1}(x,5)$ for $n=10,20,30$.

From now on, let us look at the polynomial of $S_{n,p,q}$ associated with the q-sine function and find the q-sine Bernoulli polynomials.

Example 5.

If you obtain a specific polynomial of $S_{n,p,q}$, this is the following:

$$\begin{array}{c}{S}_{0,q}(x,y)=0\hfill \\ S_{1,q}(x,y)=\frac{y}{1+q}\hfill \\ S_{2,q}(x,y)=\frac{xy}{1+q+q^2}\hfill \\ S_{3,q}(x,y)=\frac{y(x^2-q^3(1+q^2)y^2)}{(1+q)(1+q^2)}\hfill \\ S_{4,q}(x,y)=\frac{x^{3}y}{1+q+q^2+q^3+q^4}-\frac{q^3(1+q^2)x{y}^3}{1+q+q^2}\hfill \end{array}$$

Here, we will visualize the structure of the roots in $C_{n,p,q}$ and in $S_{n,p,q}$. Figure 6 shows the build-up of roots for $C_{n,p,q}$. After fixing y at five, the figure on the far left is shown at $q=0.9$ and the figure on the far right is at $q=0.1$.

Figure 6. Stacking structure of $C_{n,q}(x,5)$ for $2\le n\le 30,q=0.9,0.5,0.1$.

The following Figure 7 shows a stacked structure of roots for $S_{n,p,q}$. This is also a form obtained under the same conditions shown in Figure 6, and compared to Figure 6, the lower the value of n for $q=0.9$, the more likely it will have a slightly different change in location from $C_{n,p,q}$. While the distribution of approximation roots appears similar, we can figure out that the approximation roots themselves are different.

Figure 7. Stacking structure of $S_{n,q}(x,5)$ for $2\le n\le 30,q=0.9,0.5,0.1$.

From now on, let us find the q-sine Bernoulli polynomials.

Example 6.

The q-sine Bernoulli polynomials are the following:

$$\begin{array}{cc}\hfill {}_S{B}_{0,q}(x,y)& =0\hfill \\ \hfill {}_S{B}_{1,q}(x,y)& =\frac{y}{1+q}\hfill \\ \hfill {}_S{B}_{2,q}(x,y)& =\frac{(1+q+q^2+x+qx)y}{1+q+q^2}\hfill \\ \hfill {}_S{B}_{3,q}(x,y)& =\frac{y(2+x+x^2+q(3+2x+x^2)+q^2(5+2x+x^2)-q^6{y}^2-q^7{y}^2+q^5(1-2y^2)}{(1+q)(1+q^2)}\hfill \\ & +\frac{q^4(3+x-y^2)+q^3(4+2x-y^2))}{(1+q)(1+q^2)}\hfill \\ {}_S{B}_{4,q}(x,y)\hfill & =\frac{1}{1-q}(1-q^4)y\left(\frac{1}{1+q}+\frac{x^3}{1+q+q^2+q^3+q^4}+\frac{1+q+q^2+x+qx}{1+q}\right)\hfill \\ & -\frac{1}{1-q}(1-q^4)y\left(\frac{q^3(1+q^2)x{y}^2}{1+q+q^2}+\frac{2+x+x^2+q(3+2x+x^2)}{(1+q)(1+q^2)}\right)\hfill \\ & -\frac{1}{1-q}(1-q^4)y\left(+\frac{q^2(5+2x+x^2)}{(1+q)(1+q^2)}\right)+\cdots .\hfill \end{array}$$

The following Figure 8 shows the build-up of the roots of q-sine Bernoulli polynomials. Similar forms to the structures of q-cosine Bernoulli polynomials, which were obtained earlier, can be found, and the structure in Figure 8 shows the stacked form of approximation roots. When fixed at $y=5$, the left figure in Figure 8 is the structure that can be seen when $q=0.9$, the middle figure is the structure that can be found when $q=0.5$, and the right is when $q=0.1$. In Figure 8, blue means the value of n is small, and red appears when the value of n is 30. As a result, we can see that the stacking structure is changing as the q-number changes. From Figure 8, we can make the following assumption.

Figure 8. Stacking structure of ${}_S{B}_{n,q}(x,5)$ for $2\le n\le 30,q=0.9,0.5,0.1$.

Conjecture 7.

${}_S{B}_{n,q}(x,5)$ obtains a value for approximation roots with a diameter of four as n increases and q approaches zero.