Abstract
In this paper, we analytically dealt with the usually so-called prestressed annular membrane problem, that is, the problem of axisymmetric deformation of the annular membrane with an initial in-plane tensile stress, in which the prestressed annular membrane is peripherally fixed, internally connected with a rigid circular plate, and loaded by a shaft at the center of this rigid circular plate. The prestress effect, that is, the influence of the initial stress in the undeformed membrane on the axisymmetric deformation of the membrane, was taken into account in this study by establishing the boundary condition with initial stress, while in the existing work by establishing the physical equation with initial stress. By creating an integral expression of elementary function, the governing equation of a second-order differential equation was reduced to a first-order differential equation with an undetermined integral constant. According to the three preconditions that the undetermined integral constant is less than, equal to, or greater than zero, the resulting first-order differential equation was further divided into three cases to solve, such that each case can be solved by creating a new integral expression of elementary function. Finally, a characteristic equation for determining the three preconditions was deduced in order to make the three preconditions correspond to the situation in practice. The solution presented here could be called the extended annular membrane solution since it can be regressed into the classic annular membrane solution when the initial stress is equal to zero.
1. Introduction
Elastic membrane structures and structural components have been widely used in many advanced fields due to the properties of lightweight, high flexibility and high toughness [1,2,3,4,5,6]. The problems of membrane structure are generally shown as large deflection problems, which makes it inevitable to produce nonlinear differential equations in solving. Generally, these nonlinear differential equations will bring serious analytical difficulties even in simple boundary-value problems [7,8,9,10,11,12,13,14,15,16,17]. Thus, the closed-form solutions of these membrane problems are usually difficult to be obtained. However, the closed-form solutions are often found to be necessary when designing membrane structures and structural components.
In the existing literature, there are some analytical solutions for circular and annular membrane problems. Hencky [18] originally studied the problem of axisymmetric deformation of the circular membrane fixed at the outer edge under the uniformly-distributed loads, and presented the power series solution of the problem. A computational error in Hencky [18] was corrected by Chien [19] and Alekseev [20], respectively. This is the well-known Hencky solution and it is often cited with regard to this problem. The problem of axisymmetric deformation of the annular membrane with rigid plug in the interior fixed at the outer edge and transversely loaded at the inner edge was originally investigated by Alekseev [21], which usually called classic annular membrane problem for short. However, the solution presented by Alekseev [21] is applicable only to the case where Poisson’s ratio is under 1/3. Sun et al. [22] presented the complete solution of the classic annular membrane problem. Chien et al. [23,24] studied the problem of axisymmetric deformation of the circular membrane fixed at the outer edge under the action of uniformly-distributed loads in its central portion and the problem of axisymmetric deformation of the circular membrane fixed at the outer edge under the action of a point load at its center, and presented their solutions. Sun et al. [25] presented the solution of the problem of axisymmetric deformation of the circular membrane fixed at the outer edge and centrally loaded by a cylinder with a frictionless flat end (i.e., under the action of axisymmetric linearly-distributed loads). Recently, Lian et al. [26] resolved the well-known Hencky problem by adopting the small-rotation-angle assumption. Yang et al. [27] presented the solution of the Hencky problem by the displacement method. In addition, there are also some numerical solutions of membrane problems. Angiulli et al. [28] as well as Versaci and Morabito [29] presented a numerical approach based on shooting techniques to reconstruct the membrane profile in the device in steady-state case and provided the analytical-numerical tools for the simplified rewriting of the most important mathematical models of MEMS membrane devices for mechatronics, exploiting advanced concepts and results in the theory of curves and surfaces.
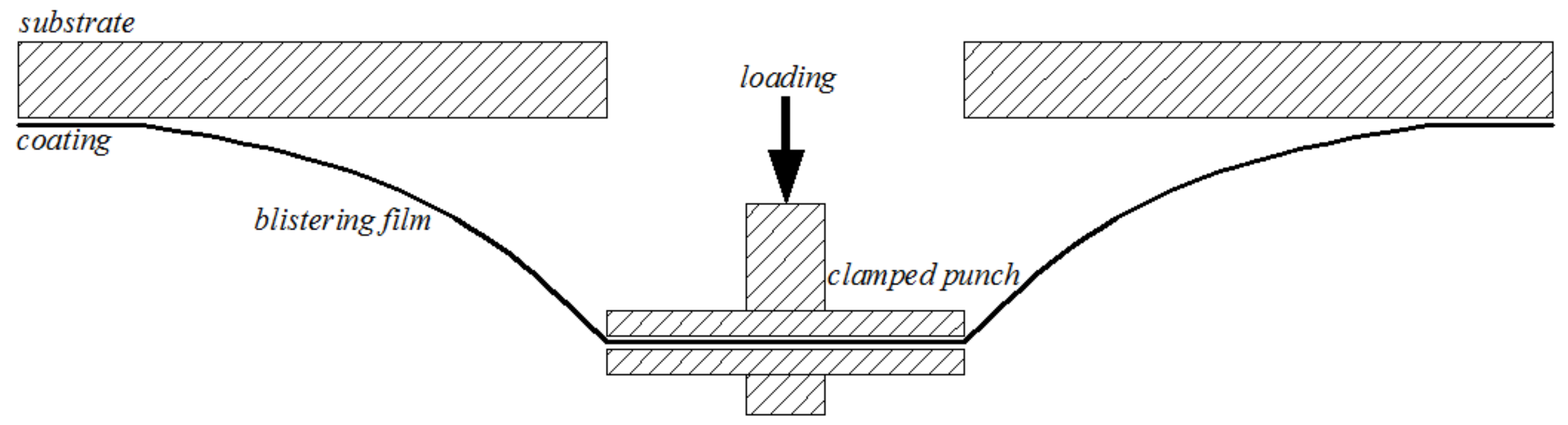
However, all the analytical solutions mentioned above are applicable only to the case where the membrane has no initial stress, i.e., the membrane is initially flat (horizontal) before subjected to a transverse load. However, in practice, the great majority of membranes in structures have initial stress [30]. In building membrane structures, for example, the initial stress applied is usually used for keeping the form of structures. A familiar example of initial stress is the residual stress in thin-film/substrate systems (coating/substrate), the tensile or compressive plane stress, which is, very easily, present in the coating due to variations in processing conditions such as the temperature, humidity, method of etching, or the order of fabrication procedures, etc. The mechanical properties of thin-film/substrate systems are often characterized by film/substrate delamination using a clamped punch-loaded blister test, as shown in Figure 1. The clamped punch-loaded blister test was usually simplified into a classic annular membrane problem. Obviously, such simplification does not take the residual stress into account. The classic annular membrane solution is not capable of dealing with the case where the coating has residual stress. The initial residual stress in the coating will have an influence on the mechanical behavior of the blistering film, and it also makes the solution to the mechanical behavior of the blistering film complicated and difficult. We here focus our attention on solving the problem of axisymmetric deformation of the coating with initial residual stress, i.e., an annular membrane problem with initial stress or simply a prestressed annular membrane problem.
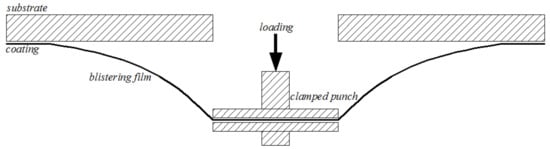
Figure 1.
Sketch of a clamped punch-loaded blister test.
The paper is organized as follows. In Section 2, the membrane equations are firstly established, then the boundary conditions with initial stress are deduced, and finally, the resulting somewhat intractable nonlinear second-order differential equation is solved by creating the integral expressions of elementary function. In Section 3, some important issues are discussed, a numerical example is conducted, and it is proved that the solution presented here can be regressed into the classic annular membrane solution when the initial stress is equal to zero. Section 4 is the concluding remarks. Table 1 is the list of symbols used in this paper.

Table 1.
List of the symbols used in this paper.
2. Membrane Equation and Its Solution
2.1. Establishment of Membrane Equations
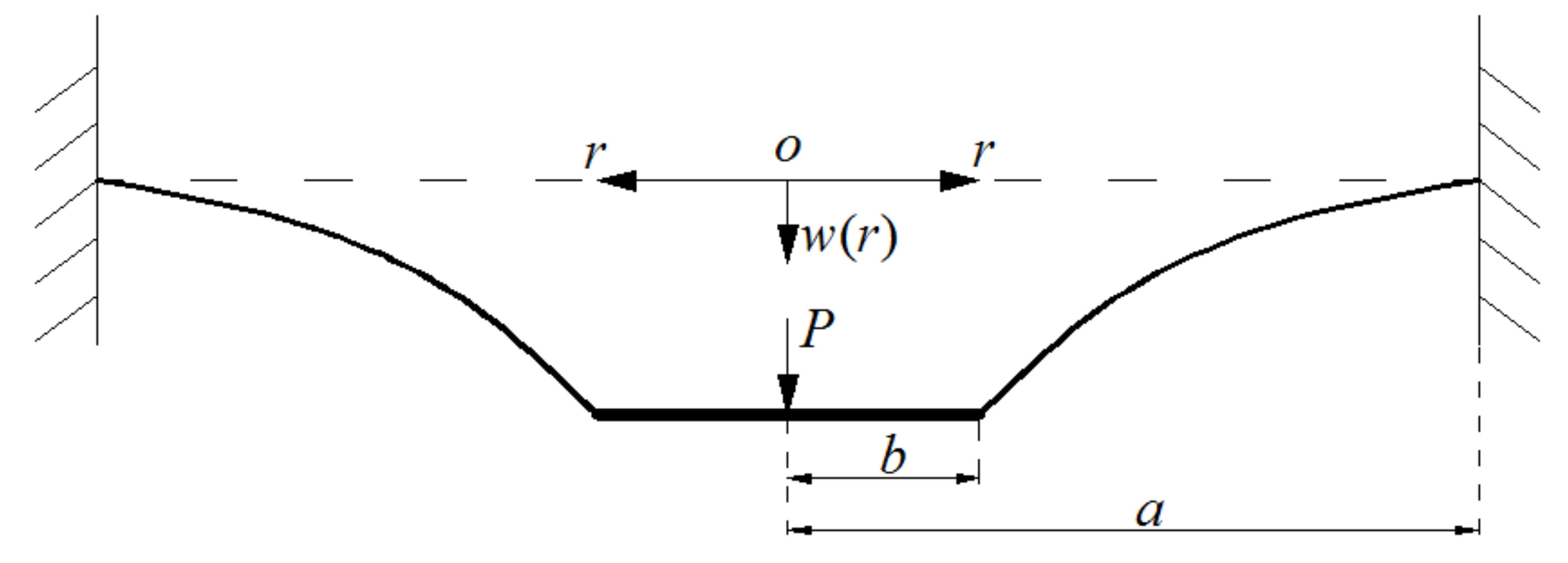
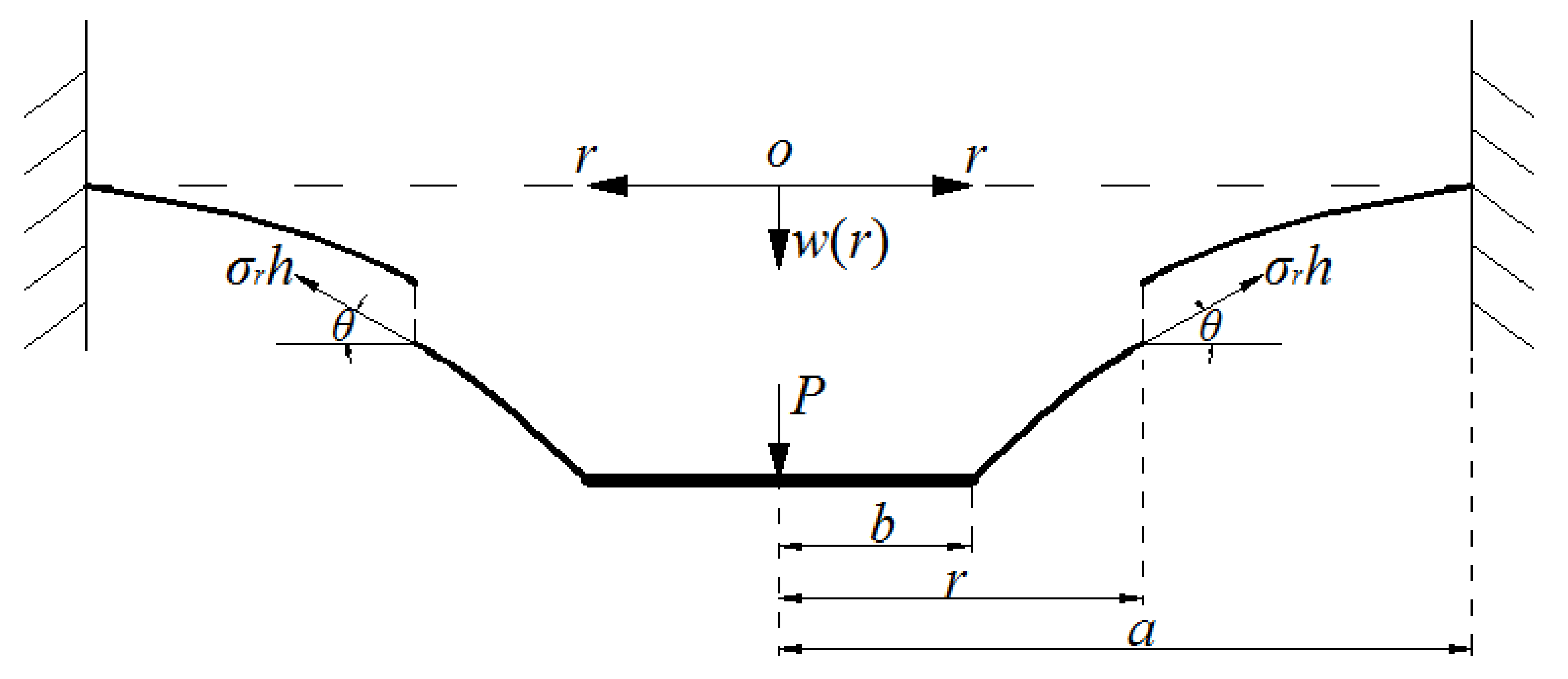
Suppose that an initially flat, linearly elastic, rotationally symmetric, taut circular membrane with Young’s modulus of elasticity E, Poisson’s ratio v, thickness h, and radius a is extended a plane radial displacement , then, the extended circular membrane is fixed at the perimeter of radius a and the central part of the extended circular membrane is clamped by two rigid circular plates of radius b. An annular membrane structure with initial stress, the so-called prestressed annular membrane structure, is thus established. We study the problem of axisymmetric deformation of this annular membrane with initial stress under the action of transverse load P at the center (loaded by a shaft at the center of the circular membrane), as shown in Figure 2, where r is the radial coordinate, w is the transverse displacement and o is the origin of the coordinates. A piece of the annular membrane, whose radius is , is taken with a view of studying the static problem of equilibrium of this membrane under the joint action of the load and the membrane force acted on the boundary, just as shown in Figure 3, where is the radial stress and is the slope angle of the deflected membrane. Right here, there are two vertical forces, i.e., the force and the total vertical force produced by the membrane force .
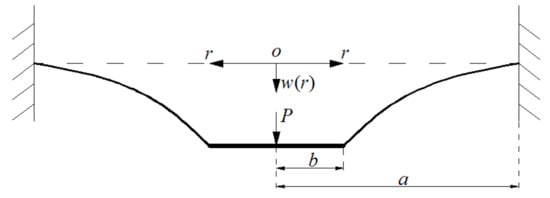
Figure 2.
Sketch of an annular membrane problem.
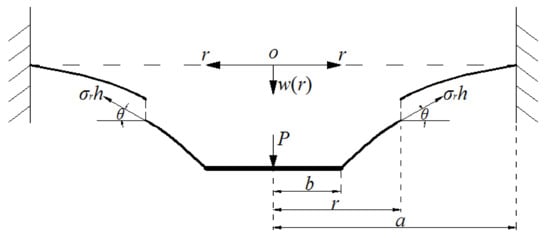
Figure 3.
Equilibrium diagram of the annular membrane of radius r (b ≤ r ≤ a).
The out-plane equilibrium condition is
Considering the physical phenomenon that the slope angle is usually less than , the following approximate expression therefore holds
Substituting Equation (2) into Equation (1), the out-plane equilibrium equation may be written as
In the plane of the membrane, there are the actions of the radial membrane force and the circumferential membrane force , where is the circumferential stress, the in-plane equilibrium equation is
If the radial strain, circumferential strain, radial displacement and transversal displacement are denoted by , , and , respectively, then there are the relations of the strain and displacement of the large deflection problem
The relations of the stress and strain are
Substituting Equation (6) into Equation (5), it may be obtained that
From Equation (7), we can finally obtain
By means of Equation (8) and Equation (4), one has
If we substitute the u of Equation (9) into the first expression of Equation (8), then
The detailed derivation from Equation (4) to Equation (10) may be obtained from any general theory of plates and shells. It is not necessary to discuss this problem here. Equations (3), (4) and (10) are three equations for the solutions of , and . The boundary conditions, under which Equations (3), (4) and (10) may be solved, must take into account the initial stress in the initially flat circular membrane, and it may be determined based on the following analysis of the plane radial stretching problem.
2.2. Establishment of Boundary Conditions Considering Initial Stress
For the axisymmetric problem of plane radial stretching, i.e., the case where the initially flat circular membrane is extended a plane radial displacement from , it is obvious that . So, from Equation (5) it may be obtained that
Substituting Equation (11) into Equation (6), it is found that
From Equations (4) and (12), one has
The boundary conditions, under which Equation (13) may be solved, are
and
So, under the conditions of Equation (14a,b), the solution of Equation (13) may be written as
Substituting Equation (15) into Equations (11) and (12), it may be obtained that
where is initial plane stress. Equation (16) indicates that for the axisymmetric plane stretching problem the radial strain is always equal to the circumferential strain at every point of the circular plane membrane, also the radial stress is always equal to the circumferential stress at every point of the circular plane membrane. Let us introduce the proportional coefficient , such that
Hence, from Equations (16) and (17), the initial plane strain may be written as
So, the boundary conditions, under which Equations (3), (4) and (10) may be solved, may finally be written as
and
and
2.3. Nondimensionalization
Let us introduce the following dimensionless variables
and transform Equations (10), (3) and (4) into
and
The boundary conditions Equation (19) can be transformed into
and
and
The boundary conditions (24a,b) may also be expressed in . So long as we eliminate from Equations (5) and (6), we may obtain . After non-dimensionalization, we may transform Equation (24a,b) into , in which may be expressed in via Equation (16).
Further, eliminating from Equations (21) and (22), we obtain an equation which contains only
Let us substitute Z for , i.e., let
Substituting Equation (26) into Equation (25), we obtain a nonlinear equation
From Equation (22), one has
Multiplying the two sides of Equation (27) with ,
After integrating,
where B is an undetermined integration constant. We take the positive value in the square-root value, then
2.4. Analytical Solution to Equation (31)
We shall solve Equation (31) under the preconditions of , and , respectively.
① The case of
From Equation (31), gives
After integrating
where k is another undetermined integration constant. Substituting Equation (20) into Equation (9), we may obtain
Then, substituting Equation (26) into Equation (34) and considering Equation (32), one has
Substituting Equation (33) into Equation (35), one has
From Equations (27) and (33), one has
Integration of Equation (37) gives
where is another undetermined integration constant. From Equations (26) and (33), one has
When (i.e., ), Equation (24a) gives, from Equation (36),
When (i.e., ), Equation (24b) gives, from Equation (36),
From Equation (38), Equation (24c) gives
From Equations (40) and (41), it may be obtained that
and
Equations (43) and (44) satisfy the form of , and each equation should have a real root and a pair of complex conjugate roots due to . We consider only the real root, such that
and
From Equations (45) and (46), it is found that
and
Further eliminating from Equations (47) and (48), the important condition of can be obtained
So, for the concrete problem where the values of , and are known in advance, if (i.e., Equation (49) holds), then this is the case of , and the value of the undetermined integration constant can be determined by Equation (47) or Equation (48) with the known , and (whose values must satisfy Equation (49), thus satisfying Equations (47) and (48)). The value of may be determined by Equation (42) with the known , and the deflection and stresses within the annular membrane can thus be determined by Equations (38), (39) and (23). Moreover, from Equations (38), (42), (45) and (46), the maximum deflection at the inner edge () may be written as
② The case of
Let us introduce the new variable φ, such that
From Equation (30), we may see that the variable transformation is valid since while . Substituting Equation (51) into Equation (31), one has
Integration of Equation (52) gives
where k is another undetermined integration constant. Substituting Equation (20) into Equation (9) and eliminating with the help of Equation (26), one has
Making use of Equations (31), (51) and (53), Equation (54) may be simplified as
From Equations (28), (51) and (52), one has
Integration of Equation (56) gives
where R is another undetermined integration constant. From Equations (26), (51) and (53), one has
If we call at as and call at as , then from Equation (53) it may be obtained that
and
Equation (59a,b) are the conditions for the determination of and with the known values of k and B. From Equation (57), Equation (24c) gives
From Equations (55) and (59b), Equation (24a) gives
From Equations (55) and (59a), Equation (24b) gives
From Equations (61) and (62), one has
From Equation (59a,b), one has
From Equations (59a) and (64), one has
From Equations (63) and (64), one has
From Equations (61), (62) and (64), one has
Hence, for the concrete problem where the values of , and are known in advance, using Equation (67) we may calculate the numerical value of with a given and the known and . With this obtained value of , we may further calculate the numerical values of B, k and v via Equations (64)–(66), respectively. If the numerical value of , obtained in this calculation, is just equal to its known value, then the corresponding numerical values of B and k are just the solution of the problem, otherwise, try another given value of and continue the numerical calculation until the obtained numerical value of is just equal to its known value. As soon as B, R and k are determined, the displacement and stresses within the annular membrane can thus be calculated. Equation (53) is the condition for the determination of from with the known values of k and B. All the calculations of numerical values can easily be finished with the help of a Microsoft Excel spreadsheet. Moreover, From Equations (57), (60) and (64), the maximum deflection at the inner edge (that is at and ) may be written as
③ The case of
Letting , from Equation (31) one has
Let us introduce the new variable φ, such that
Substituting Equation (70) into Equation (69), one has
Integration of Equation (71) gives
where k is the undetermined integration constant. Substituting Equation (20) into Equation (9) and eliminating with the help of Equation (26), one has
Making use of Equations (69), (70) and (72), Equation (73) may be simplified as
From Equations (28), (70) and (71), one has
Integration of Equation (75) gives
where R is the undetermined integration constant. From Equations (26), (70) and (72), one has
If we call at as and at as , then from Equation (72) it may be obtained that
and
Equation (78a,b) are the conditions for the determination of and with the known values of k and B. From Equation (76), Equation (24c) gives
From Equations (74) and (78b), Equation (24a) gives
From Equations (74) and (78a), Equation (24b) gives
From Equations (80) and (81), one has
From Equation (78a,b), one has
From Equations (78a) and (83), one has
From Equations (82) and (83), one has
From Equations (80)–(82), one has
Hence, for the concrete problem where the values of , and are known in advance, using Equation (86) we may calculate the numerical value of with a given and the known and . With this obtained value of , we may further calculate the numerical values of , , k and v via Equations (79), (83)–(85), respectively. If the numerical value of , obtained in this calculation, is just equal to its known value, then the corresponding numerical values of , and k, are just the solution of the problem, otherwise, try another given value of and continue the numerical calculation until the obtained numerical value of is just equal to its known value. As soon as R, and k are determined, the displacement and stress within the annular membrane can be calculated. Equation (72) is the condition for the determination of from with the known values of k and . Moreover, from Equations (76), (79) and (83), the maximum deflection at the inner edge (that is at and ) may be written as
Thus, the problem of axisymmetric deformation of the so-called prestressed annular membrane can be solved.
3. Results and Discussions
Since Equation (31) was solved under the preconditions of , and , respectively, then for solving the concrete problem where the values of , and are known in advance, the conditions of , and should be firstly specified, otherwise, we still don’t know how to use the solutions presented above. Based on a large number of numerical calculations we finally find that , and corresponds to , and , respectively, where was presented in Equation (49).
3.1. Comparison with Existing Work
An obvious difference between the annular membrane problem without initial stress and the one with initial stress (i.e., the difference between the classical problem and the problem dealt with here) is that, in the classical problem (without initial stress) the conditions of , and depends only on the Poisson’s ratio (i.e., , and correspond to , and , respectively, see Figure 7 in reference [22]), while in the problem dealt with here (with initial stress) it depends on not only and but also and ( and are introduced by the proportional coefficient , see Equations (17) and (49) in this paper). When (corresponding to ), however, Equation (49) can be regressed into Equation (34) in reference [22]. Moreover, in the classical problem the important integral constant is determined by and (see Equations (52) and (70) in reference [22]), but in the problem dealt with here it is determined by , and (see Equations (62) and (81) in this paper). When (corresponding to ), however, Equations (62) and (81) can be regressed into Equations (52) and (70) in reference [22], respectively.
From the derivation above it may easily seen that only the boundary conditions (see Equation (24)) were modified in comparison with the boundary conditions in reference [22]. All the expressions obtained here for displacements, strains and stresses have the same form as the expressions obtained in reference [22]. However, the initial stress plays an important role in the determination of numerical values of the undetermined integral constants. If , however, Equation (24) can be regressed into Equation (14) in reference [22], and consequently all the expressions obtained here can be regressed into the corresponding expressions in reference [22]. This means that the solution obtained here can be regressed into the classic annular membrane solution when the initial stress is equal to zero. Therefore, the solution presented here could be called extended annular membrane solution.
3.2. Numerical Example
The following example shows the difference between the deflection curves of the same annular polymer thin-film without and with initial stress (under the same transverse load). The outer radius of the annular polymer thin-film is mm, the inner radius is mm, the thickness is μm, the elastic modulus is MPa, the Poisson’s ratio is , the transverse load is N, and the yield stress of the polymer thin-film is found to be MPa. Suppose that the initial stress is MPa and MPa, respectively. Here . For the case of MPa, from Equation (17) it may be obtained that and hence Equation (49) gives . Consequently, the case of MPa corresponds to , and also the case of MPa corresponds to due to (see Figure 7 in reference [22]). So, the problems considered here should be approached in , i.e., the expressions obtained in the case of should be adopted. All the numerical values of , , , and have been calculated and are listed in Table 2.

Table 2.
Result of numerical values.
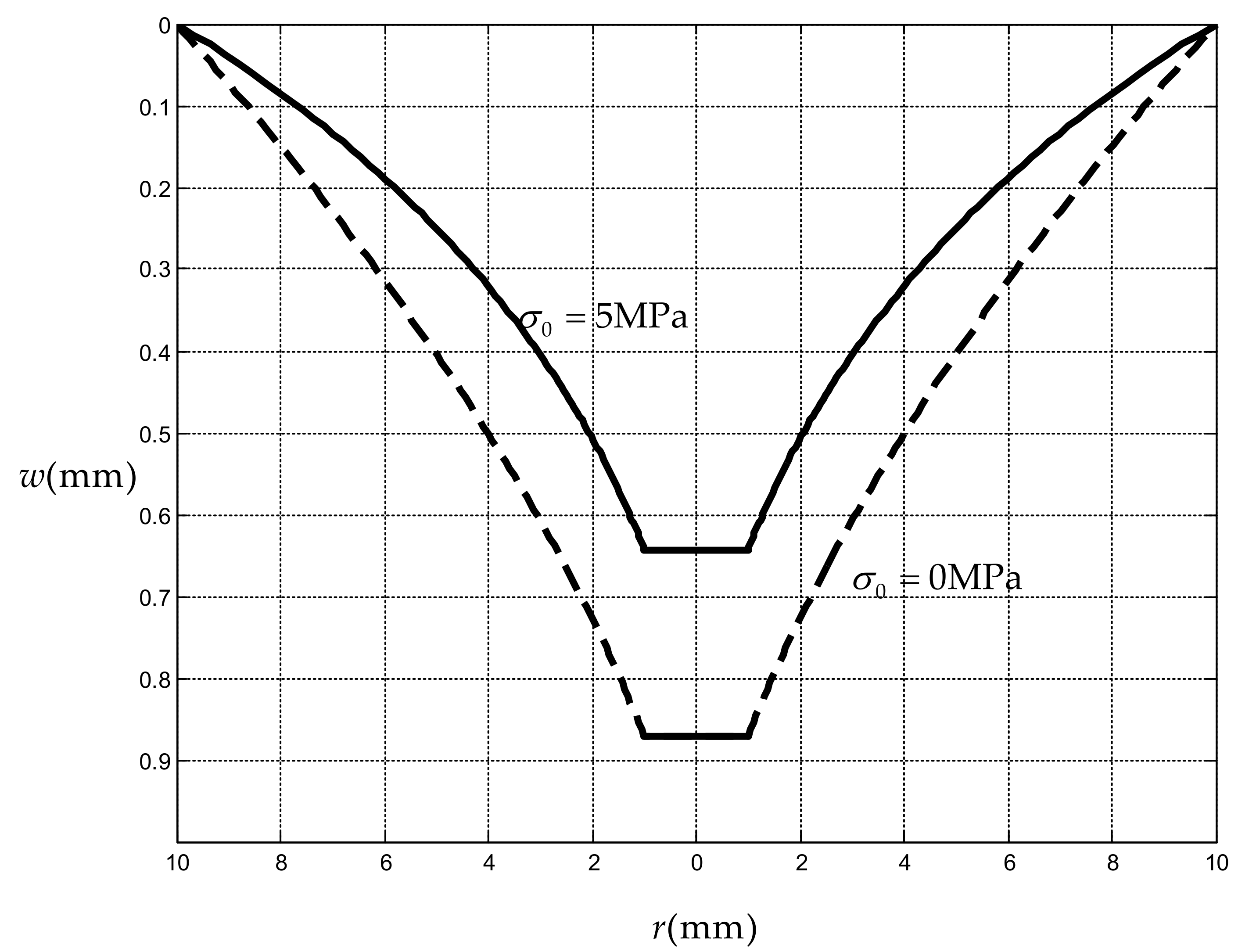
The maximum stress of the thin-film with MPa, which is at mm, is calculated to be about MPa under N. So, the thin-film is in the range of elastic deformation due to MPa. A graphical representation of deflection results is shown in Figure 4, where the solid line corresponds to MPa and the dashed line to MPa (the classic annular membrane problem). From Figure 4 we can see that the initial stress has a large influence on the mechanical behavior of the annular membrane, and we may imagine, such an influence will increase as the initial stress increases.
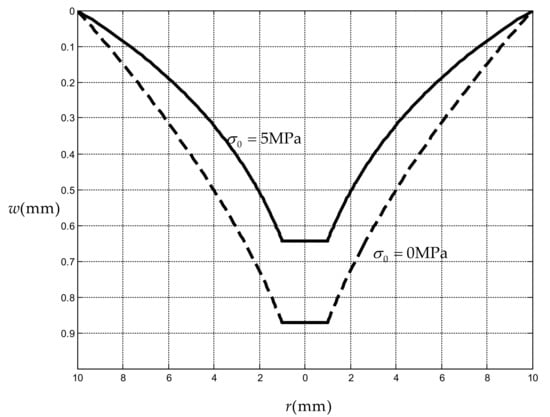
Figure 4.
Sketch of deflection curve for .
4. Concluding Remarks
In this paper, the problem of axisymmetric deformation of a prestressed annular membrane internally-connected with a rigid circular plate and transversely-loaded by a central shaft was analytically dealt with. The prestress effect, that is, the influence of the initial stress in the undeformed membrane on the axisymmetric deformation of the membrane, was taken into account by establishing the boundary condition with initial stress, rather than by establishing the physical equation with initial stress, as done in the existing work. The numerical example shows that the initial stress has a large influence on the mechanical behavior of the membrane. The closed-form solution presented here is given in the form of elementary function, which is relatively rare in solving nonlinear differential equations. So, in this sense, the work presented here has positive significance to the mathematical modeling of mechanical problems, especially to studies such as the thin-film/substrate or film/film delamination and shape finding of building film structures.
Author Contributions
Conceptualization, J.-Y.S. and X.-T.H.; methodology, J.-Y.S. and Z.-X.Y.; validation, Z.-X.Y. and X.-T.H.; writing—original draft preparation, Z.-X.Y. and Z.-H.Z.; writing—review and editing, J.-Y.S. and S.-Z.L.; visualization, Z.-H.Z. and S.-Z.L.; funding acquisition, J.-Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number No. 11772072.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Küçük, I. Optimality conditions for the control of a double-membrane complex system by a modal decomposition technique. Appl. Math. Model. 2008, 32, 562–574. [Google Scholar] [CrossRef]
- Zhao, M.; Zheng, W.; Fan, C. Mechanics of shaft-loaded blister test for thin film suspended on compliant substrate. Int. J. Solids Struct. 2010, 47, 2525–2532. [Google Scholar] [CrossRef][Green Version]
- Sun, J.-Y.; Hu, J.-L.; Zheng, Z.-L.; He, X.-T.; Geng, H.-H. A practical method for simultaneous determination of Poisson’s ratio and Young’s modulus of elasticity of thin films. J. Mech. Sci. Technol. 2011, 25, 3165–3171. [Google Scholar] [CrossRef]
- Xu, D.; Liechti, K. Analytical and experimental study of a circular membrane in adhesive contact with a rigid substrate. Int. J. Solids Struct. 2011, 48, 2965–2976. [Google Scholar] [CrossRef]
- Sun, J.-Y.; Qian, S.-H.; Li, Y.-M.; He, X.-T.; Zheng, Z.-L. Theoretical study of adhesion energy measurement for film/substrate interface using pressurized blister test: Energy release rate. Meas. 2013, 46, 2278–2287. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness. Math. 2019, 7, 1193. [Google Scholar] [CrossRef]
- Arthurs, A.M.; Clegg, J. On the Solution of a Boundary Value Problem for the Nonlinear Föppl-Hencky Equation. ZAMM 1994, 74, 281–284. [Google Scholar] [CrossRef]
- Kublanov, L.; Bottega, W. On pressing of a buckled film. Appl. Math. Model. 1995, 19, 499–507. [Google Scholar] [CrossRef]
- Plaut, R. Linearly elastic annular and circular membranes under radial, transverse, and torsional loading. Part I: Large unwrinkled axisymmetric deformations. Acta Mech. 2008, 202, 79–99. [Google Scholar] [CrossRef]
- Soares, R.M.; Gonçalves, P.B. Nonlinear vibrations and instabilities of a stretched hyperelastic annular membrane. Int. J. Solids Struct. 2012, 49, 514–526. [Google Scholar] [CrossRef]
- Long, R.; Hui, C.-Y. Axisymmetric membrane in adhesive contact with rigid substrates: Analytical solutions under large deformation. Int. J. Solids Struct. 2012, 49, 672–683. [Google Scholar] [CrossRef]
- Atai, A.; Steigmann, D. Numerical analysis of wrinkled, anisotropic, nonlinearly elastic membranes. Mech. Res. Commun. 2014, 57, 1–5. [Google Scholar] [CrossRef]
- Sun, J.-Y.; Rong, Y.; He, X.-T.; Gao, X.-W.; Zheng, Z.-L. Power series solution of circular membrane under uniformly distributed loads: Investigation into Hencky transformation. Struct. Eng. Mech. 2013, 45, 631–641. [Google Scholar] [CrossRef]
- Zhumanazarova, A.; Cho, Y.I. Asymptotic Convergence of the Solution of a Singularly Perturbed Integro-Differential Boundary Value Problem. Mathematics 2020, 8, 213. [Google Scholar] [CrossRef]
- Ahmad, B.; Alruwaily, Y.; Alsaedi, A.; Ntouyas, S.K. Existence and Stability Results for a Fractional Order Differential Equation with Non-Conjugate Riemann-Stieltjes Integro-Multipoint Boundary Conditions. Mathematics 2019, 7, 249. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Emin, S.; Bawanah, S. On the Parametrization of Caputo-Type Fractional Differential Equations with Two-Point Nonlinear Boundary Conditions. Mathematics 2019, 7, 707. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G.; Fattorusso, L.; Jannelli, A. On the uniqueness of the solution for a semi-linear elliptic boundary value problem of the membrane MEMS device for reconstructing the membrane profile in absence of ghost solutions. Int. J. Non-linear Mech. 2019, 109, 24–31. [Google Scholar] [CrossRef]
- Hencky, H. Über den Spannungszustand in kreisrunden Platten mit verschwindender Biegungssteifigkeit. Z. Math. Physik 1915, 63, 311–317. [Google Scholar]
- Chien, W.Z. Asymptotic behavior of a thin clamped circular plate under uniform normal pressure at very large deflection. Sci. Rep. Natl. Tsinghua Univ. 1948, 5, 193–208. [Google Scholar]
- Alekseev, S.A. Elastic circular membranes under the uniformly distributed loads. Eng. Corpus 1953, 14, 196–198. [Google Scholar]
- Alekseev, S.A. Elastic annular membranes with a stiff centre under the concentrated force. Eng. Corpus 1951, 10, 71–80. [Google Scholar]
- Sun, J.-Y.; Hu, J.-L.; He, X.-T.; Zheng, Z.-L. A theoretical study of a clamped punch-loaded blister configuration: The quantitative relation of load and deflection. Int. J. Mech. Sci. 2010, 52, 928–936. [Google Scholar] [CrossRef]
- Chien, W.Z.; Wang, Z.Z.; Xu, Y.G.; Chen, S.L. The symmetrical deformation of circular membrane under the action of uniformly distributed loads in its portion. Appl. Math. Mech. 1981, 2, 653–668. [Google Scholar]
- Sun, J.-Y.; Hu, J.-L.; He, X.-T.; Zheng, Z.-L.; Geng, H.-H. A Theoretical Study of Thin Film Delamination Using Clamped Punch-Loaded Blister Test: Energy Release Rate and Closed-Form Solution. J. Adhes. Sci. Technol. 2011, 25, 2063–2080. [Google Scholar] [CrossRef]
- Sun, J.-Y.; Lian, Y.S.; Li, Z.; He, X.-T.; Zheng, Z. Theoretical study on shaft-loaded blister test technique: Synchronous characterization of surface and interfacial mechanical properties. Int. J. Adhes. Adhes. 2014, 51, 128–139. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.-Y.; Yang, Z.-X.; He, X.-T.; Zheng, Z.-L. Closed-form solution of well-known Hencky problem without small-rotation-angle assumption. ZAMM 2016, 96, 1434–1441. [Google Scholar] [CrossRef]
- Yang, Z.X.; Sun, J.-Y.; Ran, G.M.; He, X.-T. A New Solution to Főppl-Hencky Membrane Equation. J. Mech. 2017, 33, N7–N11. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the membrane detection of a 1D electrostatic-driven MEMS device by the shooting method: Convergence analysis and ghost solutions identification. Comput. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Membrane Micro Electro-Mechanical Systems for Industrial Applications. Implement. Comput. Intell. Tech. Secur. Syst. Des. 2020, 139–175. [Google Scholar]
- Crăciun, E.M.; Baesu, E.; Soós, E. “General solution in terms of complex potentials in antiplane states in initial stressed and prepolarized piezoelectric crystals: Application to Mode III fracture propagation. J. Appl. Math. 2005, 70, 39–52. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).