A Density-Dependent Host-Parasitoid Model with Stability, Bifurcation and Chaos Control
Abstract
:1. Introduction
- (i)
- It is assumed that the first encounter between the parasitoid and host is random. Moreover, one viable egg is laid by a parasitoid on a single host, which is killed by the parasitoid’s progeny.
- (ii)
- Keeping in view the law of mass action, the number of encounters of resources (hosts) with consumers (parasitoids) in generation n are proportional to the product of hosts and parasitoids present densities, and consequently, one has:where a is a positive constant representing the searching efficiency of the parasitoid, and , denote the population densities of the parasitoid and host, respectively, in generation n.
- (iii)
- The next generation of parasitoids is produced due to infection of hosts in the present generation.
- (iv)
- The hosts that are not infected produce their own offspring.
2. Permanence
3. Existence of Positive Fixed Point and Stability Analysis
4. Global Stability
- (i)
- The function is non-decreasing with respect to x, and non-increasing with respect to y.
- (ii)
- The function is non-decreasing in both variables x and y.
- (iii)
- Assume that solves the following algebraic system:
5. Hopf Bifurcation
6. Chaos and Bifurcation Control
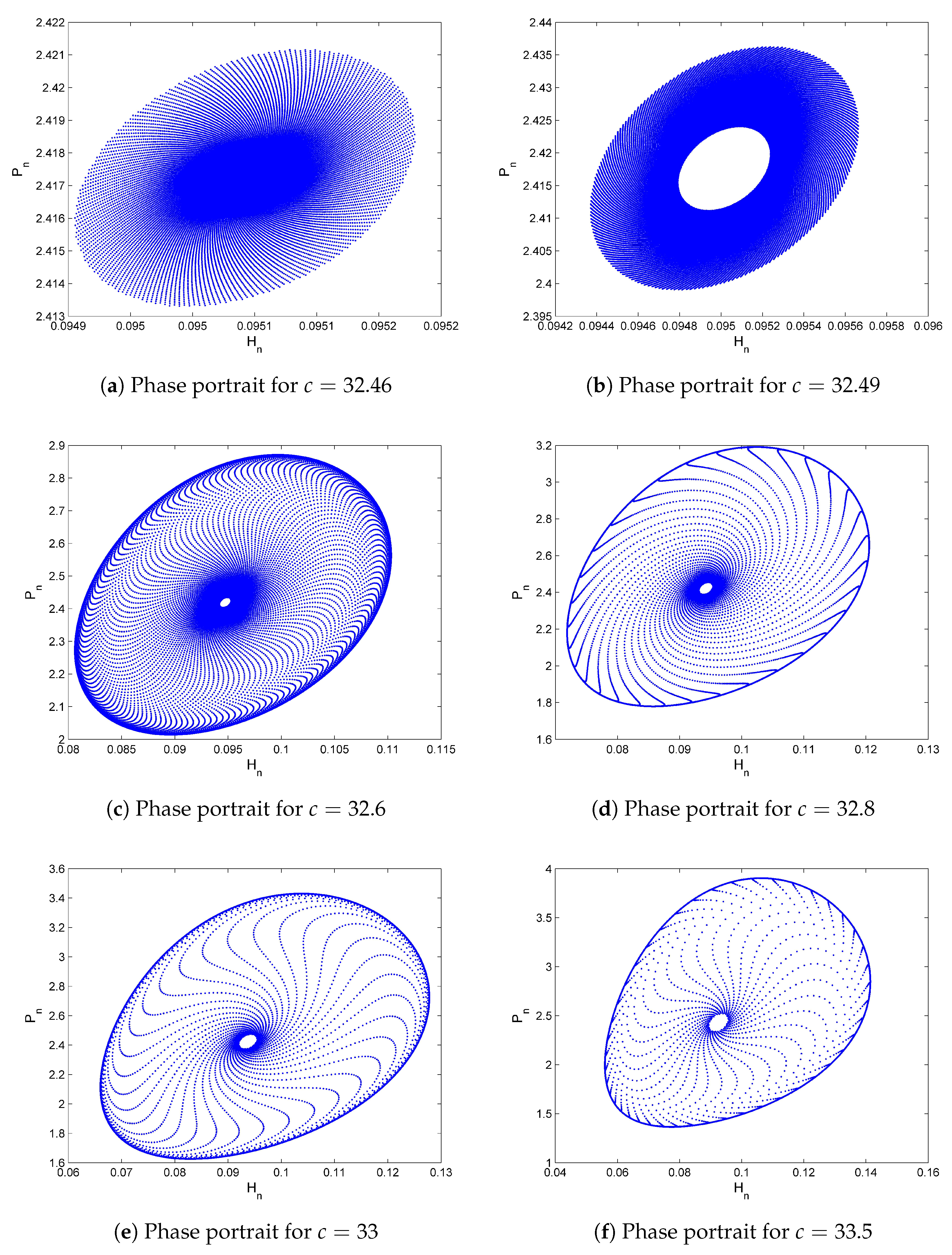
7. Numerical Simulations and Discussion
8. Concluding Remarks
9. Future Problems
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Zhang, Q.L.; Sreeram, V. Bifurcation analysis and control of a discrete harvested prey-predator system with Beddington-DeAngelis functional response. J. Franklin Inst. 2010, 347, 1076–1096. [Google Scholar] [CrossRef]
- Taylor, A.D. Parasitiod competition and the dynamics of host-parasitoid models. Am. Nat. 1988, 132, 417–436. [Google Scholar] [CrossRef]
- Kaitala, V.; Ylikarjula, J.; Heino, M. Dynamic complexities in host-parasitoid interaction. J. Theor. Biol. 1999, 197, 331–341. [Google Scholar] [CrossRef]
- Tang, S.Y.; Chen, L.S. Chaos in functional response host-parasitoid ecosystem models. Chaos Soliton Fract. 2002, 13, 875–884. [Google Scholar] [CrossRef]
- Xu, C.L.; Boyce, M.S. Dynamic complexities in a mutual interference host-parasitoid model. Chaos Soliton Fract. 2005, 24, 175–182. [Google Scholar] [CrossRef]
- Lv, S.J.; Zhao, M. The dynamic complexity of a host-parasitoid model with a lower bound for the host. Chaos Soliton Fract. 2008, 36, 911–919. [Google Scholar] [CrossRef]
- Din, Q. Global behavior of a plant-herbivore model. Adv. Differ. Equ. 2015, 2015, 119. [Google Scholar] [CrossRef] [Green Version]
- Din, Q. Global behavior of a host-parasitoid model under the constant refuge effect. Appl. Math. Model. 2016, 40, 2815–2826. [Google Scholar] [CrossRef]
- Din, Q.Ö.; Gümüş, A.; Khalil, H. Neimark-Sacker bifurcation and chaotic behaviour of a modified host-parasitoid model. Z. Naturforsch. A 2017, 72, 25–37. [Google Scholar] [CrossRef]
- Din, Q. Global stability and Neimark-Sacker bifurcation of a host-parasitoid model. Int. J. Syst. Sci. 2017, 48, 1194–1202. [Google Scholar] [CrossRef]
- Din, Q. Neimark-Sacker bifurcation and chaos control in Hassell-Varley model. J. Differ. Equ. Appl. 2017, 23, 741–762. [Google Scholar] [CrossRef]
- Din, Q. Global stability of Beddington model. Qual. Theor. Dyn. Syst. 2017, 16, 391–415. [Google Scholar] [CrossRef]
- Din, Q.; Khan, M.A.; Saeed, U. Qualitative Behaviour of Generalised Beddington Model. Z. Naturforsch. A 2016, 71, 145–155. [Google Scholar] [CrossRef]
- Din, Q. Qualitative analysis and chaos control in a density-dependent host-parasitoid system. Int. J. Dyn. Control 2018, 6, 778–798. [Google Scholar] [CrossRef]
- Din, Q.; Hussain, M. Controlling chaos and Neimark-Sacker bifurcation in a host-parasitoid model. Asian J. Control 2019, 21, 1202–1215. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, H. Global qualitative analysis of a discrete host-parasitoid model with refuge and strong Allee effects. Math. Method. Appl. Sci. 2018, 41, 2039–2062. [Google Scholar] [CrossRef]
- Jamieson, W.T. On the global behaviour of May’s host-parasitoid model. J. Differ. Equ. Appl. 2019, 25, 583–596. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, K.; Ye, Y.; Wei, Y.; Ma, M. Dynamic complexity and bifurcation analysis of a host-parasitoid model with Allee effect and Holling type III functional response. Adv. Differ. Equ. 2019, 2019, 507. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Chu, Y.; Liu, Y. Bifurcation and chaos in a host-parasitoid model with a lower bound for the host. Adv. Differ. Equ. 2018, 2018, 31. [Google Scholar] [CrossRef] [Green Version]
- Bešo, E.; Kalabušić, E.; Mujić, N.; Pilav, E. Neimark-Sacker bifurcation and stability of a certain class of a host-parasitoid models with a host refuge effect. Int. J. Bifurcat. Chaos 2019, 29, 195169. [Google Scholar]
- Bešo, E.; Mujić, N.; Kalabušić, S.; Pilav, E. Stability of a certain class of a host-parasitoid models with a spatial refuge effect. J. Biol. Dyn. 2020, 14, 1–31. [Google Scholar]
- Alba-Pérez, J.; Macias-Diaz, J.E. Analysis of structure-preserving discrete models for predator-prey systems with anomalous diffusion. Mathematics 2019, 7, 1172. [Google Scholar] [CrossRef] [Green Version]
- Suryanto, A.; Darti, I.; Panigoro, H.S.; Kilicman, A. A fractional-order predator-prey model with ratio-dependent functional response and linear harvesting. Mathematics 2019, 7, 1100. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, L.; Bai, Y. Stability and bifurcation analysis on a predator-prey system with the weak Allee effect. Mathematics 2019, 7, 432. [Google Scholar] [CrossRef] [Green Version]
- Bailey, V.A.; Nicholson, A.J. The balance of animal populations. Proc. Zool. Soc. Lond. 1935, 3, 551–598. [Google Scholar]
- Ricker, W.E. Stock and recruitment. J. Fish. Res. Board Can. 1954, 11, 559–623. [Google Scholar] [CrossRef]
- Hassell, M.P. Density—Dependence in single—Species populations. J. Anim. Ecol. 1975, 44, 283–295. [Google Scholar] [CrossRef]
- Beverton, R.J.H.; Holt, S.J. On the Dynamics of Exploited Fish Populations; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Misra, J.C.; Mitra, A. Instabilities in single-species and host-parasite systems: Period-doubling bifurcations and chaos. Comput. Math. Appl. 2006, 52, 525–538. [Google Scholar] [CrossRef] [Green Version]
- Hassell, M.P.; Varley, G.C. New inductive population model for insect parasites and its bearing on biological control. Nature 1969, 223, 1133–1137. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D. Complex dynamic behaviors of a discrete-time predator-prey system. Chaos Soliton Fract. 2007, 32, 80–94. [Google Scholar] [CrossRef]
- Grove, E.A.; Ladas, G. Periodicities in Nonlinear Difference Equations; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Robinson, C. Dynamical Systems: Stability, Symbolic Dynamics and Chaos; Taylor Francis Group: Boca Raton, NY, USA, 1999. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: New York, NY, USA, 2003. [Google Scholar]
- Wan, Y.H. Computation of the stability condition for the Hopf bifurcation of diffeomorphism on R2. SIAM J. Appl. Math. 1978, 34, 167–175. [Google Scholar] [CrossRef]
- Lynch, S. Dynamical Systems with Applications Using Mathematica; Birkhäuser: Boston, MA, USA, 2007. [Google Scholar]
- Din, Q. Complexity and chaos control in a discrete-time prey-predator model. Commun. Nonlinear Sci. Numer. Simul. 2017, 49, 113–134. [Google Scholar] [CrossRef]
- Din, Q. Bifurcation analysis and chaos control in discrete-time glycolysis models. J. Math. Chem. 2018, 56, 904–931. [Google Scholar] [CrossRef]
- Din, Q.; Donchev, T.; Kolev, D. Stability, Bifurcation Analysis and Chaos Control in Chlorine Dioxide-Iodine-Malonic Acid Reaction. MATCH Commun. Math. Comput. Chem. 2018, 79, 577–606. [Google Scholar]
- Din, Q. Controlling chaos in a discrete-time prey-predator model with Allee effects. Int. J. Dyn. Control 2018, 6, 858–872. [Google Scholar] [CrossRef]
- Din, Q. A novel chaos control strategy for discrete-time Brusselator models. J. Math. Chem. 2018, 56, 3045–3075. [Google Scholar] [CrossRef]
- Din, Q. Stability, Bifurcation Analysis and Chaos Control for a Predator-Prey System. J. Vib. Control 2019, 25, 612–626. [Google Scholar] [CrossRef]
- Din, Q.; Iqbal, M.A. Bifurcation analysis and chaos control for a discrete-time enzyme model. Z. Naturforsch. A 2019, 74, 1–14. [Google Scholar] [CrossRef]
- Abbasi, M.A.; Din, Q. Under the influence of crowding effects: Stability, bifurcation and chaos control for a discrete-time predator-prey model. Int. J. Biomath. 2019, 12, 1950044. [Google Scholar] [CrossRef]
- Din, Q.; Shabbir, M.S.; Khan, M.A.; Ahmad, K. Bifurcation analysis and chaos control for a plant-herbivore model with weak predator functional response. J. Biol. Dyn. 2019, 13, 481–501. [Google Scholar] [CrossRef] [Green Version]
- Ishaque, W.; Din, Q.; Taj, M.; Iqbal, M.A. Bifurcation and chaos control in a discrete-time predator-prey model with nonlinear saturated incidence rate and parasite interaction. Adv. Differ. Equ. 2019, 2019, 28. [Google Scholar] [CrossRef] [Green Version]
- Elsayed, E.M.; Din, Q. Period-doubling and Neimark-Sacker bifurcations of plant-herbivore models. Adv. Differ. Equ. 2019, 2019, 271. [Google Scholar] [CrossRef] [Green Version]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Romeiras, F.J.; Grebogi, C.; Ott, E.; Dayawansa, W.P. Controlling chaotic dynamical systems. Physica D 1992, 58, 165–192. [Google Scholar] [CrossRef]
- Yuan, L.-G.; Yang, Q.-G. Bifurcation, invariant curve and hybrid control in a discrete-time predator-prey system. Appl. Math. Model. 2015, 39, 2345–2362. [Google Scholar] [CrossRef]
- Bukkuri, A. A mathematical model of the effects of ascorbic acid on the onset of neurodegenerative diseases. Open J. Math. Sci. 2019, 3, 300–309. [Google Scholar] [CrossRef]
- Bukkuri, A. A mathematical model showing the potential of vitamin c to boost the innate immune response. Open J. Math. Sci. 2019, 3, 245–255. [Google Scholar] [CrossRef]
- Opoku, N.K.-D.O.; Nyabadza, F.; Ngarakana-Gwasira, E. Modelling cervical cancer due to human papillomavirus infection in the presence of vaccination. Open J. Math. Sci. 2019, 3, 216–233. [Google Scholar] [CrossRef]
- Tahir, M.; Gul Zaman, G.; Shah, A.I.A.; Muhammad, S.; Hussain, S.A.; Ishaq, M. The stability analysis and control transmission of mathematical model for Ebola Virus. Open J. Math. Anal. 2019, 3, 91–102. [Google Scholar] [CrossRef]








| ine Parameter | Description | Observed Value | Source |
|---|---|---|---|
| ineine r | Host maximum population growth rate | 40 | [27] |
| ine k | Host steady population size | 0.09 | [27] |
| ine q | Quest constant | 0.1 | [30] |
| ine m | Mutual interference constant | 0.6 | [30] |
| ine c | Intrinsic growth rate of parasitoid | Estimate | |
| ine |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Din, Q.; Rafaqat, M.; Javaid, N.; Feng, Y. A Density-Dependent Host-Parasitoid Model with Stability, Bifurcation and Chaos Control. Mathematics 2020, 8, 536. https://doi.org/10.3390/math8040536
Ma X, Din Q, Rafaqat M, Javaid N, Feng Y. A Density-Dependent Host-Parasitoid Model with Stability, Bifurcation and Chaos Control. Mathematics. 2020; 8(4):536. https://doi.org/10.3390/math8040536
Chicago/Turabian StyleMa, Xiaorong, Qamar Din, Muhammad Rafaqat, Nasir Javaid, and Yongliang Feng. 2020. "A Density-Dependent Host-Parasitoid Model with Stability, Bifurcation and Chaos Control" Mathematics 8, no. 4: 536. https://doi.org/10.3390/math8040536
APA StyleMa, X., Din, Q., Rafaqat, M., Javaid, N., & Feng, Y. (2020). A Density-Dependent Host-Parasitoid Model with Stability, Bifurcation and Chaos Control. Mathematics, 8(4), 536. https://doi.org/10.3390/math8040536





