Geometric Properties and Algorithms for Rational q-Bézier Curves and Surfaces

Abstract

In this paper, properties and algorithms of q-Bézier curves and surfaces are analyzed. It is proven that the only q-Bézier and rational q-Bézier curves satisfying the boundary tangent property are the Bézier and rational Bézier curves, respectively. Evaluation algorithms formed by steps in barycentric form for rational q-Bézier curves and surfaces are provided.

1. Introduction

The q-Bernstein basis of polynomials for some $0<q\le 1$ (see [1]) plays an important role in several areas, such as Approximation Theory and Computer Aided Design. Its impact is shown by many recent publications (see [2,3] and references in there). When $q=1$, the basis is the Bernstein basis.

Let us now introduce some notations and definitions. Let $\mathcal{U}$ be a vector space of real functions defined on a real interval $I=[a,b]$ and $U=(u_0\left(t\right),\dots ,u_n\left(t\right))$ ($t\in I$) a basis of $\mathcal{U}$. If a sequence $P_0,\dots ,P_n$ of points in ${\mathbb{R}}^k$ is given then we define a curve $\gamma \left(t\right)={\sum }_{i=0}^n{P}_i{u}_i\left(t\right)$, $t\in I$. The points $P_0,\dots ,P_n$ are called control points and the corresponding polygon $P_0\cdots P_n$ is called the control polygon of $\gamma$. In Computer-Aided Geometric Design (CAGD), it is desirable that a basis U satisfies the endpoint interpolation property and also the boundary tangent property. When the curve $\gamma$ starts at $P_0$ and ends at $P_n$ for any control polygon, it is said that the basis U satisfies the endpoint interpolation property: $\gamma \left(a\right)=P_0$, $\gamma \left(b\right)=P_n$. When the first segment of the control polygon, $P_0{P}_1$, and the last segment of the control polygon, $P_{n-1}{P}_n$, are tangent to the curve $\gamma$ at the endpoints a and b, respectively, then the basis U is said to satisfy the boundary tangent property.

For curve design purposes, a basis U has to be normalized (i.e., it forms a partition of the unity: ${\sum }_{i=0}^n{u}_i\left(t\right)=1$ for all $t\in I$) and nonnegative (i.e., $u_i\left(t\right)\ge 0$ for all $t\in I$ and $i=0,\dots ,n$). It is well known in CAGD that a curve representation presents nice properties when the corresponding normalized basis is totally positive, that is, when all its collocation matrices have nonnegative minors (see [4,5]).

The Bernstein polynomials $b_i^n\left(x\right)$, $i=0,1,\dots ,n$, of degree n are defined as

$$b_i^n\left(x\right)=\left(\genfrac{}{}{0pt}{}{n}{i}\right)x^i{(1-x)}^{n-i},x\in [0,1].$$

The Bernstein polynomials $(b_0^n,\dots ,b_n^n)$ form a normalized totally positive basis of the space of polynomials of degree at most n, ${\Pi }_n$. From the Bernstein polynomials we can construct a Bézier curve as

$$\gamma \left(x\right)={\displaystyle \sum _{i=0}^n}{P}_i{b}_i^n\left(x\right),x\in [0,1].$$

(1)

In [1] Phillips introduced a generalization of the Bernstein polynomials based on q-integers. Given a positive real number q we define a q-integer $\left[r\right]$ as

$$\left[r\right]=\left\{\begin{array}{cc}1+q+\cdots +q^{r-1}=\frac{1-q^r}{1-q},\hfill & \mathrm{if}q\ne 1,\hfill \\ r,\hfill & \mathrm{if}q=1.\hfill \end{array}\right.$$

Then we define a q-factorial $\left[r\right]!$ (see [6]) as

$$\left[r\right]!=\left\{\begin{array}{cc}\left[r\right]·[r-1]\cdots \left[1\right],\hfill & \mathrm{if}r\in \mathbb{N},\hfill \\ 1,\hfill & \mathrm{if}r=0\hfill \end{array}\right.$$

and finally, we define the q-binomial coefficient as

$$\left[\genfrac{}{}{0pt}{}{n}{r}\right]=\frac{\left[n\right][n-1]\cdots [n-r+1]}{\left[r\right]!}=\frac{\left[n\right]!}{\left[r\right]![n-r]!}$$

for integers $n\ge r\ge 0$ and as zero otherwise. The q-Bernstein polynomials of degree n for $0<q\le 1$ are defined as

$$b_{i,q}^n\left(x\right)=\left[\genfrac{}{}{0pt}{}{n}{i}\right]x^i{\displaystyle \prod _{s=0}^{n-i-1}}(1-q^{s}x),x\in [0,1],i=0,1,\dots ,n.$$

(2)

These polynomials ${\mathcal{B}}^q=(b_{0,q}^n,b_{1,q}^n,\dots ,b_{n,q}^n)$, as the usual Bernstein polynomials, also form a basis of ${\Pi }_n$. Let us observe that for the case $q=1$ the q-Bernstein polynomials coincide with the Bernstein polynomials. In [7] algorithms with high relative accuracy for solving some algebraic problems for the collocation matrices of q-Bernstein polynomials were devised.

It is well known that Bézier curves satisfy the endpoint interpolation property and also the boundary tangent property. In [8] it was shown that all rational q-Bernstein bases also satisfy the endpoint interpolation property. Section 2 recalls basic properties and algorithms of q-Bézier curves. In Section 3 we prove that the Bernstein basis is the unique basis among all q-Bernstein bases satisfying the geometric boundary tangent property. In Section 4 we recall some basic properties and algorithms of rational q-Bézier curves, analyzing and providing some new properties and algorithms. We prove that the Bernstein basis is the unique basis among all q-Bernstein bases satisfying the geometric boundary tangent property.

Algorithms formed by steps in barycentric form (that is, with real coefficients that sum up to 1) are very important in CAGD. In Section 4 we provide an algorithm with this property for rational q-Bézier curves and, in Theorem 4, we relate it with the algorithm provided in [8], which does not satisfy the property. Section 5 presents an evaluation algorithm also formed by steps in barycentric form for rational q-Bézier surfaces. Finally, in Section 6 we summarize the main conclusions of the paper.

2. q-Bézier Curves

Analogously to the case of Bézier curves we can define a q-Bézier curve as

$$\gamma \left(x\right)={\displaystyle \sum _{i=0}^n}{P}_i{b}_{i,q}^n\left(x\right),x\in [0,1],$$

(3)

where the q-Bernstein polynomials are given by (2). Observe that for $q=1$ we have the usual Bézier curve.

2.1. Properties of q-Bézier Curves

In this subsection we summarize some basic properties satisfied by q–Bézier curves either recalling where they were announced or mentioning a sketch of the proof.

• The q-Bernstein polynomials form a partition of unity:

  $${\displaystyle \sum _{i=0}^n}{b}_{i,q}^n\left(x\right)=1\mathrm{for}\mathrm{all}x\in [0,1].$$
  This property can be proved by induction by evaluating ${\sum }_{i=0}^n{b}_{i,q}^n\left(x\right)$ through Algorithm 2.
• The q-Bernstein polynomials are nonnegative: $b_{i,q}^n\left(x\right)\ge 0$ for all $x\in [0,1]$.
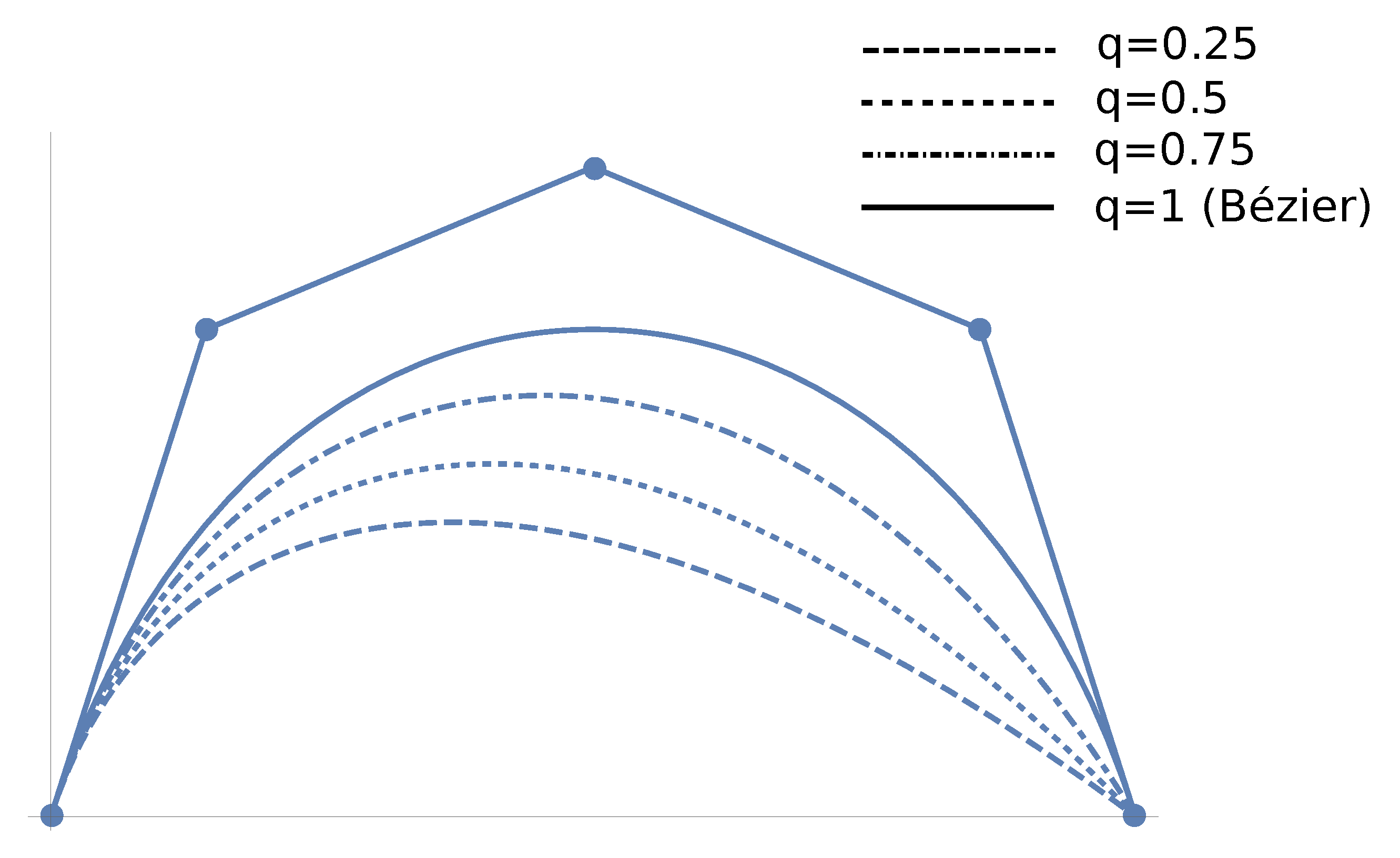
• Convex hull property: A q-Bézier curve is always contained inside the convex hull of its control points (see Section 2 of [8] for the case of rational q-Bézier curves; q-Bézier curves are a particular case of these curves).
• Affine invariance.
• Endpoint interpolation property: This is a consequence of the identities

  $$\begin{array}{c}{b}_{0,q}^n\left(0\right)=1,b_{i,q}^n\left(0\right)=0i=1,\dots ,n,\hfill \\ b_{i,q}^n\left(1\right)=0i=0,1,\dots ,n-1,b_{n,q}^n\left(1\right)=1.\hfill \end{array}$$
• Invariance under barycentric combinations:

  $${\displaystyle \sum _{i=0}^n}(\alpha P_i+\beta Q_i)b_{i,q}^n\left(x\right)=\alpha {\displaystyle \sum _{i=0}^n}{P}_i{b}_{i,q}^n\left(x\right)+\beta {\displaystyle \sum _{i=0}^n}{Q}_i{b}_{i,q}^n\left(x\right),\alpha +\beta =1.$$
• Linear precision:

  $${\displaystyle \sum _{i=0}^n}\frac{\left[i\right]}{\left[n\right]}{b}_{i,q}^n\left(x\right)=x.$$
  See Proposition 5.2 of [9].
• The q-Bernstein polynomials of degree n, $(b_{0,q}^n,\dots ,b_{n,q}^n)$, form a normalized totally positive basis (see Section 2 of [10]).
• q-Bézier curves satisfy the variation diminishing property: the q-Bézier curve has no more intersections with any line than its control polygon (see Section 2 of [10]).

2.2. q-Casteljau Algorithms

Given a sequence of control points ${\left(P_i\right)}_{0\le i\le n}$ in ${\mathbb{R}}^2$ or ${\mathbb{R}}^3$, the q-Bézier curve (3) can be evaluated by Algorithm 1 as pointed out in [11].

The previous algorithm is not formed by steps in barycentric form. In Section 2 of [12], a second de Casteljau type algorithm for computing the q-Bézier curves was given. We call it Algorithm 2.

We can observe that the previous algorithm is formed by steps in barycentric form. Although both algorithms, Algorithms 1 and 2, evaluate the same q-Bézier curve, the intermediate points are different and are related in the following form: ${\overline{f}}_i^{\left(r\right)}=q^{-ri}{f}_i^{\left(r\right)}$ (see Section 2 of [12]).

Algorithm 1 Evaluation of a q-Bézier curve

Require:${\left(P_i\right)}_{0\le i\le n}$, $q\in (0,1]$, $x\in [0,1]$ Ensure:$f_0^{\left(n\right)}\left(x\right)=\gamma \left(x\right)$  for $i=0$ to n do   $f_i^{\left(0\right)}\left(x\right)=P_i$  end for  for $r=1$ to n do   for $i=0$ to $n-r$ do    $f_i^{\left(r\right)}\left(x\right)=(q^i-q^{r-1}x)f_i^{(r-1)}\left(x\right)+x{f}_{i+1}^{(r-1)}\left(x\right)$   end for  end for

An important property of the de Casteljau algorithm in CAGD is subdivision. From Theorem 3.2 of [8] with $w_i=1$ for all i and since $f_0^{\left(i\right)}={\overline{f}}_0^{\left(i\right)}$ for $i=0,1,\dots ,n$, we derive the following result on subdivision of q-Bézier curves.

Algorithm 2 Evaluation of a q-Bézier curve

Require:${\left(P_i\right)}_{0\le i\le m}$, $q\in (0,1]$, $x\in [0,1]$ Ensure:${\overline{f}}_0^{\left(n\right)}\left(x\right)=\gamma \left(x\right)$  for $i=0$ to n do   ${\overline{f}}_i^{\left(0\right)}\left(x\right)=P_i$  end for  for $r=1$ to n do   for $i=0$ to $n-r$ do    ${\overline{f}}_i^{\left(r\right)}\left(x\right)=(1-q^{r-i-1}x){\overline{f}}_i^{(r-1)}\left(x\right)+x{q}^{r-i-1}{\overline{f}}_{i+1}^{(r-1)}\left(x\right)$   end for  end for

Theorem 1.

Let $\gamma \left(x\right)$ be a q-Bézier curve of degree n given by (3) and let $c\in (0,1)$. Then the part of the curve that corresponds to the interval $[0,c]$, denoted by ${\gamma }_{[0,c]}\left(x\right)$, is given by

$${\gamma }_{[0,c]}\left(x\right)={\displaystyle \sum _{i=0}^n}{f}_0^{\left(i\right)}\left(c\right)b_{i,q}^n\left(x\right)={\displaystyle \sum _{i=0}^n}{\overline{f}}_0^{\left(i\right)}\left(c\right)b_{i,q}^n\left(x\right),x\in [0,1],$$

where quantities $f_0^{\left(i\right)}\left(c\right)$ and ${\overline{f}}_0^{\left(i\right)}\left(c\right)$ are computed from Algorithm 1 and Algorithm 2, respectively.

2.3. Degree Elevation of q-Bézier Curves

The q-Bézier curve (3) is a polynomial curve of degree n. If the curve does not possess sufficient flexibility to model the desired shape, the degree of the curve must be elevated. So, in [10] the following result was presented.

Theorem 2.

(cf. Theorem 3.1 of [10]) Let $\gamma \left(x\right)$ be the q-Bézier curve (3) with ${\left(P_i\right)}_{0\le i\le n}$ a sequence of control points in ${\mathbb{R}}^2$ or ${\mathbb{R}}^3$. Then

$$\gamma \left(x\right)={\displaystyle \sum _{i=0}^{n+r}}{P}_i^r{b}_{i,q}^{n+r}\left(x\right),$$

where, for $n\ge 3$ and $i=0,1,\dots ,n+r$,

$$P_i^r={\displaystyle \sum _{j=0}^n}{q}^{(i-j)(n-j)}\left[\genfrac{}{}{0pt}{}{n}{j}\right]\frac{\left[\genfrac{}{}{0pt}{}{r}{i-j}\right]}{\left[\genfrac{}{}{0pt}{}{n+r}{i}\right]}{P}_j.$$

Remark 1.

Control points $P_i^r$ in the previous theorem can also be computed by applying the following recursive algorithm

$$P_i^k=\left(1-\frac{[n+r-i]}{[n+r]}\right)P_{i-1}^{k-1}+\frac{[n+r-i]}{[n+r]}{P}_i^{k-1}\left\{\begin{array}{c}k=1,2,\dots ,r,\hfill \\ i=0,1,\dots ,n+r,\hfill \end{array}\right.$$

where $P_i^0=P_i$ for $i=0,1,\dots ,n$.

3. Boundary Tangent Property for q-Bézier Curves

In this subsection we prove that the boundary tangent property holds for q-Bézier curves if and only if $q=1$, that is, for Bézier curves.

In order to study the boundary tangent property for q-Bézier curves we first need to compute ${\left(b_{i,q}^n\right)}^{\prime }\left(0\right)$ and ${\left(b_{i,q}^n\right)}^{\prime }\left(1\right)$ for $i=0,1,\dots ,n$.

Proposition 1.

Given the q-Bernstein basis $(b_{0,q}^n,\dots ,b_{n,q}^n)$ we have

$$\begin{array}{cc}\hfill & -{\left(b_{0,q}^n\right)}^{\prime }\left(0\right)={\left(b_{1,q}^n\right)}^{\prime }\left(0\right)=\left[n\right],{\left(b_{i,q}^n\right)}^{\prime }\left(0\right)=0\mathrm{for}i=2,\dots ,n,\hfill \\ \hfill & {\left(b_{i,q}^n\right)}^{\prime }\left(1\right)=-\left[\genfrac{}{}{0pt}{}{n}{i}\right]{\displaystyle \prod _{s=1}^{n-i-1}}(1-q^s)\mathrm{for}i=0,1,\dots ,n-1,{\left(b_{n,q}^n\right)}^{\prime }\left(1\right)=n.\hfill \end{array}$$

Proof. 

Differentiating the i-th q-Bernstein polynomial (2) we have

$${\left(b_{i,q}^n\right)}^{\prime }\left(x\right)=i\left[\genfrac{}{}{0pt}{}{n}{i}\right]x^{i-1}{\displaystyle \prod _{s=0}^{n-i-1}}(1-q^{s}x)-\left[\genfrac{}{}{0pt}{}{n}{i}\right]x^i{\displaystyle \sum _{s=0}^{n-i-1}}{q}^s{\displaystyle \prod _{j=0;j\ne s}^{n-i-1}}(1-q^{j}x).$$

(4)

Evaluating the previous expression at $x=0$ we have for $i=0$ and 1 that

$$\begin{array}{cc}\hfill & {\left(b_{0,q}^n\right)}^{\prime }\left(0\right)=-\left[\genfrac{}{}{0pt}{}{n}{0}\right]{\displaystyle \sum _{s=0}^{n-i-1}}{q}^s{\displaystyle \prod _{j=0;j\ne s}^{n-i-1}}(1-q^j·0)=-\left[\genfrac{}{}{0pt}{}{n}{0}\right]{\displaystyle \sum _{s=0}^{n-i-1}}{q}^s=-\frac{1-q^n}{1-q}=-\left[n\right],\hfill \\ \hfill & {\left(b_{1,q}^n\right)}^{\prime }\left(0\right)=\left[\genfrac{}{}{0pt}{}{n}{1}\right]{\displaystyle \prod _{s=0}^{n-i-1}}(1-q^s·0)=\left[\genfrac{}{}{0pt}{}{n}{1}\right]=\left[n\right],\hfill \end{array}$$

and for $i\in \{2,\dots ,n\}$ that ${\left(b_{i,q}^n\right)}^{\prime }\left(0\right)=0$. Analogously, evaluating (4) at $x=1$ we have for $i=0$ that

$${\left(b_{0,q}^n\right)}^{\prime }\left(1\right)=-\left[\genfrac{}{}{0pt}{}{n}{0}\right]{\displaystyle \sum _{s=0}^{n-1}}{q}^s{\displaystyle \prod _{j=0;j\ne s}^{n-1}}(1-q^j)=-\left[\genfrac{}{}{0pt}{}{n}{0}\right]{\displaystyle \prod _{j=1}^{n-1}}(1-q^j),$$

for $i\in \{1,\dots ,n-1\}$ that

$${\left(b_{i,q}^n\right)}^{\prime }\left(1\right)=i\left[\genfrac{}{}{0pt}{}{n}{i}\right]{\displaystyle \prod _{s=0}^{n-i-1}}(1-q^s)-\left[\genfrac{}{}{0pt}{}{n}{i}\right]{\displaystyle \sum _{s=0}^{n-i-1}}{q}^s{\displaystyle \prod _{j=0;j\ne s}^{n-i-1}}(1-q^j)=-\left[\genfrac{}{}{0pt}{}{n}{i}\right]{\displaystyle \prod _{j=1}^{n-i-1}}(1-q^j).$$

and for $i=n$ that

$${\left(b_{n,q}^n\right)}^{\prime }\left(1\right)=n\left[\genfrac{}{}{0pt}{}{n}{n}\right]=n$$

and the result follows. □

Then, as a consequence of the previous result we have the following expressions for the derivatives of a q-Bézier curve at the endpoints.

Corollary 1.

Given the q-Bézier curve $\gamma \left(x\right)$ defined by (3) we have

$$\begin{array}{cc}\hfill & {\gamma }^{\prime }\left(0\right)=\left[n\right](P_1-P_0)\hfill \\ \hfill & {\gamma }^{\prime }\left(1\right)=-{\displaystyle \sum _{i=0}^{n-1}}\left[\genfrac{}{}{0pt}{}{n}{i}\right]·\left({\displaystyle \prod _{s=1}^{n-i-1}}(1-q^s)\right)·P_i+n·P_n.\hfill \end{array}$$

From the previous result we can conclude that the first segment of the control polygon of any q-Bézier curve, $P_0{P}_1$, is tangent to the curve at $x=0$ but, in general, the last segment, $P_{n-1}{P}_n$, is not tangent to the curve at $x=1$. In the following result we determine the values of q such that the corresponding q-Bernstein bases satisfy the boundary tangent property.

Corollary 2.

The q-Bernstein basis $(b_{0,q}^n,\dots ,b_{n,q}^n)$ satisfies the boundary tangent property if and only if $q=1$, that is, if and only if it is the Bernstein basis.

Proof. 

By Corollary 1 a q-Bézier curve will satisfy the boundary tangent property if and only if the last segment of the control polygon, $P_{n-1}{P}_n$ is tangent to the curve $\gamma$ at $x=1$, that is, if there exists a value k such that ${\gamma }^{\prime }\left(1\right)=k(P_n-P_{n-1})$ for any control polygon. From Corollary 1 we deduce that a q-Bézier curve satisfies the boundary tangent property if and only if

$$\left[\genfrac{}{}{0pt}{}{n}{i}\right]·\left({\displaystyle \prod _{s=1}^{n-i-1}}(1-q^s)\right)=0\mathrm{for}i=0,1,\dots ,n-2$$

and

$$\left[\genfrac{}{}{0pt}{}{n}{n-1}\right]=\left[n\right]=n.$$

These last two expressions hold if and only if $q=1$ and the result follows. □

Figure 1 illustrates the boundary tangent property of q-Bernstein bases. We can observe that the theoretical results are confirmed: $P_0{P}_1$ is tangent to all the q-Bézier curves at $x=0$, whereas $P_{n-1}{P}_n$ is only tangent to the Bézier curve at the other endpoint $x=1$.

4. Rational q-Bézier Curves

In [8] rational q-Bézier curves were presented as a generalization of rational Bézier curves. Given a sequence ${\left(w_i\right)}_{i=0}^n$ of strictly positive weights, a rational q-Bernstein basis $(r_0^n,\dots ,r_n^n)$ was defined as

$$r_{i,q}^n\left(x\right)=\frac{w_i{b}_{i,q}^n\left(x\right)}{{\sum }_{i=0}^n{w}_i{b}_{i,q}^n\left(x\right)},x\in [0,1],\mathrm{for}i=0,1,\dots ,n,$$

(5)

and a rational q-Bézier curve as

$$\gamma \left(x\right)={\displaystyle \sum _{i=0}^n}{P}_i{r}_{i,q}^n\left(x\right)={\displaystyle \sum _{i=0}^n}{P}_i\frac{w_i{b}_{i,q}^n\left(x\right)}{{\sum }_{i=0}^n{w}_i{b}_{i,q}^n\left(x\right)},x\in [0,1].$$

(6)

where $P_i\in {\mathbb{R}}^k$ ($k=2$ or 3) are the control points of the curve.

4.1. Properties of Rational q-Bézier Curves

We now summarize some basic properties of rational q-Bézier curves.

• The functions $r_{i,q}^n\left(x\right)$ form a partition of unity:

  $${\displaystyle \sum _{i=0}^n}{r}_{i,q}^n\left(x\right)={\displaystyle \sum _{i=0}^n}\frac{w_i{b}_{i,q}^n\left(x\right)}{{\sum }_{i=0}^n{w}_i{b}_{i,q}^n\left(x\right)}=1\mathrm{for}\mathrm{all}x\in [0,1].$$
• The functions $\frac{w_i{b}_{i,q}^n\left(x\right)}{{\sum }_{i=0}^n{w}_i{b}_{i,q}^n\left(x\right)}$ are nonnegative: $\frac{w_i{b}_{i,q}^n\left(x\right)}{{\sum }_{i=0}^n{w}_i{b}_{i,q}^n\left(x\right)}\ge 0$ for all $x\in [0,1]$.
• Convex hull property: A rational q-Bézier curve is always contained inside the convex hull of its control points (see Section 2 of [8]).
• Affine invariance.
• Endpoint interpolation property: This is a consequence of the identities

  $$\begin{array}{cc}\hfill & r_{0,q}^n\left(0\right)=1,r_{i,q}^n\left(0\right)=0i=1,\dots ,n,\hfill \\ \hfill & r_{i,q}^n\left(1\right)=0i=0,1,\dots ,n-1,r_{n,q}^n\left(1\right)=1.\hfill \end{array}$$
• Invariance under barycentric combinations:

  $${\displaystyle \sum _{i=0}^n}(\alpha P_i+\beta Q_i)r_{i,q}^n\left(x\right)=\alpha {\displaystyle \sum _{i=0}^n}{P}_i{r}_{i,q}^n\left(x\right)+\beta {\displaystyle \sum _{i=0}^n}{Q}_i{r}_{i,q}^n\left(x\right),\alpha +\beta =1.$$
• The rational functions $(r_{0,q}^n,\dots ,r_{n,q}^n)$ form a normalized totally positive basis of the corresponding space of functions since any collocation matrix of this system of functions can be expressed as the product of three totally positive matrices and so it is totally positive. In fact, if we consider a collocation matrix of the system (5), it can be expressed as the product of the corresponding collocation matrix of the system $(b_{0,q}^n,\dots ,b_{n,q}^n)$ premultiplied and post multiplied by diagonal matrices with positive diagonal entries.
• Rational q-Bézier curves satisfy the variation diminishing property: the rational q-Bézier curve has no more intersections with any line than its control polygon. This property is a consequence of the previous one.

4.2. q-Casteljau Algorithms for Rational q-Bézier Curves

In Algorithm 2.1 of [8] an algorithm for the evaluation of rational q-Bézier curves was also presented. We call it Algorithm 3.

Algorithm 3 Evaluation of a rational q-Bézier curve

Require:${\left(P_i\right)}_{0\le i\le n}$, ${\left(w_i\right)}_{0\le i\le n}$, $q\in (0,1]$, $x\in [0,1]$ Ensure:$f_0^{\left(n\right)}\left(x\right)=\gamma \left(x\right)$  for $i=0$ to n do   $f_i^{\left(0\right)}\left(x\right)=P_i$   $w_i^{\left(0\right)}\left(x\right)=w_i$  end for  for $r=1$ to n do   for $i=0$ to $n-r$ do    $w_i^{\left(r\right)}\left(x\right)=(q^i-q^{r-1}x)w_i^{(r-1)}\left(x\right)+x{w}_{i+1}^{(r-1)}\left(x\right)$    $f_i^{\left(r\right)}\left(x\right)=\frac{(q^i-q^{r-1}x)w_i^{(r-1)}\left(x\right)f_i^{(r-1)}\left(x\right)+x{w}_{i+1}^{(r-1)}\left(x\right)f_{i+1}^{(r-1)}\left(x\right)}{w_i^{\left(r\right)}\left(x\right)}$   end for  end for

Algorithm 3 arose as a generalization of Algorithm 1 for rational q-Bézier curves. In particular, in [8] the following result was provided.

Theorem 3.

Each intermediate point $f_i^{\left(r\right)}\left(x\right)$ of Algorithm 3 can be expressed as

$$f_i^{\left(r\right)}\left(x\right)=\frac{{\sum }_{j=0}^r{w}_{i+j}{P}_{i+j}\left[\genfrac{}{}{0pt}{}{r}{j}\right]x^j{\prod }_{s=0}^{r-j-1}(q^i-q^{s}x)}{{\sum }_{j=0}^r{w}_{i+j}\left[\genfrac{}{}{0pt}{}{r}{j}\right]x^j{\prod }_{s=0}^{r-j-1}(q^i-q^{s}x)}$$

Analogously, we can generalize Algorithm 2 obtaining Algorithm 4.

Algorithm 4 Evaluation of a rational q-Bézier curve

Require:${\left(P_i\right)}_{0\le i\le n}$, ${\left(w_i\right)}_{0\le i\le n}$, $q\in (0,1]$ Ensure:$f_0^{\left(n\right)}\left(x\right)=\gamma \left(x\right)$  for $i=0$ to n do   ${\overline{f}}_i^{\left(0\right)}\left(x\right)=P_i$   ${\overline{w}}_i^{\left(0\right)}\left(x\right)=w_i$  end for  for $r=1$ to n do   for $i=0$ to $n-r$ do    ${\overline{w}}_i^{\left(r\right)}\left(x\right)=(1-q^{r-i-1}x){\overline{w}}_i^{(r-1)}\left(x\right)+x{q}^{r-i-1}{\overline{w}}_{i+1}^{(r-1)}\left(x\right)$    ${\overline{f}}_i^{\left(r\right)}\left(x\right)=\frac{(1-q^{r-i-1}x){\overline{w}}_i^{(r-1)}\left(x\right){\overline{f}}_i^{(r-1)}\left(x\right)+x{q}^{r-i-1}{\overline{w}}_{i+1}^{(r-1)}\left(x\right){\overline{f}}_{i+1}^{(r-1)}\left(x\right)}{{\overline{w}}_i^{\left(r\right)}\left(x\right)}$   end for  end for

We can observe that Algorithm 4 is an algorithm formed by steps in barycentric form in contrast to Algorithm 3. The following result relates both algorithms.

Theorem 4.

The intermediate values $w_i^{\left(r\right)}\left(x\right)$, $f_i^{\left(r\right)}\left(x\right)$, ${\overline{w}}_i^{\left(r\right)}\left(x\right)$ and ${\overline{f}}_i^{\left(r\right)}\left(x\right)$ of Algorithms 3 and 4 satisfy

$${\overline{w}}_i^{\left(r\right)}\left(x\right)=q^{-ir}{w}_i^{\left(r\right)}\left(x\right)\mathrm{and}{\overline{f}}_i^{\left(r\right)}\left(x\right)=f_i^{\left(r\right)}\left(x\right).$$

(7)

Proof. 

Let us prove it by induction on $r\in \{1,\dots ,n\}$. For $r=1$ we have by Algortihm 4

$${\overline{w}}_i^{\left(1\right)}\left(x\right)=(1-q^{-i}x){\overline{w}}_i^{\left(0\right)}\left(x\right)+x{q}^{-i}{\overline{w}}_{i+1}^{\left(0\right)}\left(x\right)=q^{-i}\left[(q^i-x){\overline{w}}_i^{\left(0\right)}\left(x\right)+x{\overline{w}}_{i+1}^{\left(0\right)}\left(x\right)\right].$$

From the previous expression, by Algorithm 3 and taking into account that ${\overline{w}}_i^{\left(0\right)}\left(x\right)=w_i^{\left(0\right)}\left(x\right)$ we have

$${\overline{w}}_i^{\left(1\right)}\left(x\right)=q^{-i}{w}_i^{\left(1\right)}\left(x\right),$$

(8)

that is, the first equation in (7) for $r=1$. Again by Algortihm 4 for $r=1$ we have

$$\begin{array}{cc}\hfill {\overline{f}}_i^{\left(1\right)}\left(x\right)& =\frac{(1-q^{-i}x){\overline{w}}_i^{\left(0\right)}\left(x\right){\overline{f}}_i^{\left(0\right)}\left(x\right)+x{q}^{-i}{\overline{w}}_{i+1}^{\left(0\right)}\left(x\right){\overline{f}}_{i+1}^{\left(0\right)}\left(x\right)}{{\overline{w}}_i^{\left(1\right)}}\hfill \\ \hfill & =\frac{q^{-i}\left[(q^i-x){\overline{w}}_i^{\left(0\right)}\left(x\right){\overline{f}}_i^{\left(0\right)}\left(x\right)+x{\overline{w}}_{i+1}^{\left(0\right)}\left(x\right){\overline{f}}_{i+1}^{\left(0\right)}\left(x\right)\right]}{{\overline{w}}_i^{\left(1\right)}}.\hfill \end{array}$$

Substituting (8) in the previous formula, by Algorithm 3 and taking into account that ${\overline{w}}_i^{\left(0\right)}\left(x\right)=w_i^{\left(0\right)}\left(x\right)$ and ${\overline{f}}_i^{\left(0\right)}\left(x\right)=f_i^{\left(0\right)}\left(x\right)$ we deduce that

$$\begin{array}{cc}\hfill {\overline{f}}_i^{\left(1\right)}\left(x\right)& =\frac{q^{-i}\left[(q^i-x)w_i^{\left(0\right)}\left(x\right)f_i^{\left(0\right)}\left(x\right)+x{w}_{i+1}^{\left(0\right)}\left(x\right)f_{i+1}^{\left(0\right)}\left(x\right)\right]}{q^{-i}{w}_i^{\left(1\right)}\left(x\right)}\hfill \\ \hfill & =\frac{(q^i-x)w_i^{\left(0\right)}\left(x\right)f_i^{\left(0\right)}\left(x\right)+x{w}_{i+1}^{\left(0\right)}\left(x\right)f_{i+1}^{\left(0\right)}\left(x\right)}{w_i^{\left(1\right)}\left(x\right)}=f_i^{\left(1\right)}\left(x\right),\hfill \end{array}$$

that is, the second equation in (7) for $r=1$. Now let us assume that formulas in (7) hold for some $r\in \{1,\dots ,n-1\}$ and let us prove them for $r+1$. For $r+1$ we have, by Algorithm 4, that

$$\begin{array}{cc}\hfill {\overline{w}}_i^{(r+1)}\left(x\right)& =(1-q^{r-i}x){\overline{w}}_i^{\left(r\right)}\left(x\right)+x{q}^{r-i}{\overline{w}}_{i+1}^{\left(r\right)}\left(x\right)\hfill \\ \hfill & =q^{-i}\left[(q^i-q^{r}x){\overline{w}}_i^{\left(r\right)}\left(x\right)+q^{r}x{\overline{w}}_{i+1}^{\left(r\right)}\left(x\right)\right].\hfill \end{array}$$

By the induction hypothesis we have that ${\overline{w}}_i^{\left(r\right)}\left(x\right)=q^{-ri}{w}_i^{\left(r\right)}\left(x\right)$. Applying this fact in the previous formula we have

$$\begin{array}{cc}\hfill {\overline{w}}_i^{(r+1)}\left(x\right)& =q^{-i}\left[(q^i-q^{r}x)q^{-ri}{w}_i^{\left(r\right)}\left(x\right)+q^{r}x{q}^{-r(i+1)}{w}_{i+1}^{\left(r\right)}\left(x\right)\right]\hfill \\ \hfill & =q^{-i(r+1)}\left[(q^i-q^{r}x)w_i^{\left(r\right)}\left(x\right)+x{w}_{i+1}^{\left(r\right)}\left(x\right)\right],\hfill \end{array}$$

and, by Algorithm 3, we conclude

$${\overline{w}}_i^{(r+1)}\left(x\right)=q^{-i(r+1)}{w}_i^{(r+1)}\left(x\right),$$

(9)

that is, the first formula in (7) for $r+1$. Again by Algortihm 4 for $r+1$ we have

$$\begin{array}{cc}\hfill {\overline{f}}_i^{(r+1)}\left(x\right)& =\frac{(1-q^{r-i}x){\overline{w}}_i^{\left(r\right)}\left(x\right){\overline{f}}_i^{\left(r\right)}\left(x\right)+x{q}^{r-i}{\overline{w}}_{i+1}^{\left(r\right)}\left(x\right){\overline{f}}_{i+1}^{\left(r\right)}\left(x\right)}{{\overline{w}}_i^{(r+1)}}\hfill \\ \hfill & =\frac{q^{-i}\left[(q^i-q^{r}x){\overline{w}}_i^{\left(r\right)}\left(x\right){\overline{f}}_i^{\left(r\right)}\left(x\right)+q^{r}x{\overline{w}}_{i+1}^{\left(r\right)}\left(x\right){\overline{f}}_{i+1}^{\left(r\right)}\left(x\right)\right]}{{\overline{w}}_i^{(r+1)}\left(x\right)}.\hfill \end{array}$$

Substituting (9) in the previous formula, taking into account that ${\overline{w}}_i^{\left(r\right)}\left(x\right)=q^{-ir}{w}_i^{\left(r\right)}\left(x\right)$ and ${\overline{f}}_i^{\left(r\right)}\left(x\right)=f_i^{\left(r\right)}\left(x\right)$ and by Algorithm 3 we deduce that

$$\begin{array}{cc}\hfill {\overline{f}}_i^{(r+1)}\left(x\right)& =\frac{q^{-i}\left[(q^i-q^{r}x)q^{-ir}{w}_i^{\left(r\right)}\left(x\right)f_i^{\left(r\right)}\left(x\right)+q^{r}x{q}^{-(i+1)r}{w}_{i+1}^{\left(r\right)}\left(x\right)f_{i+1}^{\left(r\right)}\left(x\right)\right]}{q^{-i(r+1)}{w}_i^{(r+1)}\left(x\right)}\hfill \\ \hfill & =\frac{(q^i-q^{r}x)w_i^{\left(r\right)}\left(x\right)f_i^{\left(r\right)}\left(x\right)+x{w}_{i+1}^{\left(r\right)}\left(x\right)f_{i+1}^{\left(r\right)}\left(x\right)}{w_i^{(r+1)}\left(x\right)}=f_i^{(r+1)}\left(x\right),\hfill \end{array}$$

that is, the second equation in (7) for $r+1$ and the theorem holds.  □

As a consequence of the previous theorem and Theorem 3, the following result follows.

Corollary 3.

Each intermediate point ${\overline{f}}_i^{\left(r\right)}\left(x\right)$ of Algorithm 4 can be expressed as

$${\overline{f}}_i^{\left(r\right)}\left(x\right)=\frac{{\sum }_{j=0}^r{w}_{i+j}{P}_{i+j}\left[\genfrac{}{}{0pt}{}{r}{j}\right]x^j{\prod }_{s=0}^{r-j-1}(q^i-q^{s}x)}{{\sum }_{j=0}^r{w}_{i+j}\left[\genfrac{}{}{0pt}{}{r}{j}\right]x^j{\prod }_{s=0}^{r-j-1}(q^i-q^{s}x)}$$

In Theorem 3.2 of [8] a result on subdivision of rational q-Bézier curves was stated. So, taking into account that result and (7) we have the following result.

Theorem 5.

Let $\gamma \left(x\right)$ be a rational q-Bézier curve of degree n given by (6) and let $c\in (0,1)$. Then the part of the curve that corresponds to the interval $[0,c]$ denoted by ${\gamma }_{[0,c]}\left(x\right)$ is given by

$${\gamma }_{[0,c]}\left(x\right)={\displaystyle \sum _{i=0}^n}{f}_0^{\left(i\right)}\left(c\right)\frac{w_0^{\left(i\right)}\left(c\right)b_{i,q}^n\left(x\right)}{{\sum }_{i=0}^n{w}_0^{\left(i\right)}\left(c\right)b_{i,q}^n\left(x\right)}={\displaystyle \sum _{i=0}^n}{\overline{f}}_0^{\left(i\right)}\left(c\right)\frac{{\overline{w}}_0^{\left(i\right)}\left(c\right)b_{i,q}^n\left(x\right)}{{\sum }_{i=0}^n{\overline{w}}_0^{\left(i\right)}\left(c\right)b_{i,q}^n\left(x\right)},x\in [0,1],$$

where quantities $w_0^{\left(i\right)}\left(c\right)$ and $f_0^{\left(i\right)}\left(c\right)$, and ${\overline{w}}_0^{\left(i\right)}\left(c\right)$ and ${\overline{f}}_0^{\left(i\right)}\left(c\right)$ are computed from Algorithm 3 and Algorithm 4, respectively.

4.3. Boundary Tangent Property for Rational q-Bézier Curves

At the beginning of this section, it was recalled that rational q-Bernstein bases satisfy the endpoint interpolation property. Now let us analyze the boundary tangent property. The following result provides the derivatives of a rational q-Bézier curve at the endpoints.

Proposition 2.

Given the rational q-Bézier curve $\gamma \left(x\right)$ defined by (6) we have

$$\begin{array}{cc}\hfill & {\gamma }^{\prime }\left(0\right)=\left[n\right]·\frac{w_1}{w_0}·(P_1-P_0),\hfill \\ \hfill & {\gamma }^{\prime }\left(1\right)=\frac{{\sum }_{i=0}^{n-1}\left[\genfrac{}{}{0pt}{}{n}{i}\right]\left({\prod }_{s=1}^{n-i-1}(1-q^s)\right)w_i(P_n-P_i)}{w_n}.\hfill \end{array}$$

Proof. 

Differentiating (6) we get

$${\gamma }^{\prime }\left(x\right)=\frac{\left({\sum }_{i=0}^n{P}_i{w}_i{\left(b_{i,q}^n\right)}^{\prime }\left(x\right)\right)\left({\sum }_{i=0}^n{w}_i{b}_{i,q}^n\left(x\right)\right)-\left({\sum }_{i=0}^n{P}_i{w}_i{b}_{i,q}^n\left(x\right)\right)\left({\sum }_{i=0}^n{w}_i{\left(b_{i,q}^n\right)}^{\prime }\left(x\right)\right)}{{\left({\sum }_{i=0}^n{w}_i{b}_{i,q}^n\left(x\right)\right)}^2}.$$

Evaluating the previous expression at $x=0$ and $x=1$ and applying Proposition 1 and that

$$\begin{array}{c}{b}_{0,q}^n\left(0\right)=1,b_{1,q}^n\left(0\right)=\cdots =b_{n,q}^n\left(0\right)=0,\hfill \\ b_{0,q}^n\left(1\right)=\cdots =b_{n-1,q}^n\left(1\right)=0,b_{n,q}^n\left(1\right)=1,\hfill \end{array}$$

(10)

the result follows.  □

Analogously to the nonrational case we can derive the following result.

Corollary 4.

The rational q-Bernstein basis $(b_{0,q}^n,\dots ,b_{n,q}^n)$ satisfies the boundary tangent property if and only if $q=1$, that is, if and only if it is the corresponding rational Bernstein basis.

Figure 2 illustrates the boundary tangent property of rational q-Bernstein bases. For the example we have considered the same control points as in the example illustrating the boundary tangent property of q-Bernstein bases with weigths ${\left(w_i\right)}_{0\le i\le 4}=(1,15,30,15,1)$. As in that case, we can observe that the theoretical results are confirmed: $P_0{P}_1$ is tangent to all the rational q-Bézier curves at $x=0$, whereas $P_{n-1}{P}_n$ is only tangent to the rational Bézier curve at the other endpoint $x=1$.

4.4. Degree Elevation of Rational q-Bézier Curves

At the end of Section 3 in [8] it was shown briefly how to elevate by 1 the degree of rational q-Bézier curves. In the following result this procedure is generalized.

Theorem 6.

Let $\gamma \left(x\right)$ be the rational q-Bézier curve (6) with ${\left(P_i\right)}_{0\le i\le n}$ a sequence of control points in ${\mathbb{R}}^2$ or ${\mathbb{R}}^3$ and ${\left(w_i\right)}_{0\le i\le n}$ a sequence of strictly positive weights. Then

$$\gamma \left(x\right)={\displaystyle \sum _{i=0}^{n+r}}{P}_i^r\frac{w_i^r{b}_{i,q}^{n+r}\left(x\right)}{{\sum }_{i=0}^{n+r}{w}_i^r{b}_{i,q}^{n+r}\left(x\right)},$$

(11)

where, for $n\ge 3$,

$$\begin{array}{cc}\hfill w_i^k& =\left(1-\frac{[n+k-i]}{[n+k]}\right)w_{i-1}^{k-1}+\frac{[n+k-i]}{[n+k]}{w}_i^{k-1},\hfill \\ \hfill P_i^k& =\frac{\left(1-\frac{[n+k-i]}{[n+k]}\right)w_{i-1}^{k-1}{P}_{i-1}^{k-1}+\frac{[n+k-i]}{[n+k]}{w}_i^{k-1}{P}_i^{k-1}}{w_i^k}\hfill \end{array}$$

for $k=1,2,\dots ,r$, and $i=0,1,\dots ,n+k$ with $w_i^0=w_i$ and $P_i^0=P_i$ for $i=0,1,\dots ,n$.

Proof. 

Denoting by

$$D\left(x\right):={\displaystyle \sum _{i=0}^n}{w}_i{b}_{i,q}^n\left(x\right)\mathrm{and}N\left(x\right):={\displaystyle \sum _{i=0}^n}{f}_i{b}_{i,q}^n\left(x\right),$$

with $f_i:=w_i{P}_i$ for $i=0,1,\dots ,n$, we have $\gamma \left(x\right)=N\left(x\right)/D\left(x\right)$. Applying Theorem 2 and Remark 1 to both $D\left(x\right)$ and $N\left(x\right)$ we deduce that

$$D\left(x\right)={\displaystyle \sum _{i=0}^{n+r}}{w}_i^r{b}_{i,q}^{n+r}\left(x\right)\mathrm{and}N\left(x\right)={\displaystyle \sum _{i=0}^{n+r}}{f}_i^r{b}_{i,q}^{n+r}\left(x\right),$$

where,

$$\begin{array}{cc}\hfill w_i^k& =\left(1-\frac{[n+k-i]}{[n+k]}\right)w_{i-1}^{k-1}+\frac{[n+k-i]}{[n+k]}{w}_i^{k-1},\hfill \\ \hfill f_i^k& =\left(1-\frac{[n+k-i]}{[n+k]}\right)f_{i-1}^{k-1}+\frac{[n+k-i]}{[n+k]}{f}_i^{k-1}\hfill \end{array}$$

for $k=1,2,\dots ,r$ and $i=0,1,\dots ,n+k$, with $w_i^0=w_i$ and $f_i^0=f_i$ for $i=0,1,\dots ,n$. Then, taking $P_i^k=f_i^k/w_i^k$ the result follows.  □

Example 1.

We have considered the rational q-Bézier curve given by (6) for $n=4$, $q=0.75$, weigths ${\left(w_i\right)}_{0\le i\le 4}=(1,15,30,15,1)$ and control points $P_0=(0,0)$, $P_1=(1,1.5)$, $P_2=(3.5,2)$, $P_3=(6,1.5)$ and $P_4=(7,0)$. Then, applying the degree elevation method for rational q-Bézier curves given in Theorem 6 for $r=3$ we obtain the rational q-Bézier curve given by (11) with weights ${\left(w_i^3\right)}_{0\le i\le 7}=(0.788899,12.0288,22.8239,23.1543,17.9863,11.4596,5.43495,0.332817)$ and control points $P_0^3=(0,0)$, $P_1^3=(0.98376,1.47564)$, $P_2^3=(2.82167,1.86236)$, $P_3^3=(3.80275,1.85416)$, $P_4^3=(4.62368,1.74692)$, $P_5^3=(5.38032,1.58936)$, $P_6^3=(6.08145,1.37782)$ and $P_7^3=(7,0)$. Figure 3 illustrates this particular example of the degree elevation of rational q-Bézier curves. The polygon with dashed line corresponds to the control polygon of the original curve, whereas the other polygon corresponds to the control polygon obtained after of the degree elevation process.

5. Rational q-Bézier Surfaces

Given a matrix of positive weights ${\left(w_{ij}\right)}_{0\le i\le m;0\le j\le n}$, a matrix of control points ${\left(P_{ij}\right)}_{0\le i\le m;0\le j\le n}$ in ${\mathbb{R}}^3$ and $q_1,q_2\in (0,1]$, we define the rational q-Bézier surface

$$F(x,y)={\displaystyle \sum _{i=0}^m}{\displaystyle \sum _{j=0}^n}{P}_{ij}\frac{w_{ij}{b}_{i,q_1}^m\left(x\right)b_{j,q_2}^n\left(y\right)}{{\sum }_{i=0}^m{\sum }_{j=0}^n{w}_{ij}{b}_{i,q_1}^m\left(x\right)b_{j,q_2}^n\left(y\right)},(x,y)\in [0,1]\times [0,1].$$

(12)

Now let us consider the evaluation of q-Bézier rational surfaces. The rational q-Bézier surface in (12) can be written as

$$F(x,y)=\frac{{\sum }_{i=0}^m\left[\left({\sum }_{j=0}^n\frac{P_{ij}{w}_{ij}{b}_{j,q_2}^n\left(y\right)}{{\sum }_{j=0}^n{w}_{ij}{b}_{j,q_2}^n\left(y\right)}\right)\left({\sum }_{j=0}^n{w}_{ij}{b}_{j,q_2}^n\left(y\right)\right)b_{i,q_1}^m\left(x\right)\right]}{{\sum }_{i=0}^m\left({\sum }_{j=0}^n{w}_{ij}{b}_{j,q_2}^n\left(y\right)\right)b_{i,q_1}^m\left(x\right)}.$$

Taking into account the previous expression of a rational q-Bézier surface, this can be evaluated by computing the evaluation of the $2m+2$ q-Bézier curves, $m+1$ rational and $m+1$ nonrational,

$$P_i\left(y\right)={\displaystyle \sum _{j=0}^n}\frac{P_{ij}{w}_{ij}{b}_{j,q_2}^n\left(y\right)}{{\sum }_{j=0}^n{w}_{ij}{b}_{j,q_2}^n\left(y\right)}\mathrm{and}{w}_i\left(y\right)={\displaystyle \sum _{j=0}^n}{w}_{ij}{b}_{j,q_2}^n\left(y\right),$$

for $i=0,1,\dots ,m$, and, finally, by computing the evaluation of the following rational q-Bézier curve:

$${\displaystyle \sum _{i=0}^m}{P}_i\left(y\right)\frac{w_i\left(y\right)b_{i,q}^m\left(x\right)}{{\sum }_{i=0}^m{w}_i\left(y\right)b_{i,q}^m\left(x\right)}$$

The evaluation of all these functions can be performed by either Algorithm 3 or Algorithm 4, obtaining Algorithm 5 and Algorithm 6, respectively.

Algorithm 5 Evaluation of a rational q-Bézier surface

Require:${\left(w_{ij}\right)}_{0\le i\le m;0\le j\le n}$, ${\left(P_{ij}\right)}_{0\le i\le m;0\le j\le n}$, $q_1,q_2$ Ensure:$F(x,y)$  for $i=0$ to m do   for $j=0$ to n do    $f_{ij}^{00}=P_{ij}$    $w_{ij}^{00}=w_{ij}$   end for  end for  for $r=1$ to n do   for $j=0$ to $n-r$ do    $w_{ij}^{0r}=(q^j-q^{r-1}y)w_{ij}^{0,r-1}+y{w}_{i,j+1}^{0,r-1}$    $f_{ij}^{0r}=\frac{(q^j-q^{r-1}y)w_{ij}^{0,r-1}{f}_{ij}^{0,r-1}+y{w}_{i,j+1}^{0,r-1}{f}_{i,j+1}^{0,r-1}}{w_{ij}^{0r}}$   end for  end for  for $r=1$ to m do   for $i=0$ to $m-r$ do    $w_{i0}^{rn}=(q^i-q^{r-1}x)w_{i0}^{r-1,n}+x{w}_{i+1,0}^{r-1,n}$    $f_{i0}^{rn}=\frac{(q^i-q^{r-1}x)w_{i0}^{r-1,n}{f}_{i0}^{r-1,n}+x{w}_{i+1,0}^{r-1,n}{f}_{i+1,0}^{r-1,n}}{w_{i0}^{rn}}$   end for  end for

Algorithm 6 Evaluation of a rational q-Bézier surface

Require:${\left(w_{ij}\right)}_{0\le i\le m;0\le j\le n}$, ${\left(P_{ij}\right)}_{0\le i\le m;0\le j\le n}$, $q_1,q_2$ Ensure:$F(x,y)$  for $i=0$ to m do   for $j=0$ to n do    ${\overline{f}}_{ij}^{00}=P_{ij}$    ${\overline{w}}_{ij}^{00}=w_{ij}$   end for  end for  for $r=1$ to n do   for $j=0$ to $n-r$ do    ${\overline{w}}_{ij}^{0r}=(q^j-q^{r-1}y){\overline{w}}_{ij}^{0,r-1}+y{\overline{w}}_{i,j+1}^{0,r-1}$    $f_{ij}^{0r}=\frac{(q^j-q^{r-1}y){\overline{w}}_{ij}^{0,r-1}{\overline{f}}_{ij}^{0,r-1}+y{\overline{w}}_{i,j+1}^{0,r-1}{\overline{f}}_{i,j+1}^{0,r-1}}{{\overline{w}}_{ij}^{0r}}$   end for  end for  for $r=1$ to m do   for $i=0$ to $m-r$ do    ${\overline{w}}_{i0}^{rn}=(q^i-q^{r-1}x){\overline{w}}_{i0}^{r-1,n}+x{\overline{w}}_{i+1,0}^{r-1,n}$    ${\overline{f}}_{i0}^{rn}=\frac{(q^i-q^{r-1}x){\overline{w}}_{i0}^{r-1,n}{\overline{f}}_{i0}^{r-1,n}+x{\overline{w}}_{i+1,0}^{r-1,n}{\overline{f}}_{i+1,0}^{r-1,n}}{{\overline{w}}_{i0}^{rn}}$   end for  end for

Taking $w_{ij}=1$ for all $i\in \{0,1,\dots ,m\}$ and $j\in \{0,1,\dots ,n\}$ in (12) a tensor product q-Bézier surface is obtained. For this particular case, Algorithms 5 and 6 are two evaluation algorithms alternative to the algorithm for the evaluation of tensor product q-Bézier surfaces proposed in [12].

As a consequence of the subdivision properties of Algorithms 3 and 4 in Theorem 5, we deduce the following subdivision properties for Algorithms 5 and 6.

Theorem 7.

Let $F(x,y)$ a rational q-Bézier surface given by (12) and let $a,b\in (0,1)$. Then the part of the surface that corresponds to $[0,a]\times [0,b]$, denoted by $F_{[0,a]\times [0,b]}(x,y)$, is given by

$$\begin{array}{cc}\hfill F_{[0,a]\times [0,b]}(x,y)& ={\displaystyle \sum _{i=0}^m}{\displaystyle \sum _{j=0}^n}{f}_{00}^{ij}(a,b)\frac{w_{00}^{ij}(a,b)b_{i,q_1}^m\left(x\right)b_{j,q_2}^n\left(y\right)}{{\sum }_{i=0}^m{\sum }_{j=0}^n{w}_{00}^{ij}(a,b)b_{i,q_1}^m\left(x\right)b_{j,q_2}^n\left(y\right)}\hfill \\ \hfill & ={\displaystyle \sum _{i=0}^m}{\displaystyle \sum _{j=0}^n}{\overline{f}}_{00}^{ij}(a,b)\frac{{\overline{w}}_{00}^{ij}(a,b)b_{i,q_1}^m\left(x\right)b_{j,q_2}^n\left(y\right)}{{\sum }_{i=0}^m{\sum }_{j=0}^n{\overline{w}}_{00}^{ij}(a,b)b_{i,q_1}^m\left(x\right)b_{j,q_2}^n\left(y\right)},(x,y)\in [0,a]\times [0,b],\hfill \end{array}$$

where quantities $f_{00}^{ij}(a,b)$ and $w_{00}^{ij}(a,b)$, and ${\overline{f}}_{00}^{ij}(a,b)$ and ${\overline{w}}_{00}^{ij}(a,b)$ are computed from Algorithm 5 and Algorithm 6, respectively.

6. Conclusions

In this paper, it is shown that many properties and efficient algorithms for Bézier curves and surfaces can be extended to q-Bézier curves and surfaces, showing some differences. The existence of evaluation algorithms formed by steps in barycentric form for the rational q-Bézier curves and surfaces is also proved. Therefore, q-Bézier curves and surfaces can be very useful, sharing many nice properties with Bézier curves and surfaces and, in addition, providing greater flexibility. We also conclude that there are some limitations with respect to Bézier curves and surfaces. For instance, with the geometric boundary tangent property. Finally, we can use for rational q-Bézier curves and surfaces algorithms with many nice properties of rational Bézier curves and surfaces.