Optimal Phase Load Balancing in Low Voltage Distribution Networks Using a Smart Meter Data-Based Algorithm

Abstract

In the electric distribution systems, the “Smart Grid” concept is implemented to encourage energy savings and integration of the innovative technologies, helping the distribution network operators (DNOs) in choosing the investment plans which lead to the optimal operation of the networks and increasing the energy efficiency. In this context, a new phase load balancing algorithm was proposed to be implemented in the low voltage distribution networks with hybrid structures of the consumption points (switchable and non-switchable consumers). It can work in both operation modes (real-time and off-line), uploading information from different databases of the DNO which contain: The consumers’ characteristics, the real loads of the consumers integrated into the smart metering system (SMS), and the typical load profiles for the consumers non-integrated in the SMS. The algorithm was tested in a real network, having a hybrid structure of the consumption points, on a by 24-h interval. The obtained results were analyzed and compared with other algorithms from the heuristic (minimum count of loads adjustment algorithm) and the metaheuristic (particle swarm optimization and genetic algorithms) categories. The best performances were provided by the proposed algorithm, such that the unbalance coefficient had the smallest value (1.0017). The phase load balancing led to the following technical effects: decrease of the average current in the neutral conductor and the energy losses with 94%, respectively 61.75%, and increase of the minimum value of the phase voltage at the farthest pillar with 7.14%, compared to the unbalanced case.

1. Introduction

The three-phase electric distribution networks (EDN) are designed and built to operate in symmetrical and balanced regimes on all phases with all elements (lines, transformers, and not least the distributed generation sources) having identical electrical parameters. In these regimes, the symmetrical current and voltage systems in each node of the system have equal values of the magnitudes of the voltage and currents on each phase, with a phase shift by 120 degrees. But, an ideal system of the currents and voltages is practically impossible to be met in the real operation conditions of the EDN because of the emergence of imbalances created mainly by the constructive conditions of some network elements (lines and transformers) or the supply of the single-phase (1-P) consumers. Thus, the operating regimes become asymmetric (unbalanced), the symmetry loss of the voltage and current systems [1].

The main causes of the imbalances in an EDN can be grouped into the following categories [2]:

• Constructive imbalances. These appear because of the spatial arrangement of the phase conductors, at the electrical lines, and the arrangement of the windings on the three columns of the ferromagnetic core, at the power transformers.
• Functional imbalances. These are created by 1-P consumers. They are connected between two phases or between a phase and the neutral point. Many of them are represented by domestic and tertiary consumers supplied from the low-voltage (LV) network, with small values of the absorbed power (up to 100 kVA). Also, there are 1-P industrial consumers. They have high absorbed powers being connected to electric medium voltage (MV) networks. The representative 1-P industrial consumers are the following: the welding installations, with absorbed powers between 100 kVA and 3 MVA, the 1-P arc furnaces, and the electric stations that supply power the railway traction network).

The current unbalances causes many issues at all voltage levels of the electric distribution networks [3]. The issues caused by current unbalance and the effects on the voltage unbalance are presented in Figure 1, adapted after [3].

It can be observed that the current and voltage unbalances cannot be separately treated. In this context, the voltage unbalances could cause current unbalances, with economic and technical losses for both partners (consumers and DNO). Concerning the attenuation measures, the current unbalances can be easier solved by the DNO. The main advantage of current balancing refers to the minimization of the current flow in the neutral conductor with benefits on the decrease of the total losses in the EDN [1].

Several phase load balancing (PLB) mechanisms are found in the literature. The PLB problem was solved in [4] using the branch and bound algorithm. The aforementioned approach uses real data of customer power demand in different periods to minimize the value of unbalance factor and find the optimal three-phase load balance in an EDN. The PLB approach used in [5] considers the reallocation of the customers to reduce the unbalance level in the EDN. Other approaches use different automatic three-phase load balancing devices [6,7,8]. The solutions for the PLB model were obtained using various techniques and technical measures: Hierarchical Petri nets [9], LV the feeder reconfiguration [10,11], or switching the consumers on the three phases [12,13,14]. The PLB problem was solved with particular metaheuristic algorithms in [15,16,17]. A PLB mechanism was proposed in [18] to be used at the MV/LV power transformer level. A particular approach, based on the optimal placement of a decentralized and autonomous battery storage system, was developed in [19,20]. A different formulation of the PLB optimization problem is presented in [21] which follows the implementation of a commutation system, with two-phase thyristor parallel contactor structure, or based on the power-line communication (PLC) and supervisory control and data acquisition (SCADA) technologies in [22,23], and not based on smart meters [24,25]. Another category of the published papers [26,27,28] regards the PLB problem at the active distribution networks (smart grids) level, using heuristic or metaheuristic methods. Moreover, an automatic phase load balancing device [29], a shunt passive compensator [30], or a controlled active filter [31] were proposed. Also, a controller was proposed in [31] to switch the connected 1-P loads from one phase to another based on an algorithm with a minimum count of loads adjustment.

To highlight the originality of the proposed algorithm, a brief description of the literature is presented in

Table 1. A comparative state-of-the-art between proposed method and the literature.

Number of Reference	Type of Network		Location of PLB		Type of Algorithm	Operation Mode
	Real	Fictive (Test)	Pillar (P)/Consumer (C)	Supply Point		Real-Time	Off-Line
[4,27]	Yes	Yes	No	Yes	Heuristic	No	Yes
[5,17,28]	Yes	No	No	Yes	Metaheuristic	No	Yes
[6,21,24]	No	Yes	No	No	Experimental	No	Yes
[7,8,26]	No	Yes	No	Yes	Heuristic	No	Yes
[9,10]	Yes	No	No	Yes	Heuristic	No	Yes
[12,13]	No	Yes	Yes	No	Metaheuristic	No	Yes
[14,29]	No	Yes	Yes	No	Experimental	Yes	No
[15,16]	No	Yes	No	Yes	Metaheuristic	No	Yes
[18,32]	No	No	No	Yes	Heuristic	No	Yes
[19,20]	Yes	No	Yes	No	Heuristic	No	Yes
[23]	No	Yes	No	No	Heuristic	Yes	No
[30,31]	No	Yes	Yes	Yes	Metaheuristic	No	Yes
Proposed approach	Yes	No	Yes	Yes	Heuristic	Yes	Yes

, based on four main characteristics: The network type, the location of PLB operation, the used algorithm, and the operation mode. Other papers from the literature indeed solve the PLB problem, but they coincide with those presented in Table 1. The objective functions refer to the minimization of unbalance factor at the pillar level or supply point (electric distribution substation).

Regardless of the algorithm used and the locations (networks) proposed for the PLB process, each consumer should have a smart phase load balancing system (SPLBS) integrated in the SMS, containing a smart meter and an automatic phase load balancing device (APBD) [27], see Figure 2.

Currently, the technical solution developed by the producers is available to be implemented by the DNOs in the EDN with a high unbalanced degree [33,34]. The solution will be introduced by the DNOs only on basis of a feasibility analysis to justify the investment.

The system contains the following main components: data concentrators, smart phase load balancing systems (SPLBS) placed to the consumers integrated into the SMS, and communication lines. The real-time data communication occurs through power line communication (PLC) wiring from the SPLBS to data concentrators and through various communication channels from the data concentrators to a central database. The use of open standard communication protocols plays a very important role in connecting SPLBS to the data concentrators. Such an approach avoids the massive investment in equipment that is not interoperable and cannot log or generate errors in the data transmission when purchased from different suppliers [35].

The analysis should identify in each stage the associated cost to implement the PLB. The main stages refer to the identification of a feasible technology, the planning of assembly at consumers, the commissioning of the system, the integration in the SMS, testing the communication with data concentrator from the supply point, and the maintenance plan [27].

Compared to the approaches from the literature, the proposed algorithm has the following advantages:

• It can be implemented in the EDNs with hybrid structures of the consumption points (switchable and non-switchable 1-P consumers). The three-phase (3-P) consumers, having identical loadings on the three phases, are not considered in the algorithm, belonging to the non-switchable consumers’ category.
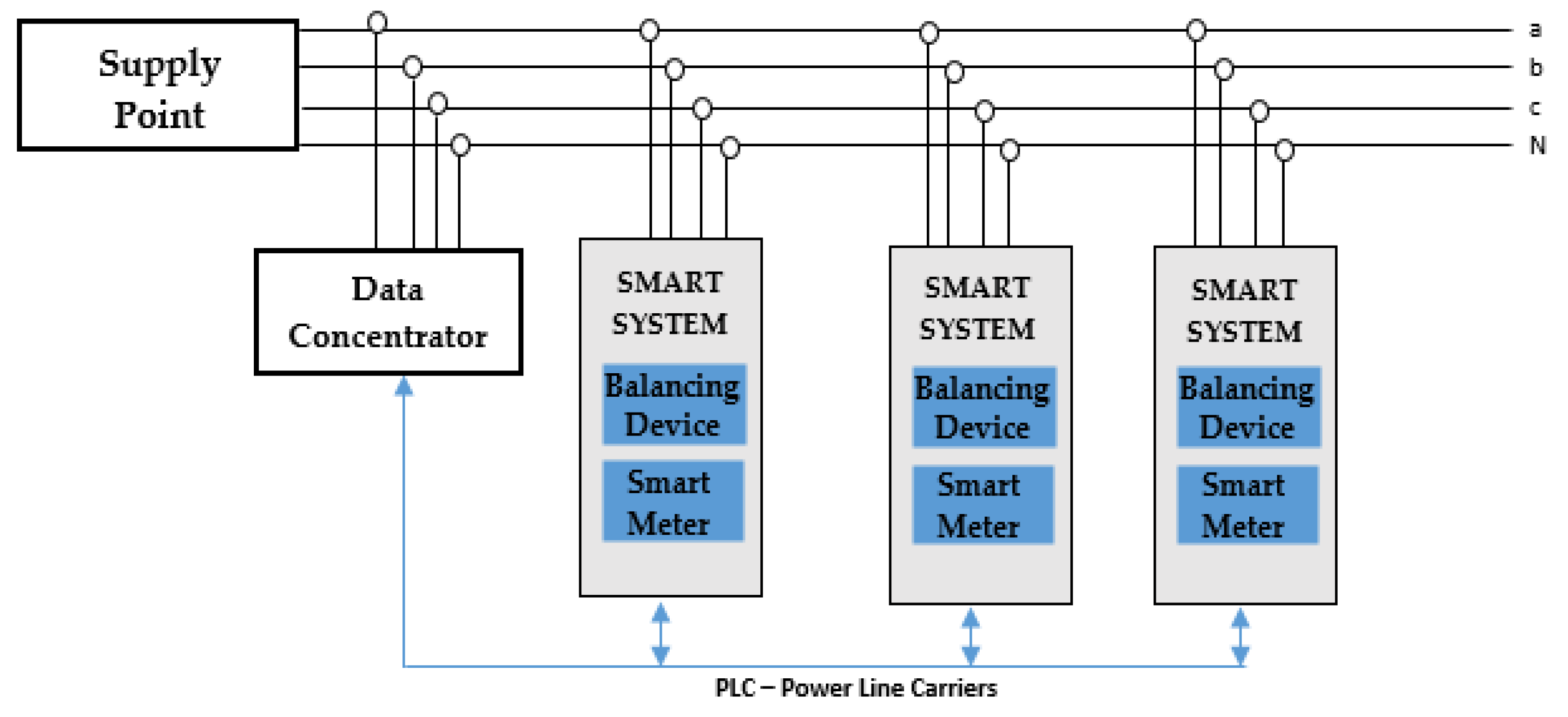
• It can work in both operation modes (real-time and off-line), uploading information from different databases of the DNO. The consumers’ characteristics (connecting pillar, allocated phase, consumption sector and class, integration in the SMS, identification number of the meter) are extracted based on the identification number of the supply point. The value of consumption and operating status of phase load balancing device (PLBD) are uploaded from the database of the SMS if the meter is integrated, or from the typical load profiles (TLPs) database if the consumer has a standard energy meter (non-integrated in the SMS).
• The convergence is rapid because of the fast recognition of the EDN topology with the help of a structure vectors-based algorithm. The optimal solutions for PLB are found at the level of each pillar such that the global solution obtained for the level of the supply point will be also optimal.

The paper has a structure organized as follows: Section 2 details the stages of the proposed PLB algorithm, accompanied by the implementation procedure. Section 3 presents the results obtained in the case of a real EDN belonging a DNO from the north-eastern of Romania and a comparison with other three algorithms to demonstrate the accuracy of the proposed algorithm. Section 4 highlights the conclusions and the future works.

2. The Proposed PLB Algorithm

The proposed algorithm can be implemented at the level of data concentrator from the supply point (electric distribution substation) to work in the real-time mode or to the decision-making central level (DMCL) of DNO for the off-line work mode helping to identify the EDNs with a high unbalanced degree and to determine the optimal solutions to decrease it. The real-time implementation in the soft architecture of the data concentrator from the supply point (SP) involves the installation of a SPLBS at the level of each consumer, as indicated in Figure 2. Also, the algorithm can be implemented in the EDN with standard and smart meters.

The PLB algorithm has the following steps:

Step 1. Identification of topology for the EDN.

The topology is identified using a two structure vectors-based algorithm [36]. The algorithm leads to the systematization of the topology, grouping the branches into vicinity levels relative to the supply point (the electric distribution substation). For an EDN with 9 nodes and 8 branches, the branches are grouped in three vicinity levels, starting from the supply point (SP): Level 1—1 branch (B2); Level 2—2 branches (B3 and B4), and Level 3—5 branches (B5, B6, B7, B8, and B9), see Figure 3. The recognition of each branch is based on the input and end nodes (pillars), being numbered relative to the end node. The input and end nodes of branches are recorded in the vectors B_i and B_e considered as input data of the algorithm.

Considering these aspects, the topology of the EDN can be described using two integer vectors, TV1 and TV2. The vector TV1 contains the number of branches from each vicinity level and the vector TV2 includes all branches in the order of the vicinity levels. The elements of vectors TV1 and TV2 are presented in

Table 2. The elements of topology vectors.

TV1	L1	L2	L3
TV2	B1	B2, B3	B5, B6, B7, B8, B9

.

Step 2. Upload the input data sequence

The algorithm uploads from the database of the DNO a data sequence that is stored in the input vectors. This input data sequence is formed from the following fields, see Figure 4:

• Supply point: Each electric distribution substation has an identification number that allows the algorithm to allocate correct data from the database to all consumers supplied from this point.
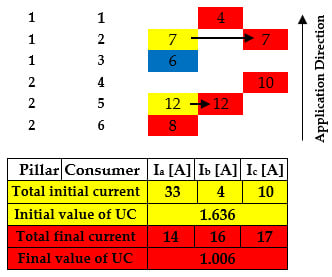
• Connecting pillar: The connecting pillar is recorded in the database to identify the position of each consumer in the network. Also, this information is very important in the calculus of a steady-state regime to evaluate the performance of the PLB measure through reducing the power/energy losses and improving the voltage level at the consumers. The vector associated with this field is noted with CP, having the size (N_C × 1), where N_C represents the total number of consumers from the EDN.
• Branching Phase: Each 1-P consumer is allocated by the DNO at one of the phases ph = {a, b, c}, and the 3-P consumers are connected at all three phases ph = {a, b, c}. The records regarding this information are found in the vector PB with the size (N_C × 1).
• Consumption Sector. The information is used to assign the consumer to the following consumption sectors: domestic, non-domestic, commercial, and industrial. The records for this information have the identification numbers from 1 to 4: 1 (domestic), 2 (non-domestic), 3 (commercial), and 4 (industrial) included in the vector CS with the size (N_C × 1).
• Consumption class. More consumption classes are allocated to each consumption sector by the DNO. As an example, a Romanian DNO has a classification in five consumption classes for consumers from the domestic sector [36]: < 400 kWh (first class), range [400 kWh, 1250 kWh] (second class), range [1250 kWh, 2500 kWh] (third class), range [2500 kWh, 3500 kWh] (the fourth class), and range [2500 kWh, 3500 kWh] (the fifth class). This information is loaded in the vector CC, having the size (N_C × 1).
• Integration in SMS. Currently, not all consumers from the LV distribution networks are integrated into the smart metering system. In this case, the value 1 (if it is integrated) and 0 (otherwise) will be recorded in the database. If the meter is integrated into the SMS, it can communicate to the central system information about the currents or active and reactive powers, which will record them in the database (see Figure 5).

If the consumer has a PLBD, then the central system will communicate both its operating status and connection phase. Thus, it will be classified by the algorithm in the category of switchable consumers, recording the value 1 in the database. Otherwise, even if the consumer integrated into the SMS and PLBD is faulty (value is 0), or has a standard meter, it cannot be allocated on other phase and will be classified in the set of non-switchable consumers, recording the value 0 in the database. The algorithm will record these values in the vectors INT (for integration mode) and BS (for the PBLD status), having the size (N_C × 1). Also, for the non-switchable consumers because of the missing data from the consumption point, the algorithm will use the hourly values from the typical load profiles (TLPs) allocated in function by Consumption Sector (vector CS) and Consumption class (vector CC).

Concerning the TLPs, these are defined by the DNO to all consumers which are not integrated in the SMS and are determined for each consumption sector (domestic, non-domestic, commercial, and industrial) having common characteristics regarding the consumption classes, days (weekend or working), and seasons (springer, summer, autumn, or winter). Finally, each consumer will have an assigned TLP, depending on the above characteristics. The profiling process to obtain the TLPs is presented in [36].

Even if these TLPs are known, the DNOs cannot implement the proposed algorithm in those networks with a high number of non-integrated consumers into the SMS. Within the proposed algorithm, they belong to the category of non-switchable consumers, so that the number of switching solutions will be limited. As the number of non-switchable consumers decreases, the number of switching options increases, leading to a solution very close to the optimal solution (in the ideal case, it is equal with 1.00).

The values of the hourly loads for all consumers are recorded in the matrix IC, with the size (N_C × H).

• Serial number. Each consumer is recognized in the database through the serial number of meter installed (smart or standard). The information is recorded in the vector SN, having the size (N_C × 1).

Step 3. The PLB procedure

The PLB procedure is characterized by a dynamic process which follows the minimization of unbalance degree (as close to 1) at the level of each pillar by allocation to other phases (e.g., phase a on phases b or c) of the switchable consumers (with SPLBS installed). The procedure is based on the decomposition and coordination of the complex distribution networks. Decomposition considers the division of the distribution network into groups of pillars and to carry out optimization on the pillar level to obtain a minimum unbalance coefficient. At the level of each pillar will be determined the optimal solution considering all combinations between the allocations of the switchable consumers on the phases. The optimal solutions at the level of each pillar are obtained by coordination of the switchable consumers, such that the global optimal solution, represented by the unbalance coefficient at the level of the supply point, will be obtained. In other words, if the balancing solutions are optimal at the level of each pillar, then the global solution at the level of the supply point is also optimal.

To evaluate if an EDN is in an unbalanced regime, an unbalance coefficient is calculated. There are formulas proposed by the IEEE (The Institute of Electrical and Electronics Engineers) and NEMA (The National Equipment Manufacturer’s Association) standards [37] for the voltage unbalance. But, there is no widespread agreement for the current unbalance. Thus, the negative and positive sequence components of the current can be used to evaluate the current unbalance [3]. This approach requires the decomposition of the current system into instantaneous positive, negative, and zero sequence components using phasor representation, which is not always possible. Easy evaluation of current unbalance in a node (pillar) of the EDN can be made based on an unbalance coefficient calculated based on the effective values of phase currents [27]. The value of this coefficient must be less than 1.1, agreed by the DNOs.

$$UC=\frac{1}{3}\cdot \left({\left(\frac{I_a}{I_{average}}\right)}^2+{\left(\frac{I_b}{I_{average}}\right)}^2+{\left(\frac{I_c}{I_{average}}\right)}^2\right)$$

(1)

where: UC—the unbalance coefficient; I_a, I_b, I_c—the currents on the phases a, b, and c; I_average—the average value of the phase currents.

The mechanism of the proposed algorithm is explained for a particular case with 2 pillars and 5 consumers, see Figure 6. For the switchable consumers, the initial phase has a yellow color, the optimal phase has a red color, and the phase of non-switchable consumers has a blue color. The optimal phase is the initial phase when the yellow color is missing. It can be observed that one consumer (3) belongs to the non-switchable consumer category, and only two consumers (2 and 5), after applying the algorithm, switched from the phases {a, a} to the phases {c, b}. Consumers 1, 4, and 6 maintained the allocations on the phases {b, c, a}.

The analysis of the obtained results highlighted that a final value of UC very close by 1 (1.006) can be reached starting from an initial high value (1.636), switching only 2 consumers on other phases.

The minimization of unbalance coefficient (UC), at each hour h = 1, …, H, and each pillar p = 1,…, Np represents the objective of the PLB problem:

$$\min (U{C}^{(p),h}),\mathrm{p}=1,\dots ,{\mathrm{N}}_{\mathrm{p}};\mathrm{h}=1,\dots ,\mathrm{H}$$

(2)

where:

$$U{C}_{}^{(p),h}=\frac{1}{3}\cdot \left({\left(\frac{I_a^{(p),h}}{I_{average}^{(p),h}}\right)}^2+{\left(\frac{I_b^{(p),h}}{I_{average}^{(p),h}}\right)}^2+{\left(\frac{I_c^{(p),h}}{I_{average}^{(p),h}}\right)}^2\right)$$

(3)

$$I_{average}^{(p),h}=\frac{1}{3}\left(I_a^{(p),h}+I_b^{(p),h}+I_c^{(p),h}\right)$$

(4)

$$I_a^{(p),h}=I_{a,ns}^{(p),h}+I_{a,s}^{(p),h}+I_a^{(d),h};\mathrm{p}=1,\dots ,{\mathrm{N}}_{\mathrm{p}};\mathrm{p}\ne \mathrm{d}$$

(5)

$$I_b^{(p),h}=I_{b,ns}^{(p),h}+I_{b,s}^{(p),h}+I_b^{(d),h};\mathrm{p}=1,\dots ,{\mathrm{N}}_{\mathrm{p}};\mathrm{p}\ne \mathrm{d}$$

(6)

$$I_c^{(p),h}=I_{c,ns}^{(p),h}+I_{c,s}^{(p),h}+I_c^{(d),h};\mathrm{p}=1,\dots ,{\mathrm{N}}_{\mathrm{p}};\mathrm{p}\ne \mathrm{d}$$

(7)

$$I_{a,ns}^{(p),h}=\left({\displaystyle \sum _{j=1}^{N_{a,ns}^{(p),h}}{I}_{a,ns,j}^{(p),h}}\right)$$

(8)

$$I_{b,ns}^{(p),h}=\left({\displaystyle \sum _{k=1}^{N_{b,ns}^{(p),h}}{I}_{b,ns,k}^{(p),h}}\right)$$

(9)

$$I_{a,ns}^{(p),h}=\left({\displaystyle \sum _{l=1}^{N_{{}_{c,ns}}^{(p),h}}{I}_{c,ns,l}^{(p),h}}\right)$$

(10)

$$I_{a,s}^{(p),h}=\left({\displaystyle \sum _{m=1}^{N_{a,s}^{(p),h}}{I}_{a,s,m}^{(p),h}}\right)$$

(11)

$$I_{b,s}^{(p),h}=\left({\displaystyle \sum _{n=1}^{N_{b,ns}^{(p),h}}{I}_{b,s,n}^{(p),h}}\right)$$

(12)

$$I_{c,s}^{(p),h}=\left({\displaystyle \sum _{o=1}^{N_{c,ns}^{(p),h}}{I}_{c,s,o}^{(p),h}}\right)$$

(13)

$$N_{C,ns}^{(p)}=N_{a,ns}^{(p),h}+N_{b,ns}^{(p),h}+N_{c,ns}^{(p),h}$$

(14)

$$N_{C,s}^{(p)}=N_{a,s}^{(p),h}+N_{b,s}^{(p),h}+N_{c,s}^{(p),h}$$

(15)

$$N_C^{(p),h}=N_{C,ns}^{(p),h}+N_{C,s}^{(p),h}$$

(16)

where: UC^(p),h—the unbalance coefficient calculated at the pillar p and hour h; I_a^(p),h, I_b^(p),h, I_c^(p),h—the currents on the phases a, b, and c, at the pillar p and hour h; I_average^(p),h—the average value of the phase currents, at the pillar p and hour h; I_a,ns^(p),h, I_b,ns^(p),h, I_c,ns^(p),h—the total current of the non-switchable consumers on the phases a, b, and c, at the pillar p and hour h; I_a,s^(p),h, I_b,s^(p),h, I_c,s^(p),h—the total current of the switchable consumers on the phases a, b, and c, at the pillar p and hour h; I_a,s^(d),h, I_b,s^(d),h, I_c,s^(d),h—the currents on the phases a, b, and c, at the pillar d (located downstream by pillar p), and hour h; I_a,ns,j^(p),h—the current of the non-switchable consumer j connected on the phase a, at the pillar p, and hour h; I_b,ns,k^(p),h—the current of the non-switchable consumer k connected on the phase b, at the pillar p, and hour h; I_c,ns,l^(p),h—the current of the non-switchable consumer l connected on the phase c, at the pillar p, and hour h; I_a,s,m^(p),h – the current of the switchable consumer m connected on the phase a, at the pillar p, and hour h; I_b,s,n^(p),h—the current of the switchable consumer n connected on the phase b, at the pillar p, and hour h; I_c,s,o^(p),h—the current of the switchable consumer o connected on the phase c, at the pillar p, and hour h; N_a,ns^(p),h, N_b,ns^(p),h, N_c,ns^(p),h—the number of the non-switchable consumers connected on the phases a, b, and c, at the pillar p, and hour h; N_a,s^(p),h, N_b,s^(p),h, N_c,s^(p),h—the number of the switchable consumers connected on the phases a, b, and c, at the pillar p, and hour h; N_C,ns^(p),h—the total number of the non-switchable consumers connected at the pillar p, and hour h; N_C,s^(p),h—the total number of the switchable consumers connected at the pillar p, and hour h; N_C^(p),h—the total number of the consumers connected at the pillar p, and hour h; N_p—the total number of the pillars; H—the analyzed time period.

The implementation procedure of the mathematical model (2)–(16) is presented in Figure 7a,b, and the details are given in

Table 3. The implementation procedure of the proposed phase load balancing (PLB) algorithm.

Steps of PLB Algorithm Based on the Smart Meter Data
Step 1. Identification of the topology for the EDN based on the vectors TV1 and TV2, built with the vectors Bi and Be which contain the input and end nodes (pillars) assigned each branch.
Step 2. Upload the input data sequence from the database of the DNO corresponding to the SP of EDN: Store the information in the vectors: CP, BP, CS, CC, INT, BS, and SN.   Determine the number of consumers supplied: NC = length (SN);   Initialize the matrices IC ∈ ℝ*(Nc×H), Ia, Ib, and Ic ∈ ℝ* (Np×H), and UC∈ ℝ*(Np×H)   for each hour h, h = 1…H      Set initial consumer index: i = 0;      while i ≤ Nc       Increase consumer index: i = i + 1;       if INT (i, h) = 1        if BS (i, h) = 1         Update IC (i, h) with the value recorded on the line SN(i) and column h of         the consumption matrix loaded from the SMS;        else         Send a warning message to the central system on the failure/missing         communication of PLBD to be repaired as soon as possible;         Update IC (i, h) with the assigned value from the TLP depending the         records from the vectors CS (i) and CC (i), day (weekend or working),         and season (springer, summer, autumn, or winter);       else         Update IC (i, h) with the assigned value from the TLP depending the         records from the vectors CS (i) and CC (i), day (weekend or working), and         season (springer, summer, autumn, or winter);
Step 3. The PLB sequence at the level of each pillar:      Set initial pillar index: p = Np;      while (p ≥ 1) and (p ≤ Np)      Initialize the vector index;      Find the index corresponding to pillar p in vector CP, and store in vector index;      Determine the number of consumers connected at the pillar p: np = length (index);      Initialize the sums of phase currents corresponding to:      switchable consumers: Ias = 0, Ibs = 0, Ics = 0;      non-switchable consumers: Ians = 0, Ibns = 0, Icns = 0;      all consumers: Iap = 0, Ibp = 0, Icp = 0;      Set initial consumer index: j = 0;      while j ≤ np       Increase consumer index: j = j + 1;       if (INT(index (j)) = 0) and (BP (index (j)) = {a})         Update sum of current to non-switchable consumers on the phase a:          Ians = Ians + IC (index (j));         if BP (index (j)) = {b})          Update sum of current to non-switchable consumers on the phase b:          Ibns = Ibns + IC (index(j));         else          Update sum of current to non-switchable consumers on the phase c:          Icns = Icns + IC (index (j));       if (INT(index (j)) = 1) and (BS (index (j)) = 0)          Changing the category of consumer j from switchable in          non-switchable;          if (BP (index (j)) = {a})           Update sum of current to non-switchable consumers on the phase a:           Ians = Ians + IC (index (j));           if BP (index (j)) = {b})             Update sum of current to non-switchable consumers on             the phase b: Ibns = Ibns + IC (index (j));           else             Update sum of current to non-switchable consumers on             the phase c: Icns = Icns + IC (index (j));       if (INT(index (j)) = 1) and (BS (index (j)) = 1)          Assigning the consumer j on each of the three phases:          case Combination 1 – allocation of the consumer j on the phase a           Compute the fictive sum of phase currents to switchable consumers:           Iasf1 = Ias + IC (index (j)); Ibsf1 = Ibs; Icsf1 = Ics;           Compute the fictive sum of the phase currents to all consumers:           Iapf1 = Ians + Iasf1; Ibpf1= Ibns + Ibsf1; Icpf1 = Icns + Icsf1;           Compute the average value of the phase currents, Iaverage1 (rel. (3))           Compute the UC1 (rel. (2));          case Combination 2 – allocation of the consumer j on the phase b           Compute the fictive sum of phase currents to switchable consumers:           Iasf2 = Ias; Ibsf2 = Ibs + IC (index (j)); Icsf2 = Ics;           Compute the fictive sum of the phase currents to all consumers:           Iapf2 = Ians + Iasf2; Ibpf2 = Ibns + Ibsf2; Icpf2 = Icns + Icsf2;           Compute the average value of the phase currents, Iaverage2, (rel. (3));           Compute the UC2 (rel. (2));          case Combination 3 – allocation of the consumer j on the phase c           Compute the fictive sum of phase current to switchable consumers:           Iasf3 = Ias; Ibsf3 = Ibs; Icsf3 = Ics + IC (index (j));           Compute the fictive sum of the phase currents of all consumers:            Iapf3 = Ians + Iasf3; Ibpf3 = Ibns + Ibsf3; Icpf3 = Icns + Icsf3;           Compute the average value of the phase currents, Iaverage3 (rel. (3));           Compute the UC3 (rel. (2));           Determine the minimum value of UC: min (UC1, UC2, UC3);           Store the number of combination with UCmin, COmin, corresponding to           one of the three phase:           if COmin = 1           Update in the vector PB the phase a: PB (index (j)) = {a};           Update the sum of phase currents to switchable consumers:           Ias = Iasf1; Ibs = Ibsf1; Ics = Icsf1;           Update the sum of phase currents to all consumers:           Iap = Iapf1; Ibp = Ibpf1; Icp = Icpf1;           if COmin = 2             Update in the vector PB the phase b: PB(index (j)) = {b};             Update the sum of phase currents to switchable consumers:             Ias = Ias2; Ibs = Ibsf2; Ics = Icsf2;             Update the sum of phase currents to all consumers:              Iap = Iapf2; Ibp = Ibpf2; Icp = Icpf2;           else             Update in the vector PB the phase c: PB(index (j)) = {c};             Update the sum of phase currents to switchable consumers:              Ias = Ias3; Ibs = Ibsf3; Ics = Icsf3;             Update the sum of phase currents to all consumers:              Iap = Iapf3; Ibp = Ibpf3; Icp = Icpf3;      Update the value of unbalanced coefficient UC (p, h) = UCmin;      Update the value of phase currents Ia (p, h) = Iap, Ib (p, h) = Ibp, and Ic (p, h) = Icp;      Decrease pillar index: p = p − 1;      According with the new allocations from vector PB the central system emits the      instructions at each PLBD;   Increase hour index: h = h + 1;   Print results: UC, Ia, Ib, Ic.

.

3. Case Study

The proposed PLB algorithm was tested in the case of a real LV EDN from a rural area, located in northeastern Romania. The structure of the network is presented in Figure 8. The structure of the network is presented in Figure 8. This network was chosen because of the very complex structure (88 pillars, a total length of 3.52 km, and many lateral branches) and the high number of consumers (163 consumers). Generally, the LV distribution networks have an average length by 1.2 km, with approximately 30 pillars, and an average number of consumers by 60 consumers [38,39]. The values of the characteristics (length, poles, and consumers) of the considered network are about three times higher than the average values. The EDN is supplied from a point (SP), through a power transformer 20/0.4 kV. The numbering of pillars is real, given by the DNO from this distribution area, beginning with Pillar 8. The distance between two successive pillars is 0.04 km, stipulated in Romanian technical normative [40]. The technical characteristics of the branches are presented in

Table 4. The technical characteristics of the branches.

Branch	Type Conductor	Cross-Section of Phase Conductors [mm2]	Cross-Section of Neutral Conductor [mm2]	Length [km]	r0 [Ω/km]	x0 [Ω/km]
SP-11	Classic	50	50	0.160	0.61	0.298
11–15	Classic	50	50	0.160	0.61	0.298
11–95	Classic	50	50	1.960	0.61	0.298
15–27	Classic	35	35	0.480	0.871	0.055
15–39	Classic	35	35	0.480	0.871	0.055
37–46	Classic	25	25	0.280	1.235	0.319
Total		50	50	2.280	0.61	0.298
		35	35	0.960	0.871	0.055
		25	25	0.280	1.235	0.319
Total				3.520

, where r₀ and x₀ represent the specific resistance and reactance. If the reactance is not known, an estimation technique can be used [41].

From the database of the DNO, the information about the characteristics of the consumers from this EDN based on the identification number of the SP was uploaded. The format of the input data was presented in Section 2, see Figure 4. The characteristics of the consumers are presented synthetically in

Table 5. Synthesis on the characteristics of the consumers from the analyzed EDN.

Consumer’ Type		Initial Phase				Consumption SECTOR
1-P	3-P	a	b	c	abc	I	II	III	IV
161	2	42	72	47	2	161	2	-	-

. Detailed information regarding the connected pillars, the branching phase, and the consumption sector are given in

Table A1. The allocation on pillar, phase, and the consumption sector.

Pillar	Consumer’ Type		Branching Phase			Consumption Sector			Pillar	Consumer’ Type		Branching Phase			Consumption Sector
	1-P	3-P	a	b	c	1	2	3		1-P	3-P	a	b	c	1	2	3
8	2	-	-	2	-	1	-	-	51	2	-	-	1	1	1	-	-
9	2	-	-	2	-	1	-	-	52	3	-	-	3	-	1	-	-
10	3	-	2	1	-	1	-	-	53	1	-	-	1	-	-	2	-
11	1	-	-	1	-	1	-	-	54	6	-	-	-	6	1	-	-
12	2	-	-	2	-	1	-	-	55	2	-	1	1	-	1	-	-
13	1	-	-	1	-	1	-	-	56	2	-	-	2	-	1	-	-
14	2	-	-	-	2	1	-	-	57	1	-	-	1	-	1	-	-
15	2	-	-	1	1	1	-	-	58	1	-	1	-	-	1	-	-
17	1	1	1	1	1	1	-	-	59	2	-	-	2	-	1	-	-
18	2	-	-	-	2	1	-	-	60	2	-	1	1	-	1	-	-
19	2	-	2	-	-	1	-	-	61	1	-	-	1	-	1	-	-
20	2	-	2	-	-	1	-	-	62	1	-	-	-	1	1	-	-
21	1	-	1	-	-	1	-	-	63	2	-	2	-	-	1	-	-
22	2	-	1	1	-	1	-	-	65	1	-	-	1	-	1	-	-
23	2	-	2	-	-	1	-	-	66	4	-	1	3	-	1	-	-
24	1	-	-	-	1	1	-	-	67	2	-	-	2	-	1	-	-
26	2	-	-	-	2	1	-	-	68	2	-	-	2	-	1	-	-
27	3	-	1	-	2	1	-	-	69	2	-	1	1	-	1	-	-
28	2	-	-	1	1	1	-	-	70	1	-	-	1	-	1	-	-
29	4	-	-	1	3	1	-	-	71	1	-	-	1	-	1	-	-
30	2	-	-	-	2	1	-	-	72	1	-	-	1	-	1	-	-
31	2	-	-	-	2	1	-	-	75	2	-	-	2	-	1	-	-
32	1	-	-	-	1	1	-	-	76	2	-	-	2	-	1	-	-
33	4	-	-	-	4	1	-	-	77	2	-	1	1	-	1	-	-
34	5	-	-	-	5	1	-	-	78	4	-	1	3	-	1	-	-
35	4	-	1	1	2	1	-	-	79	1	1	1	2	1	1	-	-
36	1	-	-	1	-	1	-	-	80	2	-		2	-	1	-	-
37	3	-	-	-	3	1	-	-	82	2	-	-	2	-	1	-	-
38	1	-	-	-	1	1	-	-	83	1	-	1	-	-	1	-	-
39	4	-	-	1	3	1	-	-	84	2	-	-	2	-	1	-	-
40	3	-	-	-	3	1	-	-	86	1	-	-	1	-	1	-	-
41	1	-	-	-	1	1	-	-	87	2	-	-	2	-	1	-	-
42	1	-	-	-	1	1	-	-	88	1	-	-	1	-	1	-	-
43	2	-	-	-	2	1	-	-	89	2	-	-	2	-	1	-	-
44	2	-	-	1	1	1	-	-	90	1	-	-	1	-	1	-	-
45	4	-	-	-	4	1	-	-	91	2	-	-	2	-	1	-	-
46	2	-	-	-	2	1	-	-	92	1	-	-	1	-	1	-	-
47	3	-	1	2	-	1	-	-	93	2	-	-	2	-	1	-	-
48	3	-	1	2	-	1	2	-	94	1	-	1	-	-	1	-	-
49	2	-	-	2	-	1	-	-	95	1	-	-	1	-	1	-	-
50	1	-	-	-	1	1	-	-

from Appendix A.

It can be observed that the vast majority of consumers (98.8%) have a 1-P branching with the following initial allocation: 25.8% on phase a, 44.2% on phase b, and 28.8% on phase c. Only 1.2% of the consumers have 3-P branching. Regarding the consumption sector, 98.8% of the consumers belong to the domestic sector, and only 1.2% are from the non-domestic sector.

From all consumers, 114 1-P consumers, representing 70.8%, are integrated into the SMS with the possibility to have PLBD installed. They will be considered from the switchable consumers’ category in our algorithm. The algorithm imports for each consumer i, i = 1,…, N_c, according to the serial number of meter recorded in the vector SN, the hourly load from the database of SMS for the analyzed period H. In our case study, the period H corresponds to a winter working day with hourly records h, h = 1, …, 24, see the supplementary file which contains the active and reactive power profiles. The other 47 1-P consumers are considered as non-switchable consumers due to the standard meters, non-integrated in the SMS. For these consumers, the algorithm uses TLPs according to the information stored in the vectors CS, associated with the consumption sector, and CC, associated with the consumption class.

The phase currents (I_a, I_b and I_c) and neutral current (I₀) in the SP (on the 0.4 kV side) were determined considering all load profiles, using the calculations of steady-state regime, see

Table 6. The currents in the conductors of the first branch, SP-Pillar 8, initial case.

Hour	Ia [A]	Ib [A]	Ic [A]	I0 [A]	UC
1	14.77	48.71	19.47	31.84	1.29
2	14.01	46.55	18.64	30.49	1.30
3	13.24	43.81	17.73	28.58	1.29
4	13.36	44.40	17.45	29.20	1.30
5	13.55	43.94	17.99	28.43	1.28
6	12.38	36.47	16.98	22.15	1.23
7	16.73	41.58	19.49	23.59	1.18
8	19.53	45.17	20.93	24.97	1.17
9	19.69	49.91	21.88	29.18	1.20
10	18.05	53.57	21.70	33.83	1.26
11	19.21	61.57	23.16	40.52	1.30
12	17.44	58.17	20.53	39.28	1.33
13	17.94	61.76	21.40	42.20	1.35
14	17.87	60.11	22.35	40.18	1.32
15	17.91	61.07	22.21	41.18	1.33
16	15.99	54.16	21.22	35.84	1.31
17	18.38	61.07	22.53	40.77	1.32
18	21.55	66.87	25.80	43.34	1.29
19	21.31	59.27	25.14	36.19	1.23
20	21.27	51.86	23.77	29.41	1.18
21	25.66	58.78	27.08	32.43	1.17
22	27.69	68.53	31.57	39.04	1.19
23	24.83	69.17	30.67	41.72	1.22
24	17.12	53.18	23.17	33.45	1.26

and Figure 9). The used algorithm is an improved version of the forward/backward sweep-based algorithm, developed in [36], to calculate the steady-state regimes to three-phase LV distribution networks in the balanced and unbalanced regime.

The analysis of the obtained results highlights a high difference between the phase currents and an important current in the neutral conductor (exceeds the current on the phases a and b), which leads to an unbalanced degree beyond the threshold (1.1) imposed by the DNO. The UC is in the range [1.17, 1.35], having an average value of 1.26.

Also, the current unbalance leads to higher power/energy losses because of current flows in the neutral conductor and a significant voltage unbalance, as shown in

Table 7. The energy losses calculated in the initial case, [kWh].

Hour	Main Conductors				Branching Conductors				Total
	a	b	c	Neutral	a	b	c	Neutral
1	0.03	0.54	0.11	0.43	0.003	0.014	0.001	0.011	1.14
2	0.03	0.49	0.10	0.39	0.003	0.013	0.001	0.011	1.04
3	0.02	0.43	0.09	0.35	0.002	0.011	0.001	0.009	0.92
4	0.02	0.44	0.09	0.35	0.002	0.012	0.001	0.010	0.93
5	0.02	0.44	0.09	0.35	0.002	0.011	0.001	0.010	0.93
6	0.02	0.31	0.08	0.25	0.002	0.006	0.001	0.006	0.67
7	0.04	0.41	0.11	0.32	0.005	0.007	0.001	0.008	0.90
8	0.05	0.50	0.12	0.38	0.007	0.009	0.001	0.011	1.08
9	0.05	0.59	0.14	0.46	0.007	0.012	0.001	0.013	1.27
10	0.04	0.66	0.13	0.52	0.005	0.017	0.001	0.015	1.40
11	0.05	0.87	0.15	0.68	0.006	0.025	0.001	0.021	1.81
12	0.04	0.77	0.12	0.60	0.005	0.025	0.001	0.020	1.58
13	0.04	0.86	0.13	0.68	0.005	0.029	0.001	0.023	1.77
14	0.04	0.82	0.14	0.65	0.005	0.025	0.001	0.020	1.71
15	0.04	0.85	0.14	0.67	0.005	0.026	0.001	0.021	1.76
16	0.04	0.67	0.13	0.53	0.004	0.019	0.001	0.015	1.40
17	0.05	0.85	0.15	0.67	0.005	0.026	0.001	0.021	1.76
18	0.06	1.04	0.19	0.82	0.007	0.028	0.002	0.024	2.17
19	0.06	0.84	0.18	0.66	0.007	0.017	0.002	0.017	1.78
20	0.06	0.66	0.16	0.51	0.007	0.011	0.001	0.013	1.43
21	0.09	0.87	0.21	0.68	0.012	0.014	0.002	0.018	1.89
22	0.10	1.18	0.29	0.93	0.012	0.019	0.002	0.022	2.55
23	0.08	1.17	0.27	0.93	0.009	0.021	0.002	0.021	2.51
24	0.04	0.66	0.15	0.53	0.004	0.014	0.001	0.012	1.42
Total	1.13	16.93	3.48	13.34	0.130	0.408	0.028	0.370	35.81

and Figure 10. The losses in the neutral conductor represent an important percent (37%) of the total energy losses such that the PLB measure must be implemented.

After the application of the proposed algorithm at each hour h = 1, …, 24, the current unbalance was significantly reduced, see

Table 8. The currents in the conductors of the first branch, SP-Pillar 8, the proposed algorithm.

Hour	Ia [A]	Ib [A]	Ic [A]	I0 [A]	UC
1	27.56	27.50	27.82	0.30	1.0000
2	26.25	26.53	26.37	0.24	1.0000
3	24.88	25.03	24.82	0.19	1.0000
4	25.29	24.88	24.99	0.36	1.0000
5	25.22	25.01	25.21	0.21	1.0000
6	21.47	22.69	21.65	1.14	1.0006
7	24.77	24.68	28.31	3.58	1.0042
8	31.90	26.76	26.93	5.06	1.0070
9	28.83	29.06	33.54	4.59	1.0050
10	30.66	30.78	31.81	1.10	1.0003
11	34.76	34.55	34.53	0.22	1.0000
12	32.61	31.65	31.78	0.91	1.0002
13	33.25	34.50	33.23	1.26	1.0003
14	33.91	33.04	33.29	0.77	1.0001
15	33.49	34.20	33.40	0.76	1.0001
16	30.88	30.23	30.18	0.68	1.0001
17	33.72	34.38	33.77	0.64	1.0001
18	38.43	37.96	37.71	0.63	1.0001
19	37.69	34.07	33.87	3.72	1.0025
20	30.67	30.70	35.48	4.79	1.0049
21	34.87	41.56	35.03	6.61	1.0070
22	40.63	46.86	40.21	6.46	1.0051
23	39.94	40.25	44.37	4.29	1.0024
24	31.96	30.73	30.71	1.24	1.0004

. The average value of UC decreased at 1.0017. It can be observed that the current in the neutral conductor decreased with 94%, from the average value of 34.08 A at 2.07 A. This aspect is highlighted in Figure 11. The effects are felt at the level of power/energy losses, see

Table 9. The energy losses calculated with the data obtained using the proposed algorithm, [kWh].

Hour	Main Conductors				Branching Conductors				Total
	a	b	c	Neutral	a	b	c	Neutral
1	0.12	0.13	0.14	0.01	0.00	0.01	0.01	0.01	0.43
2	0.11	0.13	0.12	0.01	0.00	0.01	0.01	0.01	0.39
3	0.10	0.12	0.10	0.01	0.00	0.01	0.00	0.01	0.35
4	0.12	0.10	0.10	0.01	0.01	0.01	0.00	0.01	0.35
5	0.11	0.11	0.10	0.01	0.01	0.00	0.00	0.01	0.35
6	0.08	0.08	0.08	0.00	0.00	0.00	0.00	0.01	0.26
7	0.11	0.11	0.13	0.01	0.00	0.00	0.01	0.01	0.37
8	0.17	0.12	0.13	0.01	0.01	0.00	0.00	0.01	0.45
9	0.17	0.13	0.18	0.01	0.01	0.00	0.01	0.01	0.52
10	0.15	0.17	0.17	0.01	0.01	0.01	0.01	0.01	0.54
11	0.22	0.20	0.20	0.01	0.01	0.01	0.01	0.02	0.68
12	0.19	0.16	0.17	0.01	0.01	0.01	0.01	0.02	0.59
13	0.17	0.23	0.19	0.02	0.01	0.02	0.01	0.02	0.66
14	0.21	0.19	0.18	0.01	0.01	0.01	0.01	0.02	0.64
15	0.17	0.22	0.19	0.01	0.01	0.01	0.01	0.02	0.65
16	0.17	0.15	0.16	0.01	0.01	0.01	0.01	0.01	0.52
17	0.17	0.22	0.20	0.01	0.01	0.01	0.01	0.02	0.66
18	0.23	0.27	0.24	0.01	0.01	0.01	0.01	0.02	0.82
19	0.22	0.22	0.19	0.01	0.01	0.01	0.01	0.02	0.69
20	0.16	0.18	0.20	0.01	0.00	0.01	0.01	0.01	0.58
21	0.21	0.29	0.22	0.02	0.00	0.02	0.01	0.02	0.78
22	0.28	0.35	0.32	0.02	0.00	0.02	0.01	0.02	1.01
23	0.30	0.28	0.32	0.01	0.01	0.01	0.01	0.02	0.96
24	0.16	0.18	0.16	0.01	0.00	0.01	0.01	0.01	0.54
Total	4.09	4.34	4.18	0.26	0.15	0.20	0.19	0.36	13.76

, and the voltage quality, see Figure 12.

The results were compared with other algorithms to emphasize the accuracy of the smart meter data-based proposed algorithm (SMD): from heuristic (the minimum count of loads adjustment (MCLA) algorithm [32]) and metaheuristic (particle swarm optimization (PSO) algorithm [28] and genetic algorithm (AG) [17]) categories. The computational times needed to obtain the solution are presented in

Table 10. Comparison between the computational times.

No.	Algorithm	Computational Times [Seconds]
1	SMD (Proposed)	1.26
2	MCLA	0.58
3	PSO	348
4	GA	291

for each algorithm. The algorithms with a Matlab implementation were run on a computer Intel Core i5, 3.10 GHz, 4GB RAM, WIN 10 64-bit operating system.

The values from the table correspond to 24 h. It can be observed that the lowest values were obtained for the heuristic methods (SMD and MCLA) and higher values for the metaheuristic methods (PSO and GA). Even if the computational time of MCLA is lower than SMD, this does not guarantee that effects will be better in the evaluation of the UC coefficient, the current in the neutral conductor (and implicit on the energy losses), or the voltage at the level of each pillar.

Regarding the UC coefficient, the obtained value with the proposed algorithm is identical with AG (1.0017) at the SP level, being smaller than in the case of MCLA and PSO, as shown in Figure 13.

Also, a comparison with the mathematical programming models, proposed by Arias et al. in [4] and Zhu et al. in [42], was done considering the UC coefficient. The UC coefficient was reduced from 1.17 to 1.07 (a reduction with 9.4%) using the Branch and Bound algorithm (BBA), proposed in [4], in the case of a test radial network without lateral branches. The mixed-integer programming (MIP) led at a reduction of the UC coefficient from 1.086 to 1.005 (a reduction with 8%) for a test network with 6 nodes [42]. The values are indicated in

Table 11. Comparison with the linear programming models.

No.	Algorithm	Characteristics of EDN	UCinitial	UCfinal	Improvement [%]
1	SMD (Proposed)	real/complex/88 nodes/163 consumers	1.26	1.0017	25.8
2	BBA	fictive/radial without lateral branches/51 consumers	1.17	1.07	9.4
3	MIP	fictive/radial with 2 lateral branches/6 nodes	1.086	1.005	8.0

.

The results confirm the advantages of the proposed algorithm compared with the mathematical programming algorithms. Also, the accuracy of the SMD algorithm was demonstrated in the case of a real complex EDN, compared with the other two algorithms, which were tested using fictive EDNs, with simple topologies (radial).

To highlight the effects on the decrease of the current in the neutral conductor (and implicit on the energy losses) and on improving the voltage quality at the level of each pillar, the steady-state regimes were calculated, having as input data the load matrices obtained with each algorithm (SDM, MCLA, PSO, and GA). The average value of the current in the neutral conductor, on the first branch, is shown in Figure 14, for each algorithm. It can be observed that the smallest value was obtained by applying the proposed algorithm (2.07 A), with 22.7% better than GA.

Regarding the energy losses,

Table 12. Comparison between the energy losses calculated with different algorithms, [kWh].

Algorithm	Main Conductors				Branching Conductors				Total	δΔW [%]
	a	b	c	Neutral	a	b	c	Neutral
Without	1.13	16.93	3.48	13.34	0.13	0.41	0.03	0.37	35.81	-
SMD (proposed)	4.09	4.34	4.18	0.26	0.15	0.20	0.19	0.36	13.76	61.57
MCLA	4.14	6.23	4.98	4.32	0.33	0.05	0.16	0.36	20.57	42.56
PSO	4.44	4.43	3.77	0.32	0.23	0.17	0.15	0.36	13.86	61.30
GA	3.66	4.62	4.50	0.51	0.14	0.19	0.21	0.36	14.19	60.37

presents the values calculated on the phase and neutral conductors on the branching and main conductors. The analysis of the results indicates smaller energy losses in the case of the proposed algorithm compared to the other algorithms, as shown in Table 12 and Figure 15. The energy losses decreased by 0.20%, more than in the case of AG. The difference from the MCLA algorithm is higher, with 19.01%.

Also, the saving-energy (δΔW), given in percent, are indicated in Table 12. The calculation relation is the following:

$$\delta \Delta W=\left|\frac{\Delta W_{\mathit{initial}}-\Delta W_{\mathit{algorithm}}}{\Delta W_{\mathit{initial}}}\right|\cdot 100, [\%]$$

(17)

where algorithm is SMD, MCLA, PSO, and GA.

The voltage quality was evaluated at the level of the farthest pillar (P95), and the results are presented in

Table 13. The minimum value of the phase voltages at the level of the farthest pillar (P95).

Algorithm	Phase
	a	b	c
Without	224.33	204.00	226.71
SMD (proposed)	218.81	218.58	218.94
MCLA	218.90	211.59	224.49
PSO	218.19	219.03	218.55
GA	219.41	217.28	219.07

. The minimum values are highlighted with bold to be easily identified in the analysis. It can be observed that the phase voltages are between the admissible limits (rated voltage ± 10%, where the rated voltage is 230 V). Small differences between the phase voltages, in the range [0.13V, 0.36 V], were obtained in the case of the proposed algorithm, with an improvement of value on phase b of 14.58 V (7.15%). The biggest differences, in the range [5.59 V, 12.9 V], were obtained in the case of the MCLA algorithm.

The detailed results for each algorithm are presented in

Table A2. Comparison between the hourly UC calculated with different algorithms at the SP level.

Hour	Without	SMD (Proposed)	MCLA	PSO	GA
1	1.2949	1.0000	1.0001	1.0017	1.0010
2	1.2965	1.0000	1.0005	1.0023	1.0009
3	1.2923	1.0000	1.0007	1.0024	1.0007
4	1.3016	1.0000	1.0012	1.0026	1.0011
5	1.2837	1.0000	1.0010	1.0029	1.0007
6	1.2265	1.0006	1.0005	1.0023	1.0003
7	1.1840	1.0042	1.0017	1.0010	1.0027
8	1.1700	1.0070	1.0042	1.0021	1.0046
9	1.2036	1.0050	1.0040	1.0004	1.0017
10	1.2630	1.0003	1.0022	1.0007	1.0000
11	1.3041	1.0000	1.0039	1.0018	1.0007
12	1.3339	1.0002	1.0031	1.0029	1.0019
13	1.3485	1.0003	1.0026	1.0040	1.0028
14	1.3209	1.0001	1.0028	1.0028	1.0016
15	1.3313	1.0001	1.0027	1.0031	1.0023
16	1.3078	1.0001	1.0012	1.0030	1.0013
17	1.3198	1.0001	1.0025	1.0030	1.0021
18	1.2881	1.0001	1.0018	1.0010	1.0006
19	1.2344	1.0025	1.0011	1.0001	1.0003
20	1.1843	1.0049	1.0029	1.0025	1.0032
21	1.1691	1.0070	1.0040	1.0053	1.0058
22	1.1867	1.0051	1.0031	1.0028	1.0032
23	1.2241	1.0024	1.0021	1.0007	1.0008
24	1.2562	1.0004	1.0005	1.0008	1.0001

,

Table A3. Comparison between the hourly neutral currents calculated with different algorithms, the first branch (SP-Pillar 8).

Hour	Without	SMD (Proposed)	MCLA	PSO	GA
1	31.84	0.30	0.56	2.42	1.87
2	30.49	0.24	1.23	2.68	1.72
3	28.58	0.19	1.40	2.60	1.42
4	29.20	0.36	1.81	2.71	1.74
5	28.43	0.21	1.67	2.85	1.39
6	22.15	1.14	1.06	2.21	0.87
7	23.59	3.58	2.27	1.75	2.85
8	24.97	5.06	3.90	2.79	4.10
9	29.18	4.59	4.07	1.34	2.66
10	33.83	1.10	3.11	1.70	0.30
11	40.52	0.22	4.57	3.07	1.98
12	39.28	0.91	3.78	3.67	2.92
13	42.20	1.26	3.67	4.49	3.80
14	40.18	0.77	3.73	3.76	2.85
15	41.18	0.76	3.68	3.98	3.39
16	35.84	0.68	2.19	3.52	2.34
17	40.77	0.64	3.59	3.96	3.33
18	43.34	0.63	3.39	2.58	1.89
19	36.19	3.72	2.49	0.74	1.37
20	29.41	4.79	3.68	3.39	3.90
21	32.43	6.61	4.97	5.71	6.03
22	39.04	6.46	5.02	4.75	5.12
23	41.72	4.29	3.99	2.30	2.44
24	33.45	1.24	1.53	1.90	0.79

,

Table A4. Comparison between the hourly power losses calculated with different algorithms, [kWh].

Hour	SMD (Proposed)			MCLA			PSO			GA
	a	b	c	a	b	c	a	b	c	a	b	c
1	0.40	0.03	0.43	0.60	0.03	0.63	0.40	0.03	0.43	0.43	1.68	2.11
2	0.36	0.03	0.39	0.54	0.03	0.57	0.37	0.03	0.39	0.39	1.52	1.91
3	0.32	0.02	0.35	0.48	0.02	0.50	0.33	0.02	0.35	0.35	1.35	1.70
4	0.33	0.02	0.35	0.48	0.02	0.50	0.33	0.02	0.36	0.35	1.36	1.71
5	0.33	0.02	0.35	0.49	0.02	0.51	0.33	0.02	0.36	0.35	1.38	1.73
6	0.25	0.01	0.26	0.40	0.01	0.41	0.25	0.01	0.26	0.26	1.08	1.35
7	0.35	0.02	0.37	0.55	0.02	0.57	0.35	0.02	0.37	0.37	1.51	1.88
8	0.43	0.03	0.45	0.67	0.03	0.70	0.42	0.03	0.45	0.45	1.85	2.30
9	0.48	0.03	0.52	0.74	0.03	0.77	0.48	0.03	0.51	0.52	2.06	2.58
10	0.50	0.04	0.54	0.75	0.04	0.78	0.51	0.04	0.54	0.54	2.11	2.64
11	0.63	0.05	0.68	0.91	0.05	0.96	0.64	0.05	0.69	0.68	2.59	3.27
12	0.54	0.05	0.59	0.83	0.05	0.88	0.55	0.05	0.60	0.59	2.35	2.94
13	0.60	0.06	0.66	0.92	0.06	0.97	0.61	0.06	0.67	0.66	2.60	3.25
14	0.59	0.05	0.64	0.84	0.05	0.89	0.60	0.05	0.64	0.64	2.42	3.05
15	0.60	0.05	0.65	0.86	0.05	0.91	0.61	0.05	0.66	0.65	2.46	3.11
16	0.49	0.04	0.52	0.71	0.04	0.75	0.49	0.04	0.53	0.52	2.02	2.55
17	0.61	0.05	0.66	0.87	0.05	0.92	0.62	0.05	0.67	0.66	2.50	3.16
18	0.76	0.06	0.82	1.12	0.06	1.18	0.77	0.06	0.82	0.82	3.18	3.99
19	0.65	0.04	0.69	1.01	0.04	1.05	0.65	0.04	0.69	0.69	2.79	3.48
20	0.55	0.03	0.58	0.89	0.03	0.92	0.55	0.03	0.58	0.58	2.42	3.00
21	0.73	0.04	0.78	1.15	0.04	1.19	0.73	0.04	0.77	0.78	3.16	3.94
22	0.96	0.05	1.01	1.58	0.05	1.64	0.96	0.05	1.01	1.01	4.29	5.31
23	0.91	0.05	0.96	1.48	0.05	1.53	0.91	0.05	0.96	0.96	4.02	4.98
24	0.51	0.03	0.54	0.80	0.03	0.83	0.51	0.03	0.54	0.54	2.20	2.73

and

Table A5. Comparison between the hourly phase voltages calculated with different algorithms, at the level of the farthest pillar P95, [V].

Hour	SMD (Proposed)			MCLA			PSO			GA
	a	b	c	a	b	c	a	b	c	a	b	c
1	223.25	222.85	222.25	223.28	219.05	225.96	222.50	222.46	223.38	223.81	221.64	222.90
2	223.62	222.55	223.27	223.55	219.75	226.08	222.87	222.78	223.78	224.12	222.13	223.18
3	224.01	222.94	223.69	223.91	220.40	226.29	223.28	223.20	224.17	224.45	222.65	223.54
4	223.29	223.60	223.67	223.79	220.47	226.25	223.20	223.17	224.18	224.47	222.60	223.47
5	223.33	223.55	223.59	223.82	220.35	226.26	223.30	223.07	224.10	224.35	222.57	223.55
6	224.24	224.12	224.45	224.80	221.03	226.94	224.38	223.89	224.55	224.75	223.43	224.63
7	223.33	223.16	223.14	223.26	219.58	226.72	223.09	223.16	223.38	223.64	222.57	223.42
8	221.59	223.17	222.75	222.20	218.58	226.65	222.23	222.67	222.60	222.95	221.91	222.65
9	221.36	222.83	221.88	221.84	218.08	226.07	221.69	222.03	222.35	222.69	221.29	222.08
10	222.22	221.81	221.69	221.95	218.13	225.57	221.54	221.62	222.55	222.90	220.91	221.90
11	220.73	221.02	221.25	220.94	217.16	224.83	220.43	220.62	221.95	222.37	219.82	220.81
12	221.37	221.86	221.91	223.84	216.11	225.09	221.04	221.36	222.74	223.15	220.59	221.39
13	222.15	220.28	221.45	223.49	215.53	224.75	220.57	220.86	222.45	222.89	220.05	220.93
14	220.97	221.41	221.57	221.44	217.53	224.91	220.80	220.86	222.29	222.72	220.05	221.18
15	221.95	220.37	221.35	221.37	217.39	224.85	220.71	220.76	222.20	222.70	219.83	221.14
16	221.78	222.27	222.22	222.47	218.35	225.39	221.77	221.59	222.89	223.26	220.89	222.11
17	221.85	220.34	221.23	221.31	217.20	224.85	220.73	220.63	222.06	222.56	219.66	221.19
18	220.60	219.18	220.24	220.17	215.27	224.49	219.58	219.62	220.82	221.41	218.47	220.14
19	220.78	220.07	221.17	220.96	215.62	225.34	220.40	220.60	221.03	221.63	219.37	221.01
20	222.07	220.89	221.23	221.49	216.34	226.24	221.15	221.66	221.38	221.99	220.40	221.80
21	220.83	218.92	220.42	221.29	214.22	224.53	219.60	220.66	219.91	220.66	219.12	220.39
22	219.25	218.58	218.94	218.90	211.59	225.06	218.19	219.03	218.55	219.41	217.28	219.07
23	218.81	218.91	218.98	219.75	212.05	224.71	218.55	219.04	219.11	219.98	217.33	219.38
24	222.11	221.24	222.09	222.58	217.10	225.67	221.60	221.57	222.27	222.74	220.64	222.06

from Appendix B.

4. Conclusions

In the paper, a PLB algorithm was proposed having the following advantages: It can be implemented in the EDNs with hybrid structures of the consumption points (switchable and non-switchable consumers); it can work in both operation modes (real-time and off-line), uploading information from different databases of the DNO which contain the consumers’ characteristics, real loads of the consumers integrated into the SMS, and loads from the TLPs for the consumers non-integrated in the SMS; the convergence is rapid because of the fast recognition of EDN topology with the help of a structure vectors based-algorithm.

The testing of the algorithm was made in a real rural EDN from the northeastern region of Romania, having a hybrid structure of the consumption points (114 1-P consumers (70.8%) are integrated into the SMS with the possibility to have SPLBS, the other consumers having standard meter). The obtained results were analyzed and compared with other algorithms from the heuristic category (minimum count of loads adjustment (MCLA) algorithm) and the metaheuristic category (particle swarm optimization (PSO) and genetic algorithm (AG)).

The best performances were recorded for the proposed algorithm, obtaining the smallest value of the unbalance coefficient (1.0017), in comparison with MCLA (1.0022) and PSO (1.0021) algorithms. The same value (1.0017) was also obtained in the case of AG. The average value of the current in the neutral conductor decreased with 94% from the average value of 34.08 A (initial case) at 2.07 A. This value is smaller with 22.70% than AG, 42.51% than PSO, and 43.47% than MCLA. The energy losses decreased with 61.75% compared to the initial case using the data obtained with the proposed algorithm. This value is smaller by 0.20% than AG, 0.27% than PSO, and 19.01% than MCLA.

The proposed solution can be introduced by the DNOs to ensure the transition toward the smart grids, but only on the basis of a feasibility analysis, to justify the investment. Also, the DNOs must take into account that the proposed algorithm cannot have very high efficiency in networks with many not integrated consumers into the SMS, for which the TLPs must be associated. Within the proposed algorithm, they belong to the category of non-switchable consumers, so that the number of switching options will be limited. The transition process should be mainly implemented in the “hot” areas where there are EDNs without or with small number of non-switchable consumers, leading to a solution very close to the optimal solution (in the ideal case, it is equal with 1.00).

The authors work now at an improved variant of the proposed algorithm, which considers the weight of each switchable consumer at the unbalance degree. The main objective is the determination of the optimal number of PLBD, which minimizes the unbalance coefficient and the investment costs.