Benefits and Limitations of the Artificial with Respect to the Traditional Learning of Mathematics

Abstract

The present article focuses on the role that the artificial teaching and learning of mathematics could play for education in the forthcoming era of a new industrial revolution that will be characterized by the development of an advanced Internet of things and energy, and by the cyber-physical systems controlled through it. Starting with a brief review of the traditional learning theories and methods of teaching mathematics, the article continues by studying the use of computers and of applications of artificial intelligence (AI) in mathematics education. The advantages and disadvantages of artificial with respect to traditional learning in the classroom are also discussed, and the article closes with the general conclusions and a few comments on the perspectives of future research on the subject.

1. Introduction

The first and the second industrial revolutions (IRs) that took place from the end of the 18th until the middle of the 20th century caused dramatic changes to the structures of the mainly agrarian until that time human society [1]. Their main common characteristic was that machines replaced gradually the power of the human hands and animals, enabling the massive production of goods and making easier long-distance communication among people and countries. The third IR, which started in the 1940s and is widely referred as the era of automation [1], has transformed—with the help of computers and of other “clever” machines—the human society to the digital world of our days, where technology is present in almost every aspect of our lives.

However, there were also non profitable effects for the humanity connected to those IR’s, like the negative environmental consequences that have been mainly caused by the high industrialization. The prices of energy and food are increasing in many cases, unemployment is high, the economies of many countries are in danger of collapse and recovery is not visible. Therefore, people and nations are desperately looking for a new plan that could lead the humanity to a better future.

The idea of a forthcoming new IR has appeared in the beginning of the 21st century. Famous social thinkers, like the New York Times best-selling author Jeremy Rifkin [2,3], the founder and executive chairman of the World Economic Forum Prof. Klauss Schwab [4], and others, describe in their books and articles how artificial intelligence (AI), the Internet technology, 3D-printing and the renewable energy are merging to create this new powerful revolution. The new technology will for instance facilitate the distribution of electrical energy or allow smart home and household devices to communicate via the internet. Consequently, a new advanced internet of things and energy (IoT & E) will be created, providing energy goods and services at the right time and at any place. Cyber-physical systems (CPS), examples of which are the autonomous automobile and control systems, the distance medicine, the robots, etc., will be controlled by computer programs through this powerful IoT & E. In general, our society now has the potential to improve the efficiency of services and organizations and even manage ways that can regenerate the environment from the damages caused by the previous IR’s.

Nevertheless, there are also great potential risks behind the forthcoming new IR. In fact, major changes are needed to our current political, business, educational and social structures for absorbing smoothly the resulting shifts on the purpose of getting the maximal possible profit from them and create a better future for humanity. Otherwise, the new IR could increase further the gap among rich and poor countries and people thus creating many negative consequences for the stability and coherence of our society [4]. Therefore, formal education, from elementary school to university, now faces the new big challenge of preparing students to adapt their lives to the conditions and requirements of the forthcoming era of a not explicitly known yet IR.

There is no doubt that our students should take full advantage of the potential that the new digital technologies can bring for improving their learning skills. Nevertheless, there is a question, if this should be combined with the existing traditional learning methods, or if the artificial could completely replace the traditional learning in future (e.g., see https://www.tes.com/lessons/JI7IL0ElmlD2Kg/why-computers-should-replace-teachers; https://www.quora.com/Can-artificial-Intelligence-replace-teachers; https://www.vox.com/a/new-economy-future/computers-replace-doctors-teachers, etc.). Artificial learning in this work is understood to be any kind of learning acquired by using methods and techniques of AI.

The target of the present work is to give some answers to that question through the study of the advantages and disadvantages of the artificial with respect to the traditional methods for learning mathematics, which has been recognized as the “mother” of all the other sciences many centuries ago. Historical evidence about this is the famous Ahmes (1680–1620 BC) papyrus presented in Figure 1 (retrieved from https://www.ancient-origins.net/artifacts-ancient-writings/rhind-papyrus-0013004), which proves that ancient Egyptians used first and second degree equations and numerical sequences in algebra and trigonometry applications.

The rest of the article is organized as follows: Section 2 is devoted to a brief review of the traditional learning theories and methods of teaching mathematics. Section 3 reports on the use of computers, while Section 4 studies characteristic applications of AI in mathematics education. In Section 5 the advantages and disadvantages of the artificial with respect to the traditional learning in the classroom are discussed and the article closes with the general conclusions and a brief discussion on the perspectives of future research on the subject that are presented in Section 6.

2. Traditional Learning Theories and Teaching Methods of Mathematics

Learning is one of the fundamental components of the human cognitive action. In psychology and education, it refers to a process that combines cognitive, emotional, and environmental influences for acquiring or enhancing one’s knowledge and skills. Volumes of research have been written about learning and many theories and models have been developed by the specialists for the description of its mechanisms.

There are three main philosophical frameworks under which learning theories fall:

• Behaviorism, a theory established by the American psychologist John B. Watson (1878–1958), which considers learning as the acquisition of new behavior based on environmental conditions and discounts any independent activities of the mind [5].
• Cognitivism, which replaced behaviorism during the 1960′s as the dominant theory for the process of learning and argues that knowledge can be seen as a process of symbolic mental constructions and that learning is defined as change in individual’s cognitive structures [6]. More explicitly, the learning process involves representation of the stimulus input, i.e., use of the contents of one’s memory to find the suitable input information, interpretation of the input data to produce the new knowledge, generalization of this knowledge to a variety of situations and categorization of it in the already existing learner’s cognitive schemata. In this way the individual becomes able to retrieve, when necessary, the new information from his/her proper cognitive schema and to use it for solving related problems. Changes in the learner’s behavior are in fact observed, but only as an indication of what is occurring in his/her mind. In other words, cognitive theories look beyond behavior to explain the brain-based process of learning.
• Constructivism, a philosophical framework based on Piaget’s theory for learning and formally introduced by von Clasersfeld during the 1970s, which suggests that knowledge is not passively received from the environment, but is actively constructed by the learner through a process of adaptation based on and constantly modified by the learner’s experience of the world [7]. This framework is usually referred as cognitive constructivism. The synthesis of the ideas of constructivism with Vygosky’s social development theory [8] created the issue of social constructivism [9]. According to Vygosky, learning takes place within some socio-cultural setting. Shared meanings are formed through negotiation in the learning environment, leading to the development of common knowledge. The communities of practice (CoPs), for instance, are groups of people, experts or practitioners in a particular field, with a concern for something they do and they learn how to do it better as they interact regularly, having therefore the opportunity to develop personally and professionally [10]. The basic difference between cognitive and social constructivism is that the former argues that thinking precedes language, whereas the latter supports the exactly inverse approach.

The role of teaching is to promote the learning of the corresponding subject. However, while theory provides means for analyzing learning, the process of teaching remains to a great part theoretically unsupported. In fact, theories help to analyze and explain, but they rarely provide direct guidance for practice.

Some decades ago, the dominant teaching method in mathematics education used to be the explicit instruction (EI), which is mainly based on principles of cognitivism. The teacher is in the “center” of this method and tries with clear statements and explanations of the mathematical context and by supported practice to transfer the new knowledge to students in the best possible way [11]. The main criticism against EI is that it may prevent conceptual understanding and critical analysis [12]. Therefore, many teachers, adopting ideas of constructivism, enriched the EI with a series of challenging questions so that to keep an active discourse with students, as a means to promote mathematical thinking [13].

However, following the failure of the introduction of the “new mathematics” to school education, constructivism and the socio-cultural theories for learning have become very popular during the last decades as a basis for teaching and learning mathematics, especially among teachers of the elementary and secondary education. New teaching approaches have been introduced, like the problem-based learning [14], the application-oriented teaching involving mathematical modeling [15], the inquiry-based learning through creative exploration [16], the formation of CoPs among students and teachers [10], etc.

A typical teaching method developed according those lines is the “5 E’s” instructional treatment. The acronym “5 E’s” is due to the five successive phases of that treatment including engagement, exploration, explanation, elaboration and evaluation [17]. The “5E’s” method promotes the fruitful interaction among students and teachers and facilitates the production of the new knowledge on the basis of prior knowledge and experiences. Attempts to introduce such kind of approaches for teaching mathematics in university departments of positive sciences have also been reported in the literature ([18,19], etc.), but the findings are rather intertwined.

Much progress has been made in the last 20 years on analyzing the processes by which students come to understand mathematical ideas (mathematical cognition) and how numeracy is acquired (numerical cognition). Experimental psychology, neuroimaging, and single cell recording experiments have converged to identify how these basic skills are used to support the acquisition and use of abstract mathematical concepts [20].

Predictive mathematical models are used nowadays to better understand how humans conceptualize information. For example, in [21] a model is presented that mimics pre-learned patterns of behavior through fractional differential equations. Also in [22], the effects of different delay time in human response to assess human workload state are studied, etc.

3. Computers in Mathematics Education

Computers have become in our days a valuable tool for Education providing through the web a wealth of information for teachers and learners. In mathematics education in particular, the animation of figures and of mathematical representations, obtained by using the proper software, increases the student imagination and problem-solving (PS) skills.

During the 1990′s Ed Dubinsky and his collaborators developed in the USA with the help of computers the APOS-ACE instructional treatment of mathematics [23], which highly reflects the ideas of social constructivism and of the Piaget’s theory for learning. The APOS theory argues that the teaching of mathematics should be based on orienting students to use their already existing mental structures and further to build new stronger ones for handling more and more advanced mathematics. The acronym APOS was formed by the initial letters of the words action, process, object and schema, which are the mental structures involved in that process. The interiorization of an action to a process and the categorization of a process to an object are the mental mechanisms involved in the APOS framework. The practical part (teaching schedule) of the Dubinsky’s model involves three phases, the initial letters of which form the acronym ACE. Those phases involve Activities in the classroom, use of Computers for promoting the understanding and the student skills on the new topic and Exercises given by the instructor to students as homework in order to embed the acquired new knowledge. The philosophy of the ACE teaching style is that students could be helped to be transferred from a mental structure to the next and more advanced one by participating in a suitably designed—by a specialist or by the teacher—computer activity, where they use the proper software or code to promote their learning skills. The same cycle is usually repeated several times until the categorization of the new knowledge is succeeded. More details and examples about the APOS-ACE instruction, which has been used with success - mainly in university classrooms – for teaching a wide range of mathematical topics, can be found in [23,24,25] and in many other related research reports. However, the application of this approach in classroom requires from the teacher, apart for being familiar with the corresponding computer software, to study and understand deeply first the APOS theory. This explains why the APOS-ACE method has not been used widely in school education yet.

Another general—not only for mathematics—teaching methodology that has been developed recently with the help of computers is the flipped or reverse learning (FL), which is a mixed process involving both online and traditional teaching in classroom. FL requires inverting the didactic process. Namely, the acquisition of the new knowledge is achieved outside the classroom through the use of digital technological tools (video presentations, mathematical software, etc.) that have been properly designed by the specialists. On the contrary, the traditional homework is done in the classroom directed by the teacher. This inversion promotes the effectiveness of learning and increases the time devoted to problem - solving activities [26]. FL has its roots to the works of Lage et al. [27] and of Sams and Bergmann [28], developing online teaching material, so that students could study at any place and any time. FL is highly based on the ideas of social constructivism.

The rapid technological development of the last decades created new complex problems, the solution of which requires not only critical thinking, but also another mode of advanced thinking that has been called Computational Thinking (CT). The term CT, first introduced by S. Papert [29], it was brought to the forefront of computer society by J. Wing in 2006. Wing describes CT as “involving solving problems, designing systems and understanding human behavior by drawing on principles of computer science” [30]. According to Liu and Wang [31], CT is a hybrid of other modes of reasoning including abstract, logical, algorithmic, constructive and modeling reasoning. Modeling reasoning combines all the other types of reasoning mentioned above for solving the problem at hand. Voskoglou and Buckley [32] viewed the problem as a challenge needing a solution and they developed a model elucidating the relationship between critical thinking and CT during the solution, where the existing knowledge is the link between them. The basic form of this model is graphically sketched in Figure 2 (for more details see [32]).

CT, as a synthesis of ideas from mathematics, technology and science, forms a new reasoning approach with the potential to create beneficial changes to our society. The best way to learn CT explicitly is through computer programming, which provides a framework for all sciences. However, recent studies addressed the necessity to start training in CT as soon as possible and at any case before learning programming [33].

Reports opposing the use of computers in classrooms focus on the fact that even the brightest students appear to be distracted by the presence of digital devices [34]. In general, computers should not be viewed as being capable to solve all existing problems, but rather as performing operations in high speed and therefore facilitating users to spend more time for creative reasoning [35]. The student practice with arithmetic and algebraic calculations and with the rediscovery of proofs must be continued; otherwise humans will eventually loose the ability to deal with numbers and symbols and the sense of space and time, thus becoming unable for further developments in science and technology [32].

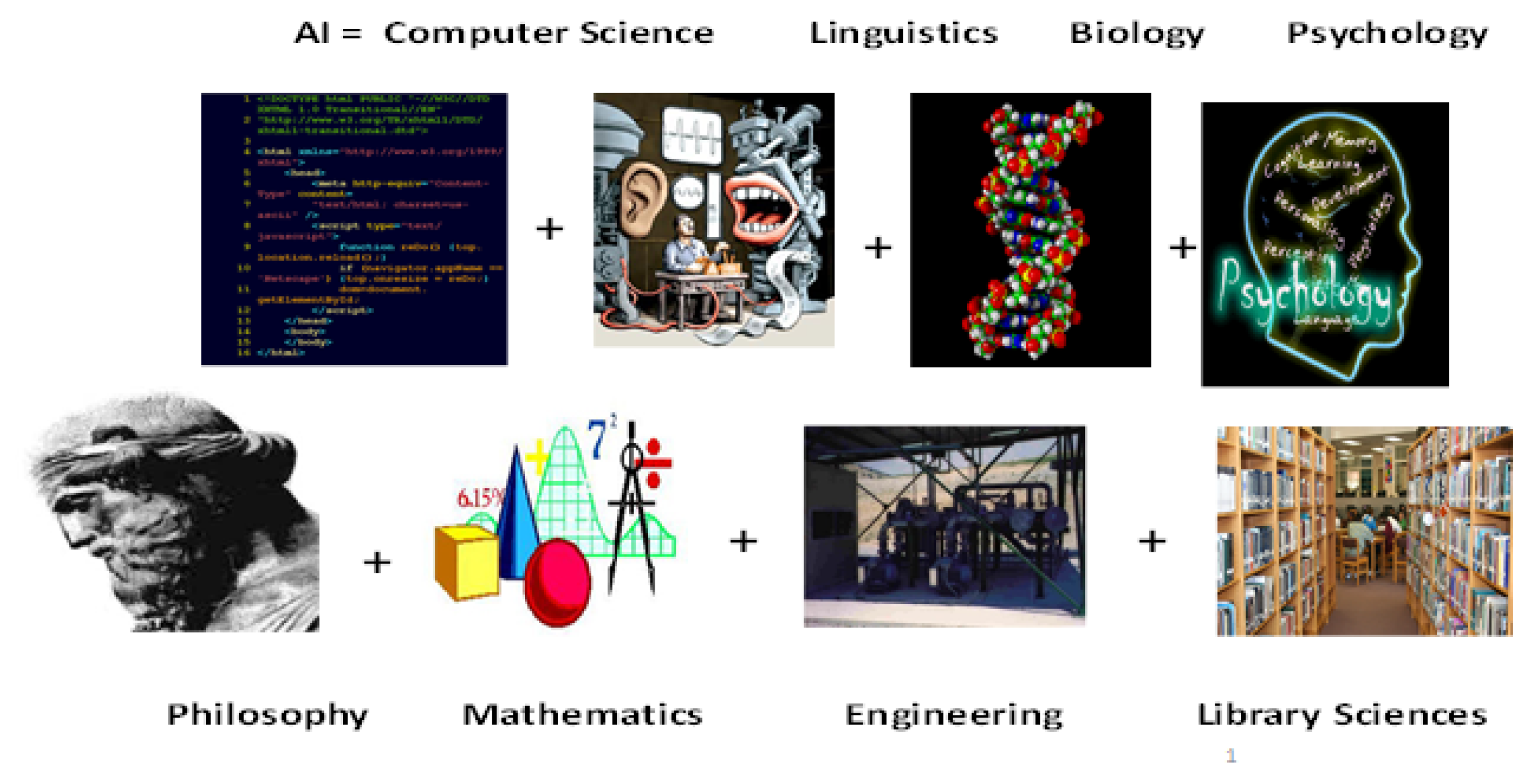
4. Artificial Intelligence in Mathematics Teaching

AI is the branch of Computer Science focusing on the theory and practice of creating “clever” machines that mimic the human intelligence and behavior, i.e., been able to think, hear, talk, walk and even feel [36,37]. In particular, AI aims to make computers capable to learn from data and make autonomous improvements without depending on commands of a program (computational intelligence). In this way computers could become able to build smart models and even to better replicate copies of them selves!

The term AI was coined by John McCarthy in 1956, when he held in Dartmouth College, USA the first academic conference on the subject [38]. The commemorative plaque for the 50th anniversary of that conference that has been placed in Dartmouth Hall in 2006 is shown in Figure 3. However, the effort to understand if machines can truly think began much earlier, even before the Alan Turing’s abstract “learning machine” invention in 1936, which has been proven capable of simulating the logic of any computer’s algorithm [39].

AI as a synthesis of ideas from mathematics, engineering, technology and science (see Figure 4) has rapidly developed since then creating a situation that has the potential to generate enormous benefits to the human society. The spectrum of AI covers many research areas and technologies, like knowledge engineering, data mining, reasoning methodologies, cognitive computing and modeling, machine learning, natural language processing and understanding, artificial planning and scheduling, vision and multimedia systems, intelligent tutoring and learning systems, etc. In this section, recent advances of introducing methods and mechanisms of AI in mathematics education, will be discussed.

The attempt to “replicate” teachers by using computers started during the 1970s. Between 1982 and 1984, several studies in the US proved that students who received individual tutoring performed much better than those who didn’t. Therefore, a new effort started to re-create the individual tutoring in a computer (adaptive learning systems). AI focuses in general on developing personalized curricula based on each student’s specific needs.

A grand experiment has started recently in China that could change the way that people learn [40]. Squirrel is one of the first China’s companies to pursue the concept of an AI tutor. Squirrel’s innovation is in its granularity and scale. For every course it offers, its engineering team works with a group of master teachers to divide the subject into the smallest possible conceptual pieces (see Figure 5, retrieved from https://www.technologyreview.com/s/614057/china-squirrel-has-started-a-grand-experiment-in-ai-education-it-could-reshape-how-the). Middle school mathematics, for example, is divided to pieces like rational and irrational numbers, properties of a triangle, calculation of areas, Pythagorean theorem, etc. The target is to determine and treat a student’s difficulties in each topic in the best possible way. Unlike Squirrel, Alo7, another big company of China, has developed an online learning platform meant to supplement a traditional classroom. AI implementation is at its beginning in elementary education of China, but in a more advanced level in higher education, especially in the field of civic education. Therefore, Chinese students are prepared and work together to create the proper situation for the future education.

The human-to-human contact that was necessary some decades ago for teaching can nowadays, thanks to the technological progress, be replaced in a great part by virtual teaching using computers, videos, etc. Consequently, it is certain that the distance learning, which is usually referred as e-learning, will become very important for our lives in future. In E-learning the learning materials are sent electronically to remote learners via a computer network [41]. For instance, the virtual CoPs through the Web appear as a very promising tool for teaching and learning mathematics, and not only, especially for developing countries, where people, due to budgetary constraints, it is not easy to travel abroad for participating in scientific, vocational and educational activities [16]. E-learning is also a very useful training tool for the modern companies and businesses, which want to be sure that their staff and partners are equipped with the adequate information and skills needed for their jobs.

Machine learning (ML) is the branch of AI that refers to any computer program that can “learn” by itself from a training data set. ML includes many types of programs that one can run across in big data analytics and data mining and it is distinguished to supervised and unsupervised learning [42]. In the former type of learning both input and output data - which play the role of the instructor - are labelled to provide a basis for future data processing. For example, having as input the sequence 1, 2, 3, 4, 5, 6, 7, …, the sequence 1, 4, 8, 16, 25, 35, 49, …. as output corresponds to the raising to the second power. Applications of supervised learning can be distinguished in two categories, classification where the output value is a linguistic expression (e.g., true or false), and regression where the output is a real value (e.g., price or weight). In the unsupervised learning only the input data provided, and the algorithms are able to function freely in order to learn more about the data. When only some of the input data are labelled with output information, then we speak about semi-supervised learning.

Deep learning (DL) is a form of ML that utilizes either supervised or unsupervised learning or both of them. The “deep” comes from the many layers that are built into the DL models, which are typically neural networks [43]. DL has become very popular for accelerating the solution of difficult computer problems, especially in the fields of computer vision and natural language processing, while much of the progress in developing self-driving cars can be attributed to advances of DL too.

A lot of different terms are used these days about the new data processing techniques. According to the IMB’s terminology the technologies that use a combination of natural language and ML to enable the interaction among humans and machines, thus extending and magnifying the human expertise and cognition, are called cognitive systems. For example, Watson, the IBM’s suite of enterprise-ready AI services, apart from its ability to win at Jeopardy, it has been also trained to “read” medical literature, like searching several forms of cancer.

Recently researchers have used ML techniques to develop through the Internet a new generation of web-based smart learning systems (SLS’s) for various educational tasks. A SLS is actually a knowledge - based software used for learning and acting as an intelligent tutor in real teaching and training situations. Such systems have the ability of reasoning and of providing inferences and recommendations by using heuristic, interactive and symbolic processing and by producing results from the big data analytics [44,45]. The successive phases for developing a SLS are:

• Construction of the knowledge base, involving collection, acquisition, and representation of the required knowledge. The success of that task presupposes the choice of the appropriate in each case among the many existing techniques (e.g., lists, trees, semantic networks, frames, production rules, cases, ontologies, etc.) that fits better to the knowledge domain and the problem to be solved.
• Selection of the suitable reasoning and inference methodology, e.g., commonsense reasoning, model-based, qualitative, causal, geometric, probabilistic or fuzzy reasoning, etc.
• Selection of intelligent authoring shells, which allow the course instructor to easily enter the knowledge domain without requiring computer programming skills. Those shells facilitate also the entry of examples/exercises including problem statements, solution steps and explanations and the integration of suitably developed by the specialists multimedia course wear. The examples may be in the form of scenarios or simulations. In addition to the course knowledge the instructor has the possibility to specify the pedagogical instruction, i.e., the best way to teach a particular student, and to choose how to assess actions and determine student mastery. The most common authoring shells are DIAG, RIDES-VIVIDS, XAIDA, REDEEM, EON, INTELLIGENT TUTOR, D3 TRAINER, CALAT, INTERBOOK, and PERSUADE [46].

In concluding, the efficiency of a SLS is based on the selection of the appropriate knowledge representation technique and reasoning methodology and the choice of the suitable authoring shell. Therefore, from the technical point of view a SLS is complex to be built and difficult to be maintained. Two are the most popular methodologies used for constructing the knowledge base of a SLS, namely ontological engineering and case-based reasoning (CBR).

The term “ontology”, having its roots to philosophy and metaphysics, refers to the nature of being. The ontologies used in computer science are knowledge-based intelligent systems designed to share knowledge among computers or among computers and people. Those types of ontologies include a relatively small number of concepts, and their main objective is to facilitate reasoning. In intelligent educational systems ontologies are used to help the search of learning materials and pedagogical resources in the internet or as a chain playing the role of a “vocabulary” among heterogeneous educational systems that have been programmed to communicate to each other (multi-agent systems) [47,48].

CBR is the process of solving problems based on the solutions of previously solved analogous problems (past cases). For example, a lawyer who advocates a particular outcome in a trial based on legal precedents is using the CBR methodology. The use of computers enables the CBR systems to preserve a continuously increasing “library” of previously solved problems, referred to as past cases, and to retrieve each time the suitable one for solving the corresponding new problem. The CBR approach, apart from commercial and business purposes, has got also a lot of attention over the last decades in mathematics education, and not only, as a new approach to PS and learning [49]. In fact, the CBR methodology organizes knowledge in cases of previous problems, each case containing a description of the problem and a solution of it. CBR’s coupling to learning occurs as a natural by-product of PS. Effective learning in CBR is referred as case-based learning. Also, when an attempt to solve a problem fails, the reason for the failure is remembered in order to avoid the same mistake in future (failure-driven learning).

CBR has been formulated for use with computers and people as a four-step process involving the following actions:

• R₁: Retrieve from the system’s library the suitable past case.
• R₂: Reuse this case for the solution of the given problem.
• R₃: Revise the solution of the retrieved case for solving the new problem
• R₄: Retain the revised solution for possible use with analogous problems in future.

Through the revision the solution is tested for success. If successful, the revised solution is directly retained in the CBR library, otherwise it is repaired and evaluated again. When the final result is a failure, the system tries to compare it to a previous analogous failure (transfer from R₃ back to R₁) and uses it in order to understand the present failure, which is finally retained in the library. A graphical representation of the above process, taken from [50], is shown in Figure 6.

More details about the history, development and applications of CBR can be found in [51] and in the related references contained in it.

The theory of Fuzzy Sets (FS’s) introduced by Zadeh in 1965 [52] and the resulting from it fuzzy logic, which is an infinite-valued logic that generalizes the traditional bi-valued logic, constitute another important topic of AI. Fuzzy mathematics has found nowadays many and important applications to almost all sectors of the human activity; e.g., see [53]: Chapter 6, [54]: Chapters 4–8, etc. From the time that Zadeh introduced the concept of FS and in the effort of tackling more effectively the uncertainty caused by the imprecision that characterizes many situations in science, technology and our everyday life, various generalizations of FS have been proposed (type-2 FS, interval-valued FS, intuitionistic FS, hesitant FS, Pythagorean FS, complex FS, neutrosophic sets, etc.), as well as several alternative theories (grey systems, rough sets, soft sets, etc.); for more details see [55]. Courses on fuzzy mathematics and logic have already appeared in the curricula of several university departments [56] and it is expected to be rapidly expanded in the near future.

Fuzzy systems, together with probabilistic reasoning and the artificial neural networks (AANs) are the three components of the wider class of soft computing. AAN’s and fuzzy systems try to emulate the operation of the human mind. The AANs, the structure of which is analogous to that of the biological neural networks, concentrate on the “hardware” of the human mind having the ability to learn and to process rabidly the information. On the contrary, fuzzy systems concentrate on the “software” emulating the human reasoning. A neuro-fuzzy system is a hybrid system that uses a learning algorithm derived from an AAN to determine its fuzzy parameters (FS and fuzzy rules). Characteristic examples are the adaptive neuro-fuzzy inference systems (ANFIS).

It would be an authors’ omission if they didn’t add a paragraph here about social robots that could play an important role in future mathematics education. One of the first to develop such kind of robots was Cynthia Breazel in MIT [57]. A social robot is an AI machine that has been designed to interact with humans and other robots. Social robots have been already used for entire job functions at home by understanding speech and facial expressions, in customer service, in education, etc. [58]. Two important examples for education are the robot Tico that has been designed to improve children’s motivation in the classroom and the robot Bandit that has been developed to teach social behaviour to autistic children. A characteristic sketch about the introduction of smart technologies and robotics in Education, which has been presented by the second author in the 23rd International Conference on Information and Software Technologies (ICIST 2017) that took place between 12 and 14 October 2017 at the Kaunas University of Technology, Lithuania, is shown in Figure 7.

5. Comparing the Artificial and the Traditional Teaching and Learning of Mathematics

The introduction of the techniques of AI has brought significant benefits for Education in general and for the teaching and learning of mathematics in particular. The most important of those benefits can be summarized as follows:

• As we have already seen in Section 3, computers provide through the Internet a wealth of information to teachers and learners, while suitably designed by the experts mathematical software packages (SLS’s) give to the instructor the opportunity to apply innovative teaching and learning methods in the class, like the ACE instruction, the flipped learning, etc., that increase the student imagination and PS skills [59,60]. Also, for the evolution of smart learning in Korean public Education, see [61].
• E-learning gives to the learner 365 days per year access to the learning subject in contrast to the traditional learning, which is scheduled as a one-time class and requires the learner’s physical presence. Another advantage of the e- learning is that it can be used at the same time by a large population spread throughout the world. The e-learning material, once developed as a course, could be easily modified in future for similar uses. Through e-learning students can learn in their own speed what is important for them by skipping unnecessary information. In addition, e-learning is obviously much cheaper than the traditional one, which involves many extra costs (travel, boarding, books, etc.). In concluding, e-learning appears today as a promising alternative to traditional classroom instruction, especially in cases of remote lifelong learning and training, while it can also be used as a complement of the classroom learning [62].
• When engaged in the CBR approach the students, with many cases available, become able to recognize more alternatives and to benefit from the failures of the others. Cases indexed by experts will reveal to students suitable ways of looking at a problem, a thing that they may not have the expertise to do without the help of a CBR system. Research reveals that students learn best when they are presented with examples of PS knowledge and then asked to apply the acquired knowledge to real situations [14]. The CBR methodology is useful in particular for cases where there is much to remember, because when reasoning analogically one tends to focus only on the few possible analogous past cases. In general, one could say that a CBR system provides the student with a model of the way that decision making must be done, i.e., what actions ought to be performed for the solution of the problem in hands.
• Apart from helping the instructor in the search of learning materials and pedagogical resources in the internet, ontologies are also useful for the evaluation of the students’ learning performance and for recommendations and grouping of them based on their learning behavior and skills. Further, they facilitate the assessment of the learning resources and of the web-based courses [63].

The impressive advances of AI in the field of Education have made these days a number of specialists on the subject to be certain that in future computers and the other “clever” machines of AI will replace teachers in educating students. “When cars invented, horses have stopped to be necessary” they argue parallelizing the two situations. However, although literature experiments have demonstrated that in certain cases artificial learning can be at least as effective as the conventional classroom learning, we are not in a position to claim that it can replace the traditional classroom instruction in general [41].

In fact, in contrast to the above-mentioned advantages, there are also certain limitations of the artificial with respect to the traditional learning. One of them is that in the distance learning the queries of a student cannot be solved instantly, as the physical presence of the teacher in the classroom guarantees. Also, students in the classroom are pushed through the course to learn, whereas not every student finds e-learning suitable for his or her style. For example, some students feel bored in front of a computer. Apart from the learner’s characteristics, there are also many other factors influencing the effectiveness of e-learning, such as media conditions, learning context, technology, etc. that must be taken seriously under consideration. In addition, other important issues like trust, authorization, individual responsibility and security of the Internet must be resolved too. Therefore, although today thousands of online courses are offered by universities all around the world, many of them leading to degree or certificate awards, several uncertain issues and technical problems have to be further investigated concerning the effectiveness and status of artificial learning.

From the philosophical point of view the authors of the present article are among those many people believing that the replacement of the teacher-led instruction by the artificial learning will never actually happen. In fact, learning is mostly a socio-cognitive activity. The acquisition of knowledge is valuable for the students, but the most important thing is to learn how to reason logically and creatively. However, this seems impossible to achieve through the help of the computers and of the other “clever” machines of AI only, because all these devices have been created and programmed by humans. Consequently, although many of them (e.g., computers) impressively exceed humans in speed, it is logical to accept that they will never reach the quality of human reasoning and therefore become able to teach students how to reason logically and creatively [32]

6. Discussion and Conclusions

The present work focused on the role that the artificial teaching and learning of mathematics could play in future education. It was concluded that it is rather difficult that computers and the other “clever” machines of AI will reach the point of replacing teachers for educating students in future. However, it is more than certain that dramatic changes will appear in the future classrooms, since the new technologies appear as having the potential to offer significant benefits for the teaching and learning of mathematics, and not only. Therefore, the investigation of the new teacher’s role in the classroom is an interesting subject for future research. This new role requires significant changes or even complete replacement of the traditional teaching methods, proper use of the new technological tools in and out of the classroom, familiarization with the ideas and techniques of distance learning, etc. Obviously, this type of research is strictly connected to the changes that the forthcoming new industrial revolution will bring to the structures of the human society, changes which are not explicitly known yet. Consequently, the ways of preparing our students to absorb smoothly those changes form an important component of this research too.

Also, more detailed information is needed with respect to the relationship of the CPS with human learning, e.g., some notions on the subject of the “extended crossover model” for human control [64] may be interesting. Today, the combination of the ML techniques with the latest knowledge acquisition and pedagogical methods has solved many of the technical problems and difficulties appearing in the design of intelligent learning and teaching systems. However, further research is needed on that topic as well for converging knowledge engineering, ML techniques, and educational technology with the forthcoming trends of the IoT & E. Such a convergence will create a new generation of intelligent learning and tutoring systems that will enhance further the on-line teaching, learning, and training processes, thus supporting the continuous growth of e-learning in future as an inseparable part of the academic and professional education.

The main limitation of the present study is that it refers to mathematics education only. However, the conclusions obtained can be generalized and extended to most other areas of education. This is among our plans for future work on this interesting subject.