Abstract
In this paper, the well-known Hencky problem—that is, the problem of axisymmetric deformation of a peripherally fixed and initially flat circular membrane subjected to transverse uniformly distributed loads—is re-solved by simultaneously considering the improvement of the out-of-plane and in-plane equilibrium equations. In which, the so-called small rotation angle assumption of the membrane is given up when establishing the out-of-plane equilibrium equation, and the in-plane equilibrium equation is, for the first time, improved by considering the effect of the deflection on the equilibrium between the radial and circumferential stress. Furthermore, the resulting nonlinear differential equation is successfully solved by using the power series method, and a new closed-form solution of the problem is finally presented. The conducted numerical example indicates that the closed-form solution presented here has a higher computational accuracy in comparison with the existing solutions of the well-known Hencky problem, especially when the deflection of the membrane is relatively large.
1. Introduction
Membrane structures or structural components have played important roles in many fields of engineering or technology, for example, the MEMS (Micro-Electro-Mechanical Systems) devices [1], heat transfer enhancement applications [2], characterization of mechanical properties [3,4], and civil engineering [5,6]. Mathematical modelling is often necessary to study the mechanical behavior of structures [7,8]. However, the large deflection phenomenon of the membrane usually gives rise to some nonlinear differential equations. The boundary value problems of these somewhat intractable nonlinear equations are usually difficult to deal with analytically [9,10,11,12,13,14,15]. Therefore, analytical solutions for membrane problems are available in a few cases, but it is usually easy to find the numerical solutions obtained by, for example, the iterative or shooting method in the existing literature. In practice, however, analytical solutions are often found to be necessary.
Hencky, a famous German scientist, originally dealt with the problem of axisymmetric deformation of a peripherally fixed circular membrane under uniformly distributed transverse loads and presented its closed-form solution in the form of power series [16]. A computational error in [16] was corrected by Chien [17] and Alekseev [18], respectively. This problem is usually called the well-known Föppl–Hencky membrane problem, or simply the well-known Hencky problem, and its solution is called the well-known Hencky solution. This solution is the first solution for circular membrane problems and is often cited in relevant studies [6,13,19,20,21]. During the derivation of the well-known Hencky solution, however, the so-called small rotation angle assumption of the membrane—that is, suppose that the rotation angle of the membrane is so small that —was adopted, which limits the applicability of the solution to the deflection of the membrane. Consequently, we gave up the small rotation angle assumption of the membrane and used to establish the out-of-plane equilibrium equation, re-solved the well-known Hencky problem, and presented the closed-form solution without the small rotation angle assumption in [21]. However, the effect of the deflection on the in-plane equilibrium equation was not considered during the derivation of the solution presented in [21], and this still limits the applicability of solution to the deflection of membrane, which will be seen from the numerical example conducted in Section 3.
In this study, the well-known Hencky problem was re-solved by simultaneously considering the improvement of the out-of-plane and in-plane equilibrium equations, and a more refined closed-form solution of well-known Hencky problem was presented. The numerical example conducted indicates that the solution presented here has a higher computational accuracy in comparison with the existing solutions. The detailed derivation of the basic equations was arranged in the next section, in which the out-of-plane equilibrium equation is established under the condition of , the in-plane equilibrium equation is, for the first time, improved by considering the effect of deflection on the equilibrium between radial stress and circumferential stress, the resulting nonlinear differential equation is successfully solved by using the power series method, and finally, a new closed-form solution of the well-known Hencky problem is presented. In Section 3, a numerical example is conducted for the identification of the validity of the closed-form solution presented and the applicability of solution to the deflection of membrane. Section 4 features the concluding remarks.
2. Membrane Equation and Its Solution
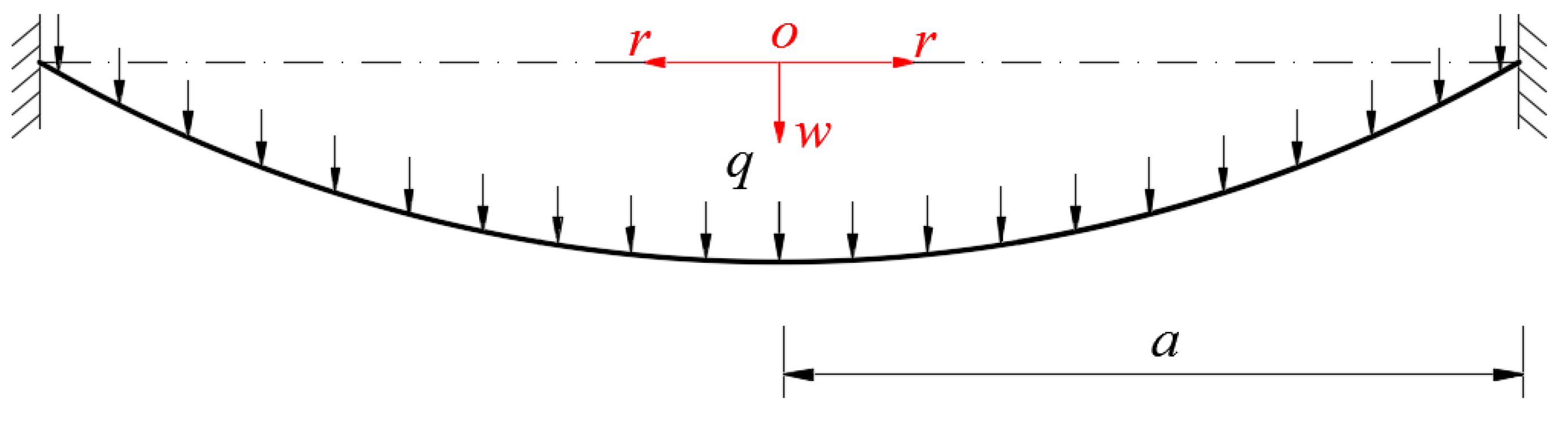
A rotationally symmetric, linearly elastic, initially-flat circular membrane with Poisson’s ratio , Young’s modulus of elasticity , radius and thickness is peripherally clamped. The uniformly distributed transverse loads is quasi-statically applied onto the surface of the membrane, as shown in Figure 1, where is the radial coordinate in a cylindrical coordinate system (where the polar coordinate plane is located in the plane in which the geometric middle plane of the initially-flat circular unstretched membrane is located) and is the transverse coordinate of the cylindrical coordinate system as well as the transverse displacement of the membrane.
Figure 1.
Sketch of the circular membrane under transverse loads q.
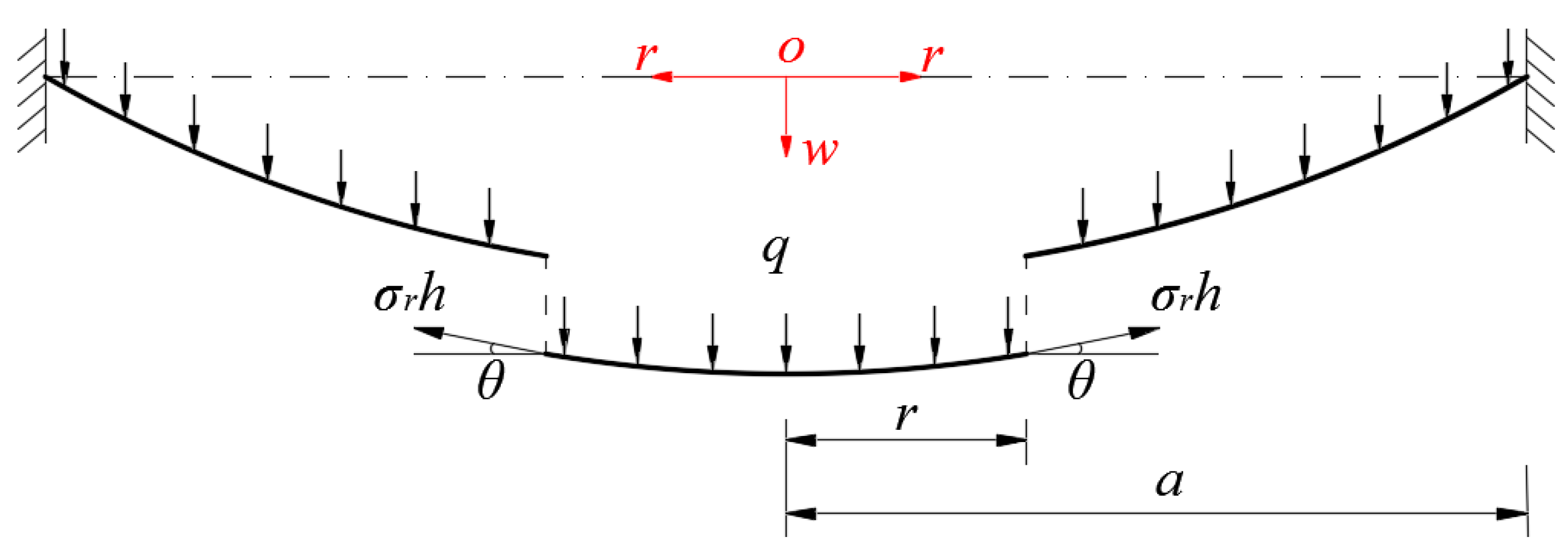
We take a piece of circular membrane with radius in the central portion of the deformed circular membrane to study the static equilibrium problem of this piece of the deformed circular membrane under the joint actions of the external loads within and the total force produced by the membrane force acting on the boundary , as shown in Figure 2, where denotes the radial stress and denotes the slope angle of the deformed membrane. Clearly, there are two vertical forces, that is, the total force (in which ) of the external loads and the total vertical membrane force that is produced by the membrane force . The so-called out-of-plane equilibrium equation is
where
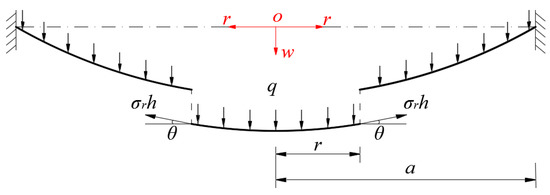
Figure 2.
Sketch of the static equilibrium of the central portion (r ≤ a).
Substituting Equation (2) into Equation (1), one obtains
While in the horizontal plane which is parallel to the initially flat circular membrane, there are two horizontal forces, the circumferential membrane force and the horizontal component of the radial membrane force , where denotes the circumferential stress. The classic in-plane equilibrium equation, i.e., , is modified and replaced by
The effect of deflection on the equilibrium between radial stress and circumferential stress is thus taken into account, and for brevity, the detailed derivation of Equation (4) is arranged in Appendix A. Suppose that we denote the radial strain by , circumferential strain by , radial displacement by , and the transversal displacement by . The relations between the strain and displacement for the large deflection problem, that is, the so-called geometric equations, may be written as
and
Moreover, the relations of the stress and strain, that is, the so-called physical equations, are still assumed to satisfy linear elasticity and can be written as
and
Substituting Equations (5) and (6) into Equations (7) and (8) yields
and
By means of Equations (9) and (10), one has
After substituting the u of Equation (11) into Equation (9), then the so-called consistency equation can be written as
Equations (3), (4) and (12) are three equations for the solutions of , and . Then, the boundary conditions, under which Equations (3), (4) and (12) may be solved, are
and
Let us employ the following nondimensionalization
and transform Equations (3), (4) and (12)–(15) into
and
In view of the physical phenomenon that the values of stress and deflection are both finite at , , and can be expanded into the power series of the , i.e., let
and
After substituting Equations (23)–(25) into Equations (17)–(19), it is found that , and (i = 1,3,5,…), while the coefficients , and (i = 2,4,6,…) can be expressed into the polynomial with regard to the coefficients and , besides (see Appendix B).
The coefficients and , as the undetermined constants depending on the concrete problem, can be determined by using the boundary conditions of Equations (21) and (22). Substituting Equations (23)–(25) into Equations (21) and (22) gives
and
Please note that Equations (26) and (27) contain only the undetermined constants and , because and the coefficients , and (i = 2,4,6,…) were expressed into the polynomial with regard to the coefficients and at this time. Therefore, for the problem in which the values of , , , and are known beforehand, the undetermined constants and can be determined by simultaneous solutions of Equations (26) and (27), and furthermore, with the known and the other coefficients , , (i = 2,4,6,…) and can be easily determined. The problem dealt with here is thus solved.
3. Results and Discussion
Let us firstly discuss the effectiveness of the solution obtained in Section 2. From the derivation of Section 2 of this paper and reference [21], we may see that only the in-plane equilibrium equation is modified to replace the classic in-plane equilibrium equation (i.e., ). However, if we let , then Equation (4) in this paper will become , i.e., the classic in-plane equilibrium equation which was adopted in reference [21]. This indicates that the solution presented here can regress into the solution presented in reference [21]. Furthermore, from the characteristic of axisymmetric deformation of the circular membrane, it is not difficult to understand that at , i.e., the boundary condition Equation (13), which has not been used yet during the derivation in Section 2. Now, let us see whether the closed-form solution obtained in Section 2 meets the boundary condition of Equation (13), i.e., at . From Equations (16) and (24) the dimensional form of the deflection can be written as
Then, the first derivative on both sides of Equation (28) is
Therefore, it is obvious that at because at while . This indicates that the closed-form solution obtained in Section 2 meets the physical phenomenon of axisymmetric deformation of the circular membrane. As a result, these two aspects discussed above, to some extent, reflect the effectiveness of the closed-form solution presented here.
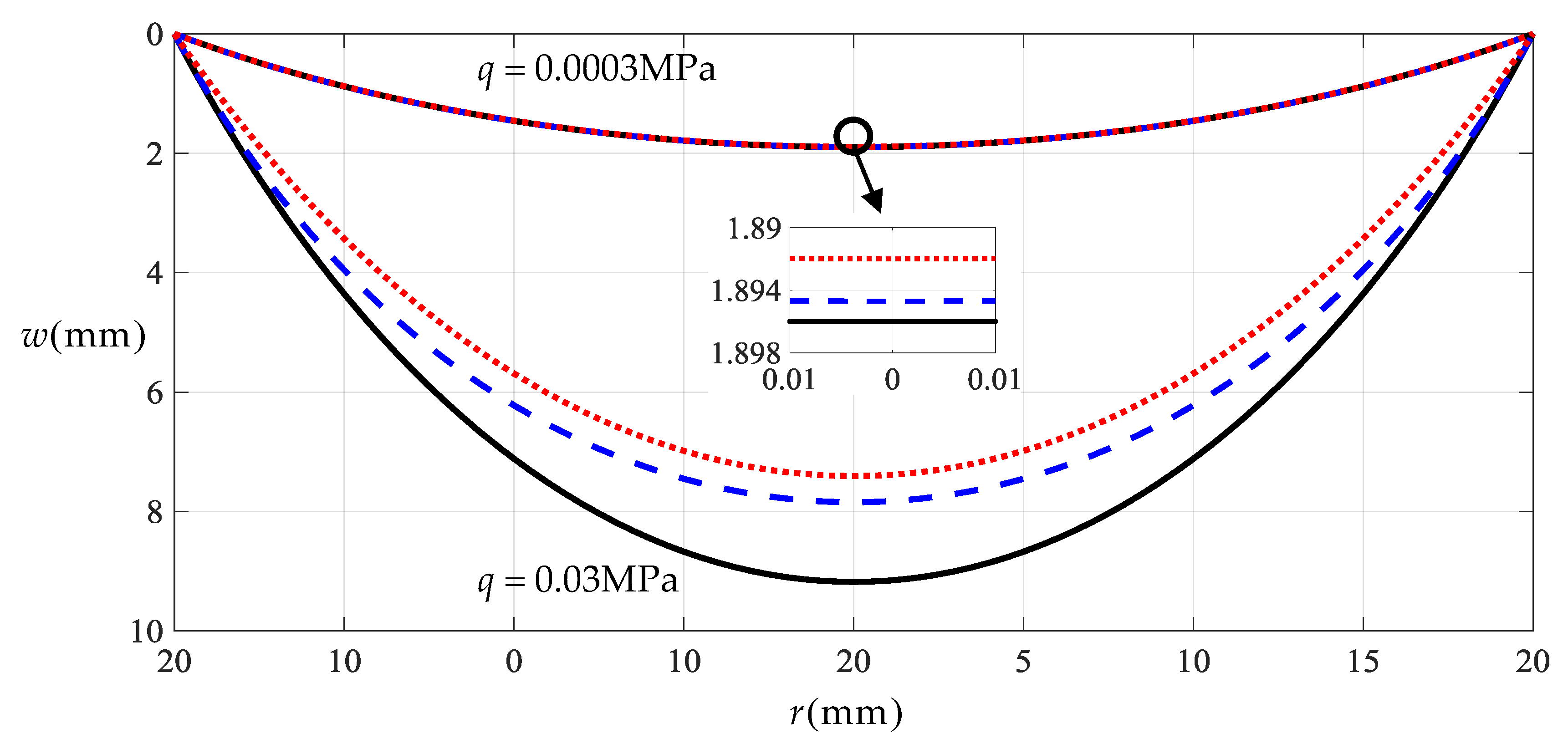
Let us consider a circular rubber membrane with radius , thickness , Young’s modulus of elasticity , Poisson’s ratio and under the action of transverse uniformly distributed loads , as an example, to discuss the applicability of solution to the deflection of membrane. Figure 3 shows the variations of the deflection with the radius when takes 0.0003 MPa and 0.03 MPa, respectively, where the solid lines represent the results obtained by the solution presented in Section 2, the dashed lines represent the results obtained by the solution presented in [21], and the dotted lines represent the results obtained by well-known Hencky solution [19].
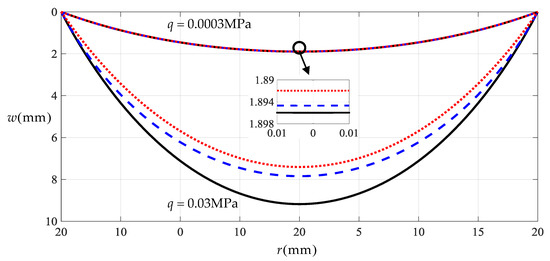
Figure 3.
Variation of with when takes 0.0003 MPa and 0.03 MPa.
From Figure 3 it may be observed that the solid line is very close to the dashed line and dotted line when takes 0.0003 MPa. This also indicates that both the closed-form solution presented here and the one presented [21] are valid, if viewed from the perspective of the well-known Hencky solution. On the other hand, along with the increase of the transverse uniformly distributed loads , the deflection of the deformed membrane will also increase. Therefore, when takes 0.03 MPa, from Figure 3, we may also see that the dashed line has a certain distance from the dotted line, while the solid line has a distinct distance from the dashed line. This indicates that the small rotation angle assumption adopted in the derivation of the well-known Hencky solution limits the applicability of the solution to the deflection of the membrane, the solution after giving up the small rotation angle assumption—that is, the solution presented in [21]—can be applied to the relatively large deflection, while compared with the solution presented in [21], the solution presented in this study can be applied to the larger deflection of the membrane. When takes 0.03 MPa, the maximum deflection is about 9.18 mm, 7.85 mm and 7.41 mm, respectively, which are calculated by the solution presented here, the solution presented in [21], and the well-known Hencky solution. The error between the maximum deflections calculated by the well-known Hencky solution and the one by the solution presented in [21] is about 5.94%, which is brought by the so-called small rotation angle assumption adopted in the derivation of the well-known Hencky solution. In particular, the error between the maximum deflection calculated by the solution presented in [21] and the one by the solution presented here is about 16.94%, which is brought about by the effect of the deflection ignored in the derivation of the classic in-plane equilibrium equation. It must be noted that such an error exceeds the allowable error of civil engineering, 15%, while the allowable error of instrument design is usually less than 3%, precision measurement usually less than 1%, including some characterizations of mechanical properties by bulge or blister test techniques [3,4,5,6,9,10].
The above discussions show that the applicability of the closed-form solution presented here to the deflection of membranes has been greatly improved, in comparison with the solution presented in [21] and the well-known Hencky solution. However, the convergence of the presented power series solution still needs to be discussed. The investigation into the convergence has to, perhaps, be arranged here, due to the fact that the coefficients , , (i = 2,4,6,…) are expressed into the somewhat intractable polynomial with regard to the coefficients and (see Appendix B) and thus there is no way to discuss the convergence of the general solutions for , and . In other words, here we can prove only the convergence of the special solutions for , and , rather than that of its general solutions, although the convergence of the general solutions, perhaps, receives the greatest attention because the special solution will converge as long as the general solution converges.
From the derivation in Section 2, we know that the general solutions for , and are the power series with regard to the nondimensional independent variable x (see Equations (23)–(25)), where the domain of the independent variable is and all the coefficients , and (i = 2,4,6,…) are expressed into the polynomial with regard to the coefficients and , besides , , (i = 1,3,5,…) and . Moreover, we also know that the undetermined constants and should be determined by simultaneous solutions of Equations (26) and (27). It seems obvious that the special solution for , and can easily be obtained as long as the undetermined constants and can be determined. However, when solving a specific definite problem it may be found that we have to substitute the partial sum of former n terms of Equations (23)–(25), rather than Equations (23)–(25), into Equations (21) and (22), otherwise the resulting Equations (26) and (27) will contain three infinite series and thus will be difficult to solve. Therefore, it seems that the undetermined constants and determined by Equations (26) and (27) will depend on the value of terms n and different n will determine the different value of and . Hence, the discussion on convergence should contain two aspects: the variation of and with terms n, and the variation of and with i for every value of terms n.
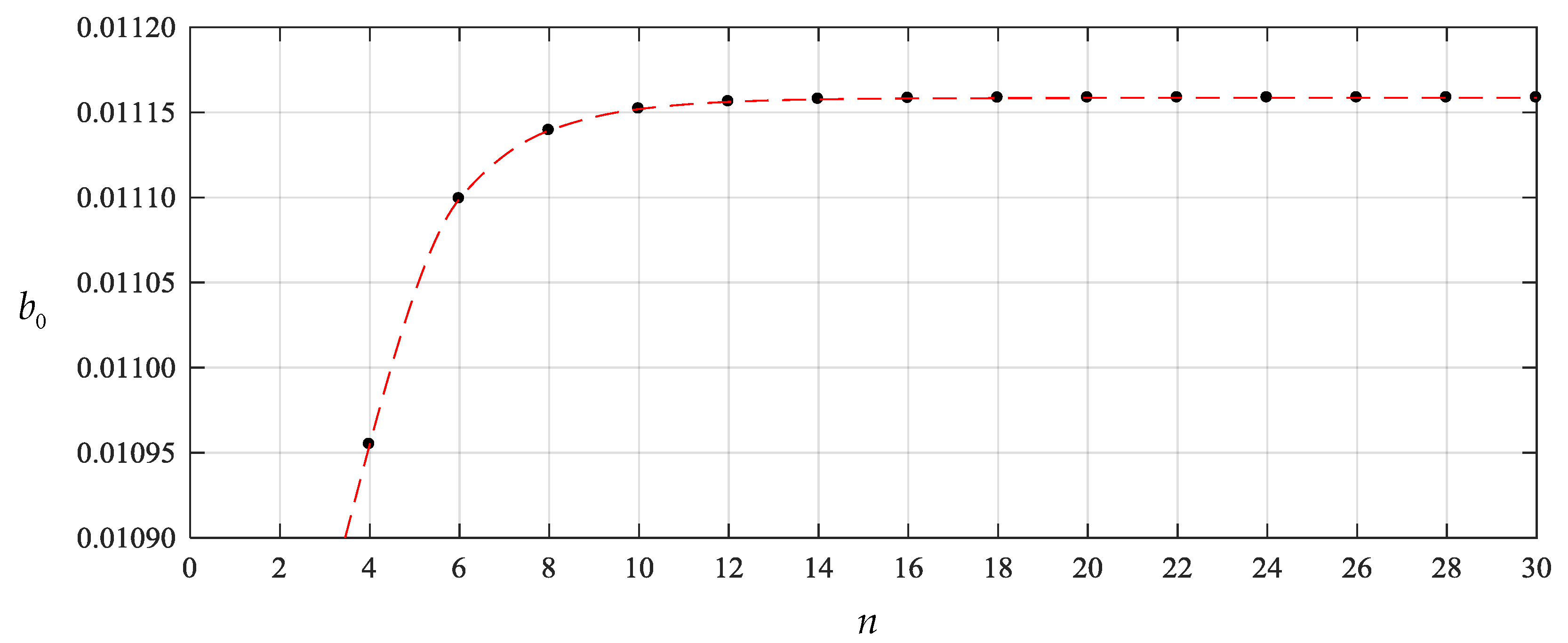
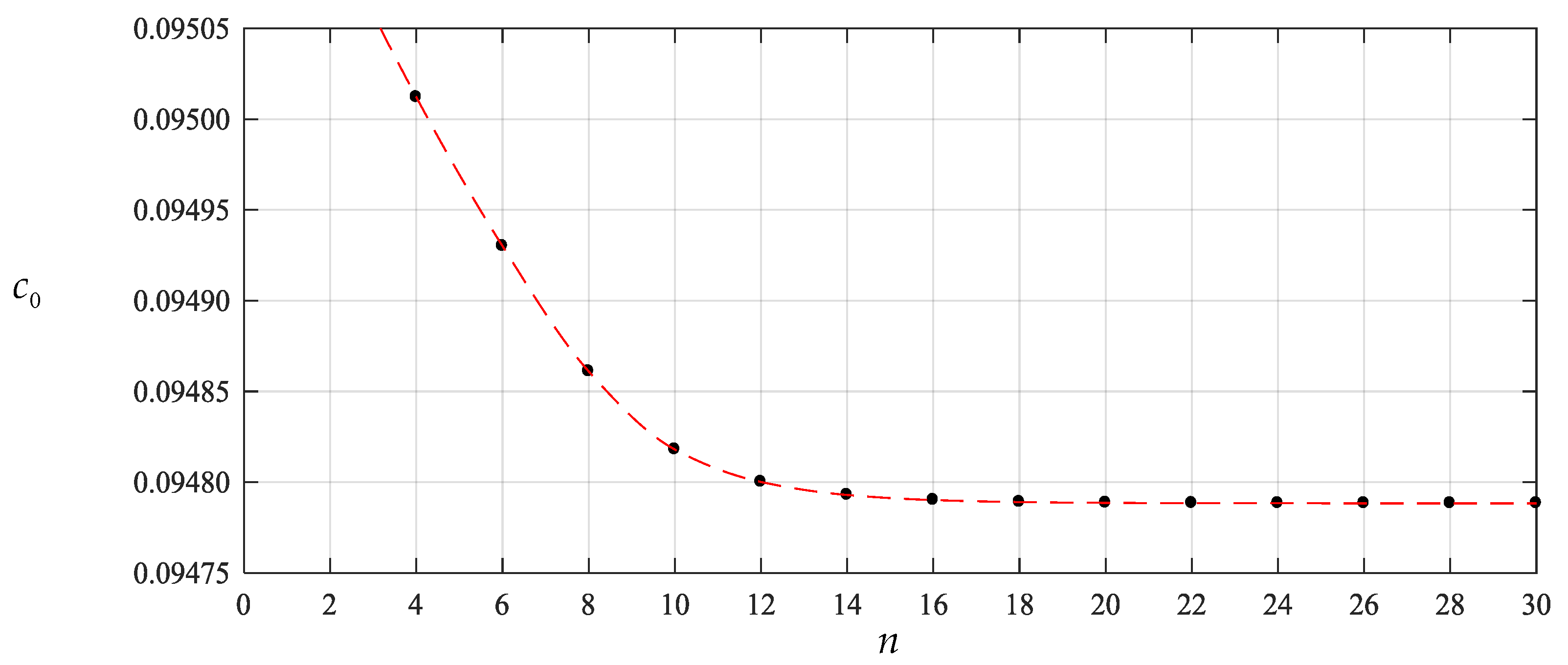
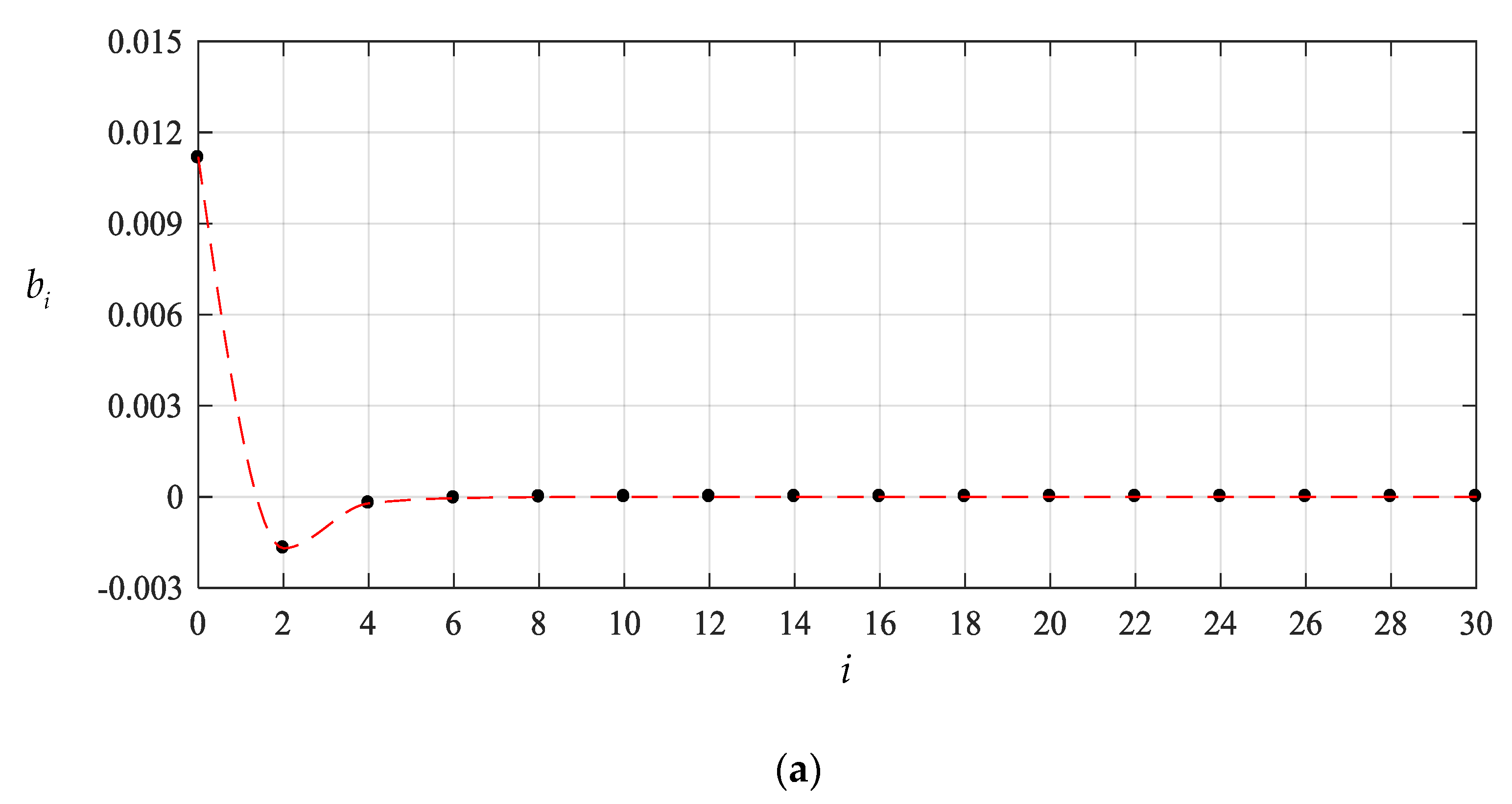
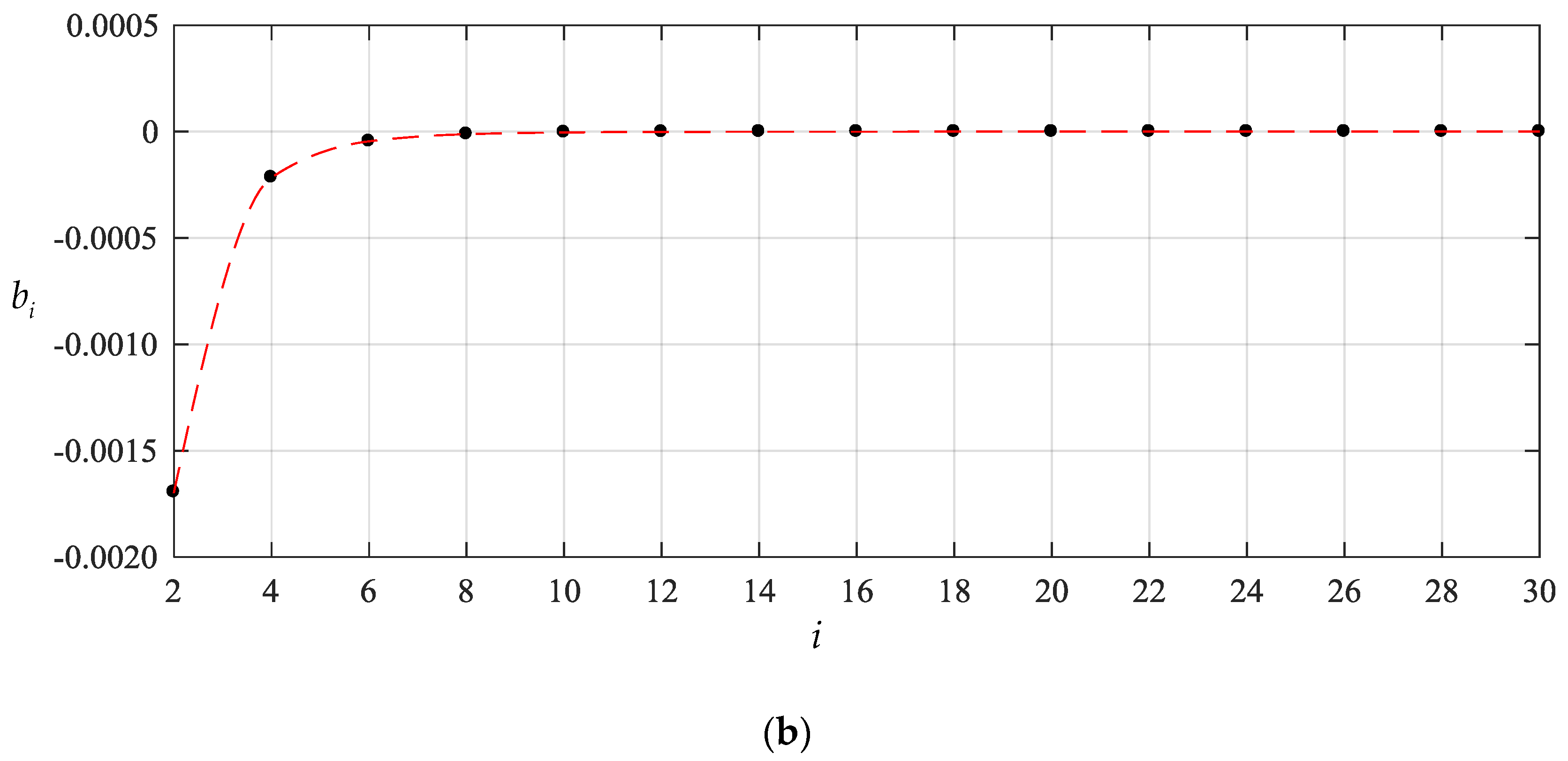
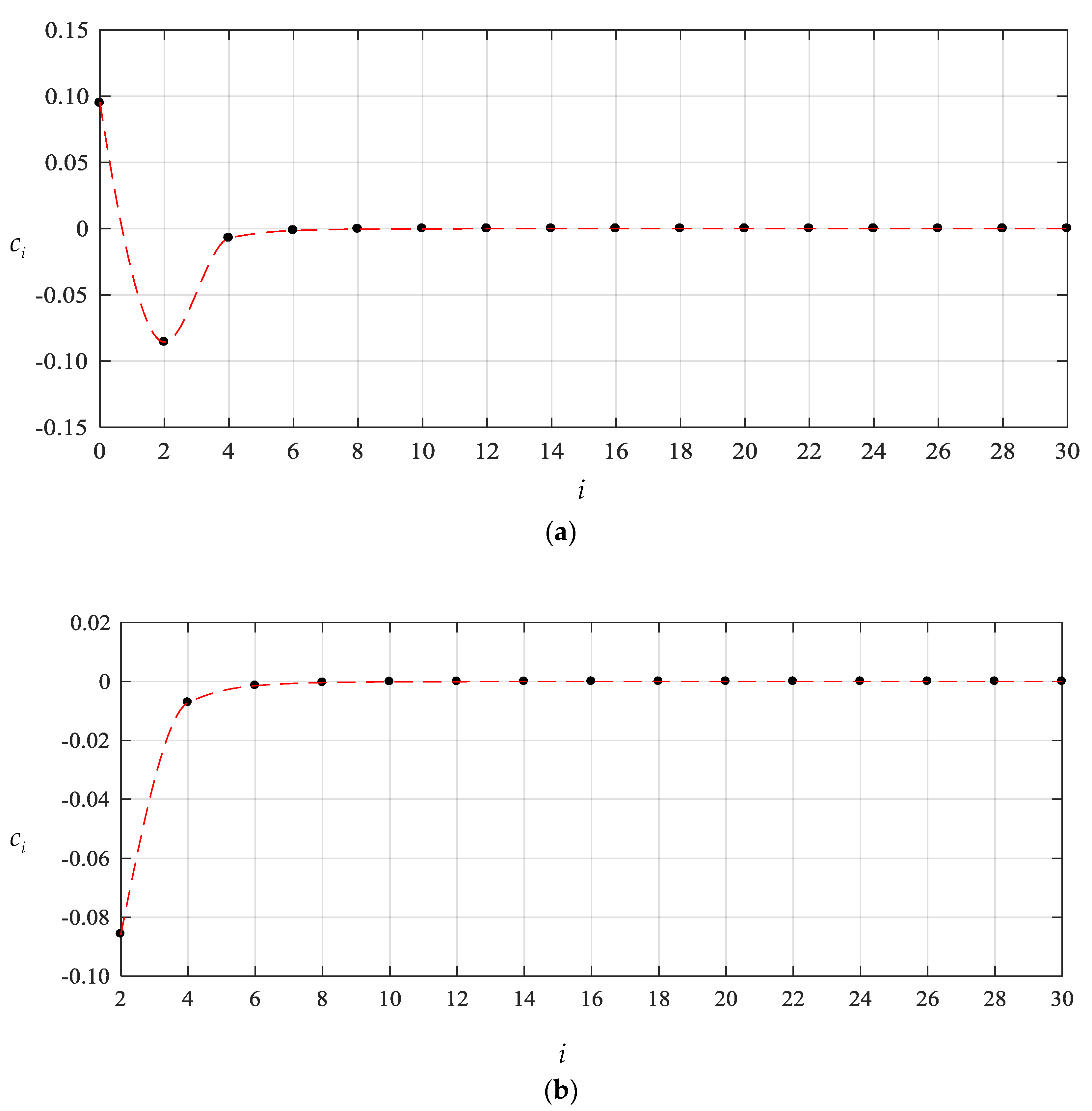
To this end, we start the numerical computation of and from , that is, start from the partial sum of the former four terms of Equations (23)–(25), and recalculate the case of q = 0.0003 MPa of the above numerical example. The obtained different numerical values of and , are listed in Table 1 and Table 2, also including the values of and corresponding to every value of and . The variation of and with terms n are shown in Figure 4 and Figure 5 separately, and the variation of and with i are, only for , shown in Figure 6 and Figure 7, respectively. From Figure 4 and Figure 5 or Table 1 and Table 2 we may see that the undetermined constants and converge reasonably well. From Figure 6 and Figure 7 or Table 1 and Table 2 we may also see that the coefficients and converge reasonably well, which indicates that the power series solutions and converge reasonably well because of . Furthermore, from Figure 4 and Figure 5 we may see that the undetermined constants and are already very close to their exact values when . So, only the coefficients , and (i = 2,4,6,…,18), which are expressed into the polynomial with regard to and , are shown in Appendix B.

Table 1.
The values of b0–b6, b8–b14, b16–b22 and b24–b30.

Table 2.
The values of c0–c6, c8–c14, c16–c22 and c24–c30.
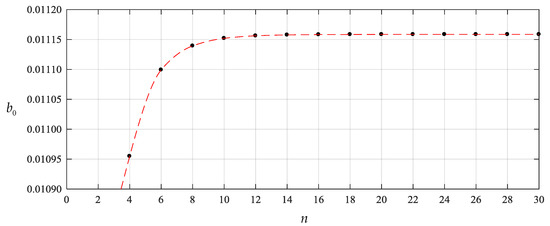
Figure 4.
Variation of with .
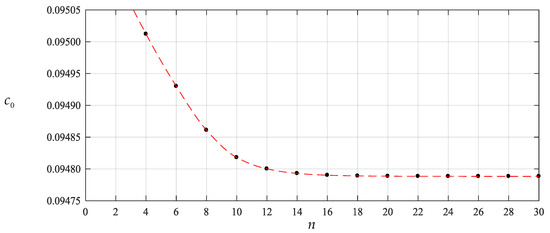
Figure 5.
Variation of with .
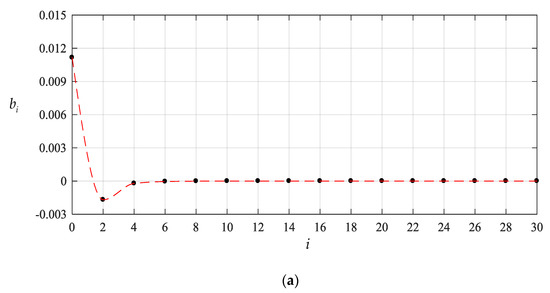
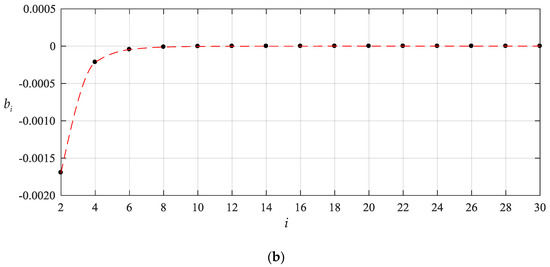
Figure 6.
Variation of with i for , where (a) for and (b) for .
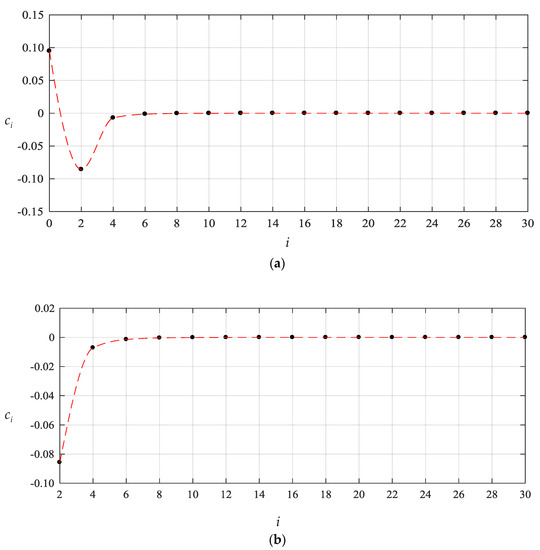
Figure 7.
Variation of with i for , where (a) for and (b) for .
4. Concluding Remarks
In this paper, the well-known Hencky problem was re-solved by simultaneously considering the improvement of the out-of-plane and in-plane equilibrium equations. From this study, the following conclusions can be drawn.
The well-known Hencky solution applies only to the case where the deflection of the membrane is relatively small.
Compared with the well-known Hencky solution, the solution after improving the out-of-plane equilibrium equation can be applied to the case where the deflection of the membrane is relatively large.
However, compared with the well-known Hencky solution and the solution that only the out-of-plane equilibrium equation is improved, the solution that the out-of-plane and in-plane equilibrium equations are simultaneously improved can be applied to the larger deflection of the membrane.
The large deflection phenomenon of the membrane is possible in many fields of engineering or technical application, for example, the delamination studies for the characterization of the surface and interfacial or thin-film/substrate mechanical properties by a so-called pressurized blister test, where the maximum deflection of the blistering thin film may reach half the radius of the circular blistering thin film, or even larger. Clearly, such a large deflection is not applicable to the solutions in existing literature. Therefore, in this sense, the work presented here should be of positive significance to these fields of technical applications.
Author Contributions
Conceptualization, X.L. and J.-Y.S.; methodology, X.L. and J.-Y.S.; validation, X.-T.H.; writing-original draft preparation, X.L. and Z.-H.Z.; writing-review and editing, X.L. and X.-T.H.; visualization, X.L. and S.-Z.L.; funding acquisition, J.-Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 11772072).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Suppose that the polar coordinate is set at the geometric middle-plane of the initially-flat circular membrane, and the original point of the coordinate (i.e., transverse coordinate) is set at the center point of the geometric mid-plane, thus the cylindrical coordinate system is established, where and are the radial and circumferential coordinate, respectively. We take a differential element that is surrounded by two meridians (,) and two parallels (,) from the deformed membrane, to study the in-plane equilibrium of this piece under the joint actions of the radial forces and circumferential force , as shown in Figure A1, where is the projection of on the polar coordinate plane, and are the radial and circumferential stress, and are the radial and circumferential increment of the element , is the maximum deflection of the circular membrane, is the radius of the circular membrane, is the thickness of the deformed circular membrane.
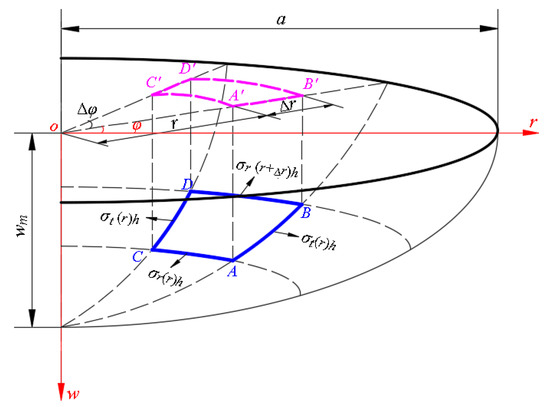
Figure A1.
Diagram of the cylindrical coordinate system and the differential element .
Figure A1.
Diagram of the cylindrical coordinate system and the differential element .
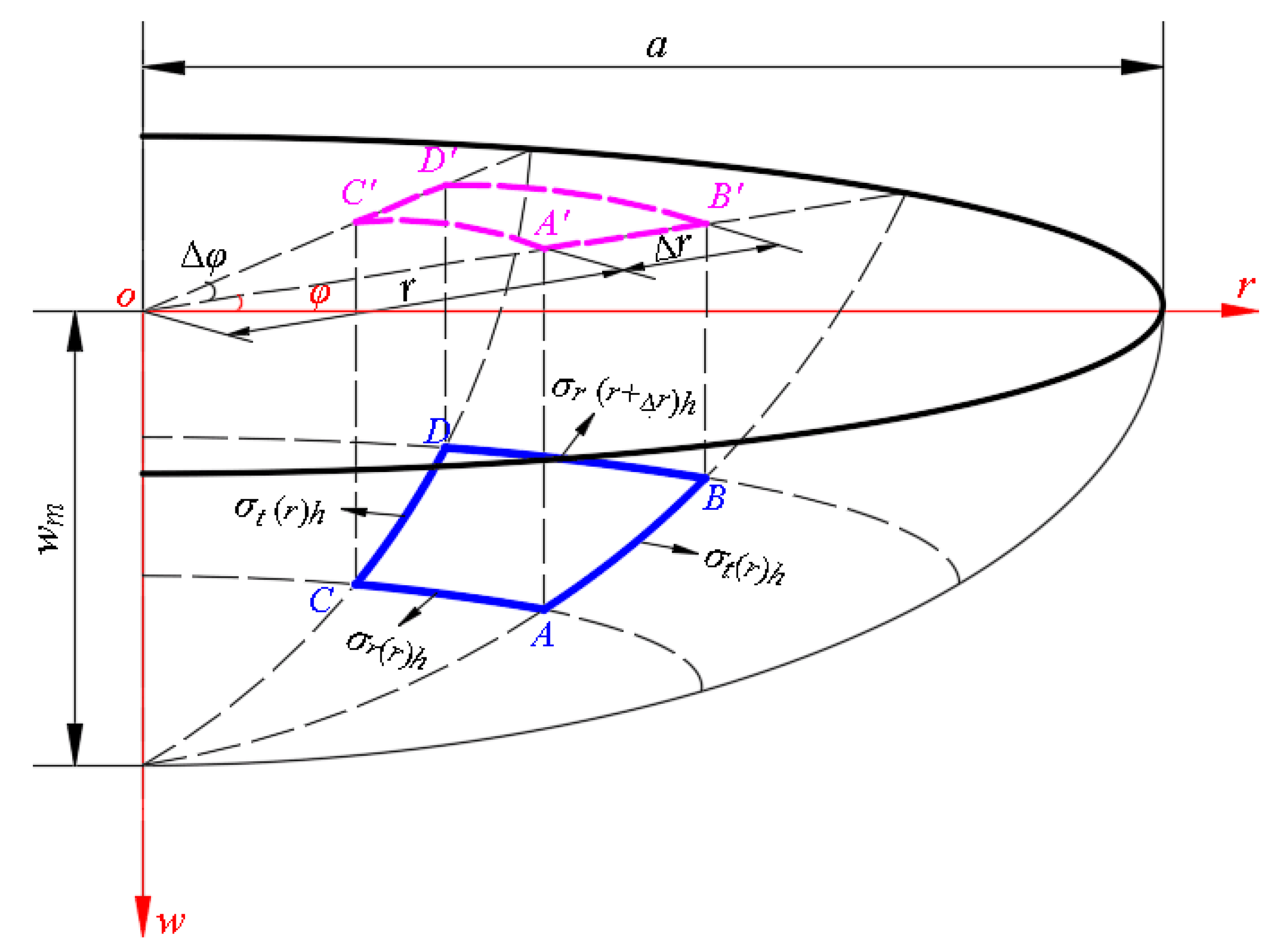
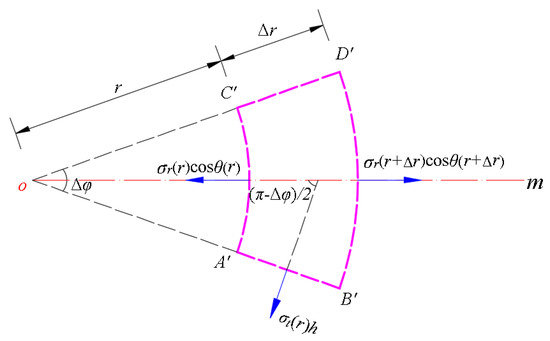
Figure A2.
Diagram of the element (the projection of ).
Figure A2.
Diagram of the element (the projection of ).
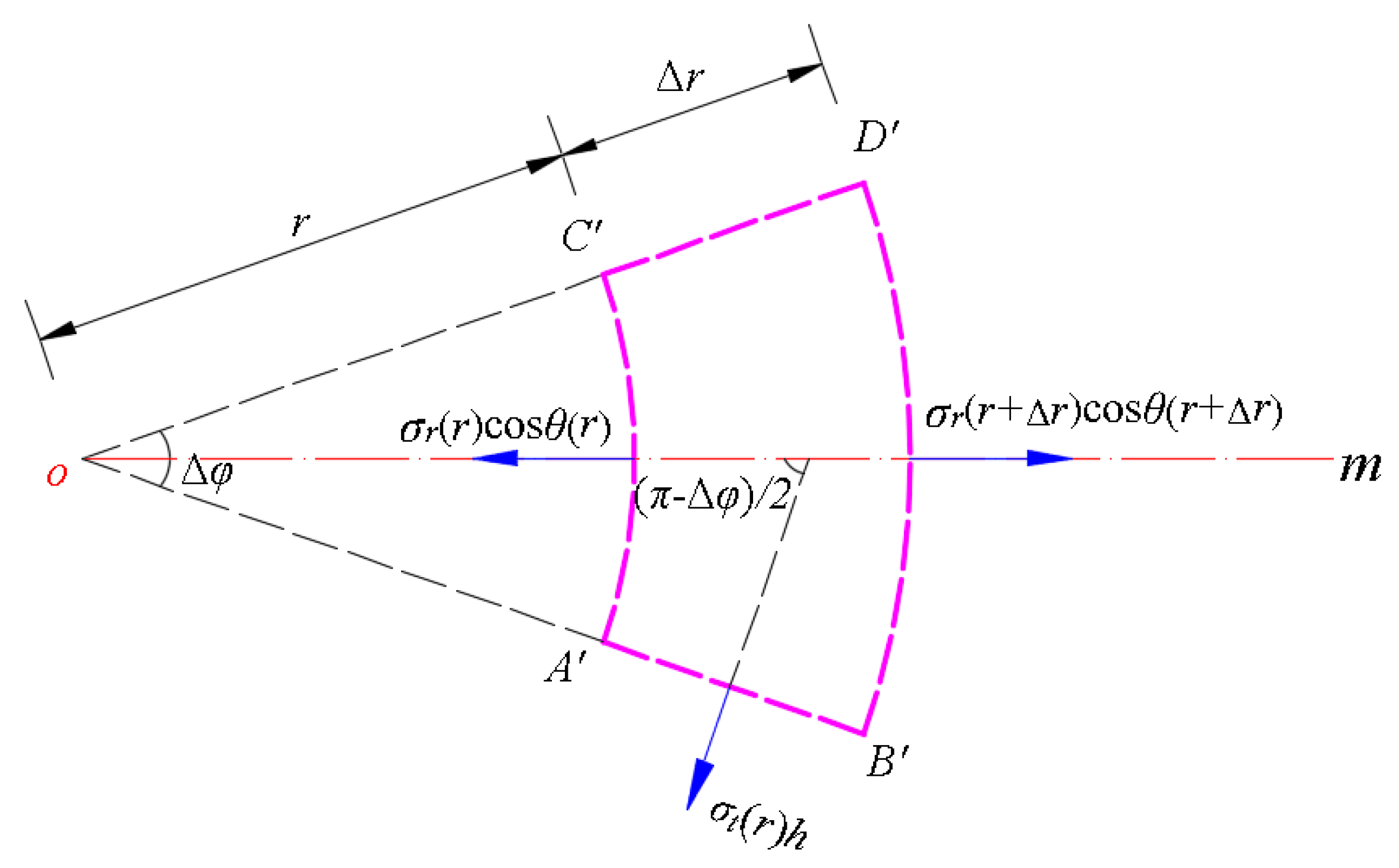
In this section, the basic assumptions are made as follows: (1) the thickness of the deformed circular membrane is supposed to be constant; (2) both the radial stress and circumferential stress refer to the mean stress on the cross section of the deformed circular membrane. Subsequently, we study the static equilibrium problem of the differential element under the total force in the horizontal direction, i.e., the direction parallel to the polar coordinate plane, as shown in Figure A2, where and denote the slope angles of the boundaries and of the differential element , is the angular bisector of . Clearly, there are four horizontal forces, i.e., the total force produced by the horizontal component of radial force acting on the boundary , the total force produced by the horizontal component of radial force acting on the boundary , two total forces produced by the circumferential force acting on the boundaries and . The total force acting on the boundary is
Similarly, the total force acting on the boundary is
Assuming that, after the membrane is deflecting, the length of the meridian is approximately equal to the length of the straight line , i.e., , we obtain
To sum up, the in-plane equilibrium equation can be written as
Due to , we can assume that and record them as . Substituting Equations (A1)–(A3) into Equation (A4), we can obtain
then we expand into the Taylor series as
The second-order and higher-order differential items in Equation (A6) may be ignored, and substituting Equation (A6) into Equation (A5) yields
after ignoring the third-order differential item and dividing the equation by , we obtain
where
Substituting Equation (A9) into Equation (A8) yields
Thus, we establish a new in-plane equilibrium equation, which is improved by considering the effect of deflection on the equilibrium between radial stress and circumferential stress.
Appendix B
References
- Di Barba, P.; Fattorusso, L.; Versaci, M. A 2D Non-linear second-order differential model for electrostatic circular membrane MEMS devices: A result of existence and uniqueness. Mathematics 2019, 7, 1193. [Google Scholar] [CrossRef]
- Rehman, A.; Salleh, Z.; Gul, T.; Zaheer, Z. The impact of viscous dissipation on the thin film unsteady flow of GO-EG/GO-W nanofluids. Mathematics 2019, 7, 653. [Google Scholar] [CrossRef]
- Sun, J.Y.; Lian, Y.S.; Li, Z.L.; He, X.T.; Zheng, Z.L. Theoretical study on shaft-loaded blister test technique: Synchronous characterization of surface and interfacial mechanical properties. Int. J. Adhes. Adhes. 2014, 51, 128–139. [Google Scholar] [CrossRef]
- Sun, J.Y.; Hu, J.L.; Zheng, Z.L.; He, X.T.; Geng, H.H. A practical method for simultaneous determination of Poisson’s ratio and Young’s modulus of elasticity of thin films. J. Mech. Sci. Technol. 2011, 25, 3165–3171. [Google Scholar] [CrossRef]
- Suo, H.; Angelotti, A.; Zanelli, A. Thermal-physical behavior and energy performance of air-supported membranes for sports halls: A comparison among traditional and advanced building envelopes. Energy Build. 2015, 109, 35–46. [Google Scholar] [CrossRef]
- Król, B.; Pielichowska, K.; Król, P.; Kędzierski, M. Polyurethane cationomer films as ecological membranes for building industry. Prog. Org. Coat. 2019, 130, 83–92. [Google Scholar] [CrossRef]
- Peride, N.; Carabineanu, A.; Craciun, E.M. Mathematical modelling of the interface crack propagation in a pre-stressed fiber reinforced elastic composite. Comp. Mater. Sci. 2009, 45, 684–692. [Google Scholar] [CrossRef]
- Sadowski, T.; Marsavina, L.; Craciun, E.M.; Kneć, M. Modelling and experimental study of parallel cracks propagation in an orthotropic elastic material. Comp. Mater. Sci. 2012, 52, 231–235. [Google Scholar] [CrossRef]
- Zhao, M.H.; Zheng, W.L.; Fan, C.Y. Mechanics of shaft-loaded blister test for thin film suspended on compliant substrate. Int. J. Solids Struct. 2010, 47, 2525–2532. [Google Scholar] [CrossRef][Green Version]
- Sun, J.Y.; Hu, J.L.; He, X.T.; Zheng, Z.L.; Geng, H.H. A theoretical study of thin film delamination using clamped punch-loaded blister test: Energy release rate and closed-form solution. J. Adhes. Sci. Technol. 2011, 25, 2063–2080. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Ge, X.M.; Yang, Z.X.; He, X.T.; Zheng, Z.L. A theoretical study of an improved capacitive pressure sensor: Closed-form solution of uniformly loaded annular membranes. Measurement 2017, 111, 84–92. [Google Scholar] [CrossRef]
- Arthurs, A.M.; Clegg, J. On the solution of a boundary value problem for the nonlinear Föppl-Hencky equation. Z. Angew. Math. Mech. 1994, 74, 281–284. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Dong, J.; Zheng, Z.L.; Yang, Z.X. Closed-form solution of axisymmetric deformation of prestressed Föppl-Hencky membrane under constrained deflecting. Struct. Eng. Mech. 2019, 69, 693–698. [Google Scholar]
- Cabada, A.; Wanassi, O.K. Existence results for nonlinear fractional problems with non-homogeneous integral boundary conditions. Mathematics 2020, 8, 255. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, C.G. Existence of positive solutions to singular φ-Laplacian nonlocal boundary value problems when φ is a sup-multiplicative-like function. Mathematics 2020, 8, 420. [Google Scholar] [CrossRef]
- Hencky, H. Über den Spannungszustand in kreisrunden Platten mit verschwindender Biegungssteifigkeit. Z. Angew. Math. Phys. 1915, 63, 311–317. [Google Scholar]
- Chien, W.Z. Asymptotic behavior of a thin clamped circular plate under uniform normal pressure at very large deflection. Sci. Rep. Natl. Tsinghua Univ. 1948, 5, 193–208. [Google Scholar]
- Alekseev, S.A. Elastic circular membranes under the uniformly distributed loads. Eng. Corpus. 1953, 14, 196–198. (In Russian) [Google Scholar]
- Sun, J.Y.; Rong, Y.; He, X.T.; Gao, X.W.; Zheng, Z.L. Power series solution of circular membrane under uniformly distributed loads: Investigation into Hencky transformation. Stuct. Eng. Mech. 2013, 45, 631–641. [Google Scholar] [CrossRef]
- Sun, J.Y.; Lian, Y.S.; Li, Y.M.; He, X.T.; Zheng, Z.L. Closed-form solution of elastic circular membrane with initial stress under uniformly-distributed loads: Extended Hencky solution. Z. Angew. Math. Mech. 2015, 95, 1335–1341. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Yang, Z.X.; He, X.T.; Zheng, Z.L. Closed-form solution of well-known Hencky problem without small-rotation-angle assumption. J. Appl. Math. Mech./Z. Angew. Math. Mech. 2016, 96, 1434–1441. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).