Orbit Growth of Periodic-Finite-Type Shifts via Artin–Mazur Zeta Function

Abstract

The prime orbit and Mertens’ orbit counting functions describe the growth of closed orbits in a discrete dynamical system in a certain way. In this paper, we prove the asymptotic behavior of these functions for a periodic-finite-type shift. The proof relies on the meromorphic extension of its Artin–Mazur zeta function.

1. Introduction

Let $(X,T)$ be a discrete dynamical system, where X is a topological space and $T:X\to X$ is a continuous map. For a point $a\in X$, the orbit of a is the set

$$\tau (a)=\{T^k(a)\mid k\in {\mathbb{N}}_0\}.$$

The point a is said to be periodic with period $n\in \mathbb{N}$ if $T^n(a)=a$. Furthermore, if $T^n(a)=a$ but $T^k(a)\ne a$ for any $k\in \{1,2,\dots ,n-1\}$, then a has least period n. In this case, its orbit

$$\tau (a)=\{a,T(a),T^2(a),\dots ,T^{n-1}(a)\}$$

is finite. Such orbit is called a (prime) closed orbit of (least) period $|\tau (a)|=n$.

Some counting functions had been introduced to describe the growth of the closed orbits in a system. The functions were inspired by the counting functions for primes in number theory. They are defined as

(i)

prime orbit counting function

$$\pi (x)={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}1,$$

(ii)

Mertens’ orbit counting functions

$$\mathcal{M}(x)={\displaystyle \prod _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\left(1-\frac{1}{e^{h\left|\tau \right|}}\right)$$

and

$$\mathcal{M}(x)={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{1}{e^{h\left|\tau \right|}}$$

where $\tau$ is the closed orbit, h is the topological entropy of the system and $x\in \mathbb{N}$. The functions are well-defined if the number of closed orbits for each period is finite.

The idea of counting closed orbits in this way arises as a dynamical analogue to counting primes in number theory. Specifically, the famous Prime Number Theorem and Mertens’ Theorem (see [1]) tell us about the asymptotic behaviors of certain counting functions for primes, which are as follows:

$${\displaystyle \sum _{p\le x}}1\sim \frac{x}{\log x},{\displaystyle \prod _{p\le x}}\left(1-\frac{1}{p}\right)\sim \frac{e^{-\gamma }}{\log x},{\displaystyle \sum _{p\le x}}\frac{1}{p}=\log \log x+M+o(1)$$

where $x\in \mathbb{N}$, p runs through primes, $\gamma$ is the Euler–Mascheroni constant and M is the Meissel–Mertens constant. Motivated by these results, we are interested to determine similar results for our counting functions for a given discrete system.

The earliest works on this idea were done by Parry and Pollicott (see [2,3]) on shifts of finite type and their suspensions. It was shown that for a mixing shift of finite type with topological entropy $h_1>0$,

$$\pi (x)\sim \frac{e^{h_1(x+1)}}{(e^{h_1}-1)x}.$$

Sharp [4] obtained the asymptotic behaviors of the counting functions for Axiom A flows. However, similar results can be deduced for a mixing shift of finite type, which are

$$\mathcal{M}(x)\sim \frac{e^{-\gamma }}{x}{\beta }_1$$

and

$$\mathcal{M}(x)=\log x+\log {\beta }_1+\gamma -C_1+o(1)$$

where ${\beta }_1$ and $C_1$ are some positive constants.

Similar results had been obtained for toral automorphisms. Waddington [5] proved that for a quasihyperbolic toral automorphism with topological entropy $h_2>0$,

$$\pi (x)\sim \frac{e^{h_2(x+1)}}{x}{\displaystyle \sum _{\rho \in U}}K(\rho )\frac{{\rho }^{x+1}}{\rho e^{h_2}-1}$$

for some finite subset U of unit circle ${\mathbb{S}}^1$ and a function $K:U\to \mathbb{Z}$. Specifically, for ergodic toral automorphism, Noorani [6] proved further that

$$\mathcal{M}(x)\sim \frac{e^{-m\gamma }}{x^m}{\beta }_2$$

where m is some positive integer and ${\beta }_2$ is some positive constant.

The proofs for the results above depend on a generating function for the number of periodic points, which is called Artin–Mazur zeta function [7]. For a system $(X,T)$, its Artin–Mazur zeta function is defined as

$$\zeta (z)=\exp \left({\displaystyle \sum _{n=1}^{\infty }}\frac{F(n)}{n}{z}^n\right)$$

(1)

where $F(n)$ is the number of periodic points of period n and $z\in \mathbb{C}$. Furthermore, the zeta function can be expressed in terms of closed orbits as

$$\zeta (z)={\displaystyle \prod _{\tau }}\frac{1}{1-z^{\left|\tau \right|}}.$$

(2)

From the formula for radius of convergence, if the sequence ${\left\{\sqrt[n]{F(n)}\right\}}_{n=1}^{\infty }$ is bounded, then the zeta function has a positive radius of convergence.

For each system above, the zeta function has a non-vanishing meromorphic extension beyond its radius of convergence. Based on the proofs, this property leads to the asymptotic behaviors of the counting functions through some combinatorial calculation. It turns out that this approach can be applied onto any system to obtain similar results on its orbit growth, as long as its zeta function has the mentioned property.

However, this approach of using zeta function may not be feasible for certain systems, for example, when the closed form of its zeta function is not readily available, or the zeta function itself is sophisticated. In recent years, there are other approaches used to obtain the orbit growth for some systems. Alsharari et al. [8] used estimates on the number of periodic points of Motzkin shift over R pairs of matching symbols and S neutral symbols to obtain that

$$\pi (x)\asymp \frac{{(R+S+1)}^x}{x}$$

and

$$\mathcal{M}(x)\asymp \log x$$

for the system. In fact, if $S=0$ in the above, we obtain the orbit growth for Dyck shift over R pairs of matching symbols (see [9]). Later, Akhatkulov et al. [10] obtained sharper results for the Dyck shift, which are

$$\pi (x)=\frac{2{(R+1)}^x}{Rx}\left(1+O\left(\frac{1}{x}\right)\right)$$

and

$$\mathcal{M}(x)=2\log x+\mathsf{\Lambda }+ϵ(x)$$

where $\mathsf{\Lambda }$ is some positive constant and $ϵ(x)\sim \frac{1}{x}$.

There are other approaches to obtain the orbit growth of a system, such as by counting in orbit monoids [11] and using orbit Dirichlet series on some algebraic systems [12,13]. However, we will not delve deeper into these topics since our focus here is on the approach via zeta function. The results shown above are enough to demonstrate the progress in this research interest in recent years. As a supplementary, interested readers may refer to our survey in [14] and the references therein for more exposure on the topic of orbit counting in discrete dynamical systems.

Béal et al. [15] introduced a new type of shift spaces, which are called periodic-finite-type shifts. These are a generalization to shifts of finite type. In fact, its zeta function had been obtained by Manada & Kashyap [16], though it is more sophisticated than for the case of shifts of finite type. Up to date, there is no result published on the orbit growth of periodic-finite-type shifts.

Hence, our aim in this paper is to obtain the orbit growth of a periodic-finite-type shift via its zeta function. Since its zeta function had been obtained in [16], it is remained to investigate the properties of its meromorphic extension.

In Section 2, we provide a key theorem with proof regarding the orbit growth of a general system via its zeta function. In Section 3, we review some properties of periodic-finite-type shifts, and proceed to determine the orbit growth by investigating their zeta function. Some basic theories on matrices and graphs are required in proving the result on their orbit growth.

2. Orbit Growth via Zeta Function

In this section, we prove the asymptotic behaviors of the counting functions $\pi (x)$, $\mathcal{M}(x)$ and $\mathcal{M}(x)$ for a general system via its zeta function. The next theorem is inspired from the results in [3,4,5,6]. The proofs in those papers depend on the closed form of the zeta functions of their particular systems. However, it turns out that the proofs work on any zeta function, as long as it satisfies certain analytic properties. Of course, there are certain parts in the proofs needed to be modified to fit our general case, especially on the combinatorial calculation. Because of that, we provide the detailed proof for completeness.

Theorem 1.

Let$(X,T)$be a discrete dynamical system with topological entropy$h>0$and Artin–Mazur zeta function$\zeta (z)$. Suppose that there exists a function$\alpha (z)$such that it is analytic and non-zero for$\left|z\right|<R{e}^{-h}$for some$R>1$, and

$$\zeta (z)=\frac{\alpha (z)}{{(1-e^{hp}{z}^p)}^m}$$

(3)

for$\left|z\right|<e^{-h}$for some$m,p\in \mathbb{N}$. Then,

(a) 

(Prime Orbit Theorem)

$$\pi (x)\sim mp·\frac{e^{hp\left(⌊\frac{x}{p}⌋+1\right)}}{(e^{hp}-1)x},$$

(b) 

(Mertens’ Orbit Theorem)

$$\mathcal{M}(x)\sim \frac{e^{-m\gamma }}{\alpha (e^{-h})·{⌊\frac{x}{p}⌋}^m}$$

where γ is Euler–Mascheroni constant, and

$$\mathcal{M}(x)=m\log ⌊\frac{x}{p}⌋+m\gamma +\log \alpha (e^{-h})-C+o(1)$$

where C is a positive constant that can be specified as

$$C={\displaystyle \sum _{\tau }}\left(\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-\frac{1}{e^{h\left|\tau \right|}}\right).$$

(4)

Proof. 

(a)

Since $\alpha (z)$ is analytic and non-zero for $\left|z\right|<R{e}^{-h}$, (3) implies that $\zeta (z)$ is also analytic and non-zero for $\left|z\right|<e^{-h}$. From (1) and (3), for $\left|z\right|<e^{-h}$,

$$\begin{array}{cc}\hfill \frac{{\alpha }^{\prime }(z)}{\alpha (z)}& =\frac{{\zeta }^{\prime }(z)}{\zeta (z)}-mp{e}^{hp}·\frac{z^{p-1}}{1-e^{hp}{z}^p}\hfill \\ & ={\displaystyle \sum _{n=1}^{\infty }}F(n)z^{n-1}-mp{\displaystyle \sum _{n=1}^{\infty }}{e}^{hpn}{z}^{pn-1}\hfill \\ & ={\displaystyle \sum _{n=1}^{\infty }}c(n)z^{n-1}\hfill \end{array}$$

where

$$c(n)=\left\{\begin{array}{cc}F(n)\hfill & \mathrm{if}p\nmid n,\hfill \\ F(n)-mp{e}^{hn}\hfill & \mathrm{if}p\mid n.\hfill \end{array}\right.$$

(5)

Equivalently, for $\left|z\right|<e^{-h}$,

$$z·\frac{{\alpha }^{\prime }(z)}{\alpha (z)}={\displaystyle \sum _{n=1}^{\infty }}c(n)z^n$$

(6)

Observe that $z·{\displaystyle \frac{{\alpha }^{\prime }(z)}{\alpha (z)}}$ is analytic for $\left|z\right|<R{e}^{-h}$ and has a power series representation ${\displaystyle {\displaystyle \sum _{n=1}^{\infty }}c(n)z^n}$ for $\left|z\right|<e^{-h}$. Recall that any analytic function has a unique power series representation (see [17,18]). Therefore, the series ${\displaystyle {\displaystyle \sum _{n=1}^{\infty }}c(n)z^n}$ is also its power series representation for $\left|z\right|<R{e}^{-h}$. Overall, (6) is also valid for $\left|z\right|<R{e}^{-h}$.

For any $S\in (1,R)$, the series ${\displaystyle {\displaystyle \sum _{n=1}^{\infty }}c(n)z^n}$ converges for $z=S{e}^{-h}$. Therefore, the terms in the series are bounded, i.e., there exists a real $M>0$ such that

$$S^n{e}^{-hn}\left|c(n)\right|\le M.$$

(7)

Now, define

$$\psi (x)={\displaystyle \sum _{n=1}^x}F(n)$$

for $x\in \mathbb{N}$. Please note that

$$\begin{array}{cc}\hfill \psi (x)& ={\displaystyle \sum _{n=1}^x}c(n)+mp{\displaystyle \sum _{n=1}^{⌊\frac{x}{p}⌋}}{e}^{hpn}\hfill \\ & ={\displaystyle \sum _{n=1}^x}c(n)+mp{e}^{hp}·\frac{e^{hp⌊\frac{x}{p}⌋}-1}{e^{hp}-1}.\hfill \end{array}$$

(8)

By using (7), it is obtained that

$$\begin{array}{cc}\hfill \left|{\displaystyle \sum _{n=1}^x}c(n)\right|& \le M{\displaystyle \sum _{n=1}^x}\frac{e^{hn}}{S^n}\hfill \\ & \le M^{\prime }·\frac{e^{hx}}{S^x}\hfill \end{array}$$

for some constant $M^{\prime }$. From here, it is easy to deduce that

$${\displaystyle \underset{x\to \infty }{\lim }}\frac{{\sum }_{n=1}^{x}c(n)}{e^{hp⌊\frac{x}{p}⌋}}=0.$$

Hence, from (8), it is obtained that

$${\displaystyle \underset{x\to \infty }{\lim }}\frac{\psi (x)}{e^{hp⌊\frac{x}{p}⌋}}=mp·\frac{e^{hp}}{e^{hp}-1}$$

or equivalently,

$$\psi (x)\sim mp·\frac{e^{hp\left(⌊\frac{x}{p}⌋+1\right)}}{e^{hp}-1}.$$

(9)

Now, we need to relate both $\psi (x)$ and $\pi (x)$. First, observe that $\psi (x)$ can be expressed in terms of closed orbits as

$$\psi (x)={\displaystyle \sum _{\begin{array}{c}\tau ,n\\ n\left|\tau \right|\le x\end{array}}}\left|\tau \right|.$$

Indeed, this is true by defining $k=n\left|\tau \right|$ and checking that

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\tau ,n\\ n\left|\tau \right|\le x\end{array}}}\left|\tau \right|& ={\displaystyle \sum _{k=1}^x}{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\mid k\end{array}}}\left|\tau \right|\hfill \\ & ={\displaystyle \sum _{k=1}^x}F(k).\hfill \end{array}$$

For a closed orbit $\tau$, the number of times for it to appear in the sum ${\displaystyle {\displaystyle \sum _{\begin{array}{c}\tau ,n\\ n\left|\tau \right|\le x\end{array}}}\left|\tau \right|}$ is $⌊{\displaystyle \frac{x}{\left|\tau \right|}}⌋$. So,

$$\begin{array}{cc}\hfill \psi (x)& ={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\left|\tau \right|·⌊\frac{x}{\left|\tau \right|}⌋\hfill \\ & \le x{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}1\hfill \\ & =x·\pi (x).\hfill \end{array}$$

(10)

Define the extension of $\pi (x)$ over $\mathbb{R}$ as

$$\tilde{\pi }(y)=\pi \left(\lfloor y\rfloor \right)$$

for $y\in \mathbb{R}$. For any real $\delta >1$, set $y\in \mathbb{R}$ such that $x=\delta y$. So,

$$\begin{array}{cc}\hfill \pi (x)& =\tilde{\pi }(y)+{\displaystyle \sum _{\begin{array}{c}\tau \\ y<\left|\tau \right|\le x\end{array}}}1\hfill \\ & \le \tilde{\pi }(y)+{\displaystyle \sum _{\begin{array}{c}\tau \\ y<\left|\tau \right|\le x\end{array}}}\frac{\left|\tau \right|}{y}\hfill \\ & \le \tilde{\pi }(y)+\frac{1}{y}{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\left|\tau \right|\hfill \\ & \le \tilde{\pi }(y)+\frac{\psi (x)}{y}.\hfill \end{array}$$

(11)

By combining (10) and (11), it is obtained that

$$1\le \frac{x·\pi (x)}{\psi (x)}\le \frac{x·\tilde{\pi }(y)}{\psi (x)}+\delta .$$

(12)

Now, we need to show that ${\displaystyle \frac{x·\tilde{\pi }(y)}{\psi (x)}}\to 0$ as $x\to \infty$ (and equivalently, $y\to \infty$). First, we will prove that ${\displaystyle \frac{\tilde{\pi }(y)}{e^{h{\delta }^{\prime }y}}}$ is bounded for any real ${\delta }^{\prime }>1$. Indeed, since $\zeta (z)$ is analytic for $\left|z\right|<e^{-h}$, this implies that $\zeta (e^{-h{\delta }^{\prime }})$ converges. From (2),

$$\begin{array}{cc}\hfill \zeta (e^{-h{\delta }^{\prime }})& ={\displaystyle \prod _{\tau }}\frac{1}{1-e^{-h{\delta }^{\prime }\left|\tau \right|}}\hfill \\ & \ge {\displaystyle \prod _{\begin{array}{c}\tau \\ \left|\tau \right|\le y\end{array}}}\frac{1}{1-e^{-h{\delta }^{\prime }\left|\tau \right|}}\hfill \\ & \ge {\displaystyle \prod _{\begin{array}{c}\tau \\ \left|\tau \right|\le y\end{array}}}\left(1+e^{-h{\delta }^{\prime }\left|\tau \right|}\right)\hfill \\ & \ge {\left(1+e^{-h{\delta }^{\prime }y}\right)}^{\tilde{\pi }(y)}\hfill \\ & \ge 1+\frac{\tilde{\pi }(y)}{e^{h{\delta }^{\prime }y}}\hfill \\ & >\frac{\tilde{\pi }(y)}{e^{h{\delta }^{\prime }y}}.\hfill \end{array}$$

Furthermore, from (9), it is easy to see that ${\displaystyle \frac{e^{hx}}{\psi (x)}}$ is also bounded.

Now, choose ${\delta }^{\prime }\in (1,\delta )$. Observe that

$$\begin{array}{c}\hfill \frac{x·\tilde{\pi }(y)}{\psi (x)}=\frac{\delta y}{e^{h(\delta -{\delta }^{\prime })y}}·\frac{\tilde{\pi }(y)}{e^{h{\delta }^{\prime }y}}·\frac{e^{hx}}{\psi (x)}.\end{array}$$

Since ${\displaystyle \frac{\tilde{\pi }(y)}{e^{h{\delta }^{\prime }y}}}$ and ${\displaystyle \frac{e^{hx}}{\psi (x)}}$ are bounded, and

$${\displaystyle \underset{y\to \infty }{\lim }}\frac{\delta y}{e^{h(\delta -{\delta }^{\prime })y}}=0,$$

it is obtained that

$${\displaystyle \underset{x\to \infty }{\lim }}\frac{x·\tilde{\pi }(y)}{\psi (x)}=0.$$

Overall, together with (12), it is shown that

$${\displaystyle \underset{x\to \infty }{\lim \inf }}\frac{x·\pi (x)}{\psi (x)}\ge 1$$

and

$${\displaystyle \underset{x\to \infty }{\lim \sup }}\frac{x·\pi (x)}{\psi (x)}\le \delta .$$

Please note that $\delta$ can be chosen arbitrarily close to 1, so it can be deduced further that

$${\displaystyle \underset{x\to \infty }{\lim \sup }}\frac{x·\pi (x)}{\psi (x)}\le 1.$$

Hence,

$${\displaystyle \underset{x\to \infty }{\lim }}\frac{x·\pi (x)}{\psi (x)}=1$$

or equivalently,

$$\pi (x)\sim \frac{\psi (x)}{x}.$$

(13)

The desired result is obtained by combining (9) and (13).

(b)

We begin with proving the result for $\mathcal{M}(x)$. From (1) and (3), it can be shown that for $\left|z\right|<e^{-h}$,

$$\begin{array}{cc}\hfill \alpha (z)& =\exp \left({\displaystyle \sum _{n=1}^{\infty }}\frac{F(n)}{n}{z}^n\right)·\exp \left(\log {\left(1-e^{hp}{z}^p\right)}^m\right)\hfill \\ & =\exp \left({\displaystyle \sum _{n=1}^{\infty }}\frac{F(n)}{n}{z}^n-m{\displaystyle \sum _{n=1}^{\infty }}\frac{e^{hpn}{z}^{pn}}{n}\right)\hfill \\ & =\exp \left({\displaystyle \sum _{n=1}^{\infty }}\frac{c(n)}{n}{z}^n\right)\hfill \end{array}$$

where $c(n)$ is given in (5). Recall that if a power series converges in an open disc, then it is analytic in the same disc (see [17,18]). Please note that the series ${\displaystyle {\displaystyle \sum _{n=1}^{\infty }}c(n)z^n}$ in (6) is analytic for $\left|z\right|<R{e}^{-h}$, and so is the series ${\displaystyle {\displaystyle \sum _{n=1}^{\infty }}{\displaystyle \frac{c(n)}{n}}{z}^n}$ by comparison.

Since any analytic function is continuous (see [17,18]), it is obtained that

$$\begin{array}{cc}\hfill \alpha (e^{-h})& ={\displaystyle \underset{\begin{array}{c}z\to e^{-h}\\ \left|z\right|<e^{-h}\end{array}}{\lim }}\alpha (z)\hfill \\ & ={\displaystyle \underset{\begin{array}{c}z\to e^{-h}\\ \left|z\right|<e^{-h}\end{array}}{\lim }}\exp \left({\displaystyle \sum _{n=1}^{\infty }}\frac{c(n)}{n}{z}^n\right)\hfill \\ & =\exp \left({\displaystyle \sum _{n=1}^{\infty }}\frac{c(n)}{n}{e}^{-hn}\right).\hfill \end{array}$$

Since $\alpha (e^{-h})>0$, for any $x\in \mathbb{N}$,

$$\begin{array}{cc}\hfill \log \alpha (e^{-h})& ={\displaystyle \sum _{n=1}^{\infty }}\frac{c(n)}{n}{e}^{-hn}\hfill \\ & ={\displaystyle \sum _{n=1}^x}\frac{c(n)}{n}{e}^{-hn}+o(1)\hfill \\ & ={\displaystyle \sum _{n=1}^x}\frac{e^{-hn}}{n}F(n)-{\displaystyle \sum _{n=1}^{⌊\frac{x}{p}⌋}}\frac{e^{-hpn}}{pn}·mp{e}^{hpn}+o(1)\hfill \\ & ={\displaystyle \sum _{n=1}^x}\frac{e^{-hn}}{n}F(n)-m{\displaystyle \sum _{n=1}^{⌊\frac{x}{p}⌋}}\frac{1}{n}+o(1).\hfill \end{array}$$

(14)

Recall that for harmonic sum,

$${\displaystyle \sum _{n=1}^{⌊\frac{x}{p}⌋}}\frac{1}{n}=\log ⌊\frac{x}{p}⌋+\gamma +o(1)$$

where $\gamma$ is the Euler–Mascheroni constant (see [19]). Therefore, (14) can be written as

$$\log \alpha (e^{-h})={\displaystyle \sum _{n=1}^x}\frac{e^{-hn}}{n}F(n)-m\log ⌊\frac{x}{p}⌋-m\gamma +o(1).$$

(15)

Now, define

$$K(x)={\displaystyle \sum _{n=1}^x}\frac{e^{-hn}}{n}F(n)$$

for $x\in \mathbb{N}$. Observe that $K(x)$ can be expressed in terms of closed orbits as

$$K(x)={\displaystyle \sum _{\begin{array}{c}\tau ,n\\ n\left|\tau \right|\le x\end{array}}}\frac{e^{-hn\left|\tau \right|}}{n}.$$

Indeed, this is true by defining $k=n\left|\tau \right|$ and checking that

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\tau ,n\\ n\left|\tau \right|\le x\end{array}}}\frac{e^{-hn\left|\tau \right|}}{n}& ={\displaystyle \sum _{k=1}^x}\frac{e^{-hk}}{k}{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\mid k\end{array}}}\left|\tau \right|\hfill \\ & ={\displaystyle \sum _{k=1}^x}\frac{e^{-hk}}{k}F(k).\hfill \end{array}$$

Furthermore, for a closed orbit $\tau$, it contributes to the sum ${\displaystyle {\displaystyle \sum _{\begin{array}{c}\tau ,n\\ n\left|\tau \right|\le x\end{array}}}\frac{e^{-hn\left|\tau \right|}}{n}}$ for $n\in \left\{1,2,\dots ,⌊{\displaystyle \frac{x}{\left|\tau \right|}}⌋\right\}$. So,

$$K(x)={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}{\displaystyle \sum _{n=1}^{⌊\frac{x}{\left|\tau \right|}⌋}}\frac{e^{-hn\left|\tau \right|}}{n}.$$

(16)

Consider the sum

$$\begin{array}{c}\hfill {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right).\end{array}$$

Since $e^{-h}<1$, it can be written as

$$\begin{array}{c}\hfill {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}{\displaystyle \sum _{n=1}^{\infty }}\frac{e^{-hn\left|\tau \right|}}{n}.\end{array}$$

(17)

From (16) and (17), it is obtained that

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-K(x)& ={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}{\displaystyle \sum _{n=⌊\frac{x}{\left|\tau \right|}⌋+1}^{\infty }}\frac{e^{-hn\left|\tau \right|}}{n}\hfill \\ & \ge 0\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-K(x)& ={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}{\displaystyle \sum _{n=⌊\frac{x}{\left|\tau \right|}⌋+1}^{\infty }}\frac{e^{-hn\left|\tau \right|}}{n}\hfill \\ & \le {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{1}{⌊\frac{x}{\left|\tau \right|}⌋+1}{\displaystyle \sum _{n=⌊\frac{x}{\left|\tau \right|}⌋+1}^{\infty }}{e}^{-hn\left|\tau \right|}\hfill \\ & \le {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{\left|\tau \right|}{x}{\displaystyle \sum _{n=2}^{\infty }}{e}^{-hn\left|\tau \right|}\hfill \\ & =\frac{1}{x}{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{\left|\tau \right|}{e^{h\left|\tau \right|}(e^{h\left|\tau \right|}-1)}.\hfill \end{array}$$

(19)

We will prove that the sum in the last line in (19) converges as $x\to \infty$ by using Riemann–Stieltjes integral with respect to $\tilde{\pi }(x)$ (see [20]). We will also use the fact that

$$A·\frac{e^{hx}}{x}\le \tilde{\pi }(x)\le B·\frac{e^{hx}}{x}$$

(20)

for some positive constants A and B. This is derived from result in part (a). Now,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{\left|\tau \right|}{e^{h\left|\tau \right|}(e^{h\left|\tau \right|}-1)}& ={\displaystyle \sum _{n=1}^x}\frac{n}{e^{hn}(e^{hn}-1)}·{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|=n\end{array}}}1\hfill \\ & ={\int }_1^x\frac{t}{e^{ht}(e^{ht}-1)}d\left(\tilde{\pi }(t)\right)\hfill \\ & ={\left[\frac{t·\pi (t)}{e^{ht}(e^{ht}-1)}\right]}_1^x-{\int }_1^x\tilde{\pi }(t)·\frac{d}{dt}\left(\frac{t}{e^{ht}(e^{ht}-1)}\right)dt\hfill \\ & \le \frac{B}{e^{hx}-1}-A{\int }_1^x\frac{e^{ht}}{t}·\frac{d}{dt}\left(\frac{t}{e^{ht}(e^{ht}-1)}\right)dt\hfill \\ & =\frac{B-A}{e^{hx}-1}+A{\int }_1^x\frac{ht-1}{t(e^{ht}-1)}dt\hfill \\ & \le \frac{B-A}{e^{hx}-1}+hA{\int }_1^x\frac{1}{e^{ht}-1}dt\hfill \\ & =\frac{B-A}{e^{hx}-1}+A{\left[\log (1-e^{-ht})\right]}_1^x\hfill \\ & =\frac{B-A}{e^{hx}-1}+A\log \left(\frac{1-e^{-hx}}{1-e^{-h}}\right).\hfill \end{array}$$

(21)

The expression in the last line in (21) converges as $x\to \infty$, and so is the sum. By using (18), (19) and (21), it is obtained that

$${\displaystyle \underset{x\to \infty }{\lim }}\left({\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-K(x)\right)=0.$$

(22)

From (14) and (22), it is deduced that

$$\begin{array}{c}\hfill {\displaystyle \underset{x\to \infty }{\lim }}\left({\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-m\log ⌊\frac{x}{p}⌋-m\gamma -\log \alpha (e^{-h})\right)=0.\end{array}$$

(23)

The desired result for $\mathcal{M}(x)$ is obtained by applying exponent and arranging terms in (23).

Now, we will prove the result for $\mathcal{M}(x)$. Using (17) and similar calculation as above, it is obtained that

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{1}{e^{h\left|\tau \right|}}& ={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}{\displaystyle \sum _{n=2}^{\infty }}\frac{e^{-hn\left|\tau \right|}}{n}\hfill \\ & \ge 0\hfill \end{array}$$

(24)

and

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{1}{e^{h\left|\tau \right|}}& ={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}{\displaystyle \sum _{n=2}^{\infty }}\frac{e^{-hn\left|\tau \right|}}{n}\hfill \\ & \le \frac{1}{2}{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}{\displaystyle \sum _{n=2}^{\infty }}{e}^{-hn\left|\tau \right|}\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{1}{2e^{h\left|\tau \right|}\left(e^{h\left|\tau \right|}-1\right)}.\hfill \end{array}$$

(25)

The sum in the last line in (25) converges as $x\to \infty$ by using Riemann–Stieltjes integral with respect to $\tilde{\pi }(x)$. Indeed, it can be checked that

$${\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{1}{2e^{h\left|\tau \right|}\left(e^{h\left|\tau \right|}-1\right)}\le \frac{B-A}{2x\left(e^{hx}-1\right)}+\frac{hA}{2}{\int }_1^x\frac{1}{t\left(e^{ht}-1\right)}dt$$

where A and B are constants in (20), and the integral converges as $x\to \infty$ by integral test. The calculation is very similar to the previous one, so it is omitted here.

Overall, from (24) and (25), the sum

$${\displaystyle \sum _{\tau }}\left(\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-\frac{1}{e^{h\left|\tau \right|}}\right)$$

converges to a positive constant C. By using (23), it is obtained that

$$\begin{array}{cc}\hfill C& ={\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\left(\log \left(\frac{1}{1-e^{-h\left|\tau \right|}}\right)-\frac{1}{e^{h\left|\tau \right|}}\right)+o(1)\hfill \\ & =m\log ⌊\frac{x}{p}⌋+m\gamma +\log \alpha (e^{-h})-{\displaystyle \sum _{\begin{array}{c}\tau \\ \left|\tau \right|\le x\end{array}}}\frac{1}{e^{h\left|\tau \right|}}+o(1).\hfill \end{array}$$

(26)

The desired result for $\mathcal{M}(x)$ is obtained by arranging terms in (26). □

Remark 1.

Please note that (3) implies that

(i) 

the radius of convergence for$\zeta (z)$about the origin is$e^{-h}<1$, and

(ii) 

there is a pole of order m at$z={\omega }^k{e}^{-h}$, where$\omega =e^{\frac{2\pi i}{p}}$is the p^th root of unity and$k\in \{0,1,\dots ,p-1\}$.

For a given system, these two properties of its$\zeta (z)$can help us to determine the suitable function$\alpha (z)$and its region of analyticity$\left|z\right|<R{e}^{-h}$. We will demonstrate this later for a periodic-finite-type shift.

3. Periodic-Finite-Type Shifts

In this section, we describe the construction of a periodic-finite-type shift and some important properties such as its graph representation and zeta function. A periodic-finite-type shift is an example of shift spaces (see [21] for details).

3.1. Construction

Let $\mathcal{A}$ be a finite set of symbols. Define the shift map $\sigma :{\mathcal{A}}^{\mathbb{Z}}\to {\mathcal{A}}^{\mathbb{Z}}$ as follows: for $\mathbf{x}={(x_i)}_{i\in \mathbb{Z}}\in {\mathcal{A}}^{\mathbb{Z}}$, its image is given by $\sigma (\mathbf{x})={(x_{i+1})}_{i\in \mathbb{Z}}$.

The element $w=w_1{w}_2\dots w_k\in {\mathcal{A}}^k$ for some $k\in \mathbb{N}$ is called a word and the element $\mathbf{x}=\dots x_{-2}{x}_{-1}{x}_0{x}_1{x}_2\dots \in {\mathcal{A}}^{\mathbb{Z}}$ is called a point. w is said to occur in $\mathbf{x}$ if there exists $j\in \mathbb{Z}$ such that $x_j{x}_{j+1}\dots x_{j+k-1}=w_1{w}_2\dots w_k$. It is denoted as $w{\prec }_j\mathbf{x}$.

For some $t\in \mathbb{N}$, consider a list of finite subsets ${\mathcal{F}}_0,{\mathcal{F}}_1,\dots ,{\mathcal{F}}_{t-1}\subset {\cup }_{k=1}^{\infty }{\mathcal{A}}^k$. Define subset $\mathsf{\Sigma }\subseteq {\mathcal{A}}^{\mathbb{Z}}$ as follows: $\mathbf{x}\in \mathsf{\Sigma }$ if and only if there exists $r\in \{0,1,\dots ,t-1\}$ such that $w{\nprec }_s{\sigma }^r(\mathbf{x})$ for all $w\in {\mathcal{F}}_{s\mathrm{mod}t}$ and all $s\in \mathbb{Z}$. The pair $(\mathsf{\Sigma },\sigma {\upharpoonright }_{\mathsf{\Sigma }})$ is called a periodic-finite-type shift of period t.

Remark 2.

(i) 

For the sake of simplicity, the restricted map$\sigma {\upharpoonright }_{\mathsf{\Sigma }}$will be denoted simply as σ from now on.

(ii) 

For the sake of this paper, we call the integer r in the above definition as the shifting value of$\mathbf{x}$. Please note that r is not necessarily unique for each$\mathbf{x}$.

It is known from [16] that given a list of subsets ${\mathcal{F}}_0,{\mathcal{F}}_1,\dots ,{\mathcal{F}}_{t-1}$, we can construct a new list of subsets ${\mathcal{F}}_0^{\prime },{\mathcal{F}}_1^{\prime },\dots ,{\mathcal{F}}_{t-1}^{\prime }$ that gives the same periodic-finite-type shift such that

(i)

all words in ${\mathcal{F}}_0^{\prime }$ have the same length ℓ, and

(ii)

${\mathcal{F}}_1^{\prime }={\mathcal{F}}_2^{\prime }=\dots ={\mathcal{F}}_{t-1}^{\prime }=\varnothing$.

A periodic-finite-type shift defined by the list of subsets with those properties is said to be in its standard form. Without loss of generality, we assume that any periodic-finite-type shift is in its standard form from now on.

By definition, a shift of finite type is indeed a periodic-finite-type shift with period 1.

3.2. Graph Representation

A periodic-finite-type shift of period t can be represented by a labeled graph. Specifically, its graph $\mathcal{G}$ is a t-partite graph with sets of vertices ${\mathcal{V}}_0,{\mathcal{V}}_1,\dots ,{\mathcal{V}}_{t-1}$ such that

(i)

${\mathcal{V}}_0={\mathcal{A}}^{\ell }\backslash {\mathcal{F}}_0$ and ${\mathcal{V}}_1={\mathcal{V}}_2=\dots ={\mathcal{V}}_{t-1}={\mathcal{A}}^{\ell }$, and

(ii)

for $u=u_1{u}_2\dots u_{\ell }\in {\mathcal{V}}_i$ and $v=v_1{v}_2\dots v_{\ell }\in {\mathcal{V}}_{i+1\mathrm{mod}t}$ where $i\in \{0,1,\dots ,t-1\}$, there exists an edge from u to v with label $v_{\ell }$ if and only if $u_2{u}_3\dots u_{\ell }=v_1{v}_2\dots v_{\ell -1}$. In this case, u and v are said to overlap progressively.

This is called the Moision–Siegel representation [15].

Recall that a sofic shift is a shift space which can be represented as a labeled graph (see [21] for details). Therefore, a periodic-finite-type shift is indeed a sofic shift.

Recall that a graph G is said to be irreducible if for each pair of vertices u and v (not necessarily distinct), there exists a path from u to v. By Perron–Frobenius Theorem [22], its adjacency matrix $A(G)$ has a Perron eigenvalue ${\lambda }_{A(G)}$. Furthermore, a labeled graph G is said to be right-resolving if for each vertex, each outgoing edge has different label. From [21], the sofic shift represented by an irreducible right-resolving graph G has topology entropy $h=\log {\lambda }_{A(G)}$.

For a periodic-finite-type shift, its Moision–Siegel representation $\mathcal{G}$ is right-resolving. Therefore, if $\mathcal{G}$ is irreducible, then its topological entropy is

$$h=\log {\lambda }_{A(\mathcal{G})}.$$

Recall that a shift space is said to be irreducible if for any pair of words u and v occurring in some points, either $uv$ occurs in some point or there exists a word w such that $uwv$ occurs in some point. From [21], if a labeled graph representing a sofic shift is irreducible, then the sofic shift itself is irreducible. However, the converse is false. In fact, there exists a periodic-finite-type shift which is irreducible, but its Moision–Siegel representation is not irreducible. This is shown in the following example.

Example 1.

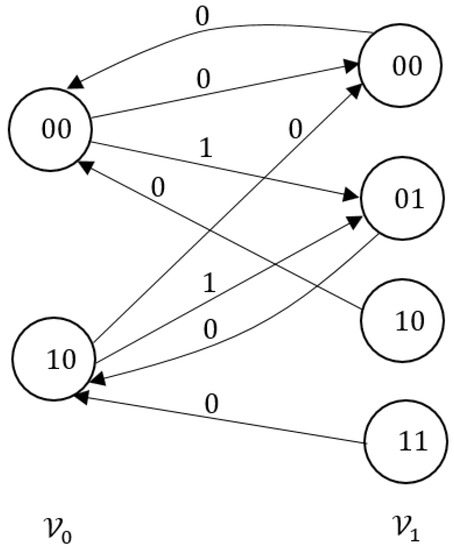
Consider the periodic-finite-type shift$(\mathsf{\Sigma },\sigma )$constructed from$\mathcal{A}=\{0,1\}$,${\mathcal{F}}_0=\{01,11\}$and${\mathcal{F}}_1=\varnothing$. Suppose that the words u and v occur in$\mathbf{x}\in \mathsf{\Sigma }$and$\mathbf{y}\in \mathsf{\Sigma }$respectively. Let r and s be the shifting value of$\mathbf{x}$and$\mathbf{y}$respectively. Let i be the position of the last symbol of u in$\mathbf{x}$, and j be the position of the first symbol of v in$\mathbf{y}$. Let${\mathbf{x}}^{-}$be the infinite string of symbols before u in$\mathbf{x}$, and${\mathbf{y}}^{+}$be the infinite string of symbols after v in$\mathbf{y}$.

Intuitively, the shifting value indicates whether the even or odd positions in the point are to be checked for the occurrence of forbidden words 01 and 11. If the value if 0, then the even positions are to be checked for those words. This is oppositely true if the value is 1. Furthermore, if the value is 0, then the symbol 1 will not occur at any odd position, since otherwise, the forbidden word 01 or 11 will occur at some even position. This is also oppositely true if the value is 1.

With the explanation above, it is easy to observe that if$r=i\mathrm{mod}2$, then the last symbol of u is either 0 or 1. However, if$r\ne i\mathrm{mod}2$, then the last symbol of u must be 0. This is similarly true for the first symbol of v.

Overall, we can check for the irreducibility of$(\mathsf{\Sigma },\sigma )$through the following cases:

(i) 

if$r=i\mathrm{mod}2$and$s=j\mathrm{mod}2$, then the word$u0v$occurs in the point${\mathbf{x}}^{-}u0v{\mathbf{y}}^{+}$;

(ii) 

if$r=i\mathrm{mod}2$and$s\ne j\mathrm{mod}2$, then the word$uv$occurs in the point${\mathbf{x}}^{-}uv{\mathbf{y}}^{+}$;

(iii) 

if$r\ne i\mathrm{mod}2$and$s=j\mathrm{mod}2$, then the word$uv$occurs in the point${\mathbf{x}}^{-}uv{\mathbf{y}}^{+}$;

(iv) 

if$r\ne i\mathrm{mod}2$and$s\ne j\mathrm{mod}2$, then the word$u0v$occurs in the point${\mathbf{x}}^{-}u0v{\mathbf{y}}^{+}$.

However, its Moision–Siegel representation is not irreducible because the vertices$10,11\in {\mathcal{V}}_1$do not have incoming edge. This is shown in Figure 1.

Figure 1. Moision–Siegel representation of| $(\mathsf{\Sigma },\sigma )$.

3.3. Zeta Function

Manada and Kashyap [16] obtained the zeta function of a periodic-finite-type shift of period t by using its Moision–Siegel representation.

Consider the set ${\{0,1\}}^t\backslash \left\{0^t\right\}$ and let $\chi ={\chi }_0{\chi }_1\dots {\chi }_{t-1}$ and ${\chi }^{\prime }$ be elements of this set. We can say that ${\chi }^{\prime }$ is cyclically equivalent to $\chi$ if there exists $q\in \{0,1,\dots ,t-1\}$ such that ${\chi }^{\prime }={\chi }_q{\chi }_{q+1}\dots {\chi }_{t-1}{\chi }_0{\chi }_1\dots {\chi }_{q-1}$. This relation partitions ${\{0,1\}}^t\backslash \left\{0^t\right\}$ into equivalent classes. Construct the set $\mathsf{\Omega }$ by taking one representative $\chi ={\chi }_0{\chi }_1\dots {\chi }_{t-1}$ from each class such that ${\chi }_0=1$.

For $\chi \in \mathsf{\Omega }$, let ${\chi }^{\ast }$ be the shortest word such that $\chi ={({\chi }^{\ast })}^k$ for some $k\in \mathbb{N}$. For convenience, denote $N_{\chi }=k$. Let $L_{\chi }$ be the length of ${\chi }^{\ast }$, and $W_{\chi }$ be the number of 1’s in ${\chi }^{\ast }$.

For $\chi \in \mathsf{\Omega }$ and its shortest word ${\chi }^{\ast }={\chi }_0{\chi }_1\dots {\chi }_{L_{\chi }-1}$, let ${\mathcal{G}}_{\chi }$ be the $L_{\chi }$-partite graph constructed as follows:

(i)

the sets of vertices ${\mathcal{V}}_0,{\mathcal{V}}_1,\dots ,{\mathcal{V}}_{L_{\chi }-1}$ are defined as

$${\mathcal{V}}_i=\left\{\begin{array}{cc}{\mathcal{A}}^{\ell }\hfill & \mathrm{if}{\chi }_i=0,\hfill \\ {\mathcal{A}}^{\ell }\backslash {\mathcal{F}}_0\hfill & \mathrm{if}{\chi }_i=1\hfill \end{array}\right.$$

for all $i\in \{0,1,\dots ,L_{\chi }-1\}$;

(ii)

for $u\in {\mathcal{V}}_i$ and $v\in {\mathcal{V}}_{i+1\mathrm{mod}{L}_{\chi }}$ where $i\in \{0,1,\dots ,L_{\chi }-1\}$, there exists an edge from u to v if and only if u and v overlap progressively.

Furthermore, let ${\mathcal{H}}_{\chi }$ be a graph constructed as follows:

(i)

the set of vertices is ${\mathcal{V}}_0={\mathcal{A}}^{\ell }\backslash {\mathcal{F}}_0$;

(ii)

for $u,v\in {\mathcal{V}}_0$, there exists an edge from u to v if and only if there is a path of length $L_{\chi }$ from u to v in ${\mathcal{G}}_{\chi }$.

Let $A({\mathcal{G}}_{\chi })$ and $A({\mathcal{H}}_{\chi })$ denote the adjacency matrix for ${\mathcal{G}}_{\chi }$ and ${\mathcal{H}}_{\chi }$ respectively.

With the notations above, the zeta function of a periodic-finite-type shift is given by

$$\zeta (z)={\displaystyle \prod _{\chi \in \mathsf{\Omega }}}{\left[\det \left(I-z·A({\mathcal{G}}_{\chi })\right)\right]}^{{(-1)}^{W_{\chi }}}\times {\displaystyle \prod _{\begin{array}{c}\chi \in \mathsf{\Omega }\\ N_{\chi }\mathrm{is}\mathrm{even},W_{\chi }\mathrm{is}\mathrm{odd}\end{array}}}\det \left(I-z^{2L_{\chi }}·A{({\mathcal{H}}_{\chi })}^2\right)$$

(27)

where I is the identity matrix.

The zeta function is a rational function, thus has a meromorphic extension to the entire complex plane.

4. Orbit Growth of a Periodic-Finite-Type Shift

In this section, we prove the orbit growth of a periodic-finite-type shift of period t by applying Theorem 1 to the zeta function in (27). For this, we need to obtain a region of analyticity beyond the radius of convergence such that its meromorphic extension is non-zero in this region.

From now on, we assume that our periodic-finite-type shift has irreducible Moision–Siegel representation $\mathcal{G}$, thus the shift itself is irreducible. Recall that for an irreducible graph, its graph period is the greatest common divisor of the lengths of cycles of any vertex. Since $\mathcal{G}$ is a t-partite graph, its graph period must be a multiple of t, i.e., $ct$ for some $c\in \mathbb{N}$.

For a square matrix $A_0$, observe that

$$\det \left(I-z·A_0\right)={\displaystyle \prod _{\mu }}(1-\mu z)$$

where $\mu$ runs through the eigenvalues of $A_0$. Therefore, the zeros and poles of the zeta function in (27) are determined by the eigenvalues of the adjacency matrices $A({\mathcal{G}}_{\chi })$ and $A({\mathcal{H}}_{\chi })$ for all $\chi \in \mathsf{\Omega }$.

Observe that for $\chi ={10}^{t-1}\in \mathsf{\Omega }$, the graph ${\mathcal{G}}_{\chi }$ is indeed the Moision–Siegel representation $\mathcal{G}$. Since $N_{\chi }=1$ is odd, there is no corresponding graph ${\mathcal{H}}_{\chi }$. Since $\mathcal{G}$ is irreducible with graph period $ct$, Perron–Frobenius Theorem [22] states that the Perron eigenvalue ${\lambda }_{A(\mathcal{G})}$ satisfies the following:

(i)

the only eigenvalues of modulus ${\lambda }_{A(\mathcal{G})}$ are of the form ${\omega }^k·{\lambda }_{A(\mathcal{G})}$ where $\omega =e^{\frac{2\pi i}{ct}}$ is $ct$^th root of unity for all $k\in \{0,1,\dots ,ct-1\}$. The eigenvalues are simple;

(ii)

if a non-negative matrix $A_0$ satisfies $A_0\le A(\mathcal{G})$, i.e., ${(A_0)}_{ij}\le {\left(A(\mathcal{G})\right)}_{ij}$ for every pair of indices i and j, then $\left|\mu \right|\le {\lambda }_{A(\mathcal{G})}$ for any eigenvalue $\mu$ of $A_0$. The equality holds if and only if $A_0=A(\mathcal{G})$.

Therefore, it is obtained that

$$\begin{array}{cc}\hfill \det \left(I-z·A(\mathcal{G})\right)& ={\displaystyle \prod _{k=0}^{ct-1}}(1-{\omega }^k·{\lambda }_{A(\mathcal{G})}·z)\times {\displaystyle \prod _{\begin{array}{c}\mu \\ \left|\mu \right|<{\lambda }_{A(\mathcal{G})}\end{array}}}(1-\mu z)\hfill \\ & =\left(1-{\lambda }_{A(\mathcal{G})}^{ct}·z^{ct}\right)\times {\displaystyle \prod _{\begin{array}{c}\mu \\ \left|\mu \right|<{\lambda }_{A(\mathcal{G})}\end{array}}}(1-\mu z)\hfill \end{array}$$

where $\mu$ runs through the eigenvalues of $A(\mathcal{G})$. Therefore, the zeta function in (27) has simple poles on the radius ${\lambda }_{A(\mathcal{G})}^{-1}$, which are contributed by $\chi ={10}^{t-1}\in \mathsf{\Omega }$. We will show that the zeros and other poles of the zeta function are located beyond the radius ${\lambda }_{A(\mathcal{G})}^{-1}$.

From now on, for a non-negative matrix $A_0$, we denote ${\lambda }_{A_0}$ as its spectral radius i.e., the largest modulus of the eigenvalues of $A_0$. In the next two lemmas, to avoid trivial case, we only consider a proper periodic-finite-type shift i.e., $t\ge 2$.

Lemma 1.

For$\chi \in \mathsf{\Omega }\backslash \left\{{10}^{t-1}\right\}$,

$${\lambda }_{A({\mathcal{G}}_{\chi })}<{\lambda }_{A(\mathcal{G})}.$$

Proof. 

For $\chi ={\chi }_0{\chi }_1\dots {\chi }_{t-1}$, let ${\mathcal{G}}_{\chi }^{\prime }$ be the graph constructed as follows:

(i)

the sets of vertices ${\mathcal{V}}_0^{\prime },{\mathcal{V}}_1^{\prime },\dots ,{\mathcal{V}}_{t-1}^{\prime }$ are defined as

$${\mathcal{V}}_i^{\prime }=\left\{\begin{array}{cc}{\mathcal{A}}^{\ell }\hfill & \mathrm{if}{\chi }_i=0,\hfill \\ {\mathcal{A}}^{\ell }\backslash {\mathcal{F}}_0\hfill & \mathrm{if}{\chi }_i=1\hfill \end{array}\right.$$

for all $i\in \{0,1,\dots ,t-1\}$;

(ii)

for $u\in {\mathcal{V}}_i^{\prime }$ and $v\in {\mathcal{V}}_{i+1\mathrm{mod}t}^{\prime }$ where $i\in \{0,1,\dots ,t-1\}$, there exists an edge from u to v if and only if u and v overlap progressively.

We will compare both graphs ${\mathcal{G}}_{\chi }$ and ${\mathcal{G}}_{\chi }^{\prime }$.

Denote $u_j^{(i)}$ to be a vertex from the set ${\mathcal{V}}_i$ in ${\mathcal{G}}_{\chi }$ for $i\in \{0,1,\dots ,L_{\chi }-1\}$, and j is simply the index for position (to be used in the notation of path later). We can use similar notation for ${\mathcal{G}}_{\chi }^{\prime }$ as well.

Let

$$\rho =u_0^{(k)}{u}_1^{(k+1\mathrm{mod}{L}_{\chi })}\dots u_l^{(k+l\mathrm{mod}{L}_{\chi })}$$

be a path of length $l\in \mathbb{N}$ in ${\mathcal{G}}_{\chi }$ for some $k\in \{0,1,\dots ,L_{\chi }-1\}$. Observe that we can associate $\rho$ with a path ${\rho }^{\prime }$ in ${\mathcal{G}}_{\chi }^{\prime }$ of the same length as

$${\rho }^{\prime }=u_0^{(k)}{u}_1^{(k+1\mathrm{mod}t)}\dots u_l^{(k+l\mathrm{mod}t)}.$$

This association is unique. Therefore, we can say that the set of paths in ${\mathcal{G}}_{\chi }$ is embedded into the set of paths in ${\mathcal{G}}_{\chi }^{\prime }$.

Let $P_l({\mathcal{G}}_{\chi })$ be the set of paths of length l in ${\mathcal{G}}_{\chi }$, and similarly $P_l({\mathcal{G}}_{\chi }^{\prime })$ for ${\mathcal{G}}_{\chi }^{\prime }$. Based on the properties of a shift of finite type constructed from a graph (see [22] for details), it is known that

$${\lambda }_{A({\mathcal{G}}_{\chi })}={\displaystyle \underset{l\to \infty }{\lim }}\sqrt[l+1]{\left|P_l({\mathcal{G}}_{\chi })\right|}.$$

This is similarly true for ${\lambda }_{A({\mathcal{G}}_{\chi }^{\prime })}$. Since $P_l({\mathcal{G}}_{\chi })$ is embedded into $P_l({\mathcal{G}}_{\chi }^{\prime })$ and so $\left|P_l({\mathcal{G}}_{\chi })\right|\le \left|P_l({\mathcal{G}}_{\chi }^{\prime })\right|$, we conclude that

$${\lambda }_{A({\mathcal{G}}_{\chi })}\le {\lambda }_{A({\mathcal{G}}_{\chi }^{\prime })}.$$

Now, observe that ${\mathcal{G}}_{\chi }^{\prime }$ is a proper subgraph of $\mathcal{G}$. Therefore, $A({\mathcal{G}}_{\chi }^{\prime })\le A(\mathcal{G})$ but $A({\mathcal{G}}_{\chi }^{\prime })\ne A(\mathcal{G})$. By Perron–Frobenius Theorem,

$${\lambda }_{A({\mathcal{G}}_{\chi }^{\prime })}<{\lambda }_{A(\mathcal{G})}.$$

The last two inequalities imply the desired result. □

Lemma 2.

For$\chi \in \mathsf{\Omega }\backslash \left\{{10}^{t-1}\right\}$,

$${\lambda }_{A({\mathcal{H}}_{\chi })}^{\frac{1}{L_{\chi }}}<{\lambda }_{A(\mathcal{G})}.$$

Proof. 

Let ${\mathcal{G}}_{\chi }^{L_{\chi }}$ be the graph constructed from the matrix $A{({\mathcal{G}}_{\chi })}^{L_{\chi }}$. Observe that ${\mathcal{H}}_{\chi }$ is a subgraph of ${\mathcal{G}}_{\chi }^{L_{\chi }}$. Using similar argument on the shift of finite type constructed from a graph as in Lemma 1, we obtain that

$${\lambda }_{A({\mathcal{H}}_{\chi })}\le {\lambda }_{A{({\mathcal{G}}_{\chi })}^{L_{\chi }}}={\lambda }_{A({\mathcal{G}}_{\chi })}^{L_{\chi }}.$$

The last inequality and Lemma 1 imply the desired result. □

Now, we are ready to prove our main theorem.

Theorem 2.

Let$(\mathsf{\Sigma },\sigma )$be a periodic-finite-type shift with period$t\in \mathbb{N}$. Suppose that its Moision–Siegel representation$\mathcal{G}$is irreducible with graph period$ct$for some$c\in \mathbb{N}$. Suppose further that the Perron eigenvalue λ for its adjacency matrix$A(\mathcal{G})$satisfies$\lambda >1$. Then,

(a) 

$$\pi (x)\sim ct·\frac{{\lambda }^{ct\left(⌊\frac{x}{ct}⌋+1\right)}}{({\lambda }^{ct}-1)x},$$

(b) 

$$\mathcal{M}(x)\sim \frac{e^{-\gamma }}{\alpha ({\lambda }^{-1})·⌊\frac{x}{ct}⌋}$$

where γ is Euler–Mascheroni constant and$\alpha (z)$is defined as in (28), and

$$\mathcal{M}(x)=\log ⌊\frac{x}{ct}⌋+\gamma +\log \alpha ({\lambda }^{-1})-C+o(1)$$

where C is a positive constant that can be specified as in (4).

Proof. 

Recall that the topological entropy of our periodic-finite-type shift is $h=\log {\lambda }_{A(\mathcal{G})}$ (or in this setting, $h=\log \lambda$). Based on Theorem 1, we need to obtain the function $\alpha (z)$ and a constant $R>1$ such that $\alpha (z)$ is analytic and non-zero for $\left|z\right|<R{\lambda }_{A(\mathcal{G})}^{-1}$.

We have the following observations:

(i)

for $\chi ={10}^{t-1}\in \mathsf{\Omega }$, the expression $\det \left(I-z·A(\mathcal{G})\right)$ gives rise to some simple poles at radius ${\lambda }_{A(\mathcal{G})}^{-1}$, and also other poles at ${\mu }^{-1}$ for other non-zero eigenvalues $\mu$ of $A(\mathcal{G})$. Since $\left|\mu \right|<{\lambda }_{A(\mathcal{G})}$ by definition of Perron eigenvalue, the other poles are located beyond the radius ${\lambda }_{A(\mathcal{G})}^{-1}$;

(ii)

for $\chi \in \mathsf{\Omega }\backslash \left\{{10}^{t-1}\right\}$, the expression $\det \left(I-z·A({\mathcal{G}}_{\chi })\right)$ gives rise to zeros or poles at ${\mu }^{-1}$ for every non-zero eigenvalue of $A({\mathcal{G}}_{\chi })$. However, Lemma 1 implies that these are located beyond the radius ${\lambda }_{A(\mathcal{G})}^{-1}$;

(iii)

for $\chi \in \mathsf{\Omega }\backslash \left\{{10}^{t-1}\right\}$, observe that

$$\det \left(I-z^{2L_{\chi }}·A{({\mathcal{H}}_{\chi })}^2\right)={\displaystyle \prod _{\mu }}(1-{\mu }^2{z}^{2L_{\chi }})$$

where $\mu$ runs through the eigenvalues of $A({\mathcal{H}}_{\chi })$. This gives rise to zeros at radius ${\mu }^{-\frac{1}{L_{\chi }}}$ for every eigenvalue of $A({\mathcal{H}}_{\chi })$. However, Lemma 2 implies that these zeros are located beyond the radius ${\lambda }_{A(\mathcal{G})}^{-1}$.

Now, set $R>1$ to be

$$R=\frac{1}{2}{\displaystyle \underset{z_0}{\min }}\left\{{\lambda }_{A(\mathcal{G})}\left|z_0\right|\right\}$$

where $z_0$ runs through zeros and poles of $\zeta (z)$ where $|z_0|>{\lambda }_{A(\mathcal{G})}^{-1}$, and define

$$\alpha (z)=\left(1-{\lambda }_{A(\mathcal{G})}^{ct}{z}^{ct}\right)·\zeta (z)$$

(28)

for $\left|z\right|<R{\lambda }_{A(\mathcal{G})}^{-1}$. Based on our observations above, the closest poles of $\zeta (z)$ are located in the radius ${\lambda }_{A(\mathcal{G})}^{-1}$, and other poles and zeros are beyond this radius. Therefore, $\alpha (z)$ is analytic and non-zero in this region. Since the conditions in Theorem 1 are satisfied, we obtain the orbit growth as desired. □

Remark 3.

In the theorem above, the assumption that$\lambda >1$is required to ensure that the shift has topological entropy$h>0$, as per condition of Theorem 1. The irreducibility of$\mathcal{G}$does not guarantee that$\lambda >1$. For example, the shift of finite type (hence, a periodic-finite-type shift) defined by$\mathcal{A}=\{0,1\}$and${\mathcal{F}}_0=\{00,11\}$has irreducible Moision–Siegel representation, but its Perron eigenvalue is$\lambda =1$.

5. Conclusions

In this paper, we have obtained the orbit growth of a periodic-finite-type shift via its zeta function as shown in Theorem 2. We can also deduce the orbit growth for a mixing shift of finite type (where $t=1$ and $c=1$) from Theorem 2, and this agrees with the results in [2,3,4]. Furthermore, this approach via zeta function works for any discrete system, as long as the zeta function satisfies the conditions stated in Theorem 1. With our demonstration here, we hope that this approach will be applied to obtain results on orbit growth for other systems in future study.