An Efficient Hybrid Genetic Approach for Solving the Two-Stage Supply Chain Network Design Problem with Fixed Costs

Abstract

This paper deals with a complex optimization problem, more specifically the two-stage transportation problem with fixed costs. In our investigated transportation problem, we are modeling a distribution network in a two-stage supply chain. The considered two-stage supply chain includes manufacturers, distribution centers, and customers, and its principal feature is that in addition to the variable transportation costs, we have fixed costs for the opening of the distribution centers, as well as associated with the routes. In this paper, we describe a different approach for solving the problem, which is an effective hybrid genetic algorithm. Our proposed hybrid genetic algorithm is constructed to fit the challenges of the investigated supply chain network design problem, and it is achieved by incorporating a linear programming optimization problem within the framework of a genetic algorithm. Our achieved computational results are compared with the existing solution approaches on a set of 150 benchmark instances from the literature and on a set of 50 new randomly generated instances of larger sizes. The outputs proved that we have developed a very competitive approach as compared to the methods that one can find in the literature.

1. Introduction

Supply chains (SCs) are considered to be worldwide networks in which the actors are: suppliers, manufacturer plants, distribution centers (DCs), retailers, and customers, and their principal objective is the fulfillment of the customer needs. In order to obtain an effective management of SC systems, researchers have emphasized the transportation system design, as it plays a significant role within the SC. A supply chain is represented usually as a multi-level structure, while its optimal design has been acknowledged to be an NP-hard problem. For more information on supply chain network design, we refer to Govindan et al. [1], Klibi et al. [2], Melo et al. [3], Wang [4], Dotoli [5,6], etc.

The goal of a transportation model is to minimize the total cost in transporting goods from a set of sources to a set of destinations, fulfilling the request of the destinations and using the capacities of the sources. In practical applications, fixed costs are associated with the arcs connecting sources to destinations, supplementary to the variable transportation costs, which are proportional to the amount of goods distributed along the arcs, resulting in a problem known in the literature as the fixed cost transportation problem (FCTP). Obviously, FCTP is a generalization of the classical transportation problem, and it was introduced by Balinski [7]. Guisewite and Pardalos [8] showed that the FCTP is $NP$-hard. For more information on the FCTP including a review of exact and heuristic approaches developed for solving the problem, we refer to Buson et al. [9].

This paper focuses on a variation of the fixed cost transportation problem in a supply chain network, namely the two-stage supply chain network design problem in which we consider two kinds of fixed costs: ones for opening the DCs and the others associated with the routes between manufacturers and DCs and between DCs and customers. In the form considered in our paper, the two-stage supply chain network design problem with fixed costs (TSSCNDP-FC) was defined by Hong et al. [10]. The same authors proposed an integer linear programming model of the problem, as well as a solution approach based on ant colony optimization tested on a set of 150 instances split into three classes: small, medium, and large sized instances. Recently, Sabo et al. [11] described a valid model of the problem and pointed out some inaccuracies regarding the paper published by Hong et al. [10].

Some other two-stage transportation problems with fixed costs considered in the literature and related to the investigated problem are:

• The two-stage transportation problem with fixed costs associated with the routes: Raj and Rajendran [12] proposed two scenarios of the two-stage transportation problem: the first one, called Scenario 1, takes into consideration fixed costs associated with the routes in addition to unit transportation costs and boundless capacities of the DCs, while the second one, called Scenario 2, considers the opening costs of the DCs in addition to unit transportation costs. The same authors developed a genetic algorithm (GA) with a particular coding scheme applicable for two-stage transportation problems, and also, they provided a set of 20 benchmark instances. Another GA dealing with the two-stage transportation problem with fixed charge associated with the routes from plants to customers through DCs was proposed by Jawahar and Balaji [13]. Pop et al. [14] proposed a hybrid method that combines a steady-state GA with a powerful local search procedure. Cosma et al. [15] described an efficient multi-start iterated local search (ILS) procedure for the total transportation cost minimization of the two-stage transportation problem, which begins with a feasible solution of the problem, makes use of a local search procedure with the goal of increasing the exploration, a perturbation mechanism, and a neighborhood operator with the scope of diversifying the search.
• The two-stage transportation problem with fixed costs for opening the distribution centers (DCs): This two-stage transportation problem was introduced by Gen et al. [16]. The present literature regarding the two-stage transportation problem with fixed costs for opening the DCs is rather limited. This optimization problem has also been investigated by Raj and Rajendran [12], who called it Scenario 2. Calvete et al. [17] proposed a hybrid evolutionary algorithm whose principal characteristic is the employment of a chromosome encoding that offers information about the DCs used within the transportation system. Cosma et al. [18] described an effective heuristic algorithm that reduces the solution search space to a subspace with a reasonable size, without losing optimal or sub-optimal solutions by means of a perturbation mechanism that allows the reconsideration of the feasible solutions that are discarded and that might lead to such solutions. Lately, Cosma et al. [19] proposed a matheuristic approach for solving the two-stage transportation problem with fixed costs associated with the routes by incorporating a linear programming optimization problem within the framework of a genetic algorithm.
• A particular case is where there exists only one plant manufacturer, and this version was considered by Molla et al. [20]. They proposed an integer linear programming mathematical model of the problem, and in addition, they described two solution approaches for solving it: a spanning tree-based genetic algorithm with a Prüfer number representation and an artificial immune algorithm. Some remarks regarding the mathematical model of the problem were published by El-Sherbiny [21]. Pintea et al. [22] proposed some hybrid algorithms, and Pintea and Pop [23] described an efficient hybrid approach combining the nearest neighbor search heuristic with a local search procedure for solving this particular two-stage transportation problem with fixed costs. Pop et al. [24] developed an innovative hybrid heuristic method achieved by combining a genetic algorithm based on a hash table coding of the individuals with a powerful local search procedure. Recently, Cosma et al. [25] described an effective hybrid heuristic approach that builds an initial feasible solution, then uses a local search procedure whose goal is to increase the exploration and a neighborhood structure for diversifying the search.
• Another two-stage transportation problem takes into consideration its effect on the environment by reducing the greenhouse gas emissions and was introduced by Santibanez-Gonzales [26] for dealing with a practical application from the public sector. For this version of the problem, Pintea et al. [27] described a set of hybrid heuristic methods, and Pop et al. [28] proposed an effective reverse distribution system for solving it.

As we can observe, the investigated supply chain network design problem generalizes the previously mentioned transportation problems by considering simultaneously two types of fixed costs: ones associated with the transportation routes and the others for opening the DCs in addition to the variable transportation costs, which are proportional to the amount of goods distributed along the arcs.

We organize the remainder of the paper as follows: in Section 2, we define the investigated two-stage supply chain problem with fixed costs and present a set of notations that will be used throughout the paper, and in Section 3, we describe a mixed integer linear formulation of the problem. The novel hybrid method, which incorporates a linear programming problem within the framework of a genetic algorithm, is presented in Section 4, and the comprehensive computational experiments with their outcomes are showcased and analyzed in Section 5. Finally, we conclude our work and discuss our plans for future work in Section 6.

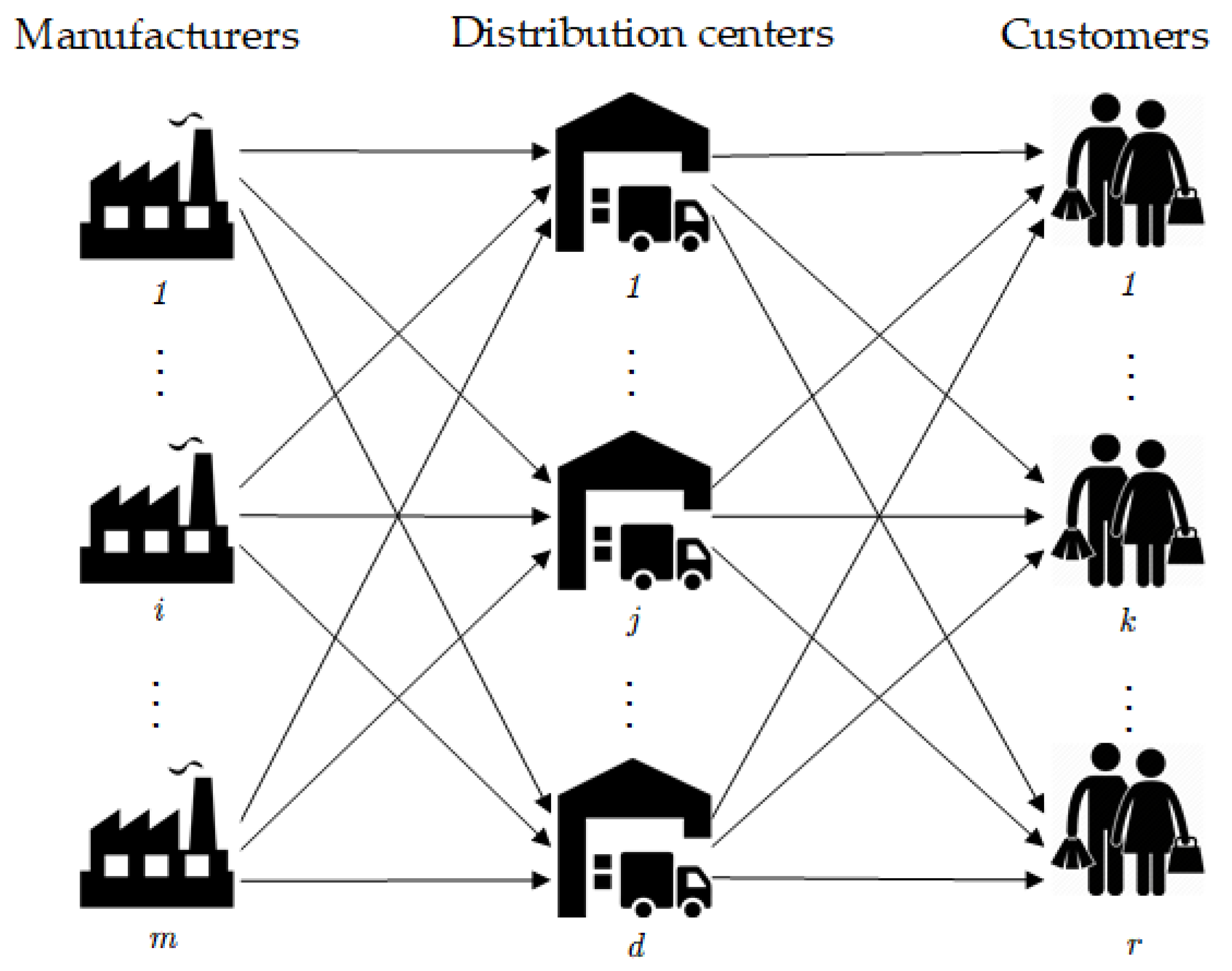
2. Definition of the Two-Stage Supply Chain Network Design Problem with Fixed Costs for Opening the Distribution Centers and Transportation Routes

In order to define and model the two-stage supply chain network design problem with fixed costs for opening the DCs and transportation routes, we consider a tripartite directed graph $G=(V,A)$ that consists of a set of vertices $V=V_1\cup V_2\cup V_3$ and a set of arcs $A=A_1\cup A_2$ defined as follows:

$$A_1=\left\{(i,j)\right|i\in V_{1}andj\in V_2\}\mathrm{and}{A}_2=\left\{(j,k)\right|j\in V_2\mathrm{and}k\in V_3\}$$

The entire set of nodes V is partitioned into three mutually exclusive sets corresponding to the set of manufacturers denoted by $V_1$ with $|V_1|=m$, the set of distribution centers denoted by $V_2$ with $|V_2|=d$, and the set of customers denoted by $V_3$ with $|V_3|=r$.

In addition, we suppose that:

• Every manufacturer $i\in V_1$ has $S_i$ units of supply; every distribution center $j\in V_2$ has a given capacity $S{C}_j$; each customer $k\in V_3$ has a demand $D_k$;
• Every manufacturer may transport to any of the q distribution centers at a transportation cost $c_{ij}^{{}^{\prime }}$ per unit from manufacturer $i\in V_1$ to DC $j\in V_2$;
• Every DC may transport to any of the r customers at a transportation cost $c_{jk}^{{}^{″}}$ per unit from DC $j\in V_2$ to customer $k\in V_3$;
• In order to open any of the DCs, we have to pay a given fixed cost denoted by $f_j$, and there exist fixed transportation costs from each manufacturer to each distribution center, denoted by $f_{ij}^{\prime }$, where $i\in V_1$ and $j\in V_2$, and from each DC to each customer, denoted by $f_{jk}^{″}$, where $j\in V_2$ and $k\in V_3$.

The aim of the two-stage supply chain network design problem with fixed costs associated with the transportation routes and for opening the DCs is to select the DCs and the routes to be opened and the corresponding transported quantities on these routes, such that the demands of the customers are satisfied, all transportation restrictions are fulfilled, and the total transportation costs are minimized.

Figure 1 illustrates the two-stage supply chain network design problem with fixed costs that we investigated.

3. A Valid Mathematical Model of the Two-Stage Supply Chain Network Design Problem with Fixed Costs

In this section, we present a valid mathematical formulation based on mixed integer programming of the investigated two-stage supply chain network design problem with fixed costs associated with the transportation routes and for opening the DCs.

We introduce the following decision variables:

• Linear variables:

  -

  $x_{\mathrm{if}}^{\prime }$, specifying the number of units shipped from plant i to the DC j;

  -

  $x_{jk}^{″}$, specifying the number of units shipped from DC j to the customer k;

• Binary variables:

  -

  $y_{\mathrm{if}}^{\prime }$, specifying if there are units transported from manufacturer plant i to the DC j ($y_{ij}^{\prime }=1$, if $x_{ij}^{\prime }>0$, and $y_{ij}^{\prime }=0$, otherwise);

  -

  $y_{jk}^{″}$, specifying if there are units transported from DC j to the customer k ($y_{jk}^{″}=1$, if $x_{jk}^{″}>0$, and $y_{jk}^{″}=0$, otherwise);

  -

  $z_j$, specifying if the DC j is open ($z_j=1$, if the DC j is open, and $z_j=0$, otherwise).

Then, the two-stage supply chain network design problem with fixed costs can be formulated as the following mixed integer problem, described by Sabo et al. [11]:

$$\begin{array}{ccc}\hfill Z=& min& \sum _{i=1}^m\sum _{j=1}^d(c_{\mathrm{if}}^{\prime }{x}_{\mathrm{if}}^{\prime }+f_{\mathrm{if}}^{\prime }{y}_{\mathrm{if}}^{\prime })+\sum _{j=1}^d\sum _{k=1}^r(c_{jk}^{″}{x}_{jk}^{″}+f_{jk}^{″}{y}_{jk}^{″})+\sum _{j=1}^d{f}_j{z}_j\hfill \end{array}$$

(1)

$$\begin{array}{cc}s.t.& \sum _{j=1}^d{x}_{ij}^{\prime }\le S_i,\forall i\in V_1\hfill \end{array}$$

(2)

$$\begin{array}{c}\sum _{j=1}^d{x}_{jk}^{″}=D_k,\forall k\in V_3\hfill \end{array}$$

(3)

$$\begin{array}{c}\sum _{i=1}^m{x}_{ij}^{\prime }=\sum _{k=1}^r{x}_{jk}^{″},\forall j\in V_2\hfill \end{array}$$

(4)

$$\begin{array}{c}\sum _{k=1}^r{x}_{jk}^{″}\le S{C}_j·z_j,\forall j\in V_2\hfill \end{array}$$

(5)

$$\begin{array}{c}{x}_{ij}^{\prime }\ge 0,\forall i\in V_1,\forall j\in V_2\hfill \end{array}$$

(6)

$$\begin{array}{c}{x}_{jk}^{″}\ge 0,\forall j\in V_2,\forall k\in V_3\hfill \end{array}$$

(7)

$$\begin{array}{c}{y}_{ij}^{\prime }\in \{0,1\},\forall i\in V_1,\forall j\in V_2\hfill \end{array}$$

(8)

$$\begin{array}{c}{y}_{jk}^{″}\in \{0,1\},\forall j\in V_2,\forall k\in V_3\hfill \end{array}$$

(9)

$$\begin{array}{c}{z}_j\in \{0,1\},\forall j\in V_2\hfill \end{array}$$

(10)

Our objective is to minimize the total transportation cost including the unit transportation costs and the fixed costs (for opening DC’s and associated with the routes). Constraint (2) guarantees that the capacity of the manufacturers is not surpassed. Constraint (3) guarantees that the customers demands are fulfilled. Constraint (4) is the flow conservation conditions and assures that the units collected by a given distribution center from manufacturers are equal to the units transported from that distribution center to the customers. Constraint (5) guarantees that the storage capacities of the distribution centers are not surpassed. Finally, the last constraint sets the ranges of the decision variables.

Hong et al. [10] described an illustrative example consisting of 2 manufacturing plants, 4 DCs, and 6 customers, whose characteristics are presented in Figure 2.

We solved this example using our proposed mixed integer programming formulation of the problem with CPLEX Version 12.7.0, and in Figure 3, we present the obtained optimal solution.

In Figure 3, we point out the capacities of the manufacturers, the storage capacities of the DCs, the demands of the customers, the transportation costs, and with red color, the fixed costs for opening the DCs and fixed costs associated with the selected transportation routes.

In order to obtain the optimal solution for this example, using our model by means of CPLEX only took 0.05 s and 30 iterations, in contrast to the model proposed by Hong et al. [10], which used the LINGO solver in order to find the optimal solution of a cost of 449,050 within 93 iterations, and their proposed ant colony approach, which provided an suboptimal solution cost of 476,138 within 0.24 s.

4. Description of the Novel Solution Approach

To solve TSSCNDP-FC, we propose a genetic algorithm, hybridized with a linear programming procedure. Genetic algorithms (GAs) were introduced by Holland [29] and are search metaheuristic techniques inspired by the Darwinian evolutionary theory based on the “survival of the fittest” concept. GAs have the capability to deliver “good” sub-optimal solutions within reasonable computational running times, making them very attractive for solving optimization problems characterized by a large feasible solution space. A genetic algorithm begins with a collection of feasible solutions, called the initial population, which are represented by chromosomes. Solutions from the current population are selected and employed to compose a new population. This is motivated by the belief that the newly created population will be better than the old one in terms of the quality of the solutions. The solutions that are picked to generate the offspring are selected according to their fitness; the more appropriate they are, the more opportunities they have to reproduce. This is repeated until some criteria (for example, the number of populations, improvement of the best solution, etc.) are fulfilled.

Our genetic algorithm builds different breeds of chromosomes that evolve separately from random populations, until evolution stagnates. Then, the breeds are merged together, hoping that the newly formed hybrid chromosomes will be better.

The operating principle of our hybrid genetic algorithm is shown in Figure 4, and the description of its blocks are described within this section.

The proposed GA makes use of an effective representation in which the genes of the chromosome represent the estimates of the flows corresponding to the optimal solution of the problem. Therefore, the chromosome contains two parts: the first one is an $m\times d$ matrix associated with the links from manufacturers to distribution centers, and the second one is a $d\times r$ matrix associated with the links from distribution centers to customers. We denote by ${\tilde{x}}_{ij}^{\prime }$ the gene corresponding to the link between manufacturer i and DC j and ${\tilde{x}}_{jk}^{″}$ the gene corresponding to the link between DC j and customer k. Initially, the chromosomes are generated randomly, with the only natural conditions that the estimates must not exceed the capacities of the manufactures, respectively the demands of the customers, i.e., ${\tilde{x}}_{ij}^{\prime }\in [0,S_i]$, for all $i\in V_1$ and $j\in V_2$, and ${\tilde{x}}_{jk}^{″}\in [0,D_k]$, for all $j\in V_2$ and $k\in V_3$.

It is unlikely that such a random chromosome would represent a correct estimate of a feasible solution of the two-stage supply chain network design problem with fixed costs for opening the DCs and associated with the routes. However, each chromosome has an associated feasible solution that can be effectively determined by solving the following linear programming problem, which is a simplified variant of the mathematical model of the TSSCNDP-FC:

$$\begin{array}{cc}min& \sum _{i=1}^m\sum _{j=1}^d{\tilde{c}}_{ij}^{\prime }{x}_{ij}^{\prime }+\sum _{j=1}^d\sum _{k=1}^r{\tilde{c}}_{jk}^{″}{x}_{jk}^{″}\hfill \\ s.t.& \left(2\right)-\left(7\right)\hfill \end{array}$$

(11)

where:

$${\tilde{c}}_{ij}^{\prime }=\{\begin{array}{c}{c}_{ij}^{\prime }+\frac{f_{ij}^{\prime }}{{\tilde{x}}_{ij}^{\prime }}+\frac{f_j}{{\tilde{x}}_j},\mathrm{if}{\tilde{x}}_{ij}^{\prime }\ne 0\\ c_{\mathrm{if}}^{\prime }+f_{\mathrm{if}}^{\prime },\mathrm{if}{\tilde{x}}_{\mathrm{if}}^{\prime }=0\mathrm{and}{\tilde{x}}_j\ne 0\\ c_{\mathrm{if}}^{\prime }+f_{\mathrm{if}}^{\prime }+f_i,\mathrm{if}{\tilde{x}}_{\mathrm{if}}^{\prime }=0\mathrm{and}{\tilde{x}}_j=0\end{array}$$

(12)

$${\tilde{c}}_{ij}^{″}=\{\begin{array}{c}{c}_{ij}^{″}+\frac{f_{ij}^{″}}{{\tilde{x}}_{ij}^{″}}+\frac{f_j}{{\tilde{x}}_j},\mathrm{if}{\tilde{x}}_{ij}^{″}\ne 0\\ c_{\mathrm{if}}^{″}+f_{\mathrm{if}}^{″},\mathrm{if}{\tilde{x}}_{\mathrm{if}}^{″}=0\mathrm{and}{\tilde{x}}_j\ne 0\\ c_{\mathrm{if}}^{″}+f_{\mathrm{if}}^{″}+f_i,\mathrm{if}{\tilde{x}}_{\mathrm{if}}^{″}=0\mathrm{and}{\tilde{x}}_j=0\end{array}$$

(13)

$${\tilde{x}}_j=\sum _{i=1}^m{\tilde{x}}_{ij}^{\prime }+\sum _{k=1}^r{\tilde{x}}_{ij}^{″}$$

(14)

The simplified variant of the mathematical model of the TSSCNDP-FC is actually a minimum cost flow problem for which there are well-known algorithms that solve it optimally in an efficient manner. We used the network simplex algorithm for solving this linear programming problem. The cost of the TSSCNDP-FC solution associated with the considered chromosome can be obtained using Relation (1) and the flows $x_{ij}^{\prime }$ and $x_{jk}^{″}$ determined by solving the simplified variant of the problem.

In order to boost the chances of discovering the optimal solution of the investigated supply chain problem with fixed costs, we developed a chromosome enhancement procedure shown in Algorithm 1, that processes all the chromosomes created throughout our genetic algorithm.

Algorithm 1: Procedure Chromosome enhancement

Each iteration of the loop in the chromosome enhancement procedure involves solving a simplified model of the TSSCNDP-FC, based on chromosome c (Step 3). The flows $x_{ij}^{\prime }$ and $x_{jk}^{″}$ determined in Step 3 are used in Step 4 to calculate the cost of the TSSCNDP-FC solution associated with chromosome c. If the solution has been improved, then the chromosome genes are updated in Step 8, using the streams determined in step 3. However, there is no guarantee that each iteration of the algorithm will enhance the TSSCNDP-FC solution associated with chromosome c. The algorithm stops when the solution worsens or a duplicate chromosome is reached. Finally, the genes of c are replaced with those of the last chromosome saved in Step 6. A chromosome $c_2$ is considered a duplicate of $c_1$ if the two chromosomes have the same corresponding TSSCNDP-FC solution.

For the newly created random chromosomes, the condition in Step 5 is changed to $\tilde{z}\le z$. This produces cleaner chromosomes in the initial population. Experiments showed that for the other chromosomes, it was better that the decision remained unchanged, because thus, there would be more diversity among the offspring.

In Figure 5, we illustrate the representation of an estimated chromosome associated with the example provided by Hong et al. [10], whose characteristics were presented in the previous section, where the entries of the matrix must not overcome the capacities of the manufacturers and the demands of the customers, and the representation of the chromosome after applying the chromosome enhancement procedure:

We remark that the chromosome $C_1$ correspond to an unfeasible solution, while the enhanced chromosome $P_1$ corresponds to a feasible solution of the problem.

For initializing the algorithm, an initial population of $2\times (m\times d+d\times r)$ enhanced chromosomes is generated by the random generator block; see Figure 4.

The admission block chooses the chromosomes that will form the current population (generation) from a pool of chromosomes that can be either from the current population or the offspring resulting from applying genetic operators (crossover and mutation). The size of each generation is kept constant at $(m\times d+d\times r)/2$ chromosomes. The admission block applies the following rules, which were adjusted based on computational experiments:

• The first two-thirds of the current population will be completed with the best chromosomes in the pool. At least half of these chromosomes must be newborn, i.e., not being part of the current population in the previous stages of evolution.
• The other chromosomes in the current population are randomly chosen from the pool.

Selection is the phase of a GA in which individual chromosomes are selected from a population for later breeding. Our selection block uses the tournament selection strategy for choosing the two chromosomes that will be selected to undergo crossover in order to form an offspring. The number of participants for each tournament was randomly settled between two and 10.

Crossover is a genetic operator that combines the genetic information of two parents in order to achieve new offspring. Our crossover block groups the chromosomes supplied by the selection block two-by-two. Then, with each pair, it forms an offspring. Each gene of the offspring is taken with the same probability either from the first parent or from the second one. The way our proposed crossover operator works is illustrated in Figure 6.

The chromosomes $C_1$ and $C_2$ in Figure 6 are two random chromosomes associated with the illustrative example presented in the previous section. By applying the chromosome enhancement procedure, they are transformed into two new chromosomes denoted by $P_1$ and $P_2$, which are feasible solutions of the TSSCNDP-FC. The offspring $O_1$ is obtained by applying the crossover operator to parents $P_1$ and $P_2$, and finally, the enhanced offspring $O_{1e}$ is obtained by applying the enhancement procedure to $O_1$. We can observe that the enhanced offspring $O_{1e}$ represents a better solution than the two feasible solutions corresponding to the parents $P_1$ and $P_2$. In Figure 6, we represent with red color the genes inherited by the offspring $O_1$ from each of the parents $P_1$ and $P_2$.

Mutation is a genetic operator whose main scope is to maintain the diversity of the chromosomes between consecutive generations of the GA. It is similar to biological mutation and usually happens with low probability. Our mutation operation was applied with a probability of 1% to each newborn chromosome. To accomplish this operation, a client k and a set of minimum 1 and maximum d DCs are randomly chosen. Then, all genes corresponding to the links between the k client and the chosen DCs are changed as follows: ${\tilde{x}}_{jk}^{″}\leftarrow randomvalue[1,D_k]$. Then, a DC j and a set of a minimum of one and a maximum of m manufacturers are randomly chosen. Then, all genes corresponding to the links between the d DCs and the chosen manufacturers are changed as follows: ${\tilde{x}}_{ij}^{\prime }\leftarrow randomvalue\in [1,S_i]$. The way the proposed mutation operator works is depicted in Figure 7.

The chromosome $O_2$ in Figure 7 represents the result of applying the mutation operator to the offspring $O_1$ presented in Figure 5. In this example, the mutation operator chooses the sixth client and a group of three DCS (1, 3, and 4), after which, it chooses the fourth DC and only one manufacturer (2). The enhanced offspring $O_{2e}$ is obtained by applying the enhancement procedure to $O_2$. This actually represents the optimal solution of the considered TSSCNDP-FC.

The genes of the chromosomes involved in the crossover and mutation examples are presented in Figure 8. The red entries in the representations of $P_1$ and $P_2$ are the genes inherited by the offspring $O_1$ and in $O_2$ are the genes that are changed by applying the mutation operator.

The evolution of a chromosome population ends when the best chromosome has not been improved in the last 25 generations. If a breed pool is available, then it is merged with the current population, using hybrid selection. The hybrid selection is different from the selection operation by the fact that it processes chromosomes from two different pools: the current population and the breed pool. One of the parent chromosomes is selected from the current population, and the other one is selected from the breed pool. The merging completes when the desired number of newborn chromosomes has been added to the offspring pool or when the desired number of crossover operations has been performed.

When the merging operation finishes, the breed pool is replaced with chromosomes taken from the current population, the existing breed pool, and the offspring. This operation is performed by the hybrid admission block, which applies the same rules as the admission block.

5. Discussion

This section is dedicated to the achieved computational results with the aim of assessing the effectiveness of our developed approach for solving the two-stage supply chain network design problem with fixed costs associated with the transportation routes and for opening the DCs.

We performed our computational experiments for solving the two-stage supply chain problem with fixed costs associated with the routes and for opening the distribution centers on a set of 200 instances randomly generated with varying characteristics in the same way as Hong et al. [10] generated. Since the test instances used by Hong et al. [10] could not be obtained in the literature, we generated new instances similar to those in Hong et al. [10]: the first 150 test instances classified into three problem classes: smaller, which consisted of 2 manufacturing plants, 5 DCs, and 10 customers, medium, which consisted of 4 manufacturing plants, 8 DCs, and 15 customers, and large, which consisted of 6 manufacturing plants, 10 DCs, and 20 customers. In addition, we generated randomly 50 test instances of the larger size consisting of 8 manufacturing plants, 12 distribution centers, and 25 customers, respectively 10 manufacturing plants, 15 distribution centers, and 30 customers. All the instances used in our computational experiments are available in [30].

We coded our algorithm in Java 8, and for each instance, we carried out 10 independent trials, on a PC with Intel Core i5-4590 3.3GHz, 4GB RAM, and the Windows 10 Education 64 bit operating system. To solve the proposed mixed integer programming formulation of the problem, we used CPLEX Version 12.7.0.

Table 1. Computational results achieved in the case of small sized instances.

Instance	CPLEX		Our Proposed Hybrid Genetic Algorithm						Improvement
	${\mathit{Z}}_{\mathit{opt}}$	${\mathit{T}}_{\mathit{cplex}}$	${\mathit{Z}}_{\mathit{min}}$	${\mathit{Z}}_{\mathit{max}}$	% $\mathit{gap}$	${\mathit{T}}_{\mathit{min}}$	${\mathit{T}}_{\mathit{max}}$	${\mathit{T}}_{\mathit{avg}.}$	Time (%)
1.	150,787	0.047	150,787	150,787	0.00	0.000	0.000	0.000	100.0
2.	156,654	0.047	156,654	156,654	0.00	0.000	0.000	0.000	100.0
3.	139,811	0.047	139,811	139,811	0.00	0.000	0.000	0.000	100.0
4.	128,859	0.047	128,859	128,859	0.00	0.000	0.000	0.000	100.0
5.	116,637	0.093	116,637	116,637	0.00	0.000	0.015	0.002	98.4
6.	87,694	0.078	87,694	87,694	0.00	0.000	0.016	0.002	97.9
7.	105,420	0.063	105,420	105,420	0.00	0.000	0.015	0.002	97.6
8.	120,077	0.063	120,077	120,077	0.00	0.000	0.015	0.002	97.6
9.	117,590	0.063	117,590	117,590	0.00	0.000	0.016	0.002	97.5
10.	131,233	0.063	131,233	131,233	0.00	0.000	0.016	0.002	97.5
11.	121,411	0.062	121,411	121,411	0.00	0.000	0.016	0.002	97.4
12.	149,525	0.109	149,525	149,525	0.00	0.000	0.016	0.003	97.1
13.	134,591	0.156	134,591	134,591	0.00	0.000	0.016	0.005	97.0
14.	105,047	0.047	105,047	105,047	0.00	0.000	0.015	0.002	96.8
15.	127,184	0.047	127,184	127,184	0.00	0.000	0.015	0.002	96.8
16.	122,630	0.094	122,630	122,630	0.00	0.000	0.016	0.003	96.7
17.	101,722	0.094	101,722	101,722	0.00	0.000	0.016	0.003	96.7
18.	132,593	0.047	132,593	132,593	0.00	0.000	0.016	0.002	96.6
19.	113,976	0.047	113,976	113,976	0.00	0.000	0.016	0.002	96.6
20.	129,436	0.172	129,436	129,436	0.00	0.000	0.016	0.006	96.4
21.	146,078	0.125	146,078	146,078	0.00	0.000	0.016	0.005	96.2
22.	119,627	0.079	119,627	119,627	0.00	0.000	0.016	0.003	96.1
23.	95,845	0.078	95,845	95,845	0.00	0.000	0.016	0.003	96.0
24.	104,190	0.078	104,190	104,190	0.00	0.000	0.016	0.003	95.9
25.	127,869	0.140	127,869	127,869	0.00	0.000	0.016	0.006	95.6
26.	100,451	0.171	100,451	100,451	0.00	0.000	0.016	0.008	95.4
27.	128,253	0.094	128,253	128,253	0.00	0.000	0.016	0.005	95.1
28.	150,379	0.125	150,379	150,379	0.00	0.000	0.016	0.006	95.0
29.	108,942	0.093	108,942	108,942	0.00	0.000	0.016	0.005	94.9
30.	137,955	0.062	137,955	137,955	0.00	0.000	0.016	0.003	94.8
31.	170,119	0.109	170,119	170,119	0.00	0.000	0.016	0.006	94.3
32.	126,603	0.079	126,603	126,603	0.00	0.000	0.016	0.005	94.2
33.	134,653	0.078	134,653	134,653	0.00	0.000	0.016	0.005	94.1
34.	142,559	0.078	142,559	142,559	0.00	0.000	0.016	0.005	94.0
35.	126,611	0.125	126,611	126,611	0.00	0.000	0.032	0.008	93.8
36.	116,869	0.047	116,869	116,869	0.00	0.000	0.015	0.003	93.6
37.	108,201	0.094	108,201	108,201	0.00	0.000	0.016	0.006	93.4
38.	129,005	0.047	129,005	129,005	0.00	0.000	0.016	0.003	93.2
39.	127,997	0.110	127,997	127,997	0.00	0.000	0.016	0.008	92.9
40.	104,891	0.109	104,891	104,891	0.00	0.000	0.047	0.008	92.8
41.	111,104	0.063	111,104	111,104	0.00	0.000	0.016	0.005	92.7
42.	108,001	0.062	108,001	108,001	0.00	0.000	0.016	0.005	92.6
43.	143,700	0.063	143,700	143,700	0.00	0.000	0.016	0.005	92.5
44.	138,510	0.078	138,510	138,510	0.00	0.000	0.016	0.006	92.1
45.	135,101	0.079	135,101	135,101	0.00	0.000	0.016	0.006	92.0
46.	129,854	0.078	129,854	129,854	0.00	0.000	0.016	0.006	91.9
47.	116,670	0.094	116,670	116,670	0.00	0.000	0.016	0.008	91.8
48.	141,467	0.047	141,467	141,467	0.00	0.000	0.016	0.005	90.2
49.	141,306	0.094	141,306	141,306	0.00	0.000	0.031	0.009	90.1
50.	125,550	0.062	125,550	125,550	0.00	0.000	0.016	0.006	90.0

,

Table 2. Computational results achieved in the case of medium sized instances.

Instance	CPLEX		Our Proposed Hybrid Genetic Algorithm						Improvement
	${\mathit{Z}}_{\mathit{opt}}$	${\mathit{T}}_{\mathit{cplex}}$	${\mathit{Z}}_{\mathit{min}}$	${\mathit{Z}}_{\mathit{max}}$	% $\mathit{gap}$	${\mathit{T}}_{\mathit{min}}$	${\mathit{T}}_{\mathit{max}}$	${\mathit{T}}_{\mathit{avg}.}$	Time (%)
1.	544,062	11.86	544,062	544,062	0.00	0.05	0.42	0.13	98.90
2.	552,793	3.44	552,793	552,793	0.00	0.05	0.13	0.09	97.43
3.	581,825	2.25	581,825	581,825	0.00	0.05	0.11	0.09	95.93
4.	558,047	3.66	558,047	558,047	0.00	0.05	0.62	0.17	95.43
5.	524,346	6.53	524,346	524,346	0.00	0.06	0.51	0.30	95.33
6.	536,344	3.00	536,344	536,344	0.00	0.05	0.65	0.15	95.08
7.	496,753	11.83	496,753	496,753	0.00	0.08	1.93	0.61	94.85
8.	632,867	5.94	632,867	632,867	0.00	0.06	1.29	0.34	94.20
9.	569,351	4.38	569,351	569,351	0.00	0.05	0.76	0.30	93.07
10.	584,386	2.47	584,386	584,386	0.00	0.05	0.61	0.19	92.14
11.	479,204	3.27	479,204	479,204	0.00	0.05	0.81	0.26	92.11
12.	573,488	1.39	573,488	573,488	0.00	0.06	0.42	0.11	91.80
13.	496,399	12.06	496,399	496,399	0.00	0.25	2.31	1.03	91.44
14.	507,962	4.20	507,962	507,962	0.00	0.08	1.94	0.38	90.99
15.	451,712	3.55	451,712	451,712	0.00	0.09	0.83	0.33	90.80
16.	439,677	10.66	439,677	439,677	0.00	0.05	3.89	0.99	90.68
17.	527,756	16.63	527,756	527,756	0.00	0.13	4.88	1.65	90.09
18.	512,029	3.88	512,029	512,029	0.00	0.11	1.11	0.39	90.04
19.	549,311	1.63	549,311	549,311	0.00	0.05	0.47	0.16	89.91
20.	495,912	6.81	495,912	495,912	0.00	0.08	1.94	0.69	89.83
21.	569,762	3.67	569,762	569,762	0.00	0.09	1.33	0.38	89.78
22.	546,127	11.19	546,127	546,127	0.00	0.06	3.52	1.19	89.40
23.	650,947	2.94	650,947	650,947	0.00	0.06	0.82	0.31	89.31
24.	625,285	2.48	625,285	625,285	0.00	0.06	0.54	0.27	89.08
25.	487,665	2.22	487,665	487,665	0.00	0.06	0.62	0.26	88.29
26.	465,159	1.61	465,159	465,159	0.00	0.06	0.64	0.19	88.25
27.	531,891	3.72	531,891	531,891	0.00	0.09	1.73	0.44	88.22
28.	525,336	1.86	525,336	525,336	0.00	0.06	0.51	0.22	88.21
29.	523,061	7.56	523,061	523,061	0.00	0.06	2.19	0.90	88.05
30.	549,113	3.06	549,113	549,113	0.00	0.08	1.10	0.38	87.45
31.	520,665	5.02	520,665	520,665	0.00	0.08	1.23	0.63	87.43
32.	516,235	6.03	516,235	516,235	0.00	0.42	1.25	0.77	87.16
33.	539,978	2.02	539,978	539,978	0.00	0.05	1.02	0.29	85.55
34.	476,725	2.25	476,725	476,725	0.00	0.06	0.56	0.34	85.10
35.	533,005	3.33	533,005	533,005	0.00	0.08	1.21	0.50	85.06
36.	572,411	2.25	572,411	572,411	0.00	0.05	1.12	0.34	84.81
37.	511,875	1.69	511,875	511,875	0.00	0.06	0.82	0.29	82.95
38.	484,094	2.55	484,094	484,094	0.00	0.06	1.55	0.44	82.67
39.	463,149	2.83	463,149	463,149	0.00	0.08	2.20	0.53	81.21
40.	610,328	2.36	610,328	610,328	0.00	0.06	0.93	0.45	80.93
41.	488,715	15.66	488,715	488,715	0.00	0.11	7.86	3.07	80.38
42.	524,444	2.58	524,444	524,444	0.00	0.03	1.39	0.52	80.02
43.	546,901	4.02	546,901	546,901	0.00	0.45	1.55	0.81	79.73
44.	546,789	2.02	546,789	546,789	0.00	0.09	2.03	0.42	79.16
45.	541,521	3.99	541,521	541,521	0.00	0.08	2.56	0.84	78.90
46.	458,557	4.28	458,557	458,557	0.00	0.08	2.90	0.92	78.44
47.	576,066	2.70	576,066	576,066	0.00	0.08	2.25	0.60	77.68
48.	566,729	5.08	566,729	566,729	0.00	0.16	2.76	1.14	77.55
49.	498,891	3.19	498,891	498,891	0.00	0.08	2.13	0.73	77.12
50.	541,012	2.36	541,012	541,012	0.00	0.09	2.32	0.58	75.47

,

Table 3. Computational results achieved in the case of large sized instances.

Instance	CPLEX		Our Proposed Hybrid Genetic Algorithm						Improvement
	${\mathit{Z}}_{\mathit{CPLEX}}$	${\mathit{T}}_{\mathit{CPLEX}}$	${\mathit{Z}}_{\mathit{min}}$	${\mathit{Z}}_{\mathit{max}}$	% $\mathit{gap}$	${\mathit{T}}_{\mathit{min}}$	${\mathit{T}}_{\mathit{max}}$	${\mathit{T}}_{\mathit{avg}.}$	Gap (%)
1.	1,498,462	>3600	1,492,959	1,498,462	0.04	7.58	179.72	70.54	0.367
2.	1,526,157	>3600	1,521,552	1,525,864	0.25	10.56	71.14	34.71	0.302
3.	1,229,762	>3600	1,226,059	1,228,900	0.16	0.73	53.58	12.97	0.301
4.	1,359,194	>3600	1,355,759	1,358,508	0.12	2.01	125.86	50.13	0.253
5.	1,506,789	>3600	1,503,253	1,506,426	0.08	0.69	171.29	54.24	0.235
6.	1,360,560	>3600	1,357,406	1,360,871	0.21	0.73	195.62	76.33	0.232
7.	1,373,481	>3600	1,370,305	1,370,305	0.00	0.33	118.06	32.24	0.231
8.	1,507,877	>3600	1,505,023	1,507,877	0.14	15.42	190.98	86.36	0.189
9.	1,313,779	>3600	1,311,341	1,313,779	0.07	3.95	187.48	56.39	0.186
10.	1,404,192	>3600	1,401,647	1,401,647	0.00	2.59	114.99	31.51	0.181
11.	1,439,014	>3600	1,436,511	1,436,511	0.00	0.59	29.36	12.94	0.174
12.	1,241,920	>3600	1,239,841	1,242,554	0.02	4.45	48.09	25.27	0.167
13.	1,182,028	>3600	1,180,055	1,182,359	0.08	5.36	185.81	67.03	0.167
14.	1,400,016	>3600	1,397,749	1,399,695	0.09	0.41	163.17	48.32	0.162
15.	1,452,499	>3600	1,450,224	1,453,131	0.04	0.58	199.54	79.30	0.157
16.	1,210,260	>3600	1,208,868	1,210,260	0.09	0.42	150.69	33.19	0.115
17.	1,172,705	>3600	1,171,392	1,173,070	0.06	11.33	192.29	92.86	0.112
18.	1,431,188	>3600	1,429,651	1,429,651	0.00	2.16	40.61	11.63	0.107
19.	1,391,275	>3600	1,389,998	1,389,998	0.00	8.58	175.24	113.26	0.092
20.	1,354,598	>3600	1,353,377	1,355,222	0.03	1.24	192.88	69.23	0.090
21.	1,401,338	>3600	1,400,090	1,400,090	0.00	4.80	97.97	34.90	0.089
22.	1,364,919	>3600	1,363,749	1,366,009	0.13	3.25	167.76	47.42	0.086
23.	1,425,663	>3600	1,424,598	1,425,663	0.04	0.59	71.56	20.01	0.075
24.	1,164,525	>3600	1,163,689	1,164,525	0.04	0.41	171.19	45.03	0.072
25.	1,485,811	>3600	1,484,745	1,485,595	0.02	1.17	91.43	37.72	0.072
26.	1,187,478	>3600	1,186,640	1,186,640	0.00	5.47	155.66	59.62	0.071
27.	1,493,211	>3600	1,492,236	1,493,511	0.01	28.94	191.48	106.28	0.065
28.	1,348,937	>3600	1,348,140	1,348,937	0.02	0.54	197.88	68.95	0.059
29.	1,306,728	>3600	1,305,967	1,305,967	0.00	5.26	167.72	48.31	0.058
30.	1,362,966	>3600	1,362,230	1,362,230	0.00	6.81	43.31	16.37	0.054
31.	1,432,828	>3600	1,432,060	1,432,060	0.00	14.73	163.45	58.88	0.054
32.	1,294,145	>3600	1,293,470	1,294,145	0.01	7.53	160.41	67.00	0.052
33.	1,367,135	>3600	1,366,494	1,367,135	0.03	8.97	185.43	58.01	0.047
34.	1,345,140	>3600	1,344,722	1,345,287	0.03	1.63	182.43	75.99	0.031
35.	1,444,708	>3600	1,444,283	1,444,708	0.01	2.39	125.75	33.11	0.029
36.	1,321,196	>3600	1,320,820	1,320,820	0.00	6.27	186.85	68.68	0.028
37.	1,488,631	>3600	1,488,259	1,488,631	0.02	18.45	196.41	99.94	0.025
38.	1,360,169	>3600	1,359,844	1,360,578	0.02	7.05	174.56	81.02	0.024
39.	1,459,280	>3600	1,458,980	1,458,980	0.00	4.57	62.32	28.49	0.021
40.	1,320,505	>3600	1,320,257	1,320,888	0.01	5.34	81.09	52.97	0.019
41.	1,515,575	>3600	1,515,301	1,515,301	0.00	0.39	29.87	12.10	0.018
42.	1,456,015	>3600	1,455,782	1,456,015	0.01	2.82	167.47	45.34	0.016
43.	1,558,119	>3600	1,557,980	1,557,980	0.00	0.39	64.55	17.19	0.009
44.	1,299,299	2071.50	1,299,299	1,299,299	0.00	3.83	81.39	24.67	0.000
45.	1,247,163	2096.72	1,247,163	1,247,163	0.00	1.32	120.01	31.05	0.000
46.	1,427,502	2686.28	1,427,502	1,427,502	0.00	2.21	94.79	25.36	0.000
47.	1,393,412	3595.30	1,393,412	1,393,412	0.00	1.85	12.64	6.86	0.000
48.	1,191,085	3507.41	1,191,085	1,191,085	0.00	0.27	5.60	1.76	0.000
49.	1,391,908	3344.05	1,391,908	1,391,908	0.00	0.30	16.08	4.50	0.000
50.	1,285,900	3348.83	1,285,900	1,285,900	0.00	0.61	14.58	4.94	0.000

,

Table 4. Computational results achieved in the case of larger sized instances (8-12-25).

Instance	CPLEX		Our Proposed Hybrid Genetic Algorithm						Improvement
	${\mathit{Z}}_{\mathit{CPLEX}}$	${\mathit{T}}_{\mathit{CPLEX}}$	${\mathit{Z}}_{\mathit{min}}$	${\mathit{Z}}_{\mathit{max}}$	% $\mathit{gap}$	${\mathit{T}}_{\mathit{min}}$	${\mathit{T}}_{\mathit{max}}$	${\mathit{T}}_{\mathit{avg}.}$	Gap (%)
1.	1,630,535	>3600	1,622,981	1,622,981	0.00	2.94	214.05	64.90	0.46
2.	1,585,431	>3600	1,581,579	1,585,261	0.11	28.37	460.47	187.29	0.24
3.	1,564,349	>3600	1,560,978	1,564,196	0.02	19.81	247.37	129.79	0.22
4.	1,688,457	>3600	1,686,019	1,688,457	0.02	16.48	444.18	255.88	0.14
5.	1,795,971	>3600	1,793,474	1,795,971	0.08	11.07	420.04	210.97	0.14
6.	1,693,447	>3600	1,691,203	1,694,066	0.06	136.12	457.29	254.00	0.13
7.	1,468,196	>3600	1,466,264	1,466,264	0.00	6.21	49.07	24.52	0.13
8.	1,670,941	>3600	1,668,943	1,669,456	0.003	6.49	294.80	122.20	0.12
9.	1,543,092	>3600	1,541,280	1,541,280	0.00	1.91	314.22	113.65	0.12
10.	1,850,860	>3600	1,848,732	1,848,732	0.00	25.34	295.75	159.96	0.11
11.	1,710,500	>3600	1,709,078	1,710,500	0.07	1.74	327.84	47.63	0.08
12.	1,616,695	>3600	1,615,417	1,615,417	0.00	13.73	494.86	122.64	0.08
13.	1,660,980	>3600	1,659,883	1,660,980	0.03	22.75	433.65	147.03	0.07
14.	1,631,768	>3600	1,631,244	1,631,244	0.00	14.33	99.50	38.02	0.03
15.	1,658,811	>3600	1,658,512	1,658,811	0.004	1.30	431.92	119.95	0.02
16.	1,583,688	>3600	1,583,449	1,583,688	0.01	6.33	289.25	119.27	0.02
17.	1,570,940	>3600	1,570,729	1,570,940	0.01	4.28	429.81	196.77	0.01
18.	1,778,786	>3600	1,778,647	1779,642	0.01	20.73	430.86	166.33	0.01
19.	1,671,547	>3600	1,671,547	1,671,547	0.00	8.60	412.75	135.36	0.00
20.	1,553,874	>3600	1,553,874	1,553,874	0.00	16.71	404.55	140.02	0.00
21.	1,618,396	>3600	1,618,396	1,618,396	0.00	2.03	120.94	25.57	0.00
22.	1,305,978	>3600	1,305,978	1,305,978	0.00	33.56	463.87	260.02	0.00
23.	1,682,622	>3600	1,682,622	1,682,622	0.00	16.56	117.56	59.01	0.00
24.	1,738,929	>3600	1,738,929	1,738,929	0.00	8.27	43.03	19.81	0.00
25.	1,539,218	>3600	1,539,218	1,539,218	0.00	73.29	398.56	215.22	0.00

and

Table 5. Computational results achieved in the case of larger sized instances (10-15-30).

Instance	CPLEX		Our Proposed Hybrid Genetic Algorithm						Improvement
	${\mathit{Z}}_{\mathit{CPLEX}}$	${\mathit{T}}_{\mathit{CPLEX}}$	${\mathit{Z}}_{\mathit{min}}$	${\mathit{Z}}_{\mathit{max}}$	%$\mathit{gap}$	${\mathit{T}}_{\mathit{min}}$	${\mathit{T}}_{\mathit{max}}$	${\mathit{T}}_{\mathit{avg}.}$	Gap (%)
1.	2,043,349	>3600	2,031,652	2,036,091	0.05	61.1	742.1	311.5	0.572
2.	2,054,648	>3600	2,046,819	2,052,230	0.09	153.3	800.4	479.5	0.381
3.	2,081,647	>3600	2,073,863	2,076,082	0.07	62.5	781.5	389.5	0.374
4.	1,928,963	>3600	1,923,043	1,926,361	0.08	67.5	782.5	463.1	0.307
5.	1,983,427	>3600	1,977,514	1,986,523	0.30	116.4	707.7	418.8	0.298
6.	1,904,794	>3600	1,899,391	1,905,847	0.18	186.9	797.8	471.1	0.284
7.	2,083,134	>3600	2,077,255	2,077,677	0.01	21.6	769.1	374.0	0.282
8.	2,054,765	>3600	2,049,041	2,050,452	0.02	106.7	763.7	22.9	0.279
9.	1,879,761	>3600	1,874,875	1,879,550	0.11	53.8	756.7	381.2	0.260
10.	2,115,385	>3600	2,110,377	2,112,099	0.04	78.4	601.4	408.8	0.237
11.	2,160,852	>3600	2,156,113	2,160,812	0.08	28.2	732.3	244.9	0.219
12.	2,151,335	>3600	2,147,165	2,151,624	0.09	162.8	696.6	400.6	0.194
13.	1,893,790	>3600	1,890,682	1,894,171	0.12	41.7	699.4	286.0	0.164
14.	2,116,378	>3600	2,113,212	2,118,729	0.18	59.4	788.1	359.1	0.150
15.	2,211,552	>3600	2,208,664	2,211,925	0.12	63.2	754.5	300.9	0.131
16.	2,234,741	>3600	2,232,117	2,234,741	0.07	45.5	685.2	338.9	0.117
17.	2,073,949	>3600	2,071,523	2,073,572	0.05	43.3	738.5	347.0	0.117
18.	2,243,637	>3600	2,241,336	2,243,637	0.05	14.4	767.2	426.0	0.103
19.	2,176,878	>3600	2,174,843	2,177,432	0.04	116.7	666.9	345.8	0.093
20.	2,112,460	>3600	2,110,653	2,113,982	0.07	170.9	648.1	383.6	0.086
21.	1,783,878	>3600	1,782,439	1,782,693	0.001	4.3	343.7	130.6	0.081
22.	1,910,476	>3600	1,909,206	1,913,753	0.05	16.8	647.0	279.0	0.066
23.	1,778,394	>3600	1,777,235	1,778,834	0.05	148.9	695.6	484.6	0.065
24.	2,101,223	>3600	2,099,976	2,103,072	0.06	24.7	764.0	415.6	0.059
25.	2,203,959	>3600	2,202,676	2,204,892	0.06	112.8	709.2	334.3	0.058

summarize the computational experiments performed for solving the considered instances using CPLEX 12.7.0 and the proposed hybrid solution approach.

In Table 1, we present the results obtained by CPLEX and the proposed hybrid genetic algorithm for solving small instances of the problem. The experimental study implied running each instance ten times. The first column displays the number of the instance; the next two columns contain the value of the optimal solution $Z_{opt}$ and the necessary computing time spent in solving the instances provided by CPLEX. The following six columns contain the results obtained by our hybrid genetic algorithm: the minimum and the maximum of the objective function achieved in the ten runs of each instance ($Z_{min}$ and $Z_{max}$), the percentage gap defined as $100\times (Z_{avg.}-Z_{min})/Z_{min}$, the minimum, maximum, and average computing times ($T_{min}$, $T_{max}$, and $T_{avg.}$) necessary for solving the instances. $Z_{avg.}$ is the average of the objective function achieved in the ten runs of each instance. The last column provides the improvement gap of the time necessary to deliver the optimal solution by the hybrid genetic algorithm in comparison to CPLEX. The improvement time gap is calculated as follows: $100\times (T_{CPLEX}-T_{avg.})/T_{CPLEX}$. The instances are ordered based on these improvements.

Analyzing the results presented in Table 1, we can remark that for all the considered small sized instances, CPLEX delivered the optimal solutions within a computational time ranging from 0.047 to 0.172 s. Our hybrid solution approach delivered as well the optimal solutions in all ten runs of each instance and the average computational time spent in solving the instances ranged from 0.000 to 0.009 s. The average improvement gap of the time spent to deliver the optimal solution by the hybrid genetic algorithm in comparison to CPLEX was greater than 95%.

In Table 2, we present the results obtained by CPLEX and the proposed hybrid genetic algorithm for solving medium instances of the problem. The columns of Table 2 are similar to those of Table 1, and we ordered the instances based on the improvement of the time necessary to deliver the optimal solution by the hybrid genetic algorithm in comparison to CPLEX.

Analyzing the results presented in Table 2, we can remark that for all the considered medium sized instances, CPLEX delivered the optimal solutions within a computational time ranging from 1.39 to 16.63 s. Our hybrid solution approach delivered as well the optimal solutions in all ten runs of each instance, i.e., $Z_{min}=Z_{max}=Z_{opt}$, and the average computational time spent in solving the instances ranged from 0.09 to 3.07 s. The average improvement gap of the time spent to deliver the optimal solution by the hybrid genetic algorithm in comparison to CPLEX was greater than 87%.

In Table 3, we present the results obtained by CPLEX and the proposed hybrid genetic algorithm for solving large instances of the problem. The first column displays the number of the instance, and the next two columns contain the value of the optimal solution $Z_{CPLEX}$ achieved by CPLEX and the necessary computing time spent in solving the instances provided by CPLEX when available, otherwise the solution determined by CPLEX when interrupting the run after 3600 s of computing time. The following six columns contain the results obtained by our hybrid genetic algorithm: the minimum and the maximum of the objective function achieved in the ten runs of each instance ($Z_{min}$ and $Z_{max}$), the percentage gap defined as $100\times (Z_{max}-Z_{min})/Z_{min}$, the minimum, maximum, and average computing times necessary for solving the instances. The last column provides the improvements of the solutions delivered by the hybrid genetic algorithm in comparison to the solutions achieved by CPLEX. The instances are ordered based on these improvements. The improvement gap is calculated as follows: $100\times (Z_{CPLEX}-Z_{min})/Z_{CPLEX}$. For the instances presented in Table 3, the running time of the algorithm was limited to 200 s.

Analyzing the computational results reported in Table 3, we can remark that for the first 43 instances, the best solution provided by our hybrid genetic algorithm improved the solution delivered by CPLEX within 3600 s, and the average computational time spent in solving the instances ranged from 11.63 to 113.26 s. The average improvement gap of the solutions delivered by the hybrid genetic algorithm in comparison to the solutions achieved by CPLEX was 0.114%. In the case of the last seven instances, CPLEX delivered the optimal solutions within a computational time ranging from 2071.50 to 3595.30 s. Our hybrid solution approach delivered as well the optimal solutions in all ten runs of each instance, i.e., $Z_{min}=Z_{max}=Z_{opt}$, but with much less computational time effort, and the average computational time spent in solving the instances ranged from 1.76 to 31.05 s. The improvement time gap ranged from 98.52% to 99.95%, and the average was greater than 99%. For 29 out of 50 instances, our proposed approach did not achieve the same solution in all ten runs, but we could observe that the average percentage gap between the minimum and the maximum of the objective function achieved ranged from 0.01% and 0.25%, a fact that proved the stability of our proposed solution approach.

In Table 4, we report the results obtained by CPLEX and the developed hybrid genetic algorithm for solving larger instances of the problem, namely with 8 manufacturing plants, 12 distribution centers, and 25 customers. The columns of Table 4 are similar to those of Table 3, and the instances are ordered based on the achieved improvement gaps. For the instances presented in Table 4, the running time of the algorithm was limited to 500 s.

Analyzing the computational results reported in Table 4, we can remark that for the first 18 instances, the best solution provided by our hybrid genetic algorithm improved the solution delivered by CPLEX within 3600 s, and the average computational time spent in solving the corresponding instances ranged from 24.52 to 255.88 s. In the case of the last seven instances, the solutions delivered by CPLEX within 3600 s were the same as the solutions achieved by our hybrid solution approach in all ten runs of each instance, but with much less computational time effort, and the average computational time spent in solving the instances ranged from 19.81 to 260.02 s. For 12 out of 25 instances, our proposed approach did not achieve the same solution in all ten runs, but we could observe that the average percentage gap between the minimum and the maximum of the objective function achieved ranged from 0.003% and 0.11%, a fact that showed the stability of our proposed solution approach.

In Table 5, we report the results obtained by CPLEX and the proposed hybrid genetic algorithm for solving larger instances of the problem, namely with 10 manufacturing plants, 15 distribution centers, and 30 customers. The columns of Table 5 are similar to those of Table 3, and the instances are ordered based on the achieved improvement gaps. For the instances presented in Table 5, the running time of the algorithm was limited to 800 s.

Analyzing the computational results reported in Table 5, we can remark that for all 25 instances, the best solution provided by our hybrid genetic algorithm improved the solution delivered by CPLEX within 3600 s, and the average computational time spent in solving the corresponding instances ranged from 22.9 to 484.6 s. In the case of these instances, our proposed approach did not achieve the same solution in all ten runs, but we can observe that the average percentage gap between the minimum and the maximum of the objective function achieved ranged from 0.001% and 0.3%, a fact that proved the stability of our proposed solution approach.

Overall, the results achieved by our hybrid genetic algorithm can be summarized as follows:

• In the case of small and medium sized instances, our algorithm delivered the optimal solution in all ten runs of each instance, but with much less computational time effort in comparison to CPLEX.
• As regards the 50 large sized instances, for seven of them, our hybrid algorithm delivered the optimal solution in all ten runs of each instance, but with much less computational time effort in comparison to CPLEX, and for the remaining instances, the best solution achieved by our algorithm improved the solution provided by CPLEX within 3600 s, but with much less computational time effort in comparison to CPLEX.
• In the case of the proposed 50 larger instances, the best solution provided by our hybrid genetic algorithm improved the solution delivered by CPLEX within 3600 s, and the average computational times spent in solving the corresponding instances were lower compared to CPLEX.
• We can remark that our developed solution outperformed in terms of the quality of the solutions and of computational times the ACO-based heuristic approach proposed by Hong et al. [10], which according to the previously mentioned authors, provided sub-optimal solutions with a gap of about $10\%$ on average from the optimal solutions.

6. Conclusions

In this paper, we investigated the two-stage supply chain network design problem in which we considered two types of fixed costs: ones for opening the DCs and the others associated with the routes. This optimization problem was introduced recently by Hong et al. [10], and it generalized the previously considered two-stage transportation problems.

The main goal of our paper was to describe an effective hybrid genetic algorithm for solving the two-stage transportation network design problem with fixed costs. Our hybrid algorithm was achieved by incorporating a linear programming optimization problem within the framework of a genetic algorithm. The method we proposed had certain important features, and here are some of these: the employment of an efficient representation in which the chromosome was generated in two stages: from an estimation of the flows to a feasible solution of the problem, the building of different breeds of chromosomes that evolved separately from random populations, until evolution stagnates, then the breeds were merged together, hoping that the newly formed hybrid chromosomes would be better.

We evaluated the effectiveness of the proposed solution approach on a set of 200 instances classified into four classes: small, medium, large, and larger sized instances. The first 150 instances were generated in the same way as Hong et al. [10] suggested, and the others were larger sized instances. The computational results that we obtained proved the efficiency of our developed hybrid genetic algorithm in yielding high quality solutions within reasonable running times, besides its superiority as compared to CPLEX and the other existing solution approaches from the literature.

It is our intention to continue our research and further improve the developed hybrid genetic algorithm through a combination with the local search methods. We intend to carry out a parallel implementation of the proposed algorithm, in order to fully benefit from the processing power of the new multicore processors and to generalize the TSSCNDP-FC model so that customers can be supplied directly by manufacturers and so that the distribution centers can also supply other distribution centers. We also plan to assess the generality and scalability of the solution approach that we suggested by testing it on even larger instances.