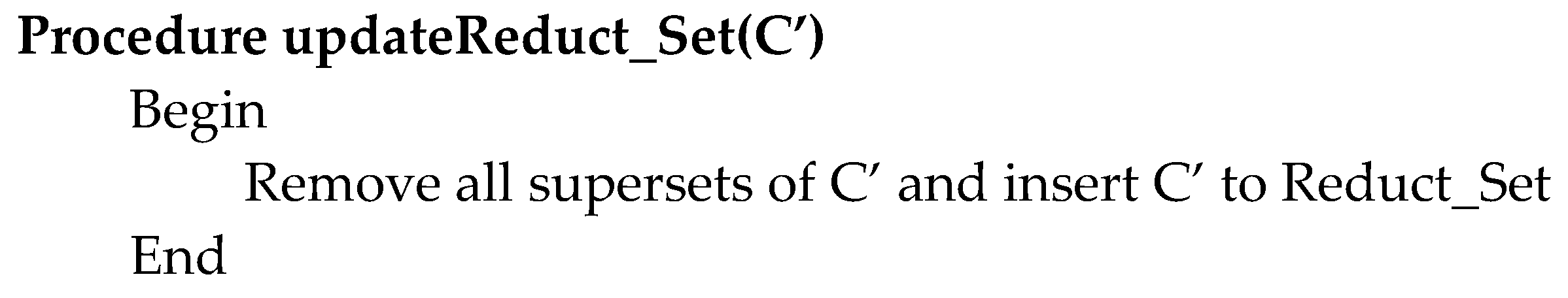Efficient Breadth-First Reduct Search

Abstract

This paper formulates the problem of determining all reducts of an information system as a graph search problem. The search space is represented in the form of a rooted graph. The proposed algorithm uses a breadth-first search strategy to search for all reducts starting from the graph root. It expands nodes in breadth-first order and uses a pruning rule to decrease the search space. It is mathematically shown that the proposed algorithm is both time and space efficient.

1. Introduction

In machine learning, feature selection is a process that selects relevant features used as the input in learning models. Its intention is to obtain optimal features so that the model can be used to accurately predict the output. Such optimal features are known as reducts in rough set theory. A reduct of an information system with conditional attributes and a decision attribute is defined as a minimal subset of a set of conditional attributes, in which its degree of dependency on the decision attribute is the same as the set of conditional attributes; (see [1] for a formal definition). A reduct could be any nonempty subset of the conditional attributes with the degree of dependency. Hence, the number of possible reducts is exponential with respect to the number of conditional attributes. With the aim of computational efficiency, a number of algorithms are proposed as a solution to finding a single reduct or multiple reducts without exhaustively investigating all of these possibilities. Therefore, many heuristic algorithms [2,3,4,5,6] and metaheuristic algorithms [7,8,9,10,11,12,13,14] have been proposed, as discussed in [15]. This class of algorithms is known as approximate algorithms. They give a single reduct or multiple reducts but not an exhausted list of reducts as the exact algorithms do. As the results of approximate algorithms requiring a parameter setting, they may produce different reducts in different runs. Moreover, they could create reducts that are not optimal. The exact algorithms are necessary if we are interested in computing the best reduct, with a given criterion, out of all reducts. However, finding all reducts involves generating and examining all possible reducts. In the literature, this can be done based on a discernibility matrix [16] and a power set tree [17,18]. Therefore, these exact algorithms have a time complexity exponential with respect to the number of conditional attributes.

In this work, we propose an exact algorithm to find all reducts without generating and examining all possible reducts. A simple representation of the possible reducts called a solution rooted graph is proposed. The rooted graph is formed by possible subsets of conditional attributes and their connections. Its root node is an n-subset attribute. The node is connected to its (n − 1)-subset nodes. Each (n − 1)-subset node is connected to its (n − 2)-subset nodes. This continues until reaching a 0-subset node. Hence, each node of the rooted graph except for a 0-subset node is a possible reduct. Furthermore, there are n node types based on their cardinalities in the search space: n-subset, (n − 1)-subset, (n − 2)-subset, …, and 1-subset. The proposed algorithm searches on the solution rooted graph with the breadth-first search. This work adopts the breadth-first search because it is complete, i.e., it assures finding all reducts. This algorithm still involves generating and examining all possible reducts from n-subset type to 1-subset type, type by type. We know that any node with a degree of dependency less than the graph root is not a reduct and its subsets are not reducts according to “the monotonic property of dependency”. Then, all of these subsets can be eliminated from consideration without losing any optimal reducts. The proposed algorithm is equipped with this rule of elimination as the pruning rule, which is the basis of its efficiency.

This paper is organized as follows. Section 2 briefly gives a sufficient background on reducts in terms of the degree of dependency. Section 3 describes the new efficient breadth-first reduct search algorithm. Analysis of the algorithm is given in Section 4. We conclude the paper in Section 5. An illustrative example is shown in Appendix A.

2. Basic Concepts

This section gives the background on reducts in terms of the degree of dependency. More details on reducts and rough sets can be found in [1].

Definition 1.

Any 4-tuple IS = <U, A = C ∪ D, V, f>; C ∩ D = Φ is called an information system; where U is a finite set of objects; A is a finite set of attributes; C is a finite set of conditional attributes; D is a finite set of decision attributes; V = ∪_{p ∈ A}Vp, where V_p is a domain of the attribute p, and f: U × A → V is a function called an information function f(x_i, q) for every q ∈ A and x_i ∈ U. An information system is denoted by IS = (U, A).

Example 1.

Let us consider the simple information system shown in

Table 1. Example dataset.

	C1	C2	C3	C4	C5	D
x1	1	2	1	3	1	2
x2	3	3	2	3	1	2
x3	3	3	2	3	1	1
x4	2	1	1	2	1	1
x5	2	2	1	1	1	2
x6	3	2	3	1	1	3
x7	2	2	3	1	1	3
x8	1	1	2	2	1	1
x9	3	3	3	1	1	3
x10	1	1	1	1	1	1

. We adopt this table to illustrate the basic concepts in the following examples.

From Table 1, let P be C₁. We have

U = {x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀},

A = {C₁, C₂, C₃, C₄, C₅, D},

VP = {1, 2, 3},

f(x₄, C₁) = {2},

and f(x₁₀, D) = {1}.

Definition 2.

Let R be any nonempty subset of A. An R-indiscernibility relation, denoted by IND(R), is defined as IND(R) = {(x_i, x_j): (x_i, x_j) ∈ U × U, a ∈ R, f (x_i, a) = f (x_j, a)}.

Note that if (x_i, x_j) ∈ IND(R), then objects x_i and x_j are called indiscernible with respect to R. The relation IND(R) is an equivalence relation. Therefore, it forms a partition U/IND(R); the equivalence classes of the R-indiscernibility relation.

Example 2.

Let R be {C₁, C₂, C₃, C₄, C₅}. We have

IND(R) = {(x₂, x₃)},

IND({C₁}) = {(x₁, x₈), (x₁, x₁₀), (x₈, x₁₀), (x₄, x₅), (x₄, x₇), (x₅, x₇), (x₂, x₃), (x₂, x₆), (x₂, x₉), (x₃, x₆), (x₃, x₉), (x₆, x₉)},

U/IND(R) = {{x₂, x₃}, {x₁}, {x₄}, {x₅}, {x₆}, {x₇}, {x₈}, {x₉}, {x₁₀}},

and U/IND({C₁}) = {{x₁, x₈, x₁₀}, {x₄, x₅, x₇}, {x₂, x₃, x₆, x₉}}.

Definition 3.

Let R be any nonempty subset of A and X be any nonempty subset of U. The R-lower approximation of X, denoted by RX, is defined as ∪ {Y ∈ U/IND(R): Y ⊆ X}. The R-lower approximation of X contains all objects with the known values of R that belong to X. The P-lower approximation of X contains all objects that with the knowledge of attributes P can be classified as belonging to concept X.

Example 3.

Let R be {C₁, C₂, C₃, C₄, C₅}. We have

U/IND (D) = {{x₁, x₂, x₅}, {x₃, x₄, x₈, x₁₀}, {x₆, x₇, x₉}},

X₁ = {x₁, x₂, x₅}, X₂ = {x₃, x₄, x₈, x₁₀}, X₃ = {x₆, x₇, x₉},

U/IND(R) = {{x₂, x₃}, {x₁}, {x₄}, {x₅}, {x₆}, {x₇}, {x₈}, {x₉}, {x₁₀}},

RX₁= {x₁} ∪ {x₅} = {x₁, x₅},

RX₂ = {x₄} ∪ {x₈} ∪ {x₁₀} = {x₄, x₈, x₁₀},

and RX₃ = {x₆} ∪ {x₇} ∪ {x₉} = {x₆, x₇, x₉}.

Definition 4.

Let R be any nonempty subset of A and X be any nonempty subset of U. Then, the positive region of the partition U/IND (D) with respect to R, denoted by POS_R (D), is defined as ${\cup }_{X\in U/IND \left(D\right)}$RX.

Example 4.

From Example 3, we have

POS_R(D) = RX₁ ∪ RX₂ ∪ RX₃ = {x₁, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀}.

Theorem 1

([19]).Let IS = (U, A = C∪ D). If B ⊆ C, then we have: POS_B (D) ⊆ POS_C (D).

Proof. 

For each x ∈ POS_B(D), there is y ∈ U/IND(D) such that [x]_IND(B) ⊆ y where [x]_IND(B) is the equivalence class of x with regard to equivalence relation IND(B). Since B ⊆ C, we have [x] _IND(C) ⊆ [x] _{IND (B)}. Thus, [x] _IND(C) ⊆ y, then x ∈ POS_C (D). Therefore, POS_B (D) ⊆ POS_C (D). □

Definition 5.

Let R be any nonempty subset of C. D depends on R in a degree k (0 ≤ k ≤ 1) where

k = γ_R (D) = |POS_R (D)|/|U|.

Example 5.

From Example 4, we have k = γ_R (D) = |POS_R(D)|/|U| = |{x₁, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀}|/|U| = 8/10 = 0.8. Then, D depends on R with degree 0.8.

Example 6.

Let R be {C₁, C₂}. We have

U/IND(D) = {{x₁, x₂, x₅}, {x₃, x₄, x₈, x₁₀}, { x₆, x₇, x₉}},

X₁ = {x₁, x₂, x₅}, X₂ = {x₃, x₄, x₈, x₁₀}, X₃ = {x₆, x₇, x₉},

U/IND(R) = {{x₂, x₃, x₉}, {x₁}, {x₄}, {x₅, x₇}, {x₆}, {x₈, x₁₀}},

RX₁ = {x₁} = {x₁},

RX₂ = {x₄} ∪ {x₈, x₁₀} = {x₄, x₈, x₁₀},

RX₃= {x₆} = {x₆},

POS_R(D) = RX₁ ∪ RX₂ ∪ RX₃ = {x₁, x₄, x₆, x₈, x₁₀},

and k = γ_R(D) = |{x₁, x₄, x₆, x₈, x₁₀}|/|U| = 5/10 = 0.5.

Definition 6.

Let C’ be any nonempty subset of C. C’ is a D-reduct (reduct with respect to D) of C, if C’ is a minimal subset of C such that γ_C(D) = γ_C’(D).

Example 7.

Let R be {C₁, C₂, C₃}. We have

U/IND(D) = {{x₁, x₂, x₅}, {x₃, x₄, x₈, x₁₀}, {x₆, x₇, x₉}},

X₁ = {x₁, x₂, x₅}, X₂ = {x₃, x₄, x₈, x₁₀}, X₃ = {x₆, x₇, x₉},

U/IND(R) = {{x₂, x₃}, {x₁}, {x₄}, {x₅}, {x₆}, {x₇}, {x₈}, {x₉}, {x₁₀}},

RX₁ = {x₁} ∪ {x₅} = {x₁, x₅},

RX₂ = {x₄} ∪ {x₈} ∪ {x₁₀} = {x₄, x₈, x₁₀},

and RX₃ = {x₆} ∪ {x₇} ∪ {x₉}= {x₆, x₇, x₉},

POS_R(D) = RX₁ ∪ RX₂ ∪ RX₃ = {x₁, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀},

and k = γ_R(D) = |{x₁, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀}|/|U| = 8/10 = 0.8.

Since each nonempty subset R’ ∈ {{C₁},{ C₂},{ C₃},{ C₁, C₂},{ C₁, C₃},{ C2, C3}} of R gives γ_R’(D) < γ_R(D), then R = {C₁, C₂, C₃} is a D-reduct of C.

Therefore, we find a reduct by obtaining a minimal subset of conditional attribute (C) so that the decision attributes (D) depend on it in the same degree as depending on C. A brute force approach to the problem is to check all subsets of C, with a minimal condition, satisfying the dependency of D on C (γ_C(D)). Each minimal subset obtained (reduct) requires checking all of its 2ⁿ − 2 subsets—excluding itself and an empty set; where n is its cardinality.

3. Efficient Breadth-First Reduct Search Algorithm

Let C = {C₁, C₂, C₃, …, C_n} be a conditional attribute of an information system IS(C, D). There are n + 1 types of subsets of C: n-subset, (n − 1)-subset, (n − 2)-subset, …, 1-subset, and 0-subset. Reducts could be any types of these subsets except for the 0-subset. The breadth-first reduct search algorithm orderly investigates the following 2ⁿ − 1 subsets, type by type: n-subset, (n − 1)-subset, (n − 2)-subset, …, and 1-subset. Thereafter, these subsets are referred to as reduct candidates. For each subset C’ in reduct candidates, if γ_C’(D) = γ_C(D), then C’ is a new element of the reduct set, and all of its supersets in the reduct set, if they exist, are eliminated. If γ_C’(D) < γ_C(D), all subsets of C’ are not reduct candidates. Each nonreduct C’ reduces 2^|c’| − 2 elements of the reduct candidates, according to Theorem 1. A reduct set is obtained once all reduct candidates are investigated.

The algorithm implements the idea above by using three data structures: Candidate Queue (the first-come first-served structure), Reduct_Set, and NonReduct_Set to maintain the reduct candidates, reducts, and nonreducts, respectively. Initially, it calculates k = γ_C(D), adds C to Candidate Queue, and sets both Reduct_Set and NonReduct_Set to an empty set. It loops to update the data of Candidate Queue, Reduct_Set, and NonReduct_Set if Candidate Queue is not empty. For each loop, it gets an element C’ from Candidate Queue and calculates γ_C’(D). If γ_C’(D) = k, then it adds C’ to Reduct_Set using the updateReduct_Set(C’) procedure. It also generates all (|C’| − 1)-subsets and insert them into Candidate Queue using the updateCandidate Queue(C’) procedure. If γ_C’(D) < k, it inserts C’ and all its subsets into NonReduct_Set using the updateNonReduct_Set(C’) procedure. The algorithm (in detail) is as shown in Figure 1.

There are three major procedures in our algorithm: updateReduct_Set(C’), updateCandidate Queue(C’), and updateNonReduct_Set(C’).

updateReduct_Set(C’)

Each element in Reduct_Set is not a reduct if we can find any of its subsets that are also reducts. Therefore, we have to test whether each reduct in Reduct_Set is a superset of a new reduct. If it is a superset, we eliminate it from Reduct_Set before putting the new reduct into it, to gain the reduct minimal condition. For example, let Reduct_Set be {{C₁, C₂, C₃, C₄, C₅}}, let C’ be {C₁, C₂, C₃}, and γ_C’(D) = γ_C(D); therefore, a new reduct is C’. However, there is a reduct {C₁, C₂, C₃, C₄, C₅} in Reduct_Set that is a superset of C’. We, therefore, remove {C₁, C₂, C₃, C₄, C₅} from the Reduct_Set and insert C’ into it. This gives the new Reduct_Set = {{C₁, C₂, C₃}}. The procedure (in detail) is as shown in Figure 2.

updateCandidate_Queue(C’)

The procedure generates all (|C’| − 1)-subsets from C’ and tests whether each is a reduct candidate. A reduct candidate is not a subset of any NonReduct_Set element. Such a candidate is appended into Candidate Queue. For example, let C’ be {C₁, C₂, C₃, C₄}, then a set of 3-subsets of C’ is {{C₁, C₂, C₃}, {C₁, C₂, C₄}, {C₂, C₃, C₄}, {C₁, C₃, C₄}}. If NonReduct_Set contains an element {C₂, C₃, C₄, C₅}, then {C₂, C₃, C₄} is not a reduct candidate since it is a subset of {C₂, C₃, C₄, C₅}. Therefore, {C₁, C₂, C₃}, {C₁, C₂, C₄}, and {C₁, C₃, C₄} are appended into Candidate Queue. The details of the procedure are shown in Figure 3.

updateNonReduct_Set(C’)

The property of the positive region as shown in Theorem 1 allows us to reduce the search space, i.e., the number of reduct candidates. We know that if C’ ⊆ C, then we have POS_C’(D) ⊆ POS_C(D). This infers that γ_C’(D) ≤ γ_C(D). In addition, if γ_C(D) = k (the degree of dependency of D on C in the original data), then C’ and its subsets are not reducts. All of the subsets can be eliminated from the candidates. For example, let C be a conditional attribute {C₁, C₂, C₃, C₄, C₅} with γ_C(D) = 0.8 and let C’ be {C₁, C₂, C₄} with γ_C’(D) = 0.6. Then, C’ and its subsets cannot be reducts according to Theorem 1. We, therefore, do not need to explore these subsets. We then remove all subsets of C’ from Candidate Queue. The proposed algorithm stores these candidates in NonReduct_Set using the procedure updateNonReduct_Set(C’). The procedure (in detail) is as shown in Figure 4.

4. Analysis of Algorithm

Let C = {C₁, C₂, C₃, …, C_n} be a conditional attribute of an IS(C, D). Additionally, let L_k be a set of k-subsets. We know that |L_k| = $\left(\begin{array}{c}n\\ k\end{array}\right)$ and ${\sum }_{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)$ = 2ⁿ. The algorithm searches for reducts from each L_k level by level starting with k = n, k = n − 1, and so on, until k = 1. Therefore, the size of its search space is ${\sum }_{k=1}^n\left(\begin{array}{c}n\\ k\end{array}\right)$ = 2ⁿ − 1. For the best case, C is the only element of Reduct_Set and each element of L_n-1 does not satisfy a reduct property. It tests C and all elements of L_n−1. The number of tests is 1 + $\left(\begin{array}{c}n\\ n-1\end{array}\right)$ = 1 + n. For the best-case scenario, the time complexity is O(n).

For the worst-case scenario, the algorithm gives a 1-subset reduct as an element of Reduct_Set. If all generated subsets satisfy a reduct property, the number of test is ${\sum }_{k=1}^n\left(\begin{array}{c}n\\ k\end{array}\right)$ = $\left(\begin{array}{c}n\\ 1\end{array}\right)$ + $\left(\begin{array}{c}n\\ 2\end{array}\right)$ + … + $\left(\begin{array}{c}n\\ n-2\end{array}\right)$ + $\left(\begin{array}{c}n\\ n-1\end{array}\right)$ + $\left(\begin{array}{c}n\\ n\end{array}\right)$. Therefore, the worst-case time complexity is O($\left(\begin{array}{c}n\\ 1\end{array}\right)$ + $\left(\begin{array}{c}n\\ 2\end{array}\right)$ + … + $\left(\begin{array}{c}n\\ n-2\end{array}\right)$ + $\left(\begin{array}{c}n\\ n-1\end{array}\right)$ + $\left(\begin{array}{c}n\\ n\end{array}\right)$) = O($\left(\begin{array}{c}n\\ m\end{array}\right)$), where m = ⌊med⌋ and med is the median of n, n − 1, n − 2, …, 1, 0. Since $\left(\begin{array}{c}n\\ m\end{array}\right)$ = n (n − 1)(n − 2)…(n − m − 1)/m!, then the worst-case time complexity is O(n^m). However, the algorithm applies a property of the positive region to reduce the search space once it finds a nonreduct subset. Each such l-subset could eliminate 2^l−1 candidate elements in L_k where k = l − 1, l − 2, …, 1. These nonreduct subsets are stored in NonReduct_Set. Any subset that is a subset of an element of NonReduct_Set is not included as an element of Candidate Queue.

In general, the space complexity of the breadth-first search algorithm is that all candidates remain in Candidate Queue. Therefore, it depends on the size of the largest Candidate Queue. For the best case, the space complexity is O(n). We observe that |L_m| is the largest among all subset levels; where m = ⌊med⌋ and med is the median of n, n − 1, n − 2, …, 1, 0. Since the algorithm generates and tests level by level, its worst-case space complexity is determined by O($\left(\begin{array}{c}n\\ m\end{array}\right)$) = O(n^m).

5. Conclusions

This paper presents a simple and efficient solution to the problem of finding all reducts in an information system. The problem is formulated as a search problem where the search space is a rooted graph. The rooted graph is a connected graph of possible reducts and their connections. Its root is a set of all conditional attributes. Each of its k-subset nodes is connected by (k − 1)-subset nodes where k is a non-negative integer not larger than the cardinality of the graph root. The proposed algorithm searches this graph using a breadth-first search strategy, starting from the graph root. It expands nodes in breadth-first order. With the monotonic property of the positive region (Theorem 1) as the pruning rule, it can prune all nonreduct nodes in the search space early. An illustrative example is given to demonstrate the algorithm. The algorithm’s efficiency is confirmed by the results of the algorithm analysis. Let n be the cardinality of conditional attributes, and m be the floor of the median of n, n − 1, n − 2, …, 1, 0; it is shown that both the time and space complexity of the algorithm are O (n) and O (n^m) for the best case and the worst case, respectively.