Exponential Stabilization of Linear Time-Varying Differential Equations with Uncertain Coefficients by Linear Stationary Feedback
Abstract
:1. Introduction
2. Preliminary Results
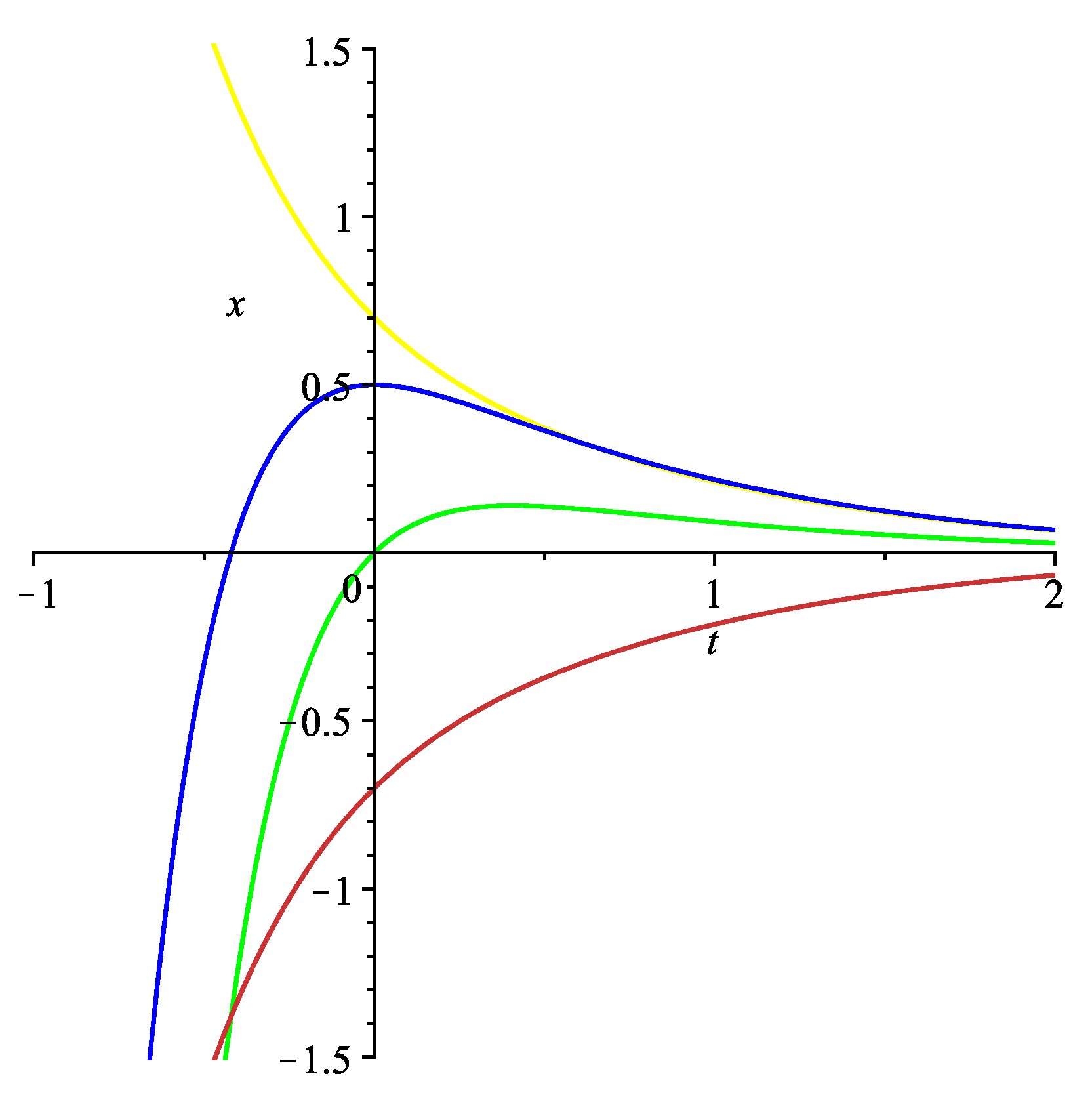
3. Time-Invariant Stabilization by Static State Feedback
4. Time-Invariant Stabilization by Static Output Feedback
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aeyels, D.; Peuteman, J. Uniform asymptotic stability of linear time-varying systems. In Open Problems in Mathematical Systems and Control Theory; Blondel, V., Sontag, E.D., Vidyasagar, M., Willems, J.C., Eds.; Springer: London, UK, 1999; pp. 1–5. [Google Scholar] [CrossRef]
- Ilchmann, A.; Owens, D.H.; Prätzel-Wolters, D. Sufficient conditions for stability of linear time-varying systems. Syst. Control Lett. 1987, 9, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Bylov, B.F.; Vinograd, R.E.; Grobman, D.M.; Nemytskii, V.V. Theory of Lyapunov Exponents; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Demidovich, B.P. Lectures on the Mathematical Stability Theory; Nauka: Moscow, Russia, 1967. [Google Scholar]
- Zhu, J.J. A necessary and sufficient stability criterion for linear time-varying systems. In Proceedings of the 28th Southeastern Symposium on System Theory, Baton Rouge, Louisiana, USA, 31 March–2 April 1996; pp. 115–119. [Google Scholar] [CrossRef]
- Levin, A.Y. Absolute nonoscillatory stability and related questions. St. Petersburg Math. J. 1993, 4, 149–161. [Google Scholar]
- Ragusa, M.A. Necessary and sufficient condition for a VMO function. Appl. Math. Comput. 2012, 218, 11952–11958. [Google Scholar] [CrossRef]
- Zhou, B. On asymptotic stability of linear time-varying systems. Automatica 2016, 68, 266–276. [Google Scholar] [CrossRef]
- Wan, J.-M. Explicit solution and stability of linear time-varying differential state space systems. Int. J. Control Autom. Syst. 2017, 15, 1553–1560. [Google Scholar] [CrossRef]
- Vrabel, R. A note on uniform exponential stability of linear periodic time-varying systems. IEEE Trans. Autom. Control 2020, 65, 1647–1651. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Tian, Y.; Lam, J. On construction of Lyapunov functions for scalar linear time-varying systems. Syst. Control Lett. 2020, 135, 104591. [Google Scholar] [CrossRef]
- Kharitonov, V.L. The asymptotic stability of the equilibrium state of a family of systems of linear differential equations. Differ. Uravn. 1978, 14, 2086–2088. [Google Scholar]
- Petersen, I.R. A stabilization algorithm for a class of uncertain linear systems. Syst. Control Lett. 1987, 8, 351–357. [Google Scholar] [CrossRef]
- Zhou, K.; Khargonekar, P.P. Robust stabilization of linear systems with norm-bounded time-varying uncertainty. Syst. Control Lett. 1988, 10, 17–20. [Google Scholar] [CrossRef]
- Khargonekar, P.P.; Petersen, I.R.; Zhou, K. Robust stabilization of uncertain linear systems: Quadratic stabilizability and H∞ control theory. IEEE Trans. Autom. Control 1990, 35, 356–361. [Google Scholar] [CrossRef]
- Xie, L.; de Souza, C.E. Robust H∞ control for linear systems with norm-bounded time-varying uncertainty. IEEE Trans. Autom. Control 1992, 37, 1188–1191. [Google Scholar] [CrossRef]
- Zhabko, A.P.; Kharitonov, V.L. Necessary and sufficient conditions for the stability of a linear family of polynomials. Autom. Remote Control 1994, 55, 1496–1503. [Google Scholar]
- Kharitonov, V.L. Robust stability analysis of time delay systems: A survey. Annu. Rev. Control 1999, 23, 185–196. [Google Scholar] [CrossRef]
- Sadabadi, M.S.; Peaucelle, D. From static output feedback to structured robust static output feedback: A survey. Annu. Rev. Control 2016, 42, 11–26. [Google Scholar] [CrossRef] [Green Version]
- Blanchini, F.; Colaneri, P. Uncertain systems: Time-varying versus time-invariant uncertainties. In Uncertainty in Complex Networked Systems. Systems and Control: Foundations and Applications; Başar, T., Ed.; Birkhäuser: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Carniato, L.A.; Carniato, A.A.; Teixeira, M.C.M.; Cardim, R.; Mainardi Junior, E.I.; Assunção, E. Output control of continuous-time uncertain switched linear systems via switched static output feedback. Int. J. Control 2018, 93, 1127–1146. [Google Scholar] [CrossRef] [Green Version]
- Gu, D.-K.; Liu, G.-P.; Duan, G.-R. Robust stability of uncertain second-order linear time-varying systems. J. Frankl. Instit. 2019, 356, 9881–9906. [Google Scholar] [CrossRef]
- Barmish, B.R. Necessary and sufficient conditions for quadratic stabilizability of an uncertain system. J. Optim. Theory Appl. 1985, 46, 399–408. [Google Scholar] [CrossRef]
- Xie, L.; Shishkin, S.; Fu, M. Piecewise Lyapunov functions for robust stability of linear time-varying systems. Syst. Control Lett. 1997, 31, 165–171. [Google Scholar] [CrossRef]
- Ramos, D.C.W.; Peres, P.L.D. An LMI approach to compute robust stability domains for uncertain linear systems. In Proceedings of the 2001 American Control Conference, Arlington, VA, USA, 25–27 June 2001. [Google Scholar] [CrossRef]
- Montagner, V.F.; Peres, P.L.D. A new LMI condition for the robust stability of linear time varying systems. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003. [Google Scholar] [CrossRef]
- Bliman, P.A. A convex approach to robust stability for linear systems with uncertain scalar parameters. SIAM J. Control Optim. 2004, 42, 2016–2042. [Google Scholar] [CrossRef] [Green Version]
- Geromel, J.C.; Colaneri, P. Robust stability of time varying polytopic systems. Syst. Control Lett. 2006, 55, 81–85. [Google Scholar] [CrossRef]
- Chesi, G.; Garulli, A.; Tesi, A.; Vicino, A. Robust stability of time-varying polytopic systems via parameter-dependent homogeneous Lyapunov functions. Automatica 2007, 43, 309–316. [Google Scholar] [CrossRef]
- Hu, T.; Blanchini, F. Non-conservative matrix inequality conditions for stability/stabilizability of linear differential inclusions. Automatica 2010, 46, 190–196. [Google Scholar] [CrossRef]
- Chesi, G. Sufficient and necessary LMI conditions for robust stability of rationally time-varying uncertain systems. IEEE Trans. Autom. Control 2013, 58, 1546–1551. [Google Scholar] [CrossRef] [Green Version]
- Gritli, H.; Belghith, S. New LMI conditions for static output feedback control of continuous-time linear systems with parametric uncertainties. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018. [Google Scholar] [CrossRef]
- Gritli, H.; Belghith, S.; Zemouche, A. LMI-based design of robust static output feedback controller for uncertain linear continuous systems. In Proceedings of the 2019 International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 19–22 March 2019. [Google Scholar] [CrossRef]
- Gelig, A.H.; Zuber, I.E. Invariant stabilization of classes of uncertain systems with delays. Autom. Remote Control 2011, 72, 1941–1950. [Google Scholar] [CrossRef]
- Zakharenkov, M.; Zuber, I.; Gelig, A. Stabilization of new classes of uncertain systems. IFAC-PapersOnLine 2015, 48, 1024–1027. [Google Scholar] [CrossRef]
- Gelig, A.H.; Zuber, I.E.; Zakharenkov, M.S. New classes of stabilizable uncertain systems. Autom. Remote Control 2016, 77, 1768–1780. [Google Scholar] [CrossRef]
- Gelig, A.K.; Zuber, I.E. Multidimensional output stabilization of a certain class of uncertain systems. Autom. Remote Control 2018, 79, 1545–1557. [Google Scholar] [CrossRef]
- Zaitsev, V.A. Modal control of a linear differential equation with incomplete feedback. Differ. Equ. 2003, 39, 145–148. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaitsev, V.; Kim, I. Exponential Stabilization of Linear Time-Varying Differential Equations with Uncertain Coefficients by Linear Stationary Feedback. Mathematics 2020, 8, 853. https://doi.org/10.3390/math8050853
Zaitsev V, Kim I. Exponential Stabilization of Linear Time-Varying Differential Equations with Uncertain Coefficients by Linear Stationary Feedback. Mathematics. 2020; 8(5):853. https://doi.org/10.3390/math8050853
Chicago/Turabian StyleZaitsev, Vasilii, and Inna Kim. 2020. "Exponential Stabilization of Linear Time-Varying Differential Equations with Uncertain Coefficients by Linear Stationary Feedback" Mathematics 8, no. 5: 853. https://doi.org/10.3390/math8050853




