Join Products K_2,3 + C_n

Abstract

The crossing number $\mathrm{cr}\left(G\right)$ of a graph G is the minimum number of edge crossings over all drawings of G in the plane. The main goal of the paper is to state the crossing number of the join product $K_{2,3}+C_n$ for the complete bipartite graph $K_{2,3}$, where $C_n$ is the cycle on n vertices. In the proofs, the idea of a minimum number of crossings between two distinct configurations in the various forms of arithmetic means will be extended. Finally, adding one more edge to the graph $K_{2,3}$, we also offer the crossing number of the join product of one other graph with the cycle $C_n$.

1. Introduction

For the first time, P. Turán described the brick factory problem. He was forced to work in a brickyard and his task was to push the bricks of the wagons along the line from the kiln to the storage location. The factory contained several furnaces and storage places, between which sidewalks passed through the floor. Turán found it difficult to move the wagon through the track passage, and in his mind he began to consider how the factory could be redesigned to minimize these crossings. Since then, the topic has steadily grown and research into the number of crosses has become one of the main areas of graph theory. This problem of reducing the number of crossings on the edges of graphs were studied in many areas.

The crossing number $\mathrm{cr}\left(G\right)$ of a simple graph G with the vertex set $V\left(G\right)$ and the edge set $E\left(G\right)$ is the minimum possible number of edge crossings in a drawing of G in the plane (for the definition of a drawing see [1].) It is easy to see that a drawing with minimum number of crossings (an optimal drawing) is always a good drawing, meaning that no edge crosses itself, no two edges cross more than once, and no two edges incident with the same vertex cross. Let D ($D\left(G\right)$) be a good drawing of the graph G. We denote the number of crossings in D by ${\mathrm{cr}}_D\left(G\right)$. Let $G_i$ and $G_j$ be edge-disjoint subgraphs of G. We denote the number of crossings between edges of $G_i$ and edges of $G_j$ by ${\mathrm{cr}}_D(G_i,G_j)$, and the number of crossings among edges of $G_i$ in D by ${\mathrm{cr}}_D\left(G_i\right)$. It is easy to see that for any three mutually edge-disjoint subgraphs $G_i$, $G_j$, and $G_k$ of G, the following equations hold:

$${\mathrm{cr}}_D(G_i\cup G_j)={\mathrm{cr}}_D\left(G_i\right)+{\mathrm{cr}}_D\left(G_j\right)+{\mathrm{cr}}_D(G_i,G_j),$$

$${\mathrm{cr}}_D(G_i\cup G_j,G_k)={\mathrm{cr}}_D(G_i,G_k)+{\mathrm{cr}}_D(G_j,G_k).$$

By Garey and Johnson [2] we already know that calculating the crossing number of a simple graph is an NP-complete problem. Recently, the exact values of the crossing numbers are known only for some special classes of graphs. In [3], Ho gave the characterization for a few multipartite graphs. So, the main purpose of this work is to extend the results concerning this topic for the complete bipartite graph $K_{2,3}$ on five vertices. In this paper we use definitions and notations of the crossing number theory presented by Klešč in [4]. In the proofs we will also use the Kleitman’s result [5] on the crossing numbers of the complete bipartite graphs. He estimated that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{with} \min \{m,n\}\le 6.$$

Again using Kleitman’s result [5], the exact values of the crossing numbers for the join product of two paths, the join product of two cycles, and also for the join product of a path and a cycle were proved in [4]. Further, some values for crossing numbers of $G+D_n$, $G+P_n$, and of $G+C_n$ for arbitrary graph G at most on four vertices are estimated in [6,7]. Let us note that the exact values for the crossing numbers of the join product G with $P_n$ and $C_n$ were also investigated for a few graphs G of order five and six in [1,8,9,10,11,12]. In all mentioned cases, the graph G contains usually at least one cycle and it is connected.

It is important to note that the methods in this paper will mostly use several combinatorial properties on cyclic permutations. If we place the graph $K_{2,3}$ on the surface of the sphere, from the topological point of view, the resulting number of crossings of $K_{2,3}+C_n$ does not matter which of the regions in the subdrawing of $K_{2,3}\cup T^i$ is unbounded, but on how the subgraph $T^i$ crosses or does not cross the edges of $K_{2,3}$ (the description of $T^i$ will be justified in Section 2). This representation of $T^i$ can best be described by the idea of a configuration utilizing some cyclic permutation on the pre-numbered vertices of the graph $K_{2,3}$. We introduce a new idea of various form of arithmetic means on a minimum number of crossings between two corresponding subgraphs $T^i$ and $T^j$. Certain parts of proofs can be also simplified with the help of software which generates all cyclic permutations of five elements due to Berežný and Buša [13].

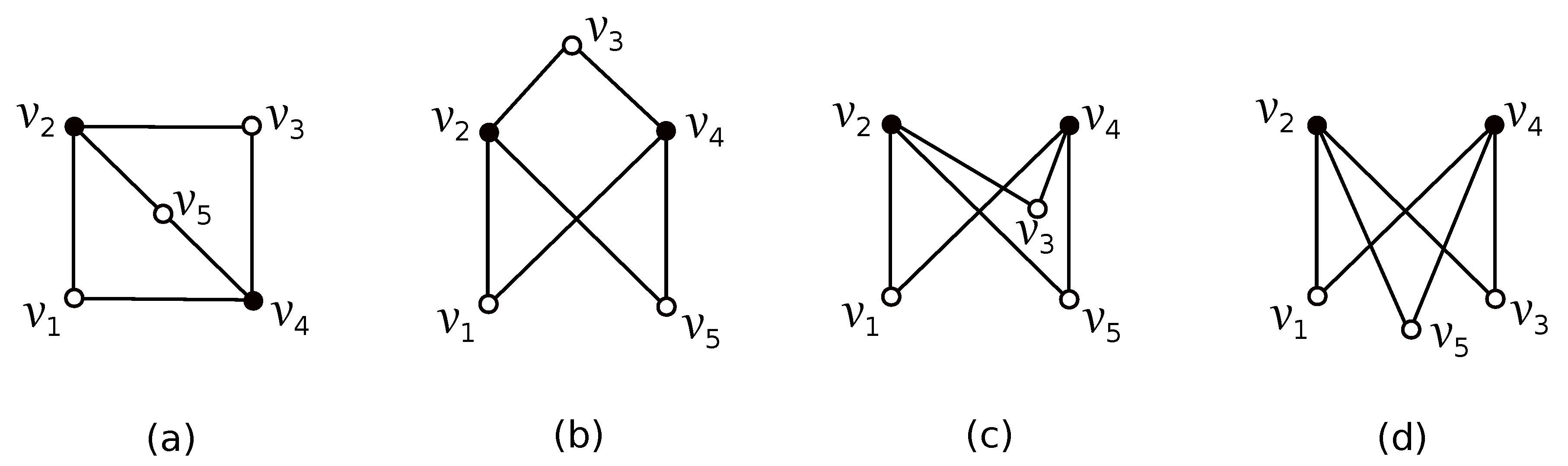
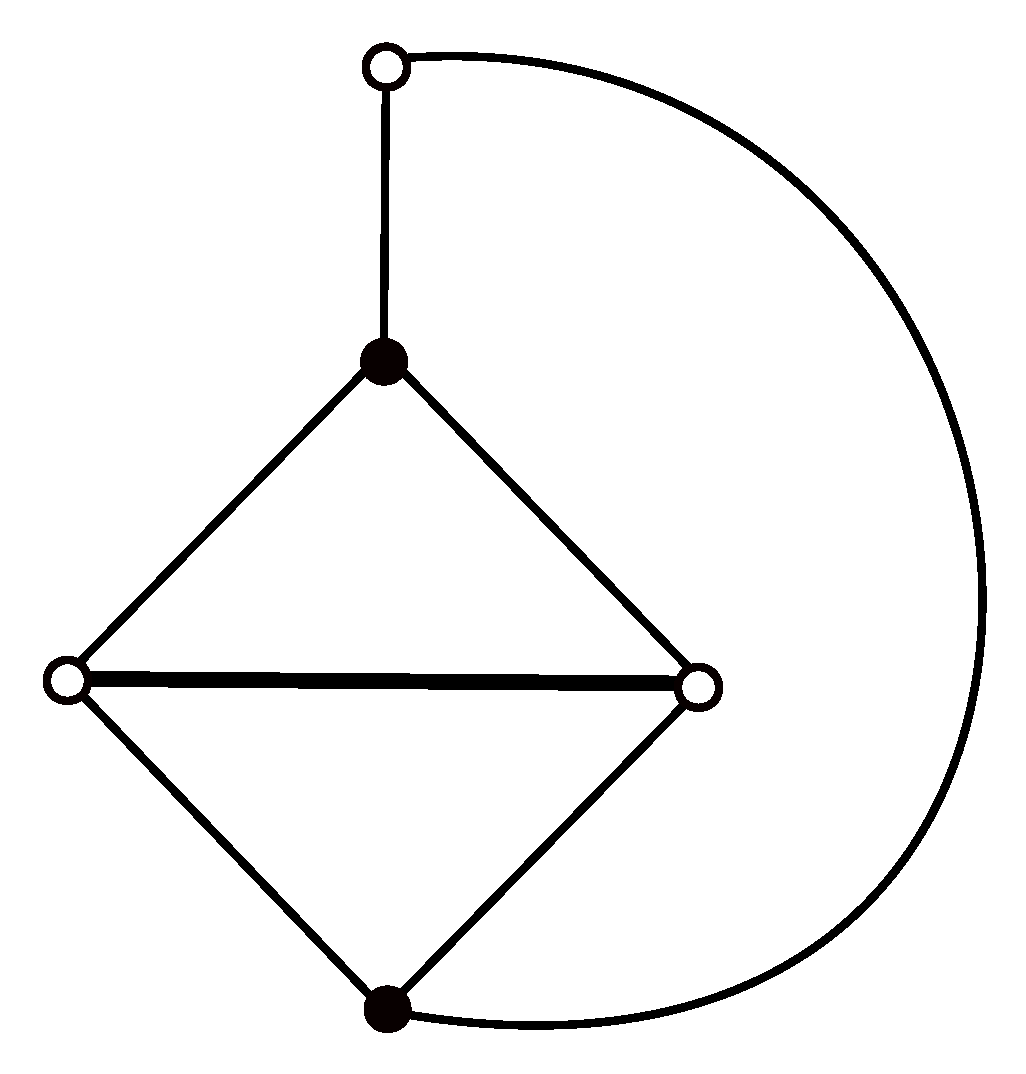
2. Possible Drawings of ${\mathit{K}}_{\mathbf{2},\mathbf{3}}$ and Preliminary Results

Let us first consider the join product of the complete bipartite graph $K_{2,3}$ with the discrete graph $D_n$ considered on n vertices. It is not difficult to see that the graph $K_{2,3}+D_n$ contains just one copy of the graph $K_{2,3}$ and n vertices $t_1,\dots ,t_n$, where each vertex $t_i$, $i=1,\dots ,n$, is adjacent to every vertex of $K_{2,3}$. For $1\le i\le n$, let $T^i$ denote the subgraph which is uniquely induced by the five edges that are incident with the fixed vertex $t_i$. This means that the graph $T^1\cup \dots \cup T^n$ is isomorphic to the graph $K_{5,n}$ and we obtain

$$K_{2,3}+D_n=K_{2,3}\cup K_{5,n}=K_{2,3}\cup \left(\bigcup _{i=1}^n{T}^i\right).$$

(1)

The graph $K_{2,3}+C_n$ contains $K_{2,3}+D_n$ as a subgraph. For all subgraphs of the graph $K_{2,3}+C_n$ which are also subgraphs of the graph $K_{2,3}+n{K}_1$ we can use the same notations as above. Let $C_n^{\ast }$ denote the cycle induced on n vertices of $K_{2,3}+C_n$ but which do not belong to the subgraph $K_{2,3}$. Hence, $C_n^{\ast }$ consists of the vertices $t_1,t_2,\dots ,t_n$ and of the edges $\{t_i,t_{i+1}\}$ and $\{t_n,t_1\}$ for $i=1,\dots ,n-1$. So we get

$$K_{2,3}+C_n=K_{2,3}\cup K_{5,n}\cup C_n^{\ast }=K_{2,3}\cup \left(\bigcup _{i=1}^n{T}^i\right)\cup C_n^{\ast }.$$

(2)

In the paper, the definitions and notation of the cyclic permutations and of the corresponding configurations of subgraphs for a good drawing D of the graph $K_{2,3}+D_n$ presented in [14] are used. By Hernández-Vélez et al. [15], the cyclic permutation that records the (cyclic) counter-clockwise order in which the edges leave a vertex $t_i$ is said to be the rotation ${\mathrm{rot}}_D\left(t_i\right)$ of the vertex $t_i$. On the basis of this, we use the notation $\left(12345\right)$ if the counter-clockwise order the edges incident with the vertex $t_i$ is $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, $t_i{v}_4$, and $t_i{v}_5$. Recall that any such rotation is a cyclic permutation. For our research, we will separate all subgraphs $T^i$ of $K_{2,3}+D_n$, $i=1,2,\dots ,n$, into three families of subgraphs depending on how many times are edges of $K_{2,3}$ crossed by the edges of the considered subgraph $T^i$ in D. For $i=1,2,\dots ,n$, let $R_D=\{T^i:{\mathrm{cr}}_D(K_{2,3},T^i)=0\}$, and $S_D=\{T^i:{\mathrm{cr}}_D(K_{2,3},T^i)=1\}$. The edges of $K_{2,3}$ are crossed at least twice by each other subgraph $T^i$ in D. For $T^i\in R_D\cup S_D$, let $F^i$ denote the subgraph $K_{2,3}\cup T^i$, $i\in \{1,2,\dots ,n\}$, of $K_{2,3}+D_n$. Clearly, the idea of dividing the subgraphs $T^i$ into three mentioned families is also retained in all drawings of the graph $K_{2,3}+C_n$. In [14], there are two possible non isomorphic drawings of the graph $K_{2,3}$, but only with the possibility of obtaining a subgraph $T^i\in R_D$ in D. Due to the arguments in the proof of Theorem 2, if we wanted to get an optimal drawing D of $K_{2,3}+C_n$, then the subdrawing $D\left(K_{2,3}\right)$ of the graph $K_{2,3}$ induced by D with at least three crossings among the edges of $K_{2,3}$ forces that the set $R_D$ must be nonempty. But, in the cases of ${\mathrm{cr}}_D\left(K_{2,3}\right)\le 2$, just one of the sets $R_D$ or $S_D$ can be empty. With these assumptions, we obtain four non isomorphic drawings of the graph $K_{2,3}$ as shown in Figure 1. The vertex notation of $K_{2,3}$ will be substantiated later in all mentioned drawings, and wherein two disjoint independent sets of vertices of the complete bipartite graph $K_{2,3}$ will be also highlighted by filled and non filled rings.

3. The Crossing Number of ${\mathit{K}}_{\mathbf{2},\mathbf{3}}+{\mathit{C}}_{\mathit{n}}$

In the proofs of the paper, several parts are based on the Theorem 1 presented in [14].

Theorem 1.

$\mathrm{cr}(K_{2,3}+D_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n$ for any $n\ge 1$.

Now we are able to prove the main results of the paper. The exact values of the crossing numbers of the small graphs $K_{2,3}+C_3$, $K_{2,3}+C_4$, and $K_{2,3}+C_5$ can be estimated using the algorithm located on the website http://crossings.uos.de/ provided that it uses an ILP formulation based on Kuratowski subgraphs and also generates verifiable formal proofs, for more see [16].

Lemma 1.

$\mathrm{cr}(K_{2,3}+C_3)=10$, $\mathrm{cr}(K_{2,3}+C_4)=15$, and $\mathrm{cr}(K_{2,3}+C_5)=24$.

Recall that two vertices $t_i$ and $t_j$ of $K_{2,3}+C_n$ are antipodal in a drawing of $K_{2,3}+C_n$ if the subgraphs $T^i$ and $T^j$ do not cross, and a drawing is said to be antipodal-free if it does not have antipodal vertices. The result in the following Theorem 2 has already been claimed by Yuan [17]. The correctness of an article written in Chinese cannot be verified because compilers cannot handle it. Therefore, such results can only be considered as unconfirmed hypotheses.

Theorem 2.

$\mathrm{cr}(K_{2,3}+C_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3$ for $n\ge 3$.

Proof of Theorem 2.

In Figure 2 there is the drawing of $K_{2,3}+C_n$ with $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3$ crossings. Thus, $\mathrm{cr}(K_{2,3}+C_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3$. Theorem 2 is true for $n=3$, $n=4$, and $n=5$ by Lemma 1. Assume $n\ge 6$. We prove the reverse inequality by contradiction. Suppose now that there is a drawing D of $K_{2,3}+C_n$ with

$${\mathrm{cr}}_D(K_{2,3}+C_n)<4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3$$

(3)

and that

$$\mathrm{cr}(K_{2,3}+C_m)\ge 4⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+m+3\mathrm{for}\mathrm{each}3\le m<n.$$

(4)

Let us show that the considered drawing D must be antipodal-free. For a contradiction suppose, with the rest of paper, that ${\mathrm{cr}}_D(T^{n-1},T^n)=0$. It is not difficult to verify in Figure 1 that if at least one of $T^{n-1}$ and $T^n$, say $T^n$, does not cross the edges of the graph $K_{2,3}$, then the edges of $T^{n-1}$ must cross the edges of $K_{2,3}\cup T^n$ at least twice, that is, ${\mathrm{cr}}_D(K_{2,3},T^{n-1}\cup T^n)\ge 2$. By [5], we already know that $\mathrm{cr}\left(K_{5,3}\right)=4$, which yields that each $T^k$, $k\ne n-1,n$, have to cross the edges of the subgraph $T^{n-1}\cup T^n$ at least four times. On the basis of this, we have

$${\mathrm{cr}}_D(K_{2,3}+C_n)={\mathrm{cr}}_D\left(K_{2,3}+C_{n-2}\right)+{\mathrm{cr}}_D(K_{5,n-2},T^{n-1}\cup T^n)+{\mathrm{cr}}_D(K_{2,3},T^{n-1}\cup T^n)+{\mathrm{cr}}_D(T^{n-1}\cup T^n)$$

$$\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+n-2+3+4(n-2)+2+0=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3.$$

This contradicts the assumption (3) and consequently confirms that D must be antipodal-free. As the graph $K_{2,3}+D_n$ is a subgraph of the graph $K_{2,3}+C_n$, by Theorem 1, the edges of $K_{2,3}+C_n$ are crossed at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n$ times, and therefore, at most two edges of the cycle $C_n^{\ast }$ can be crossed in D. This also enforces that the vertices $t_i$ of the cycle $C_n^{\ast }$ must be placed at most in two different regions in the considered good subdrawing of $K_{2,3}$. If $r=|R_D|$ and $s=|S_D|$, then the assumption (4) together with $\mathrm{cr}\left(K_{5,n}\right)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ enforce that there is at least one subgraph $T^i$ which crosses the edges of $K_{2,3}$ at most once in the drawing D. To be precise,

$${\mathrm{cr}}_D\left(K_{2,3}\right)+{\mathrm{cr}}_D(K_{2,3},K_{5,n})\le {\mathrm{cr}}_D\left(K_{2,3}\right)+0r+s+2(n-r-s)<n+3,$$

that is,

$${\mathrm{cr}}_D\left(K_{2,3}\right)+s+2(n-r-s)\le n+2.$$

(5)

This implies that $2r+s\ge n+{\mathrm{cr}}_D\left(K_{2,3}\right)-2$. Further, if ${\mathrm{cr}}_D\left(K_{2,3}\right)=0$ and $r=0$, then $s\ge n-2$. Now, we will deal with the possibilities of obtaining a subgraph $T^i\in R_D\cup S_D$ in D and we will exhibit that in all mentioned cases a contradiction with the assumption (3) is achieved.

Case 1:${\mathrm{cr}}_D\left(K_{2,3}\right)=0$. In this case, without lost of generality, we can assume the drawing with the vertex notation of $K_{2,3}$ as shown in Figure 1a. The unique subdrawing of $K_{2,3}$ induced by D contains three different regions. Hence, let us denote these three regions by ${\omega }_{1,4,3,2}$, ${\omega }_{1,4,5,2}$, and ${\omega }_{2,5,4,3}$ depending on which of vertices are located on the boundary of the corresponding region. Since the vertices of $C_n^{\ast }$ do not have to be placed in the same region in the considered subdrawing of $K_{2,3}$, two possible subcases may occur:

(a)

All vertices of $C_n^{\ast }$ are placed in two regions of subdrawing of $K_{2,3}$ induced by D. In the rest of paper, based on their symmetry, we can suppose that all vertices $t_i$ of $C_n^{\ast }$ are placed in ${\omega }_{1,4,3,2}\cup {\omega }_{1,4,5,2}$. Of course, there is no possibility to obtain a subdrawing of $K_{2,3}\cup T^i$ for a $T^i\in R_D$, that is, $r=0$. Clearly, the edges of $C_n^{\ast }$ must cross the edges of $K_{2,3}$ exactly twice. This fact, with the property (5) in the form $0+1s+2(n-s)<n+1$, confirms that $s=n$, which yields that each subgraph $T^i$ cross the edges of $K_{2,3}$ just once. If some vertices $t_i$ of $C_n^{\ast }$ are placed in ${\omega }_{1,4,3,2}$, then we deal with the configurations ${\mathcal{A}}_k$, $k\in \{1,2,3,4\}$ (they have been already introduced in [14]). For $t_i\in {\omega }_{1,4,5,2}$, there are four other ways for how to obtain the subdrawing of $F^i$ depending on which edge of $K_{2,3}$ is crossed by the edge $t_i{v}_3$ provided by there is only one subdrawing of $F^i\backslash \left\{v_3\right\}$ represented by the rotation $\left(1452\right)$. These four possibilities can be denoted by ${\mathcal{A}}_k$, for $k=5,6,7,8$ and they are represent by the cyclic permutations $\left(14532\right)$, $\left(13452\right)$, $\left(14523\right)$, and $\left(14352\right)$, respectively. Consequently, we denote by ${\mathcal{M}}_D$ the subset of all configurations that exist in the drawing D belonging to the set $\mathcal{M}=\{{\mathcal{A}}_k:k=1,\dots ,8\}$. Using the same arguments like in [14], the resulting lower bounds for the number of crossings of two configurations from $\mathcal{M}$ can be established in

Table 1. The necessary number of crossings between two different subgraphs $T^i$ and $T^j$ for the configurations ${\mathcal{A}}_k$ and ${\mathcal{A}}_l$.

-	${\mathcal{A}}_1$	${\mathcal{A}}_2$	${\mathcal{A}}_3$	${\mathcal{A}}_4$	${\mathcal{A}}_5$	${\mathcal{A}}_6$	${\mathcal{A}}_7$	${\mathcal{A}}_8$
${\mathcal{A}}_1$	4	2	3	3	1	3	2	2
${\mathcal{A}}_2$	2	4	3	3	3	1	2	2
${\mathcal{A}}_3$	3	3	4	2	2	2	1	3
${\mathcal{A}}_4$	3	3	2	4	2	2	3	1
${\mathcal{A}}_5$	1	3	2	2	4	2	3	3
${\mathcal{A}}_6$	3	1	2	2	2	4	3	3
${\mathcal{A}}_7$	2	2	1	3	3	3	4	2
${\mathcal{A}}_8$	2	2	3	1	3	3	2	4

(here, ${\mathcal{A}}_k$ and ${\mathcal{A}}_l$ are configurations of the subgraphs $F^i$ and $F^j$, where $k,l\in \{1,\dots ,8\}$).

Let us first assume that $\{{\mathcal{A}}_k,{\mathcal{A}}_{k+4}\}\subseteq {\mathcal{M}}_D$ for some $k\in \{1,2,3,4\}$. In the rest of paper, let us assume two different subgraphs $T^{n-1},T^n\in S_D$ such that $F^{n-1}$ and $F^n$ have different configurations ${\mathcal{A}}_1$ and ${\mathcal{A}}_5$, respectively. Then, ${\mathrm{cr}}_D(K_{2,3}\cup T^{n-1}\cup T^n,T^i)\ge 1+5=6$ holds for any $T^i\in S_D$ with $i\ne n-1,n$ by summing the values in all columns in two considered rows of Table 1. Hence, by fixing the subgraph $K_{2,3}\cup T^{n-1}\cup T^n$, we have

$${\mathrm{cr}}_D(K_{2,3}+C_n)\ge {\mathrm{cr}}_D\left(K_{5,n-2}\right)+{\mathrm{cr}}_D(K_{5,n-2},K_{2,3}\cup T^{n-1}\cup T^n)+{\mathrm{cr}}_D(K_{2,3}\cup T^{n-1}\cup T^n)$$

$$\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+6(n-2)+2+1\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3.$$

Due to the symmetry of three remaining pairs of configurations, we also obtain a contradiction in D by applying the same process. Now, let us turn to the good drawing D of the graph $K_{2,3}+C_n$ in which $\{{\mathcal{A}}_k,{\mathcal{A}}_{k+4}\}⊈{\mathcal{M}}_D$ for any $k=1,2,3,4$. Further, let us also suppose that the number of subgraphs with the configuration ${\mathcal{A}}_k\in {\mathcal{M}}_D$ is at least equal to the number of subgraphs with the configuration ${\mathcal{A}}_l\in {\mathcal{M}}_D$, for each possible $l\ne k$, and let $T^i\in S_D$ be such a subgraph with the configuration ${\mathcal{A}}_k$ of $F^i$. Hence,

$${\mathrm{cr}}_D(K_{5,n-1},T^i)=\sum _{j\ne i}{\mathrm{cr}}_D(T^j,T^i)\ge 3(n-2)+2-2⌊\frac{n}{7}⌋\ge \frac{5}{2}n-\frac{5}{2},$$

where an idea of the arithmetic mean of the values four, three and two of Table 1 could be exploited. Thus, by fixing the subgraph $T^i$, we have

$${\mathrm{cr}}_D(K_{2,3}+C_n)={\mathrm{cr}}_D\left(K_{2,3}+C_{n-1}\right)+{\mathrm{cr}}_D(K_{5,n-1},T^i)+{\mathrm{cr}}_D(K_{2,3},T^i)$$

$$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+n-1+3+\frac{5}{2}n-\frac{5}{2}+1\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3.$$

(b)

All vertices $t_i$ of $C_n^{\ast }$ are placed in the same region of subdrawing of $K_{2,3}$ induced by D. In the rest of paper, based also on their symmetry, we suppose that $t_i\in {\omega }_{1,4,3,2}$ for each $i=1,\dots ,n$. Whereas the set $R_D$ is again empty, there are at least $n-2$ subgraphs $T^i\in S_D$ provided by the property (5) in the form $s+2(n-s)<n+3$. For $T^i\in S_D$, we consider only one from the configurations ${\mathcal{A}}_k$, for $k=1,2,3,4$. Again, let us also assume that the number of subgraphs with the configuration ${\mathcal{A}}_k$ is at least equal to the number of subgraphs with the configuration ${\mathcal{A}}_l$, for each possible $l\ne k$, and let $T^i\in S_D$ be such a subgraph with the configuration ${\mathcal{A}}_k$ of $F^i$. Then, by fixing the subgraph $T^i$, we have

$${\mathrm{cr}}_D(K_{2,3}+C_n)={\mathrm{cr}}_D\left(K_{2,3}+C_{n-1}\right)+{\mathrm{cr}}_D(K_{5,n-1},T^i)+{\mathrm{cr}}_D(K_{2,3},T^i)$$

$$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+n-1+3+3(s-2)+2+1(n-s)+1=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋$$

$$+2n+2s-1\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+2(n-2)-1\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3,$$

wherein a simplified form of the idea of the arithmetic mean of the values of Table 1 is applied.

Case 2:${\mathrm{cr}}_D\left(K_{2,3}\right)=1$. We can choose the drawing with the vertex notation of $K_{2,3}$ like in Figure 1b. Similarly as in the previous case, we will discuss two subcases:

(a)

The cycle $C_n^{\ast }$ is crossed by some edge of the graph $K_{2,3}$. As the edges of $C_n^{\ast }$ cross the edges of $K_{2,3}$ exactly twice, there is a subgraph $T^i$ which does not cross the edges of $K_{2,3}$ provided by the property (5) in the form $1+s+2(n-r-s)\le n$. For a $T^i\in R_D$, the reader can easily verify that the subgraph $F^i=K_{2,3}\cup T^i$ is uniquely represented by ${\mathrm{rot}}_D\left(t_i\right)=\left(12345\right)$, and ${\mathrm{cr}}_D(T^i,T^j)\ge 4$ holds for any $T^j\in R_D$ with $j\ne i$ provided that ${\mathrm{rot}}_D\left(t_i\right)={\mathrm{rot}}_D\left(t_j\right)$, for more see [18]. Moreover, it is not difficult to verify in possible regions of $D(K_{2,3}\cup T^i)$ that ${\mathrm{cr}}_D(K_{2,3}\cup T^i,T^j)\ge 4$ is true for each $T^j\in S_D$. Thus, by fixing the subgraph $K_{2,3}\cup T^i$, we have

$${\mathrm{cr}}_D(K_{2,3}+C_n)\ge {\mathrm{cr}}_D\left(K_{5,n-1}\right)+{\mathrm{cr}}_D(K_{5,n-1},K_{2,3}\cup T^i)+{\mathrm{cr}}_D(K_{2,3}\cup T^i)$$

$$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4(r-1)+4s+3(n-r-s)+1=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋$$

$$+3n+(r+s)-3\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+4-3\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3,$$

where $r+s\ge 4$ holds also due to the property (5).

(b)

None edge of $C_n^{\ast }$ is crossed by the edges of $K_{2,3}$. Since all vertices $t_i$ of the cycle $C_n^{\ast }$ are placed in the same region of subdrawing of $K_{2,3}$ induced by D, they must be placed in the outer region of $D\left(K_{2,3}\right)$. If there is a $T^i\in R_D$, then the edges of $K_{2,3}\cup T^i$ are crossed at least four times by any subgraph $T^j$ with the placement of the vertex $t_j$ in the outer region of $D\left(K_{2,3}\right)$, which yields that the similar idea as in the previous subcase can be used by fixing the subgraph $K_{2,3}\cup T^i$

$${\mathrm{cr}}_D(K_{2,3}+C_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4(r-1)+4(n-r)+1$$

$$=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n-3\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3.$$

To finish the proof of this case, let us suppose that the set $R_D$ is empty. Whereas the set $R_D$ is empty, there are at least $n-1$ subgraphs $T^i\in S_D$ according to the property (5). Since the edges $v_2{v}_3$, $v_3{v}_4$, $v_2{v}_5$, and $v_1{v}_4$ of $K_{2,3}$ can be crossed by the edges $t_i{v}_4$, $t_i{v}_2$, $t_i{v}_4$, and $t_i{v}_2$, respectively, these four ways can be denoted by ${\mathcal{B}}_k$, for $k=1,2,3,4$. So, the configurations ${\mathcal{B}}_1$, ${\mathcal{B}}_2$, ${\mathcal{B}}_3$, and ${\mathcal{B}}_4$ are uniquely described by the cyclic permutations $\left(12435\right)$, $\left(13245\right)$, $\left(12354\right)$, and $\left(13452\right)$, respectively., and the aforementioned properties of the cyclic rotations imply all lower-bounds of number of crossings in

Table 2. The necessary number of crossings between two different subgraphs $T^i$ and $T^j$ for the configurations ${\mathcal{B}}_k$ and ${\mathcal{B}}_l$.

-	${\mathcal{B}}_1$	${\mathcal{B}}_2$	${\mathcal{B}}_3$	${\mathcal{B}}_4$
${\mathcal{B}}_1$	4	2	2	2
${\mathcal{B}}_2$	2	4	2	2
${\mathcal{B}}_3$	2	2	4	2
${\mathcal{B}}_4$	2	2	2	4

.

Now, let us also suppose that the number of subgraphs with the configuration ${\mathcal{B}}_k$ is at least equal to the number of subgraphs with the configuration ${\mathcal{B}}_l$, for each possible $l\ne k$, and let $T^i\in S_D$ be such a subgraph with the configuration ${\mathcal{B}}_k$ of $F^i$. Hence,

$$\sum _{T^j\in S_D,j\ne i}{\mathrm{cr}}_D(T^i,T^j)\ge 3(s-2)+2-2⌊\frac{s}{4}⌋\ge \frac{5}{2}s-4,$$

where again an idea of the arithmetic mean of the values four and two of Table 2 could be exploited. Thus, by fixing the subgraph $T^i$, we have

$${\mathrm{cr}}_D(K_{2,3}+C_n)={\mathrm{cr}}_D\left(K_{2,3}+C_{n-1}\right)+{\mathrm{cr}}_D(K_{5,n-1},T^i)+{\mathrm{cr}}_D(K_{2,3},T^i)$$

$$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+n-1+3+\frac{5}{2}s-4+1(n-s)+1=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋$$

$$+2n+\frac{3}{2}s-1\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+\frac{3}{2}(n-1)-1\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3.$$

Case 3:${\mathrm{cr}}_D\left(K_{2,3}\right)=2$. In the rest of paper, we choose the drawing with the vertex notation of $K_{2,3}$ like in Figure 1c. Obviously the set $R_D$ must be empty. As $s=n$ by the property (5), all vertices $t_i$ of the subgraphs $T^i\in S_D$ must be placed in the region of $D\left(K_{2,3}\right)$ with four vertices $v_1$, $v_2$, $v_4$, and $v_5$ of the graph $K_{2,3}$ on its boundary. For $T^i\in S_D$, there is only one possible subdrawing of $F^i\backslash \left\{v_3\right\}$ described by the rotation $\left(1245\right)$, which yields that there are exactly three ways of obtaining the subdrawing of $K_{2,3}\cup T^i$ depending on which edge of $K_{2,3}$ may be crossed by $t_i{v}_3$. In all cases of $T^i\in S_D$ represented by either $\left(12345\right)$ or $\left(12453\right)$ or $\left(12435\right)$, it is not difficult to verify using cyclic permutations that ${\mathrm{cr}}_D(T^i,T^j)\ge 2$ is fulfilling for each $T^j\in S_D$, $j\ne i$. Thus, by fixing the subgraph $T^i$, we have

$${\mathrm{cr}}_D(K_{2,3}+C_n)={\mathrm{cr}}_D\left(K_{2,3}+C_{n-1}\right)+{\mathrm{cr}}_D(K_{5,n-1},T^i)+{\mathrm{cr}}_D(K_{2,3},T^i)$$

$$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+n-1+3+2(n-1)+1\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3.$$

Case 4:${\mathrm{cr}}_D\left(K_{2,3}\right)=3$. We assume the drawing with the vertex notation of $K_{2,3}$ like in Figure 1d. As the property (5) enforces $r\ge 1$ and $r+s\ge 4$, the proof can proceed in the similar way as in the Subcase $2\mathrm{a})$.

We have shown, in all cases, that there is no good drawing D of the graph $K_{2,3}+C_n$ with fewer than $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3$ crossings. This completes the proof. □

Finally, in Figure 2, we are able to add the edge $v_1{v}_5$ to the graph $K_{2,3}$ without additional crossings, and we obtain one new graph H in Figure 3. So, the drawing of the graph $H+C_n$ with $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3$ crossings is obtained. On the other hand, $K_{2,3}+C_n$ is a subgraph of $H+C_n$, and therefore, $\mathrm{cr}(H+C_n)\ge \mathrm{cr}(K_{2,3}+C_n)$. Thus, the next result is an immediate consequence of Theorem 2.

Corollary 1.

$\mathrm{cr}(H+C_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+3$ for any $n\ge 3$.

4. Conclusions

We suppose that the application of various forms of arithmetic means can be used to estimate the unknown values of the crossing numbers for join products of some graphs on five vertices with the paths, and also with the cycles. The same we expect for larger graphs, namely for a lot of symmetric graphs of order six.