Ranking Multi-Metric Scientific Achievements Using a Concept of Pareto Optimality

Abstract

The ranking of multi-metric scientific achievements is a challenging task. For example, the scientific ranking of researchers utilizes two major types of indicators; namely, number of publications and citations. In fact, they focus on how to select proper indicators, considering only one indicator or combination of them. The majority of ranking methods combine several indicators, but these methods are faced with a challenging concern—the assignment of suitable/optimal weights to the targeted indicators. Pareto optimality is defined as a measure of efficiency in the multi-objective optimization which seeks the optimal solutions by considering multiple criteria/objectives simultaneously. The performance of the basic Pareto dominance depth ranking strategy decreases by increasing the number of criteria (generally speaking, when it is more than three criteria). In this paper, a new, modified Pareto dominance depth ranking strategy is proposed which uses some dominance metrics obtained from the basic Pareto dominance depth ranking and some sorted statistical metrics to rank the scientific achievements. It attempts to find the clusters of compared data by using all of indicators simultaneously. Furthermore, we apply the proposed method to address the multi-source ranking resolution problem which is very common these days; for example, there are several world-wide institutions which rank the world’s universities every year, but their rankings are not consistent. As our case studies, the proposed method was used to rank several scientific datasets (i.e., researchers, universities, and countries) for proof of concept.

1. Introduction

Nowadays, ranking of scientific impacts is a crucial task and it is a focus of research communities, universities, and governmental funding agencies. In this ranking, the target entities can be researchers, universities, countries, journals, or conferences. Performance analysis and benchmarking of scientific achievement has a variety of substantial purposes. At the researcher level, the research’s impact is an important measure to define the main rules of academic institutions and universities on determination of funding, hiring, and promotions [1,2,3]. From the university’s view point, university rankings are considered as a source of strategic information for governments, funding agencies, and the media in order to compare universities; then students and their parents use university rankings as a selection criterion [4]. As the assessment of scientific achievement has gained a great deal of attention for various interested groups, such as students, parents, institutions, academicians, policy makers, political leaders, donors/funding agencies, and news media; several assessment methods have been developed in the field of bibliometry and scientometrics through the utilization of mathematical and/or statistical methods [1].

In order to measure a researcher’s performance, many indicators have been proposed which can also be utilized in other scientific areas. Traditional research indicators include the numbers of publications and citations, the average number of citations per paper, and the average number of citations per year [5]. In 2005, Hirsch [6] proposed a new indicator, called h-index, which revolutionized scientometrics (informetrics). The original definition of the h-index indicator is that, “A scientist has the index h if h of his/her $N_p$ papers have at least received h citations each, and the other $N_p-h$ papers have no more than h citations each.” Later, other indicators were proposed to enhance the h-index. Additionally, h-index was defined for other scientific aggregation levels [7]. Ranking methods at researcher level tend to use only one indicator (h-index or its improved versions), but at other aggregation scientific levels they prefer to have a more comprehensive set of indicators. Research works in the scientometrics can be divided into the following two main categories: the first category includes methods which focus on introducing new indicators to enhance the performances of assessment metrics, and in the second category, methods attempt to develop enhanced ranking methods for obtaining ranks by using several various indicators.

There are various kinds of ranking methods; first, methods which focus only on one indicator; and second, methods which combine several of them. Considering only a specific indicator makes differences among the quality assessments of research outcomes very hard to be revealed. On the other hand, there are a few challenges for considering several indicators simultaneously. For instance, the method needs to find the proper weights for combining the indicators and also an efficient merging strategy to combine several different types of indicators.

In the field of optimization, an algorithm tries to find the best solution in a search space in terms of an objective function which should be minimized or maximized [8] accordingly. However, in singe-objective problems [9], there is only one objective to be optimized; in the multi-objective version, the algorithm tries to find a set of solutions based on more than one objective [10]. In the multi-objective optimization [11,12], the non-dominated sorting [13,14] is defined and used as a measure of efficiency in metaheuristic-based methods [15,16]. In [17], the basic dominance ranking was used to identify the excellent scientists according to all selected criteria. They selected all researchers in the first Pareto-front as excellent scientists, but by increasing the number of criteria (more than three) most compared entities were placed in the first Pareto front [17]. In this paper, we propose a modified, non-dominated sorting, which according to the basic dominance ranking, utilizes two main metrics and then two statistical metrics which are the computed means and medians of some ranks obtained by sorting each criterion’s value in all compared vectors. This ranking has many major advantages: (1) it can perform very well at ranking all compared vectors even with a large number of criteria; (2) each obtained Pareto front in the modified non-dominated sorting has a smaller number of vectors in compared to the basic non-dominated sorting approach; (3) it can consider the length time of academic research (called the research period) as an independent indicator, which makes it possible to compare junior and senior researchers; (4) it is independent and capable of accommodating new indicators; (5) there is no need to determine the optimal weights to combine indicators. The modified Pareto dominance ranking was used to rank two research datasets with many criteria, ranking universities (200 samples) and countries (231 samples); additionally, the basic dominance ranking was applied to rank two research datasets with a low number of the criteria, ranking computer science researchers based on h-index and period of publication (350 samples) and ranking of universities based on triple rankings resources (100 samples).

The remaining sections of this paper are organized as follows. Section 2 presents a background review which provides state-of-the-art scientific indicators and ranking methods. Section 3 describes the proposed ranking method in detail. Section 4 presents case studies and corresponding discussions. Finally, the paper is concluded in Section 5.

2. Background Review

In this section, we review several state-of-the-art scientific indicators and several recent ranking methods.

2.1. A Brief Description of State-of-the-Art Scientific Indicators

Several indicators have been proposed to measure the scientific achievements. The pioneer studies introduced some basic indicators and described how these indicators can be combined to find the general intuition of the scientific outputs for researchers [18,19]. These indicators can be categorized in the following three main groups [20,21]:

• Production based indicators: these indicators were developed to assess the quantity of production such as the total number of published papers and the number of papers published during a limited time.
• Impact based indicators: they were proposed to quantify the impact of the researchers’ publications; e.g., the total number of citations, the average number of citations per paper, the number of high-impact papers (papers with more than a specific number of citations), and the number of citations of the high-impact papers.
• Indicators based on the impact of the journals: these indicators were designed to consider journals where the papers are published; e.g., the median impact factor of the journals, relative citation rates (publication citations compared with the average citations of papers in the journal), and normalized position of the journals (computed according to position of journal in the ordered list in term of impact factor).

Some advantages and disadvantages of well-known indicators [6,22] are shown in

Table 1. A summary of advantages and disadvantages for some commonly used indicators.

Indicator	Advantage	Disadvantage
The total number of published papers	It is a proper measure to quantify the productivity.	It does not consider the impact of their publications.
The total number of received citations	It can measure the total impact.	It may be inflated by a small number of “big hits” when a paper has many co-authors. It gives a Excess weight to highly cited survey papers.
Average number of citations per publication, without counting self-citations	It can be applied to compare junior and senior scientists (not in a complete way, because the senior researchers had more time for better building up of this metric).	It is hard to find and rewards low productivity and penalizes high productivity.
Number of “significant papers” (as the number of papers with having more than y citations)	It eliminates disadvantages of the previous mentioned indicators; the total number of published papers, the total number of citations, and average number of citations per publication.	The value of “y” should be adjusted.
The number of citations to each of the q most cited papers	Similar to Number of “significant papers,” it can overcomes many of the mentioned disadvantages above.	“q” has not a single value so it is difficult to compute and compare.

.

In 2005, Hirsch dramatically changed scientometrics (informetrics) by introducing the h-index measure. Several studies have discussed and extended the validity of the h-index [23] since its introduction. The h-index has some significant properties [24,25]. It considers two aspects, the number of publications and their impacts on research. It performs better than other basic indicators (total number of papers, total number of citations, average number of significant papers, etc.) at evaluating scientific achievements. In [25], an empirical study was conducted to confirm the superiority of the h-index over other basic indicators. In addition, the h-index can effortlessly be computed by using available resources such as the ISI Web of Science. Although it was extensively utilized as a scientometrics measure, it still suffers from the following drawbacks [1,26,27,28]:

• The h-index highly depends on the length of the academic career (the research period) because it is supposed the publications and citations of researchers increase over time. The h-index of new researchers has a very low value, and so it is not applicable for comparing scientists at different stages of their academic careers.
• It is field-dependent; therefore it can be useful to compare scientists in the same field of study.
• The h-index never decreases and also it may increase even if no new papers are published because the number of received citations for scientists can be increased with time. However, the value of h-index indicates the impact of the publications; it is strongly dependent on one aspect of the research; i.e., the age of research. In order to compare two scientists fairly based on their research achievements, in addition to quality evaluation, the period of time that they have researched over is also important. In other words, for two researchers with the same value of h-index, the researcher with shorter research period is the more successful researcher. Consequently, the h-index cannot be a standalone metric to assess the rank of a scientist in terms of different criteria.
• It is insensitive to performance changes because when first h articles received at least h times h, i.e., $h^2$ citations, it does not consider the number of citations they receive.
• Additionally, the h-index suffers from the same issues as other indicators, such as self-citations and being field-dependent. Some of these issues include difficulty in finding reference standards, and also problems of collecting all required data to compute the h-index (for example, discriminating between scientists with the same names and initials is challenging).

Several variants of the h-index have been developed to overcome the drawbacks of the h-index. The m-quotient [6] was proposed to account for years since the first publication, and it is computed as follows.

$$m\text{-}\mathrm{quotient}=\frac{h\text{-}\mathrm{index}}{n},$$

(1)

where n is the number of years since the first published paper of the scientist. Batista et al. [29] introduced a complementary index as the $h_I$ index which is defined by:

$$h_I=h^2/N_a^T,$$

(2)

where $N_a^T$ is the number of authors in the considered h papers. In [30], A-index was suggested as the average number of citations of publications included in the h(Hirsch)-core which is mathematically defined as.

$$A=\frac{1}{h}\sum _{j=1}^h{cit}_j$$

(3)

The $AR$ index [31] was proposed as the square root of the sum of the average number of citations per year of articles included in the h(Hirsch)-core. The mathematical definition of the index is as bellow.

$$AR=\sqrt{\sum _{j=1}^h\frac{{cit}_j}{a_j}},$$

(4)

where $a_j$ is the age of jth paper. Liang et al. [26] suggested a new index, the R-index, which found by calculating the square root of the sum of citations in the Hirsch core without dividing by h. This indicator is mathematically defined as.

$$R=\sqrt{\sum _{j=1}^h{cit}_j}$$

(5)

Egghe [28] introduced the g index which is defined as the highest number g of papers such that the top g papers together have at least $g^2$ citations. Additionally, it has proven that there is a unique g for any set of papers and $g>h$. Egghe and Rousseau [32] proposed the citation-weighted h-index ($h_w$-index) as follows.

$$h_w=\sqrt{\sum _{j=1}^{r_0}{cit}_j},r_w\left(i\right)=\frac{{\sum }_{j=1}^i{cit}_j}{h},$$

(6)

where $ci{t}_j$ is the number of the j-th most cited paper; $r_0$ is the largest row index i such that $r_w\left(i\right)\le {cit}_i$. In general, even enhanced version of h-index metrics suffer from combining several metrics instead of considering them simultaneously.

2.2. A Brief Review of Ranking Methods

At the researcher level, all mentioned indicators can be applied to measure researchers’ achievements. Although other scientific applications such as ranking scientific journals, research teams, research institutions, and countries tend to include a more comprehensive set of indicators, it is possible to apply the scientific indicators of researcher in other scientific comparative applications. For example, h-index can be calculated for an institute: “The h-index of an institute would be $h_2$ if $h_2$ number of its researchers have an $h_1$-index of at least $h_2$ each, and the other ($N-h_2$) researchers have $h_1$-indices lower than $h_2$ each” [7]. In following, we briefly review some common ranking methods and indicators for universities. University rankings mainly use two different general categorizes of methodologies [33,34,35,36,37,38,39]; the first category uses all indicators [40,41] to calculate a single score, while the second category focuses more on a single dimension of university performance, such as the quality of research output [4], career outcomes of graduates [37], or the mean h-index [42]. The other indicators for university rankings are publication and citation counts, student/faculty ratio, percentage of international students, Nobel and other prize commonality, number of highly cited researchers and papers, articles published in Science and Nature, the h-index, and web visibility. First, some ranking methodologies of the first category are briefly described as below.

Liu and Cheng [43] proposed a ranking strategy, called Academic Ranking of World Universities (ARWU), which considers four measures: quality of education, quality of faculty, research output, and per capita performance. For comparison of four measures, the following six indicators are considered: (1) alumni of a university winning a Nobel Prize or a Fields Medal, (2) staff of a university winning a Nobel Prize or a Fields Medal, (3) highly cited researchers in 21 broad scientific fields, (4) publications in Nature and Science, (5) publications indexed in Web of Science, and (6) per capita academic performance of a university. It gives a score of 100 for the best performing university in each category and this university is considered as the benchmark against for computing the scores of all other universities. Then, the total scores of Universities are calculated as weighted averages of their individual category scores [44]. THE-QS World University Ranking (THE-QS) (http://www.topuniversities.com) was published by the Quacquarelli Symonds Company and considers six distinct indicators: academic reputation according to a large survey (40%), employer reputation (10%), the student faculty ratio (20%), citations per faculty based on the Scopus database (20%), the proportions of international professors (5%), and international students (5%). The World University Ranking was developed by Times Higher Education (www.timeshighereducation.co.uk/world-university-rankings) [41] which considers 13 indicators to rank universities. These indicators are categorized into five areas: teaching (30%), research (30%), citations (30%), industry income (2.5%), and international outlook (7.5%). They normalize the citation impact indicator to be suitable for different scientific output data.

Another global ranking is the Scimago Institutions Rankings (SIR) developed by the Scimago research group in Spain (www.scimagoir.com) [45]. SIR combines a quantity and various quality metrics. Indicators are divided into three groups: research output (total number of the publication based on the Scopus database), international collaboration, leader output, high quality publications, excellence, scientific leadership (excellence with leadership, and scientific talent pool), innovation (innovative knowledge and technological impact), and societal (web size and the number of incoming links). The Cybermetrics Lab developed the Ranking Web of World Universities or Webometrics Ranking [46,47] which uses web data extracted from commercial search engines, including the number of webpages, documents in rich formats (pdf, doc, ppt, and ps), papers indexed by Google Scholar (indicator added in 2006), and the number of external in links as a measure of link visibility or impact. Higher Education Evaluation and Accreditation Council of Taiwan [48]) conducts university ranking which applies multiple indicators in the three categories: research productivity (the number of articles published in the past 11 years (10%) and the number of articles published in the current year (15%)), research impact (number of citations in the past 11 years (15%), number of citations in the past 2 years (10%), and average number of citations in the past 11 years (10%)), and research excellence (the h-index of the last 2 years (10%), the number of highly cited papers in the past 11 years (15%), and the number of articles of the current year in high impact journals (15%)). These rankings combine multiple weighted indicators to gain a single aggregate score to rank all universities. Additionally, some universities rankings [49,50] employed I-distance method [51] to apply all indicators for computing a single score as the rank. Besides its ability to calculate a single index (by considering several indicators) and consequently ranking countries, CIDI startegy utilizes the Pearson’s coefficients of correlation, calculated using the I-distance method. In this case, the relevance of each input measure will be preserved. The I-distance method specifies the most important indicator instead of calculating numerical weights. The rank of indicator is determined by ordering them based on these correlations. In following, we mention some of ranking methodologies of the second category. The Centre for Science and Technology Studies at Leiden University published the LEIDEN Ranking (http://www.cwts.nl/ranking/LeidenRankingWebsite) [4,52] which has two main categories of indicators: impact and collaboration. The impact group includes three indicators: mean citation score, mean normalized citation score, and proportion of top 10% publications. The collaboration group includes four indicators: proportion of inter-institutional collaborative publications, proportion of international collaborative publications, proportion of collaborative publications with industry, and mean geographical collaboration distance. The Leiden Ranking considers the scientific performance instead of combining multiple indicators of university performance in a single aggregate indicator. U-Multirank [53,54] employs the variety of institutional missions and profiles and includes teaching and learning-related indicators. Additionally, it considers the importance of a user-driven approach in which the stakeholders/users are asked to determine indicators and their quality for ranking. In [37], they proposed a ranking methodology which considers only career outcomes of university graduates. This ranking focuses on the impact of universities on industry by their graduates. The mean h-index was used in [42] as a ranking metric to rank the chemical engineering, chemistry, materials science, and physics departments in Greece.

3. Proposed Methodology

As mentioned in the Section 2, several indicators and ranking methods have been proposed to measure the scientific achievements. There are two main categories of ranking methods: in the first one, the methods use all indicators (multi-metric) and in the second one, the methods focus on only one indicator (single-metric). Ranking methods by focusing on one indicator of scientific achievements cannot reveal significant differences among compared entities. In ranking methods with several indicators, first they need to assign weights for indicators which have considerable impacts on the results of these raking methods [55,56]. Finding the proper weights according to importance of indicators is a challenging task [57]. They also suffer from combining several different kinds of indicators to achieve a single score. In this paper, we modify the dominance depth ranking proposed in [13,14] utilized in the multi-objective optimization to rank scientific achievements. In 1964, Pareto [58] proposed the Pareto optimality concept, which has been applied in a wide range of application, such as economics, game theory, multi-objective optimization, and the social sciences [59]. Pareto optimality was mathematically defined as a measure of efficiency in the multi-objective optimization [12,60]. We explain Pareto optimality concepts and also the proposed method and how it can be applied to evaluate scientific achievements. Without loss of generality, it is assumed that the optimal value of each criterion as a preference be a minimal value. Seeking the optimal value among both the minimal and maximal values is analogous, and if a criterion value element $C_i$ to be maximized, it is equivalent to minimize $-C_i$.

In the following, the Pareto optimality definitions are described by the assumption of the minimal value as the optimal.

Definition 1

((Pareto Dominance) [61]). A criterion vector $u=(u_1,\cdots ,u_n)$ dominates another criterion vector $v=(v_1,\cdots ,v_n)$ (denoted as $u\prec v$) if and only if $\forall i\in \{1,\cdots ,n\},u_i\le v_i$ and $u\ne v$. This type of dominance is called weak dominance in which two vectors can be same in some objectives, but they should be different in at least one objective. However, in strict dominance, u has to be better on all objectives; i.e., it can not have the same objective value with v.

The Pareto optimality concept is defined from the dominance concept as follows.

Definition 2

(Definition (Pareto Optimality) [61]). A criterion vector u in a set of criterion vectors (S) is a Pareto optimal vector (non-dominated) if for every vector x, x does not dominate u, $x⪯u$.

Figure 1 shows Pareto optimal solutions and dominated solutions for a criterion value vectors (2D) ($f_1,f_2$). According to this definition, for a set of objective function vectors or criterion value vectors, the Pareto set is denoted as all Pareto optimal vectors which have no elements (criterion values) that can be decreased without simultaneously causing an increase in at least one of the other elements of vectors (assuming a Min-Min case).

Definition 3

(Definition (Pareto-front) [61]). For a given set S, the Pareto front is defined as set S $\{x\in S|\nexists y\in S,y\prec x\}$.

Figure 2 shows the Pareto front for two dimensional space for all four possible cases for minimizing or maximizing of two objective function vectors ($f_1,f_2$) or a two criterion value vectors ($f_1,f_2$).

Dominance depth ranking in the non-dominated sorting genetic algorithm (NSGA-II) was proposed by Deb et al. [13] to partition a set of objective function vectors (criterion value vectors) into several clusters by Pareto dominance concept. First, the non-dominated vectors in a set of criterion value vectors assigned to rank 1 and form the first Pareto front (PF1), and all these non-dominated vectors are removed. Then, non-dominated solutions are determined in the set and form the second Pareto front (PF2). This process is repeated for other remaining criterion value vectors until there is no vector left. Figure 3 illustrates an example of this ranking for a set of eight points (criterion value vectors) and

Table 2. A numerical example of computed new metrics for eight points shown in Figure 3. Four new statistical metrics are mean-ranks, median-ranks, dominated number, and nn-dominated number. Ranks-F1 and Ranks-F2 are ranks (two columns Ranks-F1 and Ranks-F2) for two criterion vectors F1 and F2.

Point	F1	F2	Ranks-F1	Ranks-F2	Mean-Ranks	Median-Ranks	Non-Dominated Number	Dominated Number
1	0.22	0.78	1	5	3	3	0	3
2	0.56	0.52	3	3	3	3	0	3
3	0.7	0.28	6	2	4	4	0	1
4	0.8	0.2	7	1	4	4	0	1
5	0.46	0.86	2	6	4	4	1	2
6	0.63	0.62	5	4	4.5	4.5	1	1
8	0.9	0.89	8	7	7.5	7.5	3	0
7	0.62	0.94	4	8	6	6	6	0

shows the coordinates of points. First points 1, 2, 3, and 4 as non-dominated solutions are ranked to rank 1. Then, for the rest of the points (points 5, 6, 7, and 8), non-dominated solutions are determined so points 5 and 6 as non-dominated solutions are ranked as 2 and removed. In the last iteration, the remaining points 7 and 8 are ranked as rank 3. The details of non-dominated sorting algorithm is presented in Algorithm 1.

Algorithm 1 Non-dominated sorting algorithm.

In [17], the dominance concept was used to identify the excellent scientists whose performances cannot be surpassed by others with respect to all criteria. The proposed method can provide a short-list of the distinguished researchers in the case of award nomination. It computes the sum of all criteria and sorts all researchers according to this calculated sum value. After that, the researcher with the maximum sum $r_{max}$ is placed in the skyline set. The second best researcher is compared with the researcher in the skyline set ($r_{skyline}$); if he/she is not dominated by $r_{max}$, he/she is added into the skyline set. This process is repeated for all remaining researchers to construct the skyline set: if they are not dominated by all researchers in the skyline set ($r_{skyline}$), then they are added into the skyline set. In fact, they select all researchers in the first Pareto front using the dominance concept. There is a well-known problem with the first Pareto created by the basic non-dominated sorting [17]. By increasing the number of criteria (more than three criteria) in the set of the criterion value vectors, a large number of the compared vectors become non-dominated vectors and are placed in the first Pareto front. By increasing the number of criteria, the chance of placing a criterion value vector while having only one better criterion value in the first Pareto front is increased. In order to demonstrate this problem,

Table 3. Indicators and the Pareto fronts from one to three by the non-dominated sorting on the country data.

Country	Rank	Documents	CI-DO	Citations	CPD	h-Index
United States	1	9,360,233	8,456,050	202,750,565	21.66	1783
Netherlands	1	746,289	682,627	16,594,528	22.24	752
Switzerland	1	541,846	501,917	12,592,003	23.24	744
Panama	1	5129	4830	137,585	26.82	142
Gambia	1	2004	1859	54,925	27.41	99
Bermuda	1	633	590	21,884	34.57	73
China	2	4,076,414	4,017,123	24,175,067	5.93	563
United Kingdom	2	2,624,530	2,272,675	50,790,508	19.35	1099
Sweden	2	503,889	471,036	10,832,336	21.5	666
Denmark	2	290,994	269,364	6,405,076	22.01	558
Iceland	2	15,625	14,353	357,678	22.89	218
Montserrat	2	95	93	2282	24.02	27
Germany	3	2,365,108	2,207,765	40,951,616	17.31	961
Canada	3	1,339,471	1,227,622	25,677,205	19.17	862
Israel	3	295,747	274,748	5,826,878	19.7	536
Faroe Islands	3	510	472	10,105	19.81	48
Guinea-Bissau	3	458	421	9357	20.43	50

shows three Pareto fronts by the non-dominated sorting for countries data extracted from the site “http://www.scimagojr.com” including five indicators: citable documents (CI-DO), citations, self-citations (SC), citations per document (CPD), and h-index; Table 3 shows the results of the non-dominated sorting method. As it can be seen from Table 3, three countries, Panama, Gambia, and Bermuda, are in the first Pareto front because they have higher values for only one criterion indicator (CPD) while other criteria values are low. Additionally, Montserrat has the rank 2 because it has the high value for only the CPD indicator.

In this paper, we propose a modified non-dominated sorting (described in Algorithm 2) to rank the scientific data. First we use the dominance depth ranking for all vectors; after that for each criterion value vector two new statistical metrics are calculated. For each vector, two metrics are the dominated number and the non-dominated number which show the number of the dominated vectors by this vector and the number of vectors which dominate this vector. Additionally, we used two other statistical measures proposed in [62]. These statistical measures are computed to sort the criterion value vectors. In [62], first for each criterion value $C_i$, all vectors are sorted according to this criterion value $C_i$ in ascending order and their ranks are assigned based on their sorting order. After that, for each criterion value vector some statistical measures like the minimum of its rank or the sum of its rank are used to make Pareto fronts.

We also sort all vectors according to each criterion value and calculate the ranks of vectors corresponding this sorting; after that we compute the mean and median of ranks of each vector as two new metrics. Table 2 shows an example of computed new metrics for eight points in Figure 3. $F_1$ and $F_2$ are the values of sample points in Figure 3 which are considered just as the numerical examples for a two-objective problem. For each point, ranks (two columns Ranks-F1 and Ranks-F2) for two criterion vectors ($F_1,F_2$) are computed according to their sorting order. Thus, we have four new statistical metrics (the mean and median of ranks, also the dominated number and the non-dominated number) which we use as criteria (objectives) to measure various levels of scientific achievement by applying dominance depth ranking again to make all Pareto fronts. We used the basic non-dominated sorting for data with two and three criteria and the modified non-dominated sorting for the data with more than three criteria. The proposed method has major advantages that are described in detail. In this method, vectors with one better criterion value than others cannot move toward the first front. Additionally, increasing the number of criteria cannot negatively influence the obtained ranks (no big portion of entities in the first front, as before); each rank corresponding to a Pareto front has a smaller number of vectors, so in total it assigns more ranks to the criterion vectors.

Algorithm 2 Modified non-dominated sorting algorithm.

In order to demonstrate the performance of this modified non-dominated sorting,

Table 4. The Pareto fronts from one to forth by the proposed method on the country data.

Country	Rank	Documents	CI-DO	Citations	CPD	h-Index
United States	1	9,360,233	8,456,050	202,750,565	21.66	1783
Netherlands	2	746,289	682,627	16,594,528	22.24	752
United Kingdom	2	2,624,530	2,272,675	50,790,508	19.35	1099
Switzerland	3	541,846	501,917	12,592,003	23.24	7444
China	3	4,076,414	4,017,123	24,175,067	5.93	563
Germany	3	2,365,108	2,207,765	40,951,616	17.31	961
Canada	3	1,339,471	1,227,622	25,677,205	19.17	862
Panama	4	5129	4830	137,585	26.82	142
Sweden	4	503,889	471,036	10,832,336	21.5	666
Denmark	4	290,994	269,364	6,405,076	22.01	558
Iceland	4	15,625	14,353	357,678	22.89	218
Japan	4	2,212,636	2,133,326	30,436,114	13.76	797
France	4	1,684,479	1,582,197	28,329,815	16.82	878

shows four Pareto fronts by the modified non-dominated sorting for extracted country data. Because the considered criteria have different scales, in all experiments, in order to apply the proposed method, they are normalized. As can be seen in the first Pareto front, only the United States is placed and Panama is in the forth Pareto front. Additionally, other countries with only one high criterion value, Gambia and Bermuda, which are in the first Pareto front by the non-dominated sorting method (as it can be seen in Table 3) are not placed in four Pareto fronts obtained by the modified non-dominated sorting method. Additionally, it can be seen that the number of countries in each Pareto front by using the modified non-dominated sorting is smaller than in basic non-dominated sorting.

In addition, we consider the period research as a new criterion value. Using Pareto dominance ranking makes it possible to have the research period as an independent indicator to be considered for ranking the scientific data. Considering the research period as the indicator provides a predication mean for some research cases. For example, suppose for comparing authors, criterion values be h-index and the research period $A_i=(h-index,time)$: two authors $A_1=(80,40)$ and $A_2=(20,10)$ would be in the same Pareto front because based on Pareto optimality concept, they do not dominate each other; therefore, we can predict that the author $A_2$ probably will be able to have the same performance as the author $A_1$ (or even better) after some years. According to observed values of indicators for universities, authors, and countries, this method can be utilized for prediction of their future performance. Additionally, the time length indicator enhances this ranking method with a traceable feature; that means by collecting data during times, we can observe how the performances of universities or researchers change and if they can improve their Pareto front ranks or not. In addition, this method can be applied to compute ranks by using obtained ranks from other ranking methods (ranking by multiple resources). In this way, each indicator is an obtained rank from a ranking method and it is expected that the non-dominated vectors in the first Pareto front contain the vectors with the minimum/maximum values of indicators, for Min-Min or Max-Max cases, respectively. Pareto dominance ranking can take into account any new kind of indicator as a new criterion value.

4. Experimental Case Studies and Discussion

We run the basic Pareto dominance ranking on the following scientific data with two and three criteria and modified Pareto dominance ranking on the following scientific data with more than three criteria. The first dataset includes 350 top computer science researchers (http://web.cs.ucla.edu/~palsberg/h-number.html) which contains a partial list of computer science researchers who each has an h-index of 40 or higher according to the Google Scholar report. This data has two indicators: research period (a low value is better) and h-index (a high value is better). The h-index values were collected from Google Scholar for the year 2016 and research period values were calculated from the year of the first publication of an author so far. The second dataset includes the 200 top universities ranked by URAP (a nonprofit organization (http://www.urapcenter.org)). This dataset has six indicators: article, citation, total document (TD), article impact total (AIT), citation impact total (CIT), and international collaboration (IC). The third dataset has 231 top countries (for the year 2015) extracted from the site SJR (http://www.scimagojr.com), including six indicators: documents, citable documents (CI-DO), citations, self-citations (SC), citations per document (CPD), and h-index. We do not consider the SC indicator because it is not certain that the maximum value or minimum value of this value is desirable. The forth dataset consists of the three ranks of 100 top common universities collected from three resources; the QS World University Rankings (https://www.topuniversities.com), URAP (http://www.urapcenter.org), and CWUR Rankings (http://cwur.org). In the following, we report all results of mentioned approaches on the four datasets in detail.

4.1. The First Case Study: Ranking Researchers

Table A1. Indicators and Pareto ranks for the author data. Indicators are h-index and the research period (RP).

Author	Rank	RP	H-Index	Author	Rank	RP	h-Index
A.Herbert	1	40	162	Burgard Wolfram	6	19	89
K.Anil	1	25	153	MllerKlaus Robert	6	18	86
Han Jiawei	1	21	136	Horrocks Ian	6	18	86
van Wil	1	18	124	Liu Bing	6	17	68
Buyya Rajkumar	1	16	98	Harman Mark	6	16	59
Perrig Adrian	1	15	82	Dongarra Jack	7	32	114
ZhouZhi-Hua	1	14	71	A.John	7	29	107
Shenker Scott	2	23	133	Nayar Shree	7	23	102
Foster Ian	2	21	117	SeidelHans-Peter	7	22	88
Salzberg Steven	2	20	116	Rexford Jennifer	7	19	86
Schölkopf Bernhard	2	18	105	Govindan Ramesh	7	18	81
Schmid Cordelia	2	17	83	Gao Wen	7	17	66
Abraham Ajith	2	15	71	Grossberg Stephen	8	35	114
Xiao Yang	2	14	59	Dubois Didier	8	32	112
Sejnowski Terrence	3	30	132	H.Randy	8	31	106
Haussler David	3	27	129	Horowitz Mark	8	29	104
I.Michael	3	25	128	Osher Stanley	8	28	101
Zisserman Andrew	3	24	121	Szeliski Richard	8	25	98
Estrin Deborah	3	22	114	H.Vincent	8	24	96
Koller Daphne	3	21	110	Malik Jitendra	8	23	95
Herrera Francisco	3	20	107	B.Mani	8	20	86
Balakrishnan Hari	3	18	100	Baraniuk Richard	8	20	86
Staab Steffen	3	17	80	Fox Dieter	8	19	85
Tan Tieniu	3	16	69	HubauxJean-Pierre	8	18	72
Wattenhofer Roger	3	15	68	Lee Wenke	8	18	72
Kanade Takeo	4	30	131	Blaauw David	8	18	72
S.Philip	4	25	126	Sahai Amit	8	17	63
Giannakis Georgios	4	24	117	Prade Henri	9	32	111
Zhang Hong Jiang	4	22	110	Vetterli Martin	9	27	96
F.Ian	4	18	96	Kumar Vipin	9	24	95
WuJie	4	17	73	Deb Kalyanmoy	9	23	93
Sukhatme Gaurav	4	17	73	Benini Luca	9	20	85
Vasilakos Athanasios	4	16	67	McCallum Andrew	9	19	84
Cao Guohong	4	15	61	Kumar Ravi	9	18	69
Garcia-MolinaHector	5	29	125	LiXiang-Yang	9	17	57
Towsley Don	5	27	117	Demaine Erik	9	17	57
Culler David	5	24	113	H.Christos	10	34	110
Jennings Nick	5	22	107	Yager Ronald	10	33	101
Halevy Alon	5	21	94	Sangiovanni-VincentelliAlberto	10	32	99
Horvitz Eric	5	20	92	Agrawal Rakesh	10	25	95
J.Alexander	5	18	90	A.Thomas	10	24	93
Abdelzaher Tarek	5	17	72	Bellare Mihir	10	23	90
Fedkiw Ronald	5	16	60	Dorigo Marco	10	21	85
Poggio Tomaso	6	34	121	Karger David	10	20	84
E.Geoffrey	6	31	117	Friedman Nir	10	19	79
Pentland Alex	6	28	112	A.Carlos	10	18	67
VanLuc	6	22	104	D.Jeffrey	11	40	104
ChangShih-Fu	6	21	91	Shneiderman Ben	11	35	103
Szalay Alex	11	26	95	Mitzenmacher Michael	14	19	66
Sheth Amit	11	25	90	Reichert Manfred	14	18	60
Shah Mubarak	11	23	86	Davis Larry	15	36	93
Jiang Tao	11	22	85	Ayache Nicholas	15	29	90
Wooldridge Michael	11	21	81	Finin Tim	15	28	86
Gross Markus	11	20	77	Bertino Elisa	15	27	83
Domingos Pedro	11	19	75	Joaquin Jose	15	24	80
H.Jason	11	18	66	Mukher jee Biswanath	15	23	79
Suri Subhash	11	18	66	Vahdat Amin	15	22	74
Zadeh Lotfi	12	40	100	J.Michael	15	22	74
H.Gene	12	38	99	Joshi Anupam	15	21	71
E.David	12	27	95	K. Sajal	15	20	69
Widom Jennifer	12	26	91	Vaidya Nitin	15	20	69
ZhangLixia	12	25	88	Thiele Lothar	15	20	69
Dumais Susan	12	23	84	Pappas George	15	19	65
Schulzrinne Henning	12	22	81	Kraut Robert	16	29	88
Freeman William	12	22	81	Pedrycz Witold	16	28	83
Bengio Yoshua	12	21	76	Abadi Martin	16	27	81
Ray LiuK.J.	12	20	75	Hendler James	16	25	80
Wagner David	12	19	72	Roy Kaushik	16	23	76
Lu Songwu	12	18	63	Rus Daniela	16	21	70
W.Bruce	13	30	93	Handley Mark	16	21	70
Jajodia Sushil	13	27	92	Qiao Chunming	16	20	66
Anderson Thomas	13	26	86	Pollefeys Marc	16	19	63
Unser Michael	13	24	83	Y.Moshe	17	33	88
Manocha Dinesh	13	23	81	Doyle John	17	31	87
Perona Pietro	13	23	81	S.Kishor	17	31	87
Darrell Trevor	13	23	81	Alon Noga	17	29	85
Tsudik Gene	13	22	76	L.Ronald	17	29	85
Pevzner Pavel	13	22	76	Sontag Eduardo	17	28	82
Karypis George	13	22	76	C.Lee	17	26	79
Nahrstedt Klara	13	21	75	Taylor Chris	17	24	74
Yao Xin	13	21	75	S.Theodore	17	23	73
Diot Christophe	13	20	74	Reiter Michael	17	21	69
Goble Carole	13	19	69	Herrera Enrique	17	20	65
Liu Huan	13	19	69	Belongie Serge	17	19	62
Tse David	13	19	69	von John	18	40	87
Alouini Mohamed-Slim	13	18	61	Yannakakis Mihalis	18	35	86
M.John	14	33	93	A.David	18	30	84
Faugeras Olivier	14	30	91	Hebert Martial	18	30	84
Chellappa Rama	14	28	90	Dally William	18	29	80
De Giovanni	14	27	87	Blake Andrew	18	28	79
Sycara Katia	14	25	83	Baldi Pierre	18	26	77
Franklin Michael	14	24	81	Greenberg Saul	18	26	77
Rost Burkhard	14	23	80	S.Daniel	18	26	77
Crowcroft Jon	14	22	75	Alur Rajeev	18	25	74
McKeown Nick	14	20	73	B.Andrew	18	24	73
Suciu Dan	14	20	73	Fua Pascal	18	24	73
Varghese George	18	23	70	Rothermel Gregg	21	21	60
Yao Yiyu	18	23	70	Gray Jim	22	39	79
LeJean-Yves	18	23	70	Y.Joseph	22	32	78
PedramMassoud	18	23	70	BezdekJames	22	31	76
Savage Stefan	18	22	69	Kiesler Sara	22	31	76
Sandholm Tuomas	18	22	69	Terzopoulos Demetri	22	29	74
D.Gregory	18	22	69	Lenzerini Maurizio	22	27	70
Leymann Frank	18	21	65	J.Haim	22	27	70
Jha Somesh	18	21	65	Peterson Larry	22	26	69
Rogaway Philip	18	21	65	Shasha Dennis	22	26	69
R.John	18	21	65	Agrawal Divyakant	22	26	69
Shenoy Prashant	18	20	63	Baeza-YatesRicardo	22	25	68
Canetti Ran	18	20	63	C.JayC	22	24	67
Gunopulos Dimitrios	18	19	61	Stolcke Andreas	22	23	65
Pearl Judea	19	30	83	L.Michael	22	23	65
Ramakrishnan Raghu	19	29	78	Alonso Gustavo	22	22	62
Waibel Alex	19	28	77	S.B.	22	22	62
Li Kai	19	27	76	V.S.Laks	22	21	59
EtzioniOren	19	26	75	S.David	23	37	78
Cohen-OrDaniel	19	25	73	Magnenat-ThalmannNadia	23	32	75
Metaxas Dimitris	19	24	70	Kaufman Arie	23	29	72
Veloso Manuela	19	24	70	Devadas Srinivas	23	27	69
Smyth Padhraic	19	22	68	Cipolla Roberto	23	25	67
Kacprzyk Janusz	19	21	64	Salesin David	23	24	65
Schaffer Alejandro	19	21	64	Kotz David	23	23	63
Voelker Geoffrey	19	20	62	Druschel Peter	23	22	61
Decker Stefan	19	19	59	L.Olvi	24	40	78
Norman Don	20	40	83	C.Fernando	24	33	74
Bertsekas Dimitri	20	31	82	S.Andrew	24	30	71
Abiteboul Serge	20	29	77	Kautz Henry	24	28	69
Hanrahan Pat	20	28	76	Dill David	24	27	68
A.Edward	20	27	75	H.Mostafa	24	26	67
Cong Jason	20	25	70	Gropp William	24	25	65
Campbell Andrew	20	23	68	Ostrovsky Rafail	24	24	62
C.Ming	20	22	67	Altman Eitan	24	24	62
Zorzi Michele	20	21	61	Smyth Barry	24	22	59
Mylopoulos John	21	33	80	Crovella Mark	24	22	59
Thalmann Daniel	21	32	79	Newell Allen	25	40	75
Adeli Hojjat	21	30	76	Samet Hanan	25	36	73
Myers Brad	21	30	76	Harel David	25	33	72
Smith Barry	21	28	74	Mitchell Tom	25	32	71
Witten Ian	21	26	70	Yuille Alan	25	30	70
K.Sankar	21	25	69	D. Hill Mark	25	30	70
Sandhu Ravi	21	25	69	Stolfo Salvatore	25	30	70
J.Ingemar	21	24	68	G.Kim	25	29	68
Stojmenovic Ivan	21	23	67	Gottlob Georg	25	28	67
Cootes Tim	21	23	67	Haralick Robert	25	27	66
Anderson Ross	21	22	66	Nisan Noam	25	26	64
van Frank	25	25	62	Shadbolt Nigel	28	25	59
W.William	25	24	61	Ishibuchi Hisao	28	24	58
Rogers Yvonne	25	22	58	Rastogi Rajeev	28	24	58
Fagin Ronald	26	38	73	Gelenbe Erol	29	39	66
W.Thomas	26	34	70	H.Russell	29	33	65
Vitter Jeffrey	26	30	69	Reif John	29	33	65
Mooney Raymond	26	30	69	Salton Gerard	29	32	64
Cohen Michael	26	29	67	Dietterich Thomas	29	30	63
Canny John	26	29	67	Kramer Jeff	29	29	61
Burns Alan	26	28	66	Bajaj Chandrajit	29	29	61
Deriche Rachid	26	27	65	Aiken Alex	29	27	60
W.Wen-Mei	26	26	62	Wiederhold Gio	29	26	59
Keutzer Kurt	26	26	62	Dasgupta Dipankar	29	24	52
Pazzani Michael	26	26	62	Wilks Yorick	30	40	66
Blum Avrim	26	25	61	Turner Jonathan	30	31	63
Nejdl Wolfgang	26	24	60	Elmagarmid Ahmed	30	28	59
de Maarten	26	22	57	Motta Enrico	30	26	58
Ceri Stefano	27	32	68	Herman Gabor	31	40	65
Levy Henry	27	30	67	F.James	31	32	62
Tambe Milind	27	28	65	Larus James	31	29	58
K.Pankaj	27	27	63	ChenMing-Syan	31	27	57
Knoblock Craig	27	27	63	LeeDer-Tsai	31	26	53
Fogel David	27	24	59	Reddy Sudhakar	32	35	62
Baruah Sanjoy	27	23	56	Beth Mary	32	30	58
Bobrow Daniel	28	40	67	I.Norman	33	37	62
Hennessy John	28	30	66	Dolev Danny	33	35	60
Ni Lionel	28	29	65	Padua David	33	33	58
Wadler Philip	28	28	64	Nicolau Alex	33	31	56
Peleg David	28	28	64	V. Aho Alfred	34	40	62
P.Michael	28	27	62	Sifakis Joseph	34	32	56
Malik Sharad	28	25	59	A.Edward	35	32	55

indicates the names of researchers, research period, h-index, and the obtained Pareto ranks from the basic Pareto dominance ranking (Pareto ranking). From Table A1, it can be seen that first Pareto ranks include researchers with high values of h-index and low research period values. For instance, the researcher “Zhi-Hua Zhou” has the minimum value of research period 14 and the researcher “A. Herbert” has the maximum value of h-index, 162. Researchers in the first Pareto front are A. Herbert, K. Anil, Han Jiawei, Van Wil, Buyya Rajkumar, Perrig Adrian, and Zhou Zhi-Hua; the second Pareto front contains Shenker Scott, Foster Ian, Salzberg Steven, Schlkopf Bernhard, Schmid Cordelia, Abraham Ajith, and Xiao Yang. Additionally, it can be observed that researchers with the maximum value of research year indicator (40) are associated with the higher rank because they are dominated by other researchers according to Pareto dominance concept. Researchers having values close to the value of h-index 52 or higher are associated with the higher rank due to the Pareto dominance concept. Figure 4 shows the ranks in terms of Pareto fronts for all researchers. It can be seen from Figure 4 that the extent of improvement for a researcher $A_i$ can change his/her Pareto front ranking by looking at researchers which dominate $A_i$ and are located in the better Pareto fronts.

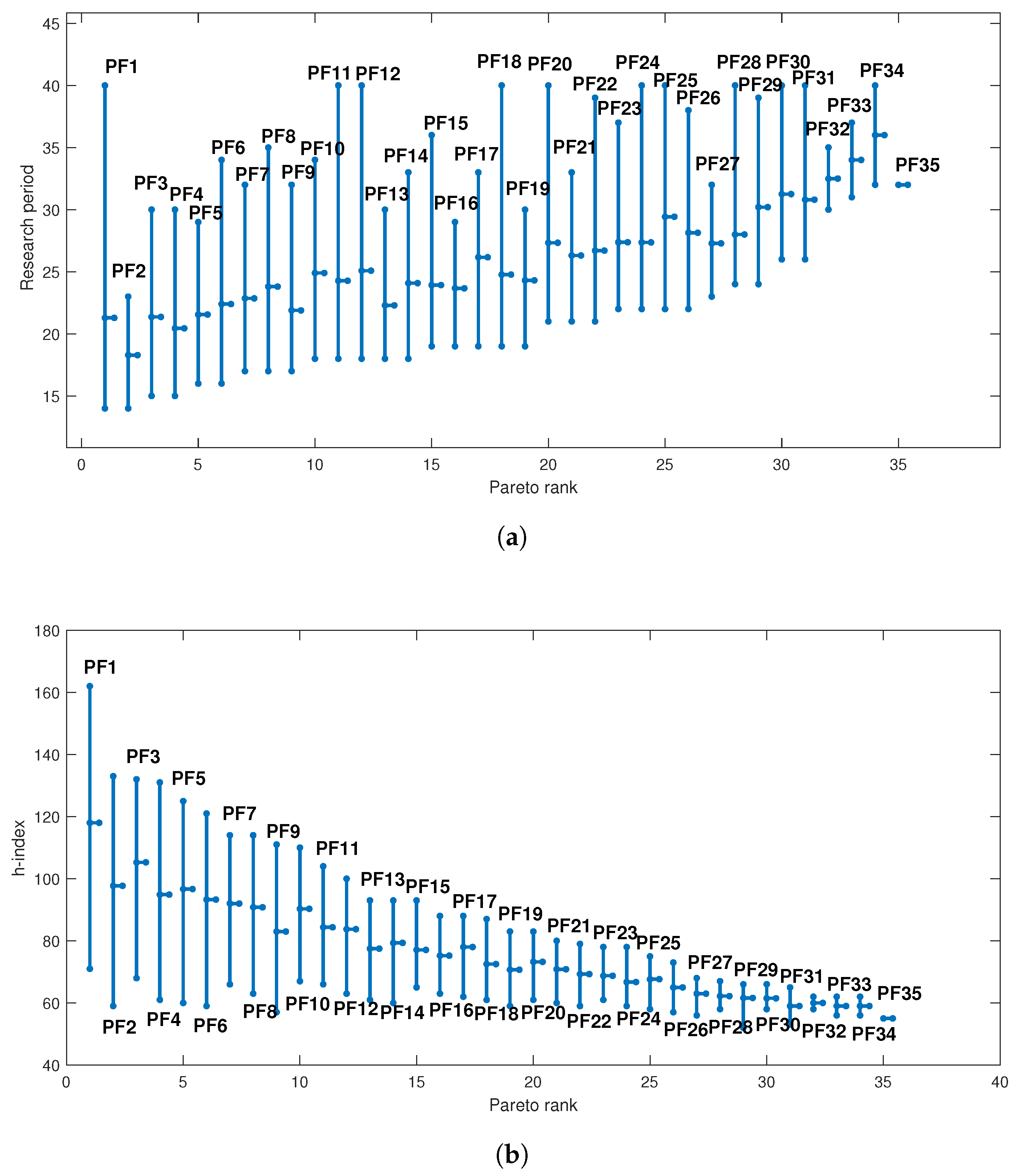
To gain a better understanding of the Pareto ranking with each indicator, we plot the obtained Pareto ranks from the first rank to the thirty fifth versus each indicator. In Figure 5, vertical lines demonstrate Pareto ranks from the first rank to the thirty fifth, which at the top of each line indicates the maximum value of the indicator; its bottom is the minimum value of the indicator; and the short horizontal tick in the middle of each line is the average value of the indicator. Figure 5 indicates that the research period of the first Pareto front includes values with the maximum and minimum of the length time. That is reasonable because it is expected that authors who have had more time have higher h-index values so they could be located in the first Pareto front, and younger authors having had shorter research periods and reasonable h-index values also could be in the first Pareto front. The average values of the research period for the beginning Pareto fronts are low values while the last Pareto fronts have higher average values. From Figure 5, we can see that the maximum, average, and minimum of h-index values for Pareto fronts decrease from the first Pareto front to the 35th. Additionally, the first Pareto front has the maximum h-index values and the last Pareto front includes the minimum h-index values.

4.2. The Second Case Study: Ranking of Universities

Six indicators of university dataset and their ranks obtained by modified Pareto dominance ranking are summarized in

Table A2. Indicators and Pareto ranks for the university data. Indicators are article, citation, Total Document (TD), Article Impact Total (AIT), Citation Impact Total (CIT), International Collaboration (IC), and the research period (RP).

University	Rank	Article	Citation	TD	AIT	CIT	IC	RP
Harvard University	1	126	126	60	108	90	90	380
University of Toronto	1	125	125	59	105.21	69.32	89	189
Stanford University	1	112.36	124.36	49.4	102.94	75.04	70.32	131
Johns Hopkins University	1	113.67	122.23	52.63	99.61	70.65	71.43	140
University of California Los Angeles	1	107.16	114.03	49.09	96.08	67.17	68.06	97
University of California San Diego	1	98.67	105.73	45.03	90.89	65.07	65.29	56
University of California Berkeley	2	105.06	117.51	44.83	103.2	74.81	71.13	148
Imperial College London	2	102.43	103.35	47.03	88.11	61.83	76.89	109
KU Leuven	2	98.43	94.22	44.4	83.16	56.85	76.42	48
Pierre & Marie Curie University - Paris 6	2	99.24	94.84	41.98	83.2	58.1	72.36	45
University of Oxford	2	115.22	119.72	51.44	103.96	72.49	85.11	920
University College London	2	116.44	113.55	54.13	97.6	65.34	84.34	190
University of Washington Seattle	2	108.58	116.21	48.95	97.19	68.28	67.17	155
Massachusetts Institute of Technology (MIT)	3	98.63	121.19	42.3	107	89	67.57	155
University of British Columbia	3	99.67	97.32	45.22	85.14	59.24	71.99	108
National University of Singapore	3	98.37	93.31	42.62	80.8	55.57	72.93	36
University of Cambridge	3	107.79	114.24	48.42	99.83	70.45	81.35	807
University of Michigan	3	114.84	113.74	51.62	97.45	64.64	68.39	199
University of Tokyo	3	108.06	101.7	46.83	87.92	57.8	66.55	139
Zhejiang University	4	111.19	89.26	44.39	77.61	51.52	60.98	119
Tsinghua University	4	107.94	89.06	41.91	79.41	53.07	60.46	105
Universidade de Sao Paulo	4	109.85	83.6	47.45	73.44	49.63	67.18	82
Seoul National University	4	102.76	89.17	44.18	75.39	51.38	59.98	70
Nanyang Technological University	4	88.18	86.44	37.67	75.84	54.57	64.08	25
University of Pennsylvania	4	105.54	113.05	49.83	93.83	66.55	63.03	276
University of Chicago	4	94.78	103.18	43.22	89.78	65.95	62.39	126
University of California San Francisco	4	93.26	107.72	45.4	85.02	65.38	60.39	143
Cornell University	4	97.05	100.49	44.67	85.3	60.8	63.24	151
University of Sydney	4	101.35	93.57	46.99	81.14	55.77	70.05	166
Monash University	4	95.25	86.58	42.4	73.35	51.78	64.32	58
Columbia University	4	103.52	109.56	47.37	93.12	66.28	66.84	262
Duke University	4	96.65	102.58	45.32	85.08	61.46	61.91	178
Shanghai Jiao Tong University	5	112.85	87.81	43.93	75.74	50.9	60.55	120
University of Melbourne	5	99.48	92.8	44.23	80.4	55.86	67.58	163
University of Queensland	5	98.53	90.06	42.98	77	53.44	67.19	107
University of California Davis	5	93.06	90.56	42.42	80.29	56.63	61.71	111
Free University of Berlin	5	88.74	86.87	41.62	71.8	52.31	62.58	68
University of Copenhagen	5	103.59	100.53	45.35	85.42	60.5	75.63	537
University of Minnesota Twin Cities	5	100.35	96.34	45.2	84.67	57.89	62	165
Central South University	6	86.42	71.48	36.15	61.6	46.73	50.01	16
Peking University	6	106.48	90.88	42.87	79.04	53.52	63	118
University of Colorado Boulder	6	95.39	95.59	42.51	81.87	59.08	59.03	140
Ohio State University	6	97.46	91.51	43.97	82.1	57.84	60.06	146
University of Florida	6	93.55	88.3	42.92	77.72	54.49	60.9	111
Aarhus University	6	90	85.21	40.03	72.48	52.05	65.48	88
University of Wisconsin Madison	6	96.46	95.44	43.5	86.34	60.62	60.17	168
University of Pittsburgh	6	94.27	98.62	45.51	81.7	58.97	58.91	229
Yale University	6	96.84	103.83	45	88.02	64.44	62.73	315
Swiss Federal Institute of Technology Zurich	7	91.5	90.14	39.43	80.86	57.2	69.92	162
California Institute of Technology	7	80.64	91.01	35.94	80.84	64.69	58.91	125
University of Paris Diderot - Paris VII	7	82.43	84.92	37.03	73.33	56.17	60.31	46
Radboud University Nijmegen	7	83.98	82.98	38.7	72.31	53.82	61.26	93
McGill University	7	95.02	91.31	43.21	79.8	56.3	67.91	195
Kyoto University	7	94.92	87.64	42.22	75.7	52.31	58.98	119
University of New South Wales	7	91.21	83.93	40.66	72.61	51.45	63.02	67
University of North Carolina Chapel Hill	7	93.35	96.13	43.42	79.93	58.08	57.65	227
Erasmus University Rotterdam	8	82.84	85.67	39.48	71.33	53.86	59.63	103
University of Calgary	8	80.47	77.12	37.76	65	48.87	56.69	50
Maastricht University	8	77.35	74.82	35.99	63.26	48.58	55.98	40
University of California Santa Cruz	8	68.71	76.1	32.27	66.59	57	49.98	51
Northwestern University	8	92.54	94.9	42.41	80.53	58.41	57.42	165
Penn State University	8	94.46	91.75	42.03	79.6	55.67	60.55	161
University of Texas Austin	8	88.6	88.4	39.15	78.45	57.02	57.21	135
University of Alberta	8	89.92	82.62	40.87	72.13	51.38	62.21	108
Ecole Polytechnique Federale de Lausanne	8	78.45	81.86	35	71.47	54.97	59	51
University of Bristol	9	81.61	79.97	37.38	71.3	52.96	57.94	85
University of Paris Descartes - Paris V	9	78.7	78.14	36.4	64.68	49.81	55.65	45
University of Manchester	9	92.82	88.76	42.55	78.18	55.6	65.72	192
Washington University (WUSTL)	9	85.81	95.32	40.77	77.39	60.3	54.55	163
Fudan University	9	96.36	84.67	39.85	71.27	51.04	56.62	111
University of Southern California	9	86.45	86.57	39.75	73.86	54.66	56.58	136
VU University Amsterdam	9	86.49	84.65	39.82	72.01	52.62	62.11	136
University of Utrecht	9	92.3	92.51	42.21	78.61	56.05	66.52	380
University of Edinburgh	9	87.11	90.17	40.58	78.94	58.37	63.87	433
National Taiwan University	9	90.25	81.46	40.39	71.78	50.26	56.72	88
University of California Irvine	10	79.5	82.59	37.07	72.39	54.64	54.56	109
University of Claude Bernard - Lyon 1	10	77.39	75.36	35.21	66.46	50.37	55.59	45
Kings College London	10	88.56	87.8	42.28	75.5	55.64	63.08	187
University of Zurich	10	86.5	86.17	39.27	75.24	56.02	65.28	183
Vanderbilt University	10	84.94	88	39.85	74.73	56.02	54.13	143
University of Arizona	10	83.28	82.38	38.22	73.32	53.9	56.68	131
Sun Yat Sen University	10	93.75	79.59	38.93	68.85	49.69	53.61	92
University of Science & Technology of China	10	87.03	79.64	36.29	70.31	50.91	53.34	58
University of Hamburg	10	80.76	77.61	36.9	69.02	52.67	57.03	97
Tel Aviv University	10	83.45	77	38.05	67.76	49.97	57.41	60
University of Barcelona	10	93.33	92.11	42.39	77	55.09	66.57	566
Ruprecht Karl University Heidelberg	10	88.26	91.02	41.16	77.82	57.81	63.37	630
Karolinska Institutet	10	90.45	90.45	41.42	73.53	54.38	67.8	206
University of Munich	10	88.4	89.24	40.73	76.67	56.6	64.03	544
Osaka University	10	87.89	81.47	39.53	69.8	50.18	54.72	85
University of Milan	10	82.84	78.7	38.18	68.29	51.19	56.66	92
University of Illinois Urbana-Champaign	11	88.61	83.81	39.34	75.86	53.9	57.68	149
Nanjing University	11	92.16	79.86	37.74	70.4	50.36	53.5	101
University of Geneva	11	78.31	80.67	36.53	71.01	54.96	59.55	140
University of Birmingham	11	79.7	78.21	38.05	69.02	52.11	56.73	116
Autonomous University of Barcelona	11	80.98	76.79	36.54	67.87	50.52	57.14	48
Universite Toulouse III - Paul Sabatier	11	77.42	75.94	34.94	65.12	49.64	56.82	47
University of Alabama Birmingham	11	75.88	78.19	36.86	64.02	49.9	50.24	47
Ghent University	11	92.24	83.31	40.58	74.82	52.29	67.23	199
New York University	11	88.57	86.84	41.02	76.06	55.34	56.61	185
Humboldt University of Berlin	11	87.79	86.45	41.06	73.29	53.69	61.82	205
Boston University	11	82.06	86.78	38.39	76.7	58.5	55.3	177
University of Montreal	11	84.99	81.52	39.57	70.85	51.58	60.52	138
Tohoku University	11	86.88	80.11	39.29	68.53	49.14	56.83	105
Universidade de Lisboa	11	84.96	75.09	37.75	67.52	48.99	60.59	105
University of Amsterdam	11	89.6	87.32	40.78	75.05	54.47	63.83	384
King Abdulaziz University	12	83.13	71.26	34.2	62.39	47.72	61.55	49
University of Maryland College Park	12	85.53	85.24	37.8	77.5	56.03	57.62	160
Huazhong University of Science & Technology	12	94.22	76.78	38.13	67.75	48.51	52.97	109
University of California Santa Barbara	12	74.07	79.24	34.15	70.92	56.17	52.51	125
King Saud University	12	81.61	70.42	35.17	60.55	46.49	61	59
Technical University of Munich	12	85.41	82.83	38.02	70.76	52.07	60.24	148
Australian National University	12	80.86	76.09	36.24	66.79	49.53	57.88	70
Jilin University	12	90.4	75.46	37.77	64.59	47.77	50.8	70
University of Groningen	12	88.8	87.97	40.77	74.11	53.71	63.99	402
University of Helsinki	13	85.98	84.46	38.79	73.96	54.45	63.63	376
Emory University	13	85.31	88.39	41.09	71.91	54.01	54.36	180
University of Oslo	13	84.56	81.86	38.4	71.61	53.18	61.9	205
Princeton University	13	79.62	84.19	35.91	76.18	58.53	55.73	270
Shandong University	13	92.53	75.48	37.9	66.61	48.45	51.74	115
University of Leeds	13	79.38	76.98	37.34	66.19	49.77	56.86	112
Newcastle University - UK	13	75.18	74.08	36.15	63.05	48.62	53.74	53
Sapienza University Rome	13	90.05	81.21	40.4	74.67	53.66	60.14	713
University of Hong Kong	13	81.72	77.6	36.83	66.37	49.24	54.98	105
Harbin Institute of Technology	13	88.78	73.47	37.14	65.59	47.69	51.92	96
Universidad Nacional Autonoma de Mexico	13	82.93	71.29	36.55	61.79	46.56	56.98	106
University of Miami	13	75.35	77.57	36.29	64.56	50.1	51.28	91
Purdue University	14	84.43	78.86	37.5	71.8	51.79	55.03	140
McMaster University	14	80.98	79.62	38.05	67.28	50.46	57.26	129
Sichuan University	14	91.37	74.89	38.2	63.79	47.25	50.46	120
Nagoya University	14	79.99	74.5	36.4	65.02	48.7	51.87	77
University of Gothenburg	14	77.19	74.76	35.24	63.31	48.54	55.41	62
Leiden University	14	83.95	85.71	38.7	72.45	54.93	60.88	441
Lund University	14	85.58	82.77	38.57	72.11	52.93	63.82	350
Hebrew University of Jerusalem	14	77.35	75.99	35.91	64.76	49.23	55.37	98
Wageningen University & Research Center	14	76.89	75.2	34.63	65.23	49.34	56.74	98
Georgia Institute of Technology	15	80.78	78.99	35.89	69.09	51.11	54.8	131
University of Waterloo	15	78.08	72.61	34.88	64.28	48.17	54.96	59
Rutgers State University	15	82.92	82.39	38.89	73.02	53.17	56.11	250
Texas A & M University College Station	15	85.21	78.81	37.8	70.59	50.83	57.22	163
University of Southampton	15	82.64	78.11	37.56	69.57	51.27	59.62	147
Michigan State University	15	83.49	79.5	37.73	70.72	51.52	55.15	161
University of Sheffield	15	78.55	75.56	36.89	67.27	50.39	55.73	111
University of Illinois Chicago	15	77.49	74.21	36.76	65.53	49.57	50.96	103
University of Paris Sud - Paris XI	15	83.29	82.86	37.31	73.7	54.24	61.5	759
Uppsala University	15	84.96	82.76	37.95	70.97	52.49	62.68	539
University of Aix-Marseille	15	85.64	81.77	38.19	71.74	52.21	61.44	607
University of Utah	16	82.83	81.24	38.29	68.1	51.19	53.08	166
University of Nottingham	16	80.15	78.05	37.97	67.01	50.12	56.48	135
University of Bonn	16	77.93	78.15	36.02	68.19	52.04	57.07	198
Yonsei University	16	87.79	76.2	38.48	65.27	47.85	52.65	131
Xian Jiaotong University	16	88.95	72.43	36.56	63.84	47.52	51.96	120
Universidade do Porto	16	79.21	72.6	36	62.61	47.42	56.16	105
Goethe University Frankfurt	16	74.56	75.63	35.37	63.9	49.5	54.17	102
University of Padua	16	85.18	81.27	38.58	71.73	53.36	59.63	794
University of Western Australia	16	84.57	80.2	38.33	67.65	50.13	60.08	457
Universite Grenoble Alpes (UGA)	16	77.79	79.09	36.13	71.06	52.39	60.35	474
University of Bern	17	79.33	76.3	36.17	67.17	51.5	58.97	182
University of Virginia	17	78.15	78.2	36.72	68.55	52.23	52.2	197
Arizona State University	17	80.2	77.56	36.18	67.63	50.64	52.32	131
University of Iowa	17	78.68	76.15	36.98	68.19	51.93	51.01	169
Korea University	17	82.74	74.18	36.72	65.69	48.43	52.28	111
Cardiff University	17	75	76.04	35.9	65.22	50.76	54.59	133
University of Cologne	17	76.7	73.92	35.31	62.77	48.49	54.45	97
Charite Medical University of Berlin	17	78.46	80.17	37.97	65.5	50.48	55.65	306
University of Liverpool	17	77.49	74.92	36.09	65.56	50	56.24	135
Kyushu University	17	80.46	73.69	36.6	63.72	47.82	51.47	105
Tongji University	17	84.92	71.28	35.94	61.55	46.65	51.38	109
Hokkaido University	17	79.61	73.24	36.18	62.39	47.2	51.53	98
University of Bologna	17	81.81	76.2	37.47	69.83	51.99	56.52	928
Universite de Toulouse	17	81.97	77.85	36.5	67.4	49.97	59.67	787
University of Glasgow	17	77.61	77.37	37	68.44	51.98	56.16	565
Stockholm University	18	75.64	74.11	33.97	65.57	50.76	55.41	138
Brown University	18	77.68	78.44	36.28	68.39	52.87	51.02	252
Dresden University of Technology	18	78.34	76.02	35.85	66.66	50.43	55.25	188
RWTH Aachen University	18	77.44	74.74	35.37	65.96	50.2	54.39	146
University of Rochester	18	74.66	76.75	35.64	66.57	51.31	51.18	166
Wuhan University	18	85.16	73.3	35.54	63.01	47.56	50.48	123
Eberhard Karls University of Tubingen	18	78.97	78.74	36.83	66.24	50.28	57.19	539
University of Basel	18	77.08	77.77	35.86	65.65	50.75	58.36	556
Technical University of Denmark	19	78.02	75.91	34.54	66.6	50.24	56.59	187
University of Gottingen	19	77.24	75.75	35.5	66.69	50.57	55.63	282
University of Ottawa	19	79.59	75.55	37.19	64.48	48.61	54.72	168
Case Western Reserve University	19	76.74	78.47	36.39	65.74	51.09	50.86	190
Western University (University of Western Ontario)	19	78.89	74	36.79	63.15	47.77	54.05	138
University of Auckland	19	76.53	71.95	35.01	63.94	48.93	54.97	133
Sungkyunkwan University	19	85.09	76.39	37	66.37	49.54	51.96	618
University of Freiburg	19	76.35	76.61	35.91	67.04	51.55	55.89	559
University of Erlangen Nuremberg	20	79.19	76.92	36.16	65.15	49.36	55.93	273
University of Adelaide	20	79.41	73.54	35.7	63.9	48.62	54.39	142
Lomonosov Moscow State University	20	82.26	69.62	36.05	64.56	48.18	54.81	261
North Carolina State University	20	79.13	73.4	35.37	64.17	48.05	51.84	129
Universite de Montpellier	20	78.34	76.42	36.02	65.05	49.07	58.46	727
Karlsruhe Institute of Technology	20	77.15	73.49	34.36	65.91	49.88	55.64	191
University of Munster	21	75.94	76.75	35.61	64.51	49.82	54.1	236
Queen Mary University London	21	73.49	74.2	35.02	64.12	50.58	52.71	231
Charles University Prague	21	79.55	73.28	36.4	65.57	49.64	56.59	668
University of Naples Federico II	22	79.04	73.63	35.99	66.4	50.47	53.7	792
University of Turin	23	76.97	74.11	35.51	64.7	49.94	53.26	612
Johannes Gutenberg University of Mainz	23	74.47	73.39	34.66	64.26	49.86	53.68	539

. As mentioned in Section 3, for fair comparison, we add the time period of academic research (the research period (RP)) mentioned in Table A2 as an indicator in the data which is calculated as the length of the university established year to present. Based on the proposed method, the first Pareto front has six universities, including top universities; for example, Harvard University, University of Toronto, and Stanford University. In the basic Pareto dominance ranking, the first Pareto front has twenty universities. Additionally, the proposed ranking clusters this data into twenty three Pareto fronts but the Pareto dominance ranking has only eight Pareto fronts. As was mentioned in the Section 3, the proposed method can assign more ranks to the criterion vectors even by increasing the number of criteria (many-metric cases).

In order to deep understand the behavior of the obtained Pareto ranks and indicators, we plot the maximum, minimum, and average of values for all indicators versus Pareto ranks in Figure 6, Figure 7 and Figure 8 as mentioned before. It can be seen from these figures—all plots for six indicators—that there is a decreasing behavior in terms of the maximum, minimum, and average values, observable from the first Pareto front to the last Pareto front. In addition, Figure 9 visualizes universities in the four top ranked Pareto fronts. Each line illustrates one university (a five dimensional vector) in which the values of five indicators are presented using vertical axes; i.e., coordinate’s value.

4.3. The Third Case Study: Ranking of Countries

Table A3. Indicators and Pareto ranks for the country data. Indicators are documents, Citable Documents (CI-DO), citations, Citations Per Document (CPD), and h-index.

Country	Rank	Documents	CI-DO	Citations	CPD	$h$-Index
United States	1	9,360,233	8,456,050	202,750,565	21.66	1783
Netherlands	2	746,289	682,627	16,594,528	22.24	752
United Kingdom	2	2,624,530	2,272,675	50,790,508	19.35	1099
Switzerland	3	541,846	501,917	12,592,003	23.24	744
China	3	4,076,414	4,017,123	24,175,067	5.93	563
Germany	3	2,365,108	2,207,765	40,951,616	17.31	961
Canada	3	1,339,471	1,227,622	25,677,205	19.17	862
Panama	4	5129	4830	137,585	26.82	142
Sweden	4	503,889	471,036	10,832,336	21.5	666
Denmark	4	290,994	269,364	6,405,076	22.01	558
Iceland	4	15,625	14,353	357,678	22.89	218
Japan	4	2,212,636	2,133,326	30,436,114	13.76	797
France	4	1,684,479	1,582,197	28,329,815	16.82	878
Gambia	5	2004	1859	54,925	27.41	99
Israel	5	295,747	274,748	5,826,878	19.7	536
Belgium	5	407,993	378,807	7,801,077	19.12	593
Italy	5	1,318,466	1,217,804	20,893,655	15.85	766
Australia	5	995,114	894,315	16,321,650	16.4	709
Bermuda	6	633	590	21,884	34.57	73
Finland	6	257,159	242,853	4,940,153	19.21	479
Spain	6	1,045,796	966,710	14,811,902	14.16	648
Montserrat	7	95	93	2282	24.02	27
Austria	7	295,668	273,467	5,052,810	17.09	487
India	7	1,140,717	1,072,927	8,458,373	7.41	426
South Korea	7	824,839	801,077	8,482,515	10.28	476
Taiwan	7	532,534	516,171	5,622,744	10.56	363
Faroe Islands	8	510	472	10,105	19.81	48
United States Minor Outlying Islands	8	30	29	710	23.67	11
Norway	8	229,276	209,259	3,951,661	17.24	439
Brazil	8	669,280	639,527	5,998,898	8.96	412
Guinea-Bissau	9	458	421	9357	20.43	50
Puerto Rico	9	13,841	13,293	248,888	17.98	166
Hong Kong	9	219,177	206,011	3,494,244	15.94	392
Greece	9	246,202	226,914	3,186,313	12.94	354
Russian Federation	9	770,491	755,186	4,907,109	6.37	421
Poland	9	475,693	460,979	4,083,631	8.58	401
Tokelau	10	2	1	43	21.5	1
Monaco	10	1586	1449	29,705	18.73	76
New Zealand	10	180,340	162,720	2,940,051	16.3	387
Singapore	10	215,553	202,089	3,135,524	14.55	392
Turkey	10	434,806	407,064	3,509,424	8.07	296
French Southern Territories	11	5	5	97	19.4	5
Bolivia	11	3569	3387	61,076	17.11	88
Ireland	11	150,552	135,523	2,382,077	15.82	364
Czech Republic	11	237,910	230,048	2,204,922	9.27	322
Mexico	11	232,828	221,611	2,305,554	9.9	316
Portugal	11	214,838	201,562	2,544,577	11.84	334
Argentina	11	159,172	150,927	1,965,624	12.35	300
Costa Rica	12	9177	8612	148,475	16.18	137
Gabon	12	2048	1936	34,704	16.95	80
Hungary	12	147,901	140,910	1,914,820	12.95	329
Kenya	12	24,458	22,347	379,560	15.52	179
South Africa	12	188,104	172,424	2,125,927	11.3	320
Iran	12	333,474	323,299	1,954,324	5.86	199
Seychelles	13	482	453	8579	17.8	44
North Korea	13	2384	2329	38,622	16.2	80
New Caledonia	13	2122	2041	34,753	16.38	73
Estonia	13	28,660	27,323	381,206	13.3	185
Chile	13	101,841	97,250	1,203,308	11.82	257
Uganda	13	11,528	10,599	171,367	14.87	128
Thailand	13	123,410	117,565	1,182,686	9.58	236
Egypt	13	137,350	133,147	1,009,954	7.35	184
Malaysia	13	181,251	175,146	888,277	4.9	190
Saint Lucia	14	99	85	1774	17.92	17
Netherlands Antilles	14	435	397	7662	17.61	44
Martinique	14	653	598	10,737	16.44	39
Philippines	14	20,326	18,658	265,737	13.07	163
Tanzania	14	11,964	11,140	170,144	14.22	122
Slovenia	14	71,408	68,494	725,498	10.16	204
Saudi Arabia	14	111,117	106,187	748,069	6.73	195
Slovakia	14	80,765	78,484	653,526	8.09	195
Romania	14	141,731	138,041	752,219	5.31	187
Malawi	15	4952	4520	77,829	15.72	104
Peru	15	14,434	13,201	192,443	13.33	154
Uruguay	15	13,702	12,971	186,793	13.63	132
Bulgaria	15	59,384	57,590	523,844	8.82	184
Venezuela	15	33,780	32,445	321,006	9.5	166
Ukraine	15	145,332	142,812	732,429	5.04	188
Croatia	15	79,154	76,097	548,687	6.93	194
French Guiana	16	956	898	15,573	16.29	56
Mozambique	16	2382	2193	37,433	15.71	73
Ecuador	16	7942	7440	96,119	12.1	111
Zimbabwe	16	7243	6691	94,533	13.05	99
Zambia	16	3992	3623	56,481	14.15	92
Cyprus	16	17,072	15,552	172,117	10.08	127
Pakistan	16	94,285	90,034	546,210	5.79	166
Colombia	16	60,402	57,407	468,135	7.75	186
Viet Nam	16	29,238	27,989	253,661	8.68	142
Lebanon	16	20,815	19,040	186,558	8.96	138
Virgin Islands (British)	17	121	111	2047	16.92	20
Mali	17	2490	2353	36,254	14.56	75
Armenia	17	12,852	12,496	130,584	10.16	135
Nigeria	17	59,372	56,630	334,059	5.63	131
Tunisia	17	58,769	55,904	342,429	5.83	123
Indonesia	17	39,719	37,729	282,788	7.12	155
Lithuania	17	36,136	35,205	271,666	7.52	144
Kuwait	17	18,468	17,687	157,888	8.55	108
Hati	18	765	683	12,231	15.99	49
French Polynesia	18	1272	1207	19,523	15.35	58
Senegal	18	7220	6752	75,373	10.44	95
Cambodia	18	2558	2292	34,654	13.55	72
Sri Lanka	18	12,557	11,532	121,696	9.69	120
Morocco	18	40,737	38,371	279,731	6.87	129
Ethiopia	18	13,363	12,625	118,656	8.88	101
Bangladesh	18	30,612	29,157	227,447	7.43	134
Guam	19	788	727	12,222	15.51	55
Cte dIvoire	19	4842	4621	52,446	10.83	89
Madagascar	19	3207	3059	39,217	12.23	74
Papua New Guinea	19	2258	2133	31,119	13.78	71
Luxembourg	19	12,562	11,567	120,570	9.6	114
United Arab Emirates	19	31,366	29,259	210,873	6.72	130
Belarus	19	30,944	30,439	202,088	6.53	133
Jordan	19	28,234	27,369	201,400	7.13	112
Nicaragua	20	1301	1233	18,269	14.04	62
Greenland	20	977	941	14,484	14.82	48
Namibia	20	2303	2125	28,985	12.59	72
Guatemala	20	2281	2085	29,034	12.73	69
Ghana	20	11,543	10,578	111,205	9.63	105
Serbia	20	53,116	50,436	258,732	4.87	118
Algeria	20	42,456	41,544	215,922	5.09	106
Cuba	20	31,690	30,382	202,503	6.39	127
Latvia	20	16,350	15,851	119,627	7.32	112
Cameroon	21	11,128	10,513	108,649	9.76	94
Democratic Republic Congo	21	517	481	7641	14.78	43
Georgia	21	11,196	10,305	105,036	9.38	114
Oman	21	12,846	11,919	87,333	6.8	91
Palau	22	149	143	2238	15.02	26
Botswana	22	5107	4545	52,195	10.22	79
Barbados	22	1690	1416	20,879	12.35	64
Nepal	22	9133	8196	85,174	9.33	94
Qatar	22	13,438	12,524	71,382	5.31	86
Congo	23	3304	3069	34,559	10.46	72
Honduras	23	995	950	13,157	13.22	51
Guinea	23	597	552	8320	13.94	46
Jamaica	23	4750	4220	48,226	10.15	75
Niger	23	1623	1553	19,835	12.22	59
Sudan	23	6099	5792	50,784	8.33	70
Syrian Arab Republic	23	5744	5459	53,601	9.33	81
Macedonia	23	8522	8167	54,409	6.38	81
Laos	24	1802	1670	20,028	11.11	59
Belize	24	330	299	4734	14.35	38
Virgin Islands (U.S.)	24	215	204	3173	14.76	31
Mongolia	24	3319	3164	33,119	9.98	72
Paraguay	24	1454	1373	17,717	12.19	60
Moldova	24	5948	5828	46,522	7.82	80
Malta	24	4500	3980	40,668	9.04	83
Trinidad and Tobago	24	5037	4561	44,146	8.76	76
Sao Tome and Principe	25	47	45	695	14.79	15
Chad	25	382	363	5122	13.41	33
Guadeloupe	25	1435	1345	17,075	11.9	52
Benin	25	3851	3681	35,470	9.21	65
Kazakhstan	25	12,124	11,809	39,700	3.27	68
Iraq	25	11,605	11,042	39,145	3.37	59
Uzbekistan	25	9259	8997	46,900	5.07	68
Palestine	25	4506	4224	30,338	6.73	60
Central African Republic	26	538	500	6940	12.9	41
Fiji	26	2400	2188	22,836	9.52	56
Liechtenstein	26	1272	1172	14,339	11.27	55
Dominican Republic	26	1101	1029	12,965	11.78	51
Azerbaijan	26	9848	9620	40,070	4.07	64
Yemen	26	2776	2698	18,951	6.83	50
Macao	26	5157	4903	25,298	4.91	57
Bahrain	26	4657	4225	24,769	5.32	55
Falkland Islands (Malvinas)	27	358	341	4628	12.93	34
American Samoa	27	162	150	2127	13.13	22
Gibraltar	27	106	94	1451	13.69	19
Mauritius	27	2206	2035	17,629	7.99	54
Rwanda	27	1759	1554	15,356	8.73	54
Myanmar	27	1543	1458	13,764	8.92	51
Reunion	27	581	544	6605	11.37	38
Bosnia and Herzegovina	27	7054	6752	30,300	4.3	61
Brunei Darussalam	27	2440	2136	16,224	6.65	52
Albania	27	3172	3028	14,759	4.65	48
Solomon Islands	28	324	296	4125	12.73	33
Svalbard and Jan Mayen	28	20	18	283	14.15	8
Tonga	28	108	105	1408	13.04	21
Sierra Leone	28	590	529	5551	9.41	31
Kyrgyzstan	28	1486	1402	9918	6.67	45
El Salvador	28	1149	1061	9994	8.7	44
Swaziland	28	1091	988	9618	8.82	43
Eritrea	28	488	468	5260	10.78	35
Bahamas	28	399	365	4535	11.37	36
Libya	28	4160	4020	18,971	4.56	51
San Marino	29	191	181	2365	12.38	23
British Indian Ocean Territory	29	19	16	267	14.05	7
Guyana	29	530	485	4898	9.24	32
Togo	29	1470	1367	8850	6.02	39
Angola	29	715	680	5422	7.58	35
Mauritania	29	482	456	4762	9.88	32
Samoa	29	249	231	2734	10.98	27
Montenegro	29	2232	2153	7346	3.29	32
Saint Vincent and the Grenadines	30	40	38	518	12.95	11
Federated States of Micronesia	30	188	175	2144	11.4	24
Grenada	30	965	824	6286	6.51	33
Afghanistan	30	791	674	5800	7.33	36
Vanuatu	30	317	295	3142	9.91	27
Tajikistan	30	1244	1209	4728	3.8	29
Lesotho	30	459	425	3524	7.68	28
Burundi	30	421	392	3761	8.93	32
Suriname	31	293	276	2921	9.97	30
Bhutan	31	551	499	3249	5.9	27
Andorra	31	172	151	1786	10.38	21
Turkmenistan	31	296	286	2291	7.74	20
Cocos (Keeling) Islands	32	14	14	162	11.57	4
Tuvalu	32	25	24	284	11.36	8
Dominica	32	266	234	2007	7.55	23
Cayman Islands	32	231	210	1857	8.04	23
Maldives	32	206	194	1833	8.9	21
Equatorial Guinea	32	153	147	1587	10.37	20
Turks and Caicos Islands	33	45	45	475	10.56	13
Saint Kitts and Nevis	33	350	240	1866	5.33	21
Liberia	33	263	216	1934	7.35	21
Comoros	33	96	89	839	8.74	13
Marshall Islands	33	84	77	827	9.85	16
Northern Mariana Islands	33	68	66	680	10	14
Cook Islands	33	64	61	658	10.28	14
Cape Verde	34	199	194	1501	7.54	17
Djibouti	35	190	178	1206	6.35	18
Aruba	36	93	74	621	6.68	12
Somalia	36	115	97	685	5.96	15
Timor-Leste	37	125	102	628	5.02	13
Mayotte	37	74	72	416	5.62	10
Antigua and Barbuda	38	114	103	550	4.82	13
Anguilla	38	36	33	201	5.58	7
South Georgia and the South Sandwich Islands	39	7	5	42	6	2
Kiribati	39	33	28	184	5.58	8
Norfolk Island	40	20	20	114	5.7	7
Nauru	40	22	21	118	5.36	6
Vatican City State	41	25	16	121	4.84	6
Christmas Island	41	7	7	38	5.43	4
Saint Helena	42	15	15	69	4.6	5
Niue	43	16	13	25	1.56	2
Bouvet Island	43	6	4	29	4.83	2
Wallis and Futuna	43	15	13	60	4	4
Western Sahara	44	11	9	22	2	3
Heard Island and McDonald Islands	45	1	1	3	3	1
Saint Pierre and Miquelon	45	5	4	6	1.2	1
Pitcairn	46	3	1	4	1.33	1

shows countries, the values of five indicators (documents, CI-DO, citations, CPD, and h-index), and the obtained Pareto ranks from the proposed method (Pareto ranking). The United States is located in the first Pareto front because it has the maximum values of four indicators: documents, CI-DO, citations, CPD, and h-index. The United States is assigned to the rank 1 and in the second Pareto front, Switzerland and the United Kingdom are placed. The proposed method ranks these countries into forty six ranks while in the Pareto dominance ranking, it has thirty Pareto fronts.

Additionally, for this data, we plot the maximum, minimum, and average of values for all indicators versus Pareto ranks in Figure 10 and Figure 11. Figures show a falling tendency of the average values from the first Pareto front to the last Pareto front. Additionally, we compute the percentage of the number of countries from the different continents (Asia, Europe, Latin America, Middle East, North America, and Pacific region) for each Pareto front. Figure 12 shows the percentage number for each continent. In Figure 12, the first largest and second largest percentages of the first Pareto front are North America and Europe. In addition, Figure 13 visualizes the values of indicators for countries in the four top ranked Pareto fronts by the parallel coordinates visualization technique. Each line illustrates one country (a five dimensional vector) in which the values of five indicators are presented using vertical axes; i.e., coordinate’s value. For instance, the value of CI-DO indicator is in interval $[1,{10}^7]$ for countries on the four first Pareto fronts.

4.4. The Forth Case Study: Resolution for Multi-Rankings of Universities

This case study collects the three ranks of 100 top common universities collected from the three mentioned resources, from which it is supposed that the criterion vectors with the lesser values for all three ranks are better vectors (i.e., Min-Min-Min).

Table A4. Pareto ranks and ranks from three sites.

University	Rank1	Rank2	Rank3	Pareto Rank
Massachusetts Institute of Technology	1	3	7	1
Stanford University	2	2	4	1
Harvard University	3	1	1	1
University of Cambridge	4	4	8	2
University of Oxford	6	5	3	2
University of Toronto	32	30	2	2
California Institute of Technology	5	11	59	3
University College London	7	31	5	3
University of Chicago	10	8	20	3
Yale University	15	10	19	3
Johns Hopkins University	17	16	6	3
University of Pennsylvania	18	14	13	3
Columbia University	20	6	14	3
University of California, Berkeley (UCB)	28	7	9	3
Swiss Federal Institute of Technology	8	96	5	4
Imperial College London	9	35	15	4
Princeton University	11	9	93	4
Cornell University	16	12	25	4
University of Michigan	23	19	10	4
University of California, Los Angeles (UCLA)	31	15	12	4
University of Tokyo	34	13	18	4
Pennsylvania State University	95	14	13	4
National University of Singapore (NUS)	12	63	29	5
The University of Edinburgh	19	55	52	5
Duke University	25	29	24	5
Northwestern University	26	21	46	5
Kyoto University	37	20	60	5
University of California, San Diego (UCSD)	40	17	17	5
University of Washington	59	27	11	5
Nanyang Technological University	13	134	66	6
Tsinghua University	24	74	38	6
The University of Manchester	29	61	49	6
McGill University	30	42	35	6
Seoul National University	35	24	50	6
Peking University	39	60	33	6
The University of Melbourne	42	89	31	6
University of British Columbia	45	57	21	6
New York University	46	22	68	6
University of Wisconsin-Madison	53	25	30	6
University of Copenhagen	68	69	16	6
The University of Hong Kong	27	169	137	7
University of Bristol	41	129	102	7
Fudan University	43	192	74	7
University of Sydney	46	95	27	7
Brown University	49	87	144	7
Carnegie Mellon University	58	67	247	7
Osaka University	63	48	101	7
University of Illinois at Urbana-Champaign	66	34	76	7
University of Texas at Austin	67	32	64	7
Ruprecht Karl University Heidelberg	72	82	51	7
University of North Carolina, Chapel Hill	78	38	43	7
Katholieke Universiteit Leuven	79	78	23	7
The Ohio State University	88	46	37	7
The Hong Kong University of Science and Technology	36	312	325	8
The University of New South Wales (UNSW Australia)	49	117	71	8
University of Queensland	51	99	41	8
Shanghai Jiao Tong University	61	166	39	8
National Taiwan University (NTU)	68	53	92	8
University of Zurich	80	93	65	8
University of California, Davis	85	49	47	8
Utrecht University	104	83	44	8
University of Warwick	51	280	208	9
Tokyo Institute of Technology	56	128	253	9
University of Amsterdam	57	111	61	9
Technical University of Munich	60	104	95	9
Monash University	65	143	57	9
Georgia Institute of Technology	71	86	125	9
Tohoku University	75	84	105	9
Boston University	89	62	79	9
University of Helsinki	91	107	72	9
Purdue University	92	56	109	9
University of Alberta	94	101	77	9
Washington University (WUSTL)	106	51	56	9
City University of Hong Kong	55	364	252	10
Delft University of Technology	62	255	210	10
University of Glasgow	63	132	130	10
Lund University	73	127	83	10
Rice University	90	114	292	10
University of Geneva	95	80	103	10
Uppsala University	98	126	89	10
Leiden University	102	112	82	10
Lomonosov Moscow State University	108	77	177	10
Durham University	74	231	258	11
The University of Nottingham	75	139	127	11
University of Birmingham	82	158	119	11
University of Southampton	87	153	110	11
Royal Institute of Technology	97	131	206	11
The University of Western Australia	102	213	104	11
University of St Andrews	77	307	348	12
The University of Auckland	81	252	195	12
Pohang University of Science And Technology (POSTECH)	83	191	349	12
The University of Sheffield	84	172	147	12
University of Leeds	93	159	138	12
Korea University	98	141	162	12
University of Science and Technology of China	104	223	113	12
Universidad de Buenos Aires (UBA)	85	372	277	13
Trinity College Dublin	98	175	263	13
Karlsruhe Institute of Technology	101	215	172	13
Sungkyunkwan University (SKKU)	106	221	139	13
Technical University of Denmark	109	168	154	13

shows universities, the values of three ranks, and the obtained Pareto ranks from Pareto dominance ranking (Pareto ranking). As we can see, three universities, “Massachusetts Institute of Technology,” “Stanford University,” and “Harvard University” are located in the first Pareto front, which has elements with the values 1 and 2 as the obtained ranks from other ranking resources. Figure 14 shows the numbers of Pareto fronts for all data. Additionally, the maximum, minimum, and average of values for three rankings versus Pareto ranks are plotted in Figure 15. It can be seen from Figure 15 that the average values of three ranks increase from the first Pareto front to 13th Pareto front.

At the end of this section, several points regarding the performance of the method and its differences with other ranking strategies are mentioned. First of all, a multi-criteria indicator is proposed for ranking the researchers, universities, and countries. Considering two or more objectives simultaneously can provide a fairer ranking. For instance, using research period along with other important criteria provides a fair comparison for senior and junior researchers to discover more-talented researchers. Secondly, since the considered criteria to assess the entities are different from indicators in other ranking strategies, the resultant rankings are completely different. In fact, they evaluate the universities in terms of different metrics. As a result, the comparison between the results of ranking strategies does not lead to a precise and meaningful conclusion. On the other hand, the proposed method clusters the entities based on multiple criteria into different levels. Accordingly, all universities in the same Pareto are ranked equally; for instance, based on this perspective, all universities in the first Pareto are the top ranked universities. Finally, this method does not actually define an evaluation measure; it gives a strategy to rank not only the case studies in the paper, but also any multi-criteria data entities. In addition, using this general platform provides the chance to utilize any metric to assess the related entities without modification to other parts of the algorithm.

5. Conclusions and Future Directions

In this paper, a modified Pareto-front based ranking was suggested as a new ranking method for measuring the scientific achievements, or in general multi and many- metric rankings. By using some dominance metrics obtained from the basic Pareto dominance depth ranking and some statistical metrics sorting compared criteria, the proposed method is able to find some different groups (clubs) for entities of a dataset having a large number of the criteria. It provides simultaneously multiple comparisons, considering the time period of academic research, and the use of other ranking methods. We selected different kinds of the scientific datasets; namely, computer science researchers, top universities, countries, and multiple rankings of universities to rank by using Pareto ranking. In future, we are planning to develop ranking strategies based on other dominance-based rankings; for example, dominance rank [61,63] which is related to the number of data entries in the set which dominates the considered point. Finally, we are interested in considering the use of other types of domination definition, such as the concepts of weak dominance, strict dominance, and $ϵ$-dominance. Additionally, many (more than three) metrics and various resources will be studied in the future.