Dynamics of Periodic Waves in a Neural Field Model
Abstract
:1. Introduction
1.1. Brain Activity and Periodic Travelling Waves
1.2. Neural Field Model
2. Stability
2.1. Linearization and Eigenvalues
2.2. Symmetric Connectivity Functions with Time Delay
2.3. Asymmetric Connectivity Function without Time Delay
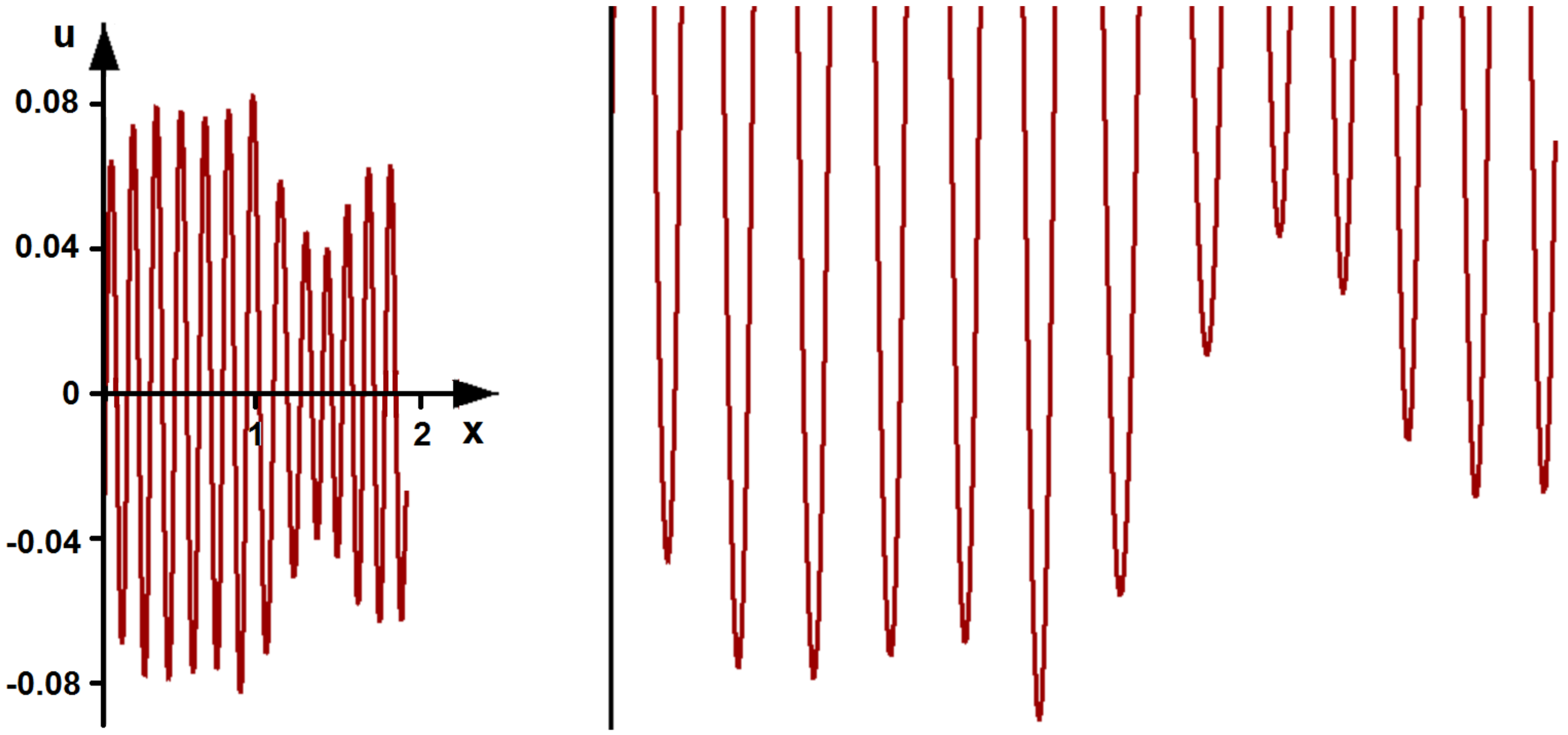
3. Numerical Results
3.1. Wave Propagation without Time Delay
3.2. Time Delay and Symmetric Connectivity Functions
3.2.1. Initial Conditions
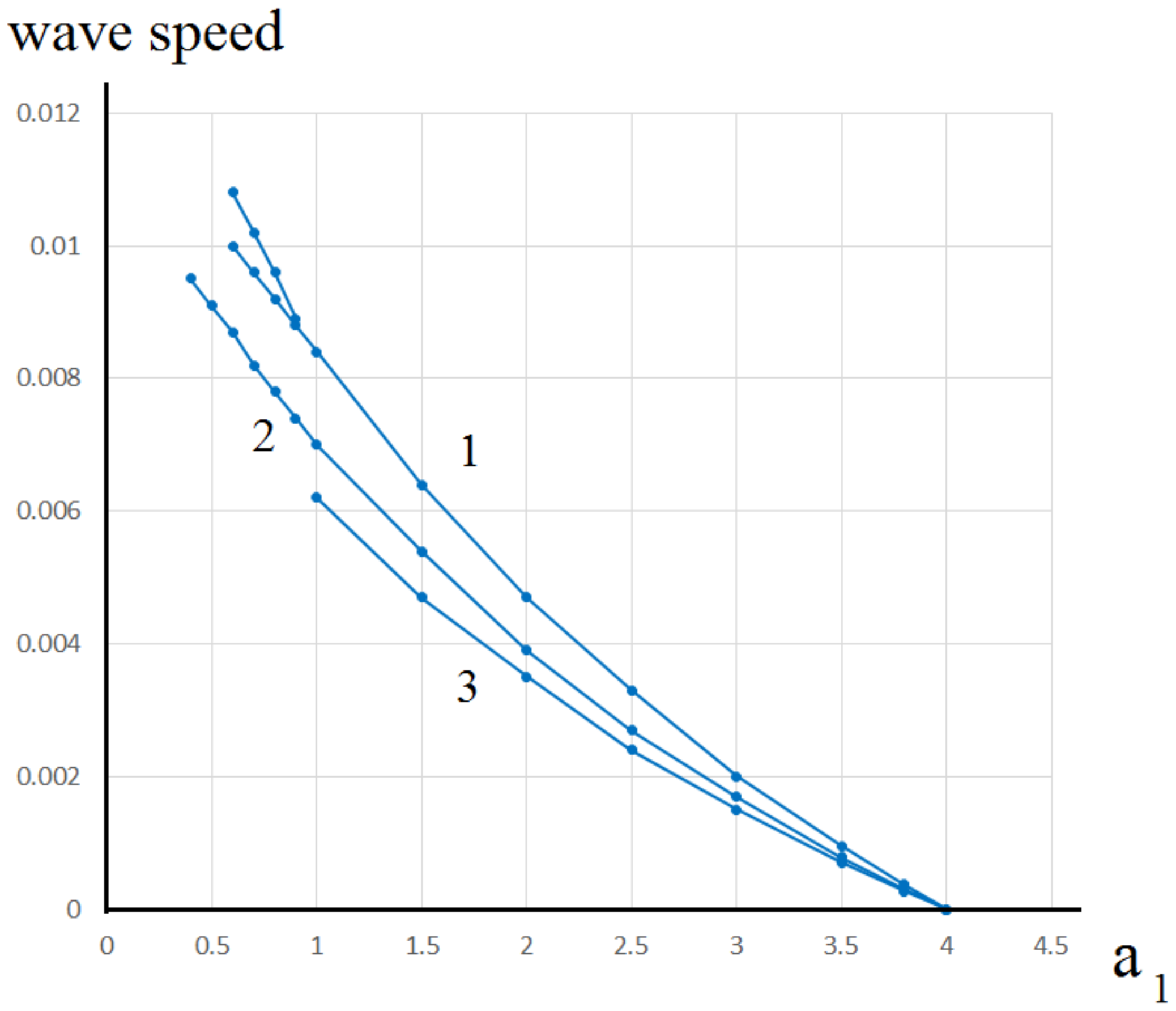
3.2.2. Multiplicity of Waves and Parameter Dependence
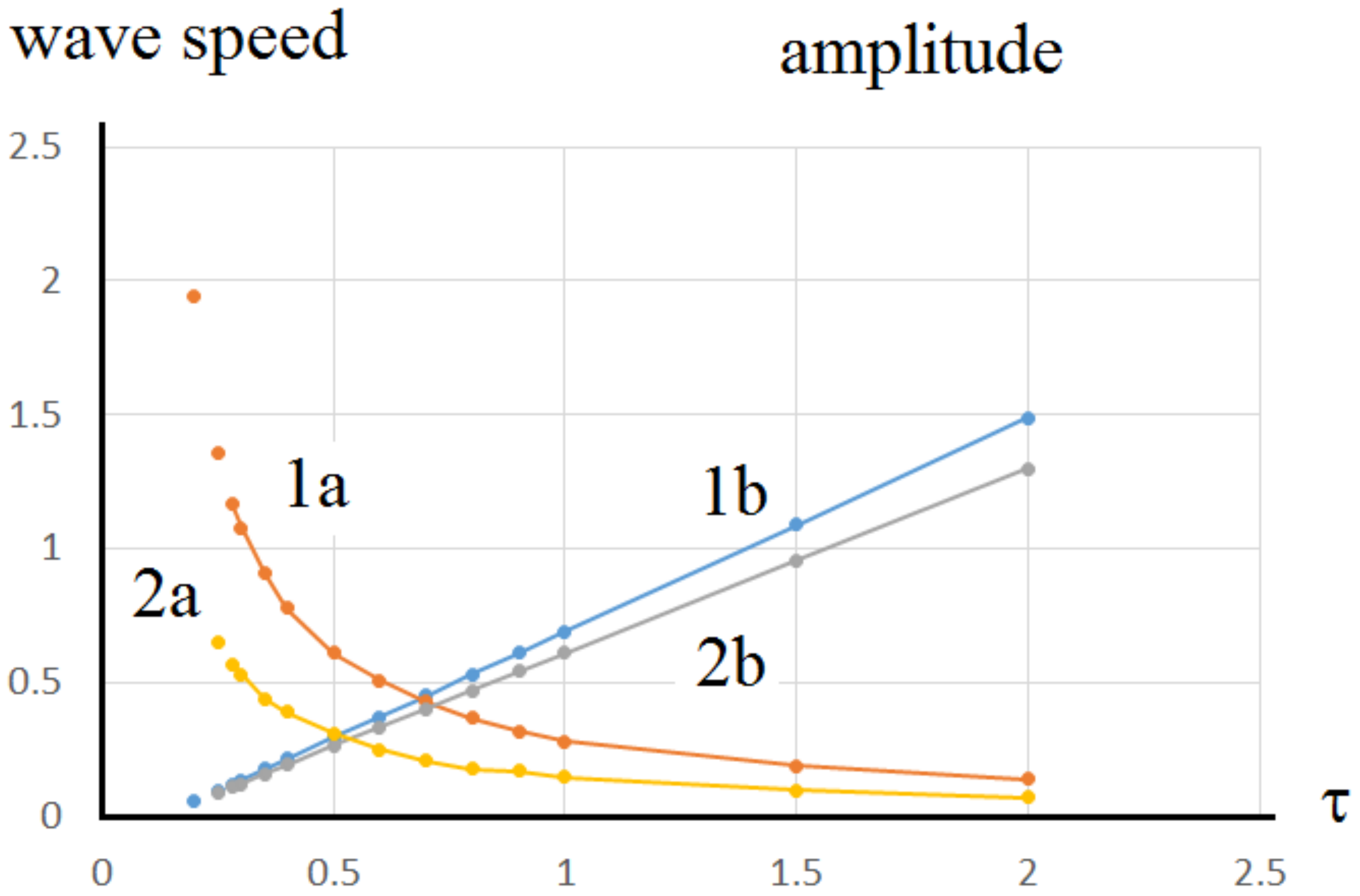
3.3. Stimulation
3.3.1. Exact Solution of the Stimulation Problem
3.3.2. Approximate Solution of the Stimulation Problem
4. Discussion
Cortex Damage and Stimulation
Author Contributions
Funding
Conflicts of Interest
Appendix A. Periodic Waves in Different Models
Appendix B. The Values of Parameters
| Parameter | Name | Unit | Typical Value |
|---|---|---|---|
| D | diffusion coefficient | length/time | |
| L | length of the interval | length | 2 |
| factors in connectivity functions | 1/length | ||
| exponents in connectivity functions | 1/length | ||
| growth rate of response functions | 1/time | 20 | |
| time delay in response functions | time | ||
| potential decay rate | 1/time |
References
- Kopell, N.; Gritton, H.J.; Whittington, M.A.; Kramer, M.A. Beyond The Connectome: The Dynome. Neuron 2014, 83, 1319–1328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sporns, O. The human connectome: Origins and challenges. NeuroImage 2013, 80, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Muller, L.; Chavane, F.; Reynolds, J.; Sejnowski, T.J. Cortical travelling waves: Mechanisms and computational principles. Nat. Rev. Neurosci. 2018, 19, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.Y.; Huang, X.; Zhang, C. Propagating Waves of Activity in the Neocortex: What They Are, What They Do. Neuroscientist 2008, 14, 487–502. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Watrous, A.J.; Patel, A.; Jacobs, J. Theta and Alpha Oscillations Are Travelling Waves in the Human Neocortex. Neuron 2018, 98, 1269–1281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Botella-Soler, V.; Valderrama, M.; Crépon, B.; Navarro, V.; Quyen, M.L.V. Large-Scale Cortical Dynamics of Sleep Slow Waves. PLoS ONE 2012, 7, e30757. [Google Scholar] [CrossRef]
- Wilson, H.R.; Cowan, J.D. A Mathematical Theory of the Functional Dynamics of Cortical and Thalamic Nervous Tissue. Kybernetik 1973, 13, 55–80. [Google Scholar] [CrossRef]
- Senk, J.; Korvasova, K.; Schuecker, J.; Hagen, E.; Tetzlaff, T.; Diesmann, M.; Helias, M. Conditions for travelling waves in spiking neural networks. arXiv 2018, arXiv:1801.06046v1. [Google Scholar]
- Atay, F.M.; Hutt, A. Neural Fields with Distributed Transmission Speeds and Long-Range Feedback Delays. SIAM J. Appl. Dyn. Syst. 2006, 5, 670–698. [Google Scholar] [CrossRef]
- Venkov, N.A.; Coombes, S.; Matthews, P.C. Dynamic instabilities in scalar neural field equations with space-dependent delays. Physica D 2007, 232, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Ermentrout, G.B.; Folias, S.E.; Kilpatrick, Z.P. Spatiotemporal Pattern Formation in Neural Fields with Linear Adaptation. In Neural Fields; Coombes, S., beim Graben, P., Potthast, R., Wright, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 119–151. [Google Scholar]
- Meijer, H.G.E.; Coombes, S. Travelling waves in a neural field model with refractoriness. J. Math. Biol. 2014, 68, 1249–1268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinotsis, D.A.; Hansen, E.; Friston, K.J.; Jirsa, V.K. Anatomical connectivity and the resting state activity of large cortical networks. Neuroimage 2013, 65, 127–138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Modolo, J.; Bhattacharya, B.; Edwards, R.; Campagnaud, J.; Legros, A.; Beuter, A. Using a virtual cortical module implementing a neural field model to modulate brain rhythms in Parkinson’s disease. Front. Neurosci. 2010, 4, 45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ermentrout, B.; McLeod, J.B. Existence and uniqueness of travelling waves for a neural network. Proc. R. Soc. Edinburgh 1994, 134A, 1013–1022. [Google Scholar] [CrossRef]
- Chen, Z.; Ermentrout, B.; Wang, X.J. Wave Propagation Mediated by GABAB Synapse and Rebound Excitation in an Inhibitory Network: A Reduced Model Approach. J. Comput. Neurosci. 1998, 5, 53–69. [Google Scholar] [CrossRef]
- Amari, S. Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 1977, 27, 77–87. [Google Scholar] [CrossRef]
- Bessonov, N.; Beuter, A.; Trofimchuk, S.; Volpert, V. Estimate of the travelling wave speed for an integro-differential equation. Appl. Math. Lett. 2019, 88, 103–110. [Google Scholar] [CrossRef]
- Buzsaki, G.; Anastassiou, C.A.; Koch, C. The origin of extracellular fields and currents—EEG, ECoG, LFP and spikes. Nat. Rev. Neurosci. 2016, 13, 407–420. [Google Scholar] [CrossRef]
- Pinto, D.J.; Ermentrout, G.B. Spatially structured activity in synapticalaly coupled neuronal networks: I. Travelling fronts and pulses. SIAM J. Appl. Math. 2001, 62, 206–225. [Google Scholar] [CrossRef] [Green Version]
- Kilpatrick, Z.P. Coupling layers regularizes wave propagation in laminar stochastic neural fields. Phys. Rev. E 2014, 89, 022706. [Google Scholar] [CrossRef] [Green Version]
- Moussaoui, A.; Volpert, V. Speed of wave propagation for a nonlocal reaction-diffusion equation. Appl. Anal. 2018, 1–15. [Google Scholar] [CrossRef]
- Rabiller, G.; He, J.-W.; Nishijima, Y.; Wong, A.; Liu, J. Perturbation of brain oscillations after ischemic stroke: a potential biomarker for post-stroke function and therapy. Int. J. Mol. Sci. 2015, 16, 25605–25640. [Google Scholar] [CrossRef] [Green Version]
- Beuter, A.; Balossier, A.; Trofimchuk, S.; Volpert, V. Modelling of post-stroke stimulation of cortical tissue. Math. Biosci. 2018, 305, 146–159. [Google Scholar] [CrossRef] [PubMed]
- Rapela, J. Travelling waves appear and disappear in unison with produced speech. arXiv 2018, arXiv:1806.09559v1. [Google Scholar]
- Pelt, J.; van Ooyen, A. Estimating neuronal connectivity from axonal and dendritic density fields. Front. Comput. Neurosci. 2013, 7, 160. [Google Scholar]
- Van Ooyen, A.; Carnell, A.; de Ridder, S.; Tarigan, B.; Mansvelder, H.D.; Bijma, F.; Gunst, M.D.; Pelt, J.V. Independently Outgrowing Neurons and Geometry- Based Synapse Formation Produce Networks with Realistic Synaptic Connectivity. PLoS ONE 2014, 9, e85858. [Google Scholar] [CrossRef]
- Carter, A.R.; Connor, L.T.; Dromerick, A.W. Rehabilitation after stroke: Current state of the science. Curr. Neurol. Neurosci. Rep. 2010, 10, 158–166. [Google Scholar] [CrossRef]
- Gross, J.; Hoogenboom, N.; Thut, G.; Schyns, P.; Panzeri, S.; Belin, P.; Garrod, S. Speech Rhythms and Multiplexed Oscillatory Sensory Coding in the Human Brain. PLoS. Biol. 2013, 11, e1001752. [Google Scholar] [CrossRef]
- Weaver, J. How Brain Waves Help Us Make Sense of Speech. PLoS Biol. 2013, 11, e1001753. [Google Scholar] [CrossRef]
- Sarubbo, S.; Benedictis, A.D.; Merler, S.; Mandonnet, E.; Balbi, S.; Granieri, E.; Duffau, H. Towards a Functional Atlas of Human White Matter. Hum. Brain Mapp. 2015. [Google Scholar] [CrossRef]
- Pinto, D.J.; Ermentrout, G.B. Spatially structured activity in synapticalaly coupled neuronal networks: II. Lateral inhibition and standing pulses. SIAM J. Appl. Math. 2001, 62, 226–243. [Google Scholar] [CrossRef] [Green Version]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bessonov, N.; Beuter, A.; Trofimchuk, S.; Volpert, V. Dynamics of Periodic Waves in a Neural Field Model. Mathematics 2020, 8, 1076. https://doi.org/10.3390/math8071076
Bessonov N, Beuter A, Trofimchuk S, Volpert V. Dynamics of Periodic Waves in a Neural Field Model. Mathematics. 2020; 8(7):1076. https://doi.org/10.3390/math8071076
Chicago/Turabian StyleBessonov, Nikolai, Anne Beuter, Sergei Trofimchuk, and Vitaly Volpert. 2020. "Dynamics of Periodic Waves in a Neural Field Model" Mathematics 8, no. 7: 1076. https://doi.org/10.3390/math8071076
APA StyleBessonov, N., Beuter, A., Trofimchuk, S., & Volpert, V. (2020). Dynamics of Periodic Waves in a Neural Field Model. Mathematics, 8(7), 1076. https://doi.org/10.3390/math8071076





