On Numerical Analysis of Carreau–Yasuda Nanofluid Flow over a Non-Linearly Stretching Sheet under Viscous Dissipation and Chemical Reaction Effects
Abstract
:1. Introduction
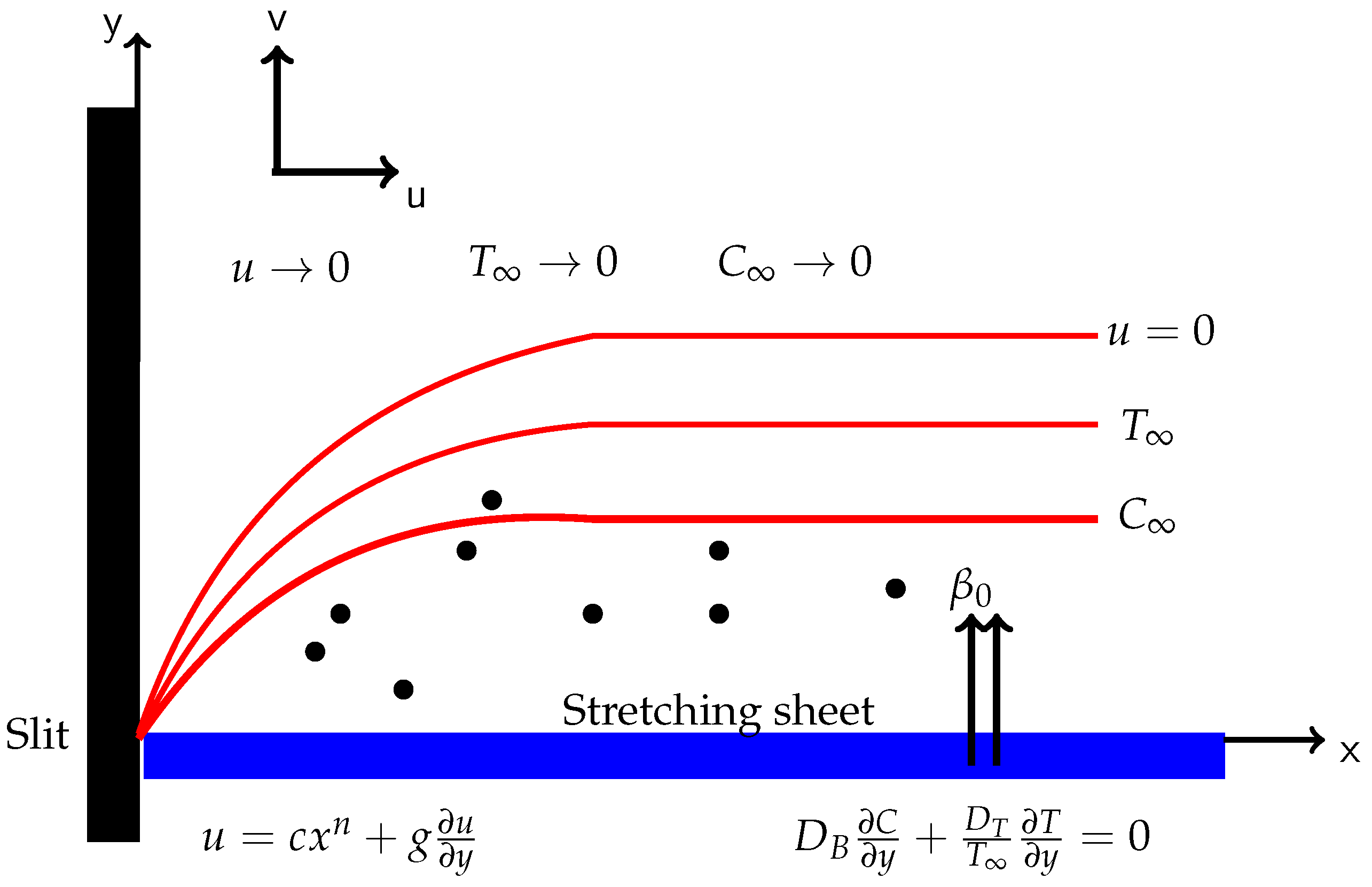
2. Mathematical Formulation
Similarity Transformations
3. Method of Solution
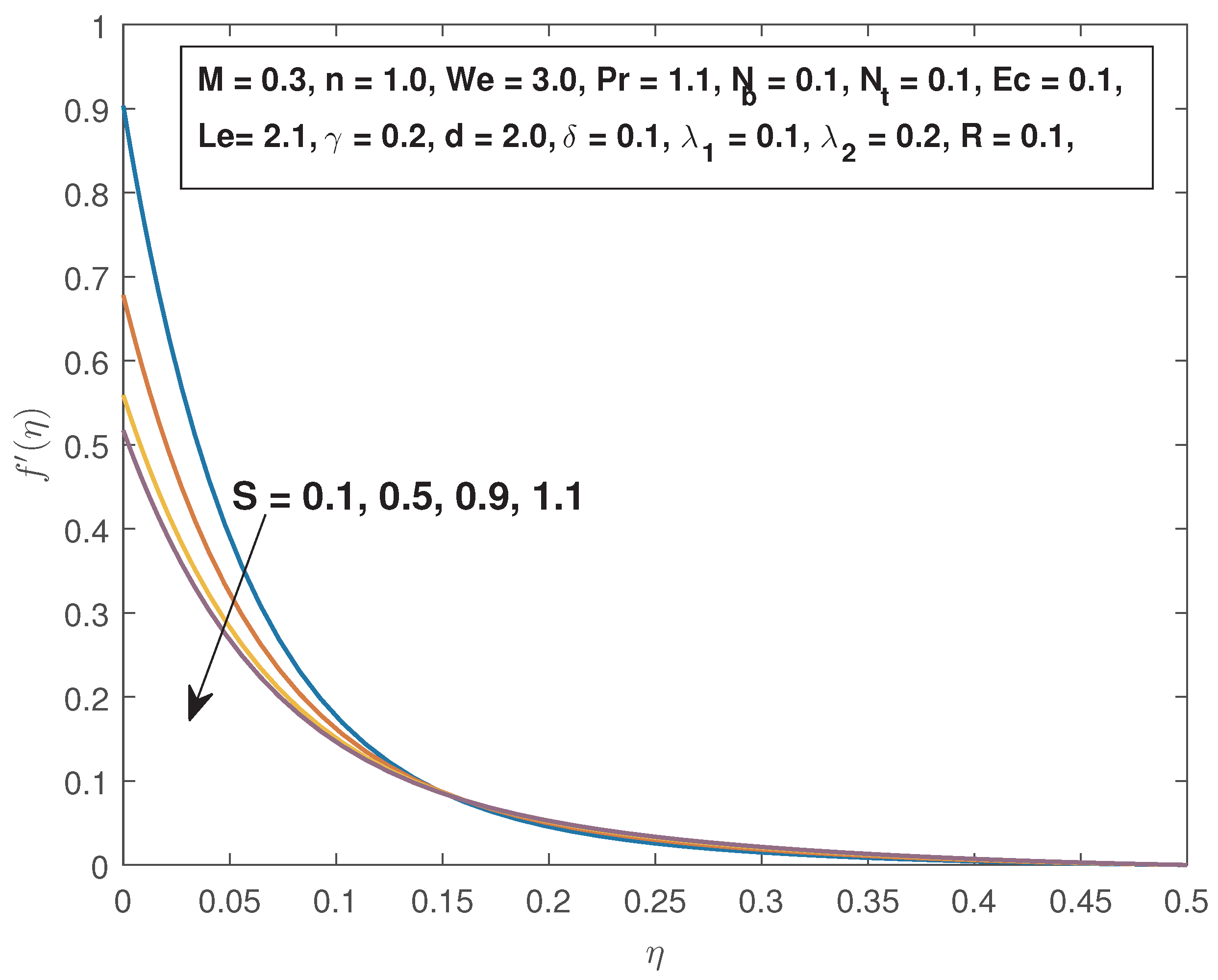
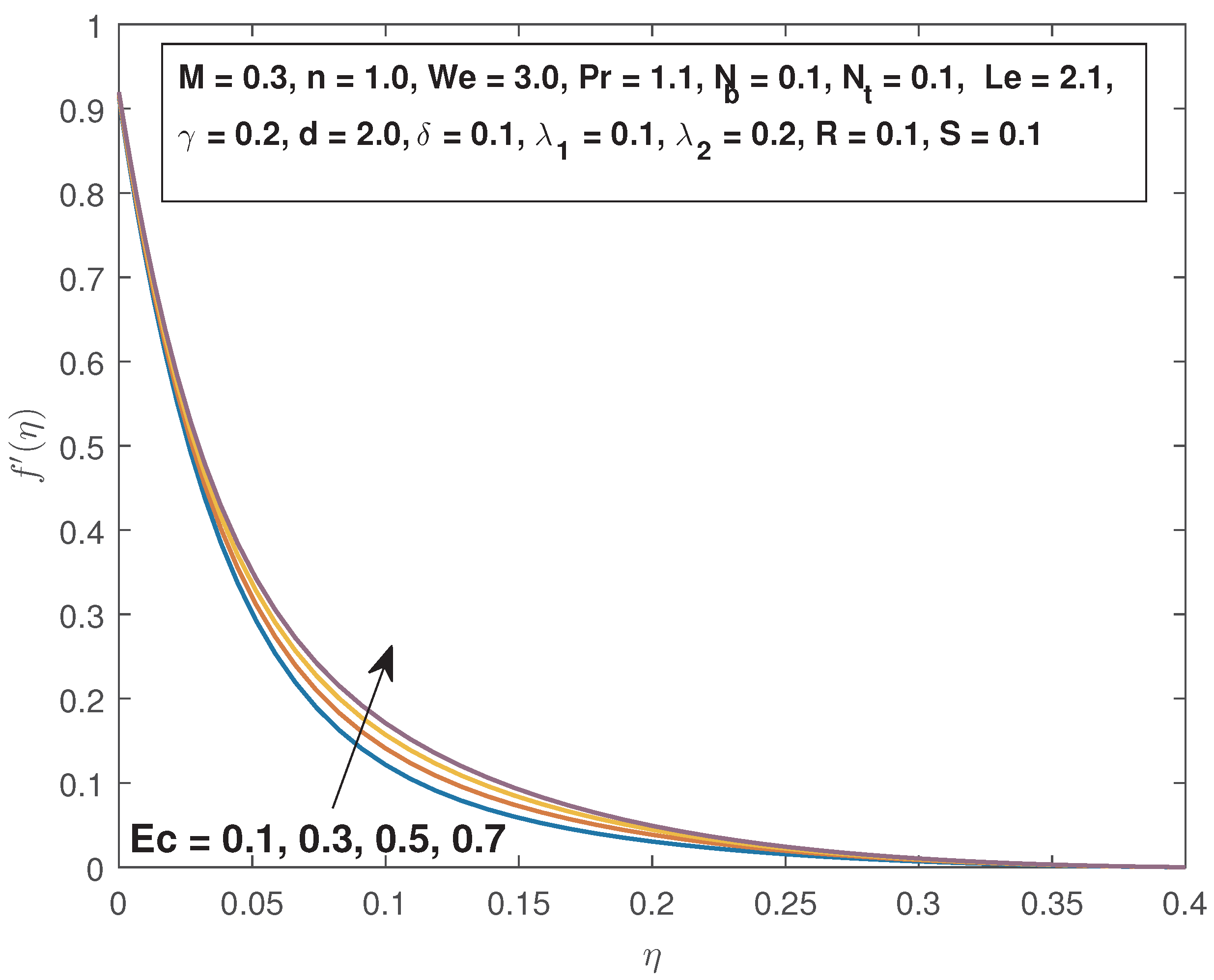
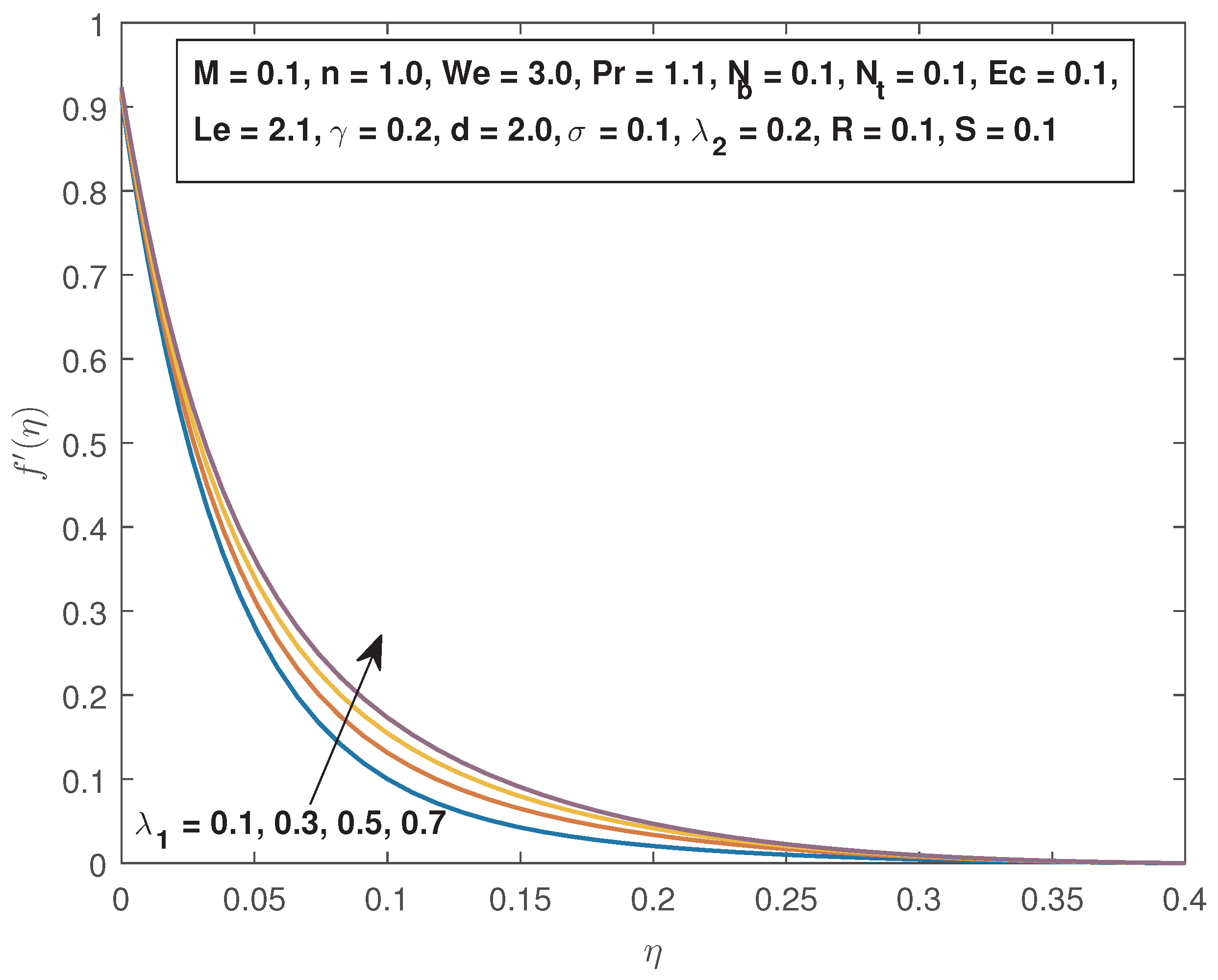
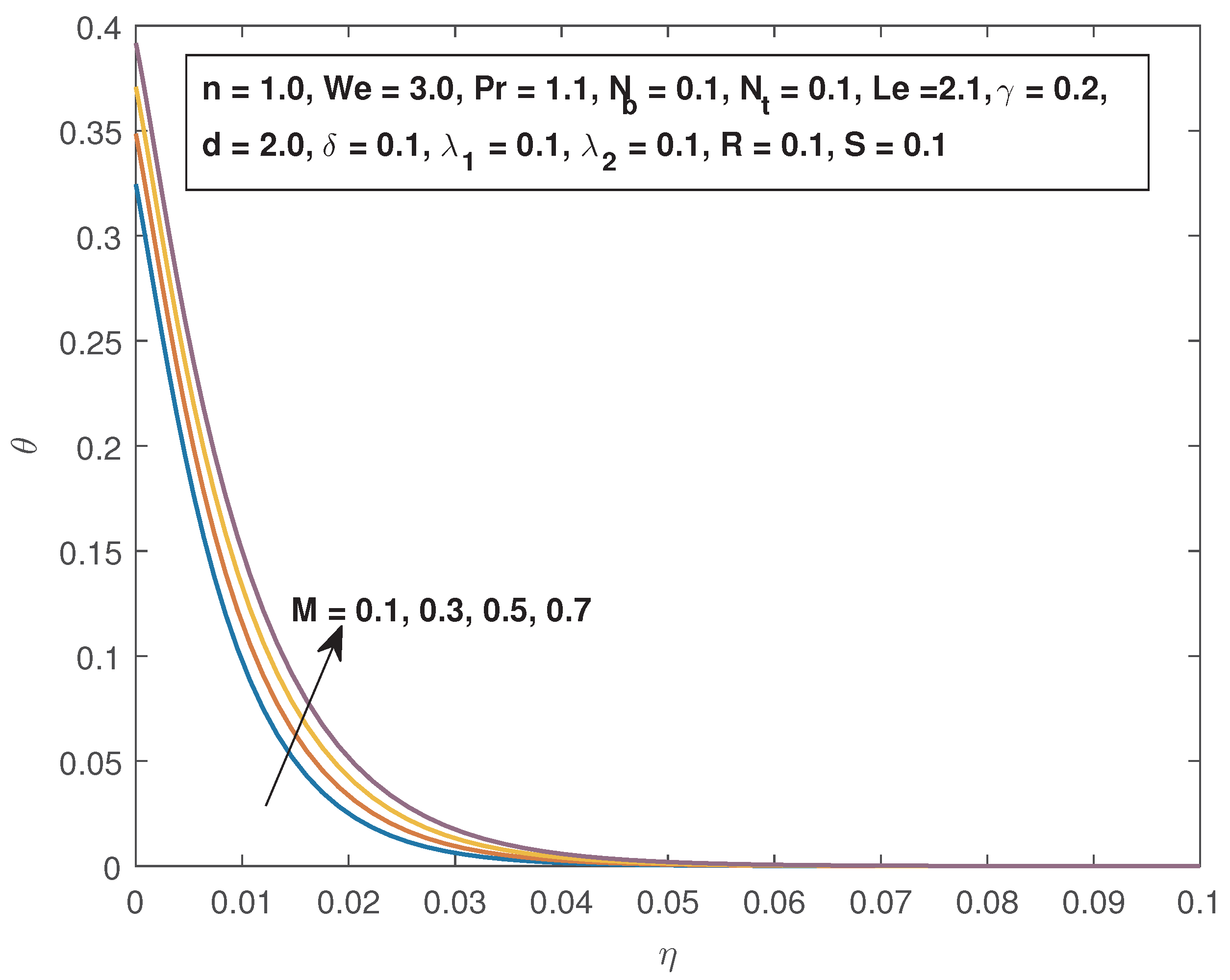
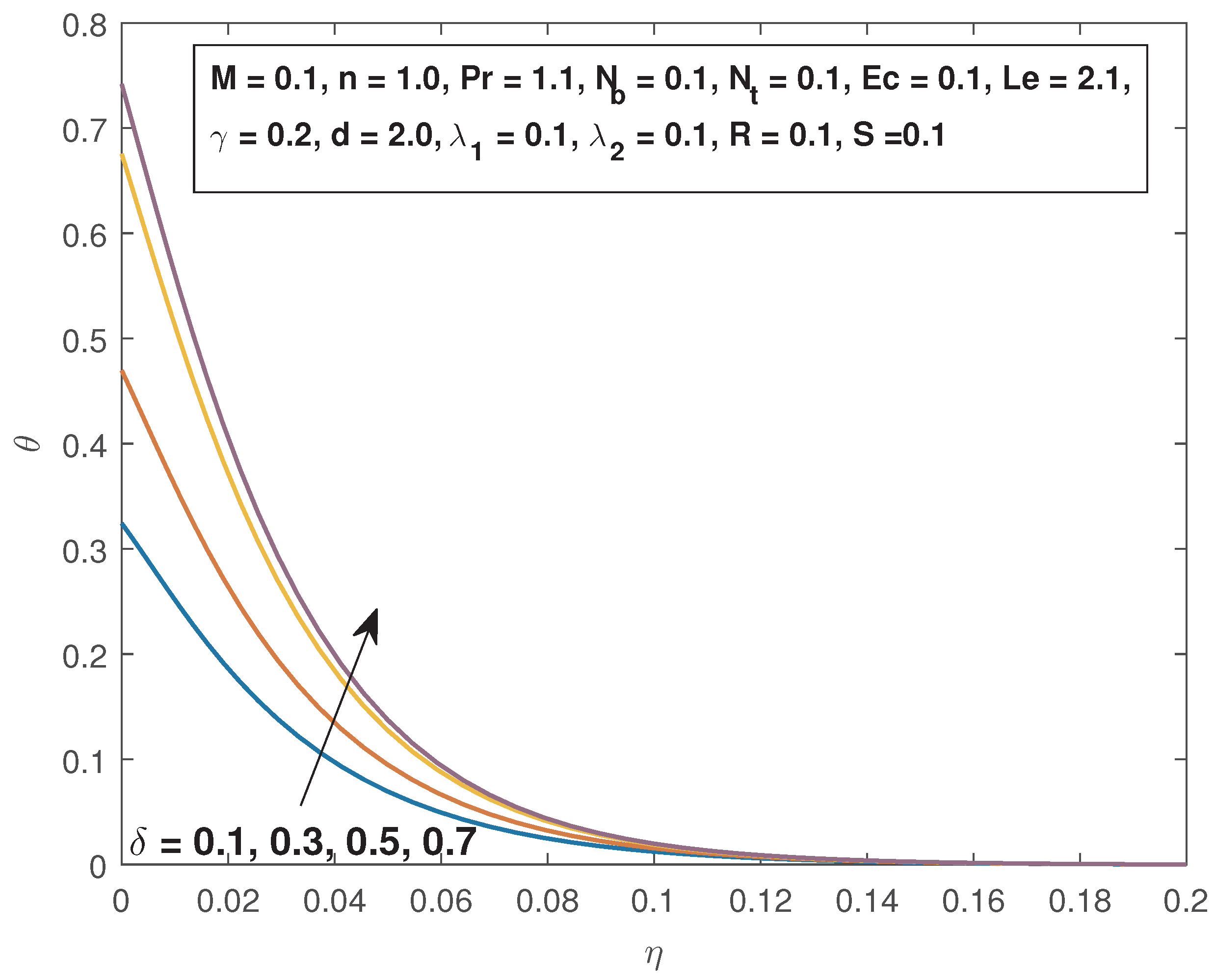
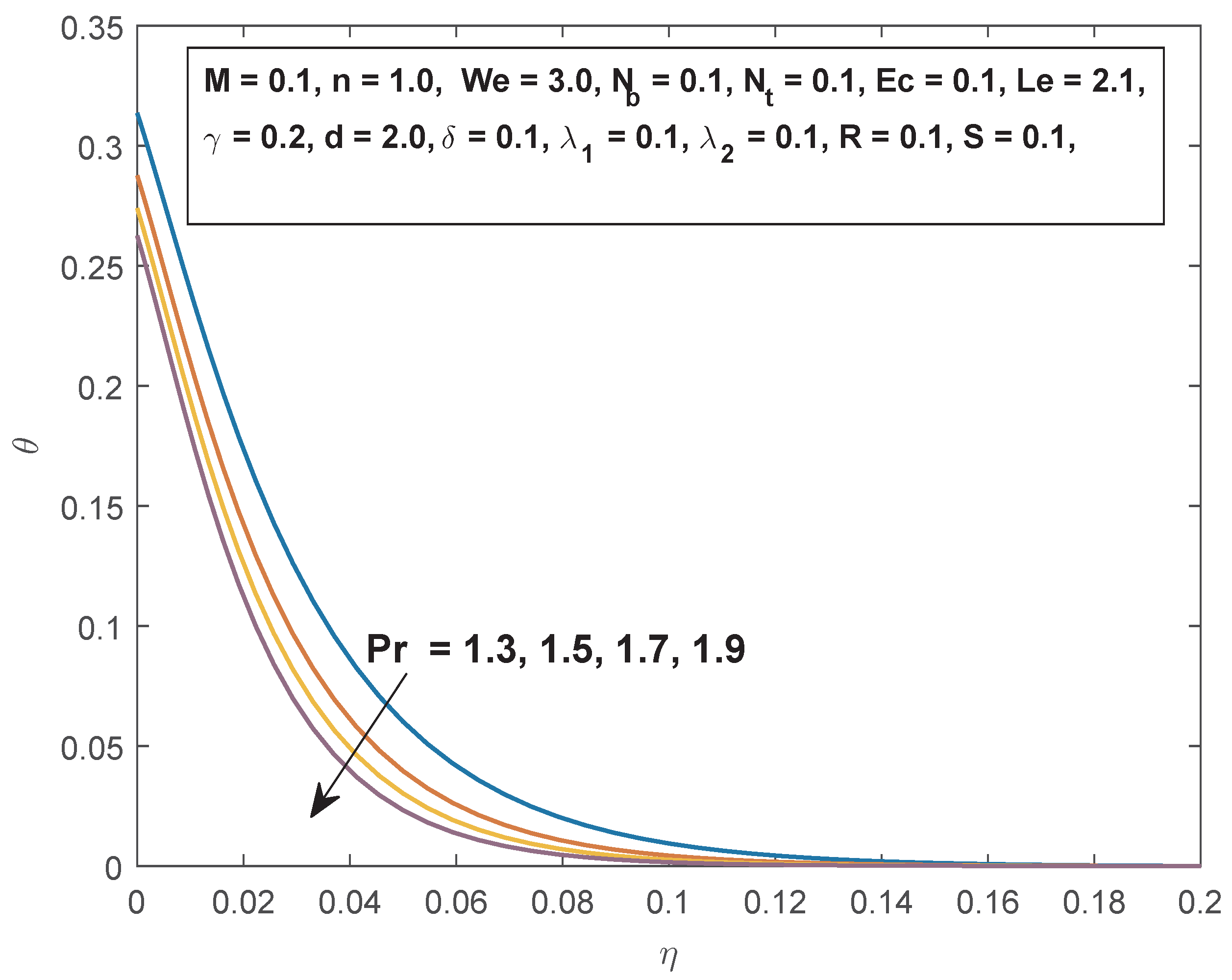
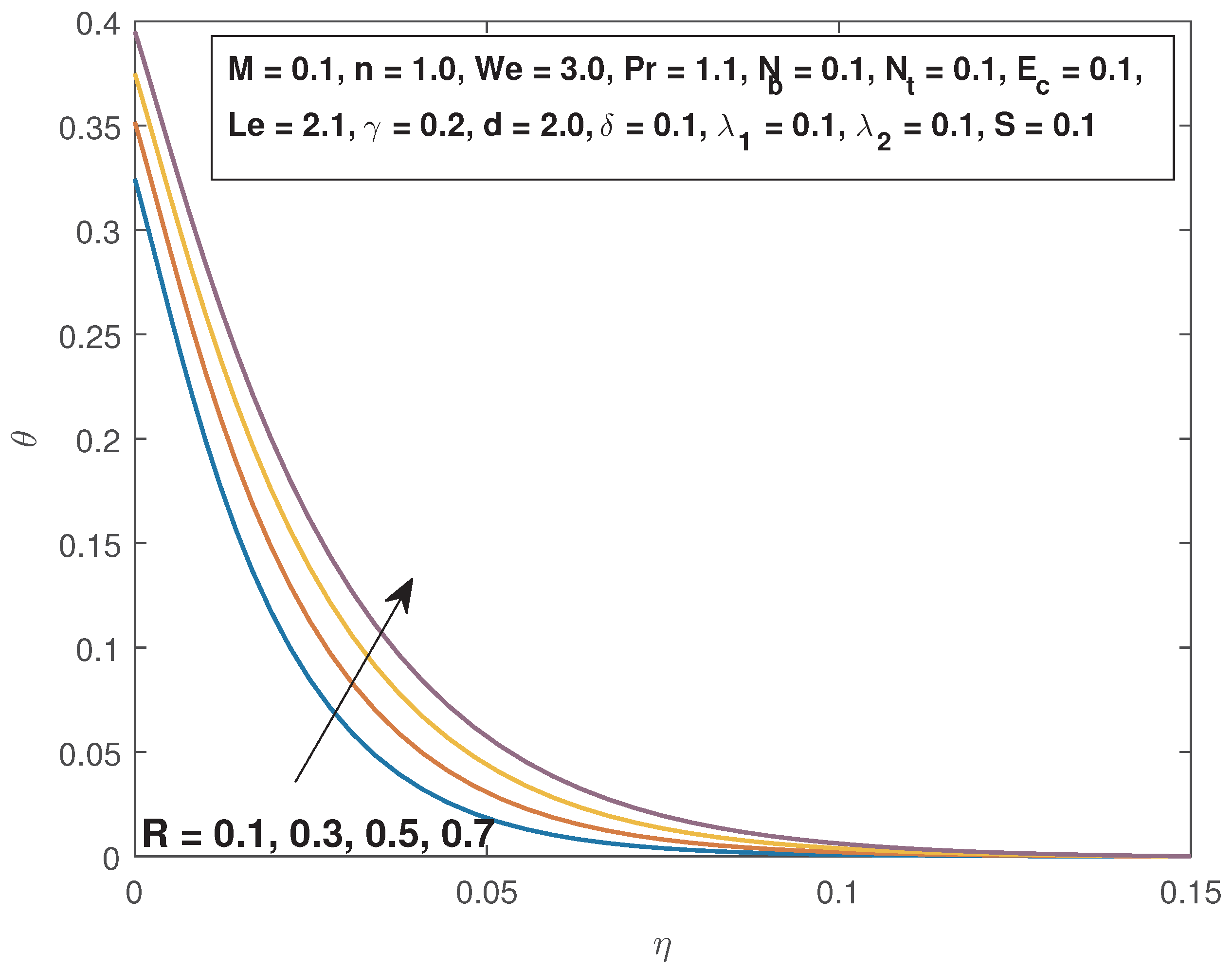
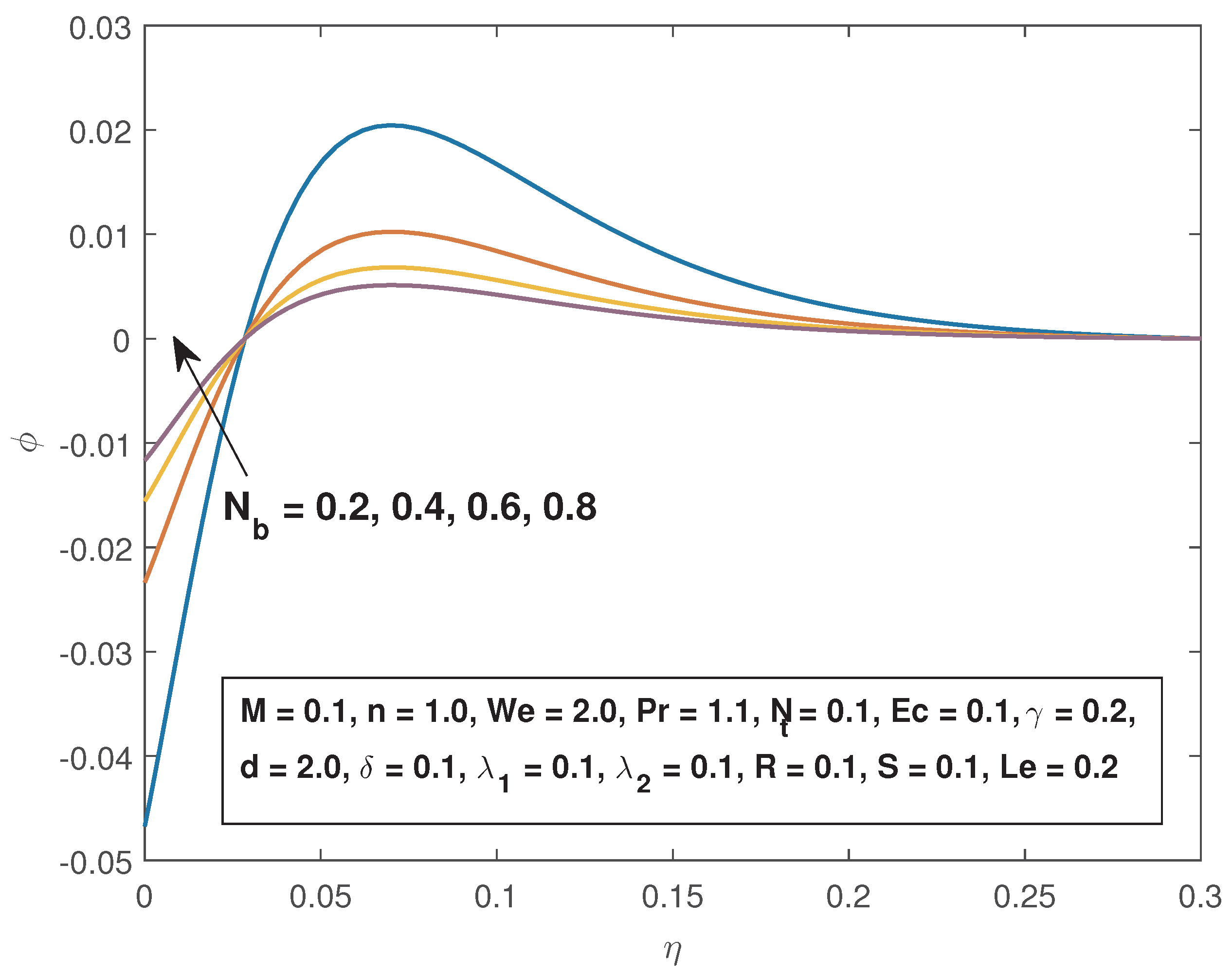
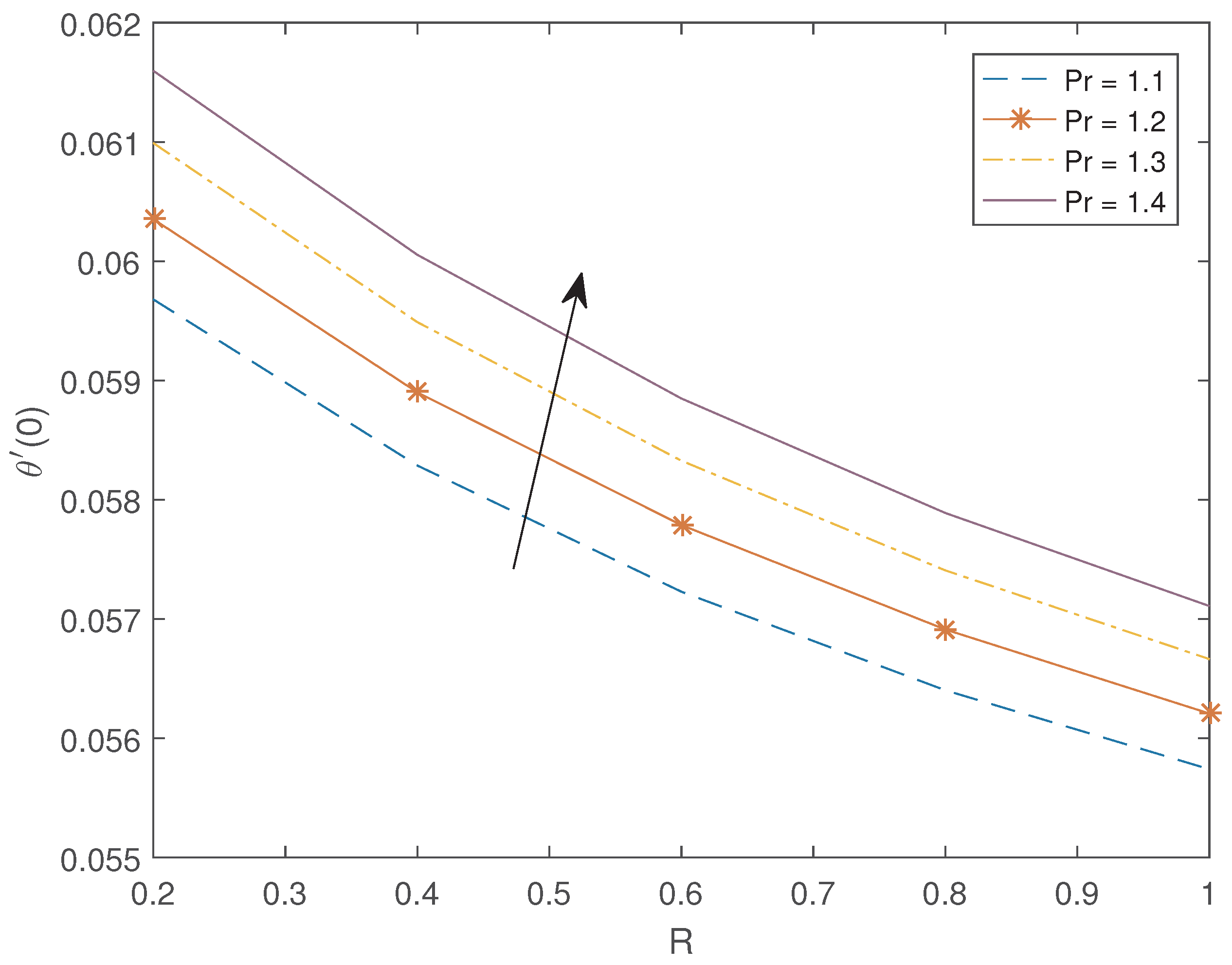
4. Results and Discussions
5. Conclusions
- The spectral quasi-linearization method is a very efficient and reliable method for solving non-linear differential equations.
- The fluid velocity and the momentum boundary layer increase with increasing Eckert number, thermal buoyancy parameter, thermal slip parameter, and decrease with the magnetic field parameter, and the velocity slip parameter.
- The fluid temperature increases with increasing magnetic field parameter, Eckert number, thermal slip parameter, and the thermal radiation parameter, and is decreased by raising the Prandtl number and thermal buoyancy parameter.
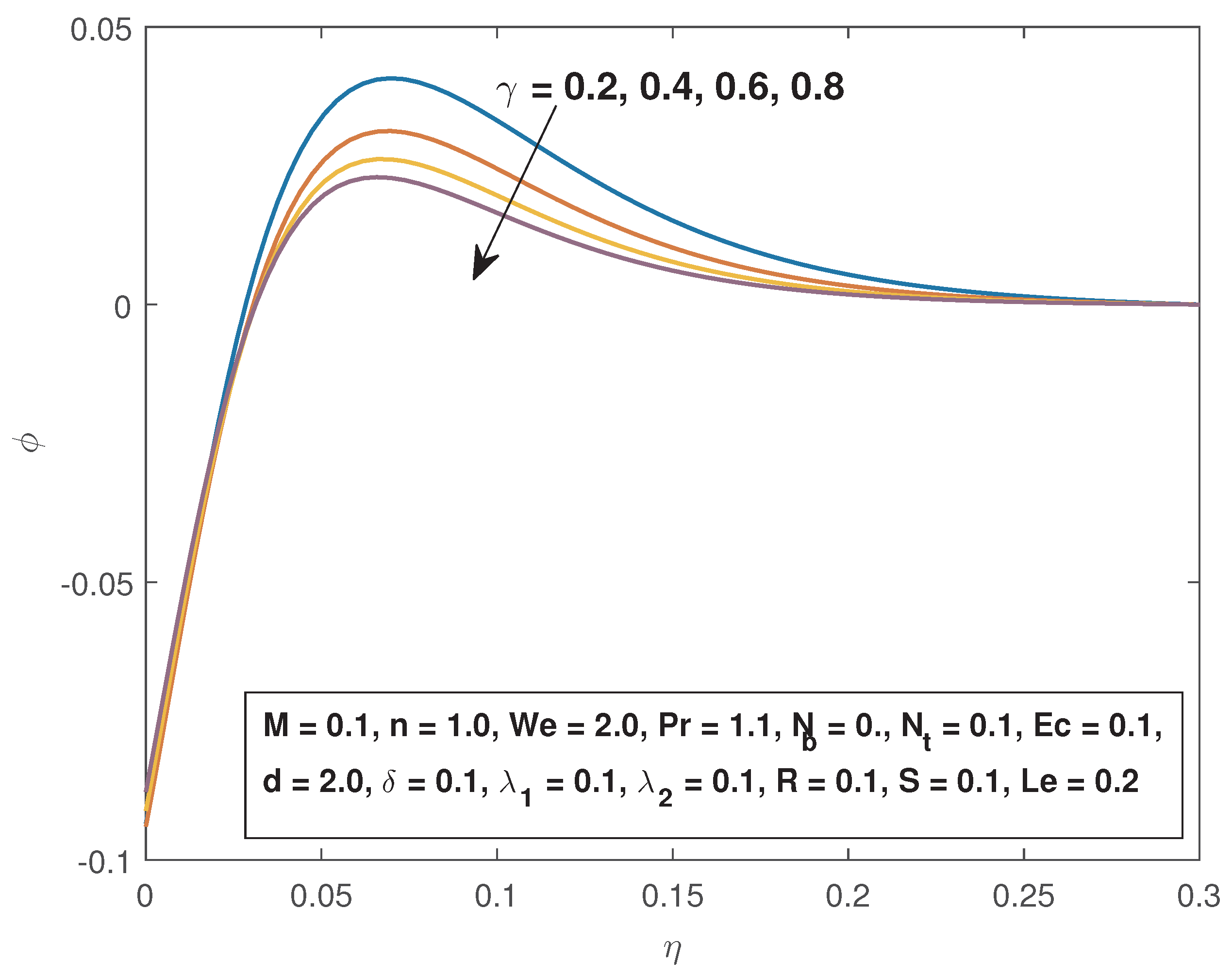
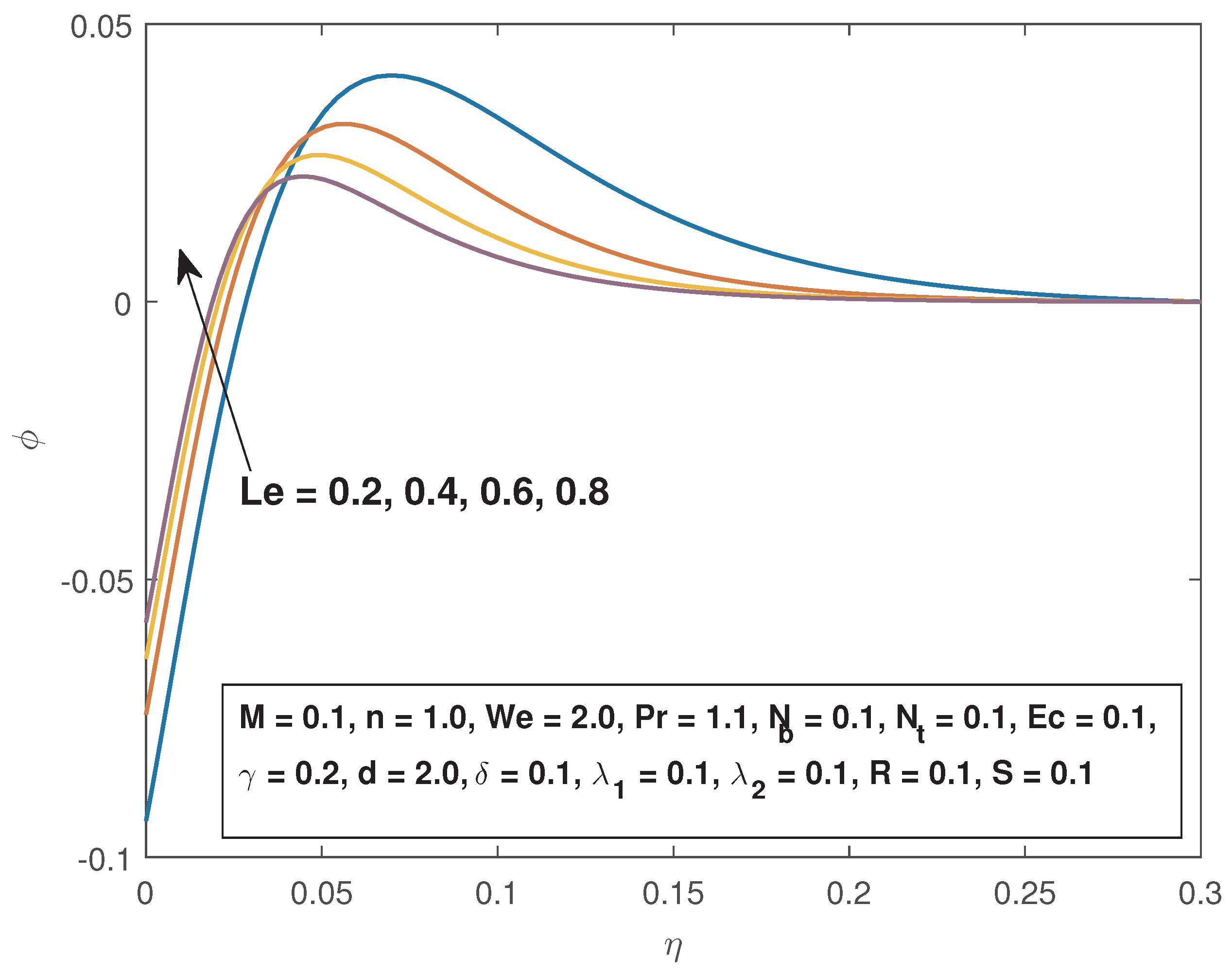
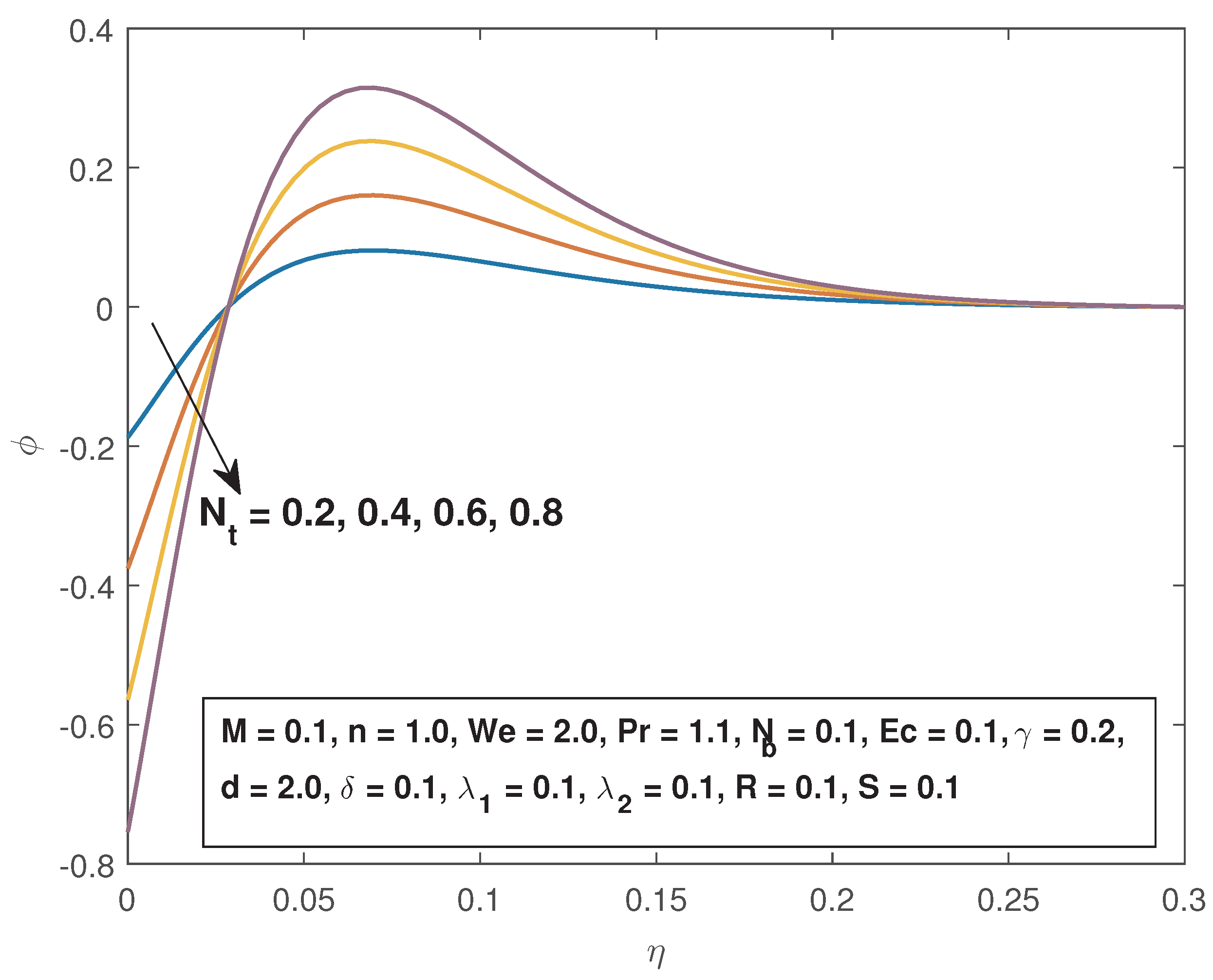
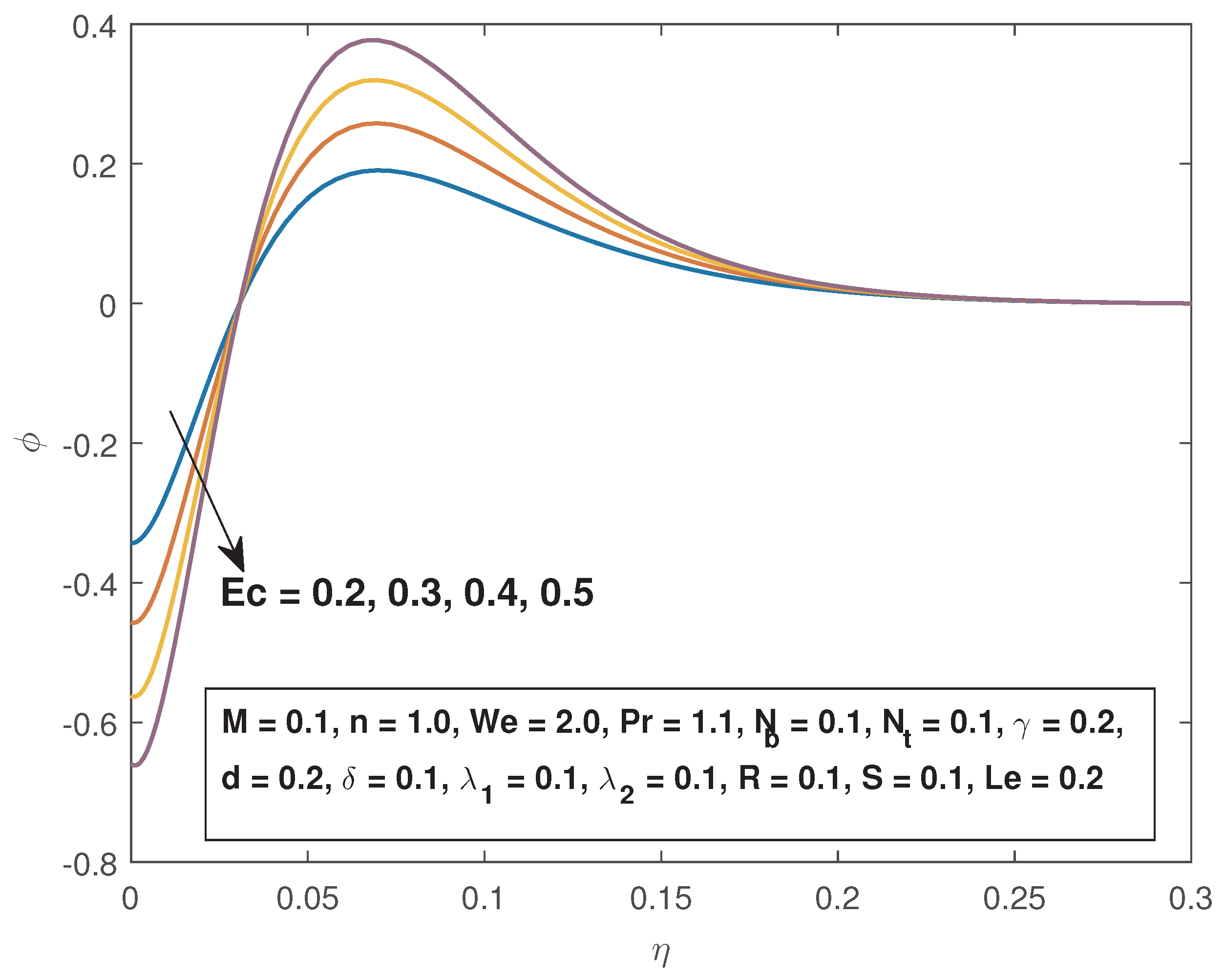
- The fluid concentration in enhanced by increasing the Lewis number and the Brownian motion parameter while it is depressed by increased thermal reaction parameter, thermophoresis parameter and the Eckert number.
- The skin friction is increases with increasing magnetic field parameter and decreases when the Eckert number, thermal buoyancy parameter and the velocity slip parameter are increased.
- The local Nusselt number increases when the Prandtl number and the thermal slip parameter are increased, while the opposite trend is observed when thermal radiation parameter and thermophoresis parameter are increased.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Rivlin–Ericksen tensor | |
| C | concentration (kg m) |
| skin friction coefficient | |
| concentration at the wall (kg m) | |
| ambient volume fraction (kg m) | |
| specific heat | |
| d | Carreau–Yasuda parameter |
| Brownian diffusion coefficient | |
| Thermophoresis diffusion coefficient | |
| Eckert number | |
| f | non-dimensional stream function |
| g | acceleration due to gravity (m s) |
| mean absorption coefficient (W m K) | |
| chemical reaction coefficient | |
| M | magnetic field parameter |
| n | power-law index |
| Brownian motion parameter | |
| thermophoresis parameter | |
| local Nusselt number | |
| Prandtl number | |
| radiative heat flux (W m) | |
| R | thermal radiation parameter |
| S | velocity slip parameter |
| local Sherwood number | |
| T | temperature (K) |
| wall temperature (K) | |
| ambient surface temperature (K) | |
| u | horizontal velocity component (m s) |
| v | vertical velocity component (m s) |
| Weissenberg number | |
| x | horizontal coordinate (m) |
| y | vertical coordinate (m) |
| Greek Symbols | |
| Stefan Boltzmann constant (W m K) | |
| electrical conductivity | |
| thermal diffusivity | |
| magnetic field strength | |
| thermal expansion coefficient | |
| concentration expansion coefficient | |
| thermal conductivity | |
| thermal buoyancy parameter | |
| solutal buoyancy parameter | |
| dimensionless radial coordinate | |
| zeros shear viscosity | |
| infinite shear viscosity | |
| material time constant | |
| non-dimensional temperature | |
| non-dimensional concentration | |
| base fluid density (kg m) | |
| chemical reaction parameter | |
| shear strain | |
| kinematic viscosity fluid | |
| heat capacity of nanoparticle | |
| heat capacity of base fluid | |
| Subscripts | |
| w | surface conditions |
| ∞ | free stream conditions |
References
- Kahshan, M.; Lu, D.; Rahimi-Gorji, M. Hydrodynamical study of flow in a permeable channel: Application to flat plate dialyzer. Int. J. Hydrogen Energy 2019. [Google Scholar] [CrossRef]
- Cioranescu, D.; Girault, V.; Rajagopal, K.R. Mechanics and Mathematics of Fluids of the Differential Type. Adv. Mech. Math. 2016. [Google Scholar] [CrossRef]
- Kheyfets, V.O.; Kieweg, S.L. Gravity-driven thin film flow of anEllis fluid. J. Nonnewton Fluid Mech. 2013, 202, 88–98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sochi, T. Analytical solutions for the flow of Carreau and Cross fluids in circular pipes and thin slits. Rheol. Acta 2015, 54, 745–756. [Google Scholar] [CrossRef] [Green Version]
- Hina, S.; Hayat, T.; Asghar, S.; Hendi, A.A. Influence of compliant walls on peristalic motion with heat/mass transfer and chemical reaction. Int. J. Heat Mass Trans. 2012, 55, 3386–3394. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Abd Elmaboud, Y. Simultaneous effects of variable viscosity and thermal conductivity on peristaltic flow in a vertical asymmetric channel. Can. J. Phys. 2014, 92, 1541–1555. [Google Scholar] [CrossRef]
- Mahmood, R.; Bilal, S.; Khan, I.; Kousar, N.; Seikh, A.H.; El-Sayed, M.S. A comprehensive finite element examination of Carreau Yasuda fluid model in a lid driven cavity and channel with obstacle by way of kinetic energy and drag and lift coefficient measurements. J. Mater. Res. Technol. 2019. [Google Scholar] [CrossRef]
- Andrade, L.C.F. The Carreau-Yasuda Fluids: A skin friction equation for turbulent flow in pipes and Kolmogorov dissipative scales. J. Braz. Soc. Mech. Sci. Eng. 2007, 29, 162–167. [Google Scholar] [CrossRef]
- Hayat, T.; Abbasi, F.M.; Ahmad, B.; Alsaedi, A. Peristaltic Transport of Carreau-Yasuda Fluid in a Curved Channel with Slip Effects. PLoS ONE 2014, 9, e95070. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Boundary layer flow of Carreau fluid over a convectively heated stretching. Appl. Math. Comput. 2014, 245, 12–22. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Alsaedi, A. Numerical analysis for MHD peristaltic transport of Carreau–Yasuda fluid in a curved channel with Hall effects. J. Magnet. Magnet. Mater. 2015, 382, 104–110. [Google Scholar] [CrossRef]
- Shamekhi, A.; Sadeghy, K. Cavity flow simulation of Carreau–Yasuda non-Newtonian fluids using PIM meshfree method. Appl. Math. Model. 2009, 33, 4131–4145. [Google Scholar] [CrossRef]
- Lashgari, L.; Pralits, J.O.; Giannetti, F.; Brandt, I. First instability of the flow of shear-thinning and shear-thickening fluids past a circular cylinder. J. Fluid Mech. 2012, 701, 201–227. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Zheng, L.; Zhang, X. Mixed Convection Heat Transfer of Non-newtonian Carreau–Yasuda Fluid Driven by Power Law Temperature Gradient. Heat Transf. Res. 2017, 48, 849–864. [Google Scholar] [CrossRef]
- Khan, M.; Shahid, A.; Malik, M.Y.; Salahuddin, T. Chemical reaction for Carreau-Yasuda nanofluid flow past a nonlinear stretching sheet considering Joule heating. Results Phy. 2018, 8, 1124–1130. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Bilal, S.; Awais, M.; Khan, I. MHD squeezed flow of Carreau-Yasuda fluid over a sensor surface. Alexandria Eng. J. 2017, 56, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Aslam, N.; Khan, M.I.; Alsaedi, A. Mixed convective peristaltic flow of Carreau–Yasuda fluid in an inclined symmetric channel. Microsyst. Technol. 2019, 25, 609–620. [Google Scholar] [CrossRef]
- Migtaa, H.M.; Al- Khafajy, D.G.S. Influence of Heat Transfer on Magnetohydrodynamics Oscillatory Flow for Carreau-Yasuda Fluid Through a Porous Medium. J. Al-Qadisiyah Comput. Sci. Math. 2019, 11, 76–88. [Google Scholar]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International mechanical engineering congress and exhibition, San Francisco, CA, USA, 12–17 November 1995; pp. 99–105. [Google Scholar]
- Nandkeolyar, R.; Mahatha, B.K.; Mahato, G.K.; Sibanda, P. Effect of Chemical Reaction and Heat Absorption on MHD Nanoliquid Flow Past a Stretching Sheet in the Presence of a Transverse Magnetic Field. Magnetochemistry 2018, 4, 18. [Google Scholar] [CrossRef] [Green Version]
- Anuar, N.S.; Bachok, N. Blasius and Sakiadis problems in nano-fluids using Buongiorno model and thermo-physical properties of nano-liquids. Eur. Int. J. Sci. Technol. 2016, 5, 65–81. [Google Scholar]
- Prakash, D.; Suriyakumar, P. Transient hydromagnetic convection flow of nanofluid between asymmetric vertical plates with heat generation. Int. J. Pure Appl. Math. 2017, 113, 1–10. [Google Scholar]
- Sharma, R.; Hussain, S.D.; Joshi, H.; Sethi, G.S. Analysis of radiative magneto-nanofluid over an accelerated plate in a rotating medium with Hall effects. Differ. Found. 2017, 11, 129–145. [Google Scholar] [CrossRef]
- Astuti, A.; Sri, P.; Kaprawi, S. Natural Convection of Nanofluids past an Accelerated Vertical Plate with Variable Wall Temperature by Presence of the Radiation. Front. Heat Mass Transfer (FHMT) 2019, 13, 3. [Google Scholar] [CrossRef] [Green Version]
- Hady, F.M.; Ibrahim, F.S.; Abdel-Gaied, S.M.; Eid, M.R. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res. Lett. 2012, 7, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shateyi, S.; Prakask, J. A new numerical approach for MHD laminar boundary layer flow and heat transfer of nanofluids over a moving surface in the presence of thermal radiation. Bound. Value Prob. 2014, 2. [Google Scholar] [CrossRef] [Green Version]
- Krishnamurthy, M.R.; Gireesha, B.J.; Prasannakumara, B.C.; Gorla, R.S.R. Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet. Nonlinear Eng. 2016, 5, 147–159. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Emam, T.G. Effects of Thermal Radiation and Heat Transfer over an Unsteady Stretching Surface Embedded in a Porous Medium in the Presence of Heat Source or Sink. Therm. Sci. 2011, 15, 477–485. [Google Scholar]
- Khan, I.; Shafquatullah, M.Y.; Malik, M.Y.; Hussain, A.; Khan, M. Magnetohydrodynamics Carreau nanofluid flow over an inclined convective heated stretching cylinder with joule heating. Results Phys. 2017, 7, 4001–4012. [Google Scholar] [CrossRef]
- Cheng, K.C.; Wu, R.S. Viscous Dissipation Effects on Convective Instability and Heat Transfer in Plane Poiseuille Flow Heated from Below. Appl. Sci. Res. 1976, 32, 327–346. [Google Scholar] [CrossRef]
- Boubaker, K.; Li, B.; Zheng, L.; Bhrawy, A.H.; Zhang, X. Effects of Viscous Dissipation on the Thermal Boundary Layer of Pseudoplastic Power-Law Non-Newtonian Fluids Using Discretization Method and the Boubaker Polynomials Expansion Scheme. ISRN Therm. 2012, 2012, 181286. [Google Scholar] [CrossRef] [Green Version]
- Lund, L.A.; Omar, Z.; Khan, I.; Kadry, S.; Rho, S.; Mari, I.A.; Nisar, K.S. Effect of Viscous Dissipation in Heat Transfer of MHD Flow of Micropolar Fluid Partial Slip Conditions: Dual Solutions and Stability Analysis. Energies 2019, 12, 4617. [Google Scholar] [CrossRef] [Green Version]
- Motsa, S.S.; Dlamini, P.G.; Khumalo, M. Spectral Relaxation Method and Spectral Quasilinearization Method for Solving Unsteady Boundary Layer Flow Problems. Adv. Math. Phys. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Alharbey, R.A.; Mondal, H.; Behl, R. Spectral Quasi-Linearization Method for Non-Darcy Porous Medium with Convective Boundary Condition. Entropy 2019, 21, 838. [Google Scholar] [CrossRef] [Green Version]
- Pal, D.; Mondal, S.; Mondal, H. Entropy generation on MHD Jeffrey nanofluid over a stretching sheet with nonlinear thermal radiation using spectral quasilinearization Method. Int. J. Ambient Energy 2019, 1–24. [Google Scholar] [CrossRef]
- Das, S.; Mondal, H.; Kundu, P.K.; Sibanda, P. Spectral quasi-linearization method for Casson fluid with homogeneous heterogeneous reaction in presence of nonlinear thermal radiation over an exponential stretching sheet. Multidiscip. Model. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Shateyi, S.; Muzara, H. On the Numerical Analysis of Unsteady MHD Boundary Layer Flow of Williamson Fluid Over a Stretching Sheet and Heat and Mass Transfers. Computation 2020, 8, 55. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; Elsevier: New York, NY, USA, 1965. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]








| M | S | |||
|---|---|---|---|---|
| 0.1 | 0.1 | 0.1 | 0.1 | 0.901165706578126 |
| 0.2 | 0.1 | 0.1 | 0.1 | 0.939430977283166 |
| 0.3 | 0.1 | 0.1 | 0.1 | 0.975901612948121 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.901165706578126 |
| 0.1 | 0.3 | 0.1 | 0.1 | 0.894342142778385 |
| 0.1 | 0.5 | 0.1 | 0.1 | 0.887855032025925 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.901165706578126 |
| 0.1 | 0.1 | 0.5 | 0.1 | 0.607698358897778 |
| 0.1 | 0.1 | 0.9 | 0.1 | 0.465481562823527 |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.901165706578126 |
| 0.1 | 0.1 | 0.1 | 0.3 | 0.877937713382835 |
| 0.1 | 0.1 | 0.1 | 0.5 | 0.856014644415950 |
| R | ||||
|---|---|---|---|---|
| 1.1 | 0.1 | 0.1 | 0.1 | 0.078548380963099 |
| 1.2 | 0.1 | 0.1 | 0.1 | 0.079117794840876 |
| 1.3 | 0.1 | 0.1 | 0.1 | 0.079609418569888 |
| 1.1 | 0.1 | 0.1 | 0.1 | 0.078548380963099 |
| 1.1 | 0.3 | 0.1 | 0.1 | 0.179932397357334 |
| 1.1 | 0.5 | 0.1 | 0.1 | 0.242732064006873 |
| 1.1 | 0.1 | 0.1 | 0.1 | 0.078548380963099 |
| 1.1 | 0.1 | 0.3 | 0.1 | 0.077003538347739 |
| 1.1 | 0.1 | 0.5 | 0.1 | 0.075588054175029 |
| 1.1 | 0.1 | 0.1 | 0.1 | 0.078548380963099 |
| 1.1 | 0.1 | 0.1 | 0.3 | 0.077003538347739 |
| 1.1 | 0.1 | 0.1 | 0.5 | 0.075588054175029 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shateyi, S.; Muzara, H. On Numerical Analysis of Carreau–Yasuda Nanofluid Flow over a Non-Linearly Stretching Sheet under Viscous Dissipation and Chemical Reaction Effects. Mathematics 2020, 8, 1148. https://doi.org/10.3390/math8071148
Shateyi S, Muzara H. On Numerical Analysis of Carreau–Yasuda Nanofluid Flow over a Non-Linearly Stretching Sheet under Viscous Dissipation and Chemical Reaction Effects. Mathematics. 2020; 8(7):1148. https://doi.org/10.3390/math8071148
Chicago/Turabian StyleShateyi, Stanford, and Hillary Muzara. 2020. "On Numerical Analysis of Carreau–Yasuda Nanofluid Flow over a Non-Linearly Stretching Sheet under Viscous Dissipation and Chemical Reaction Effects" Mathematics 8, no. 7: 1148. https://doi.org/10.3390/math8071148





