Analytical Estimation of Temperature in Living Tissues Using the TPL Bioheat Model with Experimental Verification
Abstract
1. Introduction
2. Mathematical Model
3. Laplace Transforms
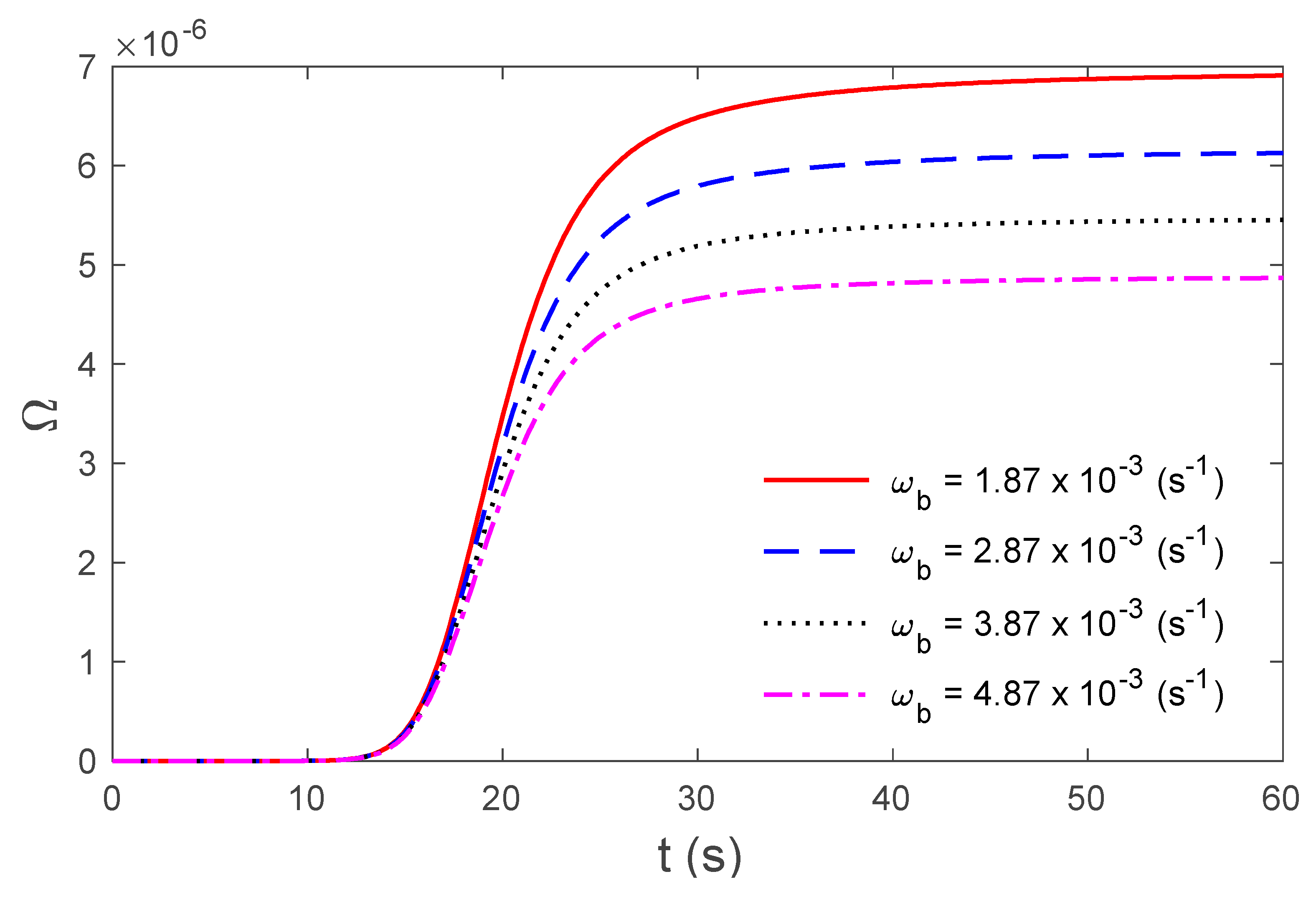
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gabay, I.; Abergel, A.; Vasilyev, T.; Rabi, Y.; Fliss, D.M.; Katzir, A. Temperature-controlled two-wavelength laser soldering of tissues. Lasers Surg. Med. 2011, 43, 907–913. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Chen, J.; Zhang, Y. Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation. Comput. Biol. Med. 2009, 39, 286–293. [Google Scholar] [CrossRef]
- Mahjoob, S.; Vafai, K. Analytical characterization of heat transport through biological media incorporating hyperthermia treatment. Int. J. Heat Mass Transf. 2009, 52, 1608–1618. [Google Scholar] [CrossRef]
- Labonte, S. Numerical model for radio-frequency ablation of the endocardium and its experimental validation. IEEE Trans. Biomed. Eng. 1994, 41, 108–115. [Google Scholar] [CrossRef] [PubMed]
- González-Suárez, A.; Berjano, E. Comparative analysis of different methods of modeling the thermal effect of circulating blood flow during RF cardiac ablation. IEEE Trans. Biomed. Eng. 2015, 63, 250–259. [Google Scholar] [CrossRef] [PubMed]
- Iasiello, M.; Andreozzi, A.; Bianco, N.; Vafai, K. The porous media theory applied to radiofrequency catheter ablation. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Hypo-and hyperthermia effects on LDL deposition in a curved artery. Comput. Therm. Sci. Int. J. 2019, 11, 95–103. [Google Scholar] [CrossRef]
- Egred, M.; Brilakis, E.S. Excimer laser coronary angioplasty (ELCA): Fundamentals, mechanism of action, and clinical applications. J. Invasive Cardiol. 2020, 32, E27–E35. [Google Scholar]
- Ho, Y.-J.; Wu, C.-C.; Hsieh, Z.-H.; Fan, C.-H.; Yeh, C.-K. Thermal-sensitive acoustic droplets for dual-mode ultrasound imaging and drug delivery. J. Control. Release 2018, 291, 26–36. [Google Scholar] [CrossRef]
- Andreozzi, A.; Iasiello, M.; Netti, P.A. A thermoporoelastic model for fluid transport in tumour tissues. J. R. Soc. Interface 2019, 16, 20190030. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Charny, C.K. Mathematical models of bioheat transfer. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1992; Volume 22, pp. 19–155. [Google Scholar]
- Nakayama, A.; Kuwahara, F. A general bioheat transfer model based on the theory of porous media. Int. J. Heat Mass Transf. 2008, 51, 3190–3199. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling heat transfer in tumors: A review of thermal therapies. Ann. Biomed. Eng. 2019, 47, 676–693. [Google Scholar] [CrossRef] [PubMed]
- Tzou, D.Y. A Unified field approach for heat conduction from macro- to micro-scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Zhu, D.; Luo, Q.; Zhu, G.; Liu, W. Kinetic thermal response and damage in laser coagulation of tissue. Lasers Surg. Med. 2002, 31, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Choudhuri, S.R. On a thermoelastic three-phase-lag model. J. Therm. Stresses 2007, 30, 231–238. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, S.; Rai, K. Analysis of classical Fourier, SPL and DPL heat transfer model in biological tissues in presence of metabolic and external heat source. Heat Mass Transf. 2016, 52, 1089–1107. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I. Finite element analyses of nonlinear DPL bioheat model in spherical tissues using experimental data. Mech. Based Des. Struct. Mach. 2020, 1–11. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I. Analytical solutions of fractional bioheat model in a spherical tissue. Mech. Based Des. Struct. Mach. 2019, 1–10. [Google Scholar] [CrossRef]
- Mondal, S.; Sur, A.; Kanoria, M. Transient heating within skin tissue due to time-dependent thermal therapy in the context of memory dependent heat transport law. Mech. Based Des. Struct. Mach. 2019, 1–15. [Google Scholar] [CrossRef]
- Kumar, R.; Chawla, V. Reflection and refraction of plane wave at the interface between elastic and thermoelastic media with three-phase-lag model. Int. Commun. Heat Mass Transf. 2013, 48, 53–60. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.S.; Abbas, I. Three-phase lag model of thermo-elastic interaction in a 2D porous material due to pulse heat flux. Int. J. Numer. Methods Heat Fluid Flow 2020. [Google Scholar] [CrossRef]
- Quintanilla, R.; Racke, R. A note on stability in three-phase-lag heat conduction. Int. J. Heat Mass Transf. 2008, 51, 24–29. [Google Scholar] [CrossRef]
- Abbas, I.A.; Zenkour, A.M. Dual-phase-lag model on thermoelastic interactions in a semi-infinite medium subjected to a ramp-type heating. J. Comput. Theor. Nanosci. 2014, 11, 642–645. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H.M. Two-temperature generalized thermoelasticity under ramp-type heating by finite element method. Meccanica 2013, 48, 331–339. [Google Scholar] [CrossRef]
- Abbas, I.A. Finite element analysis of the thermoelastic interactions in an unbounded body with a cavity. Forschung im Ingenieurwesen 2007, 71, 215–222. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abo-El-Nour, N.; Othman, M.I. Generalized magneto-thermoelasticity in a fiber-reinforced anisotropic half-space. Int. J. Thermophys. 2011, 32, 1071–1085. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. A generalized thermoelasticity problem of an annular cylinder with temperature-dependent density and material properties. Int. J. Mech. Sci. 2014, 84, 54–60. [Google Scholar] [CrossRef]
- Marin, M. Cesaro means in thermoelasticity of dipolar bodies. Acta Mech. 1997, 122, 155–168. [Google Scholar] [CrossRef]
- Marin, M.; Craciun, E. Uniqueness results for a boundary value problem in dipolar thermoelasticity to model composite materials. Compos. Part B Eng. 2017, 126, 27–37. [Google Scholar] [CrossRef]
- Hassan, M.; Marin, M.; Ellahi, R.; Alamri, S.Z. Exploration of convective heat transfer and flow characteristics synthesis by Cu–Ag/water hybrid-nanofluids. Heat Transf. Res. 2018, 49, 1837–1848. [Google Scholar] [CrossRef]
- Xu, F.; Seffen, K.; Lu, T. Non-Fourier analysis of skin biothermomechanics. Int. J. Heat Mass Transf. 2008, 51, 2237–2259. [Google Scholar] [CrossRef]
- Ahmadikia, H.; Fazlali, R.; Moradi, A. Analytical solution of the parabolic and hyperbolic heat transfer equations with constant and transient heat flux conditions on skin tissue. Int. Commun. Heat Mass Transf. 2012, 39, 121–130. [Google Scholar] [CrossRef]
- Kumar, D.; Rai, K. Three-phase-lag bioheat transfer model and its validation with experimental data. Mech. Based Des. Struct. Mach. 2020, 1–15. [Google Scholar] [CrossRef]
- Mitchell, J.W.; Galvez, T.L.; Hengle, J.; Myers, G.E.; Siebecker, K.L. Thermal response of human legs during cooling. J. Appl. Physiol. 1970, 29, 859–865. [Google Scholar] [CrossRef]
- Gardner, C.M.; Jacques, S.L.; Welch, A. Light transport in tissue: Accurate expressions for one-dimensional fluence rate and escape function based upon Monte Carlo simulation. Lasers Surg. Med. Off. J. Am. Soc. Laser Med. Surg. 1996, 18, 129–138. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro-to Micro-Scale Heat Transfer: The Lagging Behavior; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Noroozi, M.J.; Goodarzi, M. Nonlinear analysis of a non-Fourier heat conduction problem in a living tissue heated by laser source. Int. J. Biomath. 2017, 10, 1750107. [Google Scholar] [CrossRef]
- Henriques, F., Jr.; Moritz, A. Studies of thermal injury: I. The conduction of heat to and through skin and the temperatures attained therein. A theoretical and an experimental investigation. Am. J. Pathol. 1947, 23, 530. [Google Scholar]
- Moritz, A.R.; Henriques, F., Jr. Studies of thermal injury: II. The relative importance of time and surface temperature in the causation of cutaneous burns. Am. J. Pathol. 1947, 23, 695–720. [Google Scholar]
- Museux, N.; Perez, L.; Autrique, L.; Agay, D. Skin burns after laser exposure: Histological analysis and predictive simulation. Burns 2012, 38, 658–667. [Google Scholar] [CrossRef] [PubMed]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.; Alzahrani, F.; Abbas, I. Analytical Estimation of Temperature in Living Tissues Using the TPL Bioheat Model with Experimental Verification. Mathematics 2020, 8, 1188. https://doi.org/10.3390/math8071188
Hobiny A, Alzahrani F, Abbas I. Analytical Estimation of Temperature in Living Tissues Using the TPL Bioheat Model with Experimental Verification. Mathematics. 2020; 8(7):1188. https://doi.org/10.3390/math8071188
Chicago/Turabian StyleHobiny, Aatef, Faris Alzahrani, and Ibrahim Abbas. 2020. "Analytical Estimation of Temperature in Living Tissues Using the TPL Bioheat Model with Experimental Verification" Mathematics 8, no. 7: 1188. https://doi.org/10.3390/math8071188
APA StyleHobiny, A., Alzahrani, F., & Abbas, I. (2020). Analytical Estimation of Temperature in Living Tissues Using the TPL Bioheat Model with Experimental Verification. Mathematics, 8(7), 1188. https://doi.org/10.3390/math8071188




