A Fourth Order Energy Dissipative Scheme for a Traffic Flow Model

Abstract

We propose, analyze and numerically validate a new energy dissipative scheme for the Ginzburg–Landau equation by using the invariant energy quadratization approach. First, the Ginzburg–Landau equation is transformed into an equivalent formulation which possesses the quadratic energy dissipation law. After the space-discretization of the Fourier pseudo-spectral method, the semi-discrete system is proved to be energy dissipative. Using diagonally implicit Runge–Kutta scheme, the semi-discrete system is integrated in the time direction. Then the presented full-discrete scheme preserves the energy dissipation, which is beneficial to the numerical stability in long-time simulations. Several numerical experiments are provided to illustrate the effectiveness of the proposed scheme and verify the theoretical analysis.

1. Introduction

The Ginzburg–Landau equation (GLE) was first proposed by Ginzburg and Landau in 1950 and applied to model the electrodynamics, quantum mechanics and thermodynamic properties of superconductors. As a state transformation equation, the GLE is closely related to many other state transformation equations, such as Allen–Cahn equation and Chafee–Infante equation. As is well known, the GLE plays an important role in the study of state transformation and unstable wave theory. Moreover, it has been widely used in optical fiber communication. In this paper, we consider the one-dimensional GLE as a model for traffic flow [1]

$$\begin{array}{cc}\hfill u_t& =({\partial }_x+ϵ{\partial }_x^2)(6u+{\partial }_x^{2}u-u^3),\hfill \end{array}$$

(1)

subject to the initial and boundary conditions

$$\begin{array}{cc}\hfill u(x,0)& =u_0\left(x\right),x\in \Omega ,\hfill \\ \hfill u(a,t)& =u(b,t),t\ge 0,\hfill \end{array}$$

where $ϵ\ge 0$ and $\Omega =[a,b]\subseteq \mathbb{R}$ is the bounded domain. We denote the $L^2$ inner product by $〈f,g〉={\int }_{\Omega }fg\mathrm{d}x$, the $L^2$ norm ${\parallel f\parallel }^2={〈f,f〉}^{\frac{1}{2}}$. Under the periodic boundary conditions, the global energy of the GLE is

$$\begin{array}{cc}\hfill H\left(u\right)& ={\int }_{\Omega }(3u^2-\frac{1}{2}{u}_x^2-\frac{1}{4}f\left(u\right))\mathrm{d}x,\hfill \end{array}$$

where $f\left(u\right)=u^4$. Then the GLE in [1] can be rewritten as

$$\begin{array}{cc}\hfill u_t& =({\partial }_x+ϵ{\partial }_{xx})m,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill m& =\frac{\delta H\left(u\right)}{\delta u}.\hfill \end{array}$$

(3)

Taking the inner product of the Equation (2) with m and the Equation (3) with $u_t$, we obtain

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}H\left(u\right)=〈{\partial }_{x}m,m〉+〈ϵ{\partial }_{xx}m,m〉=-ϵ{\parallel {\partial }_{x}m\parallel }^2\le 0.\end{array}$$

Obviously, the GLE satisfies the energy dissipation law.

In recent years, many researchers have conducted various works about the GLE. Celledoni [1] proved that the average vector field (AVF) method can keep the energy dissipation of the Equation (1). The time-dependent GLE for the car traffic model is derived by Nagatani [2] through the perturbation method. Gunzburger and Hou [3] solved a series of problems for a Ginzburg–Landau model of superconductivity. They proposed finite element approximations for the optimality system and derived corresponding error estimates. The local well-posedness of the initial-boundary value problem for the complex GLE in bounded domains is investigated by Kuroda and Takanori [4]. Meanwhile, there are many effective ways to solve the GLE, such as the discontinuous Galerkin method [5], the semi-implicit method [6] and the trial equation method [7]. In addition, there also exist relevant studies on the fractional GLE [8,9,10,11] and the stochastic GLE [12,13,14,15,16]. However, most of previous researches can only achieve second order accuracy in the time direction. Therefore, the main challenge issue is to construct a high order energy dissipative scheme for the GLE.

The invariant energy quadratization (IEQ) approach [17] is a new method developed in recent years by introducing a Lagrange multiplier and has been successfully applied to a variety of gradient flow models [18,19,20,21,22,23,24]. By introducing a Lagrange multiplier and converting the nonlinear part to a semi-implicit scheme, a new linear system consisting of two coupled equations is calculated at each time step. A time-discretization scheme for the linear systems is constructed by Yang [25], which is easy to implement and achieve unconditionally energy stability. Liu [26] applyed two novel and efficient modified techniques based on IEQ approach to deal with nonlinear terms in gradient flows which succeeded in finding suitable positive preserving functions. Two linear and second order schemes that combine the IEQ approach with the stabilization technique are developed by Xu [27], where several extra linear stabilization terms are added and they are crucial to suppress the non-physical spatial oscillations caused by the strong anisotropy. Gong [28] presented a novel class of arbitrarily high-order and unconditionally energy-stable algorithms for gradient flow models by combining the IEQ approach and a specific class of Runge–Kutta (RK) methods. Since the solution to the Ginzburg–Landau equation shows instability very soon and this high order implicit scheme can unconditionally keep Ginzburg–Landau equation energy dissipation, we adopt this method to solve the Ginzburg–Landau equation. Ref. [28] combines IEQ approach and RK method and apply them to Cahn–Hilliard equation and Allen–Cahn equation to get the arbitrarily high-order schemes, while we apply it to the Ginzburg–Landau equation to construct a fourth order scheme in this paper.

The rest of this paper is organized as follows. In Section 2, the IEQ approach is introduced and applied to the GLE. Then the GLE is reformulated as a new system which admits a quadratic energy dissipation law. In Section 3, the Fourier pseudo-spectral method is used to obtain the semi-discrete the system of the GLE. After that, the implicit fourth order Runge–Kutta (RK4) method is applied for the time discretization to structure a full-discrete scheme. It is proved that the scheme we proposed is energy dissipative. In Section 4, the stability of the proposed scheme is verified by numerical experiments. We make a summary of this work in Section 5.

2. Invariant Energy Quadratization Approach

In this section, we present a new scheme for the GLE to preserve the energy dissipation law. By using the IEQ approach, we transform the Hamlitonian functional into a quadratic functional. We first introduce a Lagrange multiplier $r=\sqrt{f\left(u\right)}$, then the GLE is transformed into

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_t=({\partial }_x+ϵ{\partial }_{x}x)(6u+{\partial }_{xx}u-ur),\hfill \\ r_t=2u{u}_t.\hfill \end{array}\right.\end{array}$$

(4)

Theorem 1.

The system above preserves the energy dissipation law

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}H\left(u\right)\le 0,\end{array}$$

where $H\left(u\right)={\int }_{\Omega }(3u^2-\frac{1}{2}|{\partial }_x{u}^2|-\frac{1}{4}{r}^2)\mathrm{d}x.$

Proof. 

The system (4) can be rewritten as

$$\begin{array}{cc}\hfill u_t& =({\partial }_x+ϵ{\partial }_{xx})m,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill m& =6u+{\partial }_{xx}u-\frac{r}{4\sqrt{f\left(u\right)}}{f}^{\prime }\left(u\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill r_t& =\frac{f^{\prime }\left(u\right)}{2\sqrt{f\left(u\right)}}{u}_t.\hfill \end{array}$$

(7)

By taking the inner products of the Equations (5)–(7) with m, $u_t$ and $\frac{r}{2}$, respectively, we have the following equalities

$$\begin{array}{cc}\hfill 〈u_t,m〉& =〈({\partial }_x+ϵ{\partial }_{xx})m,m〉,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill 〈m,u_t〉& =〈6u+{\partial }_{xx}u-\frac{r}{4\sqrt{f\left(u\right)}}{f}^{\prime }\left(u\right),u_t〉,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill 〈r_t,\frac{r}{2}〉& =〈\frac{f^{\prime }\left(u\right)}{2\sqrt{f\left(u\right)}}{u}_t,\frac{r}{2}〉.\hfill \end{array}$$

(10)

By substituting Equations (9) and (10) into Equation (8), we obtain

$$\frac{\mathrm{d}}{\mathrm{d}t}H\left(u\right)=\frac{\mathrm{d}}{\mathrm{d}t}(-\frac{1}{2}\parallel {\partial }_{x}u{\parallel }^2+{\int }_{\Omega }(3u^2-\frac{1}{4}{r}^2)\mathrm{d}x)=〈({\partial }_x+ϵ{\partial }_{xx})m,m〉=-ϵ{\parallel {\partial }_{x}m\parallel }^2\le 0.$$

□

3. High Order Energy Dissipative Scheme

3.1. Spatial Discretization by Using Fourier Pseudo-Spectral Method

In this part, we choose the Fourier pseudo-spectral method to discretize the system (4). It is proved that the semi-discrete scheme for the GLE preserves the semi-discrete energy dissipation law.

We primarily divide the domain $\Omega =[a,b]$ into N equal intervals, where N is an even number. Afterwards, denote $h=\frac{b-a}{N}$ as the spatial step and $x_j:=a+jh(j=0,1,\cdots ,N-1)$ as the grid points. The kth-order partial differential optrator ${\partial }_x^k$ can be approximated by the Fourier spectral differential matrix $D_1^k$

$$\begin{array}{cc}\hfill {\left(D_1\right)}_{j+1,l+1}& =\left\{\begin{array}{cc}\frac{1}{2}{(-1)}^{j+l}\mu cot\left(\mu \frac{x_j-a}{2}\right),\hfill & j\ne l,\hfill \\ 0,\hfill & j=l,\hfill \end{array}\right.\hfill \end{array}$$

where $\mu =\frac{2\pi }{b-a}$, $j,l=0,1,\cdots ,N-1$. Clearly, $D_1$ is an $N\times N$ skew-symmetric matrix.

By applying Fourier pseudo-spectral method to the system (4), we acquire the semi-discrete scheme

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathbf{u}}_t=(D_1+ϵD_1^2)(6\mathbf{u}+ϵD_1^2\mathbf{u}-\mathbf{u}·\mathbf{r}),\hfill \\ {\mathbf{r}}_t=2\mathbf{u}·{\mathbf{u}}_t,\hfill \end{array}\right.\end{array}$$

(11)

where $\mathbf{u}={[u_0,u_1,\cdots ,u_{N-1}]}^{\mathrm{T}}$, $\mathbf{r}={[r_0,r_1,\cdots ,r_{N-1}]}^{\mathrm{T}}$ and $\mathbf{u}·\mathbf{r}={[u_0{r}_0,u_1{r}_1,\cdots ,u_{N-1}{r}_{N-1}]}^{\mathrm{T}}$.

Theorem 2.

The system (11) preserves the semi-discrete energy dissipation law

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}H\left(\mathit{u}\right)\le 0,\end{array}$$

where $H\left(\mathit{u}\right)=-\frac{1}{2}{\parallel D_1\mathit{u}\parallel }^2+{\sum }_{i=0}^{N-1}(3u_i^2-\frac{1}{4}{r}_i^2).$

Proof. 

The system (11) can be rewritten as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathbf{u}}_t=(D_1+ϵD_1^2)\mathbf{m},\hfill \\ \mathbf{m}=6{\mathbf{u}}^2+D_1^2\mathbf{u}-\frac{\mathbf{r}}{4\sqrt{\mathbf{f}\left(\mathbf{u}\right)}}{\mathbf{f}}^{\prime }\left(\mathbf{u}\right),\hfill \\ {\mathbf{r}}_t=\frac{{\mathbf{f}}^{\prime }\left(\mathbf{u}\right)}{2\sqrt{\mathbf{f}\left(\mathbf{u}\right)}}{\mathbf{u}}_t.\hfill \end{array}\right.\end{array}$$

(12)

Taking the inner products of the system (12) with $\mathbf{m}$, ${\mathbf{u}}_t$ and $\frac{\mathbf{r}}{2}$, respectively, we obtain the following semi-discrete energy dissipation law

$$\begin{array}{cc}\hfill \frac{\mathrm{d}}{\mathrm{d}t}H(\mathbf{u},\mathbf{r})& =\frac{\mathrm{d}}{\mathrm{d}t}(-\frac{1}{2}\parallel D_1\mathbf{u}{\parallel }^2+\sum _{i=0}^{N-1}3{\mathbf{u}}_i^2-\frac{1}{4}{\mathbf{r}}_i^2)=〈(D_1+ϵD_1^2)\mathbf{m},\mathbf{m}〉=-ϵ{\parallel D_1\mathbf{m}\parallel }^2\le 0.\hfill \end{array}$$

(13)

□

It is known that the Equation (13) is equivalent to

$$\frac{\mathrm{d}}{\mathrm{d}t}{〈\mathbf{S}\omega ,\omega 〉}_{\Omega }=2{〈\mathbf{S}\mathbf{F}\left(\omega \right),\omega 〉}_{\Omega }=2{〈\mathbf{S}{\omega }_t,\omega 〉}_{\Omega }\le 0,\forall \omega \in \Omega$$

(14)

where

$$\mathbf{S}=\left[\begin{array}{cc}3\mathbf{I}+\frac{1}{2}{D}_1^2& \mathbf{0}\\ \mathbf{0}& -\frac{\mathbf{I}}{4}\end{array}\right]$$

is a symmetric and constant matrix.

3.2. Full Discretization by Using Implicit High Order Runge–Kutta Method

In previous studies, many methods have been proposed to solve energy dissipation system, such as the second order backward differentiation formula (BDF2), the AVF method and the backward Euler method. However, these methods can only structure first or second order energy dissipative schemes in the time direction meanwhile these schemes always require a lot of iterative computations, which not only affect the efficiency, but also bring cumulative errors in the calculation processes. Therefore, we propose a new scheme to acquire high order energy dissipative schemes for the GLE.

Let $b_i,a_{ij},(i,j=1,2,\cdots ,s)$ be real numbers and $c_i={\sum }_{j=1}^s{a}_{ij}$. For given ${\mathbf{z}}^n=\mathbf{z}\left(t_n\right)$, when an s-stage RK method is applied to the Equation (1), the following intermediate values are first calculated by

$${\mathbf{z}}_i={\mathbf{z}}^n+\Delta t\sum _{j=1}^s{a}_{ij}{\mathbf{F}}_j,$$

where ${\mathbf{F}}_j=\mathbf{F}\left({\mathbf{z}}_j\right)$. Then the high order energy dissipation scheme of the GLE is updated via

$${\mathbf{z}}^{n+1}={\mathbf{z}}^n+\Delta t\sum _{i=1}^s{b}_i{\mathbf{F}}_i.$$

(15)

Proposition 1.

The RK coefficients are commonly displayed by a Butcher table

	c	A
		$b^{\mathrm{T}}$
=
$c_1$	$a_{11}$	⋯	$a_{1s}$
⋮	⋮		⋮
$c_s$	$a_{s1}$	⋯	$a_{ss}$
	$b_1$	⋯	$b_s$

where $A\in {\mathbb{R}}^{s,s}$, $b\in {\mathbb{R}}^s$ and $c=AI$ with $I={(1,1,\cdots ,1)}^{\mathrm{T}}\in {\mathbb{R}}^s$.

In consequence, we choose RK(4,4) as

$\frac{b_1}{2}$	$\frac{b_1}{2}$
$b_1+\frac{b_2}{2}$	$b_1$	$\frac{b_2}{2}$
$b_1+b_2+\frac{b_3}{2}$	$b_1$	$b_2$	$\frac{b_3}{2}$
$b_1+b_2+b_3+\frac{b_4}{2}$	$b_1$	$b_2$	$b_3$	$\frac{b_4}{2}$
	$b_1$	$b_2$	$b_3$	$b_4,$

where $b_1=-2.70309412$, $b_2=-0.53652708$, $b_3=2.37893931$, $b_4=1.86068189$.

Definition 1.

Let $\mathit{S}$ be a symmetric, constant matrix. For a dissipative system, the RK method defined by the Butcher array is said to be $\mathit{S}$-dissipative if applid to the new system (15)

$$〈{\mathit{S}\mathit{z}}^{n+1},{\mathit{z}}^{n+1}〉\le 〈{\mathit{S}\mathit{z}}^n,{\mathit{z}}^n〉$$

for all $n\ge 0$ and for all $\Delta t\ge 0$.

Theorem 3.

([29]) A RK scheme defined by the Butcher array is said to be $\mathit{S}$-dissipative, if and only if the symmetric coefficient matrix M with elements

$$\begin{array}{c}\hfill m_{ij}=b_i{a}_{ij}+b_j{a}_{ji}-b_i{b}_j,i,j=1,2,\cdots ,s\end{array}$$

(16)

are nonnegative.

Proof. 

Above all, replace ${\mathbf{z}}^{n+1}$ by the new system (15), that can be derived as

$$〈{\mathbf{Sz}}^{n+1},{\mathbf{z}}^{n+1}〉-〈{\mathbf{Sz}}^n,{\mathbf{z}}^n〉=2\Delta t\sum _{i=1}^s{b}_i〈{\mathbf{Sz}}^n,{\mathbf{F}}_i〉+\Delta t^2\sum _{i,j=1}^s{b}_i{b}_j〈\mathbf{S}{\mathbf{F}}_i,{\mathbf{F}}_j〉.$$

(17)

Substituting ${\mathbf{z}}^n={\mathbf{z}}_i-\Delta t{\sum }_{j=1}^s{a}_{ij}{\mathbf{F}}_j$ into the first term on the right hand side of the Equation (17), we get

$$\begin{array}{cc}\hfill 〈{\mathbf{Sz}}^{n+1},{\mathbf{z}}^{n+1}〉-〈{\mathbf{Sz}}^n,{\mathbf{z}}^n〉=& 2\Delta t\sum _{i=1}^s{b}_i〈{\mathbf{Sz}}_i,{\mathbf{F}}_i〉-\Delta t^2\sum _{i,j=1}^s{b}_i{a}_{ij}〈\mathbf{S}{\mathbf{F}}_i,{\mathbf{F}}_j〉\hfill \\ \hfill & -\Delta t^2\sum _{i,j=1}^s{b}_j{a}_{ji}〈\mathbf{S}{\mathbf{F}}_i,{\mathbf{F}}_j〉+\Delta t^2\sum _{i,j=1}^s{b}_i{b}_j〈\mathbf{S}{\mathbf{F}}_i,{\mathbf{F}}_j〉.\hfill \end{array}$$

Whereafter, it can be arranged as

$$〈{\mathbf{Sz}}^{n+1},{\mathbf{z}}^{n+1}〉-〈{\mathbf{Sz}}^n,{\mathbf{z}}^n〉=2\Delta t\sum _{i=1}^s{b}_i〈{\mathbf{Sz}}_i,{\mathbf{F}}_i〉-\Delta t^2\sum _{i,j=1}^s{m}_{ij}〈\mathbf{S}{\mathbf{F}}_i,{\mathbf{F}}_j〉.$$

Noticing that $〈\mathbf{S}{\mathbf{z}}_i,{\mathbf{F}}_j〉\le 0$ and $m_{ij}\ge 0$, we have

$$〈{\mathbf{Sz}}^{n+1},{\mathbf{z}}^{n+1}〉\le 〈{\mathbf{Sz}}^n,{\mathbf{z}}^n〉.$$

This completes the proof. □

In this paper, we only consider four stage and fourth order diagonally implicit RK scheme, which belongs to $\mathbf{S}$-dissipative RK scheme can be extended to higher order RK method without any necessary difficulties.

4. Numerical Simulation

In this section, we carry out two numerical experiments by applying the implicit high order energy dissipative scheme. The stability and the convergence of the new scheme (15) are verified by these numerical experiments. Meanwhile, we compare the proposed scheme (15) with the AVF method in energy errors and accuracy. The numerical iteration formula of the AVF method is

$$\begin{array}{c}\hfill \frac{{\mathbf{u}}^{n+1}-{\mathbf{u}}^n}{\Delta t}=(3E+\frac{E}{2}{D}_2)({\mathbf{u}}^{n+1}+{\mathbf{u}}^n)-\frac{E}{4}\left({\left({\mathbf{u}}^n\right)}^3+{\left({\mathbf{u}}^{n+1}\right)}^3+{\mathbf{u}}^n{\left({\mathbf{u}}^{n+1}\right)}^2+{\left({\mathbf{u}}^n\right)}^2{\mathbf{u}}^{n+1}\right),\end{array}$$

(18)

where $E=D_1+ϵD_2$. In the following text, the Newton iteration is mainly used to solve the full-discrete system.

Example 1.

We utilize the initial condition of single solitary wave given by

$$u(x,0)=e^{-M_1{(x-\frac{1}{2})}^2},x\in [-10,10]$$

(19)

to observe how the coefficient ϵ affects the energy dissipation. First, we set $M_1=0.3$, the number of grid points $N=200$ and the time step $\Delta t=0.001$. Letting $\epsilon =0,0.00025,0.0005,0.00075,0.001$ respectively, the energy variations and energy errors of the proposed scheme (15) are presented in Figure 1. Based on Figure 1a, we find the proposed scheme (15) can preserve the discrete energy conservation exactly when $ϵ=0$, and the energy dissipations of the GLE can be observed when $ϵ>0$. Obviously, with bigger ϵ, the energy dissipates faster. Taking the discrete energy obtained from the scheme (15) with $\Delta t=0.0001$ and $N=200$ as the reference discrete energy, we plot the energy errors ($\Delta t=0.001$) with various ε in Figure 1b. It shows that the proposed new scheme (15) can preserve the energy dissipation of the GLE. Meanwhile, Figure 1b indicates that the energy dissipation is a little bit influenced by the time step size. The waveforms, energy variations and energy errors obtained from the scheme (15) and the scheme (18) with $\epsilon =0.001$, $N=100$, $\Delta t=0.001$ are pictured in Figure 2. The waveforms obtained from these two schemes at $t=0.1$ are almost the same (Figure 2a). Figure 2b shows that they both can keep the energy reducing steadily. According to Figure 2c, comparatively speaking, the energy errors obtained by the proposed scheme (15) is even smaller than that by the scheme (18).

Setting $M_1=0.5$ and $\epsilon =0.001$, we list the convergence rates of the proposed new scheme (15) in

Table 1. Time accuracy test for the scheme (15) and the scheme (18) at $t=0.1$.

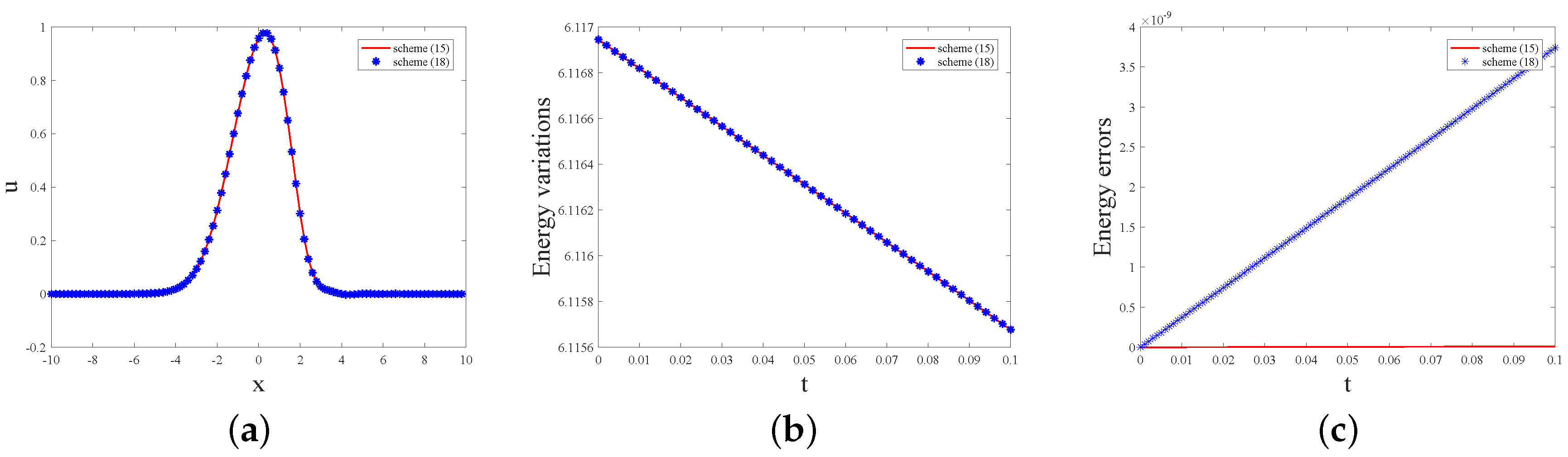
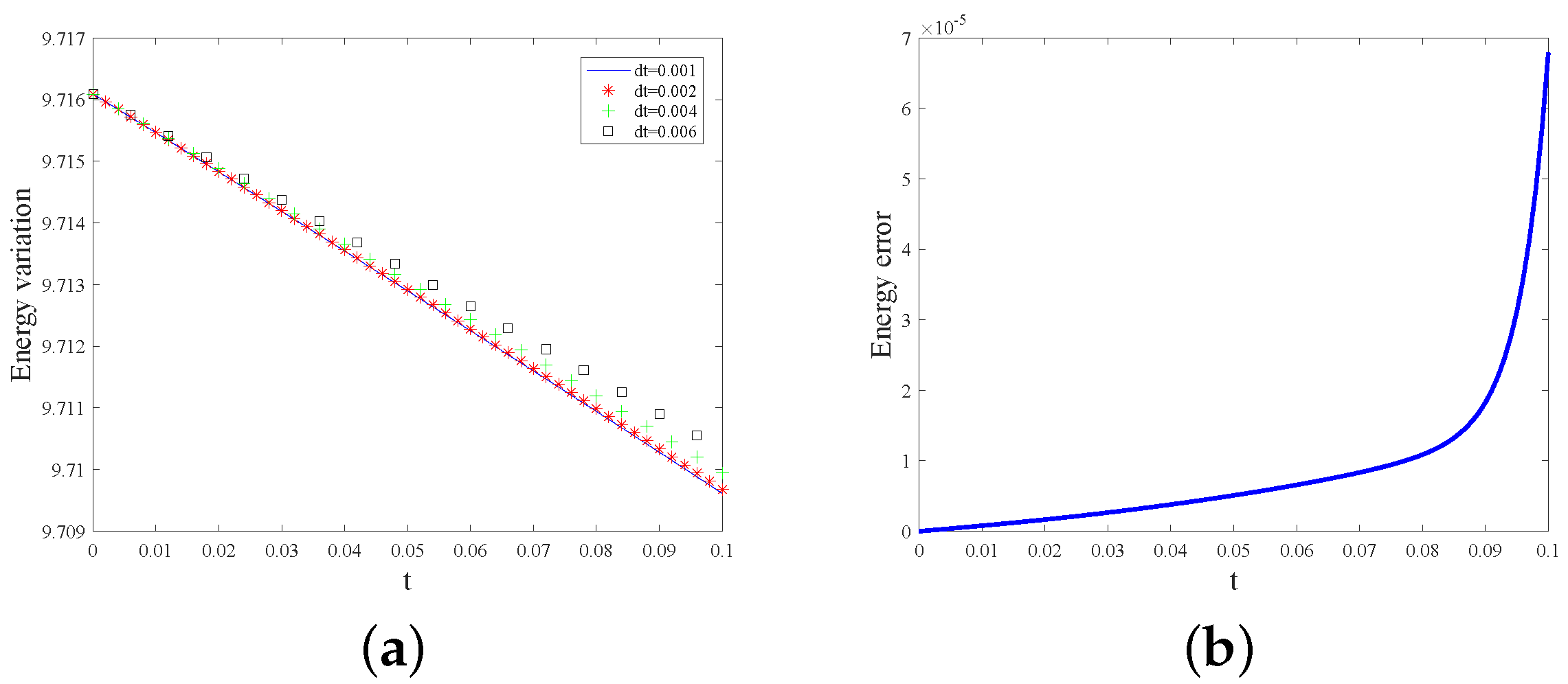
$\mathbf{\Delta }$t	New Scheme (15)	Time Order	Scheme (18)	Time Order
0.002	$3.134\times {10}^{-7}$	-	$3.074\times {10}^{-6}$	-
0.001	$1.967\times {10}^{-8}$	3.994	$7.629\times {10}^{-7}$	2.016
0.0005	$1.230\times {10}^{-9}$	3.999	$1.850\times {10}^{-7}$	2.044
0.00025	$7.688\times {10}^{-11}$	4.000	$4.046\times {10}^{-8}$	2.193

and

Table 2. Space accuracy test for the scheme (15) and the scheme (18) at $t=0.1$.

N	New Scheme (15)	Space Order	Scheme (18)	Space Order
10	$6.673\times {10}^{-2}$	-	$6.671\times {10}^{-2}$	-
20	$3.350\times {10}^{-2}$	0.994	$1.858\times {10}^{-2}$	1.844
40	$2.754\times {10}^{-5}$	10.253	$2.092\times {10}^{-5}$	9.794
80	$5.806\times {10}^{-10}$	15.533	$3.242\times {10}^{-10}$	15.978

. For the time accuracy test, we select the numerical solution with $\Delta t=0.0001$ and $N=50$ as the reference solution. Based on Table 1, the convergence order of the proposed scheme (15) in time is 4 and the scheme (18) only converges with second-order accuracy. For the space accuracy test, the scheme (15) and the scheme (18) both apply the Fourier pseudo-spectral method in space-discretization, thus the space convergence orders of them decrease in an exponential rate in Table 2 (the numerical solution with $N=560$ and $\Delta t=0.001$ is chosen as the reference solution).

Example 2.

In the second example, we investigate the energy dissipation of double solitary wave with the initial condition,

$$\begin{array}{cc}\hfill u(x,0)& =e^{M_1{(x-2)}^2+M_2{(x+2)}^2},x\in [-10,10].\hfill \end{array}$$

(20)

By setting $M_1=M_2=-1$ and $\epsilon =0.001$, we plot the waveform of double solitary wave with $N=200$ and $\Delta t=0.001$ in Figure 3a. The energy dissipation property of the GLE with various time steps can be verified in Figure 3b. It shows the new scheme (15) can keep energy dissipation at a large time step. Taking the discrete energy obtained from the new scheme (15) with $\Delta t=0.0001$ as the reference discrete energy, the energy error in Figure 3c is only about $\mathcal{O}\left({10}^{-7}\right)$. Then using the same grid, we consider the situation of $M_1=-0.2$ and $M_2=-2$ and plot the energy variation and the energy error in Figure 4. As we can see, the proposed scheme (15) still can maintain the energy dissipation property with various time steps.

5. Conclusions

In this paper, we have developed a stable and high order energy dissipative scheme for solving the GLE. By using the IEQ approach, the GLE is downgraded from fourth order to second order. The full-discrete system of GLE is obtained by using the Fourier pseudo-spectral method in the spatial direction and the diagonally implicit Runge–Kutta method in the time direction. The new scheme (15) we proposed has three main advantages. First of all, it is well-known that the implicit methods enjoy better stability in the simulation of stiff equations. Besides, it has high calculation efficiency due to the application of the diagonally implicit Runge–Kutta method. Last but not least, the high order scheme in time direction can be constructed and the energy dissipation can be preserved. The proposed implicit fourth order scheme can maintain the energy dissipation of the GLE theoretically. Moreover, the numerical results of single solitary wave and double solitary wave have verified the stability and accuracy of the proposed scheme. Compared with the scheme (18), the proposed scheme converges with fourth order in the time direction and can be generalized to construct higher order energy dissipative scheme naturally.