Decentralized Adaptive Tracking of Interconnected Nonlinear Systems by Corrupted Output Feedback
Abstract
:1. Introduction
- (i)
- (ii)
- Compared with the existing result [32], the proposed decentralized resilient control methodology ensures the robustness on unknown time-varying measurement sensitivities, without using any bounding information of the measurement sensitivities. The adaptive control strategy is proposed to compensate for unknown bounding effects of measurement sensitivities.
2. Problem Statement
3. Decentralized Adaptive Control Via Corrupted Output Measurement
3.1. Local High-Gain Observer Design
3.2. Local Adaptive Output-Feedback Controller Design
3.3. Stability Analysis
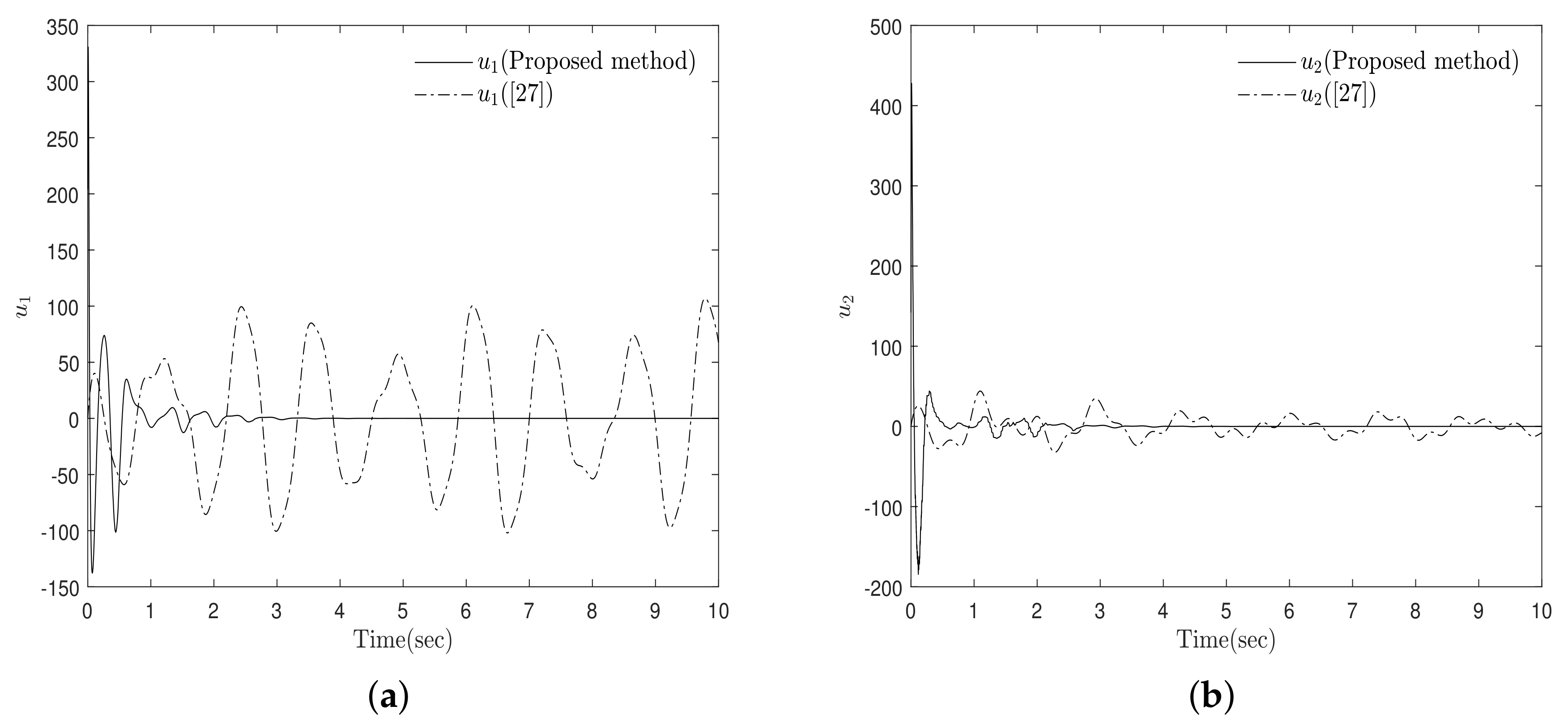
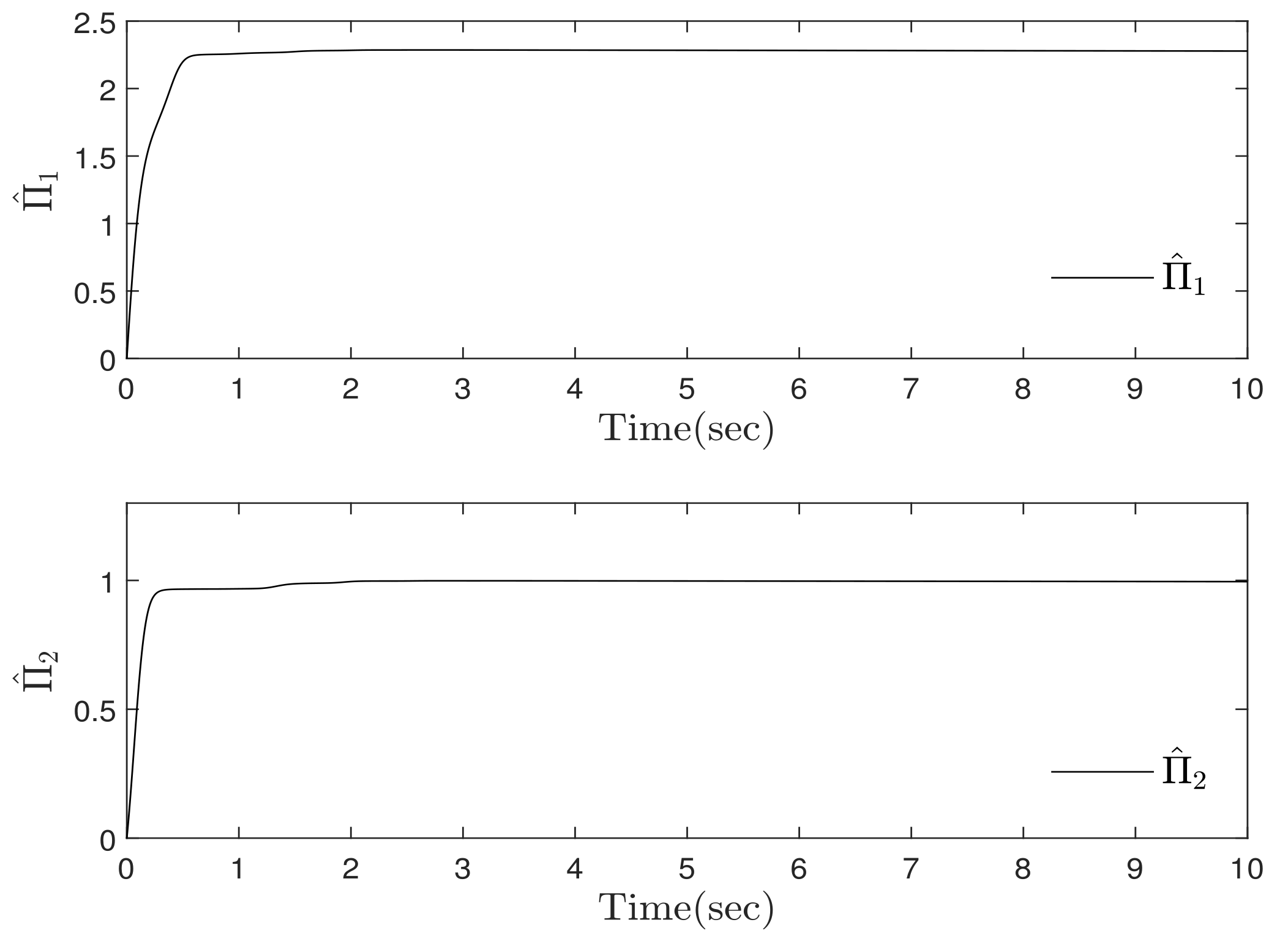
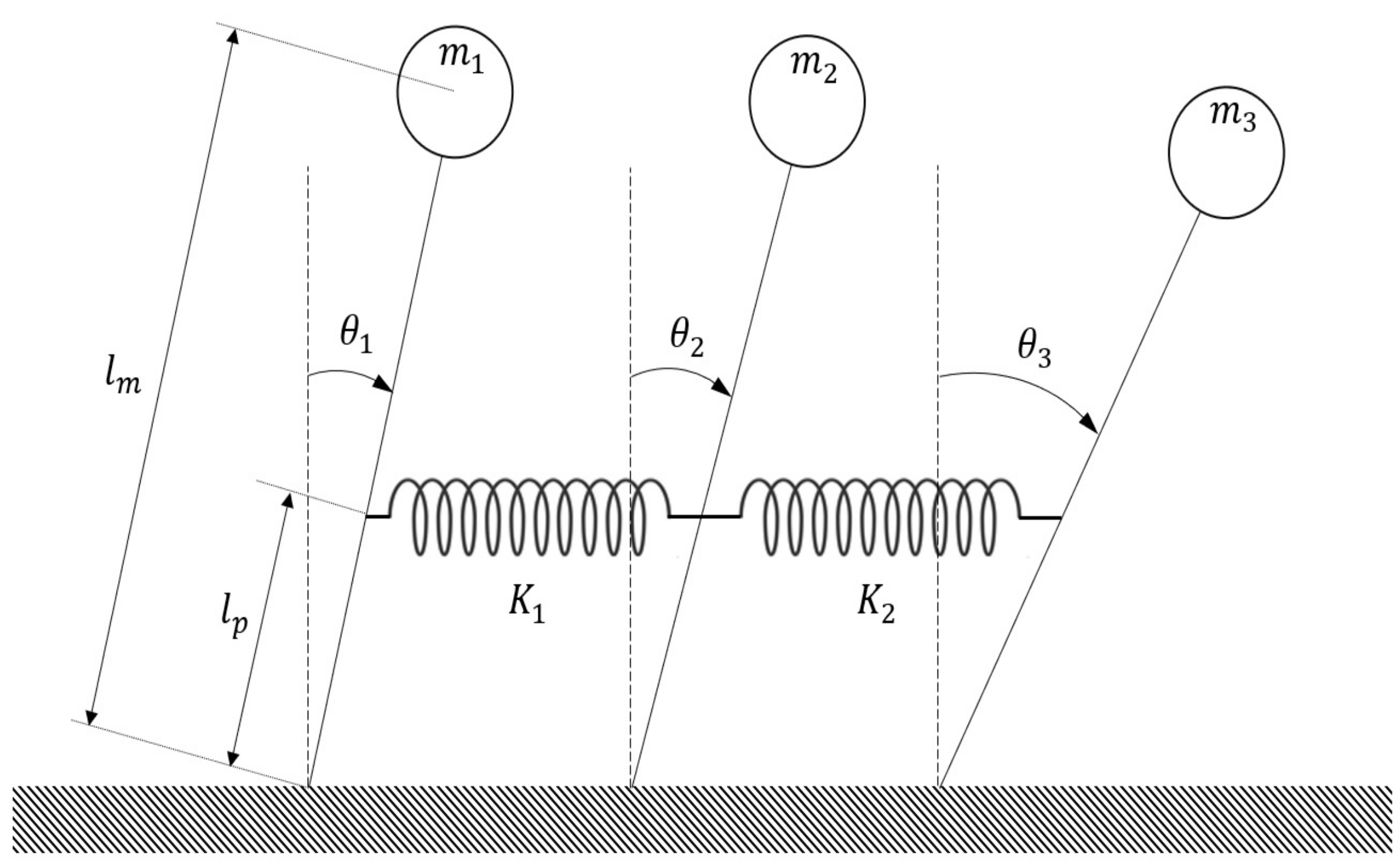
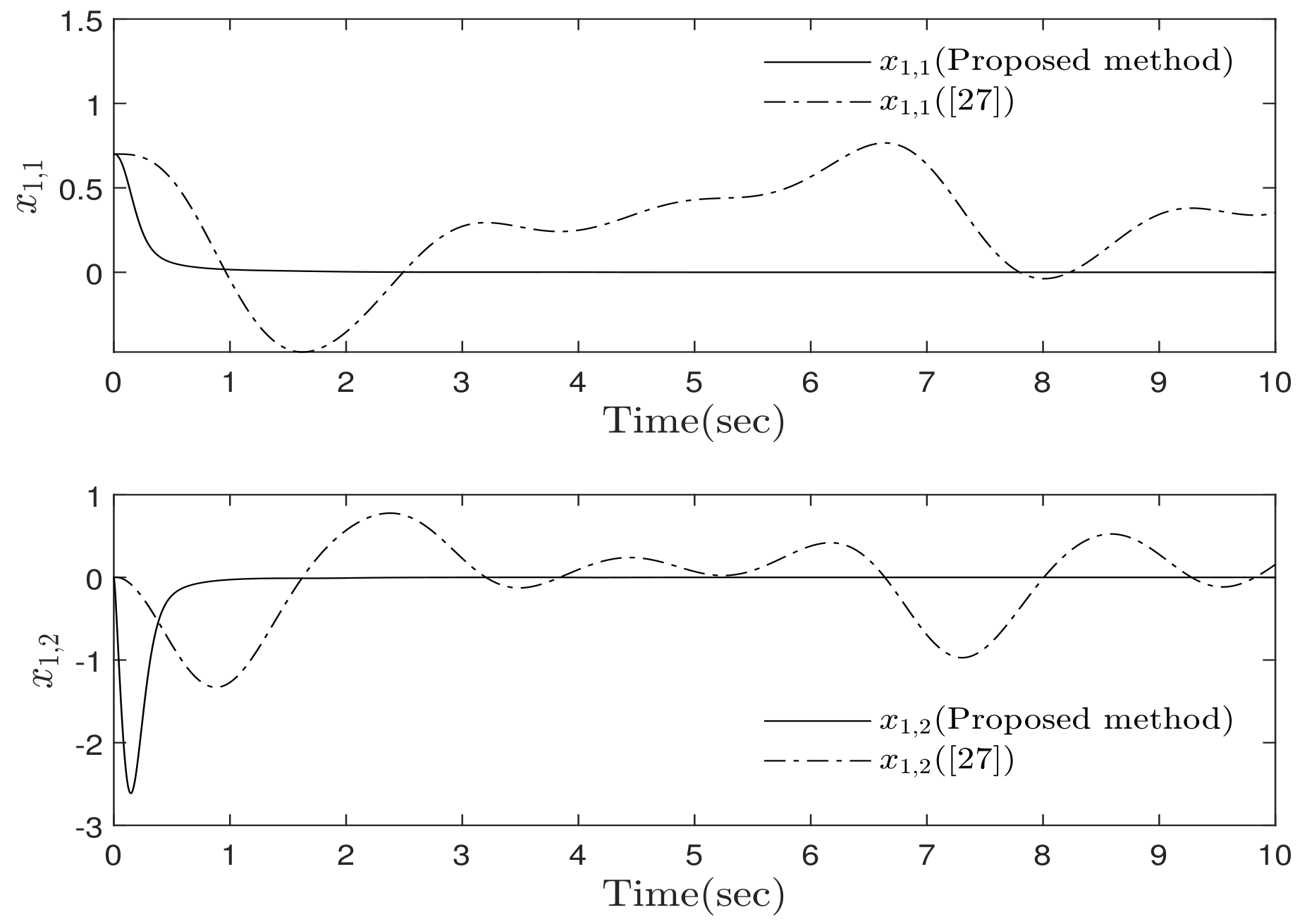
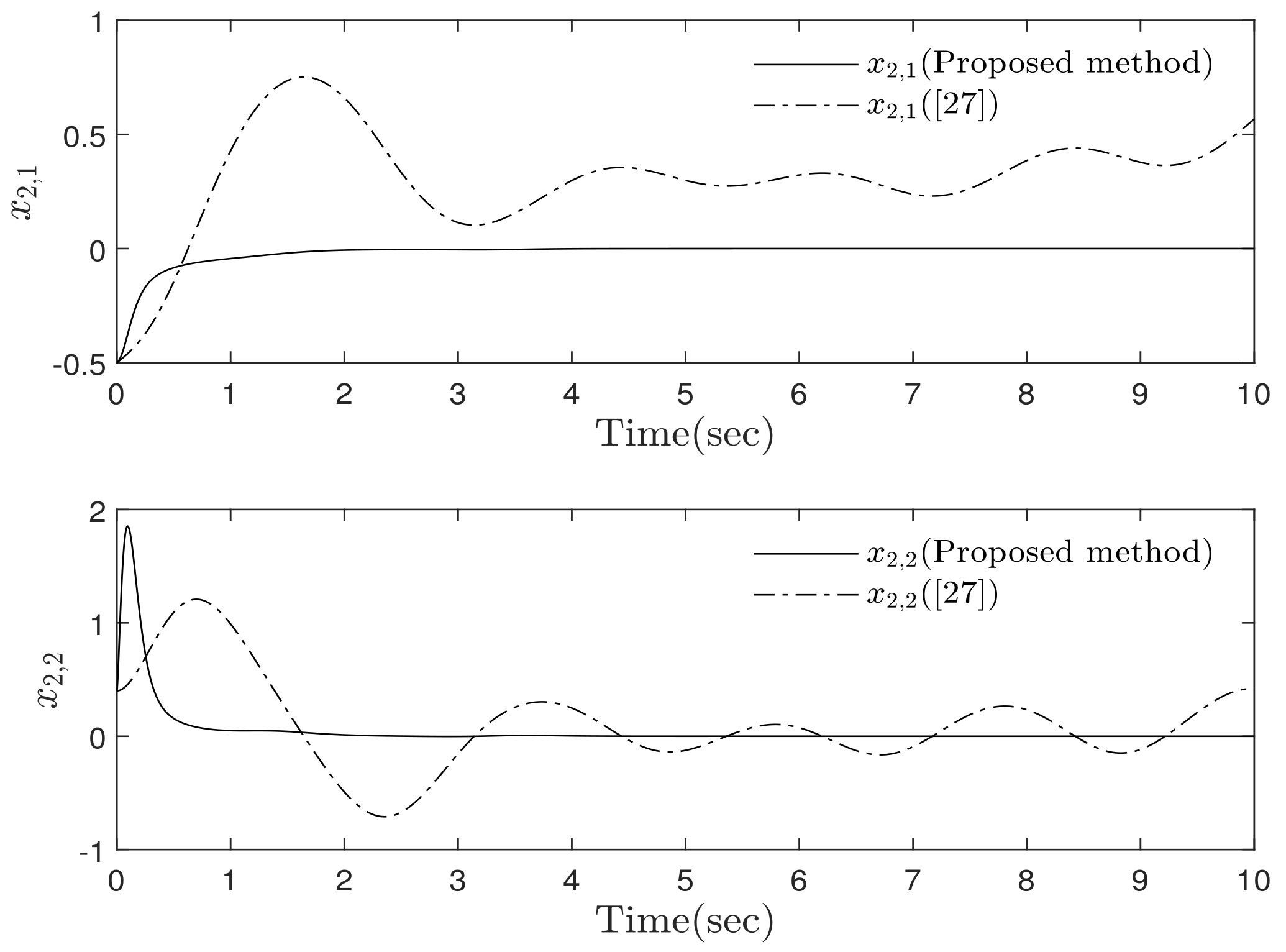
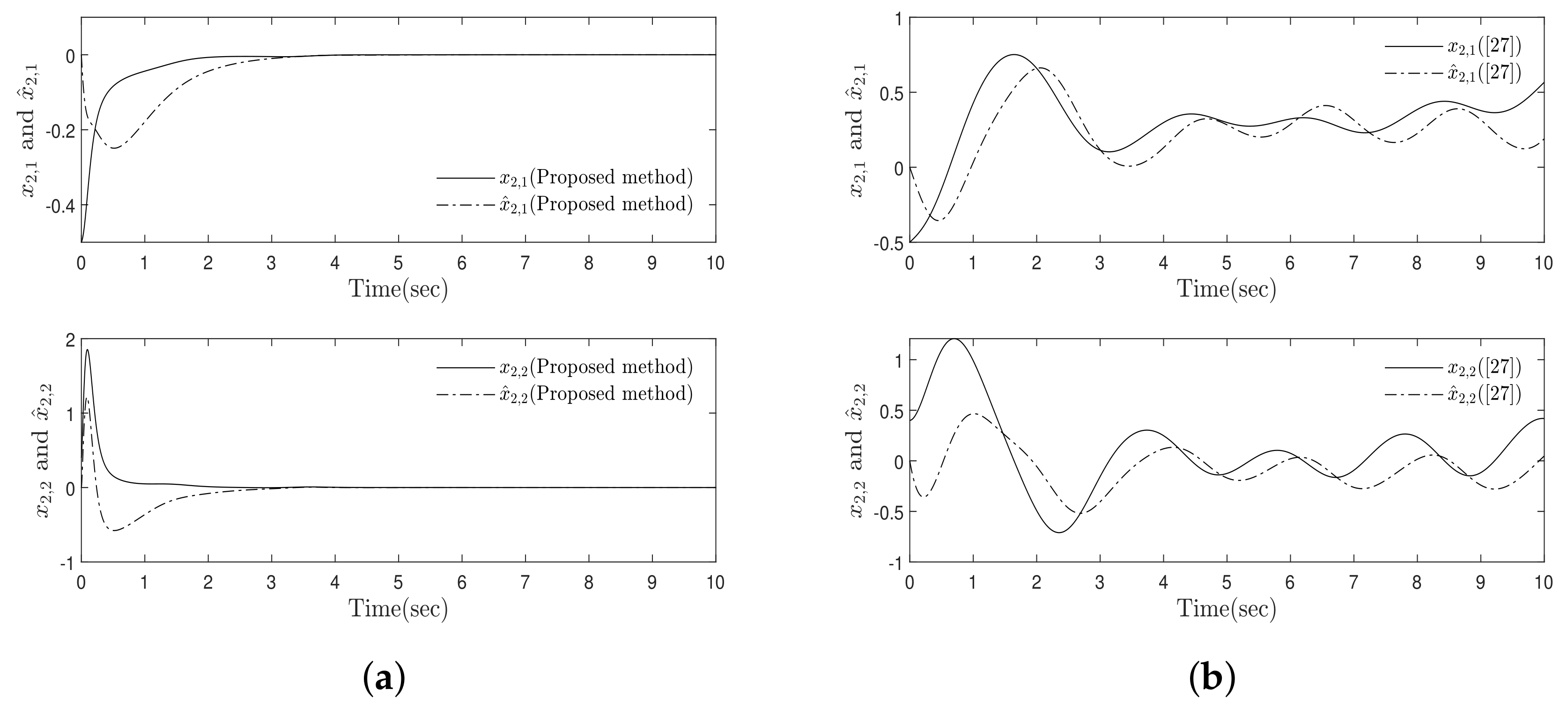
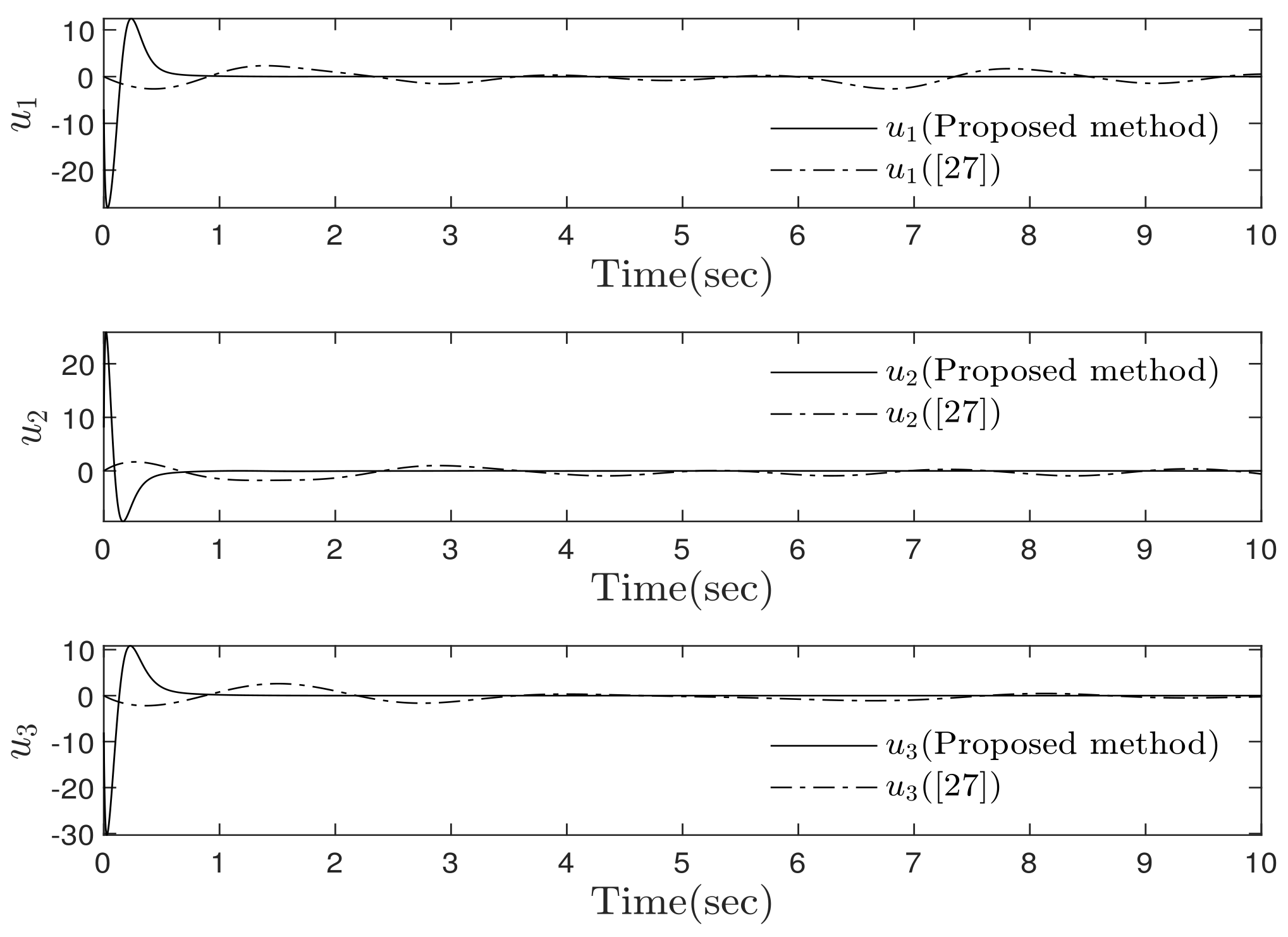
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kolovsky, M.Z. Nonlinear Dynamics of Active and Passive Systems of Vibration Protection; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Bernstein, D.S. Sensor performance specifications. IEEE Control. Syst. Mag. 2001, 21, 9–18. [Google Scholar]
- Carr, J.J.; Brown, J.M. Introduction to Biomedical Equipment Technology; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Yang, G.H.; Wang, J.L.; Soh, Y.C. Reliable H∞ controller design for linear systems. Automatica 2001, 37, 717–725. [Google Scholar] [CrossRef]
- Chen, B.; Lam, J. Reliable observer-based H∞ control of uncertain state-delayed systems. Int. J. Syst. Sci. 2004, 35, 707–718. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Qian, C. Global control of nonlinear systems with uncertain output function using homogeneous domination approach. Int. J. Robust Nonlinear Control. 2012, 22, 1543–1561. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Ai, W.Q.; Fei, S.M. Global output feedback stabilisation for a class of uncertain non-linear systems. IET Control Theory Appl. 2013, 7, 305–313. [Google Scholar] [CrossRef]
- Xie, X.J.; Li, Z.J.; Zhang, K. Semi-global output feedback control for nonlinear systems with uncertain time-delay and output function. Int. J. Robust Nonlinear Control 2017, 27, 2549–2566. [Google Scholar] [CrossRef]
- Li, Z.J.; Xie, X.J.; Zhang, K. Output feedback stabilisation for nonlinear systems with unknown output function and control coefficients and its application. Int. J. Control 2016, 90, 1027–1036. [Google Scholar]
- Ai, W.; Zhai, J.; Fei, S. Universal adaptive regulation for a class of nonlinear systems with unknown time delays and output function via output feedback. J. Frankl. Inst. 2013, 350, 3168–3187. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Du, H.B.; Fei, S.M. Global sampled-data output feedback stabilisation for a class of nonlinear systems with unknown output function. Int. J. Control 2016, 89, 469–480. [Google Scholar] [CrossRef]
- Chen, C.C.; Qian, C.; Sun, Z.Y.; Liang, Y.W. Global output feedback stabilization of a class of nonlinear systems with unknown measurement sensitivity. IEEE Trans. Autom. Control 2018, 63, 2212–2217. [Google Scholar] [CrossRef]
- Jain, S.; Khorrami, F. Decentralized adaptive output feedback design for large-scale nonlinear systems. IEEE Trans. Autom. Control. 1997, 42, 729–735. [Google Scholar] [CrossRef]
- Zhu, Y.; Pagilla, P.R. Decentralized output feedback control of a class of large-scale interconnected systems. IMA J. Math. Control Inf. 2007, 24, 57–69. [Google Scholar] [CrossRef]
- Zhai, J.; Zha, W.; Fei, S. Semi-global finite-time output feedback stabilization for a class of large-scale uncertain nonlinear systems. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3181–3189. [Google Scholar] [CrossRef]
- Wu, H.S. Decentralized adaptive robust state feedback for uncertain large-scale interconnected systems with time delays. J. Optim. Theory Appl. 2005, 126, 439–462. [Google Scholar] [CrossRef]
- Wei, C.; Luo, J.; Dai, H.; Yin, Z.; Yuan, J. Low-complexity differentiator-based decentralized fault-tolerant control of uncertain large-scale nonlinear systems with unknown dead zone. Nonlinear Dyn. 2017, 89, 2573–2592. [Google Scholar] [CrossRef]
- Shao, S.; Yang, H.; Jiang, B. Decentralized fault tolerant control for a class of interconnected nonlinear systems. IEEE Trans. Cybern. 2018, 48, 178–186. [Google Scholar] [CrossRef]
- Krstic, M.; Kanellakopoulos, I.; Kokotovic, P. Nonlinear and Adaptive Control Design; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef] [Green Version]
- Yoo, S.J.; Park, J.B. Neural-network-based decentralized adaptive control for a class of large-scale nonlinear systems with unknown time-varying delays. IEEE Trans. Syst. Man Cybern. B Cybern. 2009, 39, 1316–1322. [Google Scholar]
- Mehraeen, S.; Jagannathan, S.; Crow, M.L. Decentralized dynamic surface control of large-scale interconnected systems in strict-feedback form using neural networks with asymptotic stabilization. IEEE Trans. Neural Netw. 2011, 22, 1709–1722. [Google Scholar] [CrossRef]
- Tong, S.; Li, Y. Adaptive fuzzy decentralized output feedback control for nonlinear large-scale systems with unknown dead-zone inputs. IEEE Trans. Fuzzy Syst. 2013, 21, 913–925. [Google Scholar] [CrossRef]
- Du, P.; Liang, H.; Zhao, S.; Ahn, C.K. Neural-based decentralized adaptive finite-time control for nonlinear large-scale systems with time-varying output constraints. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Y. Nonlinear decentralized control of large-scale systems with strong interconnections. Automatica 2014, 50, 2419–2423. [Google Scholar] [CrossRef]
- Li, Y.X.; Tong, S.; Yang, G.H. Observer-based adaptive fuzzy decentralized event-triggered control of interconnected nonlinear system. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef] [PubMed]
- Frye, M.T.; Qian, C.; Colgren, R. Decentralized control of large-scale uncertain nonlinear systems by linear output feedback. Communi. Inf. Syst. 2005, 4, 191–210. [Google Scholar]
- Wang, C.; Wen, C.; Lin, Y. Decentralized adaptive backsteeping control for a class of interconnected nonlinear systems with unknown actuator failures. J. Frankl. Inst. 2015, 352, 835–850. [Google Scholar] [CrossRef]
- Choi, Y.H.; Yoo, S.J. Event-triggered decentralized adaptive fault-tolerant control of uncertina interconnected nonlinear systems with actuator failures. ISA Trans. 2018, 77, 77–89. [Google Scholar] [CrossRef]
- Wang, H.Q.; Liu, P.X.P.; Bao, J.L.; Xie, X.J.; Li, S. Adaptive neural output-feedback decentralized control for large-scale nonlinear systems with stochastic disturbances. IEEE Trans Neural Netw. Learn. Syst. 2019, 31, 972–983. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhai, D.; Dong, J. Observer-based adaptive fuzzy decentralized control of uncertain large-scale nonlinear systems with full state contraints. Int. J. Fuzzy Syst. 2019, 21, 1085–1103. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.P.; Hill, D.J. Decentralized output-feedback control of large-scale nonlinear systems with sensor noise. Automatica 2012, 48, 2560–2568. [Google Scholar] [CrossRef]
- Qian, C.; Lin, W. Output feedback control of a class of nonlinear systems: A nonseparation principle paradigm. IEEE Trans. Autom. Control 2002, 47, 1710–1715. [Google Scholar] [CrossRef] [Green Version]
- Lei, H.; Lin, W. Universal adaptive control of nonlinear systems with unknown growth rate by output feedback. Automatica 2006, 42, 1783–1789. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Kokotovic, P.V. Adaptive Systems with Reduced Models; Springer: New York, NY, USA, 1983. [Google Scholar]
- Ge, S.S.; Tee, K.P. Approximation-based control of nonlinear MIMO time-delay systems. Automatica 2007, 43, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Choi, Y.H.; Yoo, S.J. Simple adaptive output-feedback control of non-linear strict-feedback time-delay systems. IET Control Theory Appl. 2016, 10, 58–66. [Google Scholar] [CrossRef]
- Jeong, D.M.; Choi, Y.H.; Yoo, S.J. Adaptive output-feedback control of a class of nonlinear systems with unknown sensor sensitivity and its experiment for flexible-joint robots. J. Electr. Eng. Technol. 2020, 15, 907–918. [Google Scholar] [CrossRef]
- Feng, S.; Sun, Z. Biped robot walking using three-mass linear inverted pendulum model. In International Conference on Intelligent Robotics and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 371–380. [Google Scholar]
- Takei, T.; Imamura, R. Baggage transportation and navigation by a wheeled inverted pendulum mobile robot. IEEE Trans. Ind. Electron. 2009, 56, 3985–3994. [Google Scholar] [CrossRef]
- Chen, Q.; Cheng, H.; Yue, C.; Huang, R.; Guo, H. Dynamic balance gait for walking assistance exoskeleton. Appl. Bionics Biomech. 2018, 2018, 3985–3994. [Google Scholar] [CrossRef]
- Yoo, S.J.; Park, J.B.; Choi, Y.H. Decentralized adaptive stabilization of interconnected nonlinear systems with unknown non-symmetric dead-zone inputs. Automatica 2009, 45, 436–443. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, D.M.; Yoo, S.J. Decentralized Adaptive Tracking of Interconnected Nonlinear Systems by Corrupted Output Feedback. Mathematics 2020, 8, 1340. https://doi.org/10.3390/math8081340
Jeong DM, Yoo SJ. Decentralized Adaptive Tracking of Interconnected Nonlinear Systems by Corrupted Output Feedback. Mathematics. 2020; 8(8):1340. https://doi.org/10.3390/math8081340
Chicago/Turabian StyleJeong, Dong Min, and Sung Jin Yoo. 2020. "Decentralized Adaptive Tracking of Interconnected Nonlinear Systems by Corrupted Output Feedback" Mathematics 8, no. 8: 1340. https://doi.org/10.3390/math8081340
APA StyleJeong, D. M., & Yoo, S. J. (2020). Decentralized Adaptive Tracking of Interconnected Nonlinear Systems by Corrupted Output Feedback. Mathematics, 8(8), 1340. https://doi.org/10.3390/math8081340




