1. Introduction
Whitney’s 1935 article laid the groundwork for the field of combinatorial geometries and matroid [
1]. Matroid theory has been widely applied to combinatorial mathematics, combinatorial optimization and group theory [
2,
3,
4,
5,
6,
7,
8]. Based on the fuzzy set theory proposed by Zadeh in 1965 [
9], matroid theory has been generalized to various forms related to fuzzy sets. Shi [
10,
11] proposed the
-fuzzy matroid based on latticevalued fuzzy set theory and studied the base axioms of fuzzitying matroids [
12,
13,
14]. Hsueh presented a fuzzification of matroids which extends the independence axioms of matroids [
15]. Al-Hawary introduced a method to the fuzzifying of matroids which is called fuzzy C-matroids [
16,
17]. In 1988, Goetschel and Voxman proposed an important fuzzy matroid (briefly,
fuzzy matroid) in [
18]. They further studied some important concepts and their properties, such as the fuzzy bases and the fuzzy rank function [
19,
20,
21,
22]. Following them, some scholars studied the axioms, the connectedness and the structure of
fuzzy matroid, etc. [
23,
24,
25].
The intuitionistic fuzzy set (
), introduced by Atanassov originally in 1983 [
26] and made widely accessible in 1986 [
27], is a generalization of Zadeh’s fuzzy set. An
of each element is an ordered pair which is called an intuitionistic fuzzy value (
) and each
is characterized by a membership degree, a nonmembership degree and a hesitancy degree. From then on, many scholars were attracted to study the
and obtained a lot of valuable results. For ranking the
, Hong and Choi proposed the accuracy function in 2000 [
28] and Szmidt and Kacprzyk proposed a similarity function of
in 2004 [
29]. Based on the accuracy function and the similarity function, Zhang and Xu introduced a new method for ranking
in 2012 [
30]. In 2013, Rangasamy et al. proposed a method by ranking to be done using the scores and accuracy for finding the shortest hyperpath in an intuitionistic fuzzy weighted hypergraph [
31]. Some other scholars studied the aggregation operators and fuzzy clustering of
[
32,
33,
34]. After decades of effort from scholars, the relevant achievements of intuitionistic fuzzy theory became very rich. In 1999, Atanassov completed his first monograph which discussed the concept and operators of
, the interval valued
, some other extensions of
, the elements of
and the applications of
[
35]. There are some other scholars’ results worthy of learning and researching; see [
36,
37,
38]. In 2017, Li and Yi proposed an intuitionistic fuzzy matroid based on matroids and intuitionistic fuzzy sets [
39]. In [
40], Li et al. extended
fuzzy matroids and introduced a
intuitionistic fuzzy matroid and studied the induced matroid sequence and the rank function. In this paper, based on the literature [
19,
25,
40], we study the bases and the structure of a
intuitionistic fuzzy matroid (briefly,
), which are actually generalizations of some conclusions of
fuzzy matroid.
This paper is arranged as follows. Some basic definitions and results are introduced in
Section 2. The
of a
are studied in
Section 3. The judgment of an
is investigated in
Section 4. Finally, we propose the tree structure of a closed
and study its properties in
Section 5.
2. Preliminaries and Notations
We introduce some basic and useful concepts related to matroid theory here; see [
41,
42]. Firstly, we introduce the concept of the matroid.
Definition 1. Let I be a nonempty family of subsets of a finite set E and satisfy:
- 1.
.
- 2.
If, and, then.
- 3.
If, and, then there exists ansuch that.
Then the pairis called a matroid (or a crisp matroid). For any, if, then A is called an independent set; otherwise A is called a dependent set.
In matroid theory, rank function and its submodularity are very important. They are defined as follows.
Definition 2. Letbe the power set of finite set E andbe a matroid.
R is called rank function of M, whereis a mapping and is defined as follows:
From the definition of R, the following properties can be easily obtained.
If , then ;
for any ;
If , then ,
where
Definition 3. Let be a mapping, where is the power set of finite set E. σ is called submodular iffor each . Theorem 1. The rank function R of a matroid is submodular.
Next, some concepts and notations concerning fuzzy sets or intuitionistic fuzzy sets are cited; see [
9,
18,
19,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
40].
Definition 4. Let X be a fixed set. Thenis called a fuzzy set, where is the membership degree of x to A, . The collection of fuzzy sets on X is denoted by . Definition 5. Let X be a fixed set. Thenis called an (i.e., intuitionistic fuzzy set). For any , , and are called membership degree, non-membership degree and hesitancy degree, respectively, where and . The collection of on X is denoted by . If for all , , then and A is reduced to a fuzzy set. In this paper, we use to denote intuitionistic fuzzy set and to denote intuitionistic fuzzy value. For convenience and suitable for the study of intuitionistic fuzzy matroids later, an is abbreviated as and an is denoted by . Note that this notation is different from that in Definition 5.
Definition 6. Let be an . Then the accuracy function H of is denoted by Definition 7. Let be an . Then the similarity function h of for any is
In the special case , we have .
Let
X be a finite set and
be
and
. We now introduce the following notation and results; see [
40]:
.
.
.
if for any .
: for any , .
: for any , .
: and for some
: for any , .
: for any , .
: and for some .
: and .
: and .
: and .
supp.
supp.
, where .
is called the positive of .
is called the "cardinality" of an .
Definition 8. Let be two intuitionistic fuzzy sets, . and are called the union and intersection of and , respectively, where is defined by and is defined by Definition 9. Let E be a finite set and be a nonempty family of fuzzy sets. The pair is called a on E if it satisfies the following conditions:
- 1.
If , and , then .
- 2.
If , and |suppsupp, then there exists , such that:
- (a)
;
- (b)
.
Suppose that is a . is called an independent and is called the set of independent . is called a dependent .
If for any and for any , , then is actually . Thus, is reduced to .
Theorem 2. Let be a . For each r, , let
Then for each r, ,
is a matroid.
Theorem 3. Letbe a. Letbe a matroid on E defined in Theorem 2, where. Then there is a finite sequencesuch that:
- (i)
,.
- (ii)
if , if .
- (iii)
If , then , where .
- (iv)
If , then , where .
Then the sequence is called the fundamental sequence of . Moreover, if for any i, , let , then we can get a sequence of matroids which is called the matroid sequence.
Note that , where , and , so not but when .
A matroid sequence can be constructed from a above. On the contrary, a can be constructed from a matroid sequence.
Theorem 4. Let be a finite sequence. Suppose that () is a matroid sequence on a finite set E and satisfies (. For any , let and let
Then is a and its matroid sequence is , where for , .
Theorem 5. Let be a , and for each r, let , be a matroid defined by Theorem 2. Let . Then .
Theorem 6. Let be a and . Then if and only if for each .
Theorem 7. Suppose that is a with the fundamental sequence . If for any (), then is called a closed .
3. Bases of
Based on and bases of matroids or fuzzy matroids, we propose the concept of the intuitionistic fuzzy basis of a .
Definition 10. Let be a . is said to be maximal in ψ. If for any and , then . I.e., there does not exist such that ).
An intuitionistic fuzzy basis ( for short) of a is a maximal member .
Suppose that is an and . Let and ; then and . Obviously, . Therefore, here is called an intuitionistic fuzzy sub-basis ( for short) with respect to for a . Generally, there are infinite for a and their cardinality is the same as that of the corresponding .
Definition 11. An is an elementary if . If is an elementary with supp and , then is denoted by with support A and height r.
Theorem 8. Suppose that is an of a , then for each .
Proof. Assume that there exists an
such that
. Let
for each
and
Then . It follows that . However, for each , we have . Then from Theorem 6. This contradicts the hypothesis.
Here, we will use Theorem 6 to prove the next theorem. □
Theorem 9. Let be a with the fundamental sequence and suppose is an of ; then
Proof. Let be an of . Then . It follows that for each .
Assume that there is an such that . We take and let be the elementary which is defined by supp and .
If we let
, then for each
, we have
By Theorem 6, we have .
By the hypothesis, for , we have that there exists such that . Thus . Since , . This contradicts that is an . □
Theorem 10. Suppose that is a and is the fundamental sequence of . Then is closed if and only if for any , there exists an such that .
Proof. Assume that for any , there exists an such that . If is not closed.
Let
be a positive integer such that if
, then
, where
Let A be a basis of but not a basis of . Let be the elementary . Obviously, for any , and for any . It follows that .
Suppose that is an and . Then and . Since A is a crisp basis of , .
Since
and by Theorem 5 and Theorem 9, we have
Conversely, suppose that is closed. Let and , where . Let be a subsequence of and be a subsequence of such that , and for a given , there is , and for a given there is . It follows that
- (1)
;
- (2)
;
- (3)
If , then ;
- (4)
If , then .
Let be a nested sequence such that
- (a)
supp, where is a basis of ;
- (b)
For (where i is an integer), we have and is a maximal subset of in that contains ;
- (c)
For (where i is an integer), we have A is a maximal subset of in .
Let be the elementary , where . If , then we can easily get . By Theorem 6, . From the construction of , and is an for , the conclusion is established. □
4. The Judgement of an for a
From the proof of Theorem 10, we can get the following result.
Theorem 11. Suppose that is a closed with the fundamental sequence and the induced matroid sequence , where (). Let . If is an of , then supp is a basis of matroid .
Proof. Suppose that is an of . Then and for any .
Assume that supp
is not a basis of matroid
; then there exists a basis
A of
such that supp
. Let
Then , and . Thus, for any ,
and for any
,
From Theorem 6, it follows that . Since , it contradicts that is an of . □
The following necessary and sufficient condition can be used to judge whether a fuzzy set is a fuzzy basis.
Theorem 12 ([
25]).
Let be a closed fuzzy matroid on E and be the fundamental sequence. Let . Suppose is the induced matroid sequence (where ,). Then μ is a fuzzy basis of if and only if μ satisfies:- (i)
=suppμ is a basis of matroid .
- (ii)
There exists a sequence () which satisfies is a maximal subset of in () and such that for any , and for any , , where .
This result can be extended to intuitionistic fuzzy sets.
Theorem 13. Suppose is a closed with the fundamental sequence and the induced matroid sequence , where (). Let ; then is an of if and only if satisfies:
- (I)
for each ;
- (II)
The set is a crisp basis of matroid ;
- (III)
There exists a sequence () which satisfies is a maximal subset of in () and such that for any , , and for any (), .
Proof. By Theorem 8 and Theorem 11, we have
- (I)
for each ;
- (II)
The set =supp is a basis of matroid .
Now we just prove that (III) holds.
Let (). By the hypothesis, we have , That is .
Next, we will prove is a maximal subset of in , where .
Note that =supp is the basis of .
Assume that there exists () such that is not a maximal subset of in . Then there is such that and B is a maximal subset of .
Let
and
for each
, and if
, let
If
, let
where
. Then
. Since
, it follows that
, for any
, and
for any
. Then, by Theorem 6,
, which contradicts that
is an
of
.
Conversely, from condition (II) (III), supp is a crisp basis of matroid , and for any (). It follows that from Theorem 6. □
is not an of . Since and is a closed , there exists an of such that , so and suppsupp.
Case 1. supp supp. Since is an of , then for each and suppsupp is a basis of matroid . As and is a maximal subset of , where (), for any , and for any (), , for any suppsupp, we have . Since for each , . It follows that , which contradicts that , .
Case 2. supp supp. Since is an of , supp is a basis of matroid . From condition (II), supp is also a basis of matroid . Then suppsupp, which is in contradiction with suppsupp.
Therefore, is an of .
The following corollary is obvious.
Corollary 1. Suppose is a closed with the fundamental sequence and the induced matroid sequence , where (). Let . Then is an of if and only if the satisfies:
- (1)
is a crisp basis of , where .
- (2)
There exist () which satisfy and is a maximal subset of () such that for any , and for any , .
Theorem 14. Let E be a finite set. Suppose that there is the same fundamental sequence and the same induced matroid sequence for fuzzy matroid and , where (). Then is a fuzzy basis of if and only if is an of .
Proof. By the hypothesis and Theorem 12, we have is a fuzzy basis of if and only if the fuzzy set satisfies:
- (1)
is a basis of , where =supp.
- (2)
There exist which satisfy is a maximal subset of () and such that for any , , and for any .
These two conditions hold if and only if satisfies:
- (1)
is a crisp basis of matroid .
- (2)
For the above , we have for any , , and for any .
□
5. A Tree Structure of a Closed
From Theorem 13, a tree structure of a closed
is proposed below, which is similar to the tree structure introduced in [
25].
Let
be a closed
on
E,
be the fundamental sequence and
be the
-induced matroid sequence (where
(
)). Suppose that
is an
of
and
supp
is a crisp basis of matroid
. Then, from Theorem 13, there exists a sequence
(
,
) such that
is a maximal subset of
(
) in
and
. Obviously,
,
. The number of the sequence
is determined by the number of the maximal subsets of the previous maximal subset in the next level based on the same
. Obviously, each of the sequence can be constructed a brunch of a tree. All the sequences of the same
can be constructed a tree. Since there are many
, there are many trees which become a forest. The forest is called a tree structure of the closed
(
Figure 1).
Definition 12. The set of trees constructed by the sequences in Theorem 13 is the tree structure of a closed , denoted by (T for short) (Figure 1), which is defined below. Remark 1. There is one branch corresponding to a leaf in T and vice versa. From Theorem 13 and the construction of T, a branch of T and an of are one-to-one corresponding. Thus, for , the number of the is equal to the number of leaves of T.
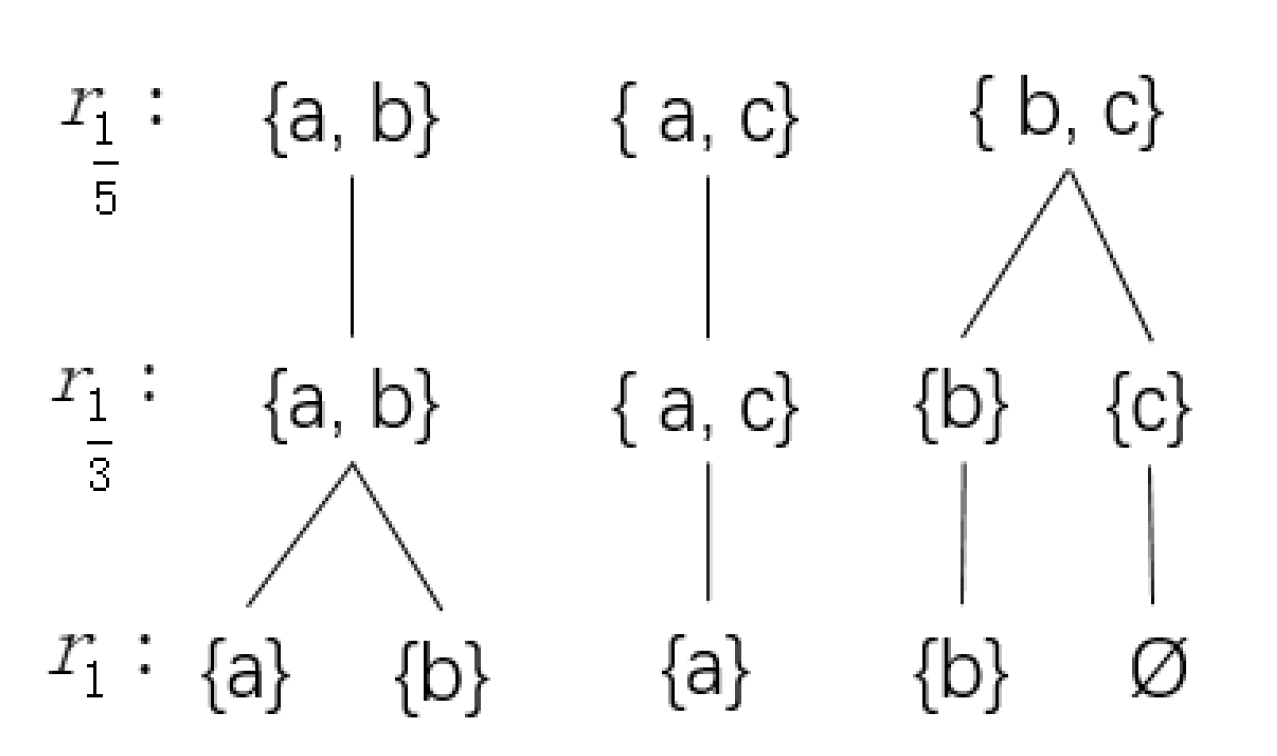
Example 1. Let , , , . Then , and are all matroids, and , , . Letand let , where . From Definition 2.16, is a closed . The tree structure T is shown in Figure 2. From
Figure 2, there are three trees and five leaves in
T. By Remark 1, there are five
of
, which are as follows:
Then the values of the similarity function
h for the five
are below:
Next, we discuss the properties of T for .
Theorem 15. Let be a closed on E, be the fundamental sequence and (where ()) be the induced matroid sequence. Let T be the tree structure of . Then each basis of the induced matroid ( is a positive integer) is in level of T.
Proof. For any i(), if , since each basis of matriod is the root of each tree in T, is in level.
If (), for any basis of matroid —since , it follows that —then there exists a basis of such that . Obviously, is a maximal subset of in . It implies that is in level of T.
Note that the converse of Theorem 15 does not hold. In Example 1, , are both the bases of matroid in the second level, but , are not the bases. □
Theorem 16. Let be a closed on E, be the fundamental sequence and (where ()) be the induced matroid sequence. Let T be the tree structure of . Suppose that is the collection of the sets in level of T, where . Let . Then .
Proof. For any , by the hypothesis, there is a basis B of matroid such that . By Theorem 15, all bases of are in level T, where . Then . It implies that . Thus, .
On the other hand, for any , there exists a set in () level of T such that . By Theorem 13, , . That implies that .
Therefore, . □
Remark 2. Let be a closed on E and T be its tree structure. Suppose that is the collection of the maximal subsets in level of T. Then the bases of () belong to .
Theorem 17. Let be a closed on E and T be its tree structure. Suppose that the sequence ( is in level) of T satisfying and . For any , let and and for any (), let . Then is the fundamental sequence of .
Proof. Let be the fundamental sequence of . By the hypothesis and Theorem 13, is a fuzzy basis of . Thus . Suppose that a sequence satisfies and . It follows that (). Then for any i () and . Thus . That implies that .
Therefore, is the fundamental sequence of . □