1. Introduction
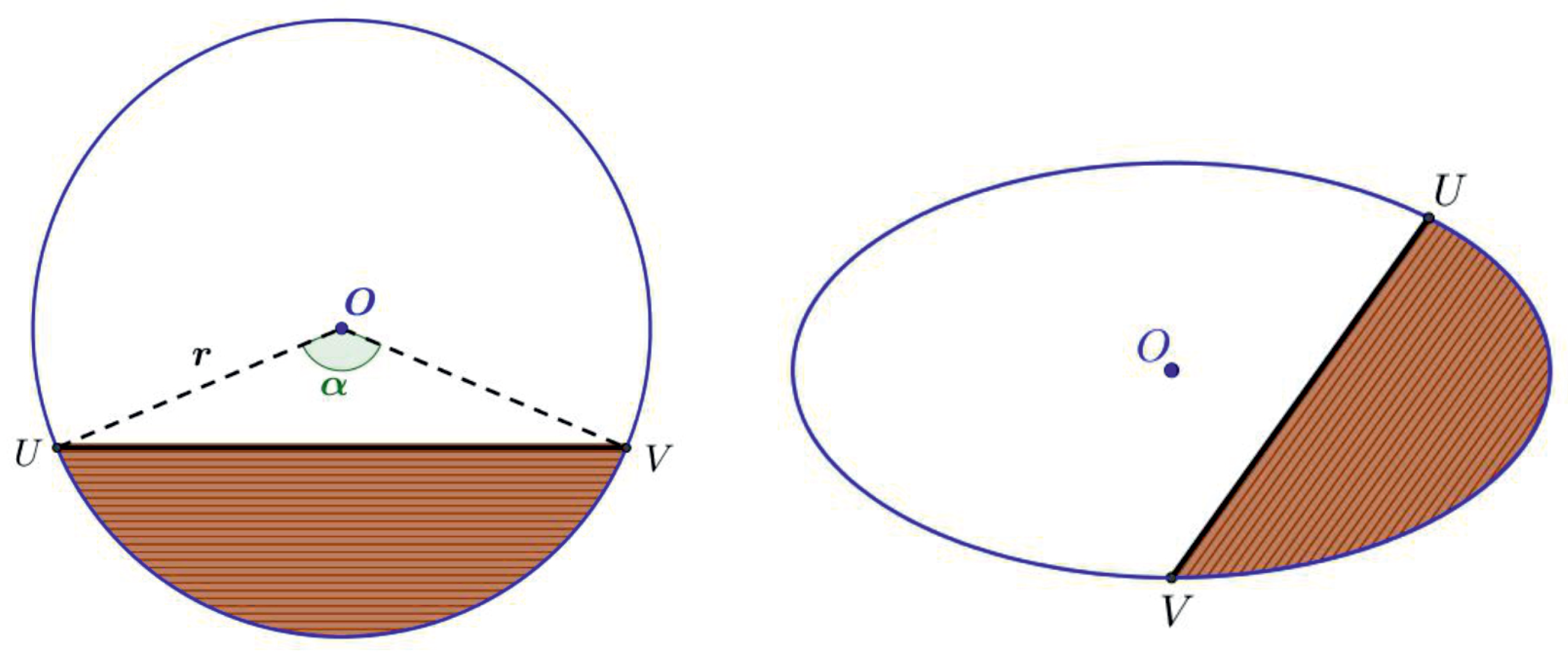
In this paper, we present the problem of calculation of the area of elliptical segment. The notion elliptical segment is a generalization of the term circular segment. In accordance with this analogy, we consider the elliptical segment as a set of points surrounded by a given elliptical arc and its chord. The figures in
Figure 1 are the segments illustrated as the shaded regions.
There exist a few formulas about how to calculate the area
A of the given circular segment. Their proving is based on the idea of subtraction of the area of the circular sector and the area of the subsistent triangle portion [
1]. In this concept, the term central angle is crucial, but it is undefined for the ellipse [
2]. The Gauss–Green formula is used to determine an elliptical sector area. It leads to an algorithm for calculating the area of the elliptical segment [
3].
Our approach to the problem of the area of the elliptical segment is different. First, we prefer analytical method. Based on the idea of definite integral, we tessellate the given segment by polygons (trapezoids) and, consecutively, we derive a formula approximately evaluated the reflected area. Finally, we present an interesting corollaries of the results related to the area of the given ellipse.
2. Elliptical Segment
First, we consider an ellipse in its central equation with center in the origin of Cartesian coordinate system
. The straight line, determined by the chord of the conic, is defined in its slope-intercept form [
4].
In Cartesian coordinate system
, the ellipse is given by the equation
for
and let
p be the line of the form
for
. The line
p must be a secant line. We show that
Generally, let us consider an arbitrary parallel line in the equation
where
.
Suppose that the line in Equation (
3) intersects the ellipse in points
. Their coordinates must be derived by solving an equation
We evaluate the discriminant
Dwhere
.
The points of intersection exist, if and only if
. It implies that
The line
p also determines the chord
of the given ellipse, if and only if
as it was necessary to prove.
It also holds true that
if , then there exists an one-to-one correspondence between the pair of points and the intercept .
These points of intersection have the coordinates
specifically
If , then and it means that . The lines in the equation are tangent lines to the given ellipse.
We label the tangent line in the equation and will be the tangent line in the equation .
The tangent lines
,
demarcate the strip in which the ellipse lies. The condition (
5) also determines that each of the lines in Equation (
3) belongs to this strip. Later, we use the points of intersection as the vertices of polygons which approximately tessellate the given elliptical segment.
Without loss of generality, in the next section, we consider that the elliptical segment lies between the lines and the line p.
3. Arithmetic Sequence of Intercepts
To determine the vertices of the polygons, we introduce the intercepts
as an arithmetic sequence
such that
for
, where
is fixed and
is a difference of the sequence. Its value is bounded too. We determine it as follows:
The inequalities (
9) result in
and we derive
for
. It implies that
This result allows us to put
This setting of the difference d has a geometric meaning. The line segment on the axis y, bounded by the points , is fragmented to n particular segments of the equal length d.
4. Approximation of Elliptical Segment
First, we construct the set of the lines, each in the equation for the arithmetical sequence with its difference d.
We determine the points of intersection with the ellipse and draw the triangle and the trapezoids for . They approximate the elliptical segment.
In this setting of the intercept
we derive that for
it holds true
where the difference
d is determined by (
12).
The area
of the elliptical segment is approximately equal to the area
where
is a height of the trapezoid.
If we label
(
Figure 2), then we derive
Example 1. Approximately calculate the area of a semi-ellipse with axes,for.
Solution. The semi-ellipse is a special case of the elliptical segment for
. If we apply it in the Formulas (
10), (
12), and (
13), then we derive
and we derive
It is evident that k is a free parameter. It has also a geometric explanation-the line p passing through the center of the ellipse divides the ellipse in half.
Due to the simplicity of the calculation, we put
and we organize data in
Table 1. Similarly, the reader can also verify some results listed in
Table 2.
The visualizations with the different partition number
n are shown in
Figure 3.
5. Estimation of Area of Ellipse
In the case, when the line
p is identical with the tangent line
, the elliptical segment is prolonged to the complete ellipse and we have
It holds that
and we derive
The result (
15) is simplified as follows:
We modify the Formula (
17) in the form
The independence on the slope
k has a geometric interpretation too. We can approximate the ellipse by many polygonal tessellations related to the value of the slope
k. They need to not be congruent, but their areas are equal. Some samples are in (
Figure 4).
We have demonstrated that the Formula (
18) can be used to numerical approximation and its value depends on
n-the number of the polygons which tessellate the given ellipse. We estimate
.
Let us consider the function for and fixed . We show that this function is bounded.
It is evident that the domain of function is
and the function is bounded from below. Its minimum is
for
. We find a maximum
M by using its derivatives:
To find a stationary point, we set
and we derive
. The second derivative
is
and it holds true that
The function
has in
a global maximum
and it implies that
6. Area of Ellipse-Exactly
The area
A of the given ellipse in Equation (
1) can be evaluated by using definite integral [
5]. It holds true that
The result implies that it holds
Finally, from (
18), we can also derive this interesting result
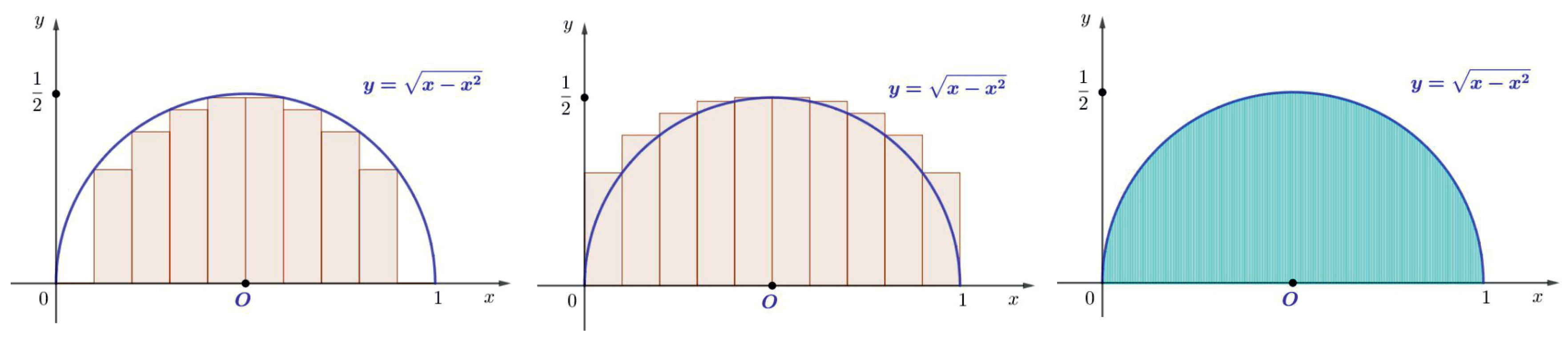
This result can be verified in geometrical way too. If we apply the idea of Darboux integral [
6], then we obtain
The
Figure 5 presents the graph of the function
. It is the semicircle with the center
and the radius
. It is evident that its area is equal to
.
Author Contributions
Investigation, D.V., J.F., and L.R.; conceptualization, D.V., J.F., and L.R.; writing—review and editing, D.V., J.F., and L.R.; writing—original draft preparation, D.V. The authors contributed equally to the work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by KEGA Grant No. 019UKF-4/2020 titled Inspirational Didactic Processes in Teaching of Projection Methods in Secondary Mathematics Education with a Focus on Requirements of Society and Practice.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments and suggestions for improving the quality of the paper.
Conflicts of Interest
The authors declare that they have no competing interest.
References
- Weisstein, E.W. Circular Segment. 2020. Available online: http://mathworld.wolfram.com/CircularSegment.html (accessed on 31 January 2020).
- Rhoad, R.; Milauskas, G.; Whipple, R. Geometry for Enjoyment and Challenge; New Edition; McDougal Littell; Houghton Mifflin Harcourt: Boston, MA, USA, 1997. [Google Scholar]
- Hughes, G.B.; Chraibi, M. Calculating ellipse overlap areas. Comput. Vis. Sci. 2012, 15, 291–301. [Google Scholar] [CrossRef]
- Bronshtein, I.N.; Semendyayev, K.A.; Musiol, G.; Mühlig, H. Handbook of Mathematics, 5th ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Mendelson, E.; Ayres, F. Schaum’s Outlines; Calculus, 5th ed.; Schaum’s Outline Series; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Spivak, M. Calculus, 3rd ed.; Publish or Perish, Inc.: Houston, TX, USA, 2008. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).