State Observation for Lipschitz Nonlinear Dynamical Systems Based on Lyapunov Functions and Functionals
Abstract
:1. Introduction
2. Stability Analysis in a Noise-Free Case
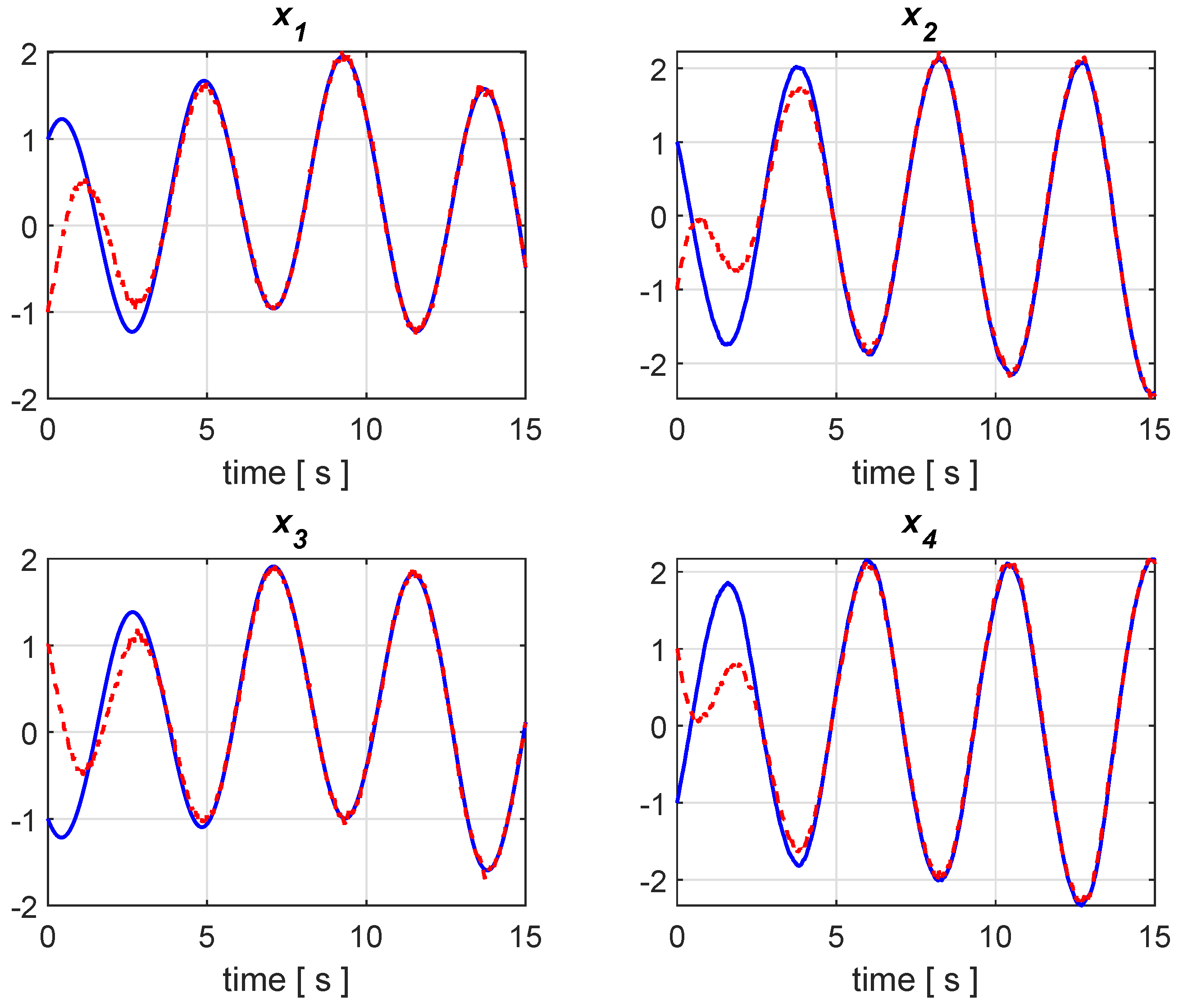
3. A Numerical Example
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ISS | input-to-state stability |
| CIBS | converging-input bounded-state |
| LMI | linear matrix inequality. |
References
- Thau, F.E. Observing the state of non-linear dynamic systems. Int. J. Control 1973, 17, 471–479. [Google Scholar] [CrossRef]
- Kou, S.R.; Elliott, D.L.; Tarn, T.J. Exponential observers for nonlinear dynamic systems. Inf. Control 1975, 29, 204–216. [Google Scholar] [CrossRef] [Green Version]
- Krener, A.J.; Isidori, A. Linearization by output injection and nonlinear observers. Syst. Control Lett. 1983, 3, 47–52. [Google Scholar] [CrossRef]
- Bestle, D.; Zeitz, M. Canonical form observer design for non-linear time-variable systems. Int. J. Control 1983, 38, 419–431. [Google Scholar] [CrossRef]
- Krener, A.J.; Respondek, W. Nonlinear observer with linearizable error dynamics. SIAM J. Control Optim. 1985, 23, 197–216. [Google Scholar] [CrossRef]
- Keller, H. Non-linear observer design by transformation into a generalized observer canonical form. Int. J. Control 1987, 46, 1915–1930. [Google Scholar] [CrossRef]
- Walcott, B.L.; Zak, S.H. State observation of nonlinear uncertain dynamical systems. IEEE Trans. Autom. Control 1987, 32, 166–170. [Google Scholar] [CrossRef]
- Slotine, J.J.; Hedrick, J.K.; Misawa, E.A. On sliding observers for nonlinear systems. J. Dyn. Syst. Meas. Control 1987, 109, 245–252. [Google Scholar] [CrossRef]
- Gauthier, J.P.; Hammouri, H.; Othman, S. A simple observer for nonlinear systems applications to bioreactors. IEEE Trans. Autom. Control 1992, 37, 875–880. [Google Scholar] [CrossRef]
- Gauthier, J.P.; Kupka, I.A.K. Observability and observers for nonlinear systems. SIAM J. Control Optim. 1994, 32, 975–994. [Google Scholar] [CrossRef]
- Astolfi, D.; Marconi, L. A high-gain nonlinear observer with limited gain power. IEEE Trans. Autom. Control 2015, 60, 3059–3064. [Google Scholar] [CrossRef] [Green Version]
- Zemouche, A.; Zhang, F.; Mazenc, F.; Rajamani, R. High-gain nonlinear observer with lower tuning parameter. IEEE Trans. Autom. Control 2019, 64, 3194–3209. [Google Scholar] [CrossRef]
- Khalil, H.; Praly, L. High-gain observers in nonlinear feedback control. Int. J. Robust Nonlinear Control 2014, 24, 993–1015. [Google Scholar] [CrossRef]
- Raghavan, S.; Hedrick, J.K. Observer design for a class of nonlinear systems. Int. J. Control 1994, 59, 515–528. [Google Scholar] [CrossRef]
- Rajamani, R. Observers for Lipschitz nonlinear nystems. IEEE Trans. Autom. Control 1998, 43, 397–401. [Google Scholar] [CrossRef]
- Hou, M.; Busawon, K.; Saif, M. Observer design based on triangular form generated by injective map. IEEE Trans. Autom. Control 2000, 45, 1350–1355. [Google Scholar] [CrossRef]
- Zemouche, A.; Boutayeb, M.; Bara, G. Observers for a class of Lipschitz systems with extension to H∞ performance analysis. Syst. Control Lett. 2008, 57, 18–27. [Google Scholar] [CrossRef]
- Sontag, E.D. The ISS philosophy as a unifying framework for stability-like behavior. In Lecture Notes in Control and Information Sciences; Isidori, A., Lamnabhi-Lagarrigue, F., Eds.; Springer Verlag: London, UK, 2000; pp. 443–467. [Google Scholar]
- Arcak, M.; Kokotovic, P. Nonlinear observer: A circle criterion design and robustness analysis. Automatica 2001, 37, 1923–1930. [Google Scholar] [CrossRef]
- Chaves, M.; Sontag, E. State-estimators for chemical reaction networks of Feinberg-Horn-Jackson zero deficiency type. Eur. J. Control 2002, 8, 343–359. [Google Scholar] [CrossRef] [Green Version]
- Shim, H.; Seo, J.H.; Teel, A.R. Nonlinear observer design via passivation of the error dynamics. Automatica 2003, 39, 885–892. [Google Scholar] [CrossRef]
- Alessandri, A. Observer design for nonlinear systems by using input-to-state stability. In Proceedings of the 43rd IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004; Volume 4, pp. 3892–3897. [Google Scholar]
- Alessandri, A.; Cervellera, C.; Macciò, D.; Sanguineti, M. Optimization based on quasi-Monte Carlo sampling to design state estimators for nonlinear systems. Optimization 2010, 59, 963–984. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Studies in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1994; Volume 15. [Google Scholar]
- Alessandri, A. On Hamilton-Jacobi approaches to state reconstruction for dynamic systems. Adv. Math. Phys. 2020, 2020, 9643291. [Google Scholar] [CrossRef] [Green Version]
- Alessandri, A. Lyapunov functions for state observers of dynamic systems using Hamilton-Jacobi inequalities. Mathematics 2020, 8, 202. [Google Scholar] [CrossRef] [Green Version]
- Alessandri, A. Sliding-mode estimators for a class of nonlinear systems affected by bounded disturbances. Int. J. Control 2002, 76, 226–236. [Google Scholar] [CrossRef]
- Alessandri, A. Design of observers for Lipschitz nonlinear systems using LMI. IFAC Proc. Vol. 2004, 37, 459–464. [Google Scholar] [CrossRef]
- Shim, H.; Son, Y.I.; Seo, J.H. Semi-global observer for multi-output nonlinear systems. Syst. Control Lett. 2001, 42, 233–244. [Google Scholar] [CrossRef]
- Sontag, E.D. Smooth stabilization implies coprime factorization. IEEE Trans. Autom. Control 1989, 34, 435–443. [Google Scholar] [CrossRef] [Green Version]
- Sontag, E.D. Remarks on stabilization and input-to-state stability. In Proceedings of the 28th Conference on Decision and Control, Tampa, FL, USA, 13–15 December 1989; pp. 1376–1378. [Google Scholar]
- Sontag, E.D. A remark on the converging-input converging-state property. IEEE Trans. Autom. Control 2003, 48, 313–314. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Sontag, E.D.; Wang, Y. On characterizations of input-to-state stability property. Syst. Control Lett. 1995, 24, 351–359. [Google Scholar] [CrossRef]
- Sontag, E.D.; Teel, A. Changing supply functions in input/state stable systems. IEEE Trans. Autom. Control 1995, 40, 1476–1478. [Google Scholar] [CrossRef] [Green Version]
- Sontag, E.D. New characterization of input-to-state stability. IEEE Trans. Autom. Control 1996, 41, 1283–1294. [Google Scholar] [CrossRef] [Green Version]
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the CACSD Conference, New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Manojlović, V. On conformally invariant extremal problems. Appl. Anal. Discret. Math. 2009, 3, 97–119. [Google Scholar] [CrossRef] [Green Version]
- Todorčević, V. Harmonic Quasiconformal Mappings and Hyperbolic Type Metrics; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Ciric, L. Some Recent results in Metrical Fixed Point Theory; Technical Report; University of Belgrade: Beograd, Serbia, 2003. [Google Scholar]
- Hosseinzadeh, M.; Yazdanpanah, M. Performance enhanced model reference adaptive control through switching non-quadratic Lyapunov functions. Syst. Control Lett. 2015, 76, 47–55. [Google Scholar] [CrossRef]
- Lu, C.; Hua, L.; Zhang, X.; Wang, H.; Guo, Y. Adaptive sliding mode control method for Z-axis vibrating gyroscope using prescribed performance approach. Appl. Sci. 2020, 10, 4779. [Google Scholar] [CrossRef]
- Angeli, D. A Lyapunov approach to incremental stability. IEEE Trans. Autom. Control 2002, 47, 410–421. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alessandri, A.; Bagnerini, P.; Cianci, R. State Observation for Lipschitz Nonlinear Dynamical Systems Based on Lyapunov Functions and Functionals. Mathematics 2020, 8, 1424. https://doi.org/10.3390/math8091424
Alessandri A, Bagnerini P, Cianci R. State Observation for Lipschitz Nonlinear Dynamical Systems Based on Lyapunov Functions and Functionals. Mathematics. 2020; 8(9):1424. https://doi.org/10.3390/math8091424
Chicago/Turabian StyleAlessandri, Angelo, Patrizia Bagnerini, and Roberto Cianci. 2020. "State Observation for Lipschitz Nonlinear Dynamical Systems Based on Lyapunov Functions and Functionals" Mathematics 8, no. 9: 1424. https://doi.org/10.3390/math8091424
APA StyleAlessandri, A., Bagnerini, P., & Cianci, R. (2020). State Observation for Lipschitz Nonlinear Dynamical Systems Based on Lyapunov Functions and Functionals. Mathematics, 8(9), 1424. https://doi.org/10.3390/math8091424




