A Multi-Carrier Waveform Design for 5G and beyond Communication Systems

Abstract

The next generation communication network (NGCN) is expected to provide higher spectral efficiency, low latency, large throughput and massive machine-to-machine type communications. In this regard, the design of the multi-carrier waveform (MCW) is posing a major research problem for the NGCN. To overcome the stated problem, a lot of state-of-the-art work exists that proposes various MCW alternative to the standard orthogonal frequency division multiplexing (OFDM) waveform. It is true that OFDM was used in a number of real-time communication systems of fourth generation (4G) networks. However, their use in the upcoming fifth generation (5G) network is not very feasible. This is because of the strict requirements of 5G communication systems, which also extend beyond 5G systems; hence rendering the use of OFDM infeasible for newer communication standards. To satisfy the requirements of upcoming communication networks, there is a dire need for MCWs with better flexibility. In this regard, a precoding-based MCW has been proposed. The proposed MCW fulfills the requirements of the NGCN in terms of low peak-to-average power ratio (PAPR), high spectral efficiency and throughput. The MCW proposed in this work uses power-domain multiplexing such as non-orthogonal multiple access (NOMA) and phase rotation by using the selective mapping (SLM) and generalized chirp-like (GCL) precoding of the input signal to the universal filtered multi-carriers (UFMC) modulations. Statistical analysis of the PAPR is presented by using the complementary cumulative distribution function (CCDF). The MATLAB^® simulations have been carried out to implement the CCDF of PAPR and results show that a PAPR gain of 5.4 dB is obtained when the proposed waveform is compared with the standard NOMA-UFMC waveform at clip rate of 10⁻³_, using 4-QAM.

1. Introduction

The fifth generation (5G) is a technology that will have a real and optimistic influence on our lives. In the past few years, many research teams across the globe have been exploring the myriad of possibilities that are offered by 5G networks. There are massive expectations for 5G networks and among them are three main application families that are going to have a huge impact. The first of these is the enhanced mobile broadband (eMBB). Due to the advent of Internet of Things (IoTs) and increasing connectivity of things, it is anticipated that 5G networks will support massive machine-type communications (MMTC). Last but not least, due to the real-time requirements of modern communication systems, the 5G network is also required to provide ultra-reliable and low latency communications (URLLC) [1,2].

The abovementioned application poses stringent demands such as uninterrupted continuous connectivity, enormous system throughput, and improved spectral efficiency [3]. Such rigorous requirements have been inciting researchers to work on new multiple access (MA) and modulation techniques in order to satisfy these requirements in 5G networks and even beyond.

It is because current technologies are not versatile and robust enough to satisfy the 5G and beyond mobile network constraints [4].

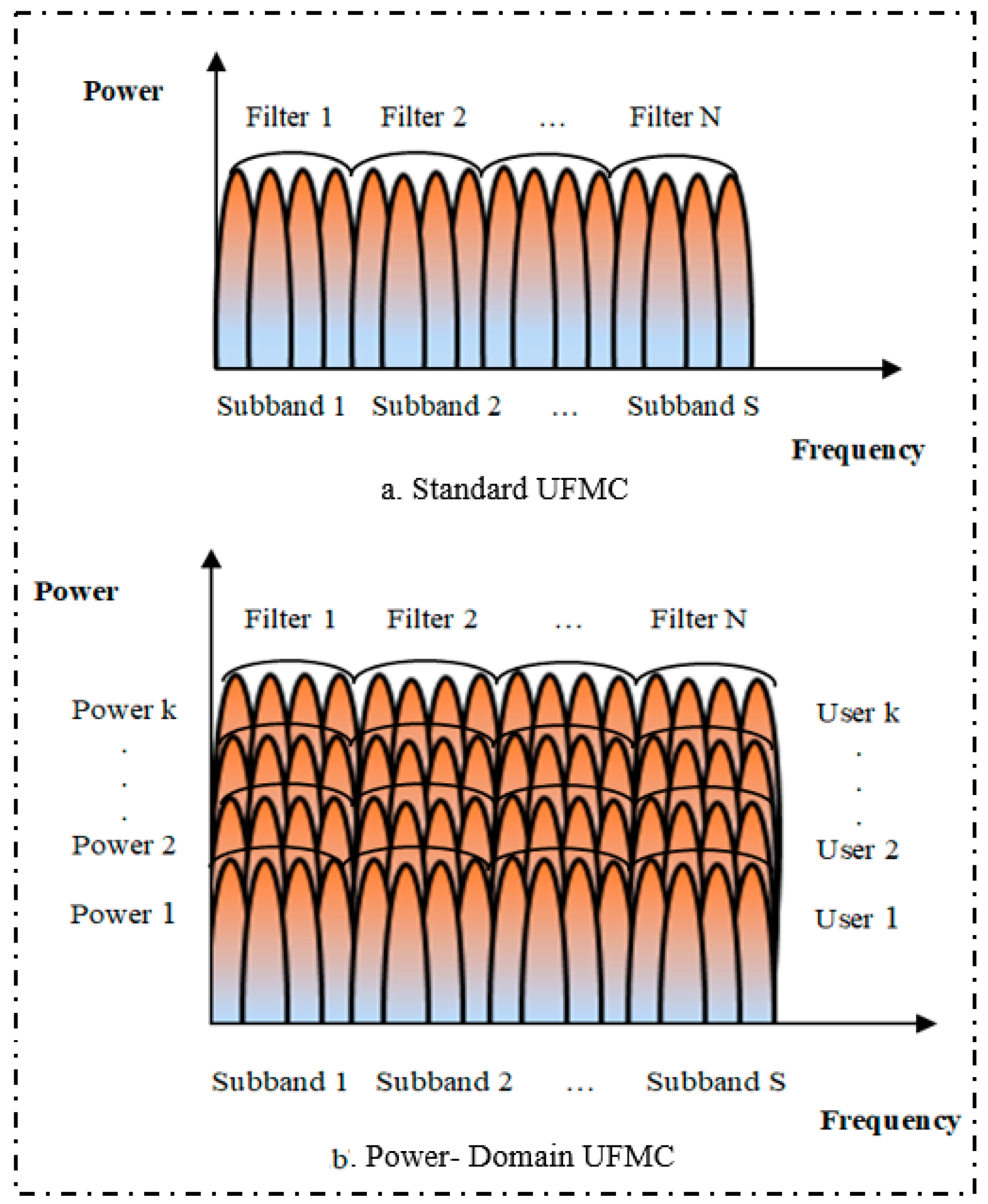
In the last few years, a significant amount of progress has been made and investigations have been carried out to determine the suitability of the universal filtered multi-carriers (UFMC) waveform for the 5G communication networks [5]. In this regard, a conceptual view of the UFMC waveform is pictorially demonstrated in Figure 1a. In this figure, the entire bandwidth is split into a number of sub-bands. Each sub-band contains a certain number of orthogonal sub-carriers. These sub-bands are filtered to reduce the out-of-band emissions (OBE). The filtering process also reduces the length of the filter significantly in comparison with the other 5G techniques proposed in the literature. Furthermore, sub-band filtering offers flexibility in design and reduces inter-symbol interference (ISI). Thus, the UFMC waveform is thought to be the most promising choice for short-burst communications [6]. The UFMC waveform achieves a good spectrum efficiency due to the lack of cyclic-prefix (CP), however, spectral inefficiency remains a silent major drawback of the standard UFMC waveform, making it infeasible for the future 5G communication networks and beyond [7,8]. Therefore, the standard UFMC waveform requires more comprehensive study and improved design to cope with the problem of spectral inefficiency.

The peak-to-average power ratio (PAPR) is yet another serious UFMC waveform problem due to its multicarrier nature. The presence of extremely large peaks in a signal ready for transmission causes a severe loss of performance, particularly when a signal is amplified by using a non-linear high-power amplifier (HPA). The HPA’s non-linearity causes two main problems, one is the in-band distortion and the other is out-of-band (OOB) radiation. Furthermore, the in-band distortion causes a higher bit error rate (BER) and on the other hand, OOB radiations increases in adjacent channel interference. Therefore, the low PAPR is one of the most desirable aspects of any communication waveform for its successful implementation.

Hence, in this paper a new multicarrier waveform with low PAPR has been designed to improve the capacity and support the large number of 5G/5G++ users. The proposed waveform uses selective mapping (SLM)-based generalized chirp-like (GCL) precoding and power domain multiplexing to manage more mobile users using the same frequency spectrum. Figure 1b illustrates the basic concept of the proposed waveform, where k users can be multiplexed in the power domain, such as non-orthogonal multiple access (NOMA), to support a large number of users. It is also shown that each of the k users consumes the same frequency band yet it has distinct power levels to increase the system capacity and throughput. There are many users who are multiplexed simultaneously. This multiplexing may cause interference with the co-channel. In order to reduce this interference, successive interference cancellation has to be used at the receiver end. In order to correctly decode the received signal, utmost attention must be paid to the allocation of the power to multiplexed users. To achieve this, the power is allocated to each user as the individual link condition (i.e., channel state or channel gain) [9,10].

The topics discussed in this paper are as follows; Section 2 presents a short review of the recent related work reported in the literature, and Section 3 briefly explains the newly designed waveform. In Section 3, the mathematical equations are derived and analyzed thoroughly. Subsequently, the numerical results are explained in Section 4 and finally, the concluding remarks about the presented work are provided in Section 5.

2. Related Work

A significant new multi-carrier waveform for upcoming modern communication systems has been suggested in the literature [5,11]. One of the most popular ones is the cyclic prefix-based orthogonal frequency division multiplexing (CP-OFDM) waveform [12]. It is being used in many fourth generation (4G) communication standards such as LTE-A, and the IEEE 802.11 family. The fundamental reason for its popularity is that this modulation scheme is capable of handling frequency selective fading channels. This is a capability that does not exist in all single-carrier-based schemes.

In CP-OFDM, the data stream is divided in a parallel manner and each stream is modulated using narrow sub-carriers. Each sub-carrier’s bandwidth is set in a way so that the transmission channels are non-coherent. This operation aids in the equalization of flat fading channels through a simple multiplication process. Moreover, the orthogonal overlap of sub-carriers in the OFDM waveform makes the frequency assignment very flexible and this in turn results in a very efficient usage of the frequency spectrum. The OFDM waveform can be easily implemented by using inverse fast Fourier transform (IFFT). The CP aspect of OFDM is introduced by copying the last part of IFFT and appending it to the start. This copy-append process gives the cyclic characteristic to the OFDM waveform and also acts as the interval guard. The length of the guard interval is determined through the length of cyclic part being appended. This process helps to reduce the inter-symbol interference (ISI). Apart from the advantages cited above, the CP-OFDM waveform has many drawbacks and shortcomings, such as high peak-to-average power ratio (PAPR), high out-of-band emissions (OBE), and higher sensitivity to synchronization errors, respectively. To counter and resolve the aforementioned disadvantages, several countermeasures have been proposed in the literature. These countermeasures include improved flexibility and better time-frequency localization. Additionally, the external guard interval in the CP-OFDM waveform is being proposed to be replaced with internal guard interval. This replacement will improve the flexibility and it will also enhance the spectral efficiency. Low implementation complexity, easy multiple input multiple output (MIMO) integration and backward compatibility still makes CP-OFDM one of the important players for new and upcoming standards; however, its rigid nature and poor coexistence with other standards further weaken its case along with the already mentioned drawbacks. Consequently, some new requirements, such as MMTC, which are unique to 5G networks, cannot be fulfilled with the existing CP-OFDM waveform [5].

The discrete Fourier transform spread OFDM (DFT-s-OFDM) is the most popular waveform employed in 4G LTE-A standard for its uplink communications due to low PAPR and robustness against multipath fading [13]. The DFT-s-OFDM waveform inherits many positive points from its predecessor CP-OFDM waveform, such as the reduced flexibility and excellent spectral efficiency. In the CP-OFDM waveform, the IDFT has high variance that can be reduced by introducing DFT operation before the IDFT. Moreover, the usage of cyclic prefix in DFT-s-OFDM enables the easy handling of the multipath channel effect. In addition to that, it has minimal implementation complexity, flexible spectrum assignment, and good MIMO adaptability. However, similar to the CP-OFDM waveform, the DFT-s-OFDM waveform also suffers from high OBE and cannot support the 5G requirements [14]. To resolve the abovementioned issues, several waveforms have been proposed in the literature. These waveforms are specifically proposed to handle the new challenges of 5G communication networks and beyond. Some of these waveforms related to the proposed work include filter bank multicarrier (FBMC) [15], multi-carrier non orthogonal multiple access (MC-NOMA) [16] and standard universal filtered multicarrier (UFMC) [17].

The FBMC waveform is one of the most investigated waveforms that offers a good frequency domain localization. This technique extends the pulse duration in the time domain along with optimally designed pulse shaping filters to achieve good frequency domain localization. The filters are designed to be applied at the sub-carrier level. This increases the flexibility of the filters and they can be used in various channel conditions and in different use cases. The FBMC can be used in different ways such as filtered multitoned FBMC and cosine modulated multitoned. However, the preferred method to implement FBMC is by using staggered modulated multitoned (SMT). SMT is also known as offset quadrature amplitude modulation FBMC (OQAM-FBMC) [18]. The ability of SMT to handle interference while handling dense symbol placement in frequency-time lattice makes it a very strong candidate for 5G networks. In OQAM-FBMC, the orthogonality between different sub-carriers is ensured through OQAM, which leads to better spectral efficiency when compared to CP-OFDM. Moreover, this technique is very suitable for mobile carriers as its well localized sub-carriers makes it very much immune to Doppler effects. On the other hand, similar to other techniques, this technique is also countered by various challenges. Some of these challenges include poor integration with MIMOs and high intrinsic interference that results from OQAM signaling [19].

The multi-carrier based non orthogonal multiple access (MC-NOMA) waveform is also one of the finest waveforms proposed in the literature to support a massive number of different users and application classes for 5G communication networks. The MC-NOMA allows overlaps in times and frequency between signals from different users. In order to eliminate the undesired interference, signals are transmitted with different power levels and a successive interference cancellation (SIC) is carried out at the receiver [20]. The MC-NOMA waveform offers significant benefits as compared to the conventional CP-OFDM waveform and is considered to be more powerful due to their reduced spectral side-lobe levels. Nevertheless, the MC-NOMA also has some implementation issues such as error propagation, channel estimation errors, complexity and nonsupport for short packet burst [21].

The UFMC is the most promising waveform proposed for the 5G communication network due to its short packet burst communication support. The UFMC waveform inherits all the advantages from FBMC and OFDM, respectively, while avoiding their drawbacks [5]. The UFMC is a technique that uses the sub-band filtering technique, where filtering is performed with a fixed granularity of frequency domain.

Likewise, the filtering process reduces the out-of-band (OOB) emissions [22]. If we look at the side lobe, compared to OFDM, UFMC has a much lower side lobe. Therefore, UFMC is comparatively more resilient than OFDM, when it comes to interferences between sub-carriers that arise from the frequency shift in the channel. It is worth mentioning that although UFMC is much better at suppressing OOB emission compared to OFDM, it has high computational complexity. However, if the UFMC is based on a Finite Impulse Response (FIR) filter rather than the conventional method, it has lower computational complexity and at the same time the impact of OOB emissions is also very low [23].

In UFMC, the use of CP depends upon the desired ISI. With the use of CP, the ISI goes down and vice versa. Normally, CP is not used in standard UFMC systems as the transition regions provide protection against ISI. To achieve orthogonality in the frequency domain, the signals are sent one after the other in time domain. However, the absence of CP in UFMC waveform requires more complicated receiver designs as compared to the CP-OFDM waveform [24].

Moreover, the use of sub-bands in the UFMC waveform gives better time localization. A coordinated multi-point reception scheme with multiple carrier-frequency offsets (CFOs) has also been proposed in the literature to support one-tap interference free equalization [6]. All the techniques discussed above provide a better OBE compared to the 4G LTE-A CP-OFDM waveform. Spectral inefficiency, however, remains a major drawback of the UFMC standard waveform, making it difficult to be used for future 5G networks.

3. Proposed Waveform

The block diagram of proposed waveform architecture is depicted in Figure 2. According to Figure 2, a k number of mobile users are communicating with the base station (BS) simultaneously, over the same frequency band, but with different powers. Assuming there are k users, where each user is utilizing an entire band with total of N sub-carriers. The Quadrature Amplitude Modulation (QAM) signal X_l of any ith user, after serial-to-parallel (S/P) conversions can be written as below:

$$X_l={[X_0,X_1,X_2,\dots X_{N-1}]}^T$$

(1)

where N is total number of sub-carriers. After S/P conversions, an entire band of having N sub-carriers for ith user is broken down into S sub-bands, where each sub-band in S is further sub-divided into a fixed number of C sub-carriers. Mathematically, for any ith user, its time domain signal with S sub-band that is the IFFT having C points can be expressed as:

$$x_{s_i}\left[n\right]=\frac{1}{\sqrt{C}}{{\displaystyle \sum }}_{l=0}^{C-1}{X}_l·e^{j2\pi \frac{n}{C}l} , 0\le n\le C-1$$

(2)

where X_l represents the SLM-based GCL precoded constellation symbols, contained in S sub-bands. After that, the C point IFFT based time domain signal is convolved with a filter f of length L, and the resultant signal can be expressed as:

$${\widehat{x}}_{s_{i,l}}=x_{s_i}\ast f_L$$

(3)

After the filtering operation, all the sub-bands are added together to get the filtered time domain UFMC signal and can be given as:

$$x_i={{\displaystyle \sum }}_{l=0}^{S-1}{\widehat{x}}_{s_{i,l}}$$

(4)

where x_i represents the UFMC signal for ith mobile user. Finally, the selected time domain UFMC signal with minimum PAPR is multiplexed in the power domain, where different power levels are assigned by the BS to each mobile user separately and each mobile user transmits the signal by using the same allocated frequency band, but with different power levels. At the receiver side, received signal denoted by y can be expressed mathematically as follows:

$$y={{\displaystyle \sum }}_{i=1}^k{h}_i\otimes x_i+w$$

(5)

where h_i is coefficients of the time domain channel for any ith mobile user and $w$ represents additive white Gaussian noise (AWGN). The multi-user diversity and successive interference cancelation (MUD-SIC) operation is applied on the received signal to separate the different users after the UFMC demodulation. Then, to combat the effect of channel and band filtering, sub-carrier equalization is carried out and eventually, data are unmapped to retrieve the original data bits.

4. Numerical Results

This section presents the study of the proposed waveform based on the analysis using computer simulations in MATLAB^®. To investigate the performance analysis, random data are generated and then modulated by using various modulation schemes such as 4-QAM, 16-QAM, 64-QAM and 256-QAM, respectively.

Table 1. Simulation parameters.

Parameters	Specification
FFT Size	512
Sub-Band Size	20
No. of Sub-Bands	10
Sub-Band Offset	156
Filter	Dolph Chebyshev
Filter Length	73
Stop-Band Attenuation	40
Modulation	4-QAM, 16-QAM, 64-QAM and 256-QAM
Subcarrier Mapping	Localized
Bits per Sub-Carriers	2, 4, 6
Sampling Frequency	15.36 MHz
PAPR Reduction Scheme	SLM, GCL Precoding
Channel Bandwidth	20 MHz

presents different parameters used for simulations and analysis in detail. According to the Table 1, the FFT size is set to be 512 where the number of sub-bands are equal to 10 and sub-carriers are equal to 20. Cubic-metric (CM) or PAPR analysis is one of the most important parameters to measure system performance. We selected PAPR analysis instead of CM because it is widely adopted in the literature to analyze the multicarrier waveform. SLM-based GCL precoding is employed for phase-rotation to lower the PAPR, and the Dolph–Chebyshev filter is used with the length of the filter given as L = 73 with stop-band attenuation 40.

The minimum PAPR of the selected time domain signal given in Equation (4) can be expressed as:

$$PAPR=\frac{peak power of x_i}{average power of x_i}$$

(6)

The complimentary cumulative distribution function (CCDF) is commonly used to evaluate the PAPR performance in the literature. It is a measure of the probability of the signal’s instantaneous power being greater than a specified level over its average power. The CCDF of the signal can be mathematically expressed as:

$$P(PAPR>PAP{R}_0=1-{(1-e^{-PAP{R}_0})}^N$$

(7)

where PAPR₀ denotes the level of clipping.

Figure 3, Figure 4, Figure 5 and Figure 6 present a CCDF comparison of the PAPR for NOMA-UFMC waveform, GCL precoding-based UFMC waveform, SLM-based GCL precoded power domain UFMC waveform using V = 2, SLM-based GCL precoded power domain UFMC waveform using V = 4, and SLM-based GCL precoded power domain UFMC waveform using V = 16 for 4-QAM, 16-QAM, 64-QAM and 256-QAM, respectively.

Table 2. Comparisons of the PAPR in dBs at 10⁻³ clip rate.

Multi-Carrier Waveform	4 QAM	16 QAM	64 QAM	256 QAM
NOMA-UFMC	11.8	11.8	11.8	11.8
GCL Precoding Based Power Domain UFMC	7.8	8.8	9.3	9.5
SLM (V = 2) and GCL Precoding Based Power Domain UFMC	7.4	8.2	8.7	8.8
SLM (V = 4) and GCL Precoding Based Power Domain UFMC	6.9	7.7	7.8	7.9
SLM (V = 16) and GCL Precoding Based Power Domain UFMC	6.4	7.2	7.4	7.5

presents a summary of the CCDF comparison of the PAPR analysis at clip rate of 10⁻³ in Figure 3, Figure 4, Figure 5 and Figure 6 by employing 4-QAM, 16-QAM 64-QAM and 256-QAM, respectively. It can be concluded from Table 2 that if we increase the size of V in SLM, which is a phase rotation factor, the PAPR of the UFMC signal will decrease, associated with the cost of increasing the system’s complexity. Furthermore, the modulation size also influences the PAPR reduction. The impact of using different QAMs is more obvious on the GCL precoded UFMC waveform and SLM-based GCL precoded power domain UFMC waveform using V = 2, 4, 16, respectively, as compared to the NOMA-UFMC waveform. PAPR performance is degraded with the higher order modulations. Hence, modulation size should be selected carefully.

Furthermore, the massive multiple input multiple output (MIMO) can be combined with the proposed waveform to enhance the future requirements of 5G and beyond communication systems significantly, at the cost of complexity. The complexity is directly proportional to the number of sub-bands and their sizes, digital modulation schemes, and number of transmit and receive antennas, and their configurations. The complexity can also be reduced by employing smaller size FFTs and a reduced number of sub-bands [25]. Recently, a hardware solution has been proposed in [26] to reduce the complexity of UFMC based waveforms. The complexity can be reduced up to 4.5 times by using poly-phase implementations.

In the end, it can be concluded that the proposed waveform with low PAPR can accommodate massive numbers of mobile users compared to the standard UFMC waveform, via power domain multiplexing. The main advantage of the proposed waveform over the other 5G candidate waveforms is capacity and throughput gain, ultra-high speed, anywhere anytime connectivity and multiple device compatibility to support a huge number of mobile users.

5. Conclusions

This paper presents a phase-rotation-based multicarrier waveform for 5G and beyond communication networks. The simulations have been conducted in MATLAB^® to investigate the PAPR performance of the designed waveform. In this research work, a joint SLM and GCL precoding was applied to improve the PAPR gain. The results of the computer simulations show that the proposed waveform gives better PAPR results when compared to standard NOMA-UFMC waveforms i.e., at clip rate of 10⁻³_, approximately 5.4 dB of PAPR gain is obtained once proposed waveform is compared with the standard NOMA-UFMC waveform by using 4-QAM. It is important to mention here that the proposed waveform has a comparatively high implementation complexity. However, the complexity of the proposed waveform can be minimized by using smaller size FFTs and by reducing the number of sub-bands. A significant advantage offered by the proposed waveform over the other waveforms is its enhanced capacity with reduced PAPR. The capacity of the proposed waveform is quite high in comparison to existing waveforms. This high capacity is because of the power domain multiplexing. Therefore, massive numbers of users can be supported under certain conditions. Hence, it can be concluded that the proposed waveform may be one of the best choices amongst the other waveforms proposed for the 5G and beyond communication networks.