Inverse Minimum Cut Problem with Lower and Upper Bounds
Abstract
:1. Introduction
2. Minimum Cut and Maximum Flow
- -
- for two non-empty sets of nodes and from , denotes the set of arcs that connects nodes from with the nodes from , i.e., ;
- -
- for a function , we define .
3. The Inverse Minimum Cut Problem with Lower and Upper Bounds
- (a)
- If the capacity of an arc is increased with the value then the difference between the value of the maximum flow in the modified network and the value of the maximum flow in the initial network is not greater than .
- (b)
- If the lower bound of an arc is decreased with the value then the difference between the value of the maximum flow in the modified network and the value of the maximum flow in the initial network is not greater than .
- AIMCUL1
- Calculate a maximum flow in ;
- Using (25) and (26) construct ;
- is an optimum solution of IMCUL1.
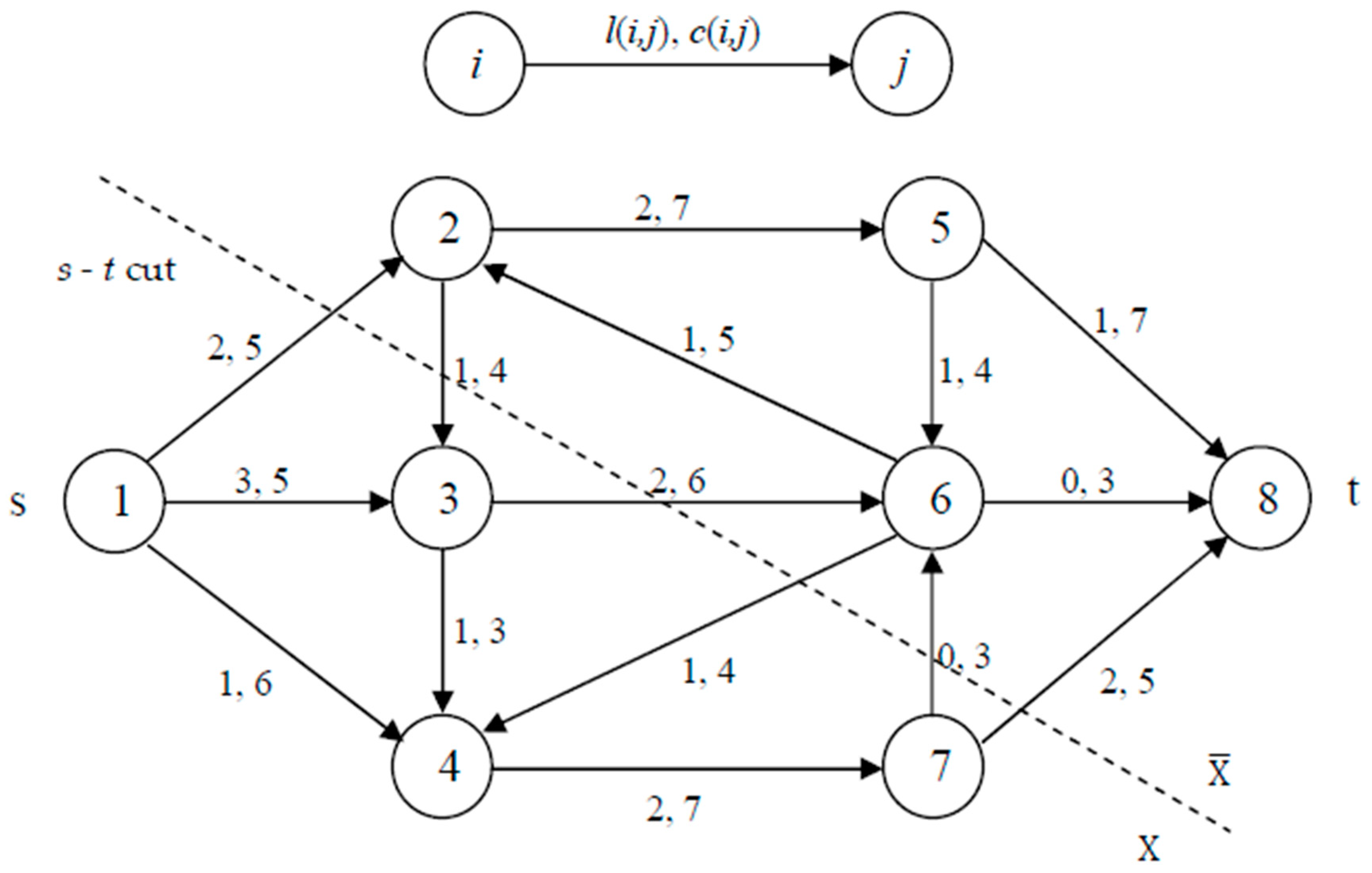
4. Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahuja, R.K.; Orlin, J.B. Combinatorial algorithms for inverse network flow problems. Networks 2002, 40, 181–187. [Google Scholar] [CrossRef] [Green Version]
- Ahuja, R.K.; Orlin, J.B. Inverse Optimization. Oper. Res. 2001, 49, 771–783. [Google Scholar] [CrossRef]
- Demange, M.; Monnot, J. An introduction to inverse combinatorial problems. In Vangelis Th. Paschos, Paradigms of Combinatorial Optimization (Problems and New Approaches); Wiley: London, UK; Hoboken, NJ, USA, 2010. [Google Scholar]
- Heuberger, C. Inverse Combinatorial Optimization: A Survey on Problems, Methods, and Results. J. Comb. Optim. 2004, 8, 329–361. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Zhang, J.; Ma, Z. Inverse maximum flow and minimum cut problems. Optimization 1997, 40, 147–170. [Google Scholar] [CrossRef]
- Deaconu, A. The inverse maximum flow problem considering L∞ norm. RAIRO Oper. Res. 2008, 42, 401–414. [Google Scholar] [CrossRef]
- Tayyebi, J.; Deaconu, A. Inverse Generalized Maximum Flow Problems. Mathematics 2019, 7, 899. [Google Scholar] [CrossRef] [Green Version]
- Tayyebi, J.; Mohammadi, A.; Kazemi, S.M.R. Reverse maximum flow problem under the weighted Chebyshev distance. RAIRO Oper. Res. 2018, 52, 1107–1121. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J. Inverse maximum flow problems under the weighted Hamming distance. J. Comb. Optim. 2006, 12, 395–408. [Google Scholar] [CrossRef]
- Deaconu, A. The inverse maximum flow problem with lower and upper bounds for the flow. Yugosl. J. Oper. Res. 2008, 18, 13–22. [Google Scholar] [CrossRef]
- Ciurea, E.; Deaconu, A. Inverse minimum flow problem. J. Appl. Math. Comput. 2007, 23, 193–203. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, M.-C. Inverse problem of minimum cuts. ZOR-Math. Methods Oper. Res. 1998, 47, 51–58. [Google Scholar] [CrossRef]
- Smith, D.K.; Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows: Theory, Algorithms, and Applications; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Orlin, J.B. Max flows in O(nm) time, or better. In Proceedings of the Forty-fifth Annual ACM Symposium on Theory of Computing, Palo Alto, CA, USA, 2–4 June 2013; pp. 765–774. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deaconu, A.; Ciupala, L. Inverse Minimum Cut Problem with Lower and Upper Bounds. Mathematics 2020, 8, 1494. https://doi.org/10.3390/math8091494
Deaconu A, Ciupala L. Inverse Minimum Cut Problem with Lower and Upper Bounds. Mathematics. 2020; 8(9):1494. https://doi.org/10.3390/math8091494
Chicago/Turabian StyleDeaconu, Adrian, and Laura Ciupala. 2020. "Inverse Minimum Cut Problem with Lower and Upper Bounds" Mathematics 8, no. 9: 1494. https://doi.org/10.3390/math8091494




