No Resistive Normal Electrons in Beginning Superconducting States
Abstract
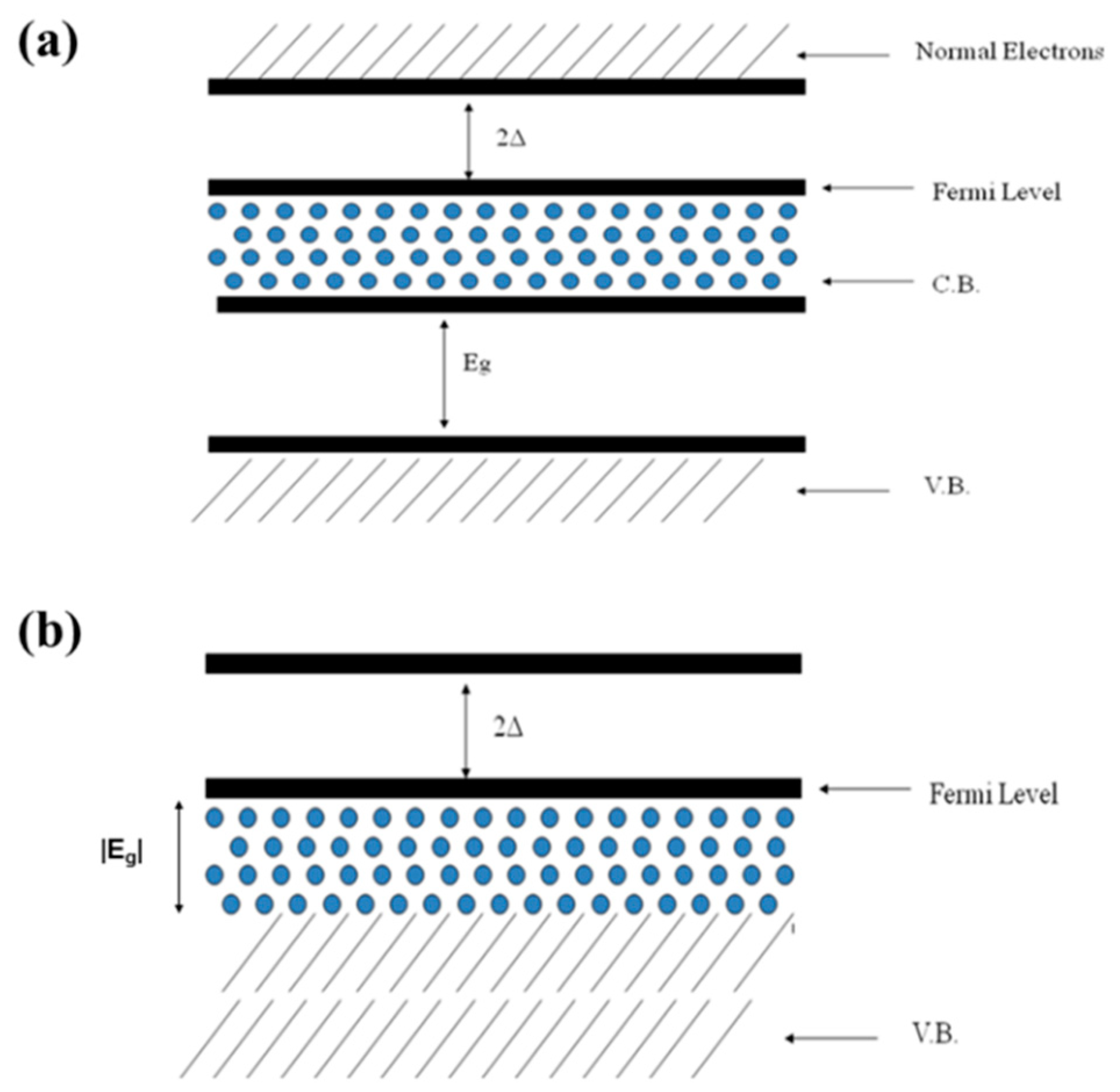
:1. Introduction
2. Model and Basic Equations
3. Results and Discussions
3.1. Criterion on Occurrence of Superconductivity
3.2. Composite Charge
- (i)
- Two-dimensional elementary excitations.
- (ii)
- A spherically isotropic distributed mode, thus yielding = 1 and e* = 0e, −2e having zero Coulomb repulsions.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schrieffer, J.R. Theory of Superconductivity; Benjamin: New York, NY, USA, 1964. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef] [Green Version]
- Bednorz, J.G.; Muller, K.A. Possible High Tc Superconductivity in the Ba-La-Cu-O System. Z. Phys. B Condens. Matter. 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Poole, C.P.; Farach, H.A.; Creswick, R.J.; Prozorov, R. Superconductivity; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Rose-Innes, A.C.; Rhoderick, E.H. Introduction to Superconductivity; Pergamon: New York, NY, USA, 1993. [Google Scholar]
- Koo, J.H.; Kim, J.H.; Jeong, J.M.; Cho, G.; Kim, J.J. Anomalous Spin Density Wave Superconductivity in Cuprate High-Tc Superconductors. Mod. Phys. Lett. B 2009, 23, 1533–1538. [Google Scholar] [CrossRef]
- Anderson, P.W. The resonating valence bond state in La2CuO4 and superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef] [PubMed]
- de Sousa, J.R.; Pacobahyba, J.T.M.; Singh, M. A theoretical study of the extinction of antiferromagnetic order by holes and dilution in La1-xSrxCu1-zZnzO4. Solid State Commun. 2009, 149, 131–135. [Google Scholar] [CrossRef]
- Bauer, J.; Hewson, A.C.; Dupuis, N. Dynamical mean-field theory and numerical renormalization group study of superconductivity in the attractive Hubbard model. Phys. Rev. B 2009, 79, 214518. [Google Scholar] [CrossRef] [Green Version]
- McMillan, W.L. Transition temperature of strong-coupled superconductors. Phys. Rev. 1968, 167, 331. [Google Scholar] [CrossRef]
- Mourachkine, A. Room-Temperature Superconductivity; Cambridge Int Science Publishing: Cambridge, UK, 2004. [Google Scholar]
- Halperin, B.I.; Refael, G.; Demler, E. BCS: 50 Years; Cooper, L.N., Feldman, D., Eds.; World Scientific: Singapore, 2011; pp. 185–226. [Google Scholar]
- Kittel, C.; McEuen, P. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1976; Volume 8. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Brooks/Cole: Pacific Grove, CA, USA, 1976. [Google Scholar]
- White, R.M.; Geballe, T.H.; Sak, J. Long Range Order in Solids. Phys. Today 1980, 33, 60. [Google Scholar] [CrossRef]
- Jewett, J.W.; Serway, R.A. Physics for Scientists and Engineers with Modern Physic; Brooks Cole: Singapore, 2010. [Google Scholar]
- Kim, D.J. New Perspectives in Magnetism of Metals; Springer Science & Business Media: Berlin, Germany, 1999. [Google Scholar]
- Touloukian, Y.S.; Buyco, E.H. Specific Heat. In Thermophysical Properties of Matter; IFI/Plenum: New York, NY, USA, 1970; Volume 4. [Google Scholar]
- Smith, D.R.; Fickett, F.R. Low-temperature properties of silver. J. Res. Natl. Inst. Stand. Technol. 1995, 100, 119. [Google Scholar] [CrossRef] [PubMed]
- Fegley, B., Jr. Practical Chemical Thermodynamics for Geoscientists; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Nielsen, N.K.; Olesen, P. Electric vortex lines from the Yang-Mills theory. Phys. Lett. B 1978, 79, 304–308. [Google Scholar] [CrossRef]
- Gasiorowicz, S. Quantum Physics; John Wiley & Sons: New York, NY, USA, 1974. [Google Scholar]
- Purcell, E.M. Berkeley Physics Course: Electricity and Magnetism; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Nambu, Y. Axial vector current conservation in weak interactions. Phys. Rev. Lett. 1960, 4, 380. [Google Scholar] [CrossRef] [Green Version]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345. [Google Scholar] [CrossRef] [Green Version]
- Nambu, Y. BCS: 50 Years; Cooper, L.N., Feldman, D., Eds.; World Scientific: Singapore, 2011; pp. 525–533. [Google Scholar]
- Anderson, P.W.; Baskaran, G.; Zou, Z.; Wheatley, J.; Hsu, T.; Shastry, B.S.; Doucot, B.; Liang, S. The theory of high-Tc superconductors—Comparisons with experiment. Phys. C Supercond. 1988, 153, 527–530. [Google Scholar] [CrossRef]
- Buckingham, M.J. A note on the energy gap model of superconductivity. II Nuovo Cim. 1957, 5, 1763–1765. [Google Scholar] [CrossRef]
- Schafroth, M.R. Remarks on the Meissner effect. Phys. Rev. 1958, 111, 72. [Google Scholar] [CrossRef]
- Fukuda, N.; Wada, Y.; Otake, S. Gauge Invariance and the Meissner Effect. Prog. Theor. Phys. 1959, 21, 343–353. [Google Scholar] [CrossRef] [Green Version]
- Wada, Y.; Fukuda, N. On the Theory of Superconductivity. Prog. Theor. Phys. 1959, 22, 775–806. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Lv, J.; Xie, Y.; Liu, H.; Ma, Y. Route to a superconducting phase above room temperature in electron-doped hydride compounds under high pressure. Phys. Rev. Lett. 2019, 123, 097001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Liang, X.; Li, G.; Liu, H.; Zhang, H.; Guo, J.; Chen, J.; Shen, K.; San, X.; Yu, W.; et al. 9.2%-efficient core-shell structured antimony selenide nanorod array solar cells. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, C.; Cho, S.; Koo, J.H. No Resistive Normal Electrons in Beginning Superconducting States. Mathematics 2020, 8, 1512. https://doi.org/10.3390/math8091512
Seo C, Cho S, Koo JH. No Resistive Normal Electrons in Beginning Superconducting States. Mathematics. 2020; 8(9):1512. https://doi.org/10.3390/math8091512
Chicago/Turabian StyleSeo, Changho, Seongsoo Cho, and Je Huan Koo. 2020. "No Resistive Normal Electrons in Beginning Superconducting States" Mathematics 8, no. 9: 1512. https://doi.org/10.3390/math8091512




