Abstract
The ACE algorithm is a candidate of the Lightweight Cryptography standardization process started by the National Institute of Standards and Technology (NIST) of the USA that passed the first round and successfully entered the second round. It is designed to achieve a balance between hardware cost and software efficiency for both authenticated encryption with associated data (AEAD) and hashing functionalities. This paper focuses on the impossible differential attack against the ACE permutation, which is the core component of the ACE algorithm. Based on the method of characteristic matrix, we build an automatic searching algorithm that can be used to search for structural impossible differentials and give the optimal permutation for ACE permutation and other SPN ciphers. We prove that there is no impossible differential of ACE permutation longer than 9 steps and construct two 8-step impossible differentials. In the end, we give the optimal word permutation against impossible differential cryptanalysis, which is , and a safer word XOR structure of ACE permutation.
1. Introduction
In 2015, to standardize lightweight cryptographic algorithms that are used in some specific situations where current standard is not applicable, the National Institute of Standards and Technology (NIST) of the USA started the Lightweight Cryptography (LWC) standardization process. NIST held two workshops in 2015 and 2016 and published the Federal Register Notice in 2018, announcing the final Submission Requirements and Evaluation Criteria for the Lightweight Cryptography Standardization Process and calling for nominations, which are cryptographic algorithms that provide authenticated encryption with associated data (AEAD) and optional hashing functionalities.
By the end of submission deadline, NIST received 57 submission packages. Among them, 56 were accepted as first round candidates in April 2019, which marks the beginning of the first round of the standardization process [1]. Due to the large number of submissions and the short timeline of the process, NIST has decided to eliminate some of the algorithms from consideration early in the first evaluation phase in order to focus analysis on the more promising submissions. In August 2019, NIST announced the 32 candidates that will be moving on to the second round.
ACE is one of the 32 candidates designed by Aagaard et al. of Department of Electrical and Computer Engineering of University of Waterloo [2]. It is designed to achieve a balance between hardware cost and software efficiency for both authenticated encryption with associated data (AEAD) and hashing functionalities, also providing sufficient security margins. In the submission package of ACE, designers analysis its security, primarily focusing on the diffusion behavior, expected upper bounds on the probabilities of differential and linear characteristics, algebraic properties and self-symmetry-based distinguishers. In this paper, we focus on the security margin of ACE against impossible differential cryptanalysis, which are not considered by any designers and attackers so far.
Impossible differential cryptanalytic method is a variant of differential cryptanalysis [3]. It can be used to build impossible differential distinguishers, distinguishing ciphers from random permutation. Impossible distinguishers can be further used to distinguish correct round keys, which can be used to recover the secret keys. The concept of impossible differential was proposed respectively by Knudsen [4] and Biham et al. [5] When studying the security of DEAL, Knudsen found that if the round function in the Feistel-structure cipher is bijective, then there will be a natural 5-round impossible differential of the cipher. In EUROCRYPTO 1999, Biham et al. proposed the concept of impossible differential in their study of Skipjack and then describe the miss-in-the-middle method of finding impossible differentials in FSE 1999 [6]. Impossible differential cryptanalysis has been used to attack many well-known iterative block ciphers with very good results (see e.g., [7,8,9,10,11,12,13]). Impossible differential distinguishers are generally of higher rounds than other distinguishers, i.e., compared to other cryptanalytic methods, impossible differential cryptanalysis can always be used to attack more rounds (or steps in this paper). For instance, the 3-round Feistel structure with a bijective round function has a provable security against differential cryptanalysis and linear cryptanalysis [14], but there is a 5-round impossible differential characteristic for it [4].
In this paper, we focus on the impossible differential cryptanalysis against ACE permutation, the core component of ACE algorithm, which are not considered by any designers and attackers so far as we know. The contribution of this paper are as follows:
- (1)
- We use the method of characteristic matrix [15] and propose that the theoretical security margin of ACE permutation against impossible differential cryptanalysis is of 9 steps.
- (2)
- We build an automatic algorithm that can be used to automatically search structural impossible differentials and apply it on ACE, giving that the actual security margin of ACE permutation against impossible differential cryptanalysis is of 8 steps.
- (3)
- We further improve our algorithm that can search for impossible differentials for all possible word permutations and XOR structures, giving an optimal permutation and an optimal XOR structure.
The automatic algorithm in this paper can further be used for other ciphers whose S-boxes are bijective and permute sub-blocks of states. We separate the step function into two parts (“XOR” and “Pbox”) and begin the automatic algorithm with the characteristic matrices of these two parts. Designers and attackers can use the algorithm by respectively entering the characteristic matrices of “XOR” and “Pbox”. For designers, they can further fix one part and traverse all the possibilities of the other part, by traversing all the possible characteristic matrix of the other part, and search for the longest impossible differentials of each, giving the optimal choice of component against impossible differential cryptanalysis.
This paper is organized as follows. In Section 2, we describe the concrete components of ACE permutation and the methodology of impossible differential cryptanalysis. In Section 3, we prove the security margin of ACE permutation, give two 8-step impossible differentials of it and present our automatic algorithm. In Section 4, by an improved algorithm, we search for the impossible differentials of all possible word permutations and test the security of other word XORing structures. Section 5 concludes the paper.
2. Preliminary
2.1. The ACE Permutation
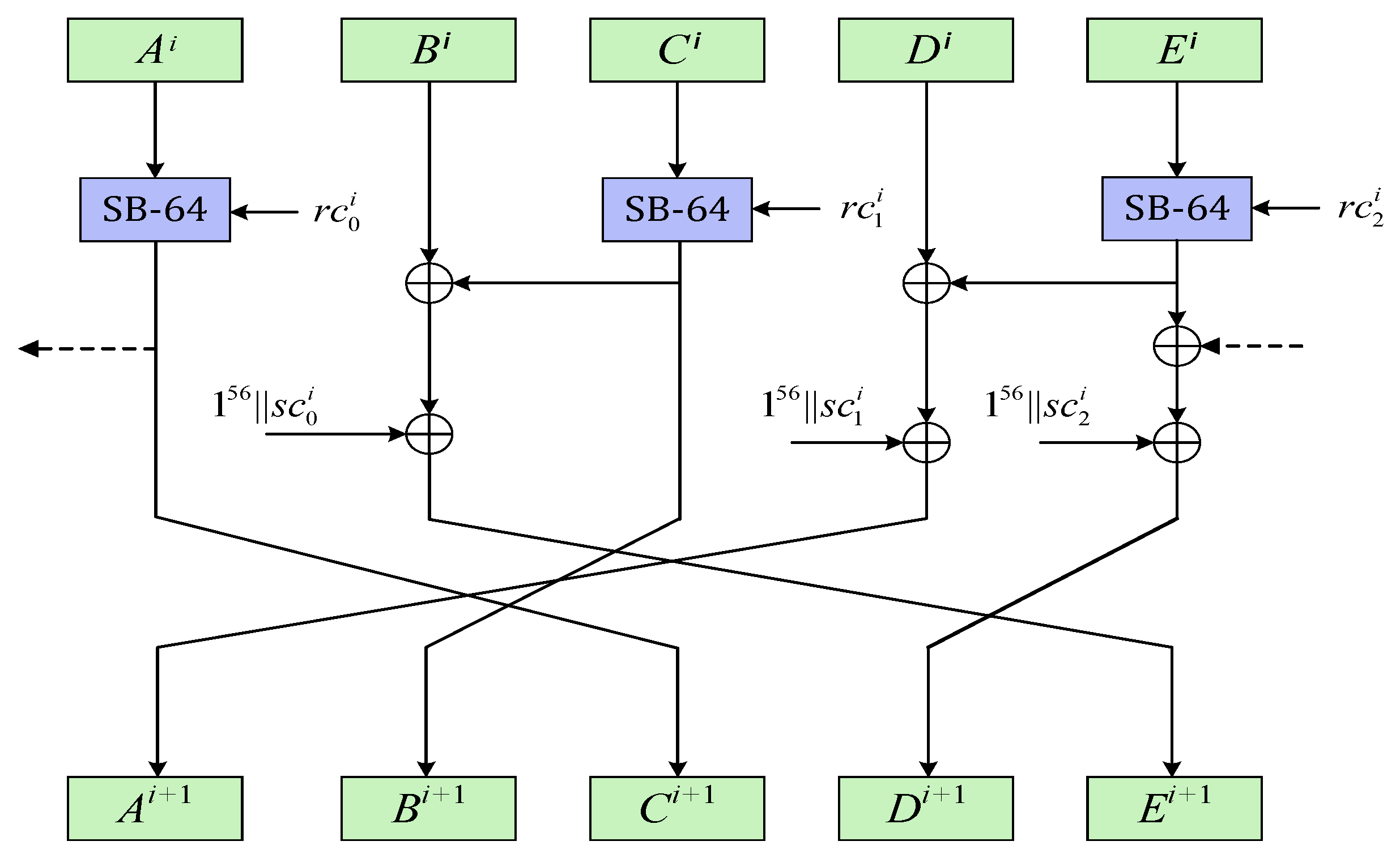
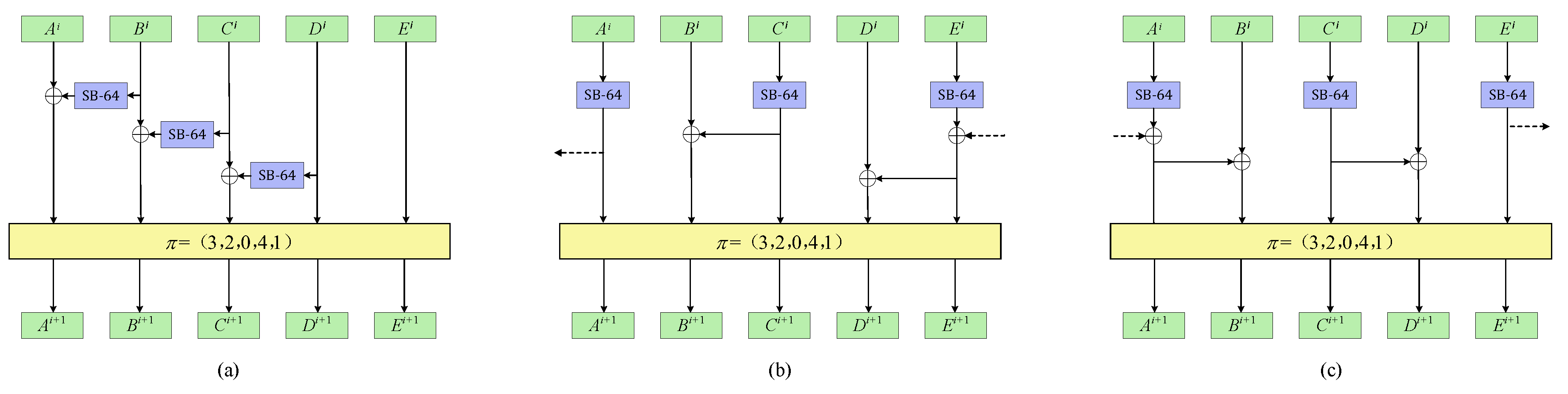
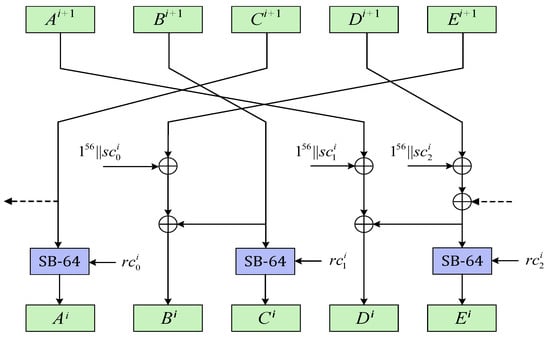
The ACE permutation is an iterative permutation with 320-bit input and a 320-bit output after iterating the step function for times. During the encryption/decryption process, the 320-bit value is arranged as the state. Each 320-bit state is divided into five 64-bit words, written as A, B, C, D, E, in every step. The step function of ACE consists of a nonlinear function and a linear function. The nonliniear function is applied on even indexed words respectively (i.e., A, C and E), where comes the permutation name. The step function is shown in Figure 1.
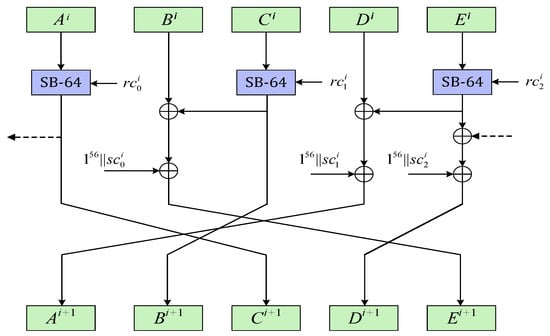
Figure 1.
ACE Step Function.
2.1.1. The Nonlinear Function SB-64
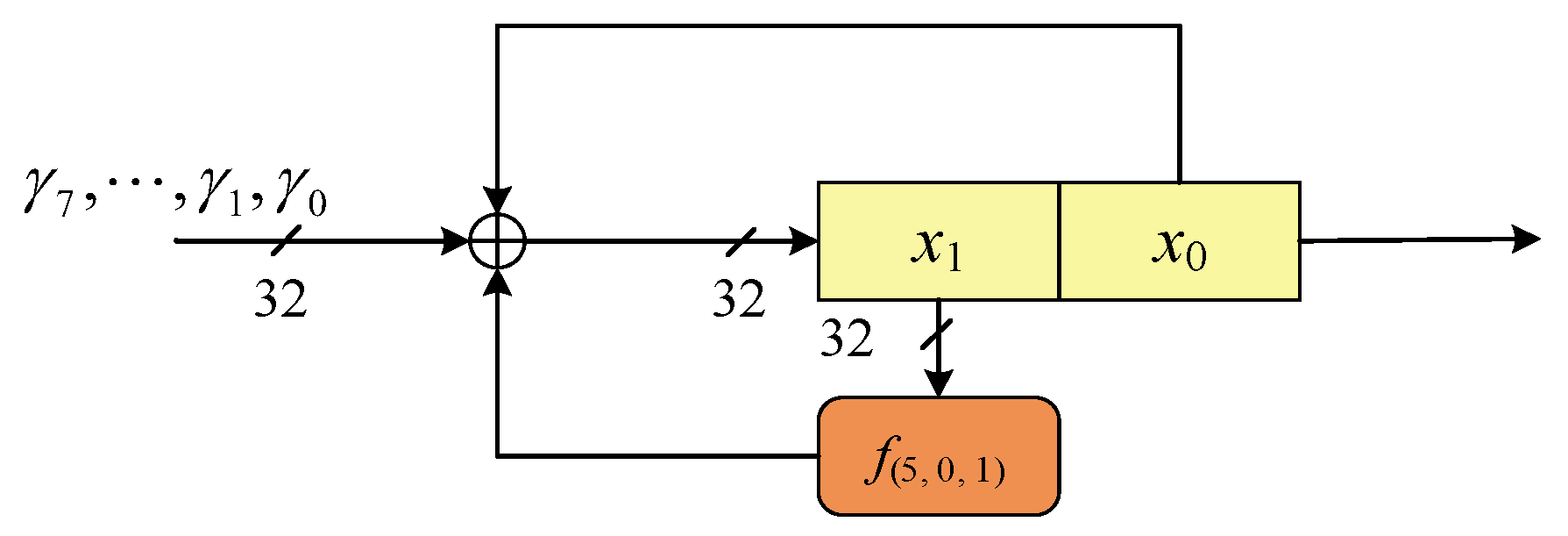
In ACE, the designers take the unkeyed 8-round Simeck block cipher with block size 64 as the nonlinear function. The Simeck block cipher uses Feistel structure, hence the reduced-round version of it is nonlinear and bijective, which meets the basic requirement of an S-box. The nonlinear function, or the S-box of ACE permutation, is denoted by SB-64. The details of SB-64 are shown in Figure 2.
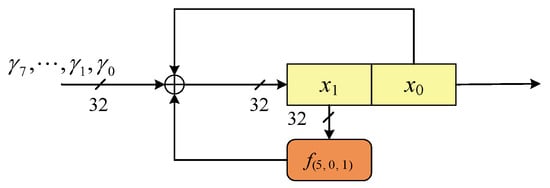
Figure 2.
Simeck Box (SB-64).
Let , where and . SB-64 iterate the Simeck-64 block cipher for 8 rounds, with round constant taking place of key addition.
2.1.2. Round and Step Constants
As Figure 1 shows, the step function of ACE is parameterized by and . For , and are both of 8-bit length, which are called round constant(of Speck-64) and step function(of ACE). The hexadecimal values of the round constant and step constant are shown in Table 1.

Table 1.
Step and round constants of ACE.
2.1.3. The Linear Function
The linear function of ACE permutation consists of two parts: a word permutation and a word XORing. We denote word permutation by . As Figure 1 shows, the origin word permutation is , i.e., after applying , the state will be transformed to . Designers choose it as the linear layer for differential cryptanalysis’s sake. This word permutation generates the largest number of active S-boxes per step.
2.2. Impossible Differential
Contrary to differential cryptanalysis, impossible differential cryptanalysis does not use high probability differential characteristics to attack ciphers and recover secret keys. Instead, it uses differential characteristics of probability 0 (i.e., impossible differential characteristics).
Definition 1
([3]).Let f denote a function on Abel group A. If for , for an arbitrary , there is , then is called a impossible differential of function f.
For instance, we denote an S-box on below:
| 00 | 01 | 10 | 11 | |
| 10 | 11 | 01 | 00 |
When the input difference is 01, we can compute directly: , , , . Then , are called an impossible differential of this S-box.
Definition 2
([3]).For an iterative block cipher, let denote the difference of input X and , denote the corresponding r-th round difference of output C and . If , then is called an r round impossible differential of the cipher.
The miss-in-the-middle method is one of the most efficient methods. For an iterative block cipher, let be a differential of probability 1 from the encryption side, and be a differential of probability 1 from the decryption side. If , then we can deduce that is an impossible differential of the cipher. For different ciphers, the way to find contradiction in the middle is different, which requires more study on the structure of the cipher itself. In this paper, we focus on structural impossible differential characteristics, which we denote by impossible differential in the next sections.
3. Impossible Differential Cryptanalysis of ACE
In this section, we propose our results of impossible differential cryptanalysis against ACE permutation. We prove that there will not be impossible differentials of ACE longer than 10 rounds and then find two 8-round impossible differentials of ACE. We also introduce an automatic algorithm searching for impossible differentials, which can be used in the cryptanalysis in other ciphers. Using the automatic algorithm, we conclude this section that the longest step of impossible differentials of ACE is 8 step, i.e., for ACE, there will not be impossible differentials longer than 9 steps.
3.1. Impossible Differential of ACE
Let F denote an iterative block cipher, and the internal state of encryption/decryption is divided into n sub-blocks. We assume that for one round of encryption, the input is denoted as () and the output is denote as ().
Definition 3
((Characteristic Matrix) [15]).(1) The encryption characteristic matrix A is an matrix. The (i, j) entry of A is set to 1 in the case that is affected by . Otherwise, the (i, j) entry is set to 0. (2) The decryption characteristic matrix B is an matrix. The (i, j) entry of B is set to 1 if is affected by . Otherwise, the (i, j) entry is set to 0.
Definition 4
([15]).Given characteristic matrix(encryption or decryption) , , we define: , where .
The definition of the multiplication between two characteristic matrices implies the transmission of effect. For two characteristic matrices X and Y, let , , where (), () and (). If the () entry of Y is 1, then would be affected by . If the () entry of X is 1, then would be affected by . On the basis of these two deductions, it is apparent that after two-step encryption/ decryption, would be affected by . On the contrary, if the () entry of Y or the () entry of X is zero (either one of them or both of them), then would not be affected by . In general, might be affected by all the n sub-blocks of y whereas might affect all the n sub-blocks of y. As long as there is one sub-block of y that delivers the effect of to , despite other sub-blocks, would definitely be affected by , which explains the reason it is Bitwise-OR that is used in the multiplication between two characteristic matrices.
The diffusion property of a cipher can be observed through characteristic matrix. An r round encryption procedure can be denoted by the characteristic matrix to the power of r. If after r round’s encryption, every element of characteristic matrix turns to 1, we can deduce that each sub-block can affect 5 sub-blocks after r rounds, i.e., a difference in one sub-block could lead to differences in every 5 sub-blocks after r rounds.
Definition 5.
Given a state difference , the corresponding difference vector is defined as follows:
The diffusion property of one round encryption/decryption can be described by left multiplying the difference vector by characteristic matrix, i.e., the state difference vector becomes / after one round of encryption/decryption. For multi-round (e.g., r-round) encryption/decryption, the state difference vector will become /.
The multiplication between a characteristic matrix and a state difference vector implies the transformation of difference. For and of ACE permutation, sub-block and are respectively affected only by one sub-block of ( and ), whereas , and are affected by more than one sub-blocks of , i.e., if the second and third sub-block of are active (), the second sub-block of is active () with probability 1 whereas the fifth sub-block is uncertain. In other words, once a sub-block of the state is affected by more than 1 sub-blocks of the state of the previous round which are all active, then this sub-block will be uncertain. Hence, we use the real number addition in this case so that we can observe the active sub-blocks by the value of difference vector’s entries.
Definition 6.
Given characteristic matrices(encryption or decryption) X, Y and a state difference vector , there is: , where
Theorem 1.
If the encryption/decryption characteristic matrix of a cipher reaches (all the entries of the matrix become 1) after r iterations, the cipher reaches structural total diffusion in the encryption/ decryption direction within r rounds.
Proof.
The iteration of characteristic matrix is denoted by the power of the matrix, and the addition in the matrix multiplication is defined as Bitwise-OR. If the entries of the encryption characteristic matrix after r iterations are all equal to 1, then any sub-block of an arbitrary input difference can affect all the n sub-blocks. The property of decryption characteristic matrix is of the same reason. □
Theorem 2.
For ACE, there will not be structural impossible differential characteristics longer than 10 steps.
Proof.
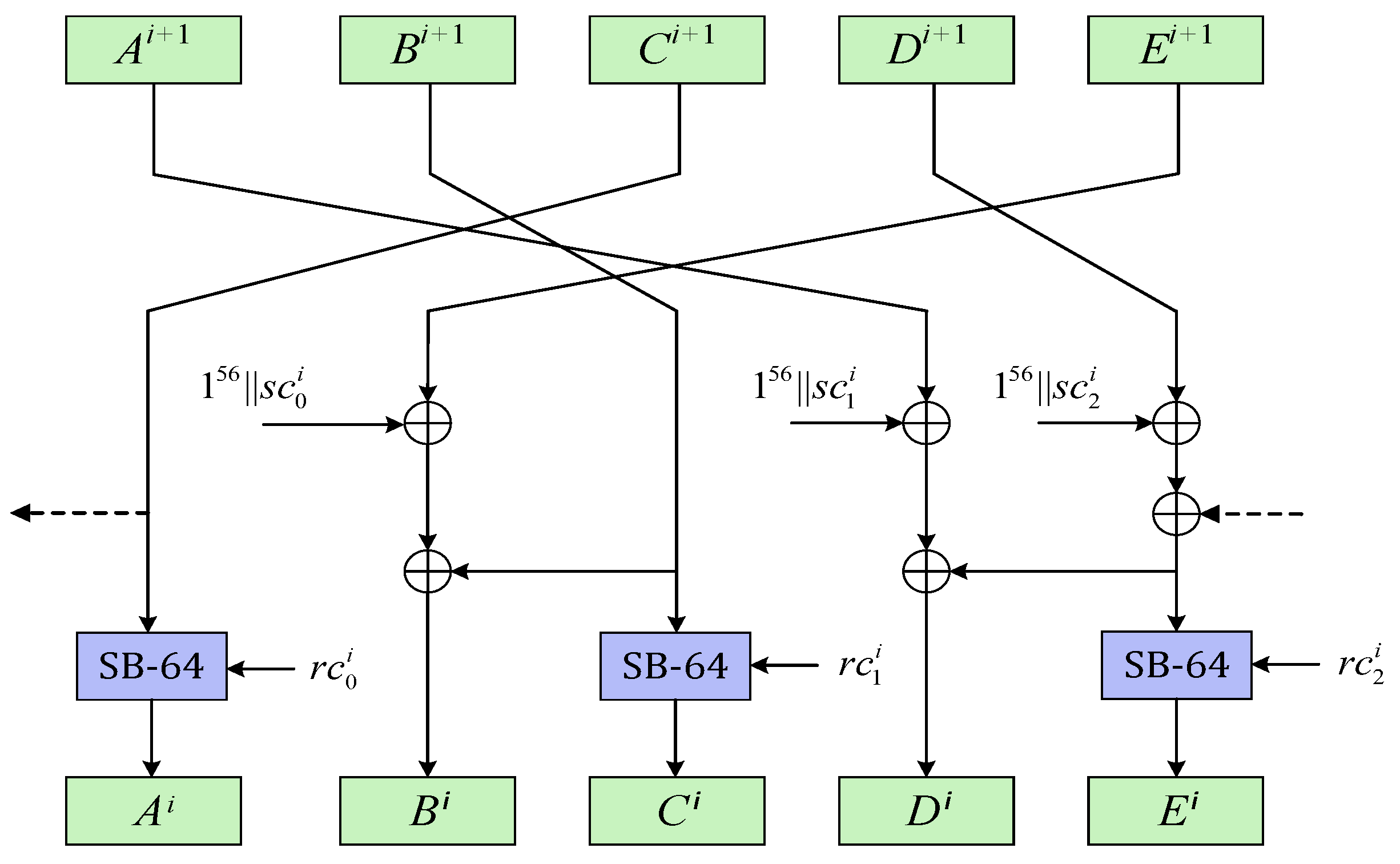
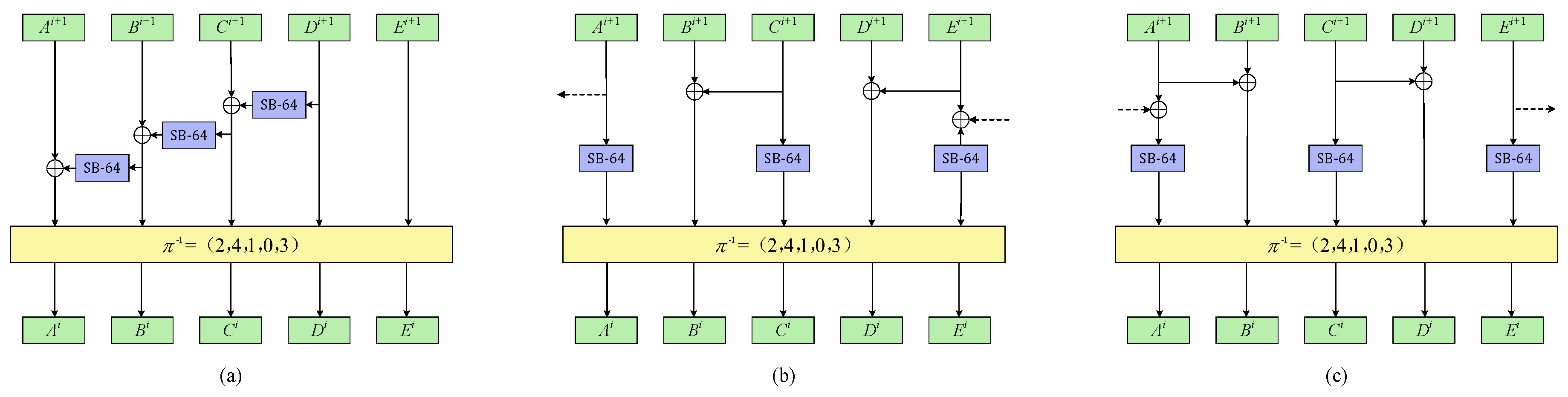
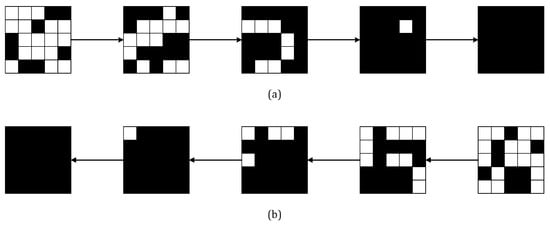
The encryption characteristic matrix of ACE permutation is , which we denote as . This matrix reaches after 5 rounds of iteration. The structure of decryption permutation is depicted in Figure 3, from which we know the decryption characteristic matrix of ACE is , denoted by . reaches after 5 rounds of iteration as well. Let be a differential of probability 1 from the encryption direction and be a differential of probability 1 from the decryption direction. If the i-th sub-block of is active whereas the i-th sub-block of is 0, then there is with probability 1. Then is an impossible differential. For ACE permutation, there will not be zero difference after 5 rounds in the encryption/decryption direction, which means there will not be contradiction in the middle. □

Figure 3.
ACE Inverse Step Function.
Theorem 3.
and are two 8-step impossible differentials of ACE.
Proof.
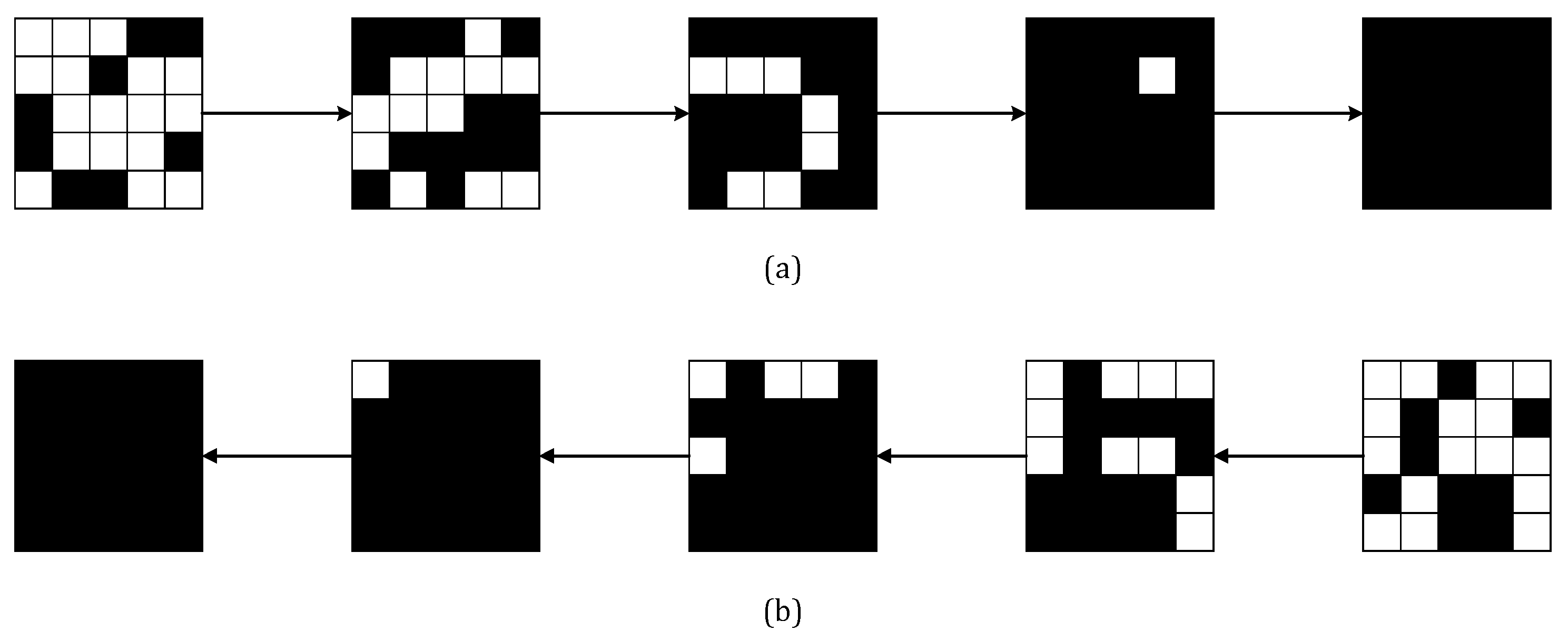
The transformation of encryption/decryption characteristic matrix of ACE is depicted in Figure 4. We can see that the entry of decryption characteristic matrix remains zero one step before . For encryption characteristic matrix, it is the entry that remains zero, i.e., cannot affect and cannot affect . If we set active and the sub-blocks of except to zero, denoting it by , then after 4 steps, the output difference will be . Similarly, we set active and the sub-blocks of except to zero, denoting it by . The differential characteristic from is depicted below:

Figure 4.
Characteristic matrix’s transformation. White box denotes an entry equaled to 1, while black box denotes an entry equaled to 0. (a) The transformation of ACE’s encryption characteristic matrix; (b) The transformation of ACE’s decryption characteristic matrix.
It is obvious that has a contradiction with in the first sub-block, then is an 8-step impossible differential of ACE. The proof of is of the same method. □
3.2. An Automatic Impossible Differential Characteristic Searching Tool
In this section, we propose our automatic impossible differential searching algorithm. By this algorithm, one can both get the number of the longest impossible differential and the actual differential characteristic.
From Section 3.1 we know that there are three circumstances of the sub-blocks of state difference: zero, active and uncertain. In these three circumstances, the value of the corresponding state difference vector’s sub-block are 0, 1 and n. The two intermediate state difference and are unequal with probability 1 when there is i such that the i-th sub-block of one is active while the i-th block of the other is zero. Equally, considering the corresponding difference vectors, this means the i-th sub-block of one equals to 1, whereas the i-th sub-block of the other equals to 0.
Theorem 4.
For two intermediate difference vector and , the existence of an i-th sub-block of equaled to 1 implies the existence of an impossible differential.
The proof of Theorem 4 is simple. Because the i-th sub-block of equals to 1 if and only if the i-th sub-block of / equals to 1 and the i-th sub-block of / equals to 0. Both two occasions imply a contradiction in the middle round.
According to Theorem 4, we can tell the existence of impossible differential by observing the sum of two intermediate difference vectors. If there is a sub-block of the sum vector equaled to 1, then there is a contradiction in the middle, which leads to an impossible differential. If not, it means there is no contradiction and no structural impossible differentials.
Theorem 5.
For ACE, there is no impossible differential longer than 9 steps.
Theorem 5 can be proved by practical computer experiment. Using the automatic searching algorithm, we find no 9-step structural impossible differential for ACE permutation. This is the security margin of ACE permutation against impossible differential cryptanalysis. If taking more details of ACE permutation into consideration, such as the details of ,we may get impossible differentials longer than that. Algorithm 1 provides the pseudo-code of the automatic algorithm for searching step impossible differentials.
| Algorithm 1. Automatic algorithm for searching step impossible differentials. |
| Input: The encryption characteristic matrix A; The decryption characteristic matrix B; The step number m from the encryption direction; The step number n from the decryption direction; Output: The ()-step impossible differential
|
4. Security of ACE Permutation
In this section, we use our algorithm to automatically try every possible word permutation and search for their longest impossible differentials. We give the safest word permutation against impossible differential attack using the improved automatic algorithm. Then we change the structure of word XORing and search for the longest impossible differentials of them. By our automatic algorithm, we give the optimal word permutation, which is , and a safer word XOR structure of ACE.
4.1. Security of Word Permutations
The step function of ACE consists of word permutation and word XORing. Hence, the characteristic matrix can also be divided to the multiplication of two matrices, and the multiplication rule is the same as the self-multiplication of characteristic matrix.
According to Definition 4, we divide the encryption/decryption characteristic matrix into “XOR” matrix and “Pbox” matrix. We fix “XOR” and traverse all possible “Pbox”. Within every possible “Pbox”, we search for the longest impossible differential, obtaining the optimal word permutation who has the minimum length of impossible differentials. Algorithm 2 depicts the pseudo-code of the automatic algorithm searching for the safest permutation.
| Algorithm 2. Automatic algorithm searching for the safest permutation. |
| Input: The XOR matrix S; The step number r Output: The characteristic matrix P of the safest permutation “Pbox”
|
4.2. Security of XOR Structures
Different XOR structures will bring different diffusion property of the cipher. If chosen improperly, it may give chance for people to attack the cipher. Hence, in this section, we change the structure of XORing in ACE and test the security margin of them, to see if the original one is the safest.
In ACE, the state is divided into five words. The three of them will be transformed by and they are structural equivalent. In this section, we consider the cases that the transformed three words being XORed to another three words and give three XOR structures that are safer than the original one as Figure 5 shows.
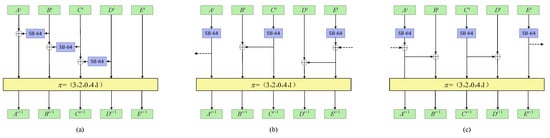
Figure 5.
Three new ways of XOR. (a) structure; (b) structure; (c) structure.
To test the diffusion property and security margin against impossible differential cryptanalysis, we depict the decryption algorithm corresponding to the three cases in Figure 6 and analyze their properties prospectively.
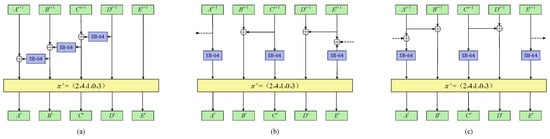
Figure 6.
The inverse structure of three new ways of XOR. (a) structure; (b) structure; (c) structure.
(1) The encryption characteristic matrix of (a) structure is . It reaches in 5 steps whereas the decryption characteristic matrix of structure (a), which is , reaches in 4 steps. This means there is also no 9-step impossible differential for (a) structure. By using the automatic algorithm, we search for all the possibilities, finding no 8-step impossible differential but one 7-step impossible differential of (a) structure.
(1) The encryption characteristic matrix of (b) structure is . It reaches in 5 steps whereas the decryption characteristic matrix of structure (b), which is , reaches in 4 steps. This means there is no 9-step impossible differential for (b) structure. By using the automatic algorithm, we search for all the possibilities, finding no 8-step impossible differential but several 7-step impossible differentials of (b) structure.
(3) The encryption characteristic matrix of (c) structure is . It reaches in only 3 steps whereas the decryption characteristic matrix of structure (c), which is , reaches in 6 steps. This means there is also no 9-step impossible differential for (c) structure. By using the automatic algorithm, we search for all the possibilities and find several 8-step impossible differential of (c) structure.
We conclude and compare these three new structures in Table 2, where m denotes the step number of reaching from the encryption direction and n denotes the step number of reaching from the decryption direction.

Table 2.
Properties of structures.
In Table 2, it is depicted that structure (a) reaches after 5 steps from the encryption direction. From the decryption direction, structure (a) reaches after 5 steps. This implies that the longest impossible differential of structure (a) may be of 8 steps. However, by using the automatic algorithm, we search for all the possibilities, finding no 8-step impossible differential but one 7-step impossible differential. For structure (b), it reaches after 5 and 4 steps from the encryption direction and decryption direction respectively while the longest impossible differential of it is of 7 steps. As for structure (c), it reaches after 3 and 6 steps from the encryption direction and decryption direction respectively while the longest impossible differential of it is of 8 steps.
From Table 2, we can observe that structure (a), (b) and (c) all have better diffusion property than ACE. Structure (a) and (b) both have higher security margin than (c) and ACE while the (a) structure have the least amount of 7-step impossible differentials, then we can conclude that among them, structure (a) is the optimal XOR structure for ACE permutation against impossible differential cryptanalysis.
5. Conclusions
In this paper, we focused on the impossible differential attack against ACE permutation, which is the core component of ACE algorithm. We used the method of characteristic matrix and built an automatic algorithm that can be used to search for the longest structural impossible differentials. We gave the security margin of ACE permutation against impossible differential cryptanalysis, which is 10, and searched the impossible differentials of ACE permutation, proving that ACE permutation does not have impossible differentials longer than 9 steps. We further improved our algorithm to search for impossible differentials for all possible word permutations and give a safer permutation . This improved algorithm can be used by designers to choose permutation with highest security margin against impossible differential cryptanalysis.
Author Contributions
Formal analysis, J.L.; Supervision, L.Q.; Methodology, J.L. and G.L.; Writing—original draft preparation, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (No. 2017YFB0802000) and the National Natural Science Foundation of China (No. 61702537).
Conflicts of Interest
The authors declare that they have no conflict of interest regarding this work.
Abbreviations
| Notation | Description |
| word | a 64-bit binary string |
| step | one round of ACE |
| s | number of steps |
| nonlinear function of ACE permutation | |
| encryption characteristic matrix of ACE permutation | |
| decryption characteristic matrix of ACE permutation | |
| the state difference in the i-th step of encryption | |
| the state difference in the i-th step of decryption | |
| the difference vector of | |
| the difference vector of | |
| , , and | the j-th sub-block of , , and |
References
- Turan, M.S.; McKay, K.A.; Çalık, Ç.; Chang, D.; Bassham, L. Status Report on the First Round of the NIST Lightweight Cryptography Standardization Process; NIST Interagency/Internal Rep. (NISTIR); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019.
- Aagaard, M.; AlTawy, R.; Gong, G.; Mandal, K.; Rohit, R. ACE: An Authenticated Encryption and Hash Algorithm; Submission to NIST-LWC; ACE: Oak Brook, IL, USA, 2019. [Google Scholar]
- Biham, E.; Shamir, A. Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 1991, 4, 3–72. [Google Scholar] [CrossRef]
- Knudsen, L. DEAL-a 128-bit block cipher. Complexity 1998, 258, 216. [Google Scholar]
- Biham, E.; Biryukov, A.; Shamir, A. Cryptanalysis of Skipjack reduced to 31 rounds using impossible differentials. J. Cryptol. 2005, 18, 291–311. [Google Scholar] [CrossRef]
- Biham, E.; Biryukov, A.; Shamir, A. Miss in the Middle Attacks on IDEA and Khufu. In International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 1999; pp. 124–138. [Google Scholar]
- Dunkelman, O.; Keller, N. An improved impossible differential attack on MISTY1. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2008; pp. 441–454. [Google Scholar]
- Lu, J.; Dunkelman, O.; Keller, N.; Kim, J. New impossible differential attacks on AES. In International Conference on Cryptology in India; Springer: Berlin/Heidelberg, Germany, 2008; pp. 279–293. [Google Scholar]
- Li, R.; Sun, B.; Zhang, P.; Li, C. New Impossible Differential Cryptanalysis of ARIA. IACR Cryptol. ePrin Arch. 2008, 2008, 227. [Google Scholar]
- Wu, W.L.; Zhang, W.T.; Feng, D.G. Impossible differential cryptanalysis of reduced-round ARIA and Camellia. J. Comput. Sci. Technol. 2007, 22, 449–456. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, W.; Feng, D. New results on impossible differential cryptanalysis of reduced AES. In International Conference on Information Security and Cryptology; Springer: Berlin/Heidelberg, Germany, 2007; pp. 239–250. [Google Scholar]
- Zhang, L.; Wu, W.; Park, J.H.; Koo, B.W.; Yeom, Y. Improved impossible differential attacks on large-block Rijndael. In International Conference on Information Security; Springer: Berlin/Heidelberg, Germany, 2008; pp. 298–315. [Google Scholar]
- Kim, J.; Hong, S.; Sung, J.; Lee, S.; Lim, J.; Sung, S. Impossible differential cryptanalysis for block cipher structures. In International Conference on Cryptology in India; Springer: Berlin/Heidelberg, Germany, 2003; pp. 82–96. [Google Scholar]
- Aoki, K.; Ohta, K. Strict evaluation of the maximum average of differential probability and the maximum average of linear probability. Ieice Trans. Fundam. Electron. Commun. Comput. Sci. 1997, 80, 2–8. [Google Scholar]
- Sun, B.; Liu, M.; Guo, J.; Rijmen, V.; Li, R. Provable Security Evaluation of Structures Against Impossible Differential and Zero Correlation Linear Cryptanalysis. In EUROCRYPT (1); Springer: Berlin/Heidelberg, Germany, 2016; pp. 196–213. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).