Fractional-Order Thermoelastic Wave Assessment in a Two-Dimensional Fiber-Reinforced
Abstract
:1. Introduction
2. Mathematical Model
3. Initial and Boundary Conditions
4. Method of Solution
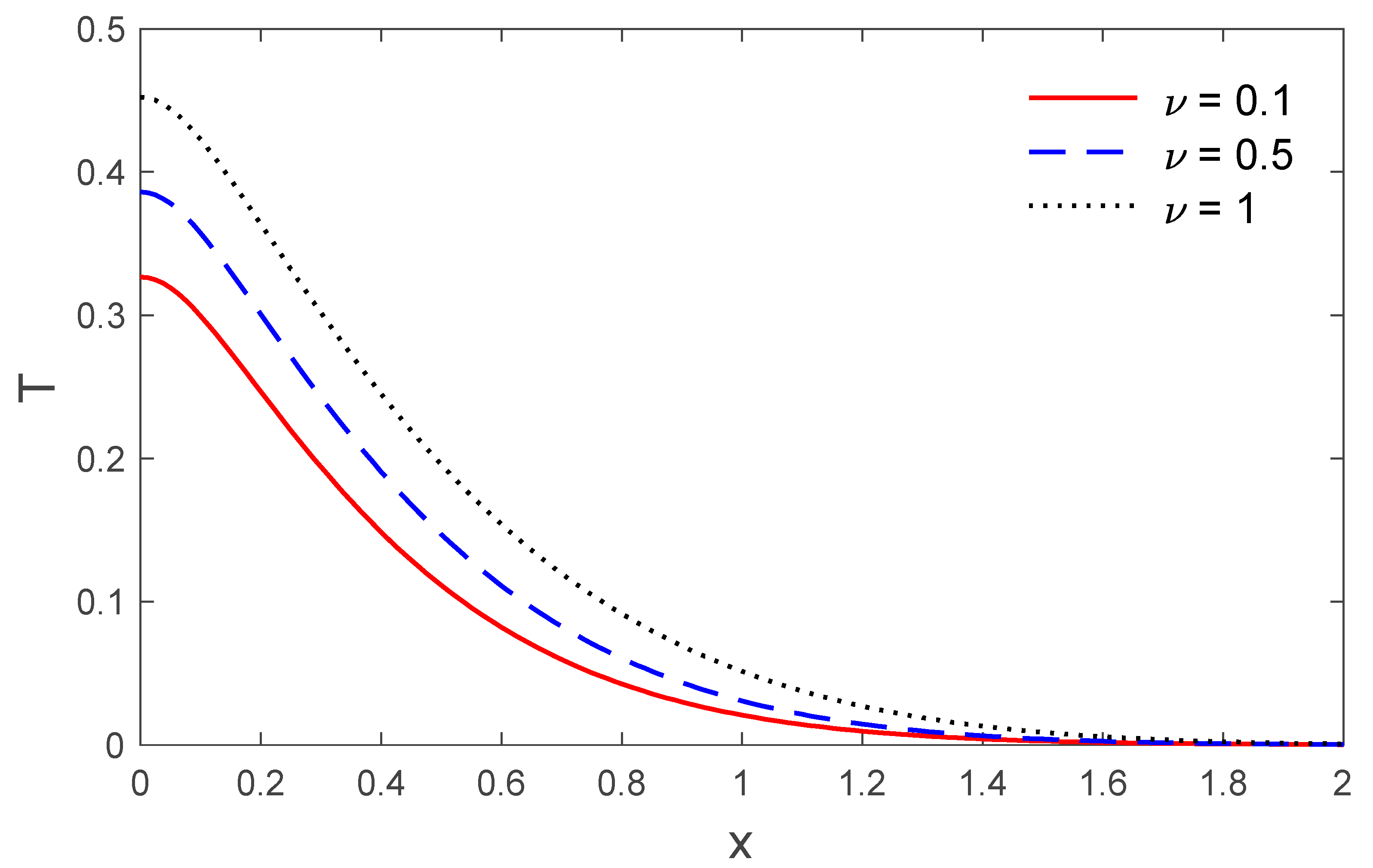
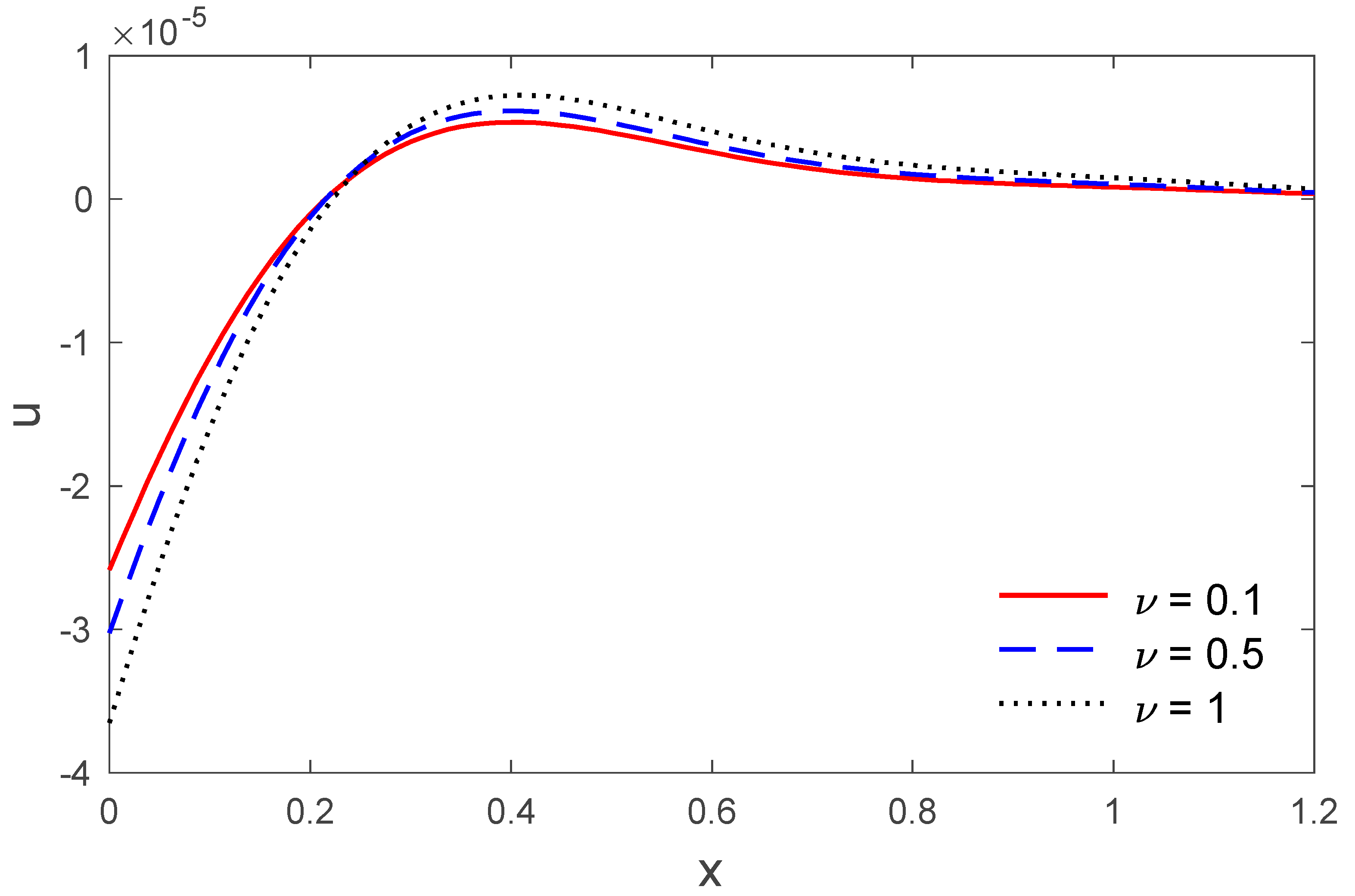
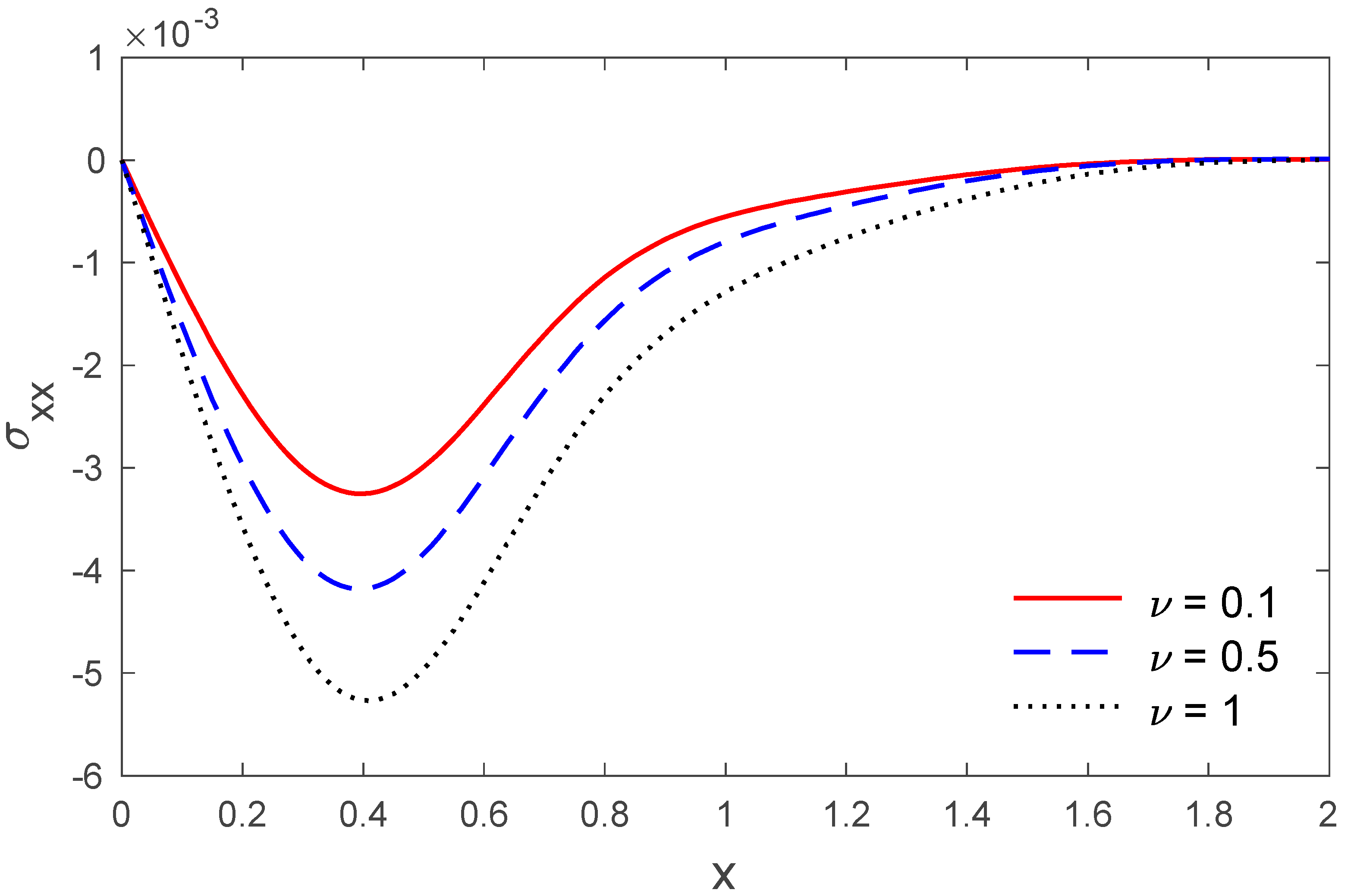
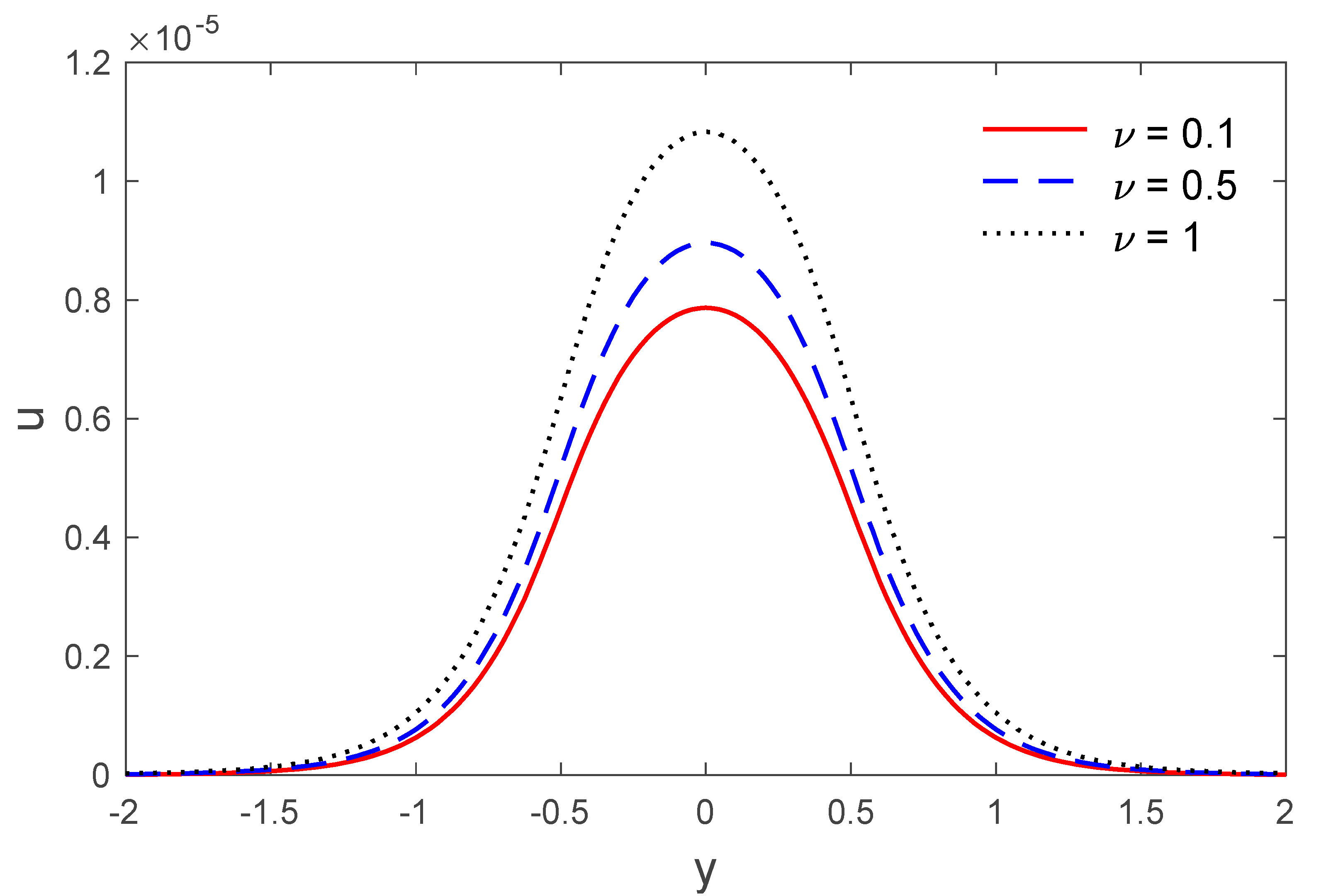
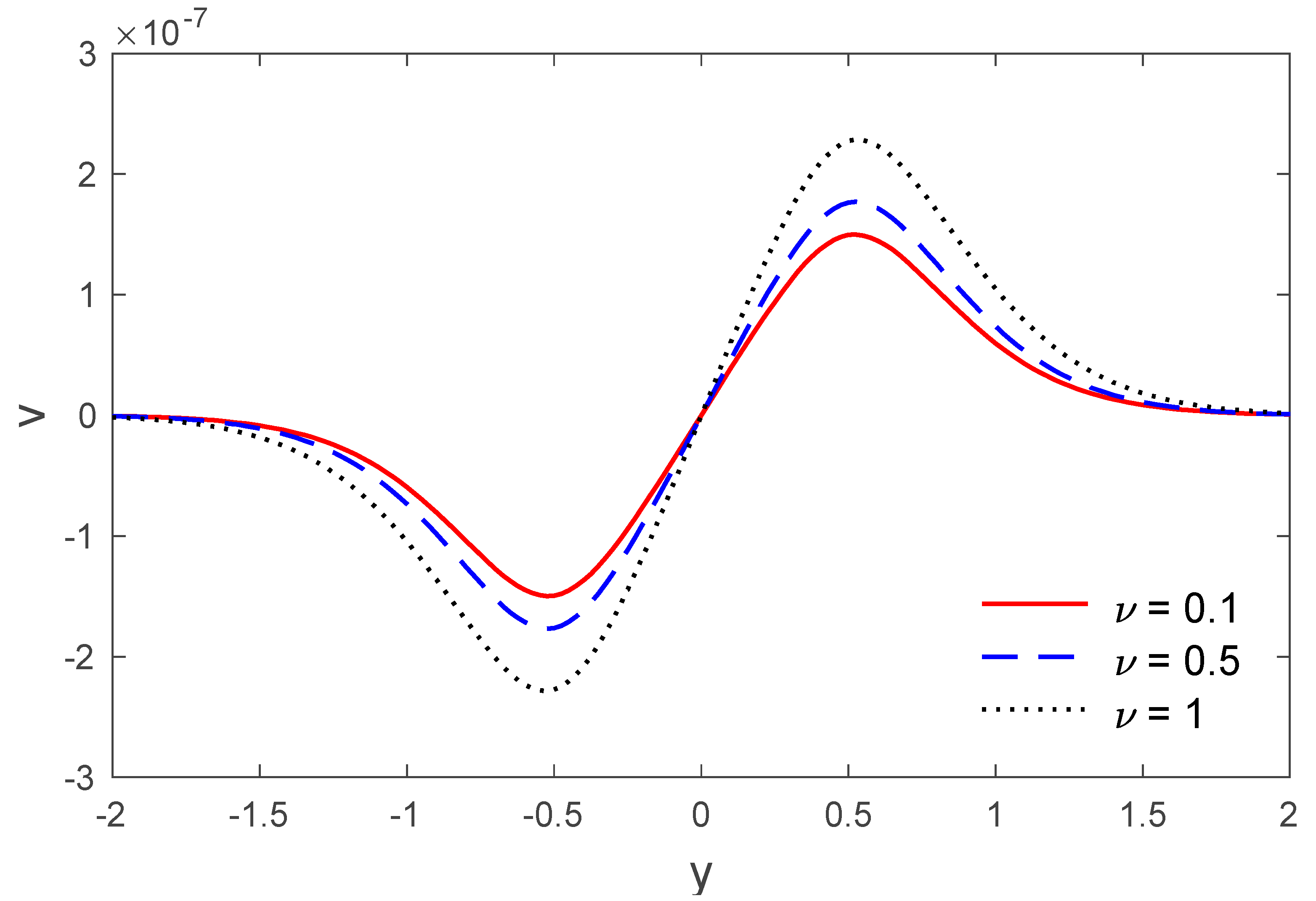
5. Numerical Result and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| are the components of displacement, | |
| , | is the increment in temperature, |
| is the medium density, | |
| is the reference temperature, | |
| are the elastic constants, | |
| are the components of stresses, | |
| is the specific heat at constant strain, | |
| are the reinforced anisotropic elastic parameters, | |
| are the components of vector where , | |
| is the thermal conductivity, | |
| is the thermal relaxation time, | |
| is the fractional parameter, where cover two types of conductivity, for normal conductivity, and for low conductivity | |
| is a constant | |
| is the Heaviside unit function | |
| is the pulse heat flux characteristic time | |
| , | are the number of components |
References
- Spencer, A.J.M. Deformations of Fibre-Reinforced Materials; Clarendon Press: Oxford, UK, 1972. [Google Scholar]
- Belfield, A.; Rogers, T.; Spencer, A. Stress in elastic plates reinforced by fibres lying in concentric circles. J. Mech. Phys. Solids 1983, 31, 25–54. [Google Scholar] [CrossRef]
- Verma, P.; Rana, O. Rotation of a circular cylindrical tube reinforced by fibres lying along helices. Mech. Mater. 1983, 2, 353–359. [Google Scholar] [CrossRef]
- Verma, P. Magnetoelastic shear waves in self-reinforced bodies. Int. J. Eng. Sci. 1986, 24, 1067–1073. [Google Scholar] [CrossRef]
- Sengupta, P.; Nath, S. Surface waves in fibre-reinforced anisotropic elastic media. Sadhana 2001, 26, 363–370. [Google Scholar] [CrossRef] [Green Version]
- Hashin, Z.; Rosen, B.W. The elastic moduli of fiber-reinforced materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Singh, B.; Singh, S.J. Reflection of plane waves at the free surface of a fibre-reinforced elastic half-space. Sadhana 2004, 29, 249–257. [Google Scholar] [CrossRef] [Green Version]
- Chattopadhyay, A.; Choudhury, S. Propagation, reflection and transmission of magnetoelastic shear waves in a self-reinforced medium. Int. J. Eng. Sci. 1990, 28, 485–495. [Google Scholar] [CrossRef]
- Nowacki, W. Dynamic Problems of Thermoelasticity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Lotfy, K.; Othman, M.I.A. The effect of magnetic field on 2-D problem for a mode-I Crack of a fiber-reinforced in generalized Thermoelasticity. Int. J. Thermophys. 2014, 35, 154–174. [Google Scholar] [CrossRef]
- Lotfy, K. Mode-I crack in a two-dimensional fibre-reinforced generalized thermoelastic problem. Chin. Phys. B 2012, 21, 014209. [Google Scholar] [CrossRef]
- Prasad, R.; Das, S.; Mukhopadhyay, S. A two-dimensional problem of a mode I crack in a type III thermoelastic medium. Math. Mech. Solids 2013, 18, 506–523. [Google Scholar] [CrossRef]
- Sherief, H.H.; El-Maghraby, N.M. A mode-I crack problem for an infinite space in generalized thermoelasticity. J. Therm. Stresses 2005, 28, 465–484. [Google Scholar] [CrossRef]
- Sherief, H.H.; El-Maghraby, N.M. An internal penny-shaped crack in an infinite thermoelastic solid. J. Therm. Stresses 2003, 26, 333–352. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach to fractional order generalized magneto-thermoelastic medium subjected to moving heat source. J. Magn. Magn. Mater. 2015, 377, 452–459. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I.; Marin, M. A GL Model on Thermo-Elastic Interaction in a Poroelastic Material Using Finite Element Method. Symmetry 2020, 12, 488. [Google Scholar] [CrossRef] [Green Version]
- Marin, M.; Craciun, E.-M.; Pop, N. Considerations on mixed initial-boundary value problems for micropolar porous bodies. Dyn. Syst. Appl. 2016, 25, 175–196. [Google Scholar]
- Sadowski, T.; Marsavina, L.; Craciun, E.-M.; Kneć, M. Modelling and experimental study of parallel cracks propagation in an orthotropic elastic material. Comput. Mater. Sci. 2012, 52, 231–235. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Thermal shock problem for a fiber-reinforced anisotropic half-space placed in a magnetic field via GN model. Appl. Math. Comput. 2014, 246, 482–490. [Google Scholar]
- Abbas, I.A.; Zenkour, A.M. The Effect of Rotation and Initial Stress on Thermal Shock Problem for a Fiber-Reinforced Anisotropic Half-Space Using Green-Naghdi Theory. J. Comput. Theor. Nanosci. 2014, 11, 331–338. [Google Scholar] [CrossRef]
- Abbas, I.A. A GN model for thermoelastic interaction in an unbounded fiber-reinforced anisotropic medium with a circular hole. Appl. Math. Lett. 2013, 26, 232–239. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, N.; Lahiri, A. The effect of gravity field on the plane waves in a fiber-reinforced two-temperature magneto-thermoelastic medium under lord-shulman theory. J. Therm. Stresses 2013, 36, 895–914. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Said, S.M. Plane waves of a fiber-reinforcement magneto-thermoelastic comparison of three different theories. Int. J. Thermophys. 2013, 34, 366–383. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Lotfy, K. The effect of magnetic field and rotation of the 2-D problem of a fiber-reinforced thermoelastic under three theories with influence of gravity. Mech. Mater. 2013. [Google Scholar] [CrossRef]
- Gupta, R.R.; Gupta, R.R. Analysis of wave motion in an anisotropic initially stressed fiberreinforced thermoelastic medium. Earthq. Struct. 2013, 4, 1–10. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Zenkour, A.M. The effect of fractional thermoelasticity on a two-dimensional problem of a mode I crack in a rotating fiber-reinforced thermoelastic medium. Chin. Phys. B 2013, 22, 108102. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Said, S.M. The effect of mechanical force on generalized thermoelasticity in a fiber-reinforcement under three theories. Int. J. Thermophys. 2012, 33, 1082–1099. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, R.R. Study of wave motion in an anisotropic fiber-reinforced thermoelastic solid. J. Solid Mech. 2010, 2, 91–100. [Google Scholar]
- Marin, M.; Vlase, S.; Ellahi, R.; Bhatti, M. On the partition of energies for the backward in time problem of thermoelastic materials with a dipolar structure. Symmetry 2019, 11, 863. [Google Scholar] [CrossRef] [Green Version]
- Marin, M.; Ellahi, R.; Chirilă, A. On solutions of Saint-Venant’s problem for elastic dipolar bodies with voids. Carpathian J. Math. 2017, 33, 219–232. [Google Scholar]
- Sadowski, T.; Marsavina, L.; Peride, N.; Craciun, E.-M. Cracks propagation and interaction in an orthotropic elastic material: Analytical and numerical methods. Comput. Mater. Sci. 2009, 46, 687–693. [Google Scholar] [CrossRef]
- Abbas, I.A.; Marin, M. Analytical solution of thermoelastic interaction in a half-space by pulsed laser heating. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 87, 254–260. [Google Scholar] [CrossRef]
- Abbas, I.A.; Kumar, R. Deformation due to thermal source in micropolar generalized thermoelastic half-space by finite element method. J. Comput. Theor. Nanosci. 2014, 11, 185–190. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Mohamed, R.; Abbas, I.A.; Abo-Dahab, S. Finite element analysis of hydromagnetic flow and heat transfer of a heat generation fluid over a surface embedded in a non-Darcian porous medium in the presence of chemical reaction. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1385–1395. [Google Scholar] [CrossRef]
- Abbas, I.A. Nonlinear transient thermal stress analysis of thick-walled FGM cylinder with temperature-dependent material properties. Meccanica 2014, 49, 1697–1708. [Google Scholar] [CrossRef]
- Abbas, I.A.; El-Amin, M.; Salama, A. Effect of thermal dispersion on free convection in a fluid saturated porous medium. Int. J. Heat Fluid Flow 2009, 30, 229–236. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. A generalized thermoelasticity problem of an annular cylinder with temperature-dependent density and material properties. Int. J. Mech. Sci. 2014, 84, 54–60. [Google Scholar] [CrossRef]
- Marin, M. Lagrange identity method for microstretch thermoelastic materials. J. Math. Anal. Appl. 2010, 363, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Marin, M.; Nicaise, S. Existence and stability results for thermoelastic dipolar bodies with double porosity. Contin. Mech. Thermodyn. 2016, 28, 1645–1657. [Google Scholar] [CrossRef]
- Das, N.C.; Lahiri, A.; Giri, R.R. Eigenvalue approach to generalized thermoelasticity. Indian J. Pure Appl. Math. 1997, 28, 1573–1594. [Google Scholar]
- Abbas, I.A. Eigenvalue approach in a three-dimensional generalized thermoelastic interactions with temperature-dependent material properties. Comput. Math. Appl. 2014, 68, 2036–2056. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach for an unbounded medium with a spherical cavity based upon two-temperature generalized thermoelastic theory. J. Mech. Sci. Technol. 2014, 28, 4193–4198. [Google Scholar] [CrossRef]
- Abbas, I.A. A dual phase lag model on thermoelastic interaction in an infinite fiber-reinforced anisotropic medium with a circular hole. Mech. Based Des. Struct. Mach. 2015, 43, 501–513. [Google Scholar] [CrossRef]
- Abbas, I.A. A two-dimensional problem for a fibre-reinforced anisotropic thermoelastic half-space with energy dissipation. Sadhana Acad. Proc. Eng. Sci. 2011, 36, 411–423. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horrigue, S.; Abbas, I.A.
Fractional-Order Thermoelastic Wave Assessment in a Two-Dimensional Fiber-Reinforced
Horrigue S, Abbas IA.
Fractional-Order Thermoelastic Wave Assessment in a Two-Dimensional Fiber-Reinforced
Horrigue, Samah, and Ibrahim A. Abbas.
2020. "Fractional-Order Thermoelastic Wave Assessment in a Two-Dimensional Fiber-Reinforced




