Delay-Dependent and Order-Dependent Guaranteed Cost Control for Uncertain Fractional-Order Delayed Linear Systems
Abstract
1. Introduction
2. Preliminary nOtions and Problem Description
3. Main Results
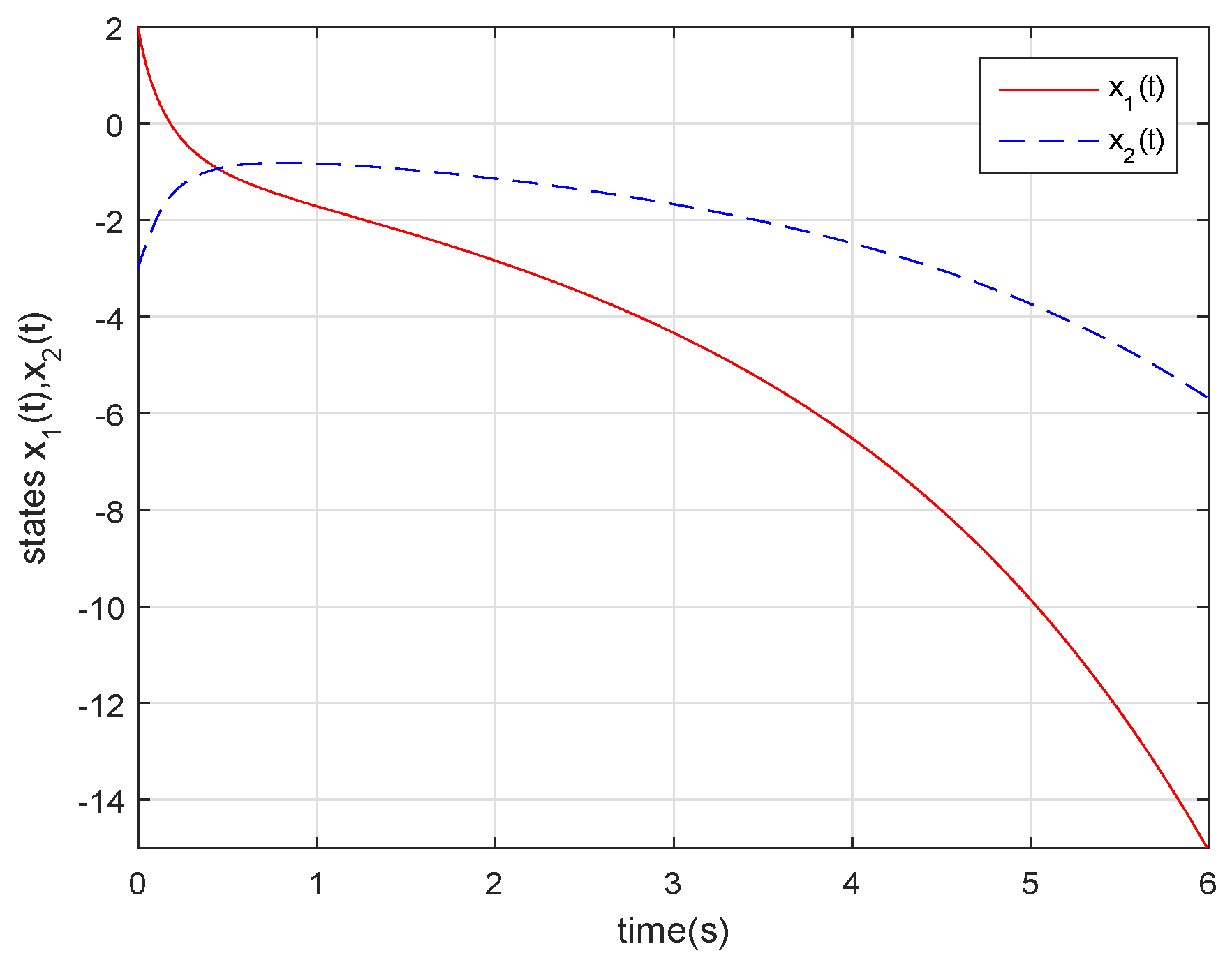
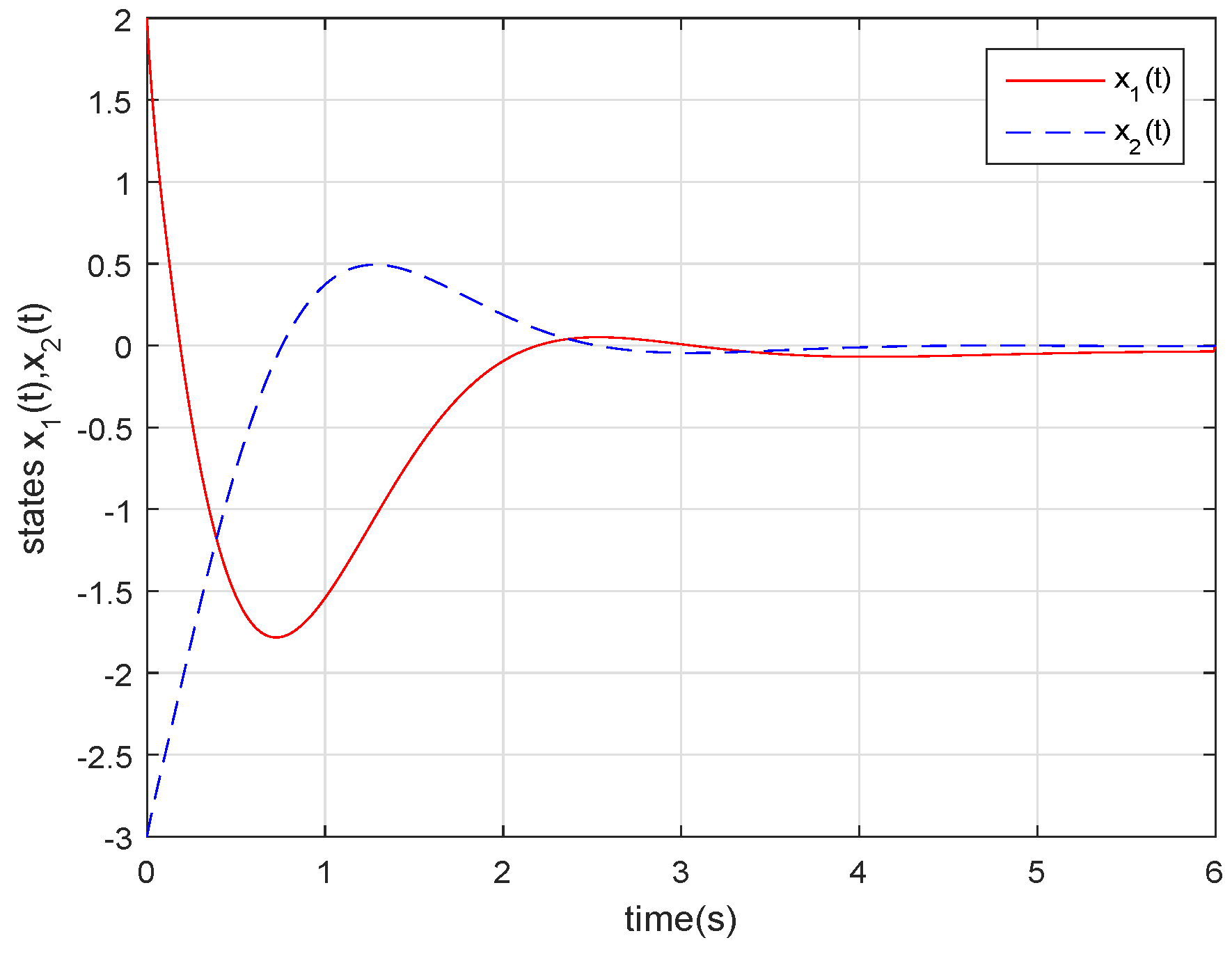
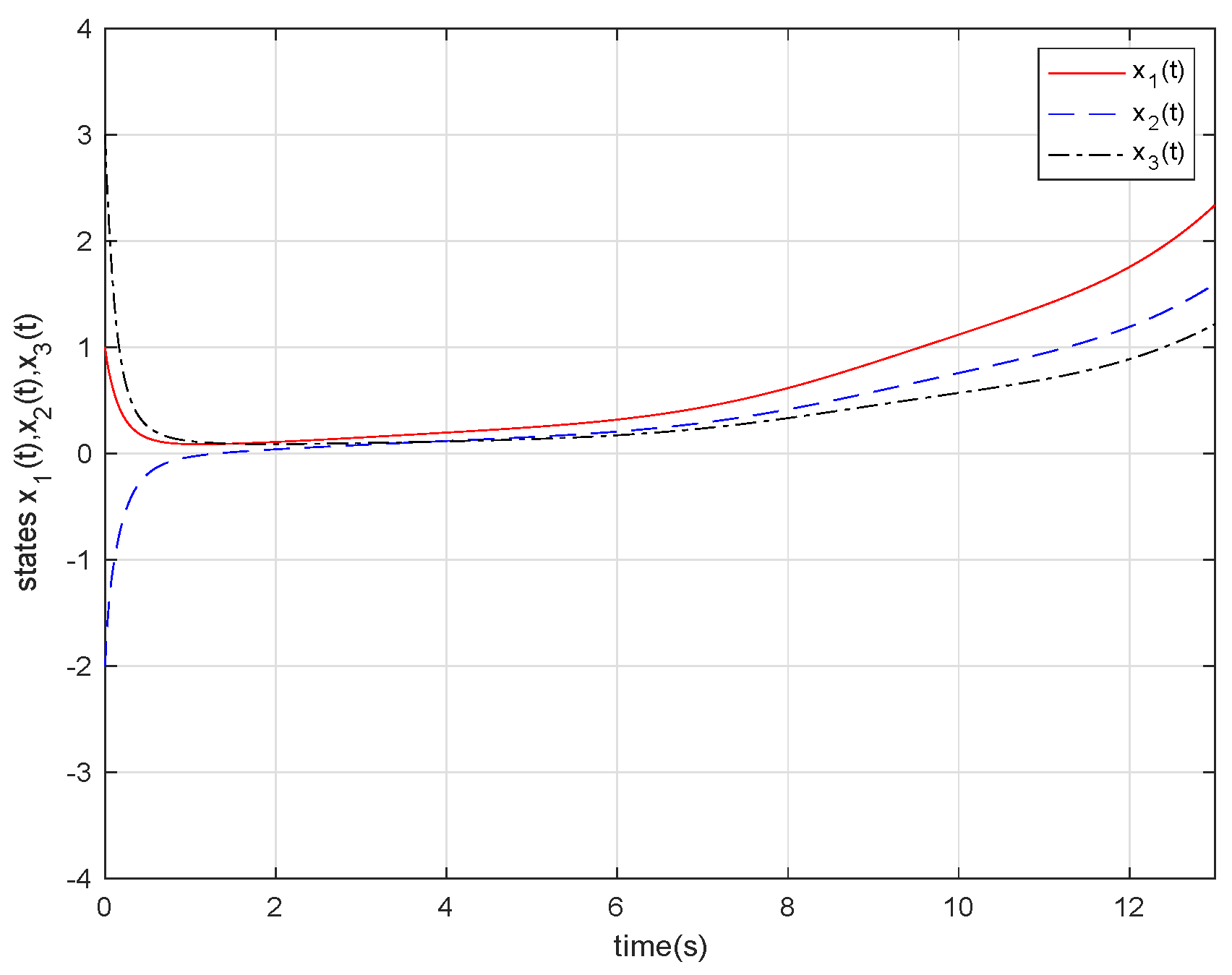
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer: Berlin, Germany, 2017. [Google Scholar]
- Yang, X. General Fractional Derivatives: Theory, Methods and Applications; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Daftardar-Gejji, V. Fractional Calculus and Fractional Differential Equations; Springer: Berlin, Germany, 2019. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Laskin, N. Fractional Quantum Mechanics; World Scientific: Singapore, 2018. [Google Scholar]
- West, B. Fractional Calculus View of Complexity: Tomorrows Science; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Singh, H.; Kumar, D.; Baleanu, D. Methods of Mathematical Modelling: Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Luo, Y.; Chen, Y. Fractional Order Motion Controls; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific: Singapore, 2015; Volume 4. [Google Scholar]
- Chen, L.; Li, T.; Chen, Y.; Wu, R.; Ge, S. Robust passivity and feedback passification of a class of uncertain fractional-order linear systems. Int. J. Syst. Sci. 2019, 50, 1149–1162. [Google Scholar] [CrossRef]
- Xue, D. Fractional-Order Control Systems: Fundamentals and Numerical Implementations; De Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Ge, F.; Chen, Y.; Kou, C. Regional Analysis of Time-Fractional Diffusion Processes; Springer: Berlin, Germany, 2018. [Google Scholar]
- Lan, Y.H.; Huang, H.X.; Zhou, Y. Observer-based robust control of a(1 ≤ a < 2) fractional-order uncertain systems: A linear matrix inequality approach. IET Control Theory Appl. 2012, 6, 229–234. [Google Scholar]
- Badri, P.; Sojoodi, M. Stability and stabilization of fractional-order systems with different derivative orders: An LMI approach. Asian J. Control 2019, 21, 2270–2279. [Google Scholar] [CrossRef]
- Chen, L.; Wu, R.; He, Y.; Yin, L. Robust stability and stabilization of fractional-order linear systems with polytopic uncertainties. Appl. Math. Comput. 2015, 257, 274–284. [Google Scholar] [CrossRef]
- Shahri, E.S.A.; Alfi, A.; Machado, J.T. Lyapunov method for the stability analysis of uncertain fractional-order systems under input saturation. Appl. Math. Model. 2020, 81, 663–672. [Google Scholar] [CrossRef]
- Mohsenipour, R.; Liu, X. Robust D-stability test of LTI general fractional order control systems. IEEE/CAA J. Autom. Sin. 2020, 7, 853–864. [Google Scholar] [CrossRef]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Ma, Y.; Lu, J.; Chen, W. Robust stability and stabilization of fractional order linear systems with positive real uncertainty. ISA Trans. 2014, 53, 199–209. [Google Scholar] [CrossRef]
- Dinh, C.H.; Mai, V.T.; Duong, T.H. New Results on Stability and Stabilization of Delayed Caputo Fractional Order Systems with Convex Polytopic Uncertainties. J. Syst. Sci. Complex. 2020, 33, 563–583. [Google Scholar] [CrossRef]
- Chang, S.; Peng, T. Adaptive guaranteed cost control of systems with uncertain parameters. IEEE Trans. Autom. Control 1972, 17, 474–483. [Google Scholar] [CrossRef]
- Chang, X.; Huang, R.; Park, J. Robust guaranteed cost control under digital communication channels. IEEE Trans. Ind. Inf. 2019, 16, 319–327. [Google Scholar] [CrossRef]
- Zong, G.; Ren, H. Guaranteed cost finite-time control for semi-Markov jump systems with event-triggered scheme and quantization input. Int. J. Robust Nonlinear Control 2019, 29, 5251–5273. [Google Scholar] [CrossRef]
- Li, Y. Optimal guaranteed cost control of linear uncertain system: an LMI approach. Control Theory Appl. 2000, 17, 423–428. [Google Scholar]
- Xu, H.; Teo, K.L.; Liu, X. Robust stability analysis of guaranteed cost control for impulsive switched systems. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 1419–1422. [Google Scholar]
- Li, H.; Wang, J.; Wu, L.; Lam, H.; Gao, Y. Optimal guaranteed cost sliding-mode control of interval type-2 fuzzy time-delay systems. IEEE Trans. Fuzzy Syst. 2018, 26, 246–257. [Google Scholar] [CrossRef]
- Xiang, C.; Petersen, I.R.; Dong, D. Performance analysis and coherent guaranteed cost control for uncertain quantum systems using small gain and Popov methods. IEEE Trans. Autom. Control 2016, 62, 1524–1529. [Google Scholar] [CrossRef]
- Yan, Z.; Park, J.H.; Zhang, W. Finite-time guaranteed cost control for Itô Stochastic Markovian jump systems with incomplete transition rates. Int. J. Robust Nonlinear Control 2017, 27, 66–83. [Google Scholar] [CrossRef]
- Gyurkovics, E. Guaranteed cost control of discrete-time uncertain systems with both state and input delays. Int. J. Control 2016, 89, 2073–2082. [Google Scholar] [CrossRef]
- Chen, W.; Xu, J.; Guan, Z. Guaranteed cost control for uncertain Markovian jump systems with mode-dependent time-delays. IEEE Trans. Autom. Control 2003, 48, 2270–2277. [Google Scholar] [CrossRef]
- Xu, S.; Lam, J.; Yang, C.; Verriest, E. An LMI approach to guaranteed cost control for uncertain linear neutral delay systems. Int. J. Robust Nonlinear Control 2003, 13, 35–53. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Liang, S.; Wu, R.; Chen, L. Adaptive pinning synchronization in fractional-order uncertain complex dynamical networks with delay. Physica A 2016, 444, 49–62. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J. Razumikhin-type stability theorems for functional fractional-order differential systems and applications. Appl. Math. Comput. 2015, 254, 63–69. [Google Scholar] [CrossRef]
- Xie, L. Output feedback H∞ control of systems with parameter uncertainty. Int. J. Control 1996, 63, 741–750. [Google Scholar] [CrossRef]
- Last, E. Linear Matrix Inequalities in System and Control Theory. Proc. IEEE 1994, 86, 2473–2474. [Google Scholar]
- Si-Ammour, A.; Djennoune, S.; Bettayeb, M. A sliding mode control for linear fractional systems with input and state delays. Commun. Nonlinear Sci. Numerical Simul. 2009, 14, 2310–2318. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, W. Fractional order nonlinear systems with delay in iterative learning control. Appl. Math. Comput. 2015, 257, 546–552. [Google Scholar]
- Geng, W.; Lin, C.; Chen, B. Observer-based stabilizing control for fractional-order systems with input delay. ISA Trans. 2020, 100, 103–108. [Google Scholar] [CrossRef]
- Choudhary, N.; Sivaramakrishnan, J.; Kar, I.N. Sliding mode control of uncertain fractional order systems with delay. Int. J. Control 2020, 93, 934–943. [Google Scholar] [CrossRef]
- Liu, H.; Xie, G.; Gao, Y. Containment control of fractional-order multi-agent systems with time-varying delays. J. Frankl. Inst. 2019, 356, 9992–10014. [Google Scholar] [CrossRef]
- Thuan, M.V.; Binh, T.N.; Huong, D.C. Finite-time guaranteed cost control of Caputo fractional-order neural networks. Asian J. Control 2020, 22, 696–705. [Google Scholar] [CrossRef]
- Thuan, M.V.; Huong, D.C. Robust guaranteed cost control for time-delay fractional-order neural networks systems. Optim. Control Appl. Methods 2019, 40, 613–625. [Google Scholar] [CrossRef]
- Chen, L.; Li, T.; Wu, R.; Lopes, A.M.; Machado, J.T.; Wu, K. Output-feedback-guaranteed cost control of fractional-order uncertain linear delayed systems. Comput. Appl. Math. 2020, 39, 1–18. [Google Scholar] [CrossRef]
- Church, K.E.; Liu, X. Cost-Effective Robust Stabilization and Bifurcation Suppression. SIAM J. Control Optim. 2019, 57, 2240–2268. [Google Scholar] [CrossRef]
- Xie, X.; Lam, J. Guaranteed cost control of periodic piecewise linear time-delay systems. Automatica 2018, 94, 274–282. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. An efficient approximate method for solving delay fractional optimal control problems. Nonlinear Dyn. 2016, 86, 1649–1661. [Google Scholar] [CrossRef]
- Wang, H.; Gu, Y.; Yu, Y. Numerical solution of fractional-order time-varying delayed differential systems using Lagrange interpolation. Nonlinear Dyn. 2019, 95, 809–822. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, F.; Chai, Y.; Chen, L.; Tenreiro Machado, J.A. Delay-Dependent and Order-Dependent Guaranteed Cost Control for Uncertain Fractional-Order Delayed Linear Systems. Mathematics 2021, 9, 41. https://doi.org/10.3390/math9010041
Qi F, Chai Y, Chen L, Tenreiro Machado JA. Delay-Dependent and Order-Dependent Guaranteed Cost Control for Uncertain Fractional-Order Delayed Linear Systems. Mathematics. 2021; 9(1):41. https://doi.org/10.3390/math9010041
Chicago/Turabian StyleQi, Fei, Yi Chai, Liping Chen, and José A. Tenreiro Machado. 2021. "Delay-Dependent and Order-Dependent Guaranteed Cost Control for Uncertain Fractional-Order Delayed Linear Systems" Mathematics 9, no. 1: 41. https://doi.org/10.3390/math9010041
APA StyleQi, F., Chai, Y., Chen, L., & Tenreiro Machado, J. A. (2021). Delay-Dependent and Order-Dependent Guaranteed Cost Control for Uncertain Fractional-Order Delayed Linear Systems. Mathematics, 9(1), 41. https://doi.org/10.3390/math9010041





