A New Smoothness Indicator of Adaptive Order Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws
Abstract
:1. Introduction
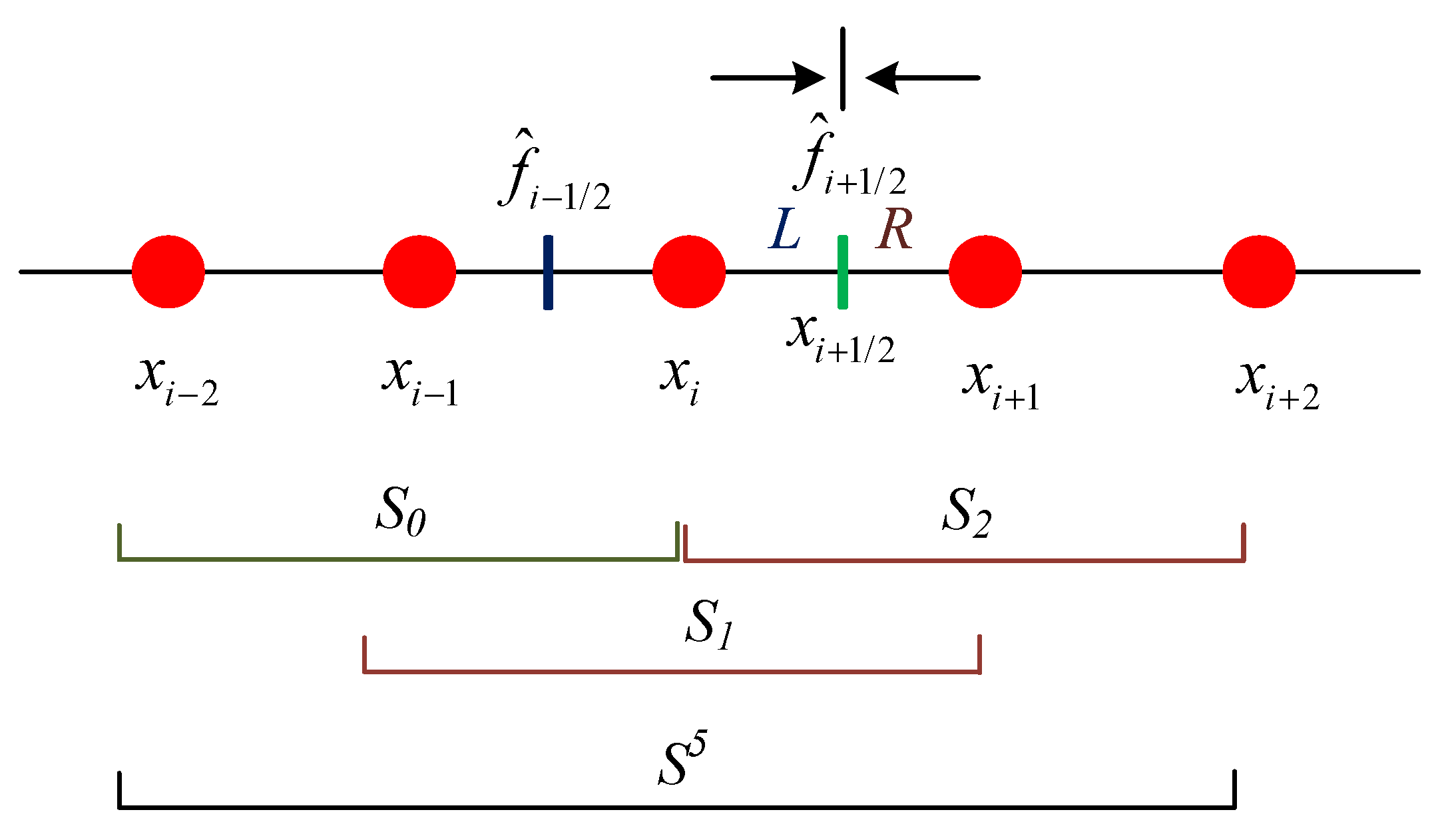
2. Finite Difference WENO Schemes
2.1. Fifth-Order WENO-JS Scheme
2.2. Fifth-Order WENO-Z Scheme
2.3. The Adaptive Order WENO Scheme
2.4. The WENO-AO-N Scheme
3. A New and Simple Smoothness Indicator
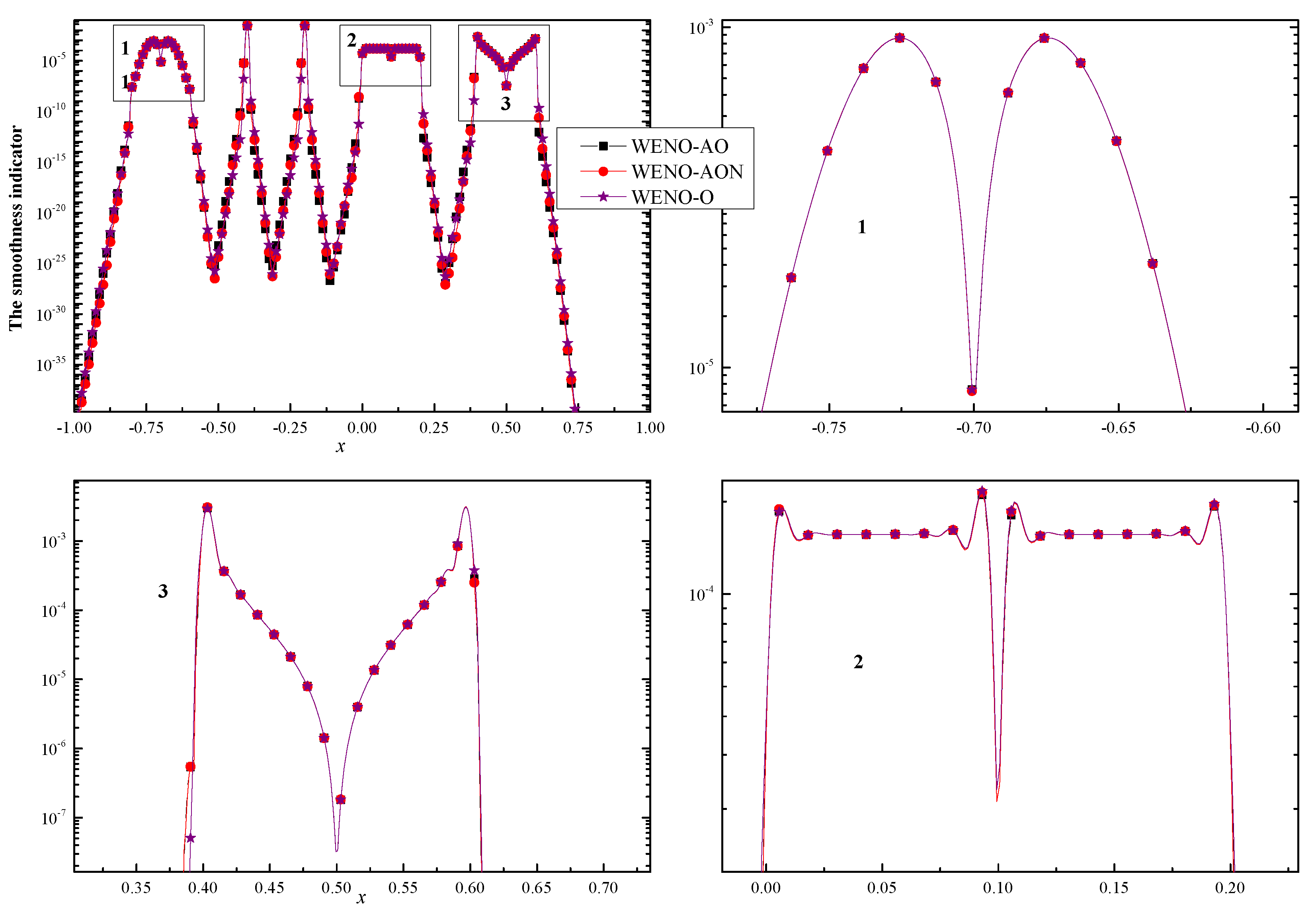
4. Analysis of the Smoothness Indicators
5. Time Integration
6. Numerical Experiments
6.1. Scalar Equation
6.1.1. Example (1)—Linear Advection of Sinusoidal Profiles
6.1.2. Example (2)—Non-Linear Burgers Equation in One Dimension
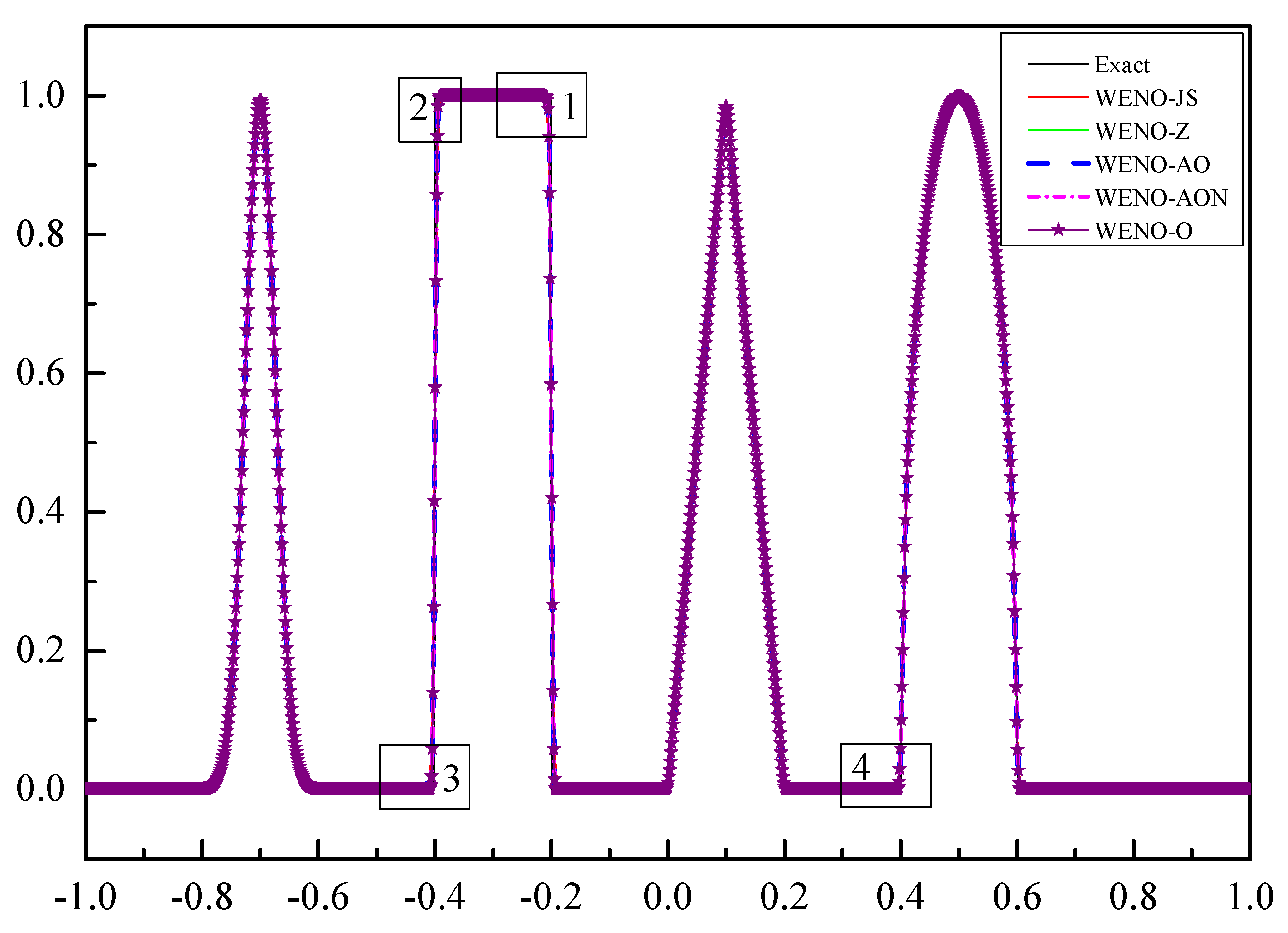
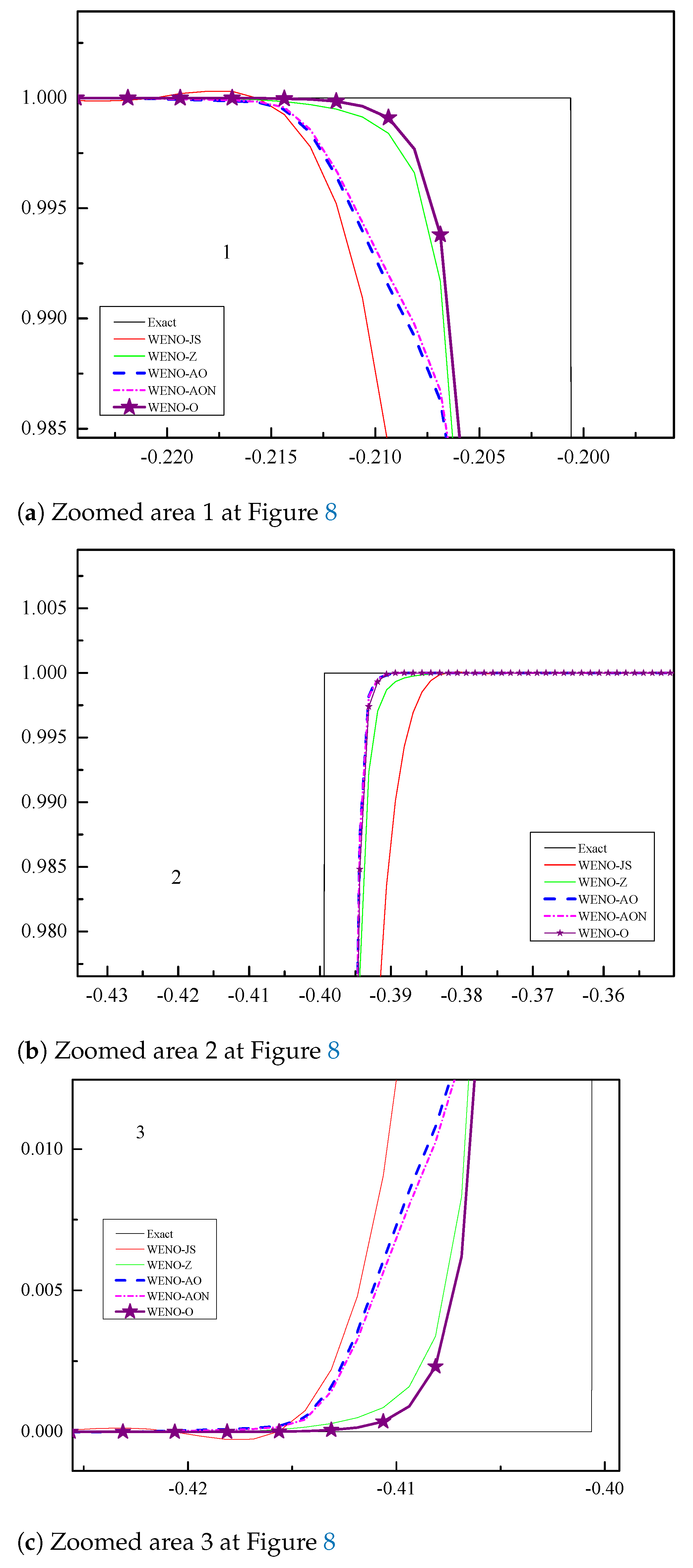
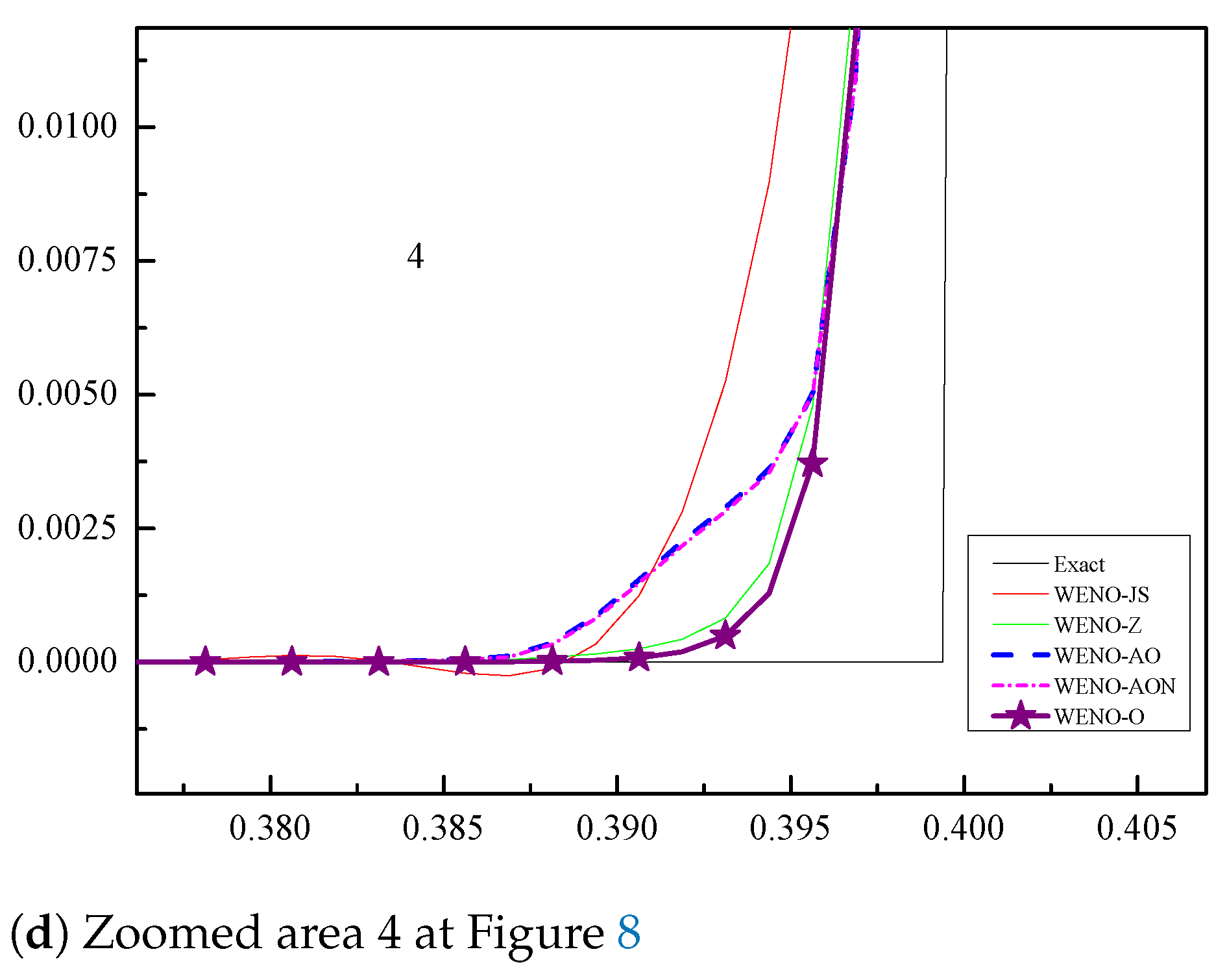
6.1.3. Example (3)—The Scalar Advection Test Problem
6.2. One-Dimensional Euler Equations
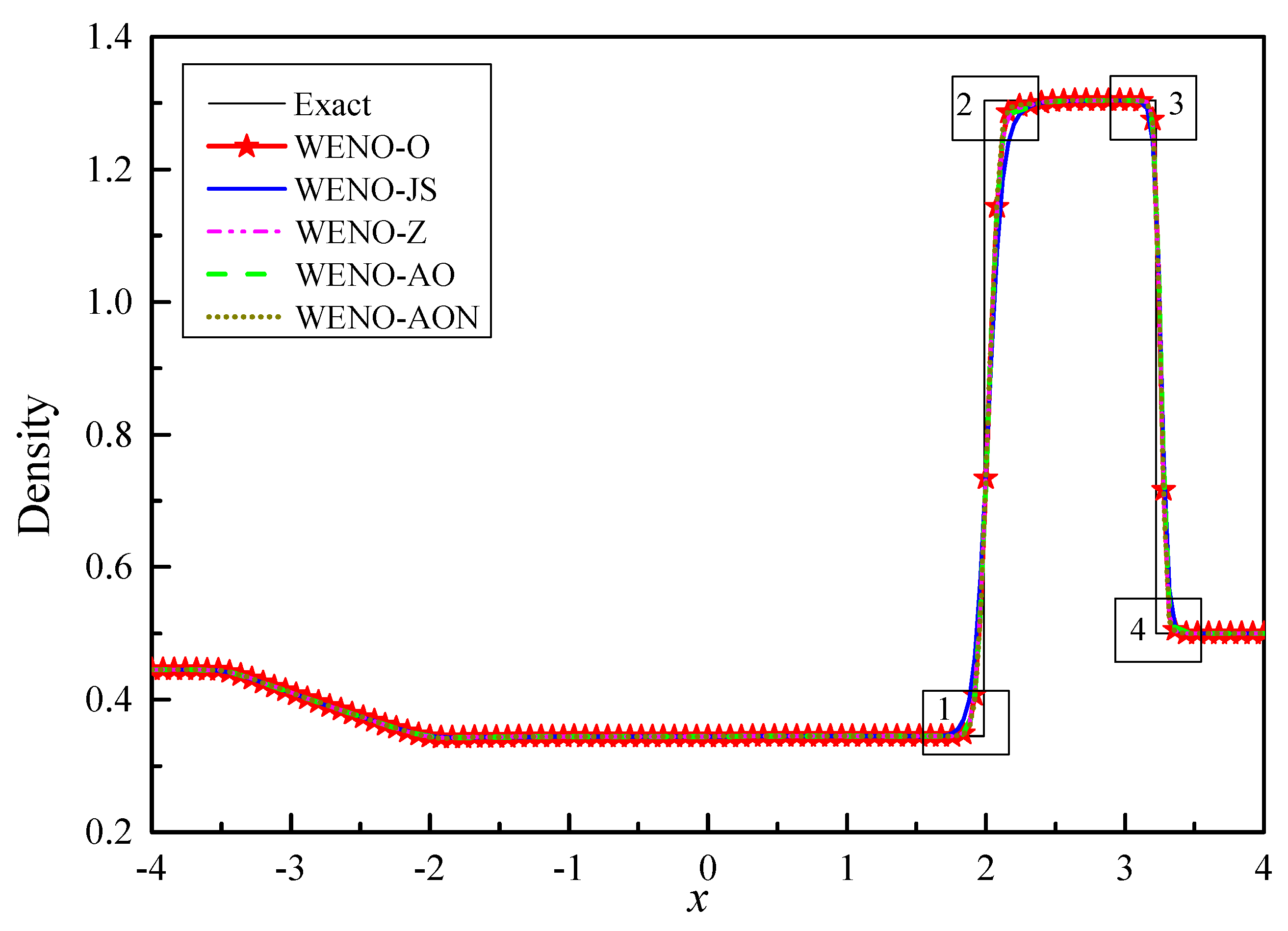
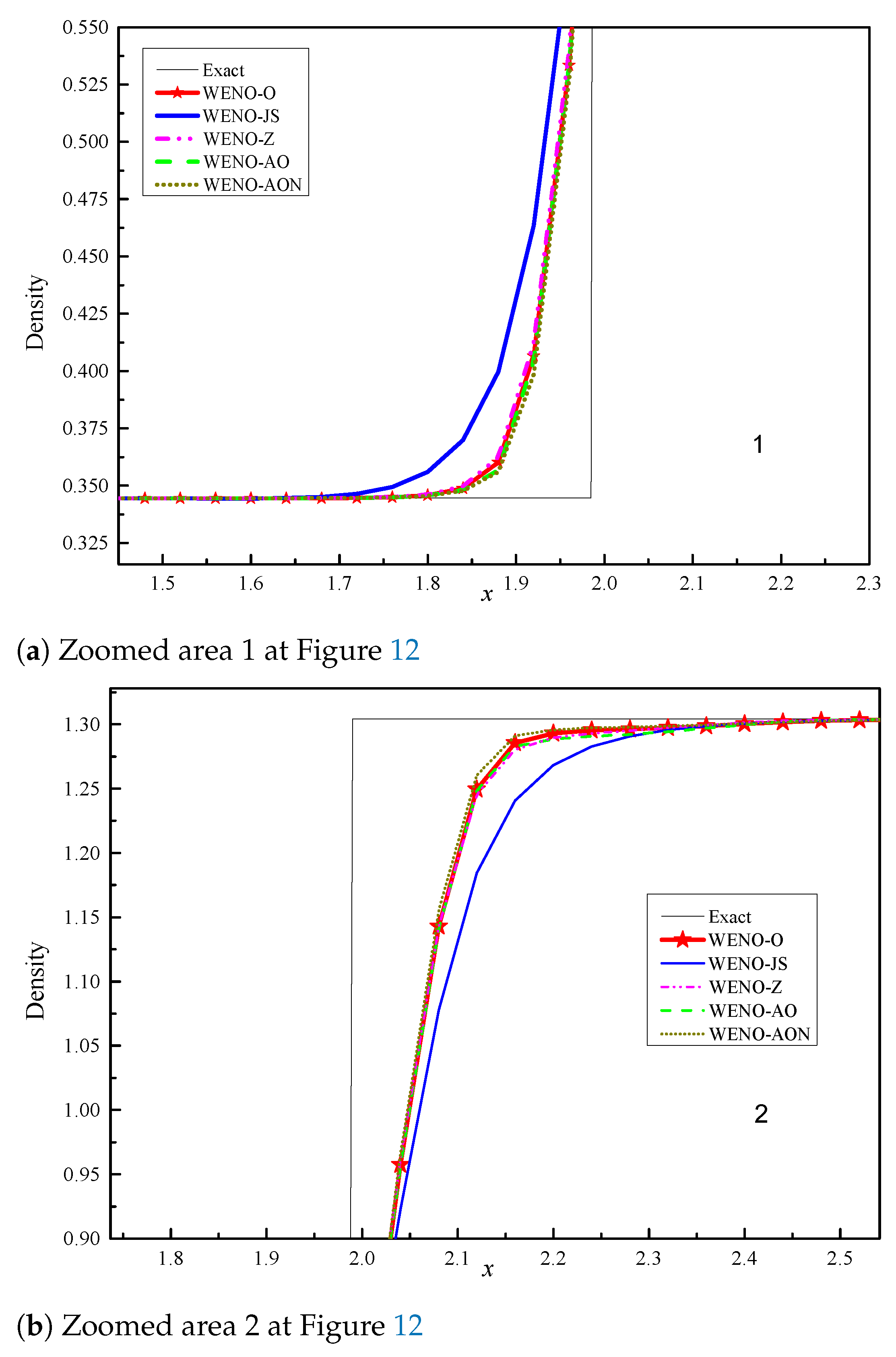
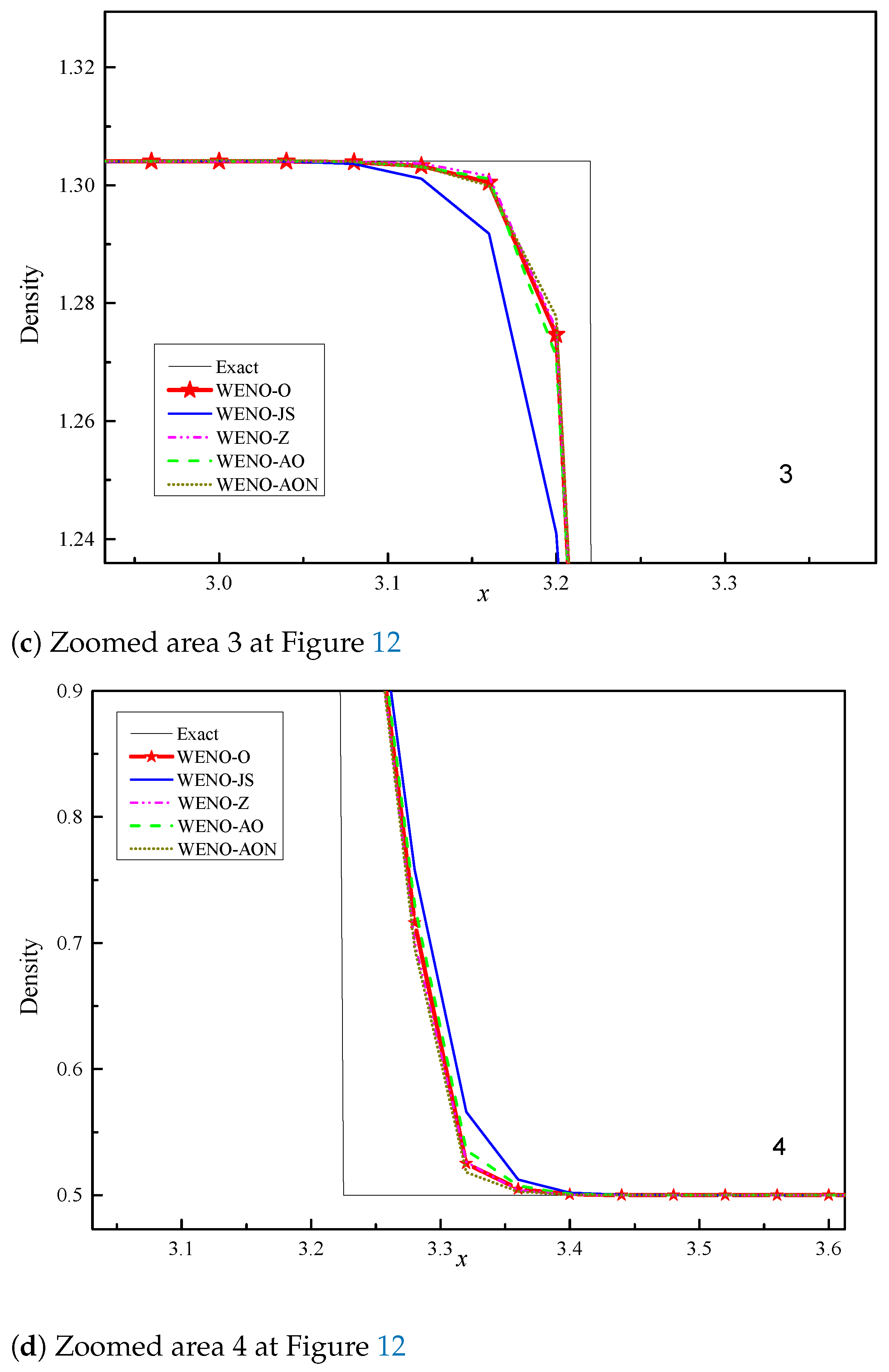
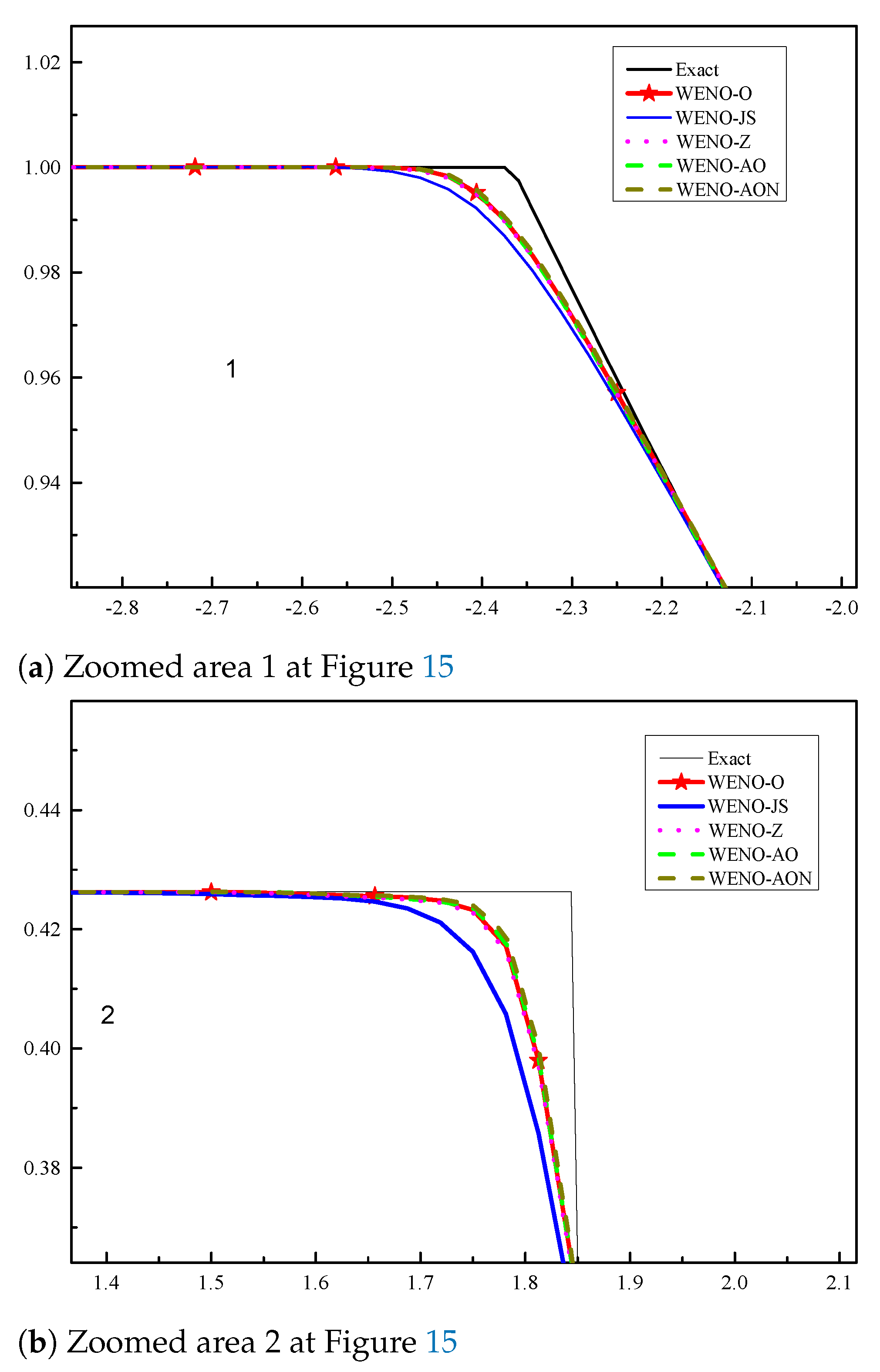
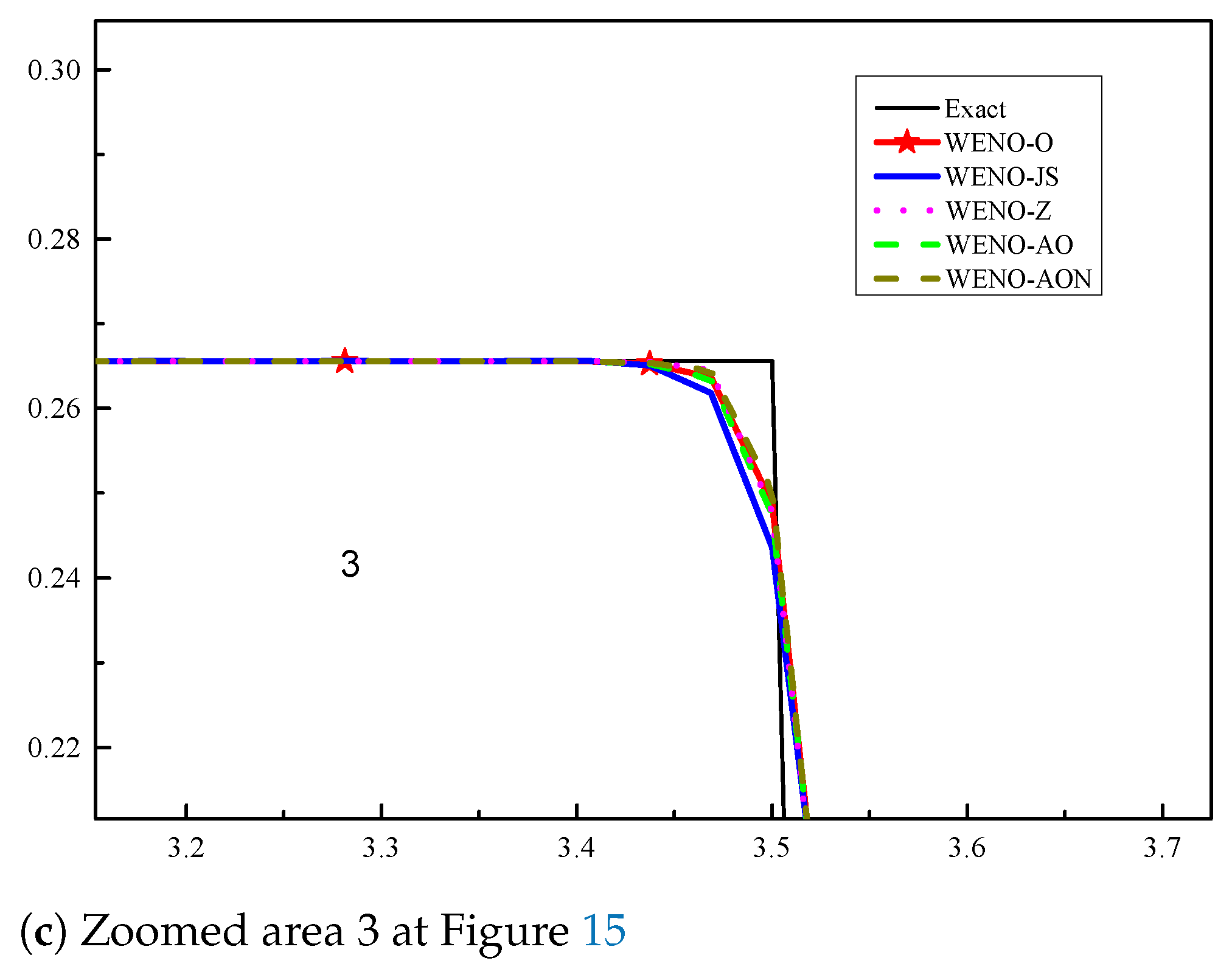
6.2.1. Example (4)—The Lax Test Problem
6.2.2. Example (5)—The Sod Test Problem
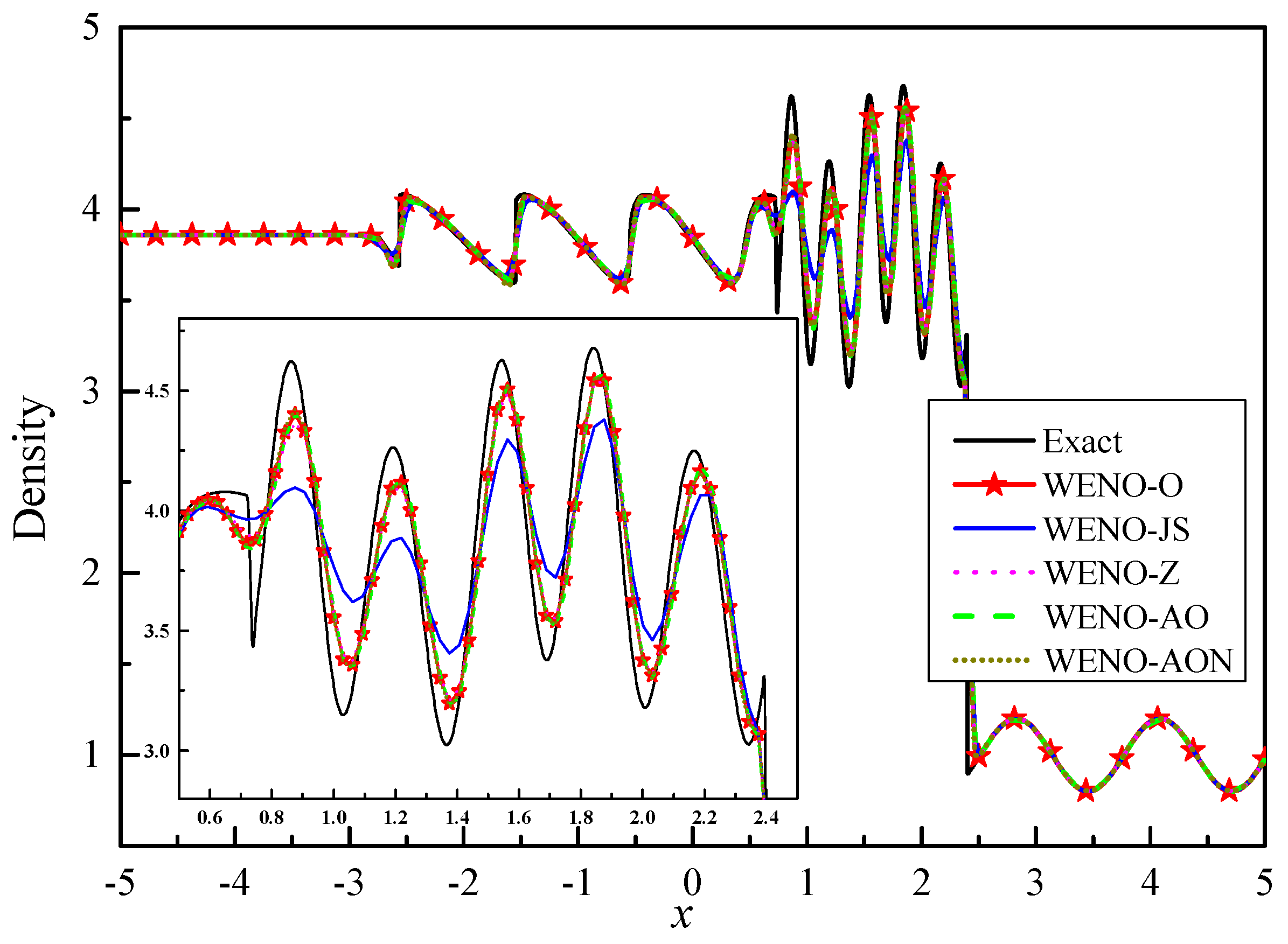
6.2.3. Example (6)—The Shu–Osher Problem
6.3. Two-Dimensional Euler Equations
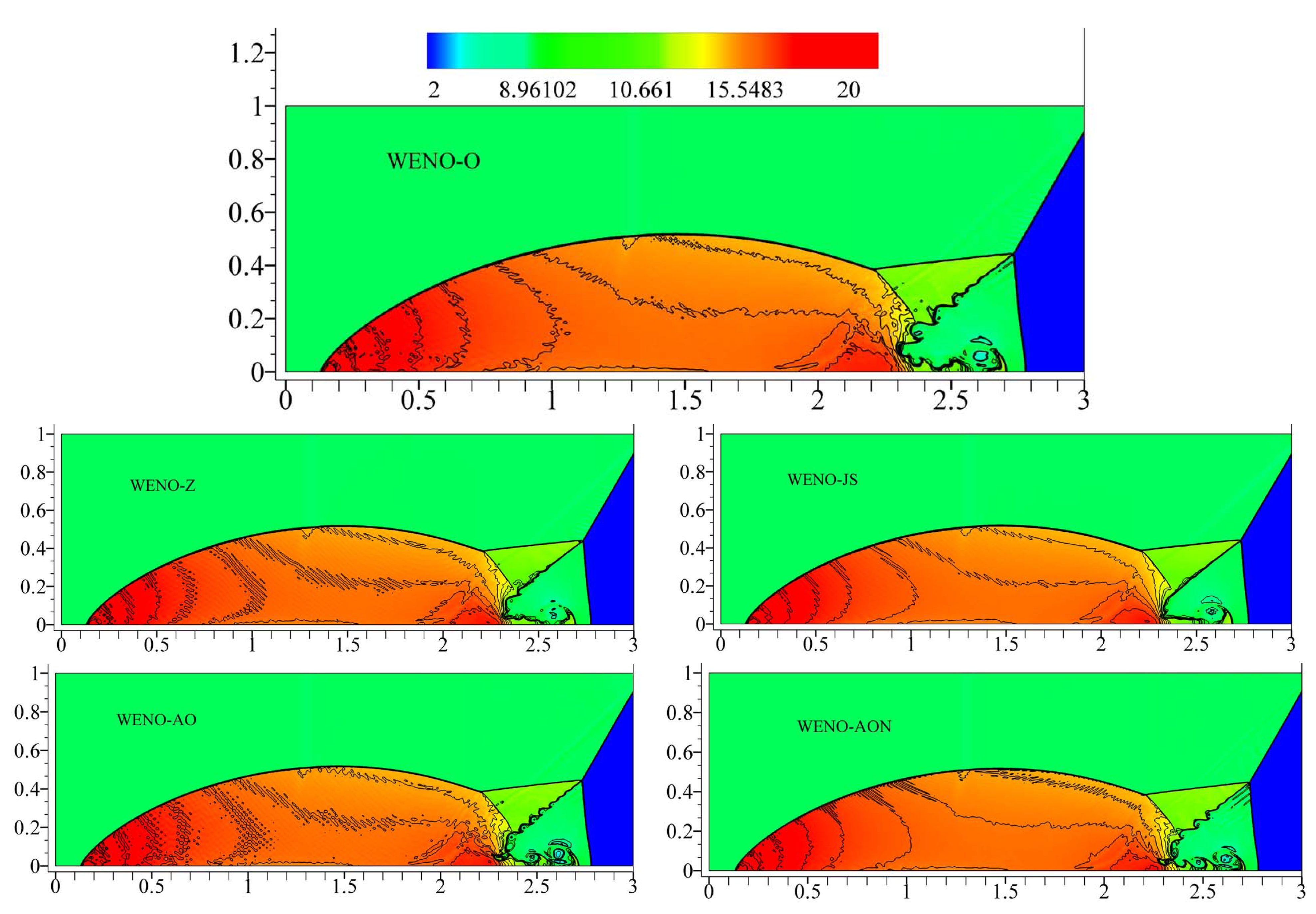
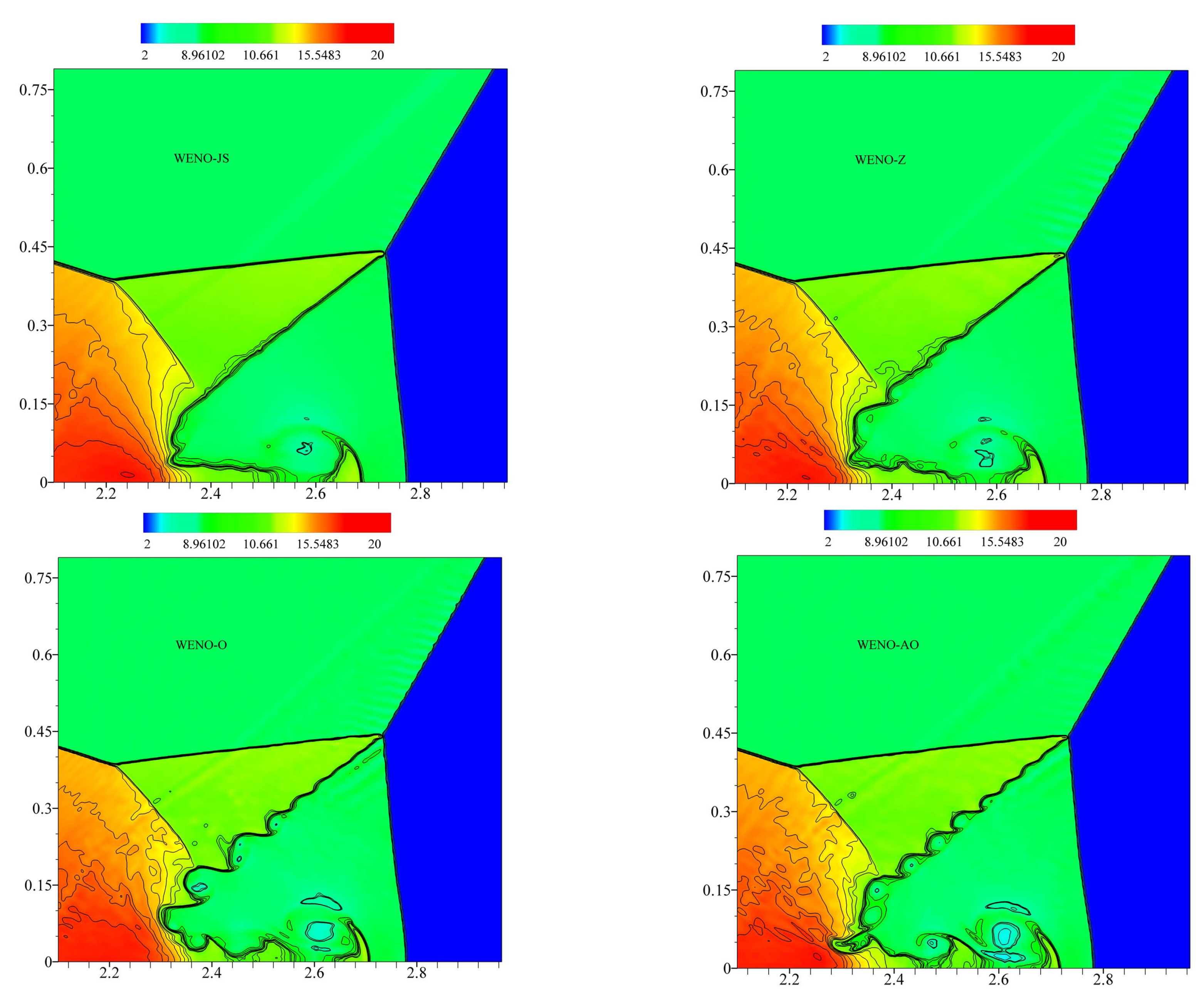
6.3.1. Example (7)—Double-Mach Reflection of Strong Shock
6.3.2. Example (8)—2-D Riemann initial data (Lax-Liu)
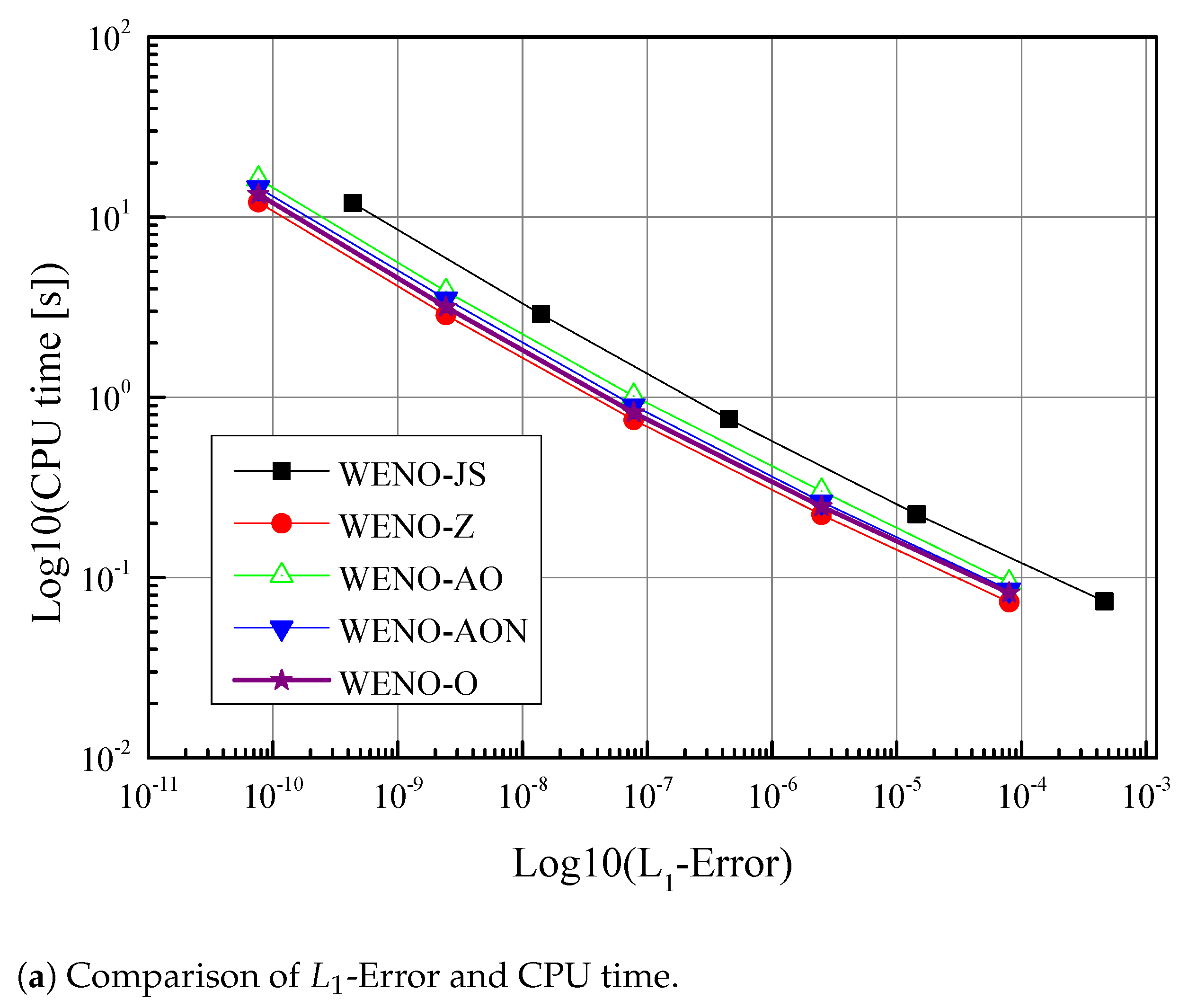
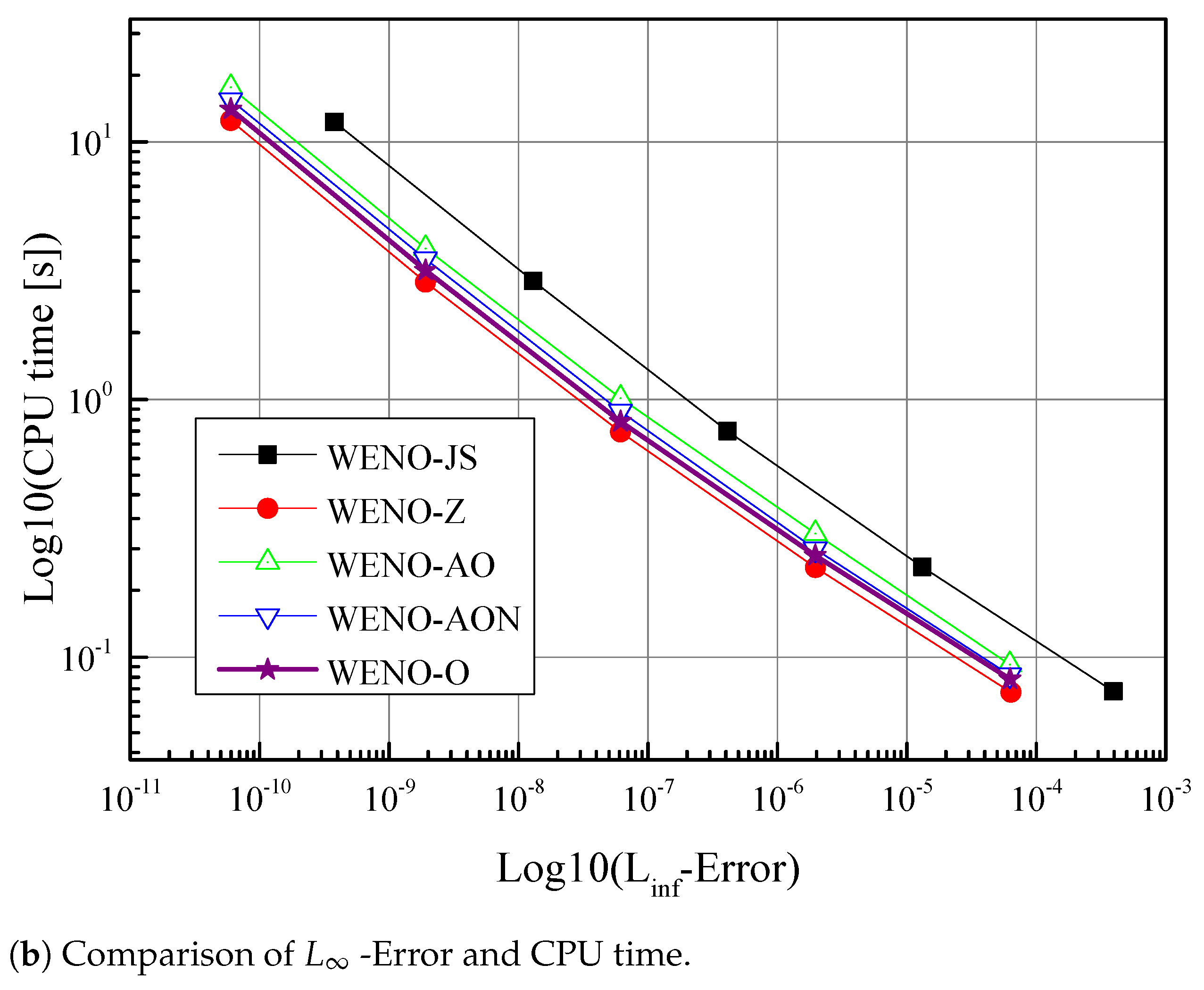
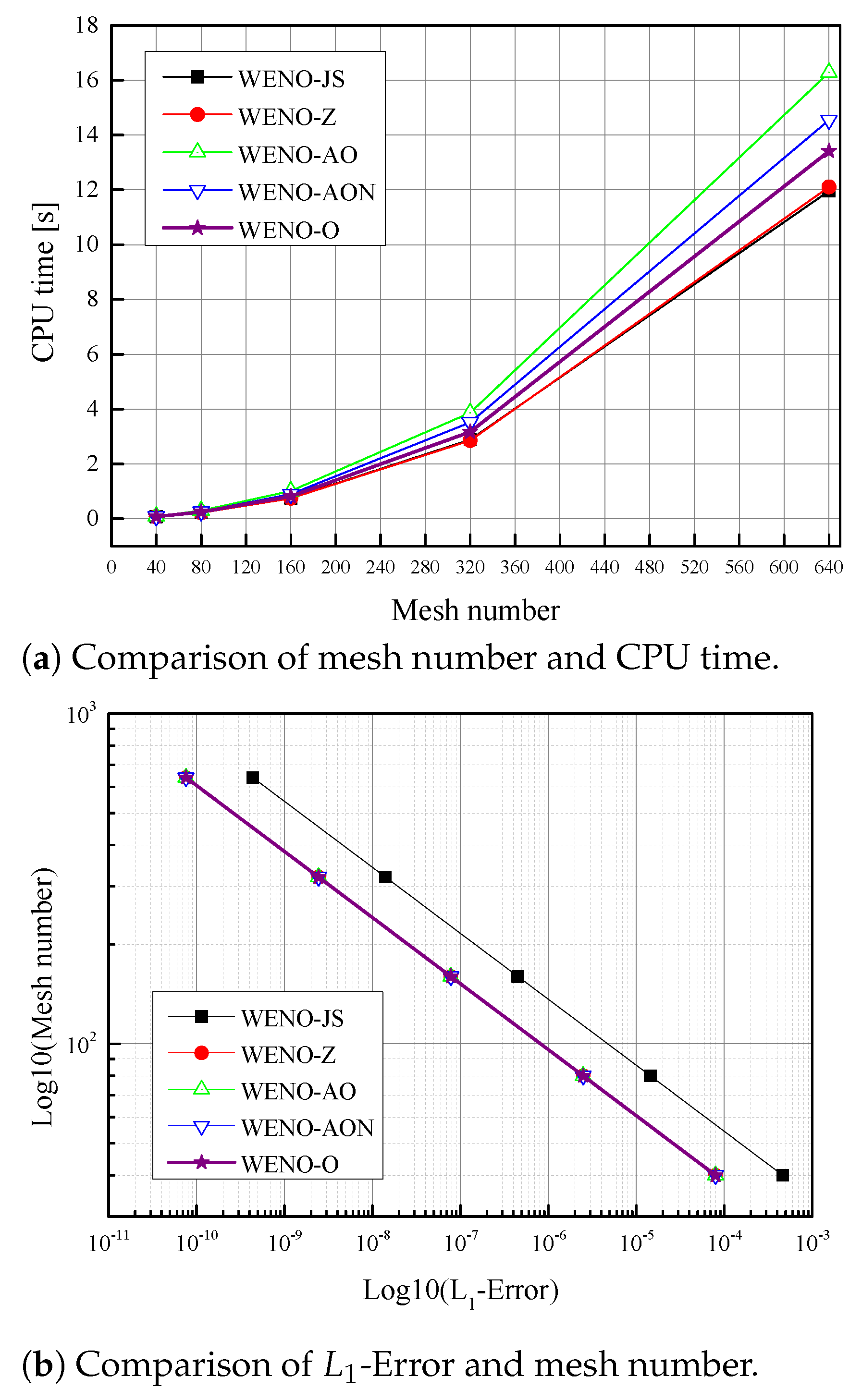
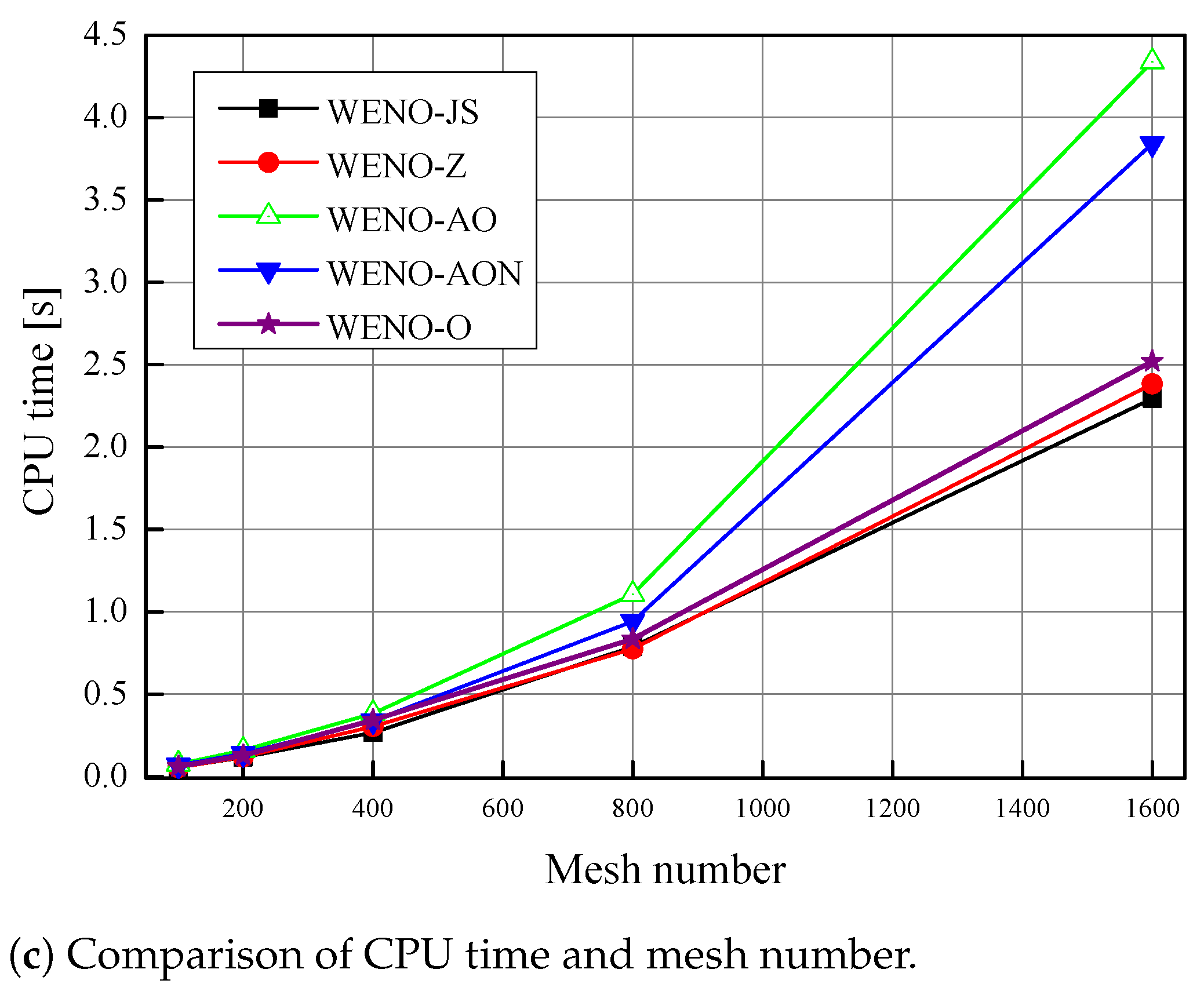
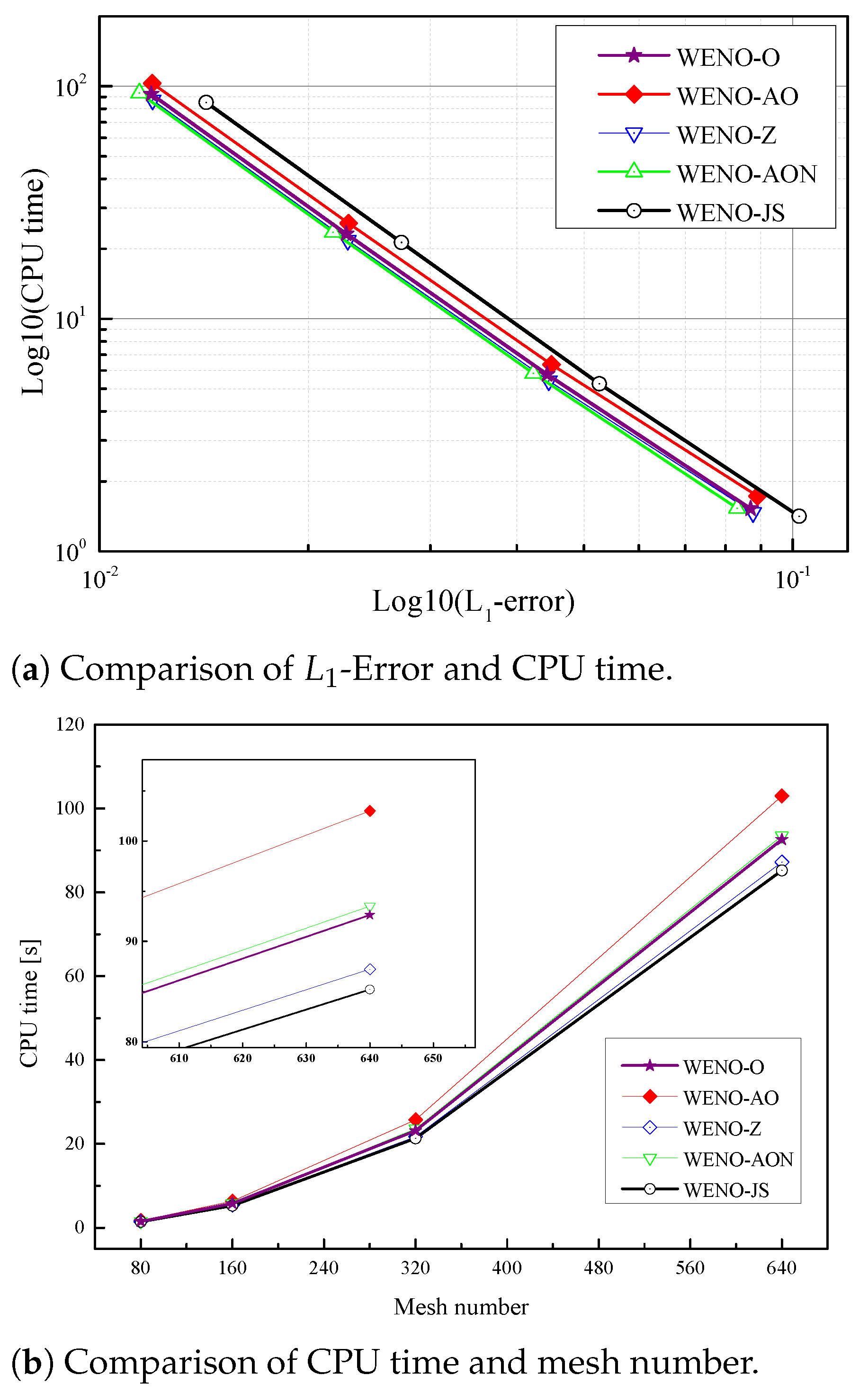
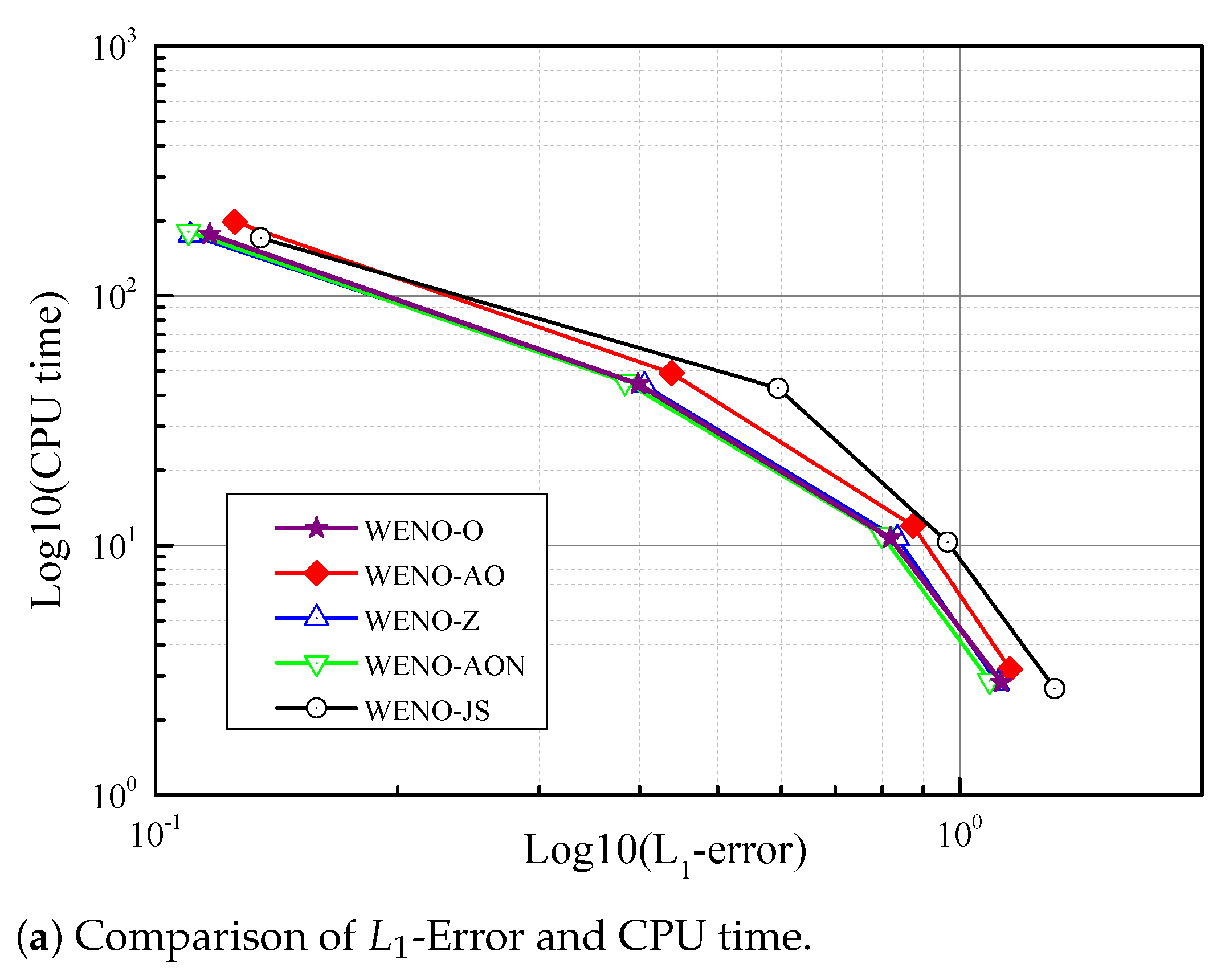
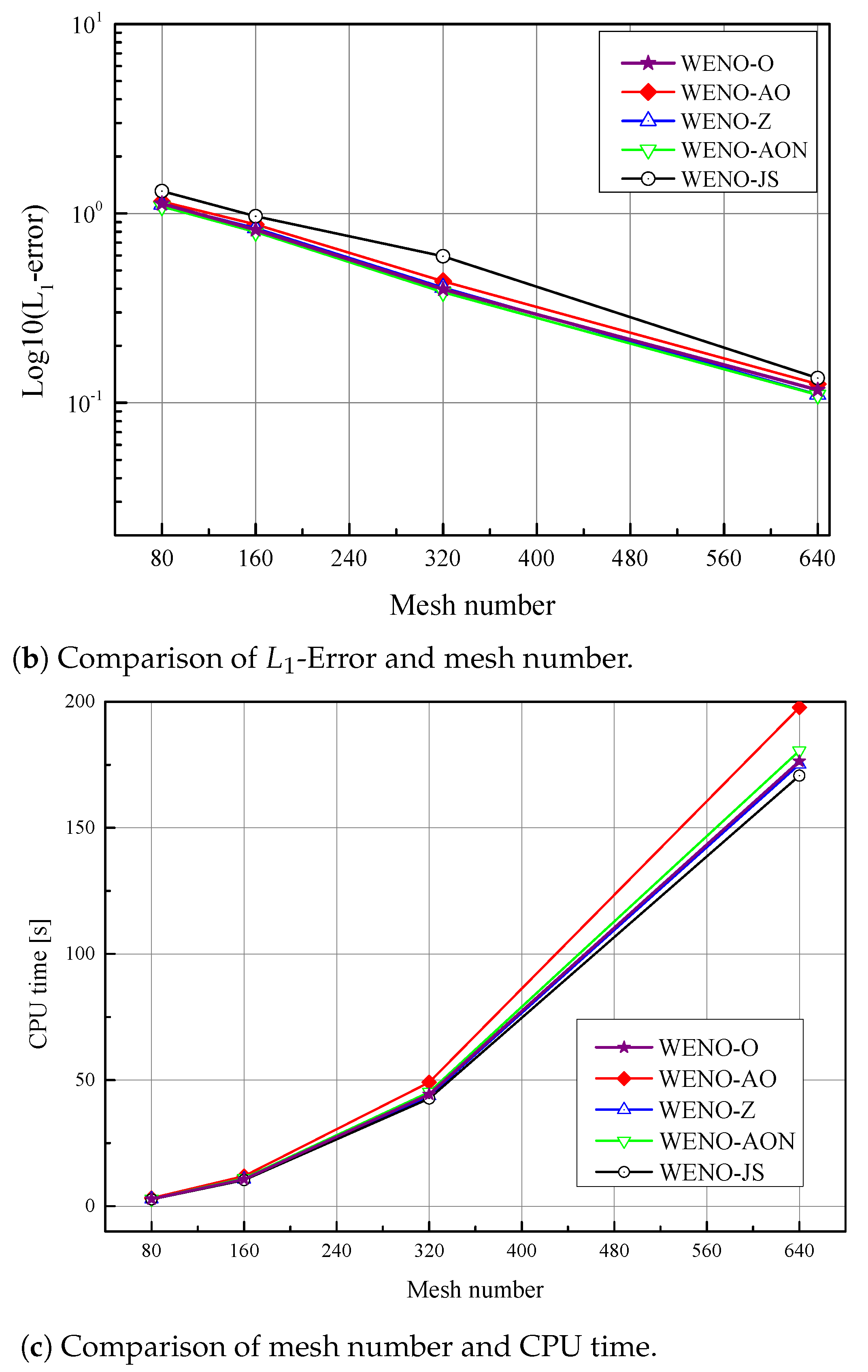
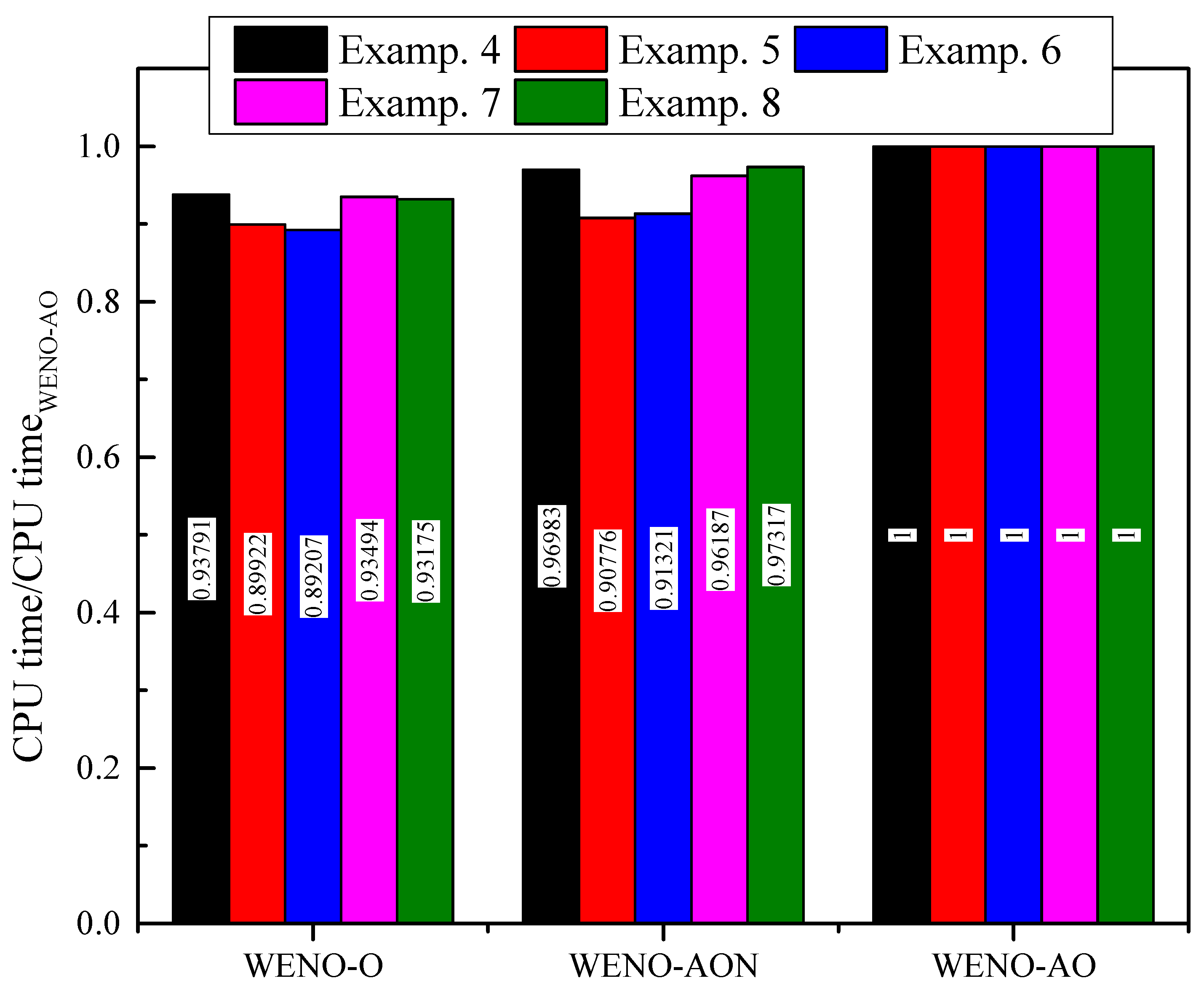
6.4. CPU Time Comparison
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly high order accurate essentially non-oscillatory schemes, III. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef] [Green Version]
- Henrick, A.K.; Aslam, T.D.; Powers, J.M. Mapped weighted essentially non-oscillatory schemes: Achieving optimal order near critical points. J. Comput. Phys. 2005, 207, 542–567. [Google Scholar] [CrossRef]
- Borges, R.; Carmona, M.; Costa, B.; Don, W.S. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 2008, 227, 3191–3211. [Google Scholar] [CrossRef]
- Musa, O.; Huang, G.; Yu, Z.; Li, Q. An improved Roe solver for high order reconstruction schemes. Comput. Fluids 2020, 207, 104591. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, J. A new fifth order finite difference WENO scheme for solving hyperbolic conservation laws. J. Comput. Phys. 2016, 318, 110–121. [Google Scholar] [CrossRef]
- Balsara, D.S.; Garain, S.; Shu, C.W. An efficient class of WENO schemes with adaptive order. J. Comput. Phys. 2016, 326, 780–804. [Google Scholar] [CrossRef] [Green Version]
- Jung, C.Y.; Nguyen, T.B. A new adaptive weighted essentially non-oscillatory WENO-θ scheme for hyperbolic conservation laws. J. Comput. Appl. Math. 2018, 328, 314–339. [Google Scholar] [CrossRef]
- Guo, J.; Jung, J.H. A RBF-WENO finite volume method for hyperbolic conservation laws with the monotone polynomial interpolation method. Appl. Numer. Math. 2017, 112, 27–50. [Google Scholar] [CrossRef]
- Fan, P. High order weighted essentially nonoscillatory WENO-η schemes for hyperbolic conservation laws. J. Comput. Phys. 2014, 269, 355–385. [Google Scholar] [CrossRef] [Green Version]
- Levy, D.; Puppo, G.; Russo, G. A third order central WENO scheme for 2D conservation laws. Appl. Numer. Math. 2000, 33, 415–422. [Google Scholar] [CrossRef]
- Yamaleev, N.K.; Carpenter, M.H. A systematic methodology for constructing high-order energy stable WENO schemes. J. Comput. Phys. 2009, 228, 4248–4272. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.; Lin, G.; Christlieb, A.J.; Qiu, J. An adaptive WENO collocation method for differential equations with random coefficients. Mathematics 2016, 4, 29. [Google Scholar] [CrossRef] [Green Version]
- Sheng, C.; Zhao, Q.; Zhong, D.; Ge, N. A Strategy to Implement High-Order WENO Schemes on Unstructured Grids. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Dong, H.; Lu, C.; Yang, H. The Finite Volume WENO with Lax–Wendroff Scheme for Nonlinear System of Euler Equations. Mathematics 2018, 6, 211. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Shen, Y. A novel weighting switch function for uniformly high-order hybrid shock-capturing schemes. Int. J. Numer. Methods Fluids 2017, 83, 681–703. [Google Scholar] [CrossRef] [Green Version]
- Rathan, S. An improved non-linear weights for seventh-order weighted essentially non-oscillatory scheme. Comput. Fluids 2017, 156, 496–514. [Google Scholar] [CrossRef]
- Wu, X.; Liang, J.; Zhao, Y. A new smoothness indicator for third-order WENO scheme. Int. J. Numer. Methods Fluids 2016, 81, 451–459. [Google Scholar] [CrossRef]
- Xu, W.; Wu, W. Improvement of third-order WENO-Z scheme at critical points. Comput. Math. Appl. 2018, 75, 3431–3452. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, J.; Chen, Y.; Qiu, J. A new hybrid WENO scheme for hyperbolic conservation laws. Comput. Fluids 2019, 179, 422–436. [Google Scholar] [CrossRef]
- Huang, C. WENO scheme with new smoothness indicator for Hamilton—Jacobi equation. Appl. Math. Comput. 2016, 290, 21–32. [Google Scholar] [CrossRef]
- Huang, C.; Chen, L.L. A simple smoothness indicator for the WENO scheme with adaptive order. J. Comput. Phys. 2018, 352, 498–515. [Google Scholar] [CrossRef]
- Kumar, R.; Chandrashekar, P. Simple smoothness indicator and multi-level adaptive order WENO scheme for hyperbolic conservation laws. J. Comput. Phys. 2018, 375, 1059–1090. [Google Scholar] [CrossRef] [Green Version]
- Gottlieb, S.; Shu, C.W. Total variation diminishing Runge-Kutta schemes. Math. Comput. Am. Math. Soc. 1998, 67, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Lax, P.D. Weak solutions of nonlinear hyperbolic equations and their numerical computation. Commun. Pure Appl. Math. 1954, 7, 159–193. [Google Scholar] [CrossRef]
- Sod, G.A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes, II. J. Comput. Phys. 1989, 83, 32–78. [Google Scholar] [CrossRef]
- Woodward, P.; Colella, P. The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comput. Phys. 1984, 54, 115–173. [Google Scholar] [CrossRef]
- Lax, P.D.; Liu, X.D. Solution of two-dimensional Riemann problems of gas dynamics by positive schemes. SIAM J. Sci. Comput. 1998, 19, 319–340. [Google Scholar] [CrossRef] [Green Version]
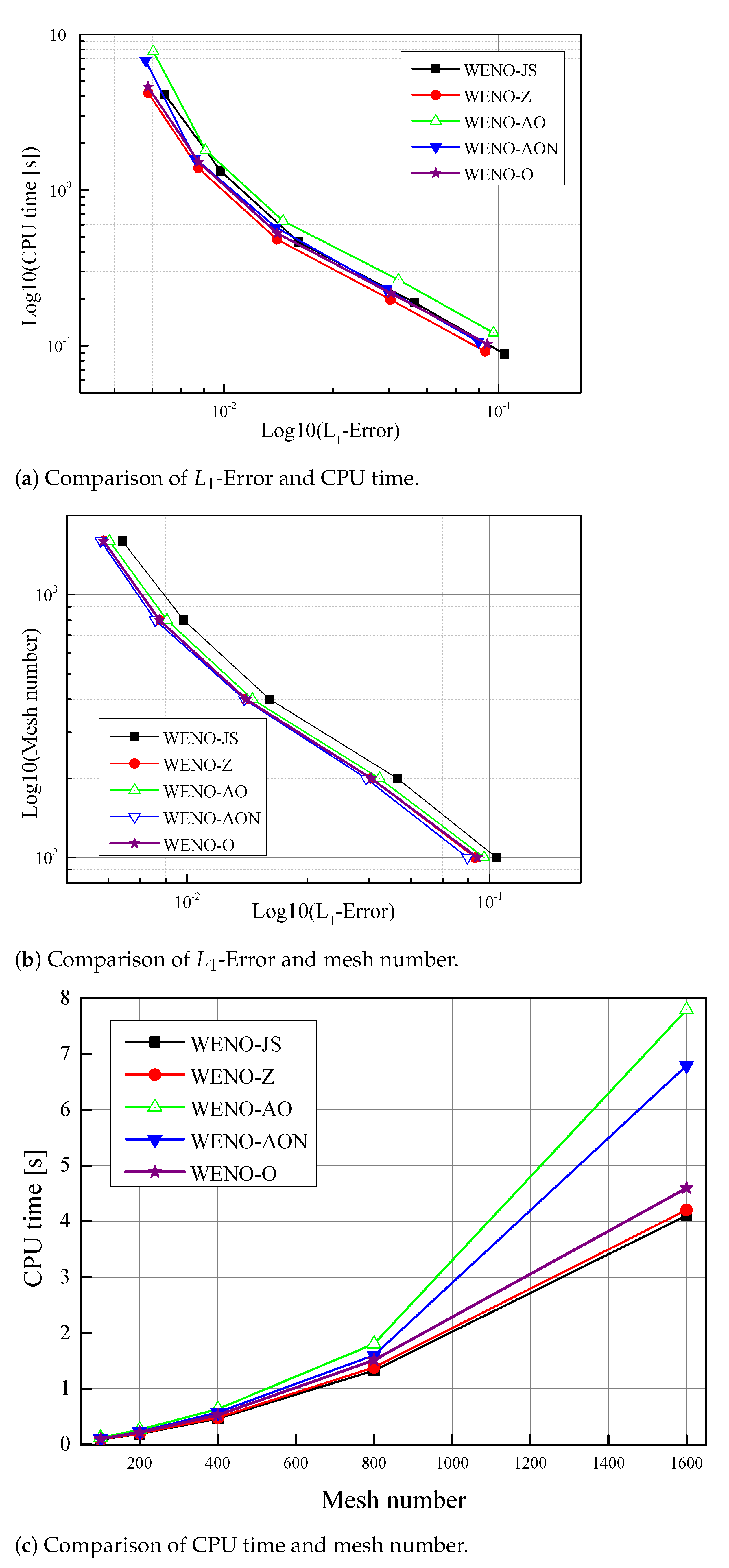
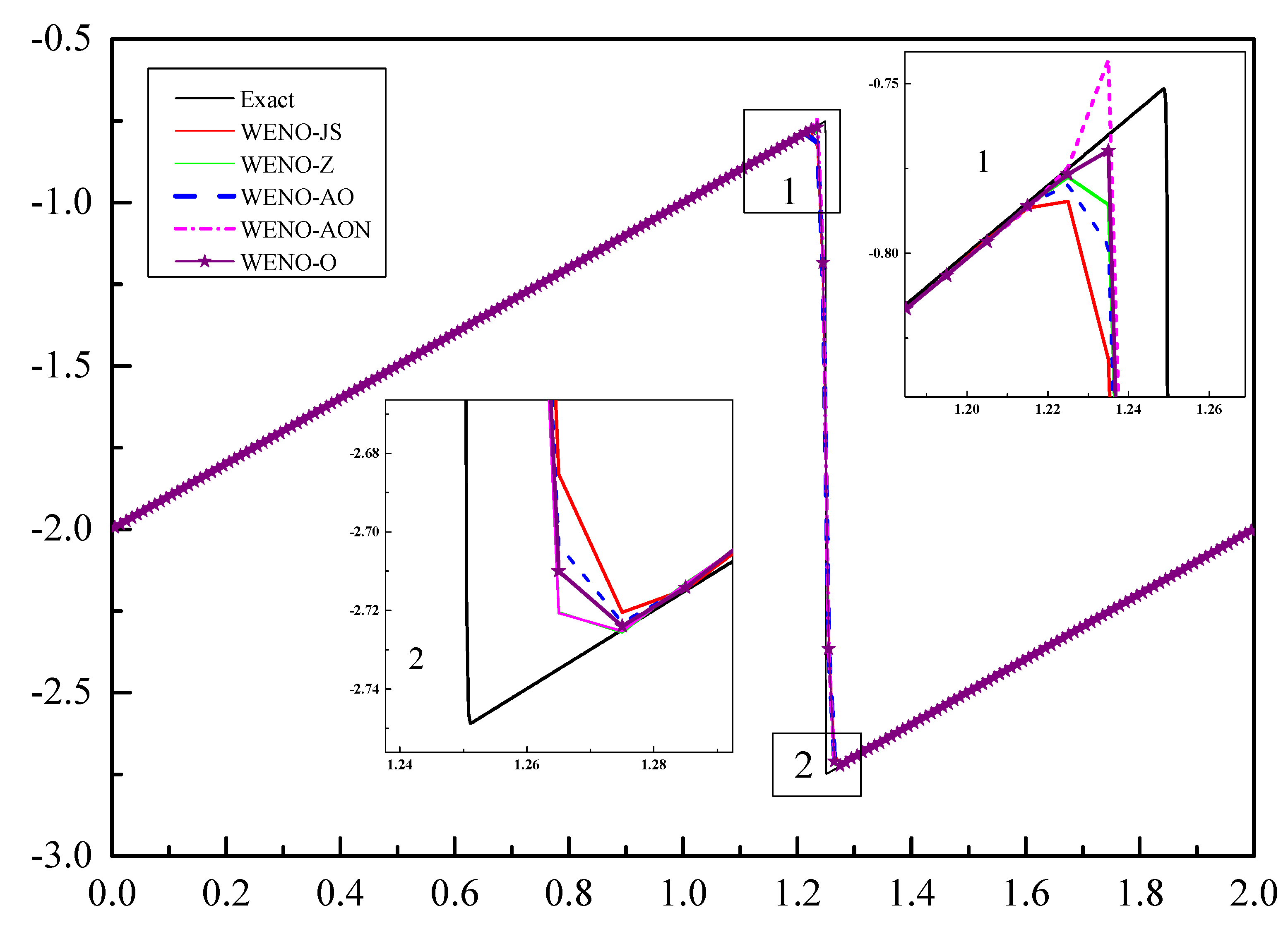
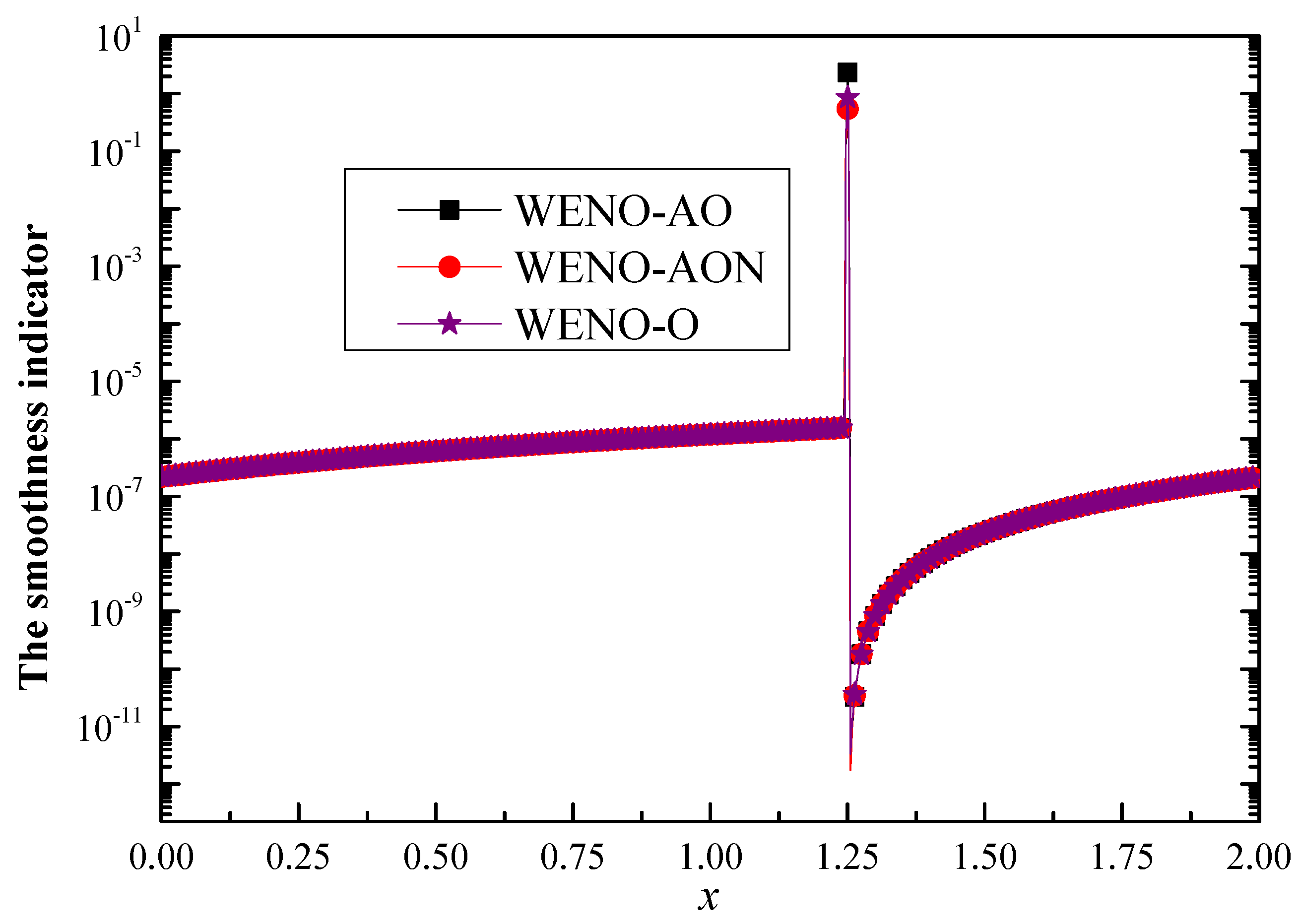
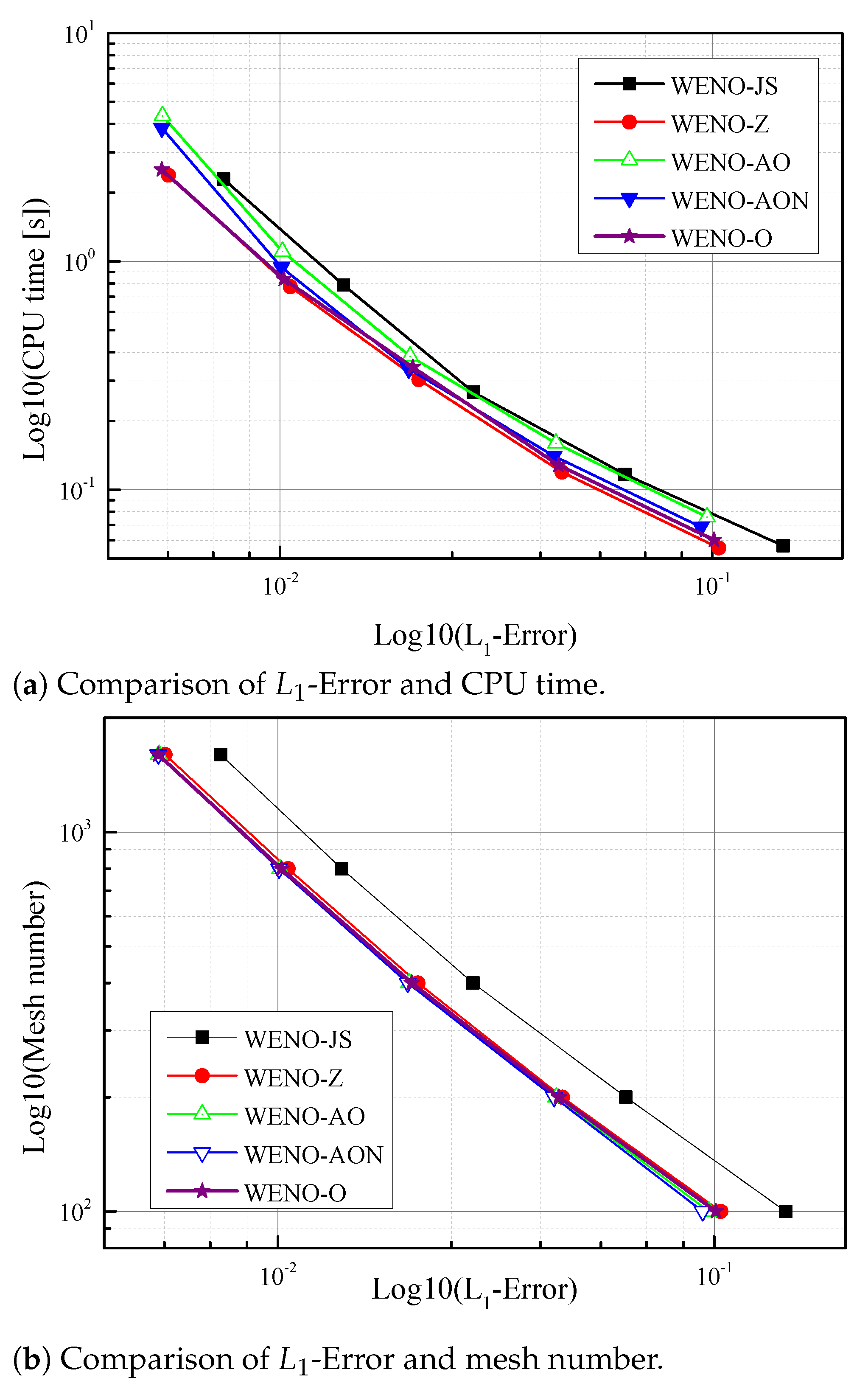


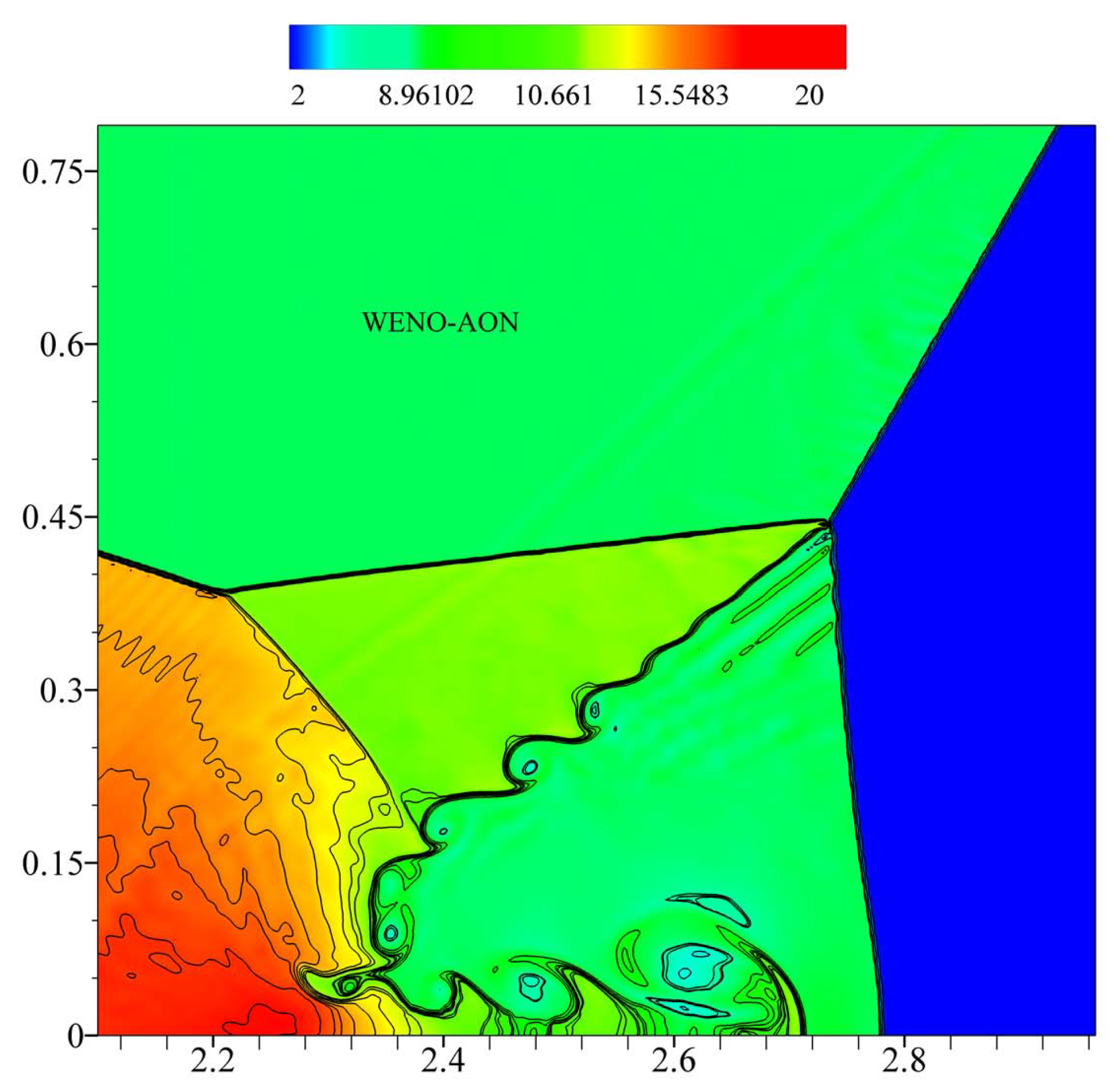
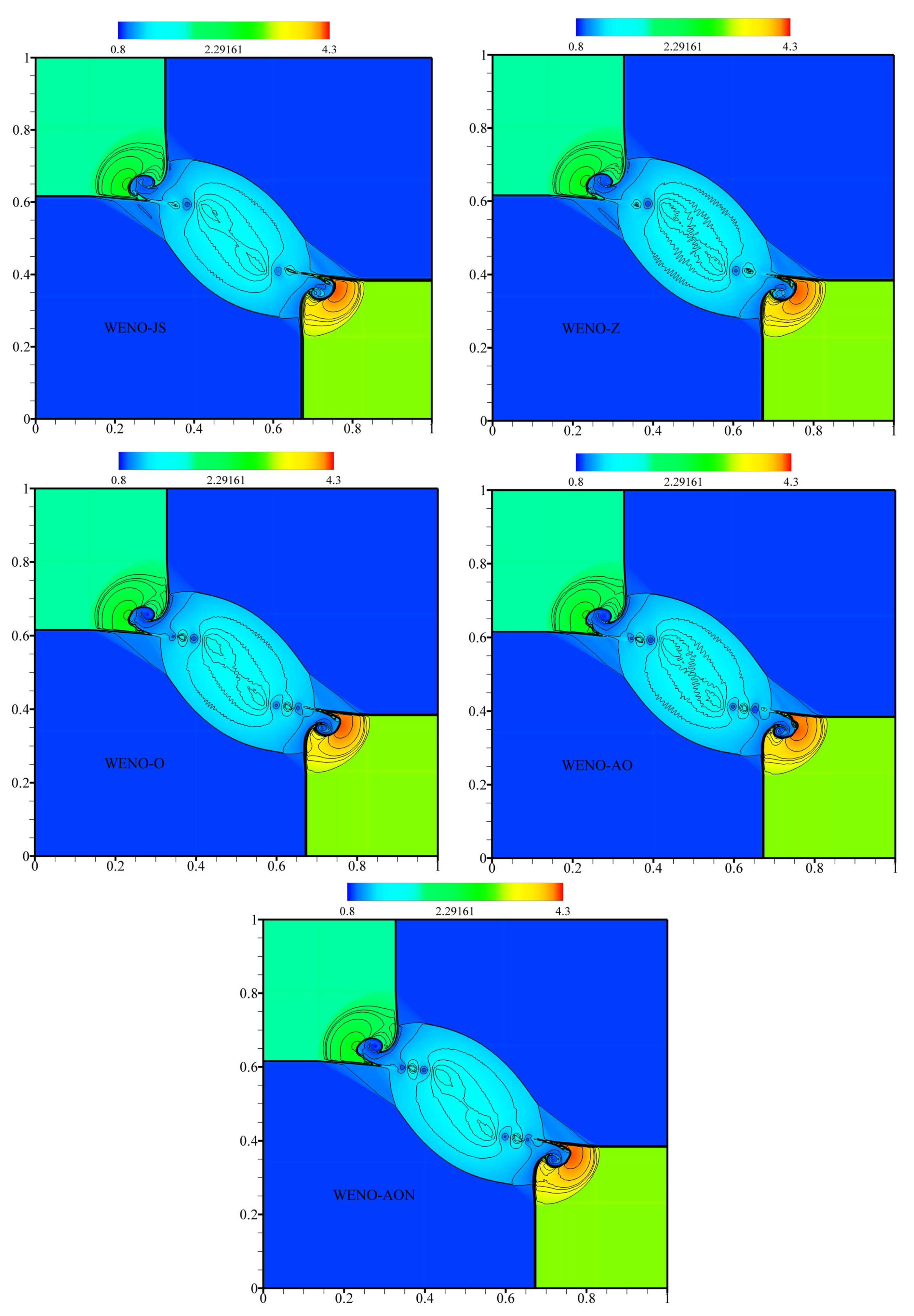
| Scheme | Flux Function |
|---|---|
| WENO-O | |
| WENO-AO | |
| WENO-AON |
| Scheme | Smoothness Indicator |
|---|---|
| WENO-O | |
| WENO-AO | |
| WENO-AON |
| Method | N | 40 | 80 | 160 | 320 | 640 |
|---|---|---|---|---|---|---|
| -norm error | 4.6300 × 10 | 1.4500 × 10 | 4.5100 × 10 | 1.4100 × 10 | 4.3700 × 10 | |
| WENO-JS | -norm error | 3.9447 × 10 | 1.3153 × 10 | 4.1205 × 10 | 1.2966 × 10 | 3.7797 × 10 |
| CPU time | 0.0737 | 0.2244 | 0.7555 | 2.8856 | 11.9590 | |
| accuracy | - | 5.00096 | 5.00143 | 5.00257 | 5.00925 | |
| -norm error | 7.9900 × 10 | 2.5000 × 10 | 7.8000 × 10 | 2.4400 × 10 | 7.6200 × 10 | |
| WENO-Z | -norm error | 6.3800 × 10 | 1.9714 × 10 | 6.1381 × 10 | 1.9160 × 10 | 5.9857 × 10 |
| CPU time | 0.07316 | 0.22302 | 0.7488 | 2.8570 | 12.1060 | |
| accuracy | - | 5.00101 | 4.99947 | 4.99982 | 4.99964 | |
| -norm error | 7.9644 × 10 | 2.4949 × 10 | 7.8014 × 10 | 2.4383 × 10 | 7.6215 × 10 | |
| WENO-AO | -norm error | 6.2539 × 10 | 1.9595 × 10 | 6.1272 × 10 | 1.9151 × 10 | 5.9855 × 10 |
| CPU time | 0.0936 | 0.3021 | 1.0136 | 3.8675 | 16.2850 | |
| accuracy | - | 4.99651 | 4.99911 | 4.99979 | 4.99966 | |
| -norm error | 7.9644 × 10 | 2.4949 × 10 | 7.8014 × 10 | 2.4383 × 10 | 7.6214 × 10 | |
| WENO-AON | -norm error | 6.2540 × 10 | 1.9595 × 10 | 6.1272 × 10 | 1.9150 × 10 | 5.9843 × 10 |
| CPU time | 0.0853 | 0.2628 | 0.8998 | 3.5138 | 14.5450 | |
| accuracy | - | 4.99651 | 4.99911 | 4.99979 | 4.99968 | |
| -norm error | 7.9645 × 10 | 2.4949 × 10 | 7.8014 × 10 | 2.4383 × 10 | 7.6215 × 10 | |
| WENO-O | -norm error | 6.2573 × 10 | 1.9595 × 10 | 6.1272 × 10 | 1.9151 × 10 | 5.9863 × 10 |
| CPU time | 0.0822 | 0.2482 | 0.8219 | 3.1722 | 13.4120 | |
| accuracy | - | 4.99653 | 4.99911 | 4.99979 | 4.99966 |
| Method | N | 100 | 200 | 400 | 800 | 1600 |
|---|---|---|---|---|---|---|
| -norm error | 10.5320 × 10 | 4.9560 × 10 | 1.8770 × 10 | 9.7500 × 10 | 6.1100 × 10 | |
| WENO-JS | CPU time | 0.0884 | 0.1893 | 0.4628 | 1.3257 | 4.1040 |
| accuracy | - | 1.08739 | 1.40112 | 0.94452 | 0.67477 | |
| -norm error | 8.9590 × 10 | 4.0470 × 10 | 1.5630 × 10 | 8.0900 × 10 | 5.3100 × 10 | |
| WENO-Z | CPU time | 0.0918 | 0.1978 | 0.4818 | 1.3818 | 4.2026 |
| accuracy | - | 1.14656 | 1.37206 | 0.95128 | 0.60665 | |
| -norm error | 9.5970 × 10 | 4.328 × 10 | 1.6460 × 10 | 8.5900 × 10 | 5.5400 × 10 | |
| WENO-AO | CPU time | 0.1210 | 0.2654 | 0.6338 | 1.8035 | 7.7902 |
| accuracy | - | 1.14886 | 1.39521 | 0.93783 | 0.63237 | |
| -norm error | 8.4530 × 10 | 3.9110 × 10 | 1.5450 × 10 | 7.8600 × 10 | 5.1900 × 10 | |
| WENO-AON | CPU time | 0.1061 | 0.2305 | 0.5772 | 1.6001 | 6.7917 |
| accuracy | - | 1.11204 | 1.33956 | 0.97565 | 0.5972 | |
| -norm error | 9.1120 × 10 | 4.067 × 10 | 1.5680 × 10 | 8.1000 × 10 | 5.3000 × 10 | |
| WENO-O | CPU time | 0.1025 | 0.2170 | 0.5269 | 1.5128 | 4.5968 |
| accuracy | - | 1.16402 | 1.3749 | 0.95213 | 0.61221 |
| Method | N | 100 | 200 | 400 | 800 | 1600 |
|---|---|---|---|---|---|---|
| -norm error | 14.5820 × 10 | 6.2810 × 10 | 2.8020 × 10 | 1.4020 × 10 | 7.4000 × 10 | |
| WENO-JS | CPU time | 0.0567 | 0.1167 | 0.2670 | 0.7877 | 2.2937 |
| accuracy | - | 1.21512 | 1.16454 | 0.99897 | 0.92189 | |
| -norm error | 10.3540 × 10 | 4.4910 × 10 | 2.0940 × 10 | 1.0560 × 10 | 5.5200 × 10 | |
| WENO-Z | CPU time | 0.0555 | 0.1193 | 0.3035 | 0.7751 | 2.3831 |
| accuracy | - | 1.20508 | 1.10078 | 0.98765 | 0.93587 | |
| -norm error | 9.7320 × 10 | 4.3500 × 10 | 2.0000 × 10 | 1.0130 × 10 | 5.3400 × 10 | |
| WENO-AO | CPU time | 0.0758 | 0.1596 | 0.3838 | 1.1061 | 4.3390 |
| accuracy | - | 1.16172 | 1.12102 | 0.98137 | 0.92372 | |
| -norm error | 9.4160 × 10 | 4.2970 × 10 | 1.9850 × 10 | 1.0100 × 10 | 5.3200 × 10 | |
| WENO-AON | CPU time | 0.0686 | 0.1403 | 0.3382 | 0.9420 | 3.8419 |
| accuracy | - | 1.13178 | 1.11419 | 0.97764 | 0.922 | |
| -norm error | 10.0930 × 10 | 4.4060 × 10 | 2.0280 × 10 | 1.0200 × 10 | 5.3300 × 10 | |
| WENO-O | CPU time | 0.0602 | 0.1281 | 0.3436 | 0.8360 | 2.5197 |
| accuracy | - | 1.19581 | 1.11941 | 0.99149 | 0.93636 |
| Method | N | 100 | 200 | 400 | 800 |
|---|---|---|---|---|---|
| -norm error | 2.2053 × 10 | 1.2080 × 10 | 5.8170 × 10 | 3.2700 × 10 | |
| WENO-JS | CPU time | 0.5005 | 1.6318 | 6.4533 | 25.3660 |
| accuracy | - | 0.86835 | 1.05427 | 0.83098 | |
| -norm error | 1.7743 × 10 | 9.6730 × 10 | 4.4950 × 10 | 2.5640 × 10 | |
| WENO-Z | CPU time | 0.5018 | 1.6433 | 6.2886 | 25.2070 |
| accuracy | - | 0.87521 | 1.10564 | 0.80992 | |
| -norm error | 1.8416 × 10 | 9.9480 × 10 | 4.5600 × 10 | 2.6200 × 10 | |
| WENO-AO | CPU time | 0.5849 | 1.7990 | 7.3039 | 29.1650 |
| accuracy | - | 0.88848 | 1.12442 | 0.79821 | |
| -norm error | 1.7110 × 10 | 9.2890 × 10 | 4.3090 × 10 | 2.4750 × 10 | |
| WENO-AON | CPU time | 0.5442 | 1.8045 | 7.0549 | 28.2850 |
| accuracy | - | 0.88124 | 1.10817 | 0.79992 | |
| -norm error | 1.7887 × 10 | 9.6990 × 10 | 4.4730 × 10 | 2.5580 × 10 | |
| WENO-O | CPU time | 0.5149 | 1.7442 | 6.8033 | 27.3540 |
| accuracy | - | 0.88300 | 1.11659 | 0.80623 |
| Method | N | 80 | 150 | 320 | 640 |
|---|---|---|---|---|---|
| -norm error | 10.217 × 10 | 5.2620 × 10 | 2.7250 × 10 | 1.4250 × 10 | |
| WENO-JS | CPU time | 1.4147 | 5.2543 | 21.3190 | 85.1990 |
| accuracy | - | 0.95729 | 0.94936 | 0.93529 | |
| -norm error | 8.7670 × 10 | 4.4480 × 10 | 2.2810 × 10 | 1.1930 × 10 | |
| WENO-Z | CPU time | 1.4665 | 5.4114 | 21.7280 | 87.2130 |
| accuracy | - | 0.97893 | 0.96349 | 0.93507 | |
| -norm error | 8.8940 × 10 | 4.4880 × 10 | 2.2870 × 10 | 1.1910 × 10 | |
| WENO-AO | CPU time | 1.7262 | 6.3594 | 25.7530 | 103 |
| accuracy | - | 0.98676 | 0.97262 | 0.94128 | |
| -norm error | 8.3130 × 10 | 4.2260 × 10 | 2.1720 × 10 | 1.1420 × 10 | |
| WENO-AON | CPU time | 1.5325 | 5.8208 | 23.577 | 93.4990 |
| accuracy | - | 0.97608 | 0.96027 | 0.92746 | |
| -norm error | 8.6990 × 10 | 4.4230 × 10 | 2.2690 × 10 | 1.1870 × 10 | |
| WENO-O | CPU time | 1.5241 | 5.7645 | 23.1690 | 92.6200 |
| accuracy | - | 0.97582 | 0.96297 | 0.93474 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musa, O.; Huang, G.; Wang, M. A New Smoothness Indicator of Adaptive Order Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws. Mathematics 2021, 9, 69. https://doi.org/10.3390/math9010069
Musa O, Huang G, Wang M. A New Smoothness Indicator of Adaptive Order Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws. Mathematics. 2021; 9(1):69. https://doi.org/10.3390/math9010069
Chicago/Turabian StyleMusa, Omer, Guoping Huang, and Mingsheng Wang. 2021. "A New Smoothness Indicator of Adaptive Order Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws" Mathematics 9, no. 1: 69. https://doi.org/10.3390/math9010069
APA StyleMusa, O., Huang, G., & Wang, M. (2021). A New Smoothness Indicator of Adaptive Order Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws. Mathematics, 9(1), 69. https://doi.org/10.3390/math9010069







