A Sampling-Based Sensitivity Analysis Method Considering the Uncertainties of Input Variables and Their Distribution Parameters
Abstract
:1. Introduction
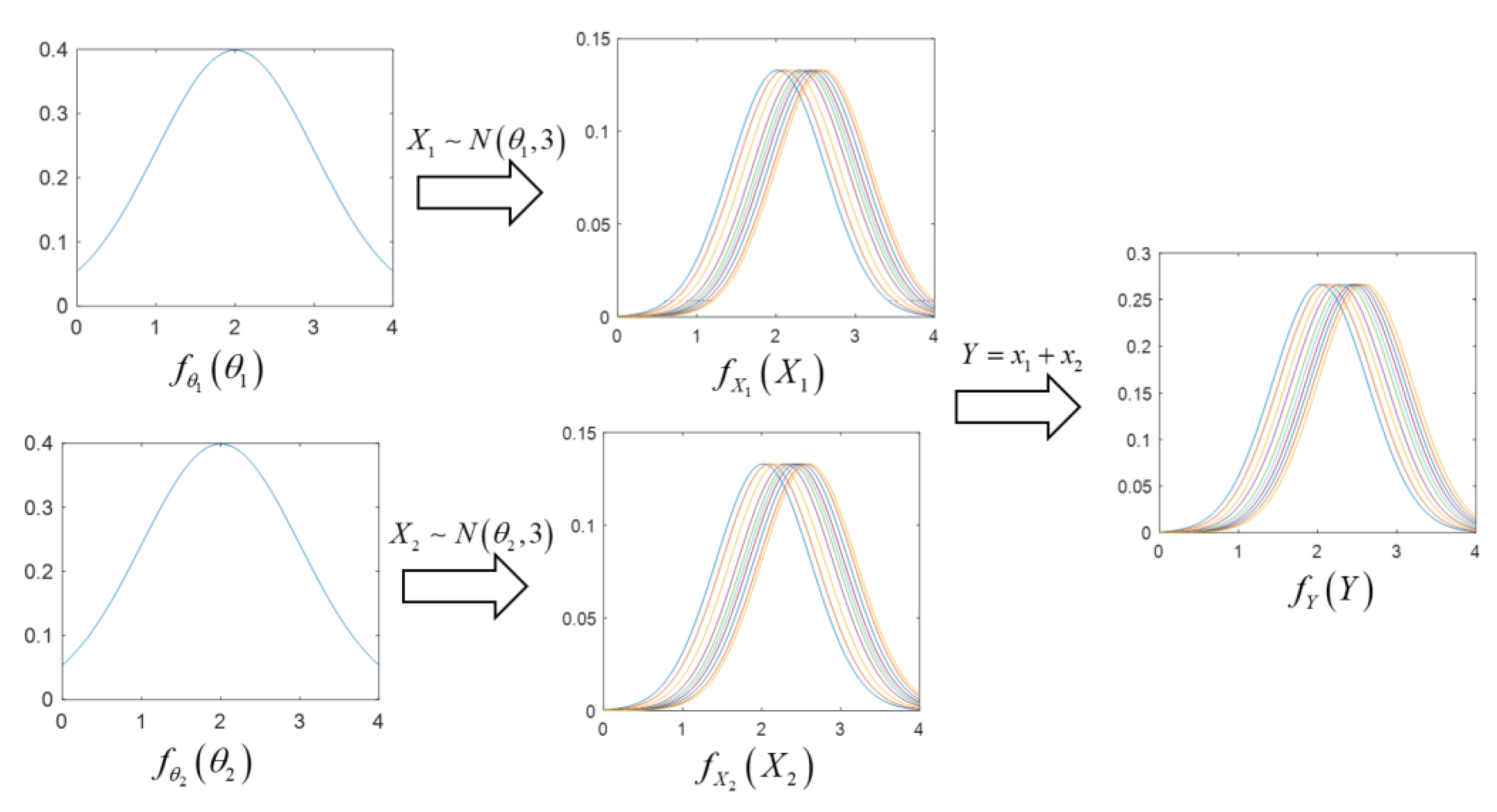
2. Problem Formulation
- (1)
- There is a nested double loop in the uncertainty analysis of performance function , which is complex and computationally expensive. With the increase in the total number of , the computational time increases exponentially. For example, there are 10 uncertainty variables, which have 2 uncertainty distribution parameters for every uncertainty variables. The sampling points for every distribution parameter is 1000. For considering the uncorrelation between 20 distribution parameters, the total sampling point of uncertainty distribution parameters is increased along with the number of distribution parameters; therefore, the total sampling point of distribution parameters is 20 × 1000 = 2 × 104; For every group of sampling points of distribution parameters, the sampling points of 10 uncertainty variables is 10 × 1000 = 104. The total number of sampling points will, therefore, be , which is time-consuming, especially for an engineering system whose performance function at every sampling point is difficult to calculate or analyze.
- (2)
- Considering the uncertainty of distribution parameters , the performance function is a function of uncertain input variables and distribution parameters simultaneously. Therefore, the SA of and should be analyzed. The analytical expression of function is difficult to obtain. Therefore, calculating the SA values is another challenge.
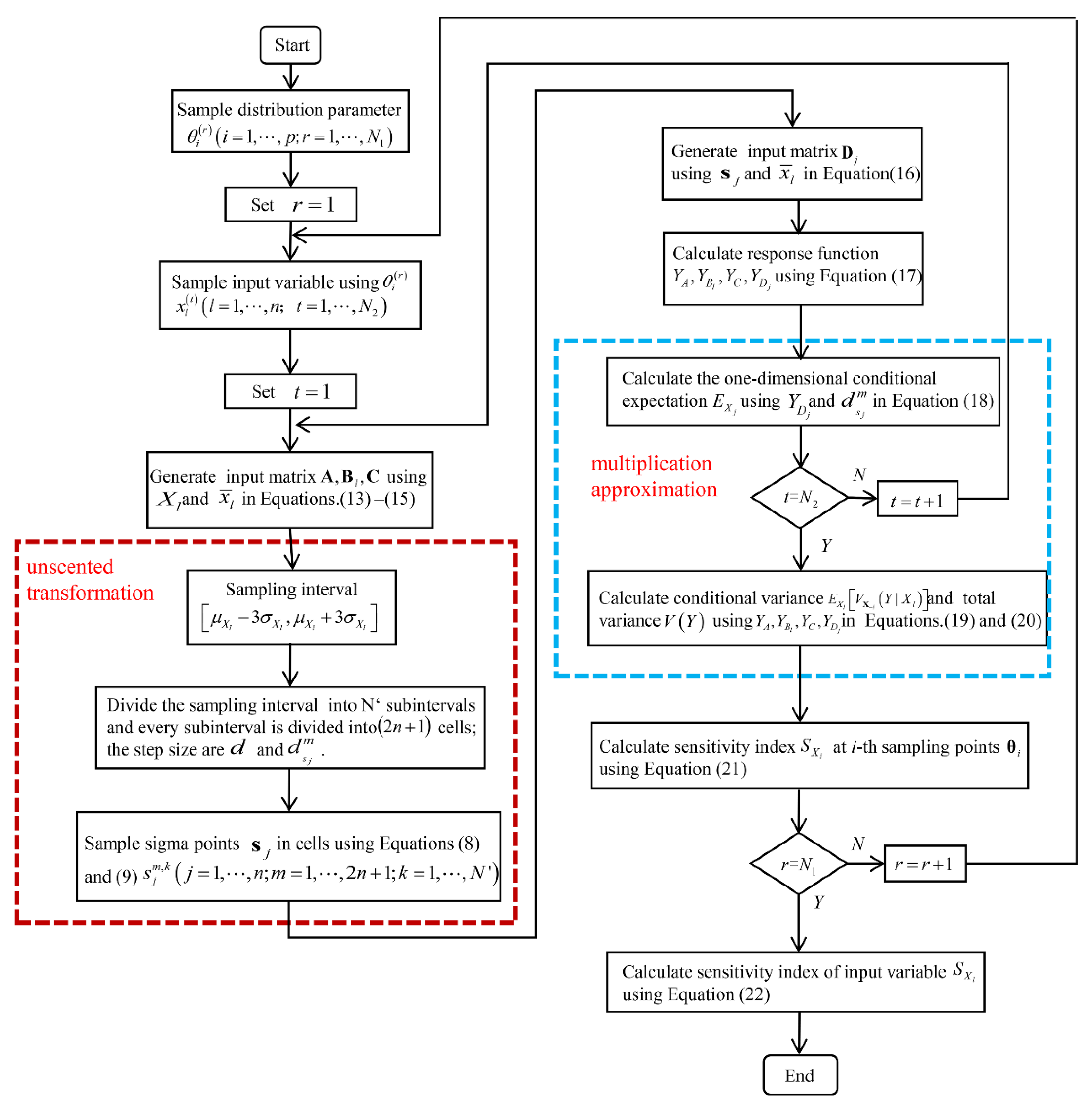
3. An Efficient Sampling-Based SA Method Based on Unscented Transformation
4. Implementation of the Proposed Sensitivity Calculation Algorithm
4.1. Calculation of the First-Order Sensitivity Index of the Input Variables
4.2. Calculation of the First-Order Sensitivity Index of the Distribution Parameters
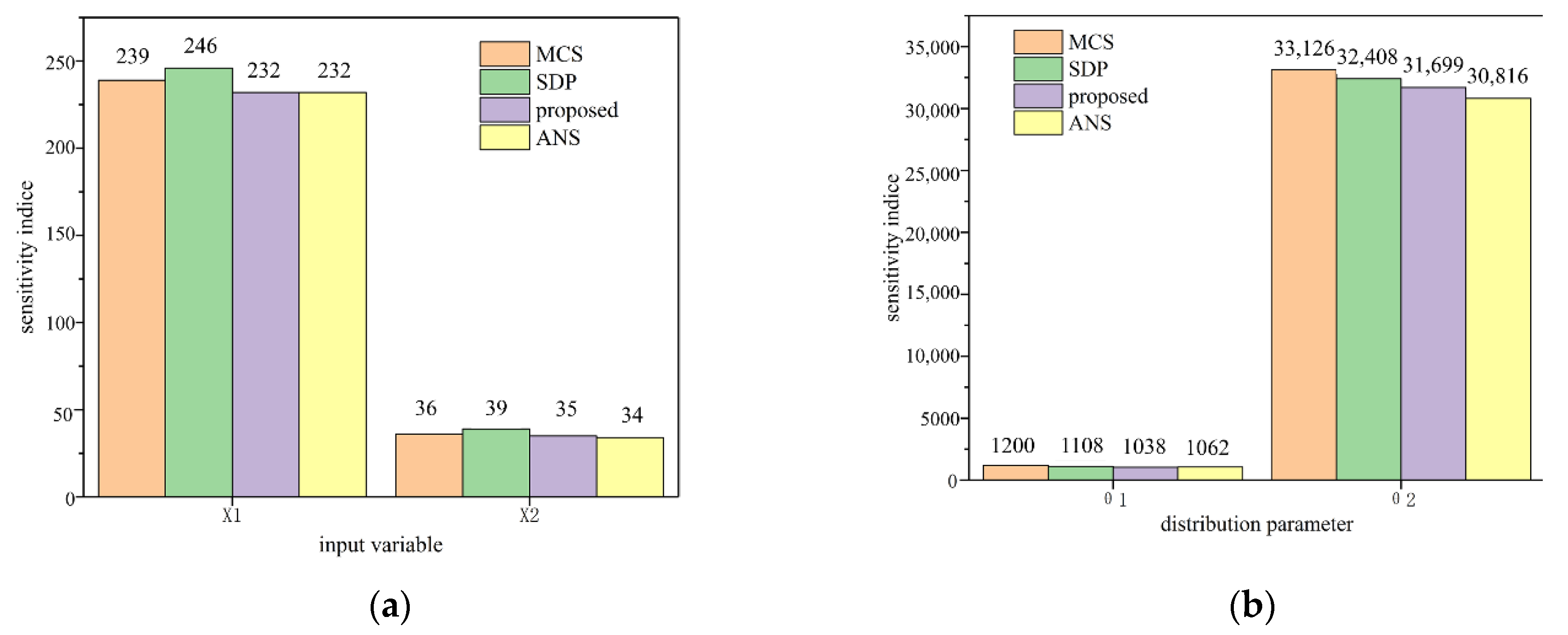
4.3. Computational Effort and Comparison to the Crude Monte-Carlo
5. Numerical and Engineering Examples
5.1. Numerical Example 1
5.2. Numerical Example 2
5.3. Numerical Example 3
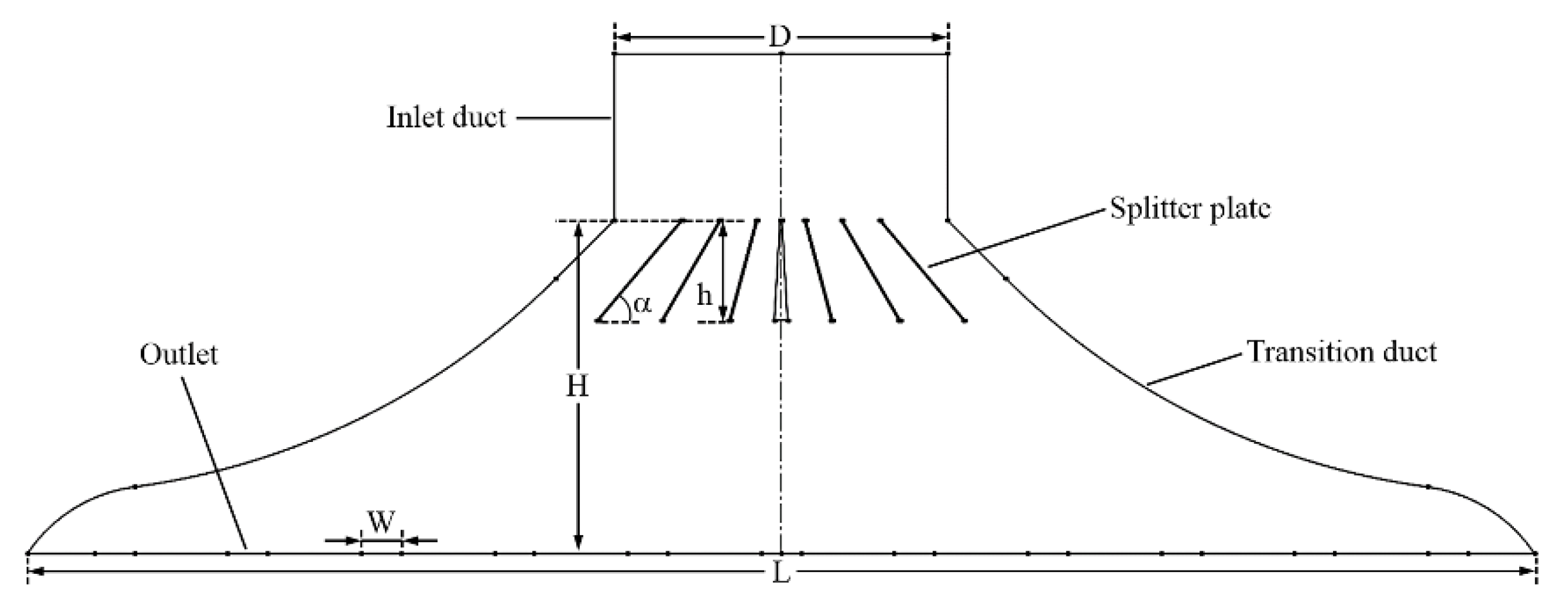
5.4. Engineering Example: Inlet Header of Heat Exchanger
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yeratapally, S.R.; Glavicic, M.G.; Argyrakis, C.; Sangid, M.D. Bayesian uncertainty quantification and propagation for validation of a microstructure sensitive model for prediction of fatigue crack initiation. Reliab. Eng. Syst. Saf. 2017, 164, 110–123. [Google Scholar] [CrossRef]
- Cheng, J.; Lu, W.; Liu, Z.; Wu, D.; Gao, W.; Tan, J. Robust optimization of engineering structures involving hybrid probabilistic and interval uncertainties. Struct. Multidiscip. Optim. 2021, 63, 1327–1349. [Google Scholar] [CrossRef]
- Wang, C.-N.; Dang, T.-T.; Nguyen, N.-A.-T. A Computational Model for Determining Levels of Factors in Inventory Management Using Response Surface Methodology. Mathematics 2020, 8, 1210. [Google Scholar] [CrossRef]
- Kala, Z.; Valeš, J. Global sensitivity analysis of lateral-torsional buckling resistance based on finite element simulations. Eng. Struct. 2017, 134, 37–47. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Probabilistic evaluation of tunnel face stability in spatially random soils using sparse polynomial chaos expansion with global sensitivity analysis. Acta Geotech. 2017, 12, 1415–1429. [Google Scholar] [CrossRef]
- Neggers, J.; Allix, O.; Hild, F.; Roux, S. Big Data in Experimental Mechanics and Model Order Reduction: Today’s Challenges and Tomorrow’s Opportunities. Arch. Comput. Methods Eng. 2017, 25, 143–164. [Google Scholar] [CrossRef] [Green Version]
- Yun, W.; Lu, Z.; Jiang, X. An efficient method for moment-independent global sensitivity analysis by dimensional reduction technique and principle of maximum entropy. Reliab. Eng. Syst. Saf. 2019, 187, 174–182. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity analysis practices: Strategies for model-based inference. Reliab. Eng. Syst. Saf. 2006, 91, 1109–1125. [Google Scholar] [CrossRef]
- Mara, T.A.; Tarantola, S. Variance-based sensitivity indices for models with dependent inputs. Reliab. Eng. Syst. Saf. 2012, 107, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.; Liu, Z.; Tang, M.; Tan, J. Robust optimization of uncertain structures based on normalized violation degree of interval constraint. Comput. Struct. 2017, 182, 41–54. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Zhou, Z.; Hu, L. An efficient multi-objective optimization method based on the adaptive approximation model of the radial basis function. Struct. Multidiscip. Optim. 2021, 63, 1385–1403. [Google Scholar] [CrossRef]
- Helton, J.; Johnson, J.; Sallaberry, C.; Storlie, C. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Pedersen, N.L.; Pedersen, P. Local analytical sensitivity analysis for design of continua with optimized 3D buckling behavior. Struct. Multidiscip. Optim. 2017, 57, 293–304. [Google Scholar] [CrossRef]
- Proppe, C. Local reliability based sensitivity analysis with the moving particles method. Reliab. Eng. Syst. Saf. 2021, 207, 107269. [Google Scholar] [CrossRef]
- Morozov, E.; Pagano, M.; Peshkova, I.; Rumyantsev, A. Sensitivity Analysis and Simulation of a Multiserver Queueing System with Mixed Service Time Distribution. Mathematics 2020, 8, 1277. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, Z.; Qian, Y.; Zhou, Z.; Tan, J. Non-Probabilistic Robust Equilibrium Optimization of Complex Uncertain Structures. J. Mech. Des. 2019, 142, 1–44. [Google Scholar] [CrossRef]
- Antoniadis, A.; Lambert-Lacroix, S.; Poggi, J.-M. Random forests for global sensitivity analysis: A selective review. Reliab. Eng. Syst. Saf. 2021, 206, 107312. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chowdhury, R. A hybrid approach for global sensitivity analysis. Reliab. Eng. Syst. Saf. 2017, 158, 50–57. [Google Scholar] [CrossRef]
- Papaioannou, I.; Breitung, K.; Straub, D. Reliability sensitivity estimation with sequential importance sampling. Struct. Saf. 2018, 75, 24–34. [Google Scholar] [CrossRef]
- Steiner, M.; Bourinet, J.-M.; Lahmer, T. An adaptive sampling method for global sensitivity analysis based on least-squares support vector regression. Reliab. Eng. Syst. Saf. 2019, 183, 323–340. [Google Scholar] [CrossRef] [Green Version]
- Cheng, K.; Lu, Z.; Zhang, K. Multivariate output global sensitivity analysis using multi-output support vector regression. Struct. Multidiscip. Optim. 2019, 59, 2177–2187. [Google Scholar] [CrossRef]
- Lo Piano, S.; Ferretti, F.; Puy, A.; Albrecht, D.; Saltelli, A. Variance-based sensitivity analysis: The quest for better estimators and designs between explorativity and economy. Reliab. Eng. Syst. Saf. 2021, 206, 107300. [Google Scholar] [CrossRef]
- Zhang, Z.; Buisson, M.; Ferrand, P.; Henner, M. Integration of Second-Order Sensitivity Method and CoKriging Surrogate Model. Mathematics 2021, 9, 401. [Google Scholar] [CrossRef]
- Rajabi, M.M.; Ataie-Ashtiani, B.; Simmons, C.T. Polynomial chaos expansions for uncertainty propagation and moment independent sensitivity analysis of seawater intrusion simulations. J. Hydrol. 2015, 520, 101–122. [Google Scholar] [CrossRef]
- Shi, Y.; Lu, Z.; Cheng, K.; Zhou, Y. Temporal and spatial multi-parameter dynamic reliability and global reliability sensitivity analysis based on the extreme value moments. Struct. Multidiscip. Optim. 2017, 56, 117–129. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Z.; Cheng, K.; Yun, W. A Bayesian Monte Carlo-based method for efficient computation of global sensitivity indices. Mech. Syst. Signal Process. 2019, 117, 498–516. [Google Scholar] [CrossRef]
- Hu, Z.; Mahadevan, S. Global sensitivity analysis-enhanced surrogate (GSAS) modeling for reliability analysis. Struct. Multidiscip. Optim. 2016, 53, 501–521. [Google Scholar] [CrossRef]
- Cadini, F.; Lombardo, S.S.; Giglio, M. Global reliability sensitivity analysis by Sobol-based dynamic adaptive kriging importance sampling. Struct. Saf. 2020, 87, 101998. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B. Global sensitivity analysis in the context of imprecise probabilities (p-boxes) using sparse polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2019, 187, 129–141. [Google Scholar] [CrossRef] [Green Version]
- Xiao, S.; Lu, Z.; Wang, P. Global sensitivity analysis based on distance correlation for structural systems with multivariate output. Eng. Struct. 2018, 167, 74–83. [Google Scholar] [CrossRef]
- Xu, L.; Lu, Z.; Xiao, S. Generalized sensitivity indices based on vector projection for multivariate output. Appl. Math. Model. 2019, 66, 592–610. [Google Scholar] [CrossRef]
- Li, L.; Lu, Z. A new method for model validation with multivariate output. Reliab. Eng. Syst. Saf. 2018, 169, 579–592. [Google Scholar] [CrossRef]
- Li, L.; Lu, Z. Variance-based sensitivity analysis for models with correlated inputs and its state dependent parameter solution. Struct. Multidiscip. Optim. 2017, 56, 919–937. [Google Scholar] [CrossRef]
- Decarlo, E.C.; Mahadevan, S.; Smarslok, B.P. Efficient global sensitivity analysis with correlated variables. Struct. Multidiscip. Optim. 2018, 58, 2325–2340. [Google Scholar] [CrossRef]
- Cacciola, M.; La Foresta, F.; Morabito, F.C.; Versaci, M. Advanced use of soft computing and eddy current test to evaluate mechanical integrity of metallic plates. NDT E Int. 2007, 40, 357–362. [Google Scholar] [CrossRef]
- Alruwaili, M.; Siddiqi, M.H.; Javed, M.A. A robust clustering algorithm using spatial fuzzy C-means for brain MR images. Egypt. Inform. J. 2020, 21, 51–66. [Google Scholar] [CrossRef]
- Zhao, Y.-G.; Zhang, X.-Y.; Lu, Z.-H. Complete monotonic expression of the fourth-moment normal transformation for structural reliability. Comput. Struct. 2018, 196, 186–199. [Google Scholar] [CrossRef]
- Peng, X.; Gao, Q.; Li, J.; Liu, Z.; Yi, B.; Jiang, S. Probabilistic Representation Approach for Multiple Types of Epistemic Uncertainties Based on Cubic Normal Transformation. Appl. Sci. 2020, 10, 4698. [Google Scholar] [CrossRef]
- Sankararaman, S.; Mahadevan, S. Likelihood-based representation of epistemic uncertainty due to sparse point data and/or interval data. Reliab. Eng. Syst. Saf. 2011, 96, 814–824. [Google Scholar] [CrossRef]
- Peng, X.; Li, J.; Jiang, S. Unified uncertainty representation and quantification based on insufficient input data. Struct. Multidiscip. Optim. 2017, 56, 1305–1317. [Google Scholar] [CrossRef]
- Wang, P.; Lu, Z.; Xiao, S. Variance-based sensitivity analysis with the uncertainties of the input variables and their distribution parameters. Commun. Stat. Simul. Comput. 2017, 47, 1103–1125. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Lamboni, M. Multivariate sensitivity analysis: Minimum variance unbiased estimators of the first-order and total-effect covariance matrices. Reliab. Eng. Syst. Saf. 2019, 187, 67–92. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Efficient computation of global sensitivity indices using sparse polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2010, 95, 1216–1229. [Google Scholar] [CrossRef]
- Yun, W.; Lu, Z.; Jiang, X. An efficient sampling approach for variance-based sensitivity analysis based on the law of total variance in the successive intervals without overlapping. Mech. Syst. Signal Process. 2018, 106, 495–510. [Google Scholar] [CrossRef]
- Rocco Sanseverino, C.M.; Ramirez-Marquez, J.E. Uncertainty propagation and sensitivity analysis in system reliability assessment via unscented transformation. Reliab. Eng. Syst. Saf. 2014, 132, 176–185. [Google Scholar] [CrossRef]
- Yun, W.; Lu, Z.; Zhang, K.; Jiang, X. An efficient sampling method for variance-based sensitivity analysis. Struct. Saf. 2017, 65, 74–83. [Google Scholar] [CrossRef]
- Bartoň, M.; Calo, V.M. Optimal quadrature rules for odd-degree spline spaces and their application to tensor-product-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2016, 305, 217–240. [Google Scholar] [CrossRef] [Green Version]
- Bartoň, M.; Calo, V.M. Gauss–Galerkin quadrature rules for quadratic and cubic spline spaces and their application to isogeometric analysis. Comput. Des. 2017, 82, 57–67. [Google Scholar] [CrossRef] [Green Version]
- Hiemstra, R.R.; Calabrò, F.; Schillinger, D.; Hughes, T.J.R. Optimal and reduced quadrature rules for tensor product and hierarchically refined splines in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2017, 316, 966–1004. [Google Scholar] [CrossRef] [Green Version]
- Johannessen, K.A. Optimal quadrature for univariate and tensor product splines. Comput. Methods Appl. Mech. Eng. 2017, 316, 84–99. [Google Scholar] [CrossRef]
- Zhang, X.; Pandey, M.D. Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method. Struct. Saf. 2013, 43, 28–40. [Google Scholar] [CrossRef]
- Richter, J. Reliability estimation using unscented transformation. In Proceedings of the 2011 3rd International Workshop on Dependable Control of Discrete Systems, Saarbrucken, Germany, 15–17 June 2011; pp. 102–107. [Google Scholar]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Peng, X.; Qiu, C.; Li, J.; Jiang, S. Thermal Compensation Effect of Passage Arrangement Design for Inlet Flow Maldistribution in Multiple-Stream Plate-Fin Heat Exchanger. Heat Transf. Eng. 2018, 40, 1239–1248. [Google Scholar] [CrossRef]
- Lalot, S.; Florent, P.; Lang, S.; Bergles, A. Flow maldistribution in heat exchangers. Appl. Therm. Eng. 1999, 19, 847–863. [Google Scholar] [CrossRef]




| Sensitivity Indices | Accurate Values | Proposed Method | MCS | ||
|---|---|---|---|---|---|
| 324 | 324.30 | 0.09% | 323.91 | 0.03% | |
| 87 | 86.96 | 0.05% | 87.13 | 0.15% | |
| 175 | 175.05 | 0.03% | 176.06 | 0.60% | |
| 0 | 0 | 0 | 0 | 0 | |
| 1328 | 1316.32 | 0.89% | 1323.52 | 0.34% | |
| 2736 | 2879.15 | 4.97% | 2864.03 | 4.47% |
| Sensitivity Indices | Proposed Method | MCS | |
|---|---|---|---|
| 0.47 | 0. 48 | 2.13% | |
| 0.11 | 0. 12 | 9.10% | |
| 0.92 | 0. 93 | 1.09% | |
| 0.73 | 0. 70 | 4.11% |
| Sensitivity Indices | Proposed Method | MCS |
|---|---|---|
| 0.95 | 0.95 | |
| 0.05 | 0.05 | |
| 0.95 | 0.93 | |
| 0.78 | 0.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Xu, X.; Li, J.; Jiang, S. A Sampling-Based Sensitivity Analysis Method Considering the Uncertainties of Input Variables and Their Distribution Parameters. Mathematics 2021, 9, 1095. https://doi.org/10.3390/math9101095
Peng X, Xu X, Li J, Jiang S. A Sampling-Based Sensitivity Analysis Method Considering the Uncertainties of Input Variables and Their Distribution Parameters. Mathematics. 2021; 9(10):1095. https://doi.org/10.3390/math9101095
Chicago/Turabian StylePeng, Xiang, Xiaoqing Xu, Jiquan Li, and Shaofei Jiang. 2021. "A Sampling-Based Sensitivity Analysis Method Considering the Uncertainties of Input Variables and Their Distribution Parameters" Mathematics 9, no. 10: 1095. https://doi.org/10.3390/math9101095






