A Generalized Quasi Cubic Trigonometric Bernstein Basis Functions and Its B-Spline Form
Abstract
1. Introduction
2. Materials and Methods
2.1. Bernstein Basis Functions and Bézeir Curves
2.2. Extended Chebyshev Space and Blossom Theory
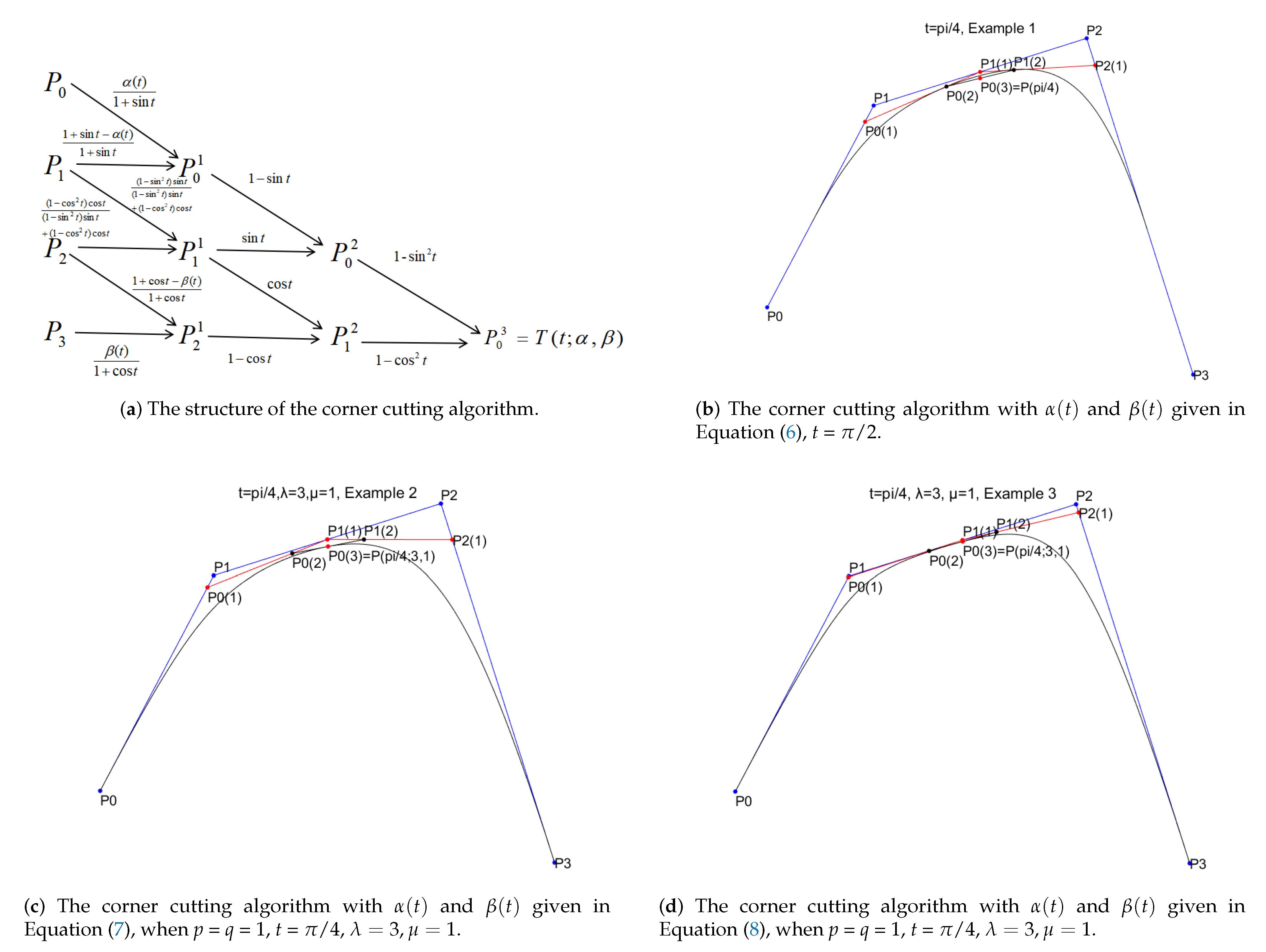
3. Generalized Quasi Cubic Trigonometric Bernstein Basis Functions
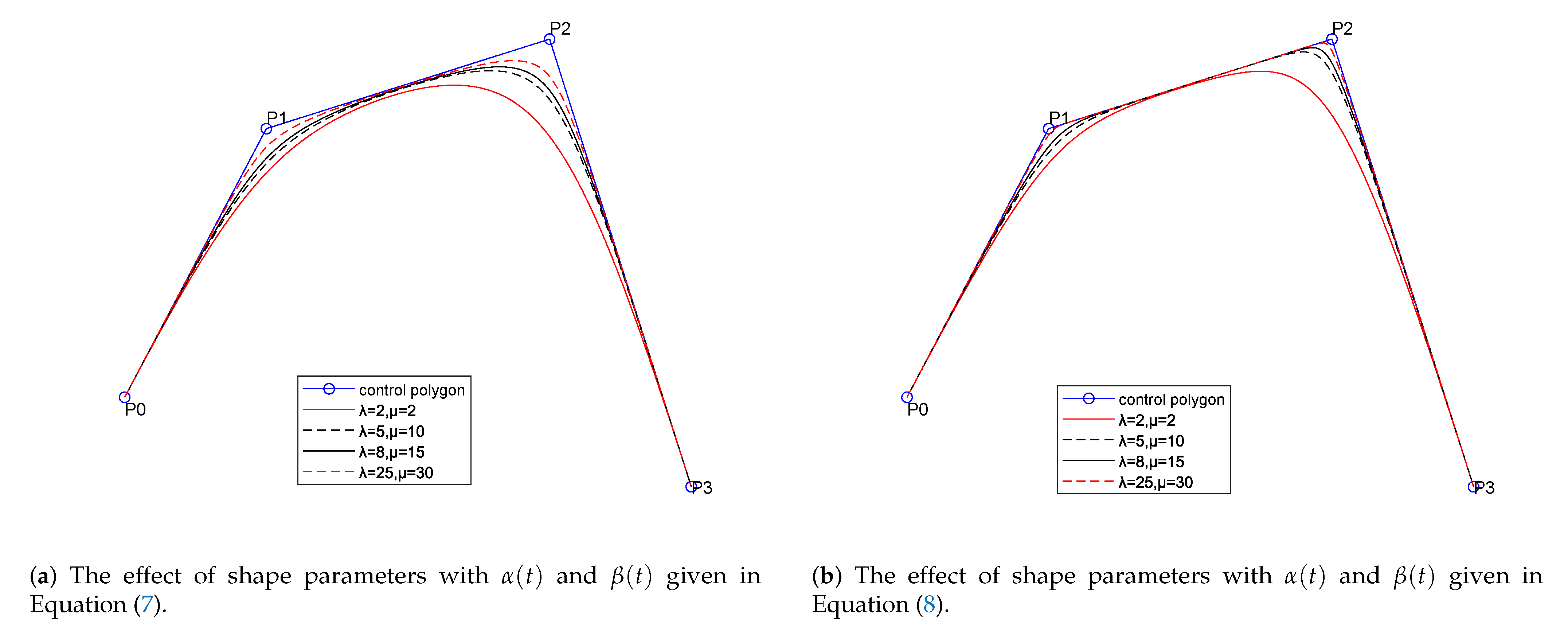
3.1. Construction and Properties
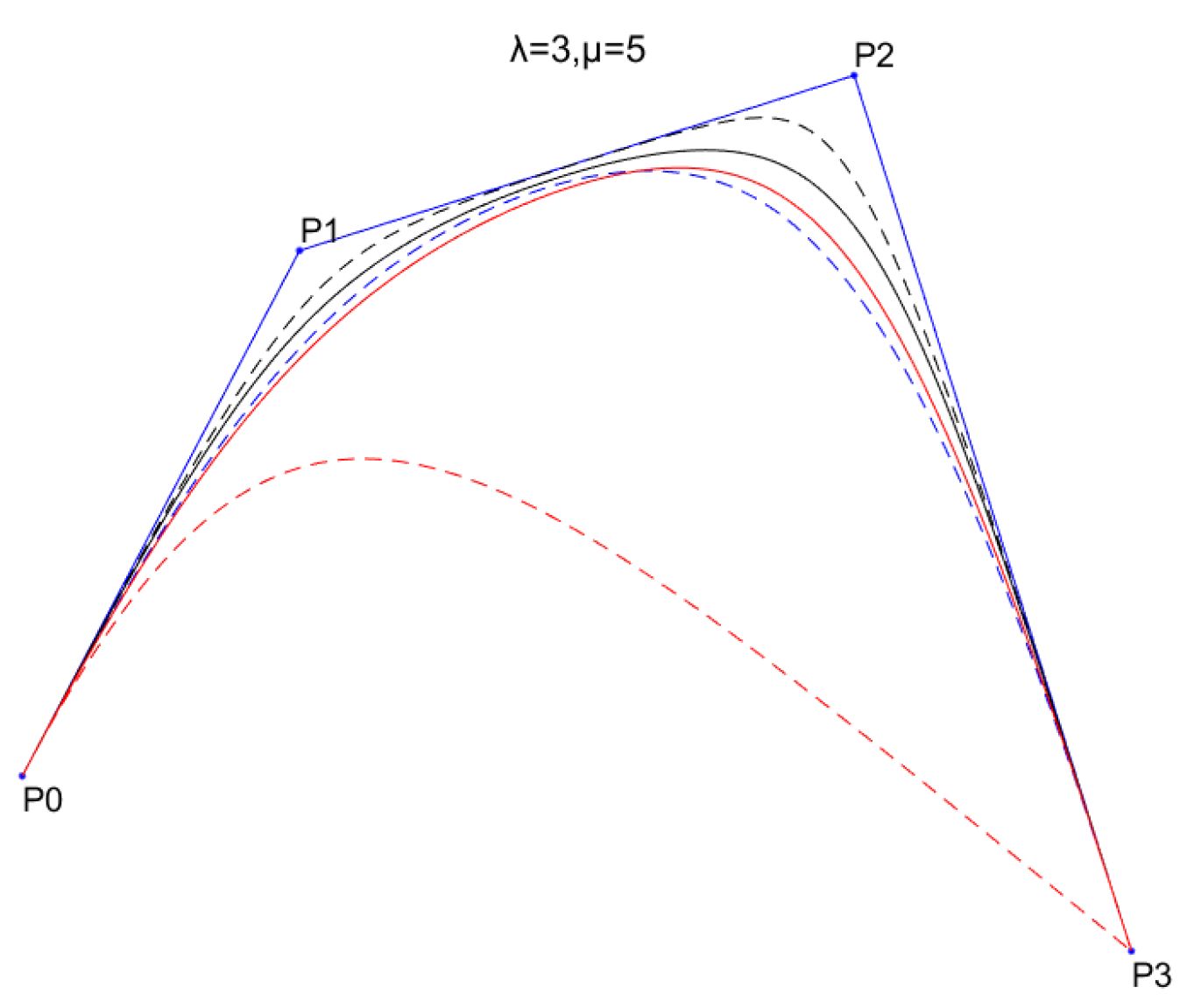
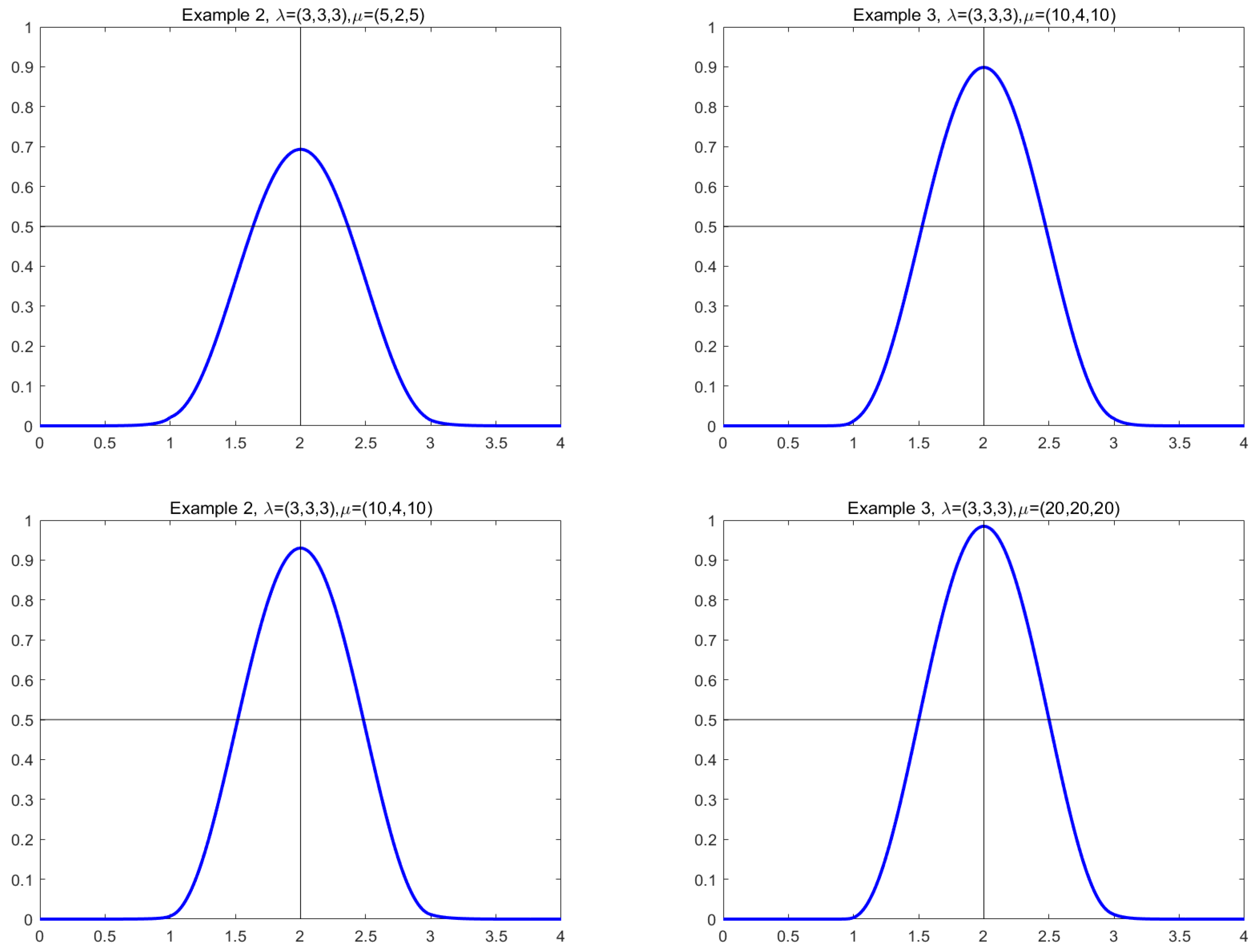
3.2. New Generalized Quasi Cubic Trigonometric Bézier Curve
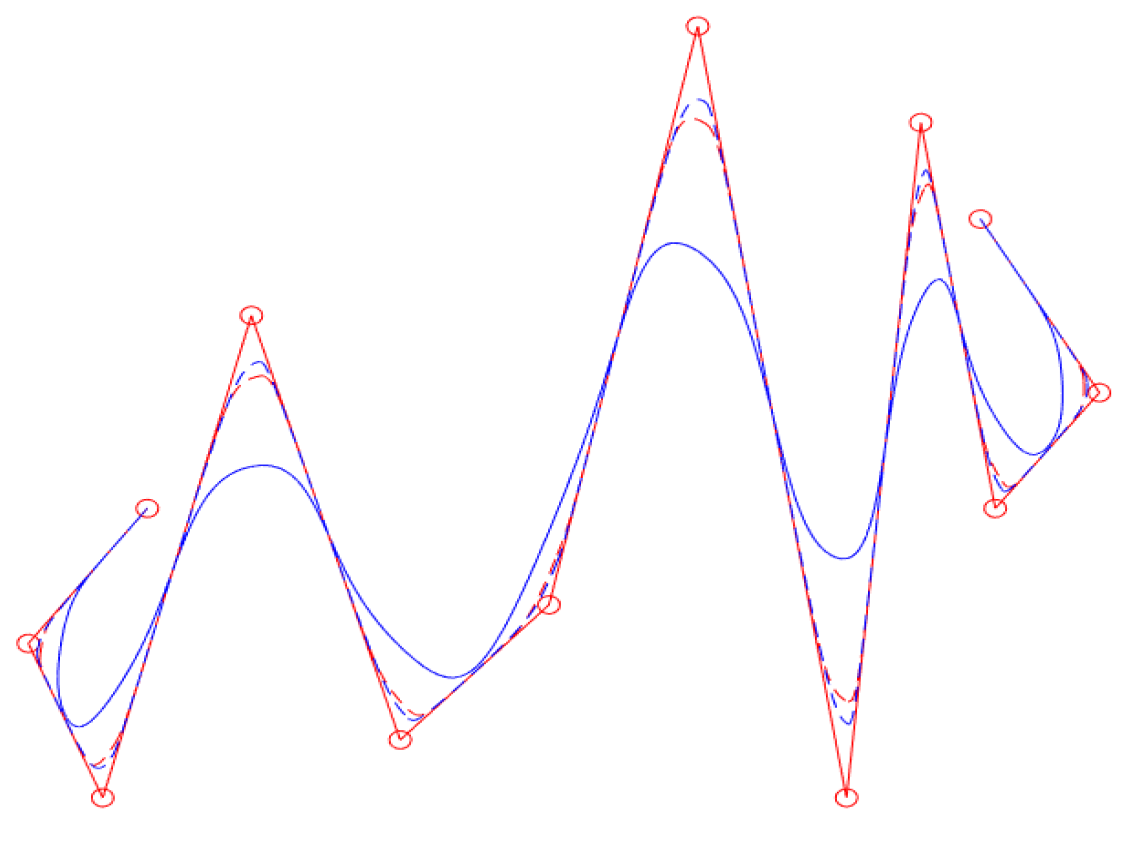
4. New Generalized Quasi Cubic Trigonometric B-Spline Basis with Two Shape Functions
4.1. New Generalized Quasi Cubic Trigonometric B-Spline Basis Functions
4.2. Properties of the New Generalized Quasi Cubic Trigonometric B-Spline Basis Functions
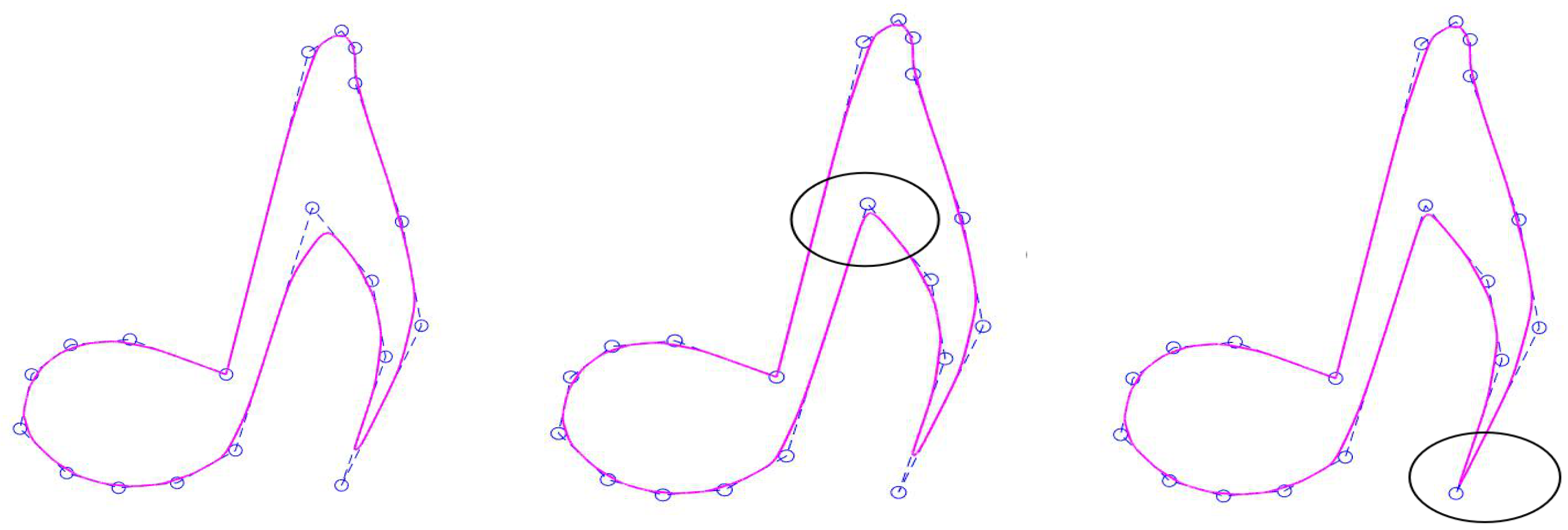
4.3. New Generalized Quasi Cubic Trigonometric B-Spline Curves
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EC | Extended Chebychev |
| ECC | Extended Complete Chebychev |
References
- Nielson, G.M. A locally controllable spline with tension for interactive curve design. Comput. Aided Geom. Des. 1984, 1, 199–205. [Google Scholar] [CrossRef]
- Brian, A.B. Local control of bias and tension in Beta-splines. ACM Trans. Graph. 1983, 2, 109–134. [Google Scholar] [CrossRef]
- Costantini, P. Curve and surface construction using variable degree polynomial splines. Comput. Aided Geom. Des. 2000, 17, 419–446. [Google Scholar] [CrossRef]
- Shen, W.Q.; Wang, G.Z.; Yin, P. Explicit representations of changeable degree spline basis functions. J. Comput. Appl. Math. 2013, 238, 39–50. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. New cubic rational basis with tension shape parameters. Appl. Math. J. Chin. Univ. Ser. B 2015, 30, 273–298. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L.; Liu, S.J. Curve construction based on four αβ-Bernstein-like basis functions. J. Comput. Appl. Math. 2015, 273, 160–181. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. Curves and surfaces construction based on new basis with exponential functions. Acta Appl. Math. 2014, 129, 183–203. [Google Scholar] [CrossRef]
- Ramshaw, L. Blossoming: A Connect-the-Dots Approach to Splines; Digital Systems Research: Palo Alto, CA, USA, 1987. [Google Scholar]
- Mazure, M.L.; Laurent, P.J. Piecewise smooth spaces in duality: Application to blossoming. J. Approx. Theory 1999, 98, 316–353. [Google Scholar] [CrossRef]
- Mazure, M.L. Quasi-Chebychev splines with connexion matrices: Application to variable degree polynomial splines. Comput. Aided Geom. Des. 2001, 18, 287–298. [Google Scholar] [CrossRef]
- Mazure, M.L. Blossoms and optimal bases. Adv. Comput. Math. 2004, 20, 177–203. [Google Scholar] [CrossRef]
- Costantini, P.; Lyche, T.; Manni, C. On a class of weak Tchebysheff systems. Numer. Math. 2005, 101, 333–354. [Google Scholar] [CrossRef]
- Mazure, M.L. On dimension elevation in Quasi Extended Chebyshev spaces. Numer. Math. 2008, 109, 459–475. [Google Scholar] [CrossRef]
- Costantini, P.; Pelosi, F.; Sampoli, M.L. New spline spaces with generalized tension properties. BIT Numer. Math. 2008, 48, 665–688. [Google Scholar] [CrossRef]
- Han, X.L. Cubic trigonometric polynomial curves with a shape parameter. Comput. Aided Geom. Des. 2004, 21, 535–548. [Google Scholar] [CrossRef]
- Wu, X.Q.; Han, X.L.; Luo, S. Quadratic trigonometric polynomial Bézier curves with a shape parameter. J. Eng. Graph. 2008, 1, 82–87. [Google Scholar] [CrossRef]
- Han, X.A.; Ma, Y.C.; Huang, X.L. The cubic trigonometric Bézier curve with two shape parameters. Appl. Math. Lett. 2008, 22, 226–231. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. New trigonometric basis possessing exponential shape parameters. J. Comput. Math. 2015, 33, 642–684. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, G.C.; Nhon, N.T. New trigonometric basis possessing denominator shape parameters. Math. Probl. Eng. 2018, 9569834. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Liu, Z. A class of trigonometric Bernstein-type basis functions with four shape parameters. Math. Probl. Eng. 2019. [Google Scholar] [CrossRef]
- Han, X.L.; Zhu, Y.P. Curve construction based on five trigonometric blending functions. BIT Numer. Math. 2012, 52, 953–979. [Google Scholar] [CrossRef]
- Majeed, A.; Abbas, M.; Qayyum, F.; Miura, K.T.; Misro, M.Y.; Nazir, T. Geometric modeling using new cubic trigonometric B-spline functions with shape parameter. Mathematics 2020, 8, 2102. [Google Scholar] [CrossRef]
- Peña, J.M. Shape Preserving Representations in Computer-Aided Geometric Design; Nova Science Publishers: Hauppauge, NY, USA, 1999. [Google Scholar]
- Peña, J.M. Shape preserving representations for trigonometric polynomial curves. Comput. Aided Geom. Des. 1997, 14, 5–11. [Google Scholar] [CrossRef]
- Carnicer, J.M.; Peña, J.M. Total positive bases for shape preserving curve design and optimality of B-splines. Comput. Aided Geom. Des. 1994, 11, 635–656. [Google Scholar] [CrossRef]
- Pottmann, H. The geometry of Tchebycheffian splines. Comput. Aided Geom. Des. 1993, 10, 181–210. [Google Scholar] [CrossRef]
- Mazure, M.L. Blossoming: A Geometrical Approach. Constr. Approx. 1999, 15, 33–68. [Google Scholar] [CrossRef]
- Mazure, M.L. Which spaces for design? Numer. Math. 2008, 110, 357–392. [Google Scholar] [CrossRef]
- Farin, G. Curves and Surfaces for Computer Aided Geometric Design; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Gori, L.; Pitolli, F. Totally positive refinable functions with general dilation M. Appl. Numer. Math. 2017, 112, 17–26. [Google Scholar] [CrossRef]
- Goodman, T.N. Total Positivity and the Shape of Curves. In Total Positivity and Its Applications; Gasca, M., Micchelli, C.A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; pp. 157–186. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Zhu, Y. A Generalized Quasi Cubic Trigonometric Bernstein Basis Functions and Its B-Spline Form. Mathematics 2021, 9, 1154. https://doi.org/10.3390/math9101154
Fu Y, Zhu Y. A Generalized Quasi Cubic Trigonometric Bernstein Basis Functions and Its B-Spline Form. Mathematics. 2021; 9(10):1154. https://doi.org/10.3390/math9101154
Chicago/Turabian StyleFu, Yunyi, and Yuanpeng Zhu. 2021. "A Generalized Quasi Cubic Trigonometric Bernstein Basis Functions and Its B-Spline Form" Mathematics 9, no. 10: 1154. https://doi.org/10.3390/math9101154
APA StyleFu, Y., & Zhu, Y. (2021). A Generalized Quasi Cubic Trigonometric Bernstein Basis Functions and Its B-Spline Form. Mathematics, 9(10), 1154. https://doi.org/10.3390/math9101154