Application of Delaunay Triangulation and Catalan Objects in Steganography

Abstract

This paper presents a new method of steganography based on a combination of Catalan objects and Voronoi–Delaunay triangulation. Two segments are described within the proposed method. The first segment describes the process of embedding data and generating a complex stego key. The second segment explains the extraction of a hidden message. The main goal of this paper is to transfer a message via the Internet (or some other medium) using an image so that the image remains absolutely unchanged. In this way, we prevented the potential attacker from noticing some secret message hidden in that picture. Additionally, the complex stego key consists of three completely different parts (the image, the encrypted Delaunay triangulation, and the array R_k in Base64 code), which are very difficult to relate with each other. Finally, a few security analyses of the proposed method are conducted, as well as the corresponding steganalysis.

1. Introduction

When we talk about protecting the privacy of data in an image—that is, hiding a message within an image—we can say that this is a new challenge in cyberspace. The image as a carrier of a secret message and its design, encryption schemes, creation of algorithms, and methods have attracted the attention of many researchers. Thus, in [1], the authors mentioned many techniques used in image encryption which attackers encounter. Some of these techniques are Fridrich image encryption schemes, frameless diffusion, and so on. In contrast to the mentioned techniques, the proposed technique is based on a combination of Delaunay’s triangulation of the binary record of an image, Catalan objects (as the mixing key), and stack permutation as the encryption method.

Encouraged by the fact that, in this paper, we prevent the attacker from accessing the secret message, we came up with the idea that the bearer of the secret message is an image that will not change its original form after installing the secret message. The main motivation was how to hide the message in the picture and not change its shape. Then, we study the procedure of disassembling the stego key so that the attacker would be confused when creating the attack method. The basic question is this: how can an attacker get a secret message even if, in some cases, he manages to connect the parts in the stego key?

The method we are presenting aims to use the image to transmit hidden information to the desired user via the Internet. This steganography algorithm, in the encryption process, is based on encoding an image into a binary record, converting a secret message (hidden information) into a binary record, and creating a Delaunay triangulation of a binary record of an image whose vertices are the carriers of the secret message bit. After that, by applying the stack permutation method and Catalan objects over the coordinates (x,y) of the Delaunay vertex, a completely new encrypted triangulation is obtained whose vertex coordinates (x,y) are placed in a sequence.

The original image, an encrypted string with vertex coordinates (x,y) in the form of Base64 code and an encrypted Delaunay triangulation, are sent to the user via the medium (Internet). Finally, in the process of decryption, by reapplying the Catalan object and the stack permutation method, the original Delaunay triangulation of the binary record of the image is created, and the original information is revealed.

The paper is organized as follows. Section 2 gives a brief survey of the previous results in the field of the research. Section 3 contains some preliminary considerations about Voronoi–Delaunay triangulations, Catalan objects, and the stack permutation method, followed by the presentation of the proposed steganographic method, concerning both embedding data and stego key generation, and extraction of the hidden data. In Section 4, we present the results of the stego analysis and security testing. At the end, concluding remarks and further research suggestions are given in Section 5.

2. Related Work

The authors have worked in their previous investigations with Catalan numbers and objects in many areas, such as cryptography, steganography, computational geometry, and combinatorics. A few applications of combinatorics in steganography are presented in [2,3,4]. In [5], the authors studied the properties of the Catalan numbers and the lattice path as well as their application in cryptography. Saračević et al. in [6] investigated applications of Catalan numbers in steganography. Additional data hiding techniques based on binary (Dyck) words appeared in [7].

In [8], a steganography method using pixel intensity value decomposition and well-known number sequences (Fibonacci, Lucas, and Catalan–Fibonacci) are offered. It is defined as a method which uses two generators of random numbers. The first is the generator of the Catalan numbers, while the second one generates Lucas number sequences. The list of image steganography techniques is presented in [9]. The combinatorics results also can be used in steganography as presented by Bhaskari et al. [10]. In [11], a secret key method based on random numbers is presented. The superior security is the main advantage of the proposed technique, because the original image and the stego images are unchanged.

In [12,13,14], an image steganography method improving the embedding capacity in stego objects is proposed. This method, based on pixel overlapping, uses both the modulus function and overlapped PVD. The number of bits per pixel, as well as the execution time, are compared to the existing methods. Suitable RS analysis demonstrates the method’s security. Besides that, a multi-stego image method introduced in [15] uses modified least significant bit matching to improve the embedding capacity as well as image quality. A bit flipping technique of hiding data within the image is proposed in [16].

Recently, the authors of [1] analyzed many techniques of steganography and image encryption. One of the mentioned techniques is an iterative reconstruction of the scheme for the compression of encrypted binary image files using a random Markov field for the characterization of the corresponding ordinary images in the spatial domain. In addition, in relation to Mark’s random fields, decoding and decompression are based on a factorial graph methodology, using a two-part graph representing the factorization of functions in some subfunctions [17].

3. Proposed Steganographic Method

First, we will expose some preliminaries about Voronoi–Delaunay triangulation, Catalan numbers and objects, and the stack permutation method as well.

3.1. Voronoi–Delaunay Triangulation

Let $P=\left\{p_1,p_2,\dots ,p_n\right\}$ denote a set of points in a plane given by their (x,y) coordinates. These points we denote as centers or sites. Delaunay triangulation of set $P$ is a unique triangulation where no triangle-circumscribing circle contains other sites in its interior. On the other hand, the counterpart of Delaunay triangulation is the Voronoi diagram. A Voronoi diagram for some set of sites also partitions a plane into the regions, where every region consists of all points closer to a site $p_i$ than to any other site.

To more clearly describe the process of Delaunay triangulation of a binary image record, let us first explain the process of obtaining the Delaunay triangulation. It is essentially based on the fact that in the circle drawn around the triangle, there must be no more than three points on the circle and inside it. In the process of creating the Delaunay triangulation, we will first explain the term, namely the edges of the Delaunay diagram. We say that the edge $\overline{p_i{p}_j}$ belongs to the Delaunay diagram if there is a circle $C_{ij}$ to which $p_i$ and $p_j$ belong, no other center from $P$ lies inside the circle, and the center of the circle $C_{ij}$ lies on the edge of the Voronoi diagram defined with $V\left(p_i\right)$ and $V\left(p_j\right)$. The three points $p_i$, $p_j$, and $p_k$ are the chords of the Delaunay diagram of the set $P$ if and only if the circle through the points $p_i$, $p_j$, and $p_k$ does not contain other points from $P$ within the circle. The following definition of the Delaunay triangulation applies to this statement.

Definition 1.

For the triangulation $\mathcal{T}$of a set of points in the plane$P$, we say that it is a Delaunay triangulation if and only if the drawn circle of any triangle in $\mathcal{T}$does not contain points from $P$within the circle. Triangulation defined in this way is also called a legal Delaunay triangulation. Figure 1 shows the Delaunay triangulation.

It can be noticed that within the circles $C\left(p_i p_j p_m\right)$ and $C\left(p_i p_j p_k\right)$, legal triangulations $\Delta p_i p_j p_m$ and $\Delta p_i p_j p_k$ are formed. If a point (vertex) happens to appear by chance, as in our case with topic $p_l$, then these triangulations would be illegal Delaunay triangulations. If we want to legalize them, it is necessary to remove the line $\overline{p_m{p}_j}$ and to form a new one:$\overline{p_l{p}_i}$. The process of edge legalization is defined by the legalize edge algorithm [18]. The Voronoi diagram and the Delaunay triangulation are completely dual (i.e., the vertices of the Delaunay triangulation are the Voronoi areas in the division of space). Some of Voronoi–Delaunay triangulation’s useful properties are uniqueness and independence from the starting point, formed triangles being in the form of equilateral triangles, there being no other point in the circles of the triangles (circle property), the convex set being triangulated, the segment obtained from the nearest pair of points being in triangulation, and the segment obtained from the point and its nearest point being the side of the triangle in triangulation.

3.2. Catalan Numbers and Catalan Objects

Catalan numbers are calculated by the following Equation [19]:

$$C_n=\frac{\left(2n\right)!}{\left(n+1\right)!n!}=\frac{1}{n+1}\left(\begin{array}{c}2n\\ n\end{array}\right),n\ge 0$$

(1)

These numbers count a series of combinatorial objects. Hence, objects counted by a Catalan number are referred to as Catalan objects. Here, we use Catalan objects as Catalan keys. For the selected $n$, $C_n$ is the total number of bit strings that contain exactly $n$ ‘1’ bits and $n$ ‘0’ bits and satisfy the inherent bit balance. A simple example of generating $C_3=5$ Catalan keys for $n=3$ is shown in Figure 2. For example, for $n=4$, according to Equation (1), we have a set of $C_n=14$ values that satisfy the bit balancing property. The decimal equivalents of these bit strings are 170, 172, 178, 180, 184, 202, 204, 210, 212, 216, 226, 228, 232, and 240, while these bit strings are as follows: 10101010, 10101100, 10110010, 10110100, 10111000, 11001010, 11001100, 11010010, 11010100, 11011000, 11100010, 11100100, 11101000, and 11110000.

3.3. Stack Permutation Method

In the process of encrypting the vertex coordinates of the Delaunay triangles, we mentioned the stack permutation method of the Catalan key. The stack is an abstract type of data structure with two basic operations: push and pop. Stack permutations, as a method for solving combinatorial problems, can also be generated based on the properties of the Catalan key:

• If the current bit in the key is “1”, the push operation is needed, and the number of occurrences of this bit in the record is entered on the left;
• If the bit value “0” appears, the pop operation is needed, and the bit is ejected from the stack.

We will give here an example of encoding one of the coordinates (x, y) of the Delaunay triangle vertex for the triangle in the image using stack permutations. The x coordinate has a value of x = 1430. Its binary record is 1430₁₀ = 10110010110₂, which has $n=11$ bits. The value of the Catalan key is K = 2816098. Its binary record is 2816098₁₀ = 1010101111100001100010₂, which has $2n=22$ bits. Figure 3 describes the details.

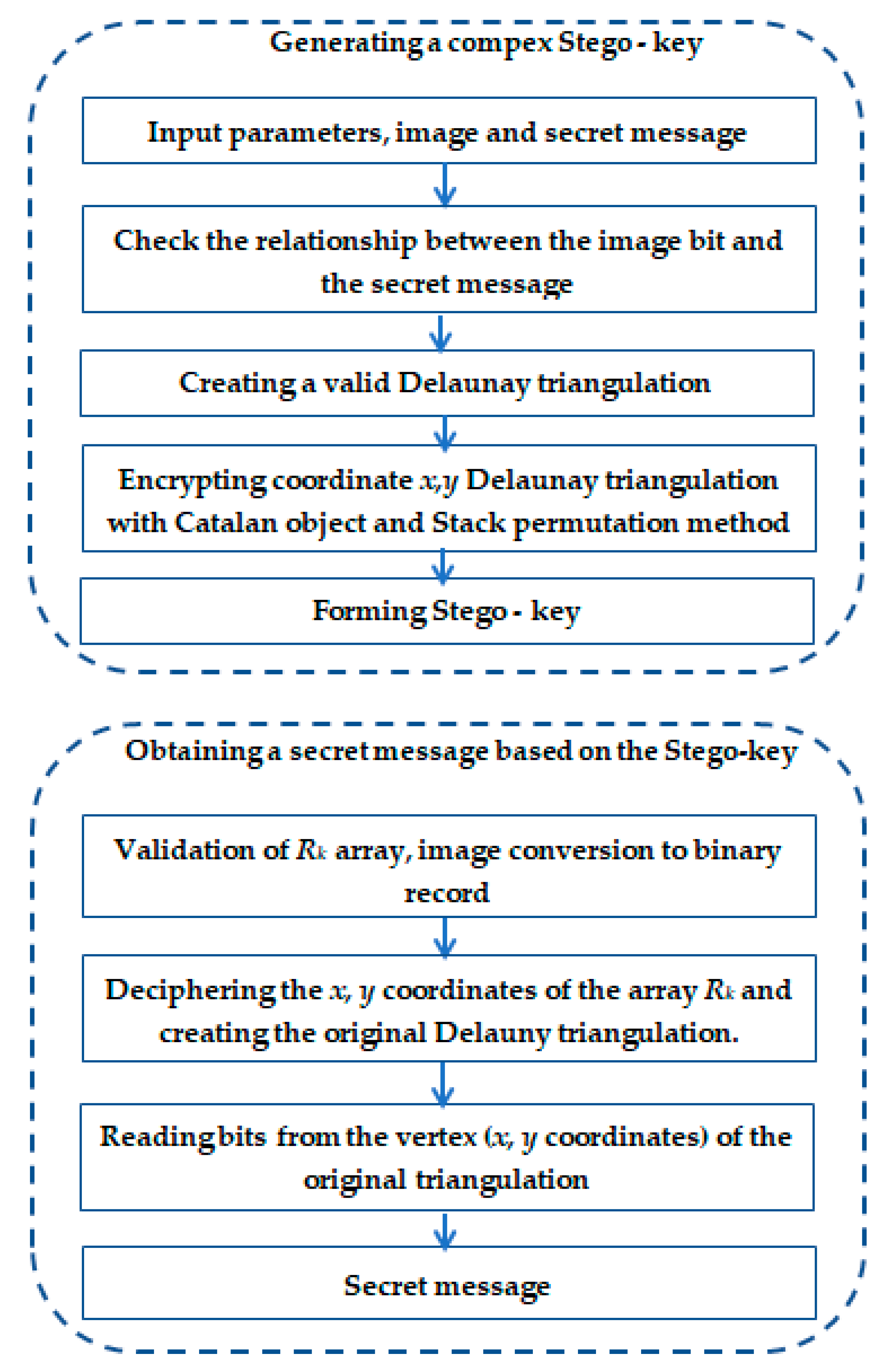
3.4. Steganographic Method

In its functioning, the Steganographic system uses several techniques and methods to create a hidden channel of information transmission. Our method is based on the standard principle of the steganographic system in relation to Steganographic medium = Hidden message + Message carrier + Steganographic key. The condition of all conditions is that the sender and recipient know the value of the Catalan object, because it is the main factor in the process of protecting the secret message from a potential attacker. Below, approximately how the system works as well as a partial description of the stego method can be seen [7].

In the first phase, an image of a given resolution is selected. It is then converted to Base64 and then to binary notation. After selecting the image, a secret message is entered into the system, which is also translated into a binary record.

In the second phase, the ratio of 0 and 1 bits in the image and in the secret message is checked. It is important to mention that the number of 0 bits appearing in the image must always be greater than or equal to the number of 0 bits appearing in the message. The same is true for the occurrence of 1 bits. In this way, we examined the maximum length of the secret message that could be embedded in relation to a given image resolution.

In the third phase, a “valid Delaunay triangulation” is required (i.e., the vertices with x, y coordinates that must correspond to a given bit from the message are randomly selected).

In the fourth phase, the x, y coordinates of the Delaunay triangulation vertex are encrypted using the stack permutation and Catalan object methods. In this way, we receive an encrypted array R_k which is translated into Base64 code.

In the fifth phase, the original image, the encrypted Delaunay triangulation, and the array R_k (explained in detail in the next section) in the Base64 code are combined into a stego key.

We will now explain the process of obtaining secret messages from the stego key.

In the first step, we convert array R_k with coordinates from Base64 to an integer. Then, we create a Delaunay triangulation from it and thus check whether the created and obtained Delaunay triangulations are the same (i.e., whether the array R_k is correct). Additionally, the resulting original image is converted into Base64 and then into binary notation.

In the second step, using the Catalan object and the stack permutation, we decipher array R_k and obtain the original triangulation.

In the third step, we read the bits of the image obtained by the vertex of the Delaunay triangulation.

In the fourth step, we divide the obtained bits into groups of 8 bits and convert the obtained sections into text, thus obtaining a secret message. Figure 4 presents the complete procedure of the secret message method.

3.4.1. Example of the Steganographic Method with Details

At the very beginning, it is necessary to convert a randomly selected image into a binary record. In order to do a conversion of selected image to a binary record, it is necessary to first convert it to Base64 code and only then to a binary record. The starting point has the coordinates $\left(x,y\right)$ of each vertex of the Delaunay triangulation be the carrier of the “0” or “1” bit of the hidden information (Figure 5).

Our method of encrypting a binary image record is based on the application of the Delaunay triangulation incremental algorithm (i.e., encrypting the coordinates $\left(x,y\right)$ of each randomly obtained vertex that carries one bit of “0” or “1” hidden information). As was already mentioned, the process of the vertex coordinates’ encryption is based on the application of the stack permutation method of binary representations of Catalan objects.

Now, we can present the method of encrypting hidden information in an image. The first step is to turn the desired information we want to hide into a binary record. In our example, this information is the word “ENCRYPTION” = 01000101 01001110 01000011 01010010 01011001 01010000 01010100 01001001 01001111 01001110. We notice that each letter is converted with 8 bits. It is also necessary to enter each bit of this word in one array $S$, because we need to access the bits later in the algorithm to check their values. In the second step, we select an image that we convert to a binary record. Each pixel of this image represents one “0” or “1” bit that will be a potential carrier of the hidden information. It is important to note that any image with a defined resolution can be taken. The resolution is important because it is connected with the Catalan key (e.g., if the Catalan key has, for example, $2n$ bits, it can convert the coordinates $\left(x, y\right)$ of the Delaunay triangulation vertex, which are contained in the range of $2n/2$ bits (Figure 6)).

The third step approaches the process of creating a Delaunay triangulation over a binary image representation. Since we have the number of bits of the hidden information (the length of the string $S$ from step 1) as well as the bits themselves in the string, our Delaunay triangulation will have as many vertices as the length of the string $S$. In other words, the number of bits of the hidden information in our case is 8 (characters) * 10 = 80 bits, so in this example, 80 vertices with $\left(x, y\right)$ coordinates are needed to form the Delaunay triangulation. The Delaunay triangulation vertices are chosen randomly using the incremental algorithm [18]. When randomly selecting vertices, a control is introduced where each vertex corresponds to one bit from the array of bits $S$ that carries the hidden information. If this does not happen, the process of vertex selection is repeated by calling the random() function in Algorithm 1 and returning to the beginning of the loop using goto() functions until the appropriate bit is found and so on until the Delaunay triangulation is created.

The $\left(x,y\right)$ coordinates of each vertex carry one bit of the hidden information and are stored in the array $R$ that we need due to the encryption process. The fourth step is reserved for the stack permutation method, which encrypts the $\left(x, y\right)$ coordinates of the vertex from the array $R$ of the newly formed Delaunay triangulation triangles with the selected Catalan key (known to both the sender and the receiver), and it is stored in the array $R_k$ required for the process of decryption. At this point, the resulting $R_k$ array is converted to Base64 code. For the user to find out the hidden information, it is necessary to send the original image, the encrypted Delaunay triangulation, and the array $R_k$ to access the decryption process. It should be noted that the encrypted Delaunay triangulation is sent for control or prevention of errors in the decryption process. Below, we present a

Table 1. Secret message encryption scenario of the word “ENCRYPTION”.

Original Image	Binary Image Record	Secret Message	Binary Secret Message Record S	Delaunay Triangulation of Binary Secret Message Record (Array R)	Catalan Key	Encrypted Delaunay Triangulation Using Stack Permutation (Array Rk)	Array Rk in Base64 Code Form
	011001000110000101110100011000010011101001101001011011010110000101100111011001010010111101101010011100000011	E	0	vertex 1: x = 68, y = 44	281609810 = 10101011111000011000102	vertex 1: x = 20, y = 164	WCA9IDIwLCBZPSAxNjQsICBYID0gMjMyLCBZPSA1NiwgIFggPSAyMjEsIFk9IDEyNCwgIFggPSA0OCwgWT0gMTk5LCAgWCA9IDc5LCBZPSAxNTcsICBYI
			1	vertex 2: x = 58, y = 98		vertex 2: x = 232, y = 56
			0	vertex 3: x = 95, y = 118		vertex 3: x = 221, y = 124
			0	vertex 4: x = 96, y = 157		vertex 4: x = 48, y = 199
			0	vertex 5: x = 151, y = 79		vertex 5: x = 79, y = 157
			1	vertex 6: x = 68, y = 188		vertex 6: x = 20, y = 230
			0	vertex 7: x = 94, y = 230		vertex 7: x = 220, y = 62
			1	vertex 8: x = 179, y = 43		vertex 8: x = 107, y = 169
		N	0	vertex 9: x = 197, y = 134		vertex 9: x = 23, y = 14
			1	vertex 10: x = 231, y = 118		vertex 10: x = 63, y = 124
			0	vertex 11: x = 195, y = 187		vertex 11: x = 27, y = 235
			0	vertex 12: x = 178, y = 230		vertex 12: x = 106, y = 62
			1	vertex 13: x = 159, y = 261		vertex 13: x = 207, y = 261
			1	vertex 14: x = 123, y = 299		vertex 14: x = 249, y = 425
			1	vertex 15: x = 87, y = 321		vertex 15: x = 93, y = 273
			0	vertex 16: x = 150, y = 337		vertex 16: x = 78, y = 337

with an example of encryption of the secret message “ENCRYPTION”.

The described hidden message encryption scenario was realized using Algorithms 1 and 2.

Algorithm 1 Delaunay triangulation of binary presented picture $p_r,\overline{p_i p_j} ,\mathcal{T}$

1. Require: Randomly selected image (converted in binary represent) and array $S$ (bit of secret message). 2. Make initial set of triangles $\mathcal{T}$ containing $\Delta p_{-1}{p}_{-2}{p}_{-3}$. 3. for  r = 1 to N  (length of $S$ array)  do  (Put ${\mathit{p}}_r$ in $\mathcal{T}$) 4.  if ($p_r$) or ($p_r$) (Dependency which is a bit (0 or 1) of secret message in array $S$) 5.           then 6.               Find $\Delta p_i{p}_j{p}_k\in \mathcal{T}$, which contains $p_r$ 7.               Put the $p_r$ coordinates $\left(x,y\right)$ into array $R$. 8.                             if $p_r$ in the interior of the $\Delta p_i{p}_j{p}_k$ 9.                             then 10.                                  LegalizeEdge ($p_r,\overline{p_i p_j} ,\mathcal{T}$) 11.                                  LegalizeEdge ($p_r,\overline{p_j p_k} ,\mathcal{T}$) 12.                                       LegalizeEdge ($p_r,\overline{p_k p_l} ,\mathcal{T}$) 13.                                 else ($p_r$ on an edge of $\Delta p_i{p}_j{p}_k\in \mathcal{T}$, say the edge $\overline{p_i p_j}$) 14.                                  LegalizeEdge ($p_r,\overline{p_i p_l} ,\mathcal{T}$) 15.                                  LegalizeEdge ($p_r,\overline{p_l p_j} ,\mathcal{T}$) 16.                                  LegalizeEdge ($p_r,\overline{p_j p_k} ,\mathcal{T}$) 17.                                        LegalizeEdge ($p_r,\overline{p_k p_l} ,\mathcal{T}$) 18.  else 19.        Call random()  to find $p_r$  pixel which contains “0” or “1” 20.        (Dependency which is a bit (0 or 1) of secret message in array $S$ 21.            goto() line 4. 22.  Discard $\Delta p_{-1}{p}_{-2}{p}_{-3}$ with all their incident edges from $\mathcal{T}$. 23. Output: $\mathcal{D}$ (triangulated binary presented picture or subset triangles of the set $\mathcal{T}$).

Algorithm 2 Delaunay triangulated encryption of binary presented picture ($p_r,\overline{p_i p_j} ,\mathcal{T}$)

1. Require: Triangulation $\mathcal{D}$ resulting from Algorithm 1 and array $R$. 2. for r = 1 to N (length of $S$ array) do (Access $p_r$ in the array $R$) 3. Convert $\left(x,y\right)$ coordinates of $p_r$ in binary record 4. Call Stack permutation method based on chosen Catalan key. 5. Convert $p_s$ in the decimal record (after permutation, bit $p_r$ becomes $p_s$ 6. Put $\left(x,y\right)$ coordinates of $p_s$ in array R_k. 7. Make the initial set of triangles ${\mathcal{T}}_s$ containing $\Delta p_{-1}{p}_{-2}{p}_{-3}$. 8. for s = 1 to N (length of $S$ array) do (Put $p_s$ in ${\mathcal{T}}_s$) 9.       Find $\Delta p_i p_j p_k\in {\mathcal{T}}_s$, which contains $p_s$ 10.           Access $\left(x,y\right)$ coordinates of $p_s$ in array $R_k$ 11.            if $p_s$ in the interior of the $\Delta p_i p_j p_k$ 12.                 then 13.                      LegalizeEdge ($p_s, \overline{p_i p_j} {\mathcal{T}}_s$) 14.                      LegalizeEdge ($p_s,\overline{p_j p_k} ,{\mathcal{T}}_s$) 15.                      LegalizeEdge ($p_s, \overline{p_k p_i},{\mathcal{T}}_s$) 16.                 else ($p_s$ on an edge of $\Delta p_i p_j p_k$, say the edge $\overline{p_i p_j}$ 17.                      LegalizeEdge ($p_s,\overline{p_i p_l} ,{\mathcal{T}}_s$) 18.                      LegalizeEdge ($p_s,\overline{p_l p_j} ,{\mathcal{T}}_s$) 19.                      LegalizeEdge ($p_s,\overline{p_j p_k} ,{\mathcal{T}}_s$) 20.                      LegalizeEdge ($p_s,\overline{p_k p_i} ,{\mathcal{T}}_s$) 21.  Convert array $R_k$  from decimal value to Base64 code. 22.  Discard $\Delta p_{-1}{p}_{-2}{p}_{-3}$ with all their incident edges from ${\mathcal{T}}_{\mathrm{s}}$. 23.  Output: ${\mathcal{D}}_{\mathrm{s}}$ (triangulated binary presented picture or subset triangles of the set ${\mathcal{T}}_s$).

The process of decryption consists of the fact that both the sender and the recipient of the message (the image, Delaunay triangulation, and array $R_k$) know the value of the Delaunay key because it is something that must not come to the possession of a potential attacker in the process of sending messages. Now that the recipient (end user) has everything he or she needs, the decryption process can start.

The first step is to convert the $R_k$ array from Base64 code to the string. The $\left(x, y\right)$ coordinates are extracted from the obtained string, and an integer array $R_k$ is formed. The process of creating the Delaunay triangulation is started, and the encrypted Delaunay triangulation is obtained. At this moment, the obtained triangulation and the one sent with the original image are checked. The check is performed by overlapping the triangulations over each other. If they are the same, this indicates that the recipient of the message is on a good path in the decryption process, which means that the array $R_k$, which is sent in the form of Base64 code, is not damaged (i.e., it was not affected by a potential attacker). Let us also consider a case where the attacker did not attack the sent string $R_k$ and that, based on the sent Delaunay triangulation, he or she found out about the coordinates of its vertices. The next question is this: how is it possible to find out the content of the secret message?

The answer to this question lies in the Catalan key and the fact that the secret message is contained in the binary representation of the original image which, in this method, the attacker has no basis to find out. Below, the original image is reconverted to the binary record, and the original Delaunay triangulation is created using the selected Catalan key. In other words, the original array $R$ with the original vertex coordinates $\left(x, y\right)$ is obtained from the $R_k$ string. Since it is the original image and the original binary record, each vertex contains one bit of the original message. Of course, the value of each element of the array $R$ is placed in a new array $S_k$, which needs to be converted back to the string in sequences of 8 bits to thus find out the real message. After a detailed explanation of the encryption–decryption process of a secret message, we will present the creation of a specific Delaunay triangulation of the binary image representation for the specified secret message “ENCRYPTION”.

Step 1. In this step, the secret message is converted to a binary record by converting each letter to 8 bits (“ENCRYPTION” = 01000101 01001110 01000011 01010010 01011001 01010000 01010100 01001001 01,001111 01001110). Each bit of the secret message is entered in the array S because the values of the bits must be exactly known due to the decryption process. In this case, it is 80 bits, and it will also be the length of the array $S$.

Step 2. In this step, a random image is selected and converted to a binary record. This binary record of the image is considered its binary representation, starting from the assumption that its every bit is a potential carrier of the secret message bit.

Step 3. The process of creating a Delaunay triangulation is approached by taking the binary image representation aid the array $S$ from step 1 as the background. The triangulation is performed using the incremental algorithm. As said, each bit from the array $S$ is joined by one vertex $p_r$ (Algorithm 1) Delaunay triangulation with coordinates $\left(x, y\right)$. For example, p1 = ((68, 44)==0), p2 = ((58, 98)==1), p3 = ((95, 118)==0), p4 = ((96, 157)==0), p5 = ((151, 79)==0), p6 = ((68, 188)==1), p7 = ((94, 230)==0), p8 = ((179, 43)==1), p9 = ((197, 134)==0), p10 = ((231, 118)==1), p11 = ((195, 187)==0), p12 = ((178, 230)==0), p13 = ((159, 261)==1), p14 = ((123, 299)==1), p15 = ((87, 21)==1), p16 = ((150, 337)==0), p17 = ((296, 63)==0), p18 = ((305, 100)==1), p19 = ((314, 137)==0), p20 = ((311, 173)==0), p21 = ((268, 188)==0), p22 = ((276, 246)==0), p23((251, 283)==1), p24 = ((286, 323)==1), p25 = ((177, 337)==0), p26 = ((141, 378)==1), p27 = ((178, 394)==0), p28 = ((213, 412)==1), p29 = ((250, 392)==0), p30 = ((357, 376)==0), p31 = ((396, 375)==1), p32 = ((412, 301)==0), p33 = ((96, 390)==0), p34 = ((86, 430)==1), p35 = ((40, 298)==0), p36 = ((14, 428)==1), p37 = ((349, 174)==1), p38 = ((412, 120)==0), p39 = ((386, 190)==0), p40 = ((452, 117)==1), p41 = ((514, 247)==0), p42 = ((504, 192)==1), p43 = ((450, 265)==0), p44 = ((442, 374)==1), p45 = ((468, 375)==0), p46 = ((403, 415)==0), p47 = ((359, 450)==0), p48 = ((276, 468)==0), p49 = ((532, 41)==0), p50 = ((460, 78)==1), p51 = ((459, 153)==0), p52 = ((378, 302)==1), p53 = ((604, 134)==0), p54 = ((467, 41)==1), p55 = ((542, 341)==0), p56 = ((314, 245)==0), p57 = ((604, 192)==0), p58 = ((449, 176)==1), p59 = ((352, 285)==0), p60 = ((260, 337)==0), p61 = ((342, 432)==1), p62 = ((169, 413)==0), p63 = ((87, 465)==0), p64 = ((425, 470)==1), p65 = ((658, 43)==0), p66 = ((562, 63)==1), p67 = ((590, 97)==0), p68 = ((578, 211)==0), p69 = ((579, 395)==1), p70 = ((432, 249)==1), p71 = ((331, 283)==1), p72 = ((461, 448)==1), p73 = ((678, 207)==0), p74 = ((596, 359)==1), p75 = ((635, 431)==0), p76 = ((611, 466)==0), p77 = ((551, 483)==1), p78 = ((542, 284)==1), p79 = ((581, 134)==1), and p80 = ((713, 393)==0). These vertices are entered into the array $R$ that we need to encrypt the binary representation of the image, and this is presented in Table 1.

Step 4. In this step, the Delaunay triangulation vertices are converted to a binary record and encrypted using the stack permutation and the selected Catalan key (in this case, it is 2816098₁₀ = 1010101111100001100010₂). The rule is that both the sender and the recipient of the message know the selected Catalan key. The encrypted vertices are in the following order: p_s1 = (20, 164), p_s2 = (232, 56), p_s3 = (221, 124), p_s4 = (48, 199), p_s5 = (79, 157), p_s6 = (20, 230), p_s7 = (220, 62), p_s8 = (107, 169), p_s9 = (23, 14), p_s10 = (63, 124), p_s11 = (27, 235), p_s12 = (106, 62), p_s13 = (207, 261), p_s14 = (249, 425), p_s15 = (93, 273), p_s16 = (78, 337), p_s17 = (416, 237), p_s18 = (353, 52), p_s19 = (488, 131), p_s20 = (365, 167), p_s21 = (388, 230), p_s22 = (324, 126), p_s23 = (251, 457), p_s24 = (460, 281), p_s25 = (99, 337), p_s26 = (135, 504), p_s27 = (106, 394), p_s28 = (87, 454), p_s29 = (250, 386), p_s30 = (309, 496), p_s31 = (390, 381), p_s32 = (454, 421), p_s33 = (48, 270), p_s34 = (92, 430), p_s35 = (160, 424), p_s36 = (140, 422), p_s37 = (469, 174), p_s38 = (454, 240), p_s39 = (266, 238), p_s40 = (278, 117), p_s41 = (520, 127), p_s42 = (498, 18), p_s43 = (282, 385), p_s44 = (490, 380), p_s45 = (342, 381), p_s46 = (331, 463), p_s47 = (317, 282), p_s48 = (324, 342), p_s49 = (580, 161), p_s50 = (406, 156), p_s51 = (411, 195), p_s52 = (504, 428), p_s53 = (724, 14), p_s54 = (347, 161), p_s55 = (716, 341), p_s56 = (488, 119), p_s57 = (724, 18), p_s58 = (275, 98), p_s59 = (304, 453), p_s60 = (260, 337), p_s61 = (348, 354), p_s62 = (163, 455), p_s63 = (93, 339), p_s64 = (419, 350), p_s65 = (586, 169), p_s66 = (616, 237), p_s67 = (668, 49), p_s68 = (536, 91), p_s69 = (537, 395), p_s70 = (354, 243), p_s71 = (409, 457), p_s72 = (407, 274), p_s73 = (558, 159), p_s74 = (596, 317), p_s75 = (761, 431), ps76 = (569, 346), ps77 = (557, 315),ps78 = (716, 452), p_s79 = (533, 14), and p_s80 = (659, 387).

All the above vertices are located in the $R_k$ array.

Step 5. In this step, the string $R_k$ is converted to Base64 code, which for the above example looks like this:

• WCA9IDIwLCBZPSAxNjQsICBYID0gMjMyLCBZPSA1NiwgIFggPSAyMjEsIFk9IDEyNCwgIFg PSA0OCwgWT0gMTk5LCAgWCA9IDc5LCBZPSAxNTcsICBYID0gMjAs
• IFk9IDIzMCwgIFggPSAyMjAsIFk9IDYyLCAgWCA9IDEwNywgWT0gMTY5LCAgWCA9IDIzLCBZPSAxNCwgIFggPSA2MywgWT0gMTI0LCAg...wgWT0gMjc0LCBYID0gNTU4LCBZPSAxNTksIFggPSA1OTYsIFk9IDMxNywgWCA9IDc2MSwgWT0gNDMxLCBYID0gNTY5LCBZPSAzNDYsIFggPSA1NTcsIFk9IDMxNSwgWCA9IDcxNiwgWT0gNDUyLCBYID0gNTMzLCBZPSAxNCwgWCA9IDY1OSwgWT0gMzg3.

Step 6. Upon completion of the encryption process, the $R_k$ array, the original image, and the encrypted Delaunay triangulation of the binary representation of the image is sent via some medium (the Internet) to the recipient. To discover the right message, the recipient needs to approach the decryption process already described. Figure 6 explains the steps described above.

3.4.2. Algorithm Complexity and Maximum Length of the Secret Message in Characters

Let us consider the complexity of Algorithm 1. The number of triangles created by the Delaunay triangulation algorithm is, at most, $9n+1$, and the time complexity of this algorithm is $\mathcal{O}\left(n\log n\right)$ using $\mathcal{O}\left(n\right)$ memory locations, as was proven in [18] (Lemma 9.11, Theorem 9.12). Here, Algorithm 1 is also a Delaunay triangulation algorithm, with the added control of bits carrying a secret message. However, it cannot increase the number of returns in the loop starting at line three, retaining the same proportionality of the time cost with respect to the number of points $n$.

When talking about the maximum length of a secret message that can be embedded into an image of a given resolution (e.g., 800 × 600), we must first of all respect the relationship that will be checked before the process of embedding the message in the image, and that is expressed as

B_0s > = B_0p and B_1s > = B_1p

(1)

where B_0s is the total number of 0 bits in the picture, B_1s is the number of 1 bits in the picture, B_0p counts the 0 bits in the secret message, and B_1p is the number of 1 bits in the secret message. It should be noted that our method is not based on removing bits from the image. The basic idea is to hide the secret message without changing the look of the image, even in a single pixel. Therefore, we will consider the case of reducing the BPP from 1/20 to a smaller ratio, such as 1/10. If we analyzed the data arising from an image of a certain resolution (800 × 600), the length of the secret message would be (480000/10)/8 = 6000, which is twice the length of the secret message that can be placed in the image than the BPP used in the LSB technique. It is a BPP of 1/20. We did not disturb the original appearance of the image in any single pixel. As a verification that this statement is true, we will create one Delauny triangulation (Figure 7) in a 10 × 8 pixel grid where the 1/10 ratio is respected.

This means that one bit of the hidden message is placed in each 5 × 2 pixel subnet. Overall, it is one character.

It can be observed that there are still remaining opportunities to reduce the BPP while avoiding transformation of the Delaunay triangulation into a network (each bit of the secret message belongs to one pixel).

4. Steganalysis and Security Testing

Guided by the goal of steganography, which involves the transmission of a secret message by concealing its existence, we used the LSB (least significant bit) algorithm, based on the replacement of the least significant bit as a method of steganography. This algorithm replaces the least significant bit of each pixel with the bitstream of the encrypted message. Since only the LSB pixel changes, it is visually invisible to humans [20]. To assess the safety of the presented solution, the following analyses were performed: entropy of approximate values (original vs. stego image), as well as the bit distribution in the stego image (black or RGB(Read Green Blue)). The realization of the steganization test was done in several steps. In the first step, 150 images (JPG format) created on the same device with the same resolution were selected. Then, 24 bits of the image were taken for analysis, and finally, the amount of information per pixel that we would hide was determined.

As a basis for the realization of this test, we used the recommendations of the previous stego analysis research [2]. In these studies, it was learned that no existing tool could detect the LSB algorithm where the information is 0.005 bpp. Testing determined the admissible parameters of the LSB algorithm for a safe steganographic channel. A comparative analysis was presented which showed that the classifier had similar or better performance than the existing algorithm.

Approximate entropy. If we look at the results, we notice that the entropy of both images remained the same, so this is a desirable property of the method. Figure 8 shows the test results of the frequency of occurrence of all possible overlaps of the n-bit patterns within the series. Additionally, we can see that the entropy (indeterminacy) of the stego image was in a stable plane or greater than the original image.

Bit distribution. To obtain a uniform bit distribution, we applied a message bit permutation before embedding. Figure 9 shows the bit distribution for one selected image, in which the secret data was embedded by the Catalan stego method. Only embedded bits with a value of ‘1’ are shown, while bits with a value of ‘0’ are omitted (Octave GUI (Graphical User Interface) environment).

Regarding this criterion, which refers to the uniform distribution of hidden bits, it is important to emphasize that in our method, it is defined by Delaunay triangulation, which is always random. However, with the LSB technique, there is always a predetermined array of bits that are placed in the least significant (important) positions or bits. In this way, we achieved much better entropy in our testing.

Determining the amount of information to hide. The authors were guided by recommendations from previous research on LSB steganalysis, where it was found that no tool can detect an LSB algorithm where the information is 0.005 bpp (bits per pixel).

By embedding the secret information in the image, the authors tested some additional options. One of them was displaying additional parameters that indicated whether the process was successfully implemented with respect to the amount of information installed per pixel.

This technique does not change the image (carrier), but in combination with a specific key, it allows efficient message extraction. That is why this technique belongs to the category of steganographic methods; it enables the hiding and automatic generation of secret information, but with the existence of a complex stego key.

Table 2. Comparative analysis of the speed (in seconds) of extracting a secret message.

T	Secret Message Length (in Bytes)	Image Size (Resolution)	DTM	DCM [2]	LSB [20]
1	500	800 × 600	0.36	0.33	0.27
2	1000	800 × 600	0.47	0.41	0.38
3	1500	800 × 600	0.89	0.79	0.62
4	3000	1280 × 960	1.12	1.15	0.94
5	5000	1280 × 960	2.51	2.69	1.74
6	10,000	1280 × 960	4.68	5.17	3.51
7	20,000	1280 × 1024	8.87	9.97	8.74
8	50,000	1280 × 1024	10.17	12.47	12.17
9	100,000	1280 × 1024	14.89	16.74	15.14
10	150,000	1920 × 1080	17.85	19.11	18.55
11	200,000	1920 × 1080	22.51	23.08	22.99
12	300,000	1920 × 1080	24.78	26.44	25.73

presents a comparative analysis of the speed (in seconds) of extracting a secret message for the following three steganographic methods:

• DTM: the Delaunay triangulation method (our proposed method);
• DCM: the decomposition Catalan method (presented in [2]);
• LSB: the least significant bit method (technique presented in [20]).

As can be seen, our proposed technique has the advantages of increasing the image resolution and increasing the length of the secret message. It is noticed that our technique spent the least amount of time reaching the highest values (length of a secret message) in testing. This can be seen in the chart below (see Figure 10).

5. Conclusions

As a method of steganography in this paper, Catalan objects and Voronoi–Delaunay triangulation are used in particular. The performed steganalysis deals with the bit distribution in a stego image. In the case of an attack, it cannot be detected whether only one or more bases were used in the database generation, so the bit positions in the message carrier cannot be determined with certainty. It is also not possible to detect how many message carriers contain a hidden message. The main benefits of this method are the use of an image to hide a secret message while keeping it in its original form. Since the stego key consists of three independent parts, we can send each of its independent parts via a medium (e.g., the Internet) in three different time intervals and thus additionally prevent the attacker from revealing a secret message. In addition, one of the benefits of this method is that the attacker cannot find out the secret message without choosing the Catalan object and using the encryption method, or even discover the true value of the R_k array or, in some cases, get the encrypted Delaunay triangulation. In the future, our proposed method may be developed in the direction of being combined with some other additional techniques. First of all, it can be extended by the model originating from [21], where the authors presented adaptive payload distribution in multiple image steganography based on image texture features. In addition, a new approach related to a new payload partition strategy in color image steganography from [17] can be considered. In future work, we will try to connect our steganographic technique with the cubic reference table-based image steganography presented in [22].