1. Introduction
Let
be a graph with vertex set
and edge set
, where
and
. If the vertices
and
are adjacent, we write
. For
, let
be the degree of the vertex
. The
maximum degree of a graph
G will be denoted by
. A vertex
of degree 1 is called a
pendant vertex (also known as
leaf), the edge incident with a pendant vertex is called a
pendant edge. For any two nonadjacent vertices
and
of a graph
G, we let
be the graph obtained from
G by adding the edge
. For a subset
W of
, let
be the subgraph of
G obtained by deleting the vertices of
W and the edges incident with them. Similarly, for a subset
of
, we denote by
the subgraph of
G obtained by deleting the edges of
. If
and
, the subgraphs
and
will be written as
and
for short, respectively. The
chromatic number of a graph
G, denoted by
, is the minimum number of colors such that vertices of
G can be colored with these colors in order that no two adjacent vertices have the same color. A
clique of graph
G is a subset
of
such that in
, the subgraph of
G induced by
, any two vertices are adjacent. The
clique number of
G, denoted by
, is the number of vertices in a largest clique of
G. For two vertex-disjoint graphs
and
, we denote by
the graph which consists of two components
and
. As usual,
,
,
and
, denote, respectively, the path, the cycle, the star and the complete bipartite graph on
n vertices. Other undefined notations and terminology on the graph theory can be found in [
1].
A topological descriptor is a numerical descriptor of the topology of a molecule. These topological descriptors are used for predicting the physico-chemical and/or biological properties of molecules in quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR) studies [
2,
3]. In the literature, several degree- and distance-based topological descriptors were proposed and studied by some researchers [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. Very recently, a new degree-based molecular structure descriptor was introduced, the Sombor index is denoted by
and is defined as follows [
18]:
Many fundamental mathematical properties such as lower and upper bounds can be found in, e.g., [
3,
10,
18,
19,
20,
21,
22,
23,
24,
25,
26]. This topological index was motivated by the geometric interpretation of the degree radius of an edge
, which is the distance from the origin to the ordered pair
.
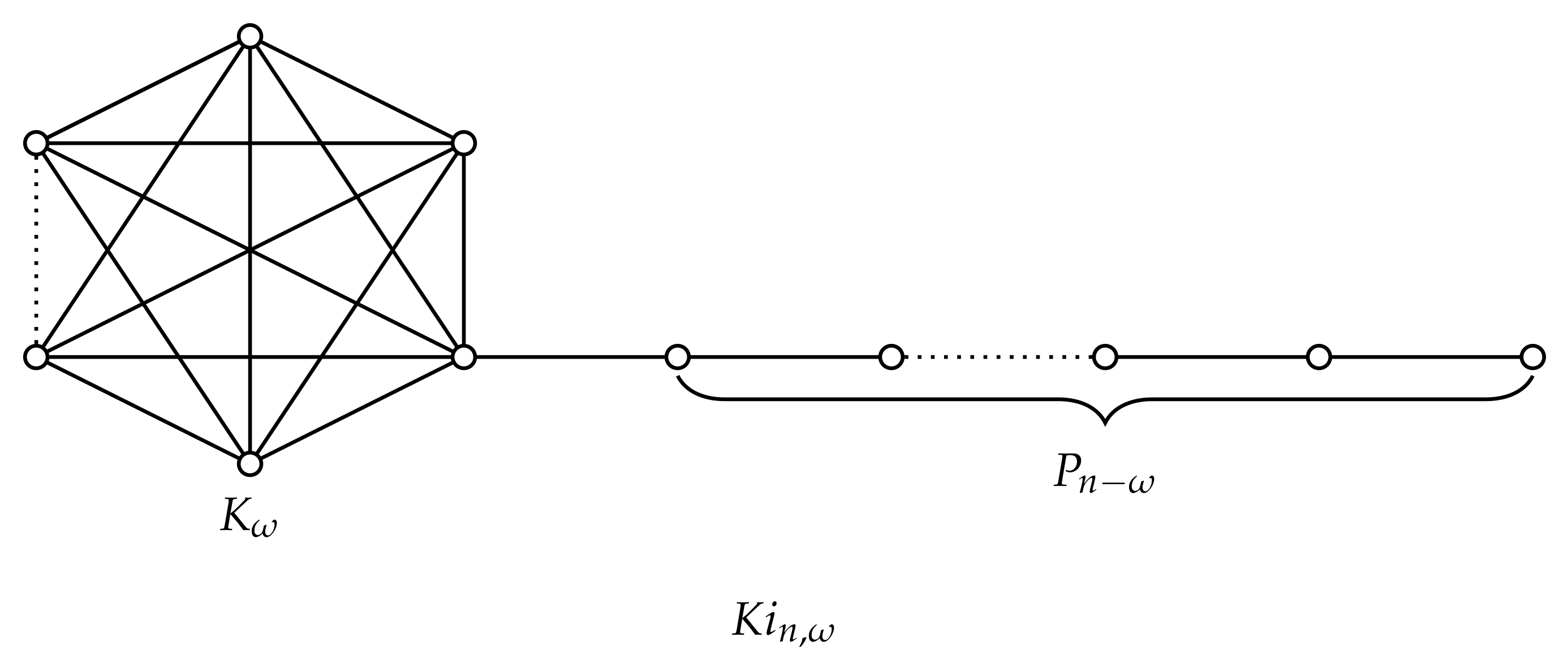
Denote by
the set of connected graphs of order
n with clique number
. The long kite graph
(see,
Figure 1) is a graph of order
n obtained from a clique
and a path
by adding an edge between a vertex from the clique and an endpoint from the path. In particular, for
,
. Let
. For
, we have
and hence
In this paper, we present a lower bound on of graph G in terms of n and clique number , and characterize the extremal graphs.
Theorem 1. Let . Then with equality holding if and only if .
Corollary 1. [
18]
Let G be a connected graph of order n. Then with equality holding if and only if . Proofof Corollary 1. Let
be the clique number of graph
G. Then
. Therefore one can easily see that
hence we obtain the required result. □
Let be the set of connected graphs of order n with chromatic number k. Recall that the Turán graph is a complete k-partite graph of order n whose partition sets differ in size by at most 1. When , the only graph in is . So, we now assume that where , i.e., in . We now give an upper bound on of graph G in terms of n and chromatic number k, and characterize the extremal graphs.
Theorem 2. For any graph , we havewith equality holding if and only if . Recall that a short kite graph
obtained by adding
pendant vertices to the unique vertex of clique
; see
Figure 2. Let
. We have
and hence
Finally we give an upper bound on Sombor index in terms of n, p pendant vertices, and characterize the extremal graphs.
Theorem 3. Let G be a graph of order n with p pendant vertices. Thenwith equality holding if and only if . 3. Proofs
Proof of Theorem 1. For
, we have
and hence the equality holds. For
,
is a subgraph of
G as
. Hence by Lemma 1, we obtain
with equality if and only if
. For
, we have
or
is a subgraph of
G, where
is a tree of order
n. By Lemmas 1 and 2, we have
. Moreover,
if and only if
.
Otherwise,
. Since the clique number of
G is
, we can assume that a clique of
G is
. Let
H be a connected graph with
such that
and
, where
are the trees with
,
,
and
. Moreover,
. By Lemma 1, we have
with equality if and only if
. For
, we have
and
. Moreover,
for
and
. Thus, we have
Claim 1. For , with equality if and only if .
For
, then
the equality holds in
Claim 1. For
, then
as
, the inequality strictly holds in
Claim 1. Otherwise,
. First we assume that
. Thus, we have
or
. When
, we obtain
as
and
. When
, we obtain
as
and
.
Next we assume that
. Since
with Lemma 3, we obtain
Claim 2.
with equality if and only if
with
.
Since
and
, we have
. For
, we have
the equality holds in
Claim 2. Otherwise,
. We have
. First we assume that
. Thus, we have
or
. If
, then we obtain
The equality holds in Claim 2. Otherwise, . We consider two cases:
Case 1. . In this case
as
.
Case 2. . We obtain
as
and
.
Next we assume that . Then . If , then and one can easily check that Otherwise, . We consider the following two cases:
Case 3. . Let
be a vertex adjacent to
in tree
. Then
as
. First suppose that
. Then
. One can easily see that
as
.
Next suppose that
. In this case
. Since
is a tree of order
, by Lemma 3, we obtain
Case 4. . For
, one can easily check that
. So now we have
. Since
and
is a tree,
, (say), where
is a tree of order
with
. Thus, we have
. Let
be a vertex in
such that
, where
. We now prove that
First we assume that
. Then by Lemma 3,
. We obtain
the result strictly holds in (
4).
Next we assume that
. For
, we have
,
for
, and hence we obtain
The equality holds in (
4). Otherwise,
. In this case
and
for
. If
, then one can easily check that the result holds in (
4). Otherwise,
. We obtain
or
One can easily check that
Again the result holds in (3).
Using the result in (3), we obtain
If
, then from (
5), we obtain
as
. Otherwise,
. In this case
. From (
5), we obtain
as
.
Claim 2 is proved. □
Using
Claim 1 and
Claim 2, we obtain
with equality if and only if
and
with
, i.e.,
.
Since
, we have
and
. Using the above result in (
3), we obtain
This completes the proof of the theorem. □
Let be positive integers with . Denote by a complete k-partite graph of order n whose partition sets are of size , respectively. We will determine the extremal graph in with respect to Sombor index of graphs G. For this we first prove a related lemma below.
Lemma 5. Let be a graph defined as above with for . Then Proof. Without loss of generality, we can assume that
. This lemma will be proved if we can prove the following:
By the definition of Sombor index, we obtain
Then, in view of the fact that
, we obtain
Proof of Claim 3. Since
, we have
that is,
that is,
that is,
that is,
which finishes the proof of
. □
Proof of Claim 4. Since
, we have
From the above results, we obtain
that is,
which finishes the proof of
Claim 4. □
Since
, we have
and hence
for
. Using the above result with
Claims 3 and
4, from (
6), we obtain
This completes the proof of the lemma. □
We are now ready to proof of Theorem 2.
Proof of Theorem 2. From the definition of chromatic number, any graph
G from
has
k color classes each of which is an independent set. Suppose that these
k classes have order
, respectively. By Lemma 1, we obtain
with equality holding if and only if
. We now apply Lemma 5 several times (if needed) and we obtain
with equality holding if and only if
. From the above two results with
we obtain the required result. This finishes the proof of this theorem. □
Proof of Theorem 3. Let
be the set of pendant vertices in
G. Let
be a graph obtained from
G such that any two vertices
and
join by an edge, where
is the number of pendant vertices adjacent to the vertex
and
,
. Then by Lemma 1, one can easily see that
. If
, then the equality holds in (
2). Otherwise,
. Let
. Since
, we obtain
Claim 5. , where and .
Proof of Claim 5. First we assume that
. Thus, we have
. In this case we have to prove that
that is,
that is,
that is,
after squaring both sides, one can easily check that the above result is true. Hence the
Claim 5 is true for
.
Next we assume that
. In this case we have to prove that
Using this, from the above, we have to prove that
that is,
that is,
that is,
that is,
that is,
which is always true as
. This completes the proof of
Claim 5. □
Claim 6. , where , and .
Proof of Claim 6. We have to prove that
that is,
that is,
that is,
that is,
which is true always. This completes the proof of
Claim 6. □
Claim 7. .
Proof of Claim 7. We have to prove that
that is,
that is,
which is true always. This completes the proof of
Claim 7. □
Using (
8), (
9) with
Claim 7 in (
7), we obtain
. Using this result several times (if needed), we obtain
as
. Hence
This completes the proof of the theorem. □