A Two-Parameter Model: Properties and Estimation under Ranked Sampling
Abstract
:1. Introduction
- Draw m random samples with a size n from the desired population such that m = n;
- Without taking any measurements, rank the samples in each dataset according to the criterion determined by the experimenter;
- Choose a sample for true judgment by involving the smallest ordered unit in the first set and the second-smallest ordered unit in the second set. The operation is continued in this manner until the largest-ranked unit is chosen from the final set;
2. HLITL Model Characterizations
3. Basic Properties of the HLITL Distribution
3.1. Useful Representation
3.2. HLITL Entropy
3.3. Quantile Function
3.4. Moments and Related Measures
3.5. Bonferroni and Lorenz Curves
4. Parameters Estimation
4.1. Parameter Estimation under SRS
4.2. ML Estimation under RSS
4.3. Simulation Procedures
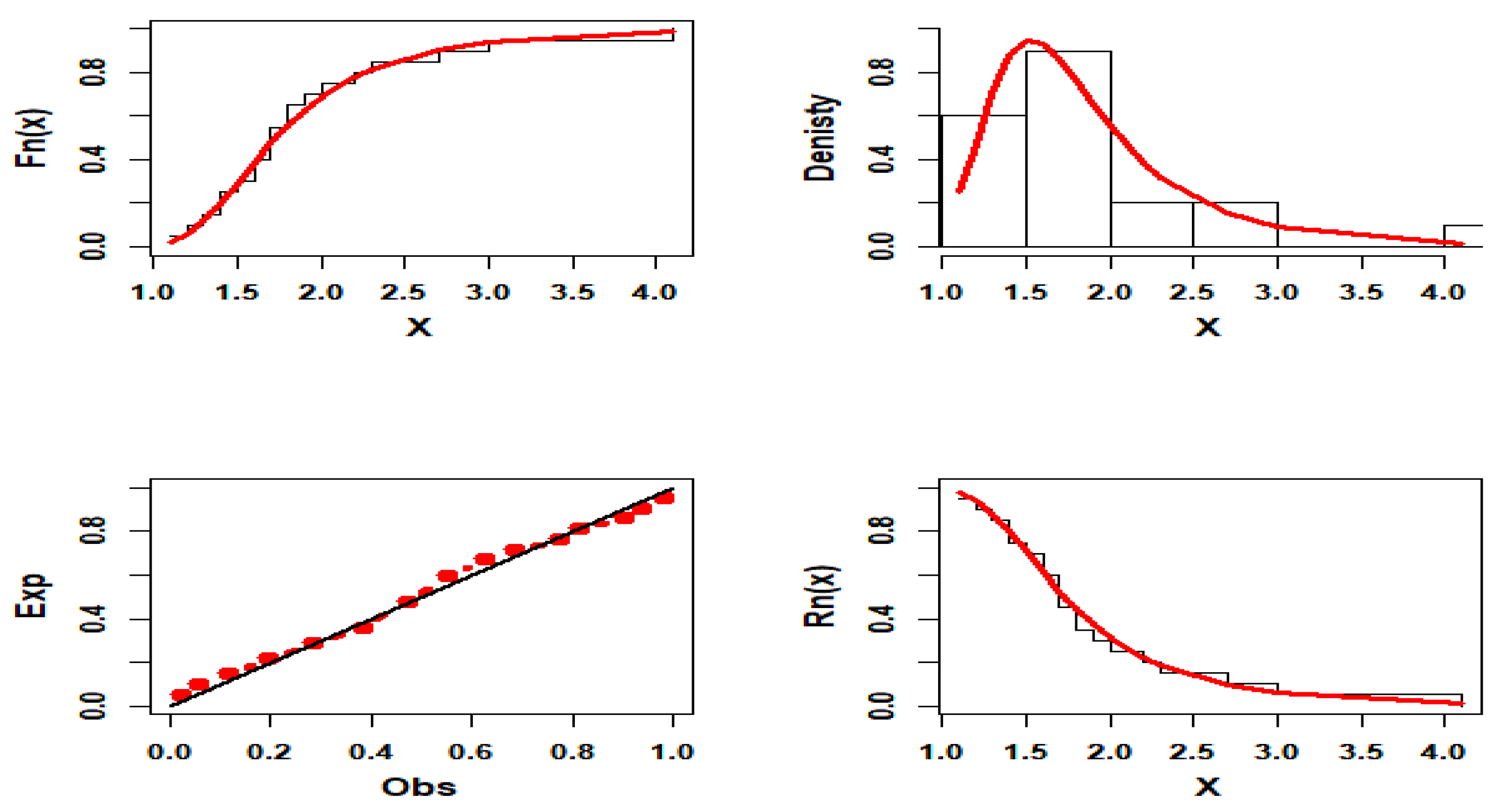
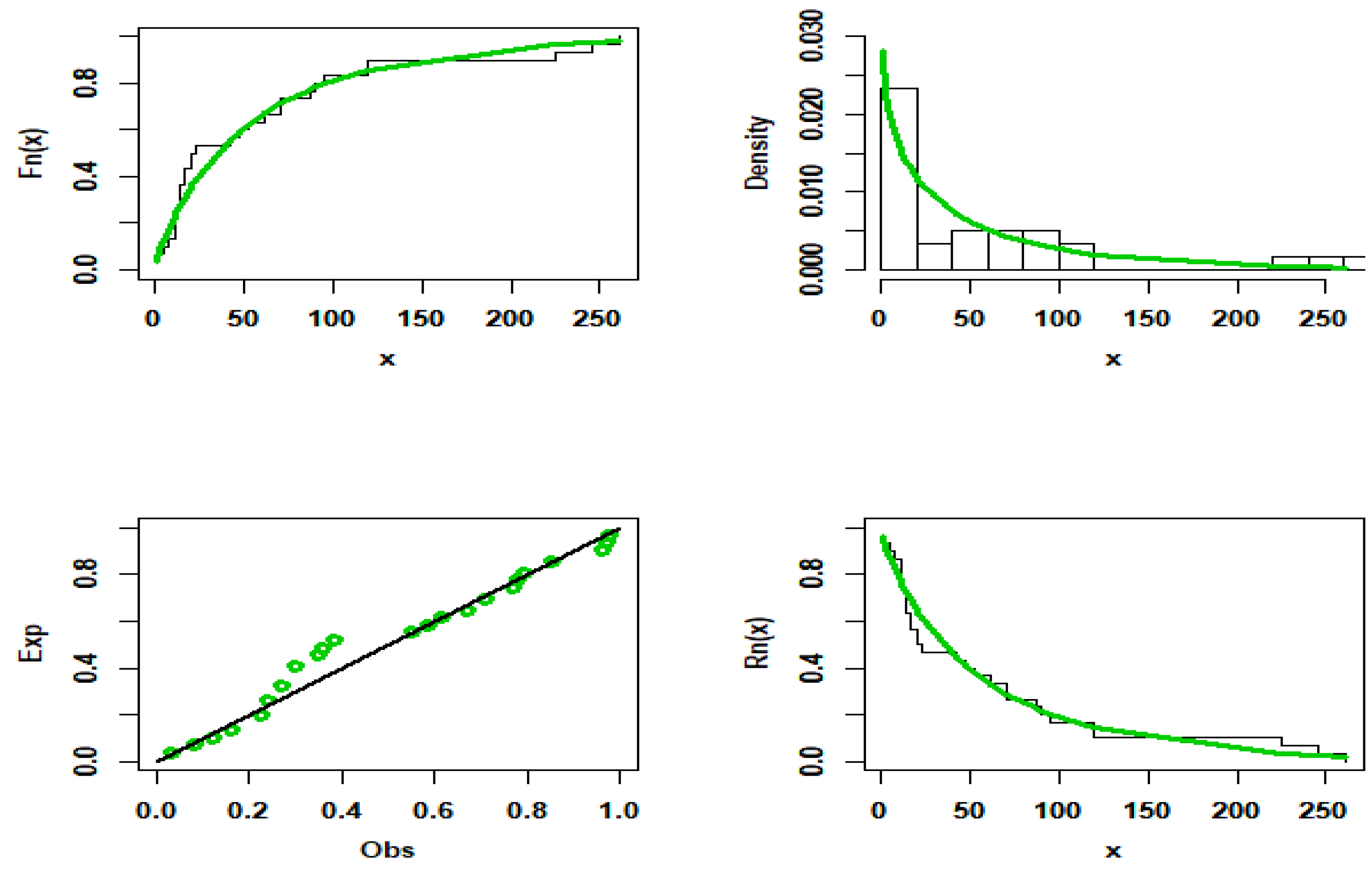
5. Applications to Real Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nadarajah, S.; Kotz, S. Moments of some J-shaped distributions. J. Appl. Stat. 2003, 30, 311–317. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Kotz, S.; Xie, M. On some reliability measures and their stochastic orderings for the Topp–Leone distribution. J. Appl. Stat. 2005, 32, 715–722. [Google Scholar] [CrossRef]
- Zghoul, A.A. Record values from a family of J-shaped distributions. Statistica 2011, 71, 355–365. [Google Scholar]
- Genc, A.I. Estimation of P(X>Y) with Topp–Leone distribution. J. Stat. Comput. Simul. 2013, 83, 326–339. [Google Scholar] [CrossRef]
- Keller, A.Z.; Kamath, A.R.R. Alternative reliability models for mechanical systems. In Proceedings of the 3rd International Conference on Reliability and Maintainability, Toulouse, France, 26 February 2015. [Google Scholar]
- Sharma, V.K.; Singh, S.K.; Singh, U.; Agiwal, V. The inverse Lindley distribution: A stress-strength reliability model with application to head and neck cancer data. J. Ind. Prod. Eng. 2015, 32, 162–173. [Google Scholar] [CrossRef]
- Abd AL-Fattah, A.M.; EL-Helbawy, A.A.; AL-Dayian, G.R. Inverted Kumaraswamy distribution: Properties and estimation. Pak. J. Stat. 2017, 33, 37–61. [Google Scholar]
- Tahir, M.H.; Cordeiro, G.M.; Ali, S.; Dey, S.; Manzoor, A. The inverted Nadarajah–Haghighi distribution: Estimation methods and applications. J. Stat. Comput. Simul. 2018, 88, 2775–2798. [Google Scholar] [CrossRef]
- Hassan, A.S.; Abd-Allah, M. On the Inverse Power Lomax Distribution. Ann. Data Sci. 2018, 6, 259–278. [Google Scholar] [CrossRef]
- Hassan, A.S.; Mohamed, R.E. Parameter estimation for inverted exponentiated Lomax distribution with right censored data. Gazi Univ. J. Sci. 2019, 32, 1370–1386. [Google Scholar]
- Hassan, A.S.; Elgarhy, M.; Ragab, R. Statistical properties and estimation of inverted Topp-Leone distribution. J. Stat. Appl. Probab. 2020, 9, 319–331. [Google Scholar]
- Hassan, A.S.; Elgarhy, M. Kumaraswamy Weibull-generated family of distributions with applications. Adv. Appl. Stat. 2016, 48, 205–239. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Alizadeh, M.; Marinho, P.R.D. The type I half-logistic family of distributions. J. Stat. Comput. Simul. 2015, 86, 707–728. [Google Scholar] [CrossRef]
- Al-Shomrani, A.; Arif, O.; Hanif, S.; Shahbaz, M.Q.; Shawky, A. Topp–Leone Family of Distributions: Some Properties and Application. Pak. J. Stat. Oper. Res. 2016, 12, 443. [Google Scholar] [CrossRef] [Green Version]
- Hassan, A.S.; Hemeda, S.E.; Maiti, S.S.; Pramanik, S. The generalized additive Weibull-G family of probability distributions. Int. J. Stat. Probab. 2017, 6, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Hassan, A.S.; Nassr, S.G. Power Lindley-G family of distributions. Ann. Data Sci. 2019, 6, 189–210. [Google Scholar] [CrossRef]
- Hassan, A.S.; Elgarhy, M.; Ahmad, Z. Type II generalized Topp–Leone family of distributions: Properties and applications. J. Data Sci. JDS 2019, 17, 638–659. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Hassan, A.S.; Elgarhy, M.; Shakil, M. Type II half logistic family of distributions with applications. Pak. J. Stat. Oper. Res. 2017, 13, 245–264. [Google Scholar]
- Hassan, A.S.; Elgarhy, M.; Haq, M.A.; Alrajhi, S. On type II half logistic Weibull distribution with applications. Math. Theory Modeling 2019, 19, 49–63. [Google Scholar]
- Haq, M.A.; Almarashi, A.M.; Hassan, A.S.; Elgarhy, M. Type II half logistic Rayleigh: Properties & estimation based on censored samples. J. Adv. Math. Comput. Sci. 2018, 19, 1–19. [Google Scholar]
- Hassan, A.S.; Elgarhy, M.; Mohamed, R.E. Statistical properties and estimation of type II half logistic Lomax distribution. Thail. Stat. 2020, 18, 290–305. [Google Scholar]
- Zeineldin, R.A.; Haq, M.A.U.; Hashmi, S.; Elsehety, M.; Elgarhy, M. Type II half logistic Kumaraswamy distribution with applications. J. Funct. Spaces 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Bantan, R.; Hassan, A.S.; Elsehetry, M.; Golam Kibria, B.M. Half-logistic xgamma distribution: Properties and estimation under censored samples. Discret. Dyn. Nat. Soc. 2020. [Google Scholar] [CrossRef]
- McIntyre, G. A method for unbiased selective sampling, using ranked sets. Aust. J. Agric. Res. 1952, 3, 385–390. [Google Scholar] [CrossRef]
- Zamanzade, E. New ranked set sampling for estimating the population mean and variance. Hacet. J. Math. Stat. 2015, 46, 1891–1905. [Google Scholar] [CrossRef]
- Haq, A.; Brown, J.; Moltchanova, E.; Al-Omari, A.I. Paired Double Ranked Set Sampling. Commun. Stat. Theory Methods 2015, 45, 2873–2889. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Almanjahie, I.M.; Hassan, A.S.; Nagy, H.F. Estimation of the stress-strength reliability for exponentiated pareto distribution using median and ranked set sampling methods. Comput. Mater. Contin. 2020, 64, 835–857. [Google Scholar] [CrossRef]
- Bantan, R.; Hassan, A.S.; Elsehetry, M. Zubair Lomax distribution: Properties and estimation based on ranked set sampling. Comput. Mater. Contin. 2020, 65, 2169–2187. [Google Scholar] [CrossRef]
- Hassan, A.S.; Al-Omari, A.; Nagy, H.F. Stress-strength reliability for the generalized inverted exponential distribution using MRSS. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 641–659. [Google Scholar] [CrossRef]
- Mathematica, Version 9.0; Wolfram Research Inc.: Champaign, IL, USA, 2012.
- Lee, P.N.; Gross, A.J.; Clark, V.A. Survival distributions: Reliability applications in the biomedical sciences. J. R. Stat. Soc. Ser. C Appl. Stat. 1976, 25, 303. [Google Scholar] [CrossRef]
- Linhart, H.; Zucchini, W. Model Selection; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Mahadavi, A.; Kundu, D. A new method of generating distribution with an application to exponential distribution. Commun. Stat. Theory Methods. 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- Dey, S.; Ghosh, I.; Kumar, D. Alpha power transformed Lindley distribution: Properties and associated inference with application to earthquake data. Ann. Data Sci. 2019, 6, 623–650. [Google Scholar] [CrossRef]
- Alrajhi, S.H. The odd Fréchet inverse exponential distribution with application. J. Nonlinear Sci. Appl. 2019, 8, 535–542. [Google Scholar] [CrossRef] [Green Version]
- Elgarhy, M.; Alrajhi, S.H. The odd Fréchet inverse Rayleigh distribution: Statistical properties and applications. J. Nonlinear Sci. Appl. 2019, 12, 291–299. [Google Scholar] [CrossRef] [Green Version]
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]






| Parameters | |||
|---|---|---|---|
| 0.245 | −0.193 | −0.321 | |
| 0.386 | 0.06 | −0.022 | |
| 0.449 | 0.141 | 0.064 | |
| 0.486 | 0.186 | 0.111 | |
| 0.513 | 0.216 | 0.142 | |
| 0.533 | 0.239 | 0.165 | |
| 0.043 | −0.321 | −0.437 | |
| 0.167 | −0.095 | −0.167 | |
| 0.216 | −0.031 | −0.099 | |
| 0.244 | 0.0022 | −0.065 | |
| 0.263 | 0.023 | −0.044 | |
| 0.277 | 0.038 | −0.029 | |
| −0.041 | −0.38 | −0.491 | |
| 0.076 | −0.165 | −0.233 | |
| 0.121 | −0.107 | −0.172 | |
| 0.145 | −0.078 | −0.143 | |
| 0.161 | −0.061 | −0.125 |
| 0.334 | 0.555 | 0.716 | 0.844 | 0.951 | 1.044 | |
| 0.336 | 0.646 | 0.928 | 1.188 | 1.431 | 1.659 | |
| 0.804 | 1.597 | 2.376 | 3.14 | 3.889 | 4.626 | |
| 5.137 | 10.268 | 15.389 | 20.498 | 25.594 | 30.677 | |
| 0.225 | 0.338 | 0.415 | 0.475 | 0.526 | 0.569 | |
| 5.079 | 4.398 | 4.176 | 4.071 | 4.011 | 3.973 | |
| 84.146 | 66.827 | 61.804 | 59.545 | 58.306 | 57.546 | |
| CV | 1.418 | 1.048 | 0.9 | 0.816 | 0.762 | 0.723 |
| 0.233 | 0.381 | 0.484 | 0.565 | 0.63 | 0.686 | |
| 0.137 | 0.259 | 0.367 | 0.464 | 0.552 | 0.633 | |
| 0.148 | 0.291 | 0.43 | 0.563 | 0.692 | 0.816 | |
| 0.261 | 0.521 | 0.779 | 1.034 | 1.286 | 1.535 | |
| 0.083 | 0.114 | 0.132 | 0.145 | 0.155 | 0.162 | |
| 3.249 | 2.732 | 2.566 | 2.489 | 2.447 | 2.421 | |
| 23.342 | 18.335 | 16.955 | 16.367 | 16.065 | 15.891 | |
| CV | 1.232 | 0.889 | 0.751 | 0.674 | 0.624 | 0.587 |
| Parameters | SRS | RSS | RE | |||||
|---|---|---|---|---|---|---|---|---|
| MLE | Bias | MSE | MLE | Bias | MSE | |||
| 30 | 2.24665 | 0.24665 | 0.44814 | 2.05599 | 0.05599 | 0.07258 | 6.17398 | |
| 5.42395 | 0.42395 | 2.15164 | 5.09999 | 0.09999 | 0.40560 | 5.30488 | ||
| 50 | 2.13933 | 0.13933 | 0.18853 | 2.02705 | 0.02705 | 0.02444 | 7.71307 | |
| 5.24674 | 0.24674 | 0.96227 | 5.05890 | 0.05890 | 0.12829 | 7.50083 | ||
| 100 | 2.02133 | 0.02133 | 0.06865 | 2.01428 | 0.01428 | 0.00672 | 10.21169 | |
| 5.12873 | 0.12873 | 0.42011 | 5.02657 | 0.02657 | 0.03839 | 10.94189 | ||
| 200 | 1.98450 | −0.01550 | 0.04086 | 1.99913 | −0.00087 | 0.00271 | 15.06497 | |
| 4.96450 | −0.03550 | 0.19184 | 4.98999 | −0.01001 | 0.01459 | 13.14884 | ||
| 300 | 2.00841 | 0.00841 | 0.02286 | 1.99921 | −0.00079 | 0.00099 | 23.08329 | |
| 5.01792 | 0.01792 | 0.14397 | 4.99748 | −0.00252 | 0.00564 | 25.50732 | ||
| Parameters | SRS | RSS | RE | |||||
|---|---|---|---|---|---|---|---|---|
| MLE | Bias | MSE | MLE | Bias | MSE | |||
| 30 | 3.49833 | 0.49833 | 1.51722 | 3.06551 | 0.06551 | 0.18998 | 7.98617 | |
| 5.54666 | 0.54666 | 1.87525 | 5.08473 | 0.08473 | 0.27925 | 6.71538 | ||
| 50 | 3.17527 | 0.17527 | 0.39593 | 3.01343 | 0.01343 | 0.05829 | 6.79289 | |
| 5.23404 | 0.23404 | 0.74310 | 5.01014 | 0.01014 | 0.11053 | 6.72327 | ||
| 100 | 3.06525 | 0.06525 | 0.22305 | 3.01564 | 0.01564 | 0.02158 | 10.33606 | |
| 5.10540 | 0.10540 | 0.36652 | 5.01876 | 0.01876 | 0.03375 | 10.85922 | ||
| 200 | 3.06158 | 0.06158 | 0.12887 | 3.01063 | 0.01063 | 0.00599 | 21.49613 | |
| 5.05276 | 0.05276 | 0.20716 | 5.01286 | 0.01286 | 0.00901 | 22.98753 | ||
| 300 | 3.04510 | 0.04510 | 0.07566 | 3.00965 | 0.00965 | 0.00249 | 30.38488 | |
| 5.00445 | 0.00445 | 0.11340 | 5.01317 | 0.01317 | 0.00432 | 26.24375 | ||
| Parameters | SRS | RSS | RE | |||||
|---|---|---|---|---|---|---|---|---|
| MLE | Bias | MSE | MLE | Bias | MSE | |||
| 30 | 1.07235 | 0.07235 | 0.07101 | 1.01680 | 0.01680 | 0.01125 | 6.31288 | |
| 8.76351 | 0.76351 | 7.54481 | 8.27698 | 0.27698 | 1.62355 | 4.64711 | ||
| 50 | 1.05411 | 0.05411 | 0.04031 | 1.00142 | 0.00142 | 0.00504 | 7.99685 | |
| 8.61090 | 0.61090 | 4.96154 | 8.09470 | 0.09470 | 0.67902 | 7.30688 | ||
| 100 | 1.02216 | 0.02216 | 0.01626 | 0.99950 | −0.00050 | 0.00107 | 15.16481 | |
| 8.36669 | 0.36669 | 2.78284 | 7.99541 | −0.00459 | 0.15104 | 18.42416 | ||
| 200 | 1.01110 | 0.01110 | 0.00669 | 1.00159 | 0.00159 | 0.00031 | 21.29228 | |
| 8.15951 | 0.15951 | 0.98182 | 8.02785 | 0.02785 | 0.04678 | 20.98708 | ||
| 300 | 0.99242 | −0.00758 | 0.00389 | 0.99977 | −0.00023 | 0.00017 | 23.37761 | |
| 7.99837 | −0.00163 | 0.52617 | 8.00809 | 0.00809 | 0.02578 | 20.41341 | ||
| Parameters | SRS | RSS | RE | |||||
|---|---|---|---|---|---|---|---|---|
| MLE | Bias | MSE | MLE | Bias | MSE | |||
| 30 | 2.11451 | 0.11451 | 0.23930 | 2.04546 | 0.04546 | 0.08626 | 2.77425 | |
| 8.14470 | 0.14470 | 2.72208 | 8.13691 | 0.13691 | 0.95506 | 2.85016 | ||
| 50 | 2.10872 | 0.10872 | 0.17984 | 2.01079 | 0.01079 | 0.02425 | 7.41578 | |
| 8.30965 | 0.30965 | 2.20228 | 8.01382 | 0.01382 | 0.32892 | 6.69551 | ||
| 100 | 2.07331 | 0.07331 | 0.08344 | 2.01130 | 0.01130 | 0.00753 | 11.07905 | |
| 8.10855 | 0.10855 | 1.24516 | 8.04232 | 0.04232 | 0.10381 | 11.99414 | ||
| 200 | 2.00342 | 0.00342 | 0.03284 | 1.99796 | −0.00204 | 0.00277 | 11.84549 | |
| 7.95718 | −0.04282 | 0.46577 | 7.99595 | −0.00405 | 0.03844 | 12.11569 | ||
| 300 | 2.02033 | 0.02033 | 0.02537 | 1.99699 | −0.00301 | 0.00103 | 24.59269 | |
| 8.09456 | 0.09456 | 0.38287 | 7.98655 | −0.01345 | 0.01498 | 25.55199 | ||
| Parameters | SRS | RSS | RE | |||||
|---|---|---|---|---|---|---|---|---|
| MLE | Bias | MSE | MLE | Bias | MSE | |||
| 30 | 3.41418 | 0.41418 | 1.27229 | 3.09333 | 0.09333 | 0.15659 | 8.12492 | |
| 8.55175 | 0.55175 | 4.23735 | 8.20260 | 0.20260 | 0.50519 | 8.38760 | ||
| 50 | 3.22376 | 0.22376 | 0.58594 | 2.99541 | −0.00459 | 0.06124 | 9.56734 | |
| 8.39282 | 0.39282 | 1.95568 | 7.99319 | −0.00681 | 0.25080 | 7.79780 | ||
| 100 | 3.12361 | 0.12361 | 0.21725 | 3.01169 | 0.01169 | 0.02121 | 10.24074 | |
| 8.19048 | 0.19048 | 1.01699 | 8.03179 | 0.03179 | 0.08586 | 11.84500 | ||
| 200 | 3.04516 | 0.04516 | 0.11087 | 3.00666 | 0.00666 | 0.00635 | 17.44767 | |
| 8.05130 | 0.05130 | 0.40836 | 8.00759 | 0.00759 | 0.02846 | 14.35016 | ||
| 300 | 3.04564 | 0.04564 | 0.07322 | 3.00014 | 0.00014 | 0.00382 | 19.15888 | |
| 8.08202 | 0.08202 | 0.30526 | 8.00310 | 0.00310 | 0.01608 | 18.98614 | ||
| n | Min | Max | Mean | Median | SK | KU | |
|---|---|---|---|---|---|---|---|
| Data 1 | 20 | 1.1 | 4.1 | 1.9 | 1.7 | 1.862 | 4.185 |
| Data 2 | 30 | 1 | 261 | 59.6 | 22 | 1.784 | 2.569 |
| Model | MLE and SE | MLE and SE |
|---|---|---|
| HLITL () | 39.964 (25.292) | 7.027 (1.394) |
| OFIR (α, θ) | 1.623 (0.182) | 1.462 (0.265) |
| APL () | 10540 (15462.663) | 1.884 (0.174) |
| APE () | 16530 (23359.046) | 1.488 (0.161) |
| OFIE () | 1.073 (0.0618) | 2.929 (0.518) |
| Model | MLE and SE | MLE and SE |
|---|---|---|
| HLITL () | 4.519 (1.2539) | 0.612 (0.115) |
| OFIR () | 6.85 (1.761) | 0.229 (0.034) |
| APL () | 0.1 (0.104) | 0.024 (5.127 × 10−3) |
| APE () | 8.688 × 10−10 (5.698 × 10−8) | 8.536 × 10−4 (2.844 × 10−3) |
| OFIE () | 4.082 (0.7770) | 0.47 (0.069) |
| Model | AIC | CAIC | BIC | HQIC | A* | W* |
|---|---|---|---|---|---|---|
| HLITL | 34.894 | 35.599 | 33.496 | 35.282 | 0.1702 | 0.0308 |
| OFIR | 35.476 | 36.181 | 34.078 | 35.864 | 0.23635 | 0.0399 |
| APL | 74.416 | 75.122 | 73.018 | 74.804 | 0.75697 | 0.09802 |
| APE | 75.411 | 76.117 | 74.013 | 75.8 | 0.94478 | 0.10762 |
| OFIE | 35.078 | 35.784 | 33.68 | 35.467 | 0.19209 | 0.03343 |
| Model | AIC | CAIC | BIC | HQIC | A* | W* |
|---|---|---|---|---|---|---|
| HLITL | 315.459 | 315.904 | 314.414 | 316.356 | 0.8386 | 0.1152 |
| OFIR | 341.187 | 341.893 | 340.141 | 342.083 | 1.53147 | 0.1613 |
| APL | 370.83 | 371.274 | 369.784 | 371.727 | 1.2629 | 0.1778 |
| APE | 358.775 | 359.22 | 357.729 | 359.672 | 1.5844 | 0.1978 |
| OFIE | 332.232 | 332.677 | 331.186 | 333.129 | 1.4387 | 0.1817 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bantan, R.; Elsehetry, M.; Hassan, A.S.; Elgarhy, M.; Sharma, D.; Chesneau, C.; Jamal, F. A Two-Parameter Model: Properties and Estimation under Ranked Sampling. Mathematics 2021, 9, 1214. https://doi.org/10.3390/math9111214
Bantan R, Elsehetry M, Hassan AS, Elgarhy M, Sharma D, Chesneau C, Jamal F. A Two-Parameter Model: Properties and Estimation under Ranked Sampling. Mathematics. 2021; 9(11):1214. https://doi.org/10.3390/math9111214
Chicago/Turabian StyleBantan, Rashad, Mahmoud Elsehetry, Amal S. Hassan, Mohammed Elgarhy, Dreamlee Sharma, Christophe Chesneau, and Farrukh Jamal. 2021. "A Two-Parameter Model: Properties and Estimation under Ranked Sampling" Mathematics 9, no. 11: 1214. https://doi.org/10.3390/math9111214
APA StyleBantan, R., Elsehetry, M., Hassan, A. S., Elgarhy, M., Sharma, D., Chesneau, C., & Jamal, F. (2021). A Two-Parameter Model: Properties and Estimation under Ranked Sampling. Mathematics, 9(11), 1214. https://doi.org/10.3390/math9111214








