Neural Architecture Search for Lightweight Neural Network in Food Recognition
Abstract
:1. Introduction
1.1. Model Scaling for Convolutional Neural Network
1.2. Neural Architecture Search
2. Methodology
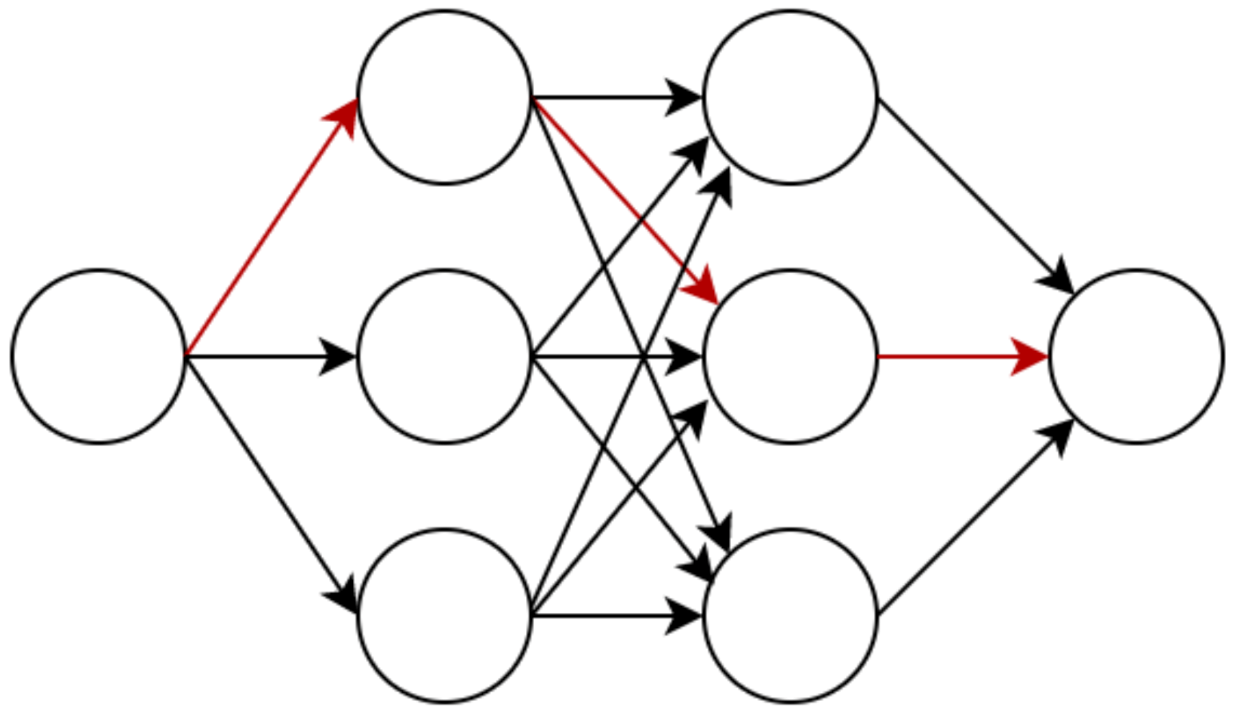
2.1. Search Space
2.2. Search Strategy
3. Experiments and Results
3.1. Settings
3.2. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammadbeigi, A.; Asgarian, A.; Moshir, E.; Heidari, H.; Afrashteh, S.; Khazaei, S.; Ansari, H. Fast food consumption and overweight/obesity prevalence in students and its association with general and abdominal obesity. J. Prev. Med. Hyg. 2018, 59, E236–E240. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, A.; Vadiveloo, M.; Greaney, M.; Risica, P.; Gans, K.; Mena, N.; Tovar, A. Dietary Contributors to Food Group Intake in Preschool Children Attending Family Childcare Homes. Curr. Dev. Nutr. 2020, 4, 268. [Google Scholar] [CrossRef]
- Fitt, E.; Cole, D.; Ziauddeen, N.; Pell, D.; Stickley, E.; Harvey, A.; Stephen, A.M. DINO (Diet In Nutrients Out)—An integrated dietary assessment system. Public Health Nutr. 2014, 18, 234–241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.S.; Wong, J.E.; Ayob, A.F.; Othman, N.E.; Poh, B.K. Can Malaysian Young Adults Report Dietary Intake Using a Food Diary Mobile Application? A Pilot Study on Acceptability and Compliance. Nutrients 2017, 9, 62. [Google Scholar] [CrossRef] [Green Version]
- Khishe, M.; Caraffini, F.; Kuhn, S. Evolving Deep Learning Convolutional Neural Networks for Early COVID-19 Detection in Chest X-ray Images. Mathematics 2021, 9, 1002. [Google Scholar] [CrossRef]
- Tan, R.Z.; Chew, X.; Khaw, K.W. Quantized Deep Residual Convolutional Neural Network for Image-Based Dietary Assessment. IEEE Access 2020, 8, 111875–111888. [Google Scholar] [CrossRef]
- Yanai, K.; Kawano, Y. Food image recognition using deep convolutional network with pre-training and fine-tuning. In Proceedings of the 2015 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Turin, Italy, 29 June–3 July 2015; pp. 1–6. [Google Scholar]
- Michele, A.; Colin, V.; Santika, D.D. MobileNet Convolutional Neural Networks and Support Vector Machines for Palmprint Recognition. Procedia Comput. Sci. 2019, 157, 110–117. [Google Scholar] [CrossRef]
- Kc, K.; Yin, Z.; Wu, M.; Wu, Z. Depthwise separable convolution architectures for plant disease classification. Comput. Electron. Agric. 2019, 165, 104948. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Freeman, I.; Roese-Koerner, L.; Kummert, A. Effnet: An Efficient Structure for Convolutional Neural Networks. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 6–10. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural Architecture Search: A Survey. arXiv 2019, arXiv:1808.05377. [Google Scholar]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl. Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Asadulaev, A.; Kuznetsov, I.; Stein, G.; Filchenkov, A. Exploring and Exploiting Conditioning of Reinforcement Learning Agents. IEEE Access 2020, 8, 211951–211960. [Google Scholar] [CrossRef]
- Ben-Nun, T.; Hoefler, T. Demystifying Parallel and Distributed Deep Learning: An In-Depth Concurrency Analysis. ACM Comput. Surv. 2019, 52, 65. [Google Scholar] [CrossRef]
- Hanif, M.S.; Bilal, M. Competitive residual neural network for image classification. ICT Express 2020, 6, 28–37. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; An, Z.; Jiang, X.; Qian, W.; Ji, S. Batch-normalized deep neural networks for achieving fast intelligent fault diagnosis of machines. Neurocomputing 2019, 329, 53–65. [Google Scholar] [CrossRef]
- Wu, S.; Li, G.; Deng, L.; Liu, L.; Wu, D.; Xie, Y.; Shi, L. L1-Norm Batch Normalization for Efficient Training of Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 2043–2051. [Google Scholar] [CrossRef] [Green Version]
- Guo, K.; Sui, L.; Qiu, J.; Yu, J.; Wang, J.; Yao, S.; Han, S.; Wang, Y.; Yang, H. Angel-Eye: A Complete Design Flow for Mapping CNN onto Embedded FPGA. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 37, 35–47. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Wang, Y.; Li, Z.; Li, N.; Su, J. A novel effective and efficient capsule network via bottleneck residual block and automated gradual pruning. Comput. Electr. Eng. 2019, 80, 106481. [Google Scholar] [CrossRef]
- Lee, D. Comparison of Reinforcement Learning Activation Functions to Improve the Performance of the Racing Game Learning Agent. J. Inf. Process. Syst. 2020, 16, 1074–1082. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, D.; Lee, D.-J. IIRNet: A lightweight deep neural network using intensely inverted residuals for image recognition. Image Vis. Comput. 2019, 92, 103819. [Google Scholar] [CrossRef]
- Horiguchi, S.; Ikami, D.; Aizawa, K. Significance of Softmax-based Features in Comparison to Distance Metric Learning-based Features. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1279–1285. [Google Scholar] [CrossRef] [Green Version]
- Bhagat, S.; Banerjee, H.; Tse, Z.T.H.; Ren, H. Deep Reinforcement Learning for Soft, Flexible Robots: Brief Review with Impending Challenges. Robotics 2019, 8, 4. [Google Scholar] [CrossRef] [Green Version]
- Weng, J.; Jiang, X.; Zheng, W.-L.; Yuan, J. Early Action Recognition with Category Exclusion Using Policy-Based Reinforcement Learning. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 4626–4638. [Google Scholar] [CrossRef]
- Bohme, M.; Pham, V.-T.; Roychoudhury, A. Coverage-Based Greybox Fuzzing as Markov Chain. IEEE Trans. Softw. Eng. 2019, 45, 489–506. [Google Scholar] [CrossRef]
- Chen, M.; Beutel, A.; Covington, P.; Jain, S.; Belletti, F.; Chi, E. Top-K Off-Policy Correction for a REINFORCE Recommender System. arXiv 2020, arXiv:1812.02353. [Google Scholar]
- Chaudhari, P.; Soatto, S. Stochastic Gradient Descent Performs Variational Inference, Converges to Limit Cycles for Deep Networks. arXiv 2018, arXiv:1710.11029. [Google Scholar]
- Park, J.; Yi, D.; Ji, S. A Novel Learning Rate Schedule in Optimization for Neural Networks and It’s Convergence. Symmetry 2020, 12, 660. [Google Scholar] [CrossRef]
- Oyedotun, O.K.; Shabayek, A.E.R.; Aouada, D.; Ottersten, B. Improved Highway Network Block for Training Very Deep Neural Networks. IEEE Access 2020, 8, 176758–176773. [Google Scholar] [CrossRef]
- Yunus, R.; Arif, O.; Afzal, H.; Amjad, M.F.; Abbas, H.; Bokhari, H.N.; Haider, S.T.; Zafar, N.; Nawaz, R. A Framework to Estimate the Nutritional Value of Food in Real Time Using Deep Learning Techniques. IEEE Access 2019, 7, 2643–2652. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Kutzner, C.; Páll, S.; Fechner, M.; Esztermann, A.; de Groot, B.L.; Grubmüller, H. More bang for your buck: Improved use of GPU nodes for GROMACS 2018. J. Comput. Chem. 2019, 40, 2418–2431. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.; Zhang, Z.; Niu, X.; Zhang, Y.; Cao, C.; Xiao, F.; Gao, X. Retinal vessel segmentation of color fundus images using multiscale convolutional neural network with an improved cross-entropy loss function. Neurocomputing 2018, 309, 179–191. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. arXiv 2018, arXiv:1807.11164. [Google Scholar]
- Kawano, Y.; Yanai, K. Real-Time Mobile Food Recognition System. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Portland, OR, USA, 23–28 June 2013; pp. 1–7. [Google Scholar]
- Martinel, N.; Piciarelli, C.; Micheloni, C. A supervised extreme learning committee for food recognition. Comput. Vis. Image Underst. 2016, 148, 67–86. [Google Scholar] [CrossRef]
- Bossard, L.; Guillaumin, M.; Van Gool, L. Food-101—Mining Discriminative Components with Random Forests. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2014; Volume 8694, pp. 446–461. ISBN 978-3-319-10598-7. [Google Scholar]
- Pandey, P.; Deepthi, A.; Mandal, B.; Puhan, N.B. FoodNet: Recognizing Foods Using Ensemble of Deep Networks. IEEE Signal Process. Lett. 2017, 24, 1758–1762. [Google Scholar] [CrossRef] [Green Version]




| Model | 50th Epoch | 100th Epoch | 150th Epoch | 200th Epoch |
|---|---|---|---|---|
| LNAS-NET | 56.9% | 74.2% | 88.3% | 89.1% |
| MobileNet | 51.9% | 71.3% | 87.7% | 87.8% |
| MobileNetV2 | 28.3% | 73.0% | 82.0% | 85.1% |
| ShuffleNet | 57.8% | 72.0% | 83.0% | 84.4% |
| ShuffleNetV2 | 55.5% | 77.1% | 85.0% | 85.4% |
| Model | 50th Epoch | 100th Epoch | 150th Epoch | 200th Epoch |
|---|---|---|---|---|
| LNAS-NET | 32.8% | 49.3% | 67.1% | 70.7% |
| MobileNet | 23.7% | 49.1% | 63.5% | 68.3% |
| MobileNetV2 | 5.6% | 17.4% | 27.3% | 35.8% |
| ShuffleNet | 20.5% | 36.5% | 51.5% | 57.6% |
| ShuffleNetV2 | 23.8% | 44.0% | 61.4% | 66.3% |
| Model | Parameter | Time Spent (mins) | Top-1 Acc | Top-5 Acc |
|---|---|---|---|---|
| LNAS-NET | 1.73M | 132 | 89.1% | 99.2% |
| MobileNet | 3.22M | 143 | 87.8% | 99.0% |
| MobileNetV2 | 2.26M | 211 | 85.1% | 98.6% |
| ShuffleNet | 0.90M | 312 | 86.5% | 98.9% |
| ShuffleNetV2 | 1.27M | 187 | 87.4% | 99.0% |
| Model | Parameter | Time Spent (mins) | Top-1 Acc | Top-5 Acc |
|---|---|---|---|---|
| LNAS-NET | 1.84M | 689 | 75.9% | 93.5% |
| MobileNet | 3.32M | 760 | 73.6% | 92.5% |
| MobileNetV2 | 2.32M | 1180 | 39.4% | 68.9% |
| ShuffleNet | 1.01M | 1805 | 62.6% | 87.0% |
| ShuffleNetV2 | 1.36M | 1032 | 72.2% | 92.0% |
| Author | Method | Accuracy Rate |
|---|---|---|
| The Proposed Model | LNAS-NET | 75.90% |
| Kawano et al. [36] | Liner SVM with a fast χ2 kernal | 53.50% |
| Martinel et al. [37] | Extreme Learning Machine | 55.89% |
| Bossard et al. [38] | Deep CNN | 56.40% |
| Yanai et al. [7] | Pre-trained DCNN | 70.41% |
| Pandey et al. [39] | Ensemble CNN | 72.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, R.Z.; Chew, X.; Khaw, K.W. Neural Architecture Search for Lightweight Neural Network in Food Recognition. Mathematics 2021, 9, 1245. https://doi.org/10.3390/math9111245
Tan RZ, Chew X, Khaw KW. Neural Architecture Search for Lightweight Neural Network in Food Recognition. Mathematics. 2021; 9(11):1245. https://doi.org/10.3390/math9111245
Chicago/Turabian StyleTan, Ren Zhang, XinYing Chew, and Khai Wah Khaw. 2021. "Neural Architecture Search for Lightweight Neural Network in Food Recognition" Mathematics 9, no. 11: 1245. https://doi.org/10.3390/math9111245
APA StyleTan, R. Z., Chew, X., & Khaw, K. W. (2021). Neural Architecture Search for Lightweight Neural Network in Food Recognition. Mathematics, 9(11), 1245. https://doi.org/10.3390/math9111245






