Lie Symmetry Analysis, Self-Adjointness and Conservation Law for a Type of Nonlinear Equation
Abstract
:1. Introduction
2. Lie Symmetries of Equation (2)
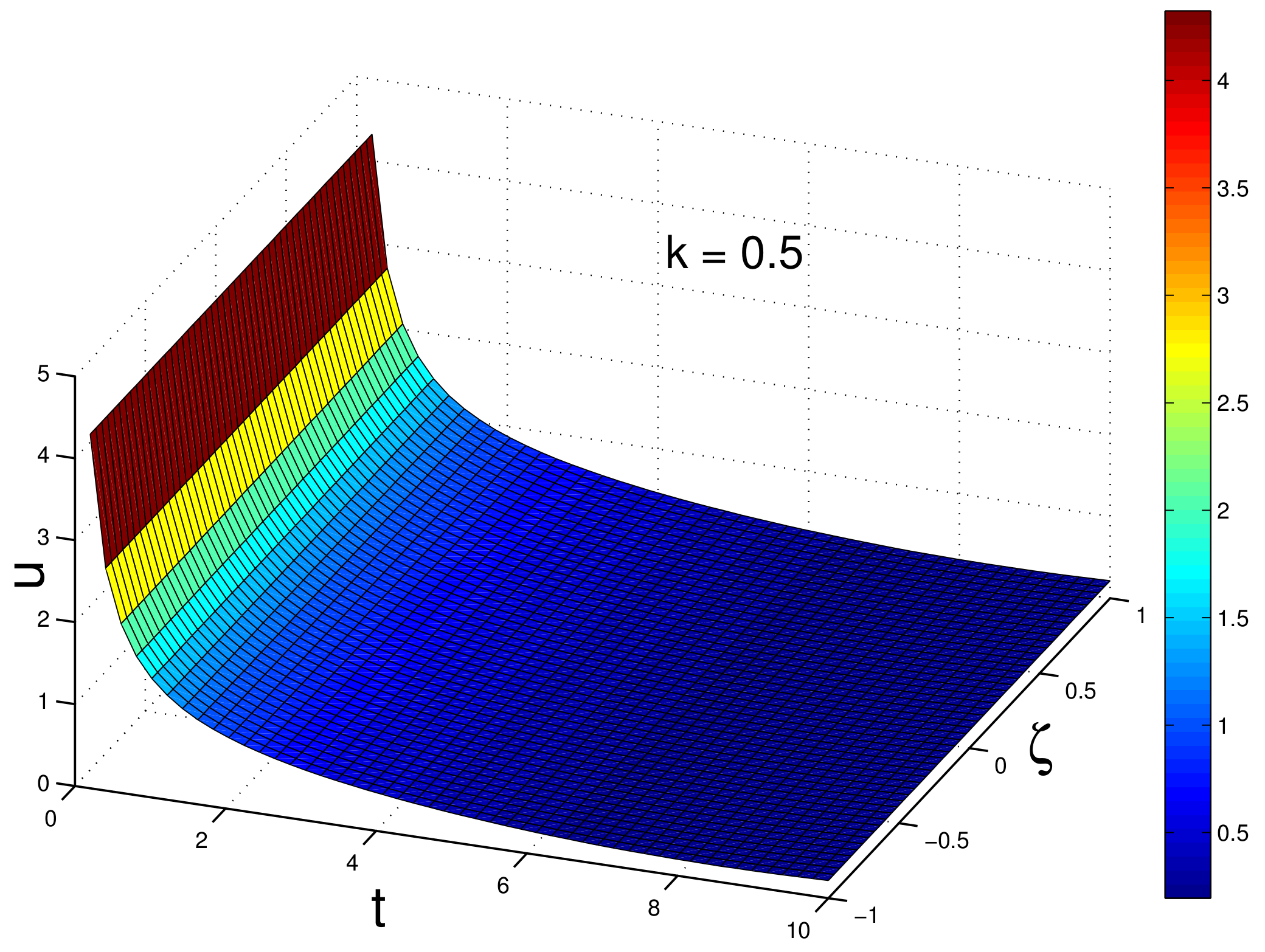
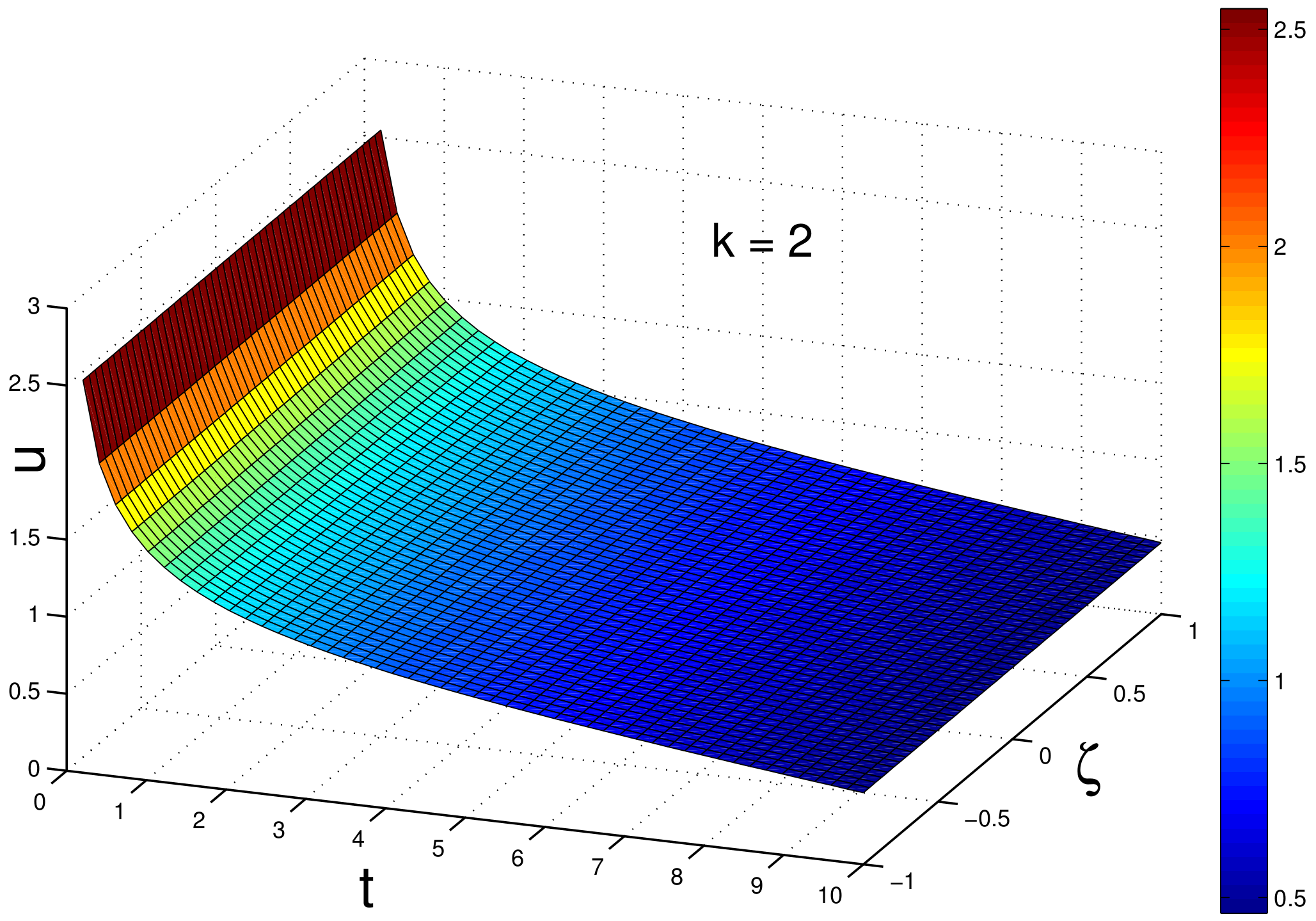
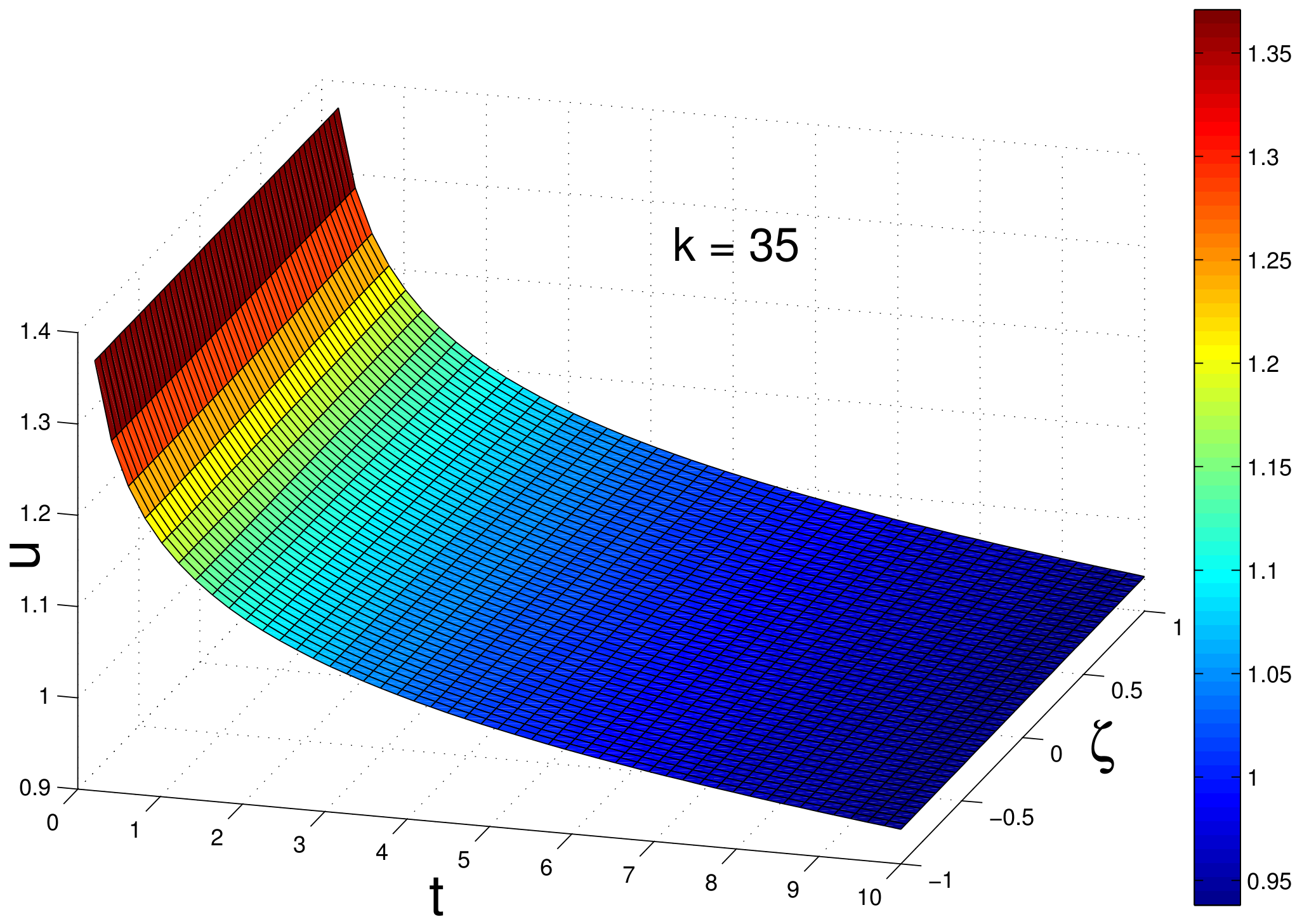
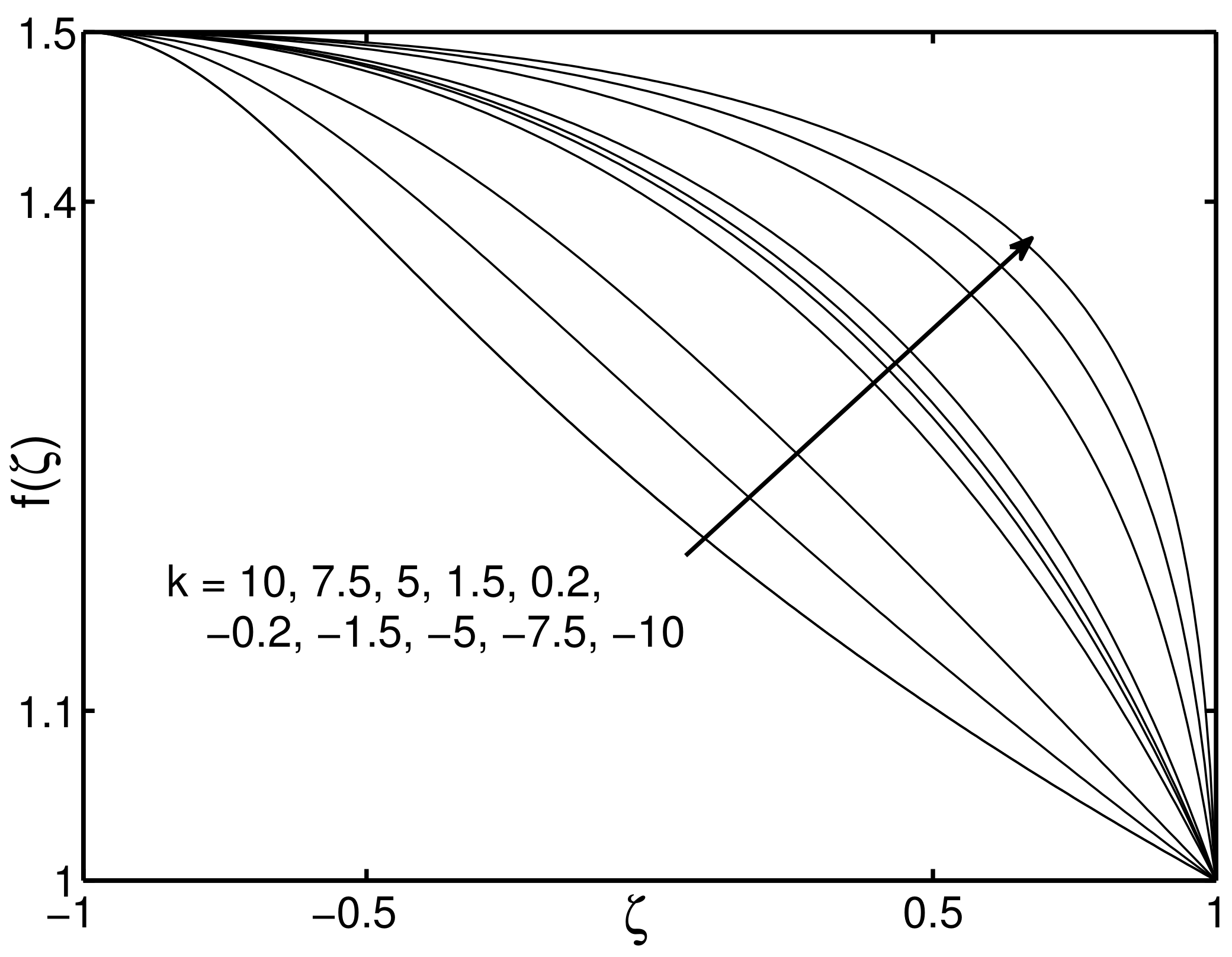
3. Similarity Reductions for Equation (2)
4. Nonlinear Self-Adjointness and Conservation Law
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Elsevier: Cambridge, MA, USA, 1982. [Google Scholar]
- Ibragimov, N.H. Transformation Groups Applied to Mathematical Physics; Reidel Publishing Company: Dort, NL, USA, 1985. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Grauate Texts in Mathematics; Springer: New York, NY, USA, 1993; Volume 107. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; World Publishing Corp.: New York, NY, USA, 1989. [Google Scholar]
- Bluman, G.W.; Anco, S.C. Symmetry and Integration Methods for Differential Equations; Applied Mathematical Sciences; Springer: New York, NY, USA, 2002; Volume 154. [Google Scholar]
- Kannan, R.; Wang, Z.J. A high order spectral volume solution to the Burgers equation using the Hopf—Cole transformation. Int. J. Numer. Meth. Fluids 2012, 69, 781–801. [Google Scholar] [CrossRef]
- Kannan, R. A High Order Spectral Volume Formulation for Solving Equations Containing Higher Spatial Derivative Terms II: Improving the Third Derivative Spatial Discretization Using the LDG2 Method. Commun. Comput. Phys. 2012, 12, 767–788. [Google Scholar] [CrossRef]
- Noether, E. Invariante Variationsprobleme, Königliche Gesellschaft der Wissenschaften zu Göttingen, Nachrichten. Mathematisch-Physikalische Klasse 1918, 2, 235–257, English transl.: Transp. Theory Statist. Phys. 1971, 1, 186–207. [Google Scholar]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.X. Conservation laws by symmetries and adjoint symmetries. Discrete Cont. Dyn.-A 2018, 11, 707–721. [Google Scholar] [CrossRef]
- Kozlov, R. Lie point symmetries of Stratonovich stochastic differential equations. J. Phys. A-Math. Theor. 2018, 5. [Google Scholar] [CrossRef]
- Liu, H.Z.; Li, J.B. Lie symmetry analysis and exact solutions for the short pulse equation. Nonlinear Anal.-Theor. 2009, 71, 2126–2133. [Google Scholar] [CrossRef]
- Liu, H.Z.; Li, J.B.; Liu, L. Lie group classifications and exact solutions for twovariable-coefficient equations. Appl. Math. Comput. 2009, 215, 2927–2935. [Google Scholar]
- Liu, H.Z.; Li, J.B. Lie Symmetries, Conservation Laws and Exact Solutions for Two Rod Equations. Acta Appl. Math. 2010, 110, 573–587. [Google Scholar] [CrossRef]
- Liu, H.Z.; Li, J.B.; Liu, L. Lie symmetry analysis, optimal systems and exact solutions to the fifth-order KdV types of equations. J. Math. Anal. Appl. 2010, 368, 551–558. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.Z.; Li, J.B.; Liu, L. Group Classifications, Symmetry Reductions and Exact Solutions to the Nonlinear Elastic Rod Equations. Adv. Appl. Cliffor. Algebr. 2012, 22, 107–122. [Google Scholar] [CrossRef]
- Nadjafikhah, M.; Ahangari, F. Symmetry Analysis and Conservation Laws for the Hunter—Saxton Equation. Commun. Theor. Phys. 2013, 59, 335–348. [Google Scholar] [CrossRef]
- Qin, C.Y.; Tian, S.F.; Zou, L.; Zhang, T.T. Lie Symmetry Analysis, Conservation Laws and Exact Solutions of Fourth-order Time Fractional Burgers Equation. J. Appl. Anal. Comput. 2018, 8, 1727–1746. [Google Scholar]
- Rashidi, S.; Hejazi, S.R. Lie symmetry approach for the Vlasov-Maxwell system of equations. J. Geom. Phys. 2018, 132, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Yong, X.L.; Chen, Y.F. Symmetry analysis for Whitham-Broer-Kaup equations. J. Nonlinear Math. Phys. 2008, 15, 383–397. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.F.; Mei, J.Q.; Zhang, X.Z. Symmetry properties and explicit solutions of some nonlinear differential and fractional equations. Appl. Math. Comput. 2018, 337, 408–418. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Han, B. On optimal system, exact solutions and conservation laws of the Broer-Kaup system. Eur. Phys. J. Plus 2015, 130, 223. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Han, B. Lie symmetry analysis of the Heisenberg equation. Commun. Nonlinear Sci. Numer. Simulat. 2017, 45, 220–234. [Google Scholar] [CrossRef]
- Qiao, Z.J. New integrable hierarchy, its parametric solutions, cuspons, one-peak solitons, and M/W-shape peak solitons. J. Math. Phys. 2007, 48, 082701. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Z.J.; Liu, L.P. A new integrable equation with no smooth solitons. Chaos Soliton Fractals 2009, 41, 587–593. [Google Scholar] [CrossRef]
- Sakovich, S. Smooth soliton solutions of a new integrable equation by Qiao. J. Math. Phys. 2011, 52. [Google Scholar] [CrossRef] [Green Version]
- Humphreys, J.E. Introduction to Lie Algebras and Representation Theory; Springer: New York, NY, USA, 1972. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zou, Z.; Shen, X. Lie Symmetry Analysis, Self-Adjointness and Conservation Law for a Type of Nonlinear Equation. Mathematics 2021, 9, 1313. https://doi.org/10.3390/math9121313
Wang H, Zou Z, Shen X. Lie Symmetry Analysis, Self-Adjointness and Conservation Law for a Type of Nonlinear Equation. Mathematics. 2021; 9(12):1313. https://doi.org/10.3390/math9121313
Chicago/Turabian StyleWang, Hengtai, Zhiwei Zou, and Xin Shen. 2021. "Lie Symmetry Analysis, Self-Adjointness and Conservation Law for a Type of Nonlinear Equation" Mathematics 9, no. 12: 1313. https://doi.org/10.3390/math9121313
APA StyleWang, H., Zou, Z., & Shen, X. (2021). Lie Symmetry Analysis, Self-Adjointness and Conservation Law for a Type of Nonlinear Equation. Mathematics, 9(12), 1313. https://doi.org/10.3390/math9121313