Modular and Self-Scalable Origami Robot: A First Approach
Abstract
:1. Introduction
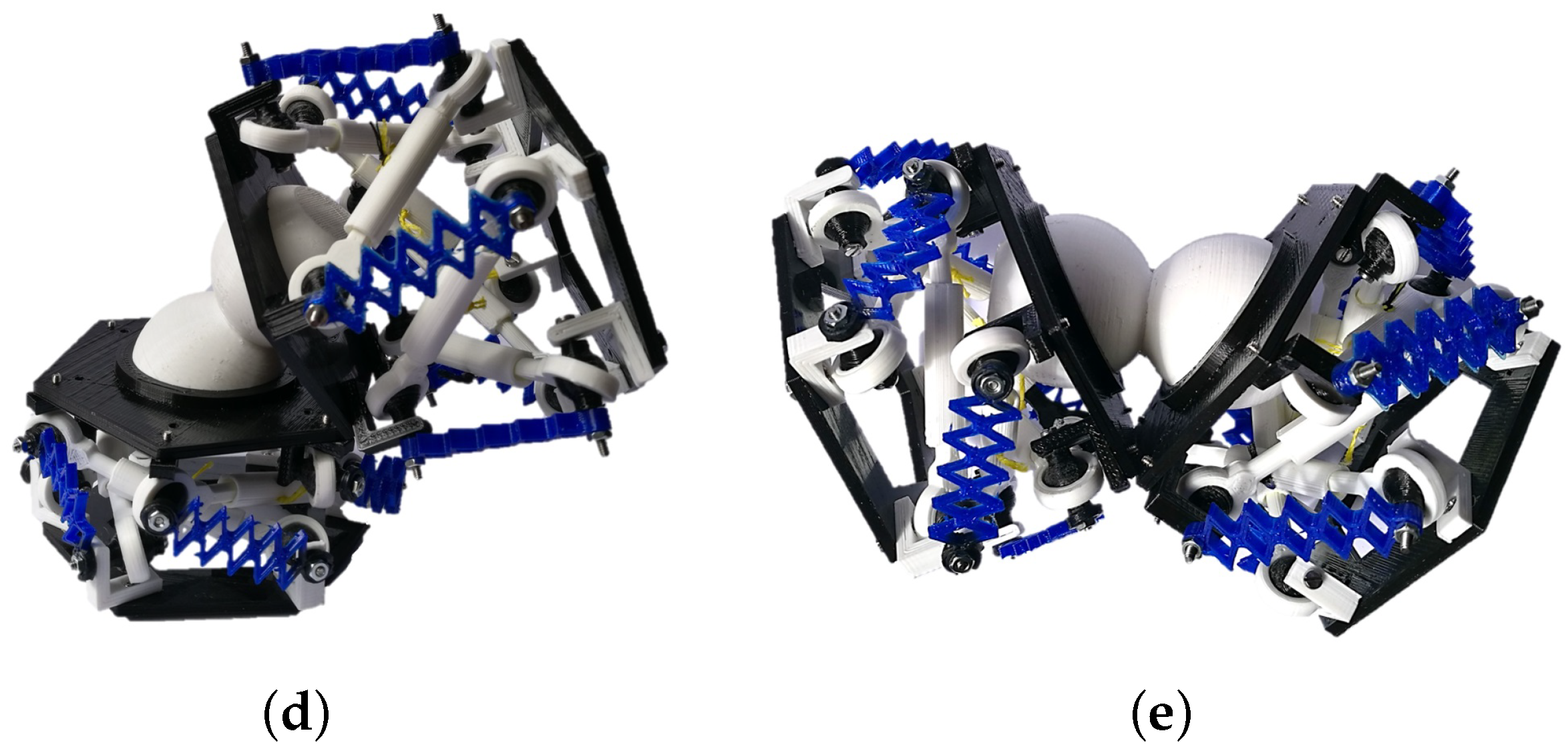
- A single link capable of changing its size individually (self-scalable) is the first proposed design option. This link could be connected to other links with similar features, this way achieving the modularity property.
- Design and prototyping of a self-scalable link as a proof of concept. While being inspired by the origami technique, the final prototype integrates both rigid and soft materials in its structure, instead of paper. This novel approach is a real contribution to the state of the art.
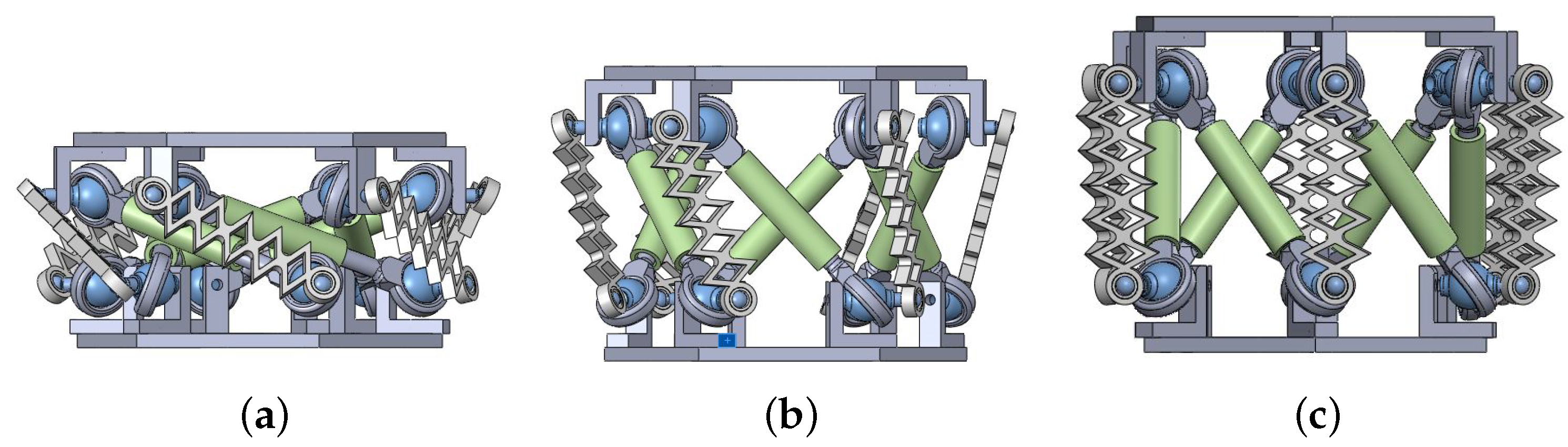
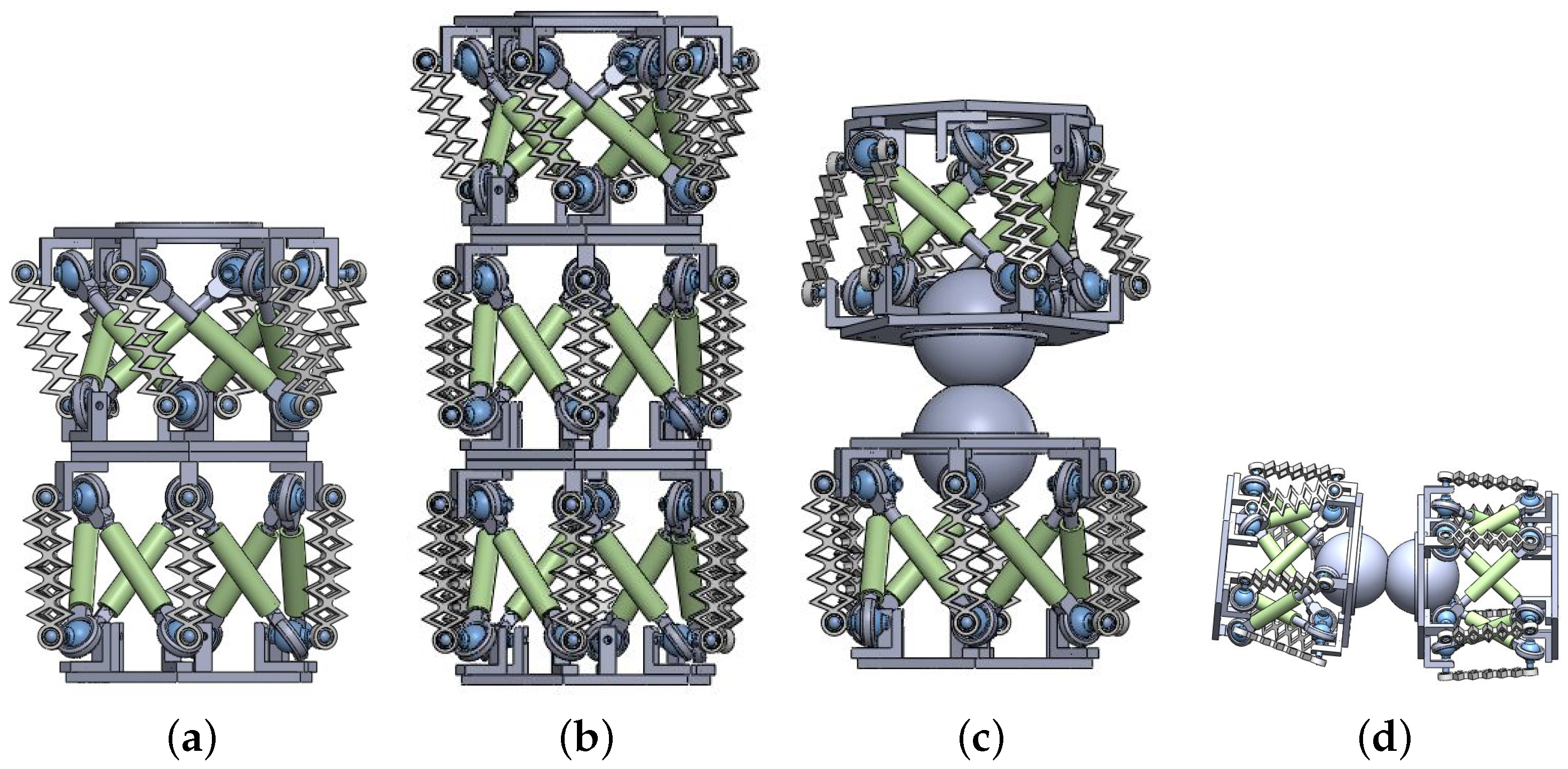
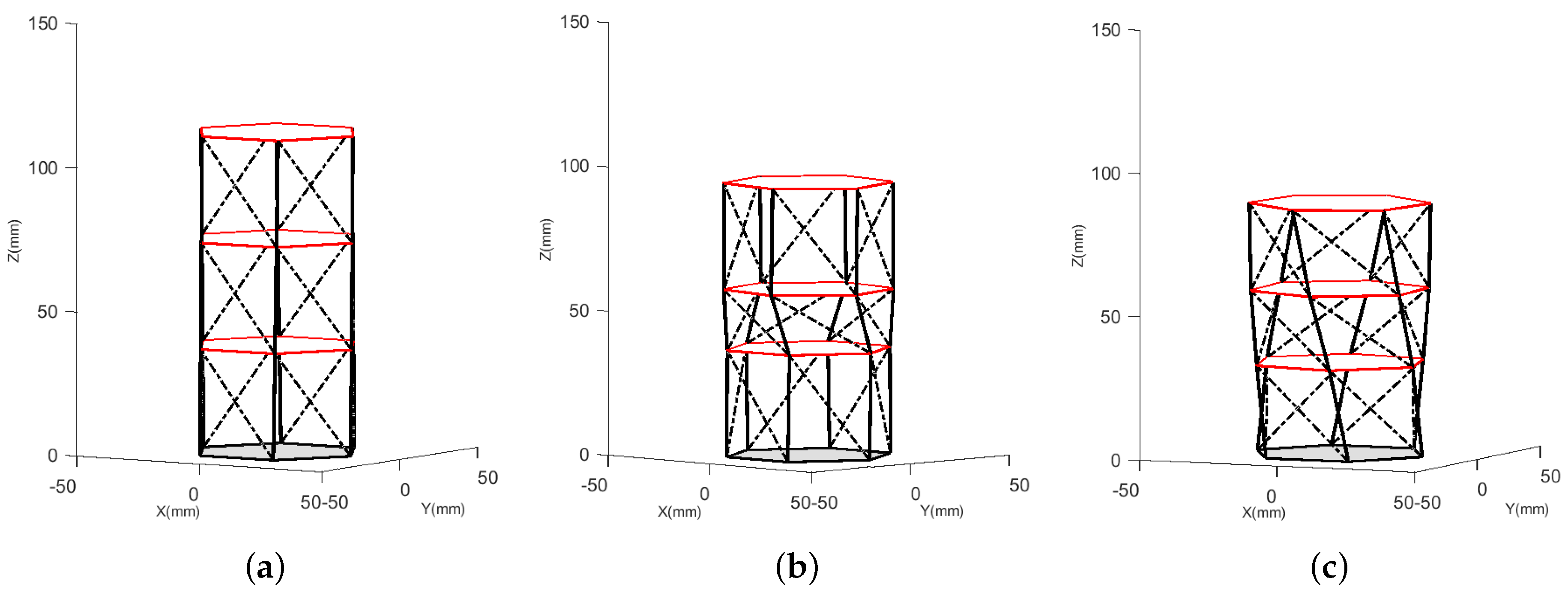
- Design of a complete modular robot with interconnected scalable links. A linkage joint is proposed that allows modularity for three DOF configurations, enabling a wider range of applications.
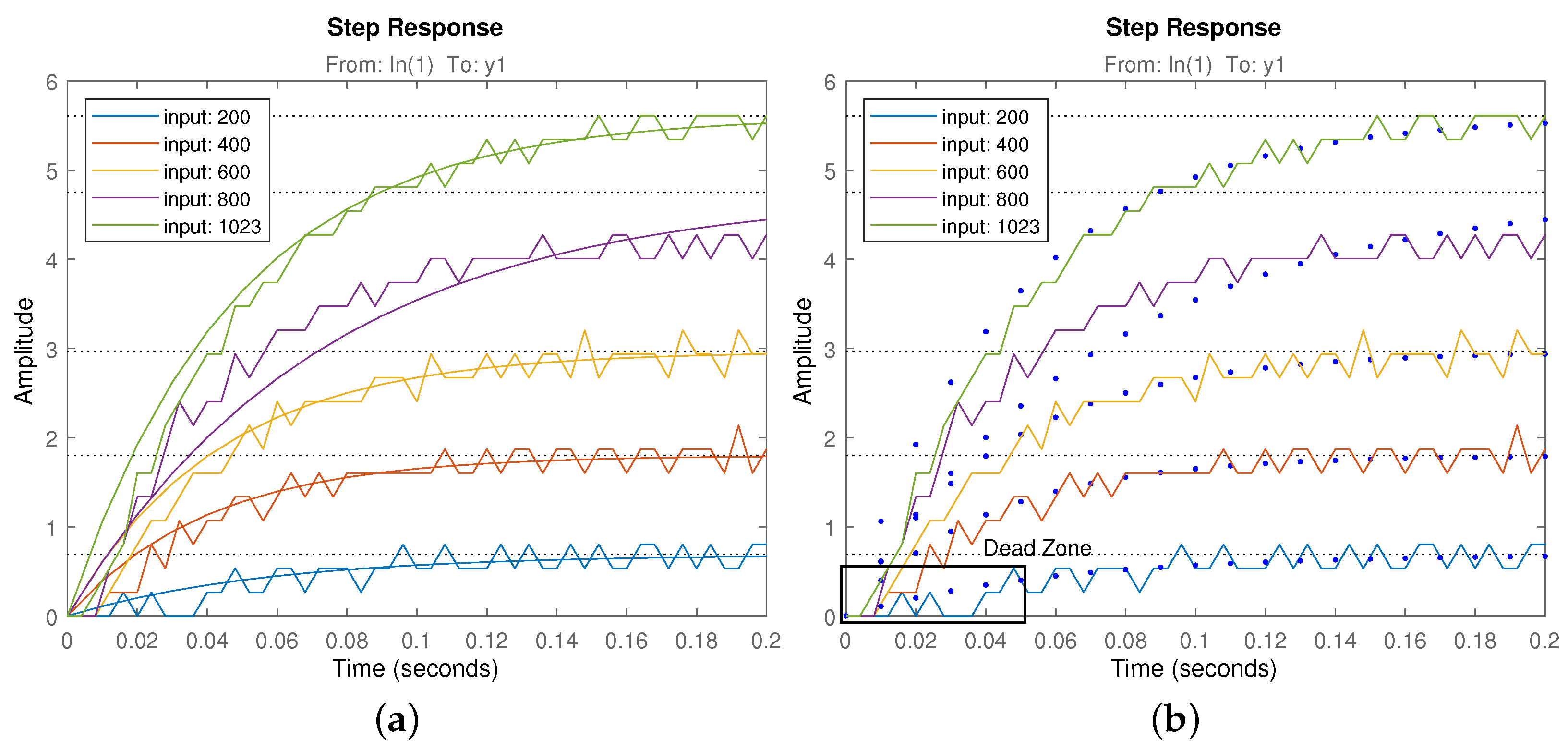
- The final prototype is a 3D printed low cost solution that allows for the validation of the scalability in an autonomous way through the design and implementation of a control system. The control problem of these robotic structures is not generally faced in the majority of the works dealing with these designs, this being another important contribution of this paper. In addition, solutions to common control problems like motor’s dead zones or saturation are addressed in this work.
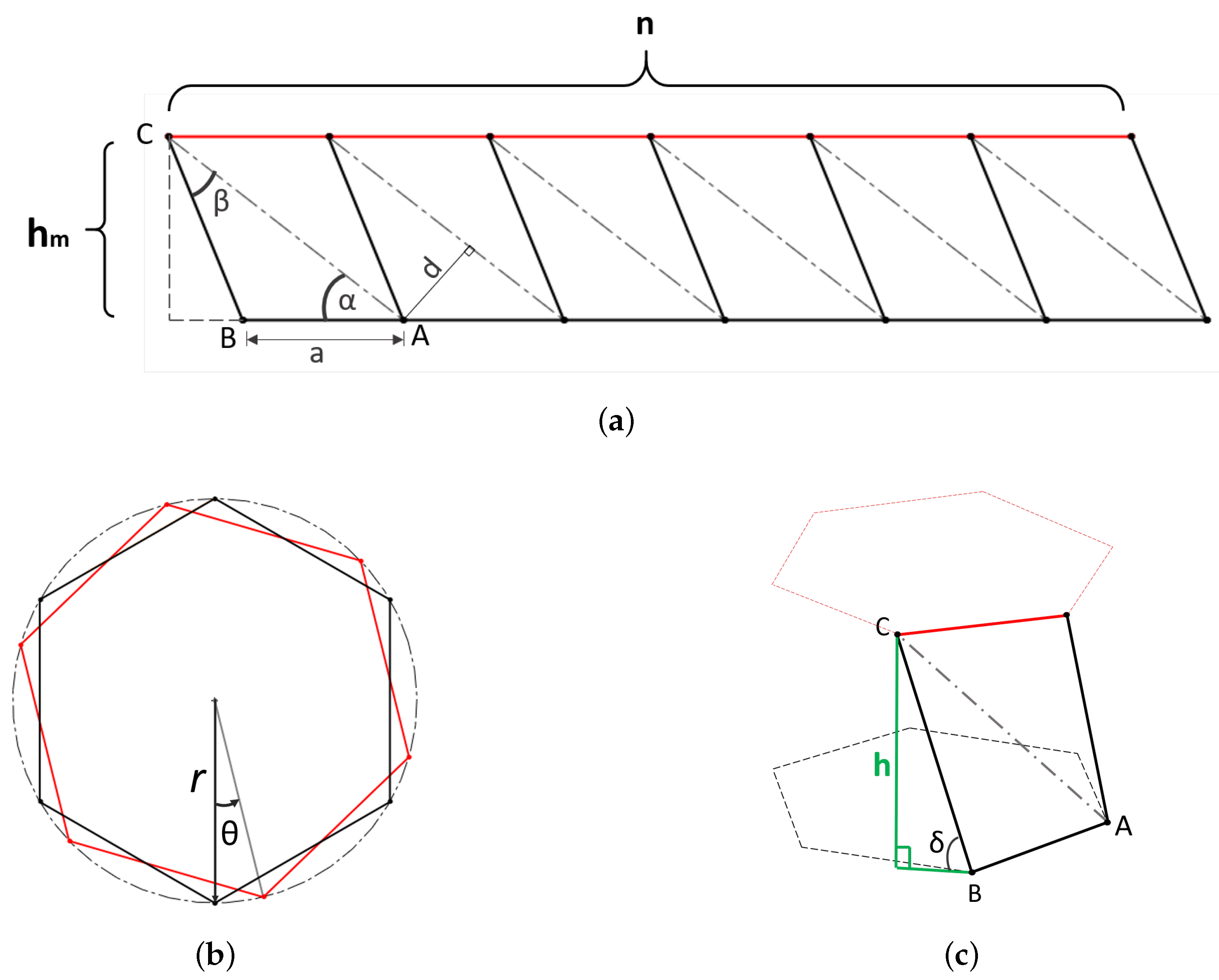
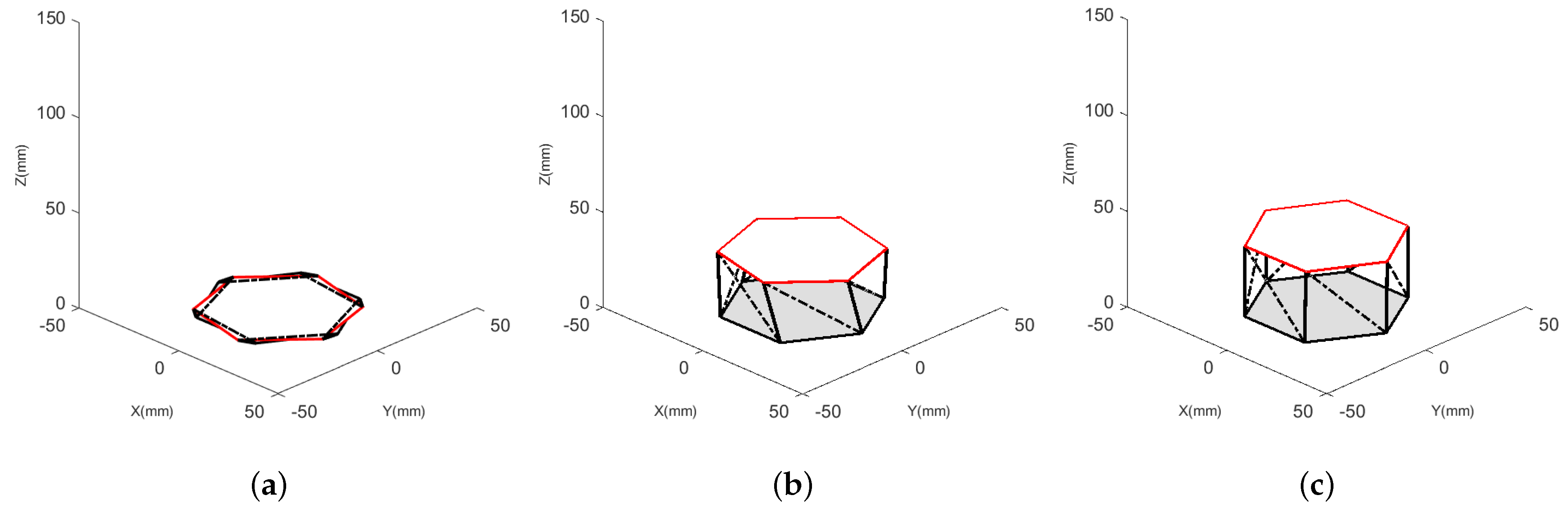
2. Soft Origami-Based Design
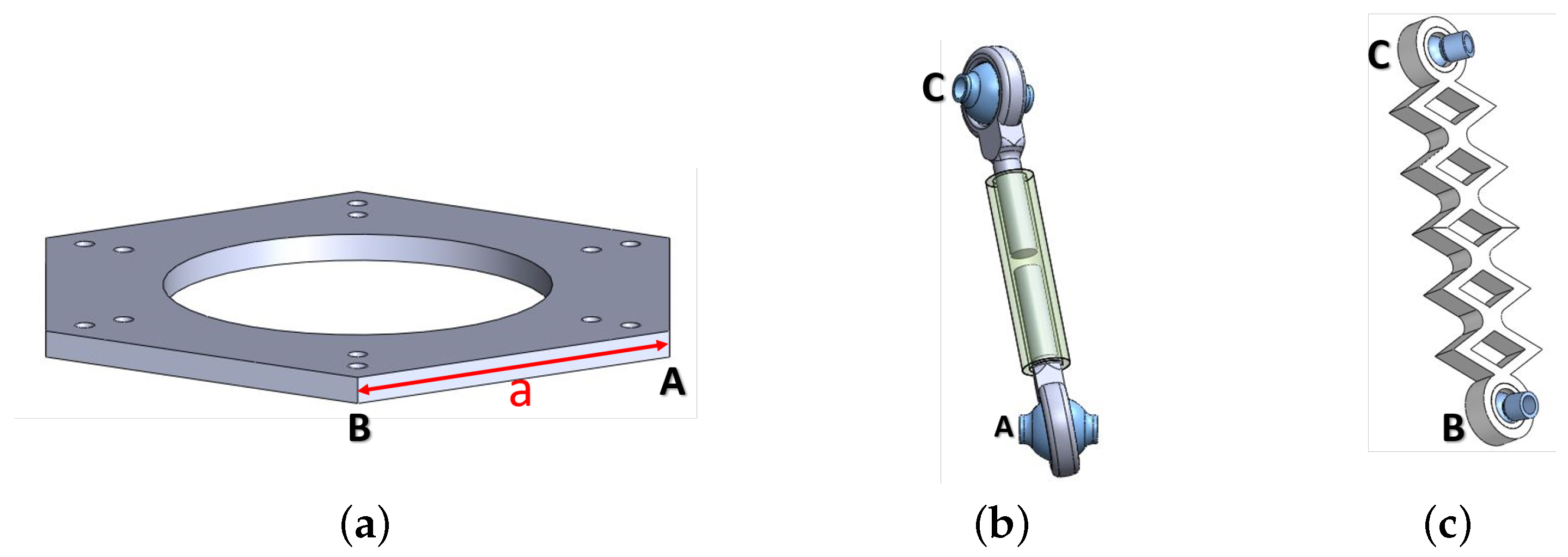
Link Prototype
3. Cable-Driven Prototype
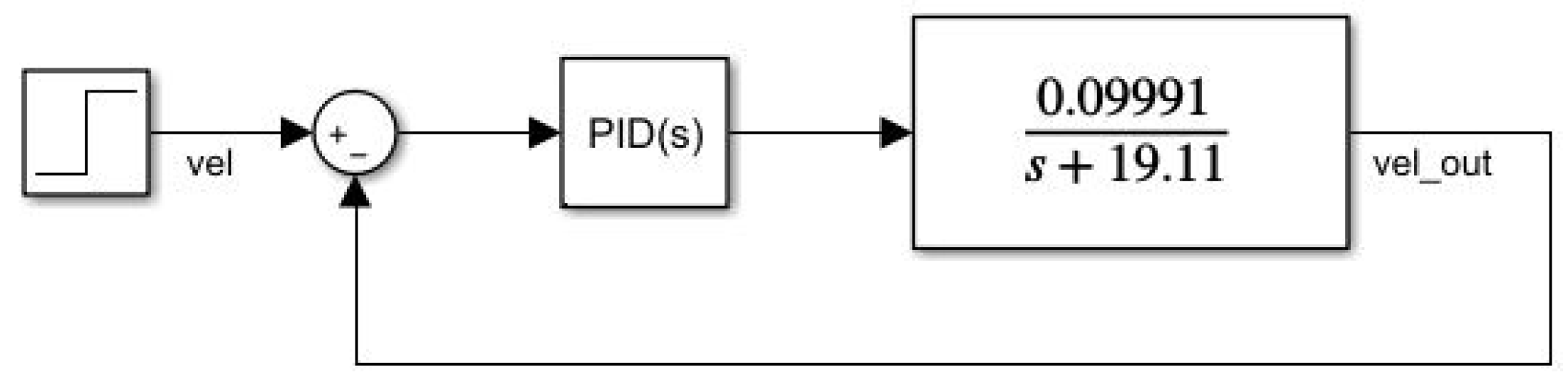
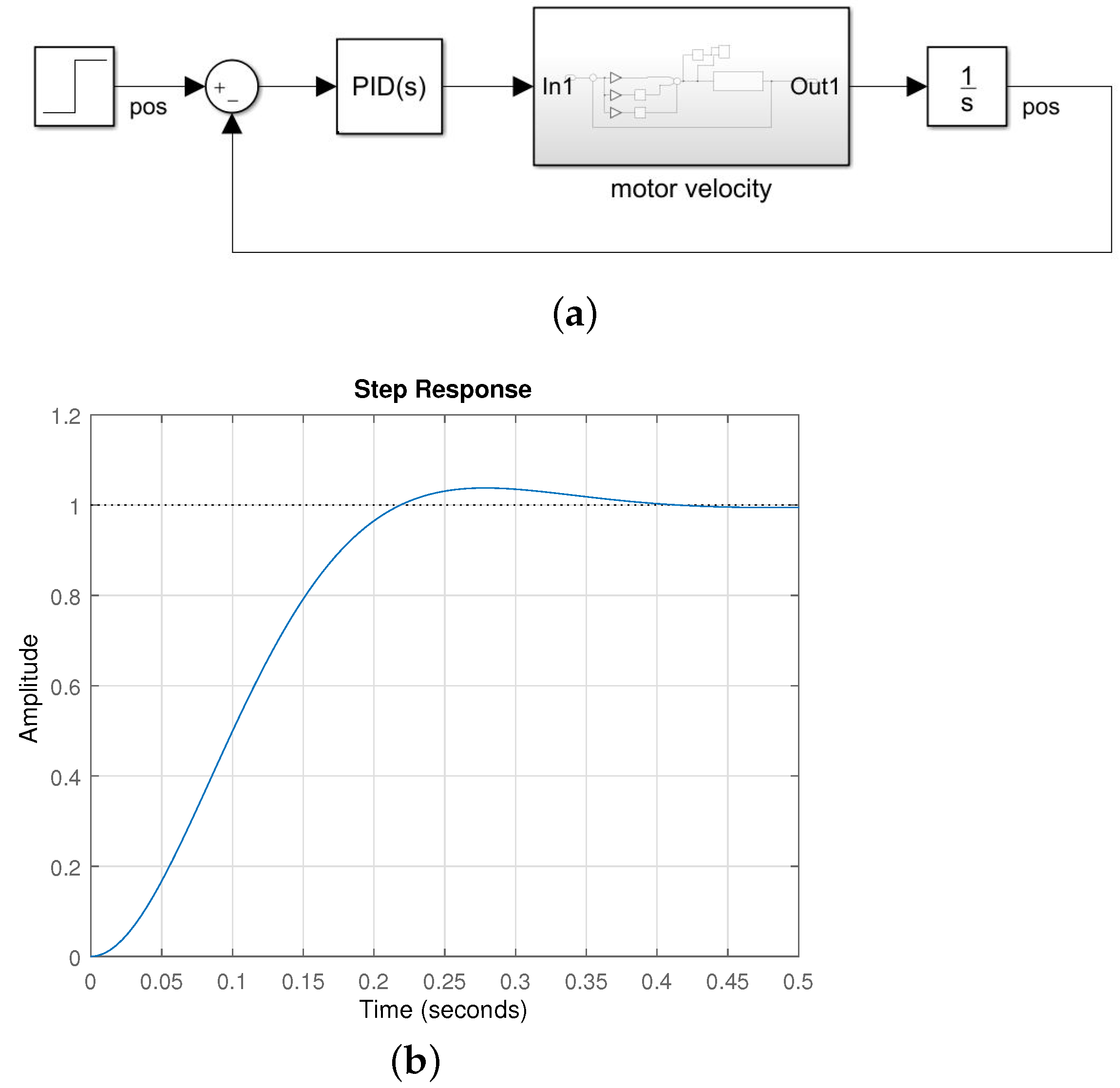
3.1. Motor System Identification
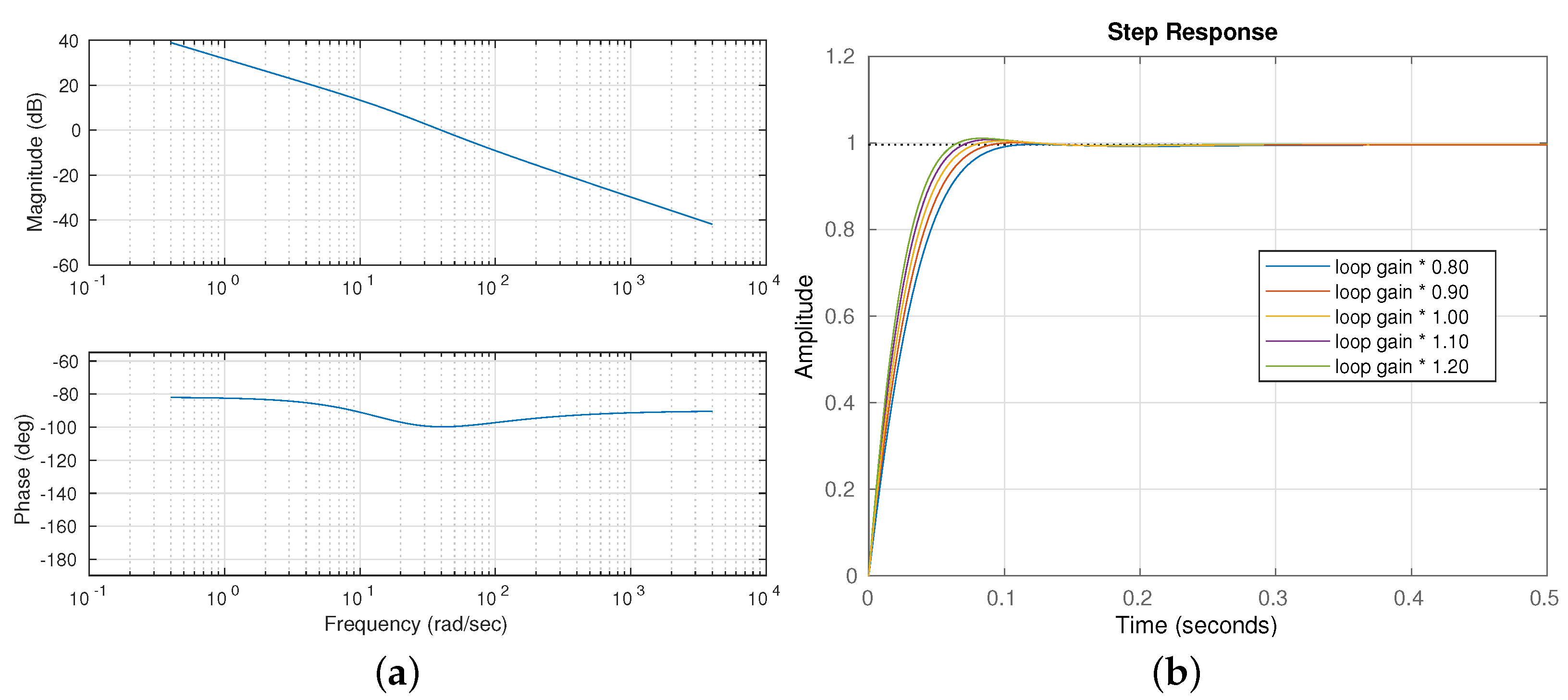
3.2. Controller Design
3.3. Whole System Behavior
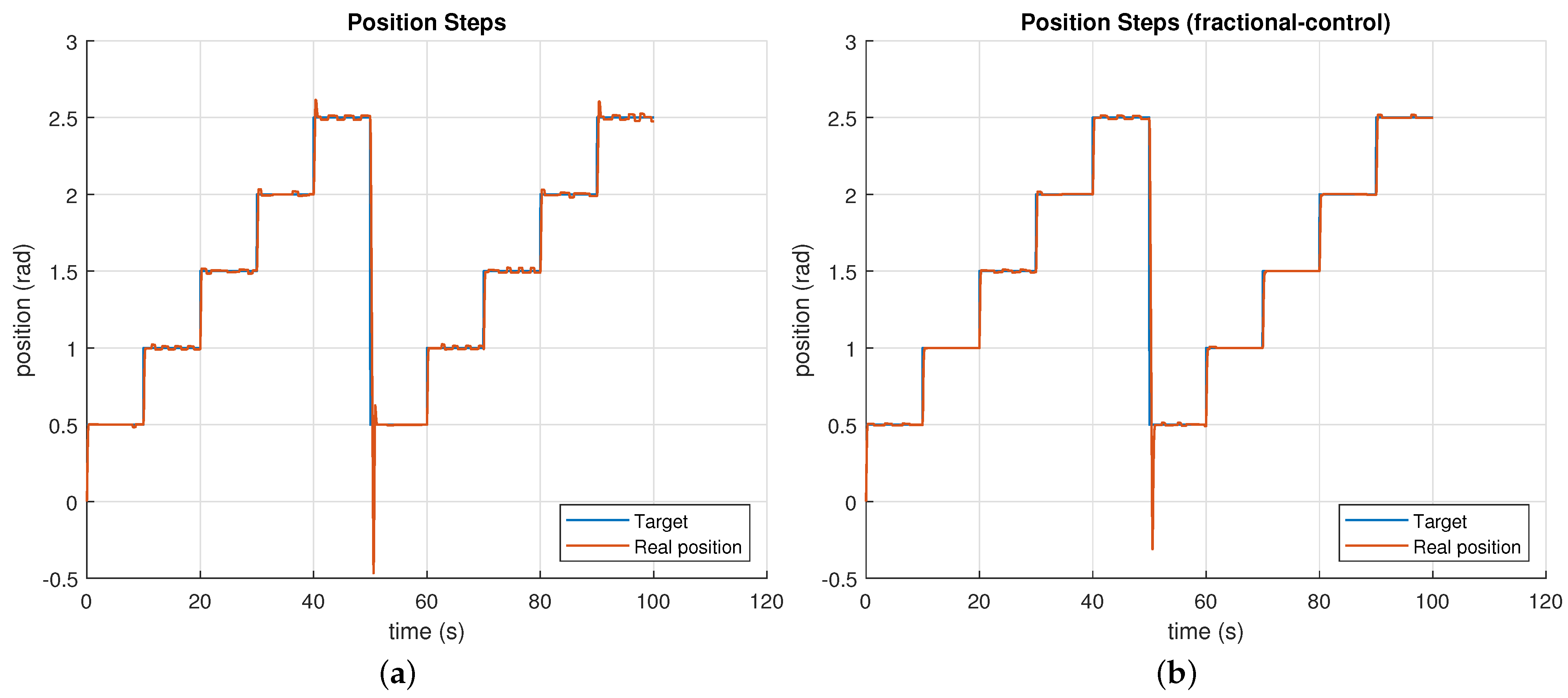
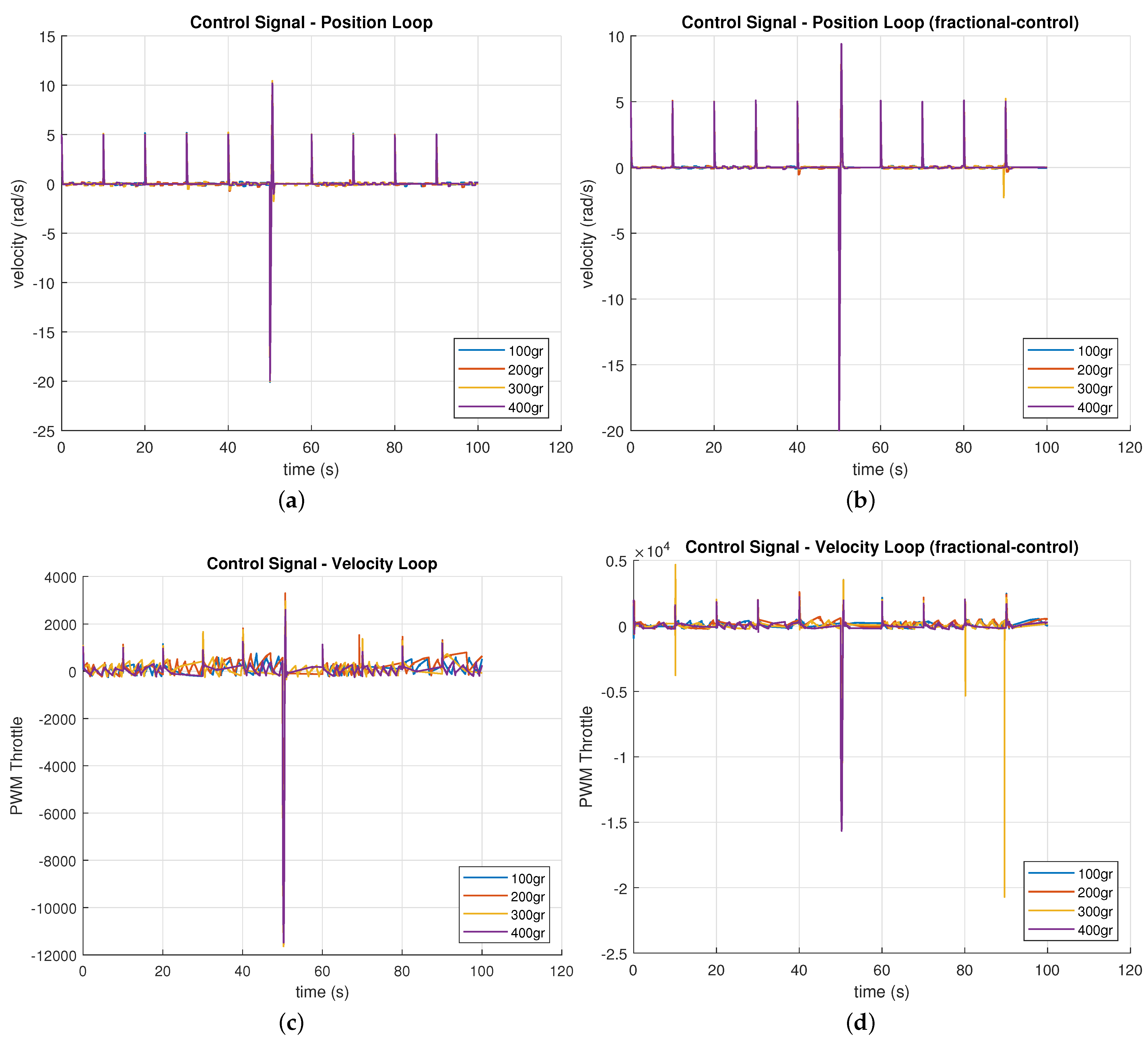
4. Results
Single Link Cable-Driven Prototype Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MRS | Modular robotic system |
| MITE | Module, information, task, and environment |
| DoF | Degrees of freedom |
References
- Fukuda, T.; Nakagawa, S. Approach to the dynamically reconfigurable robotic system. J. Intell. Robot. Syst. 1988, 1, 55–72. [Google Scholar] [CrossRef]
- Schmitz, D. The CMU Reconfigurable Modular Manipulator System; Technical Report; The Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 1988. [Google Scholar]
- Ahmadzadeh, H.; Masehian, E.; Asadpour, M. Modular robotic systems: Characteristics and applications. J. Intell. Robot. Syst. 2016, 81, 317–357. [Google Scholar] [CrossRef]
- Yim, M. A reconfigurable modular robot with multiple modes of locomotion. In Proceedings of the 1993 JSME Conference on Advanced Mechatronics, Tokyo, Japan, August 1993. [Google Scholar]
- Qiao, G.; Song, G.; Wang, W.; Zhang, Y.; Wang, Y. Design and implementation of a modular self-reconfigurable robot. Int. J. Adv. Robot. Syst. 2014, 11, 47. [Google Scholar] [CrossRef] [Green Version]
- Murata, S.; Kurokawa, H.; Kokaji, S. Self-assembling machine. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; IEEE: New York, NY, USA, 1994; pp. 441–448. [Google Scholar]
- Murata, S.; Kurokawa, H. Prototypes of self-organizing robots. In Self-Organizing Robots; Springer: Tokyo, Japan, 2012; pp. 105–130. [Google Scholar]
- Inou, N.; Kobayashi, H.; Koseki, M. Development of pneumatic cellular robots forming a mechanical structure. In Proceedings of the 7th International Conference on Control, Automation, Robotics and Vision, 2002, ICARCV 2002, Singapore, 2–5 December 2002; IEEE: New York, NY, USA, 2002; Volume 1, pp. 63–68. [Google Scholar]
- Romanishin, J.W.; Gilpin, K.; Rus, D. M-blocks: Momentum-driven, magnetic modular robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–8 November 2013; IEEE: New York, NY, USA, 2013; pp. 4288–4295. [Google Scholar]
- Wolfe, K.C.; Moses, M.S.; Kutzer, M.D.; Chirikjian, G.S. M 3 Express: A low-cost independently-mobile reconfigurable modular robot. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; IEEE: New York, NY, USA, 2012; pp. 2704–2710. [Google Scholar]
- Hong, W.; Wang, S.; Shui, D. Reconfigurable robot system based on electromagnetic design. In Proceedings of the 2011 International Conference on Fluid Power and Mechatronics, Beijing, China, 17–20 August 2011; IEEE: New York, NY, USA, 2011; pp. 570–575. [Google Scholar]
- Sadjadi, H.; Mohareri, O.; Al-Jarrah, M.A.; Assaleh, K. Design and implementation of HexBot: A modular self-reconfigurable robotic system. J. Frankl. Inst. 2012, 349, 2281–2293. [Google Scholar] [CrossRef]
- Davey, J.; Kwok, N.; Yim, M. Emulating self-reconfigurable robots-design of the SMORES system. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; IEEE: New York, NY, USA, 2012; pp. 4464–4469. [Google Scholar]
- Lyder, A.; Garcia, R.F.M.; Stoy, K. Genderless connection mechanism for modular robots introducing torque transmission between modules. In Proceedings of the ICRA Workshop on Modular Robots, State of the Art, Anchorage, Alaska, 3 May 2010; pp. 77–81. [Google Scholar]
- Yu, C.H.; Haller, K.; Ingber, D.; Nagpal, R. Morpho: A self-deformable modular robot inspired by cellular structure. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: New York, NY, USA, 2008; pp. 3571–3578. [Google Scholar]
- Galloway, K.C.; Jois, R.; Yim, M. Factory floor: A robotically reconfigurable construction platform. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; IEEE: New York, NY, USA, 2010; pp. 2467–2472. [Google Scholar]
- Lyder, A.; Garcia, R.F.M.; Stoy, K. Mechanical design of odin, an extendable heterogeneous deformable modular robot. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: New York, NY, USA, 2008; pp. 883–888. [Google Scholar]
- Shimizu, M.; Ishiguro, A.; Kawakatsu, T. A modular robot that exploits a spontaneous connectivity control mechanism. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; IEEE: New York, NY, USA, 2005; pp. 1899–1904. [Google Scholar]
- Donald, B.R.; Levey, C.G.; McGray, C.D.; Paprotny, I.; Rus, D. An untethered, electrostatic, globally controllable MEMS micro-robot. J. Microelectromechan. Syst. 2006, 15, 1–15. [Google Scholar] [CrossRef]
- Suzuki, R.; Zheng, C.; Kakehi, Y.; Yeh, T.; Do, E.Y.L.; Gross, M.D.; Leithinger, D. ShapeBots: Shape-changing Swarm Robots. In Proceedings of the 32nd Annual ACM Symposium on User Interface Software and Technology, New Orleans, LA, USA, 20–23 October 2019; pp. 493–505. [Google Scholar]
- Matsuo, H.; Asada, H.H.; Takeda, Y. Design of a Novel Mutliple-DOF Extendable Arm With Rigid Components Inspired by a Deployable Origami Structure. IEEE Robot. Autom. Lett. 2020, 5, 2730–2737. [Google Scholar] [CrossRef]
- Hatori, K. History of Origami in the East and the West before Interfusion. In Origami 5: Fifth International Meeting of Origami Science, Mathematics and Education; Singapore Management University: Singapore, 2010; pp. 1–13. [Google Scholar]
- Miura, K. Method of packaging and deployment of large membranes in space. Title Inst. Space Astronaut. Sci. Rep. 1985, 618, 1. [Google Scholar]
- Santoso, J.; Skorina, E.H.; Luo, M.; Yan, R.; Onal, C.D. Design and analysis of an origami continuum manipulation module with torsional strength. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: New York, NY, USA, 2017; pp. 2098–2104. [Google Scholar]
- Firouzeh, A.; Paik, J. An under-actuated origami gripper with adjustable stiffness joints for multiple grasp modes. Smart Mater. Struct. 2017, 26, 055035. [Google Scholar] [CrossRef]
- Kuribayashi, K.; Tsuchiya, K.; You, Z.; Tomus, D.; Umemoto, M.; Ito, T.; Sasaki, M. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil. Mater. Sci. Eng. A 2006, 419, 131–137. [Google Scholar] [CrossRef]
- Zirbel, S.A.; Wilson, M.E.; Magleby, S.P.; Howell, L.L. An origami-inspired self-deployable array. In Proceedings of the ASME 2013 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Snowbird, UT, USA, 16–18 September 2013. [Google Scholar]
- Paez, L.; Agarwal, G.; Paik, J. Design and analysis of a soft pneumatic actuator with origami shell reinforcement. Soft Robot. 2016, 3, 109–119. [Google Scholar] [CrossRef]
- Kidambi, N.; Wang, K. Dynamics of Kresling origami deployment. Phys. Rev. E 2020, 101, 063003. [Google Scholar] [CrossRef] [PubMed]
- Kresling, B.; Abel, J.F. Natural twist buckling in shells: From the hawkmoth’s bellows to the deployable Kresling-pattern and cylindrical Miura-ori. In Proceedings of the 6th International Conference on Computation of Shell and Spatial Structures, Ithaca, NY, USA, 28–31 May 2008; Volume 11, pp. 12–32. [Google Scholar]
- Zhai, Z.; Wang, Y.; Jiang, H. Origami-inspired, on-demand deployable and collapsible mechanical metamaterials with tunable stiffness. Proc. Natl. Acad. Sci. USA 2018, 115, 2032–2037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hunt, G.W.; Ario, I. Twist buckling and the foldable cylinder: An exercise in origami. Int. J. Non-Linear Mech. 2005, 40, 833–843. [Google Scholar] [CrossRef]
- Jianguo, C.; Xiaowei, D.; Ya, Z.; Jian, F.; Yongming, T. Bistable behavior of the cylindrical origami structure with Kresling pattern. J. Mech. Des. 2015, 137. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, J.; Li, M.; Feng, J. Bistable behaviour of a deployable cylinder with Kresling pattern. In Proceedings of the 7th International Meeting on Origami in Science, Mathematics and Education (7OSME), Oxford, UK, 4–7 September 2018. [Google Scholar]
- Muñoz, J.; Monje, C.A.; Nagua, L.F.; Balaguer, C. A graphical tuning method for fractional order controllers based on iso-slope phase curves. ISA Trans. 2020. [Google Scholar] [CrossRef] [PubMed]
- Nise, N.S. Frequency response techniques. In Control Systems Engineering; Wiley: Pomona, CA, USA, 2019; Chapter 10; pp. 525–612. [Google Scholar]
- Chen, Y.; Moore, K.L. Relay Feedback Tuning of Robust PID Controllers with Iso-damping Property. IEEE Trans. Syst. Man Cybern. Part B 2005, 35, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Monje, C.A.; Vinagre, B.M.; Santamaría, G.E.; Tejado, I. Auto-tuning of fractional order PIλDμ controllers using a PLC. In Proceedings of the 2009 IEEE Conference on Emerging Technologies Factory Automation, Palma de Mallorca, Spain, 22–25 September 2009; IEEE: New York, NY, USA, 2009; pp. 1–7. [Google Scholar] [CrossRef]













| x (m) | M (kg) |
|---|---|
| 0.13 | 0 |
| 0.128 | 0.1 |
| 0.105 | 0.2 |
| 0.092 | 0.3 |
| 0.082 | 0.4 |
| Physical | Effect | Closed Loop | Open Loop |
|---|---|---|---|
| Meaning | Defined | Specification | Specification |
| Damping ratio | Overshoot | Resonant peak | Phase margin |
| Response speed | Peak time | Bandwidth | Crossover frequency |
| h (mm) | (deg) | (deg) | |
|---|---|---|---|
| Collapsed state | 0 | 0 | −13.32 |
| Deploying state | 30 | 54.3 | −12.27 |
| Deployed state | 36.93 | 90 | 1.04 |
| (mm) | (mm) | (mm) | (mm) | |
|---|---|---|---|---|
| Completely deployed link | 36.93 | 36.93 | 36.93 | 110.8 |
| Only one section folding | 36.93 | 20.55 | 36.93 | 94.43 |
| Three sections folding | 31.73 | 25.55 | 30 | 87.29 |
| Real | Simulation | Error | |||||
|---|---|---|---|---|---|---|---|
| Position (rad) | h (mm) | (deg) | (deg) | h (mm) | (deg) | h (mm) | (deg) |
| 0.5 | 35.69 | 64.46 | −12.11 | 38.88 | −12.28 | 3.18 | −0.1635 |
| 1 | 31.94 | 53.85 | −12.72 | 34.79 | −12.89 | 2.84 | −0.1637 |
| 1.5 | 28.19 | 45.45 | −13.06 | 30.71 | −13.23 | 2.51 | −0.1660 |
| 2 | 24.44 | 38.16 | −13.28 | 26.64 | −13.45 | 2.19 | −0.1634 |
| 2.2 | 22.94 | 35.45 | −13.35 | 24.99 | −13.52 | 2.04 | −0.1642 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mena, L.; Muñoz, J.; Monje, C.A.; Balaguer, C. Modular and Self-Scalable Origami Robot: A First Approach. Mathematics 2021, 9, 1324. https://doi.org/10.3390/math9121324
Mena L, Muñoz J, Monje CA, Balaguer C. Modular and Self-Scalable Origami Robot: A First Approach. Mathematics. 2021; 9(12):1324. https://doi.org/10.3390/math9121324
Chicago/Turabian StyleMena, Lisbeth, Jorge Muñoz, Concepción A. Monje, and Carlos Balaguer. 2021. "Modular and Self-Scalable Origami Robot: A First Approach" Mathematics 9, no. 12: 1324. https://doi.org/10.3390/math9121324
APA StyleMena, L., Muñoz, J., Monje, C. A., & Balaguer, C. (2021). Modular and Self-Scalable Origami Robot: A First Approach. Mathematics, 9(12), 1324. https://doi.org/10.3390/math9121324






