Second-Order Weak Approximations of CKLS and CEV Processes by Discrete Random Variables

Abstract

In this paper, we construct second-order weak split-step approximations of the CKLS and CEV processes that use generation of a three−valued random variable at each discretization step without switching to another scheme near zero, unlike other known schemes (Alfonsi, 2010; Mackevičius, 2011). To the best of our knowledge, no second-order weak approximations for the CKLS processes were constructed before. The accuracy of constructed approximations is illustrated by several simulation examples with comparison with schemes of Alfonsi in the particular case of the CIR process and our first-order approximations of the CKLS processes (Lileika– Mackevičius, 2020).

1. Introduction

We are interested in weak second-order approximations for the Chan–Karolyi– Longstaff–Sanders (CKLS) model [1]

$$\mathrm{d}{X}_t=(\theta -\beta X_t)\mathrm{d}t+\sigma X_t^{\gamma }\mathrm{d}{B}_t,X_0=x\ge 0,$$

(1)

with parameters $(\theta ,\beta ,\sigma ,\gamma )\in {\overline{\mathbb{R}}}_{+}\times \mathbb{R}\times {\mathbb{R}}_{+}\times [1/2,1)$, where ${\mathbb{R}}_{+}:=(0,\infty )$ and ${\overline{\mathbb{R}}}_{+}:=[0,\infty )$. In particular, when $\theta =0$ and $\beta <0$, we have the constant elasticity of variance (CEV) model [2], and when $\gamma =1/2$ and $\beta \ge 0$, we have the well-known Cox–Ingersoll–Ross (CIR) model [3]. The main problem in developing numerical methods for such a diffusion equation/model is that the diffusion coefficient has unbounded derivatives near zero, and therefore standard methods (see, e.g., Milstein and Tretyakov [4]) are not applicable: discretization schemes that (explicitly or implicitly) involve the derivatives of the coefficients usually lose their accuracy near zero, especially for large $\sigma$. This problem for the CIR processes was solved by modifying the scheme considered by switching near zero to another scheme, which is (1) sufficiently regular and (2) sufficiently accurate near zero; we refer, for example, to [5,6,7] and references therein. Typically, a second-order approximation near zero is constructed by discrete random variables matching three or four moments with those of the true solution.

The main result of this paper is the construction of second-order weak split-step approximations of the CKLS and CEV processes by discrete random variables. To the best of our knowledge, no second-order weak approximations of the CKLS process have been constructed before, except for the particular case of the CIR process (Alfonsi [5], Mackevičius [7]). Our construction method is significantly different from that of the first-order approximation in our previous paper [8]. Another novel feature of our result is that in our schemes, no switching between schemes near zero is used, in contrast to [5,7]. This simplifies the implementation of approximations. We illustrate the accuracy of our approximations by several simulation examples with comparison with schemes of Alfonsi in the particular case of the CIR process and our first-order approximations of the CKLS processes constructed in [8].

Why are second-order schemes better than first-order ones? On the one hand, the former are more accurate when using the same discretization step size. On the other hand, by the former, we can reach the same accuracy under larger step sizes, which implies lower computation costs. Of course, if high accuracy is not required, first-order approximations suffice.

The paper is organized as follows. In Section 2, we recall some definitions and results. In Section 3, we derive sufficient conditions for a discretization scheme to be a potential second-order approximation for the stochastic part ($\mathrm{d}{S}_t=\sigma S_t^{\gamma }\mathrm{d}{B}_t$) of the CKLS and CEV equations. In Section 4, we construct second-order approximations for the CIR equation by three-valued discrete random variables. In Section 5, we apply the approach of Section 4 to the CKLS and CEV equations. In Section 6, we give several simulation examples illustrating our results. Finally, in the Appendix A, we derive some exact formulas for moments of the stochastic parts of the CKLS equations, which we need for simulation examples.

2. Preliminaries

In this section, we give some definitions for the general one-dimensional stochastic differential equation

$$X_t^x=x+{\int }_0^{t}b(X_s^x)\mathrm{d}s+{\int }_0^t\sigma (X_s^x)\mathrm{d}{B}_s,t\ge 0,x\in \mathbb{D}\subset \mathbb{R}.$$

(2)

We assume that the equation has a unique weak solution $X_t^x$ such that $\mathbb{P}(X_t^x\in \mathbb{D},t\ge 0)=1$ for all $x\in \mathbb{D}$. For example, for Equation (1), we can take $\mathbb{D}={\overline{\mathbb{R}}}_{+}$.

Having a fixed time interval $[0,T],$ consider an equidistant time discretization ${\Delta }^h=\{ih,i=0,1,\dots ,[T/h],h\in (0,T]\}$, where $\left[a\right]$ is the integer part of a. By a discretization scheme of Equation (2) we mean a family of discrete-time homogeneous Markov chains ${\widehat{X}}^h=\{{\widehat{X}}^h(x,t),x\in \mathbb{D},t\in {\Delta }^h\}$ with initial values ${\widehat{X}}^h(x,0)=x$ and one-step transition probabilities $p^h(x,\mathrm{d}z)$, $x\in \mathbb{D}$, in $\mathbb{D}$. For convenience, we only consider steps $h=T/n$, $n\in \mathbb{N}$. For brevity, we write ${\widehat{X}}_t^x$ or $\widehat{X}(x,t)$ instead of ${\widehat{X}}^h(x,t)$. Note that because of the Markovity, a one-step approximation ${\widehat{X}}_h^x$ of the scheme completely defines the distribution of the whole discretization scheme ${\widehat{X}}_t^x$, so that we only need to construct the former.

We denote by $C^{\infty }(\mathbb{D})$ the space of $C^{\infty }$ functions $f:\mathbb{D}\to \mathbb{R}$, by $C_0^{\infty }(\mathbb{D})$ the functions $f\in C^{\infty }(\mathbb{D})$ with compact support in $\mathbb{D}$, and by $C_{\mathrm{pol}}^{\infty }(\mathbb{D})$ the functions $f\in C^{\infty }(\mathbb{D})$ such that

$$\begin{array}{c}\hfill |f^{(n)}(x)|\le C_n{(1+|x|}^{k_n}),x\in \mathbb{D},n\in {\mathbb{N}}_0:=\{0,1,2,\dots \},\end{array}$$

for some sequence $(C_n,k_n)\in {\mathbb{R}}_{+}\times {\mathbb{N}}_0$. Following [5], we say that such a sequence $\{(C_n,k_n),n\in {\mathbb{N}}_0\}$ is a good sequence for f.

We will write $g(x,h)=O(h^n)$ if, for some $C>0$, $k\in \mathbb{N}$, and $h_0>0$,

$$\left|g(x,h)\right|\le {C(1+|x|}^k)h^n,x\ge 0,0<h\le h_0.$$

If, in particular, the function g is expressed in terms of another function $f\in {\mathrm{C}}_{\mathrm{pol}}^{\infty }(\mathbb{R})$ and the constants C, k, and $h_0$ only depend on a good sequence for f, then we will write, instead, $g(x,h)=\mathcal{O}(h^n)$.

Definition 1.

A discretization scheme ${\widehat{X}}^h$ is a weak νth-order approximation for the solution $(X_t^x,t\in [0,T])$ of Equation (2) if for every $f\in C_0^{\infty }(\mathbb{D})$, there exists $C>0$ such that

$$\begin{array}{c}\hfill |\mathbb{E}f(X_T^x)-\mathbb{E}f({\widehat{X}}_T^x)|\le C{h}^{\nu },h>0.\end{array}$$

Definition 2.

Let $Lf=b{f}^{\prime }+\frac{1}{2}{\sigma }^2{f}^{″}$ be the generator of the solution of Equation (2). Suppose $Lf\in C_{\mathrm{pol}}^{\infty }(\mathbb{D})$ for all $f\in C_{\mathrm{pol}}^{\infty }(\mathbb{D})$, that is, $b,{\sigma }^2\in C_{\mathrm{pol}}^{\infty }(\mathbb{D})$. The νth-order remainder of a discretization scheme ${\widehat{X}}_t^x$ for $X_t^x$ is the operator $R_{\nu }^h:C_{\mathrm{pol}}^{\infty }(\mathbb{D})\to C(\mathbb{D})$ defined by

$$R_{\nu }^{h}f(x):=\mathbb{E}f({\widehat{X}}_h^x)-\left[f(x)+\sum _{k=1}^{\nu }\frac{L^{k}f(x)}{k!}{h}^k\right],x\in \mathbb{D},h>0.$$

(3)

A discretization scheme ${\widehat{X}}_t^x$ is a local νth-order weak approximation of Equation (2) if

$$R_{\nu }^{h}f(x)=O(h^{\nu +1}),h\to 0,$$

for all $f\in C_{\mathrm{pol}}^{\infty }(\mathbb{D})$ and $x\in \mathbb{D}$.

Remark 1.

Iterating the Dynkin formula $\mathbb{E}f(X_h^x)=f(x)+{\int }_0^h\mathbb{E}Lf(X_s^x)\mathrm{d}s$, we have

$$\begin{array}{cc}\hfill \mathbb{E}f(X_h^x)& =f(x)+\sum _{k=1}^{\nu }\frac{L^{k}f(x)}{k!}{h}^k\hfill \\ & +{\int }_0^h{\int }_0^{s_1}\dots {\int }_0^{s_{\nu }}\mathbb{E}{L}^{\nu +1}f(X_{s_{\nu +1}}^x)\mathrm{d}{s}_{\nu +1}\dots \mathrm{d}{s}_2\mathrm{d}{s}_1,\hfill \end{array}$$

which motivates Definition 2: If $L^{\nu +1}f$ behaves “well” (e.g., $b,{\sigma }^2,f\in C_0^{\infty }(\mathbb{D})$, and $\mathbb{E}{L}^{\nu +1}f$ is bounded), then for the “one-step” $\nu$th-order weak approximation scheme ${\widehat{X}}_h^x$, we have

$$|\mathbb{E}f(X_h^x)-\mathbb{E}f({\widehat{X}}_h^x)|=O(h^{\nu +1}),h\to 0.$$

(4)

We may expect that in “good” cases, a local $\nu$th-order weak discretization scheme is a $\nu$th-order (global) approximation. Rigorous statements require certain uniformity of (4) with respect to f and regularity of L.

Definition 3.

A discretization scheme ${\widehat{X}}_t^x$ is a potential νth-order weak approximation for Equation (2) if for every $f\in C_{\mathrm{pol}}^{\infty }(\mathbb{D})$,

$$\begin{array}{c}\hfill |R_{\nu }^{h}f(x)|=\mathcal{O}(h^{\nu +1}).\end{array}$$

Definition 4.

A discretization scheme ${\widehat{X}}_t^x={\widehat{X}}^h(x,t)$, $h>0$, has uniformly bounded moments if there exists $h_0>0$ such that

$$\begin{array}{c}\hfill \underset{0<h\le h_0}{sup}\underset{t\in {\Delta }^h}{sup}\mathbb{E}(|{\widehat{X}}^h(x,t){|}^n)<+\infty ,n\in \mathbb{N},x\in \mathbb{D}.\end{array}$$

We say that a potential νth-order weak approximation is a strongly potential νth-order weak approximation if it has uniformly bounded moments.

Remark 2.

Typically, a strongly potential $\nu$th-order discretization is a $\nu$th-order weak approximation in the sense of Definition 1. At least, we do not know any counterexample. A rigorous proof for the CIR equation is given by Alfonsi [9] (see also [10]).

We split Equation (1) into the deterministic part

$$\begin{array}{cc}\hfill \mathrm{d}{D}_t^x& =(\theta -\beta D_t^x)\mathrm{d}t,D_0^x=x\ge 0,\hfill \end{array}$$

and the stochastic part

$$\mathrm{d}{S}_t^x=\sigma {(S_t^x)}^{\gamma }\mathrm{d}{B}_t,S_0^x=x\ge 0.$$

(5)

The solution of the deterministic part is positive for all $(x,t)\in {\overline{\mathbb{R}}}_{+}\times (0,T]$, namely:

$$\begin{array}{c}\hfill D_t^x=D(x,t)=\left\{\begin{array}{cc}\hfill x{\mathrm{e}}^{-\beta t}+\frac{\theta }{\beta }(1-{\mathrm{e}}^{-\beta t}),& \beta \ne 0,\hfill \\ \hfill x+\theta t,& \beta =0.\hfill \end{array}\right.\end{array}$$

The solution of the stochastic part is not explicitly known. The following theorem allows us to reduce the construction of a weak second-order approximation to that of the stochastic part. Let ${\widehat{S}}_t^x=\widehat{S}(x,t)$ be a discretization scheme for the stochastic part (5).

Theorem 1

([5] (Thm. 1.17)). Let ${\widehat{S}}_t^x$ be a potential second-order weak approximation of the stochastic part (5) of Equation (1). Then the (split-step) composition

$${\widehat{X}}^h(x,h):=\left\{\begin{array}{cc}\hfill D\left(\widehat{S}\left(D(x,h/2),h\right),h/2\right),& h>0,\hfill \\ \hfill x,& h=0,\hfill \end{array}\right.$$

(6)

defines a potential second-order weak approximation of Equation (1).

Corollary 1.

If ${\widehat{S}}_t^x$ is a strongly potential second-order weak approximation of the stochastic part (5) of Equation (1), then composition (6) is a strongly potential second-order weak approximation of Equation (1).

The theorem and corollary allow us to restrict ourselves, without loss of generality, on the (strongly) potential second-order weak approximations of the stochastic part $\mathrm{d}{S}_t^x=\sigma {(S_t^x)}^{\gamma }\mathrm{d}{B}_t$ of Equation (1).

3. A Strongly Potential Second-Order Approximation of the Stochastic Part of the CKLS and CEV Equations

Let ${\widehat{S}}_h^x$ be any discretization scheme. Denote $a:={\sigma }^2$. Using Taylor’s formula for $f\in C^6(\mathbb{R})$, we get

$$\begin{array}{cc}\hfill \mathbb{E}f({\widehat{S}}_h^x)& =f(x)+f^{\prime }(x)\mathbb{E}({\widehat{S}}_h^x-x)+\frac{f^{″}(x)}{2}\mathbb{E}{({\widehat{S}}_h^x-x)}^2+\frac{f^{‴}(x)}{6}\mathbb{E}{({\widehat{S}}_h^x-x)}^3\hfill \\ & +\frac{f^{(4)}(x)}{4!}\mathbb{E}{({\widehat{S}}_h^x-x)}^4+\frac{f^{(5)}(x)}{5!}\mathbb{E}{({\widehat{S}}_h^x-x)}^5\hfill \\ & +\frac{1}{5!}\mathbb{E}{\int }_x^{{\widehat{S}}_h^x}{f}^{(6)}(s){({\widehat{S}}_h^x-s)}^5\mathrm{d}s.\hfill \end{array}$$

It is worth noting that further technical calculations were mainly made by using MAPLE software.

Since the first and second power of the generator of stochastic part (5) are (see Definition (3))

$$\begin{array}{cc}\hfill L_{0}f(x)& =\frac{1}{2}a{x}^{2\gamma }{f}^{″}(x)\mathrm{and}\hfill \\ \hfill L_0^{2}f(x)& =\gamma \left(\gamma -\frac{1}{2}\right)a^2{x}^{4\gamma -2}{f}^{″}(x)+\gamma a^2{x}^{4\gamma -1}{f}^{‴}(x)+\frac{1}{4}{a}^2{x}^{4\gamma }{f}^{(4)}(x),\hfill \end{array}$$

the second-order remainder for ${\widehat{S}}_h^x$ is

$$\begin{array}{cc}\hfill R_2^{h}f(x)& =\mathbb{E}f({\widehat{S}}_h^x)-\left[f(x)+L_{0}f(x)h+L_0^{2}f(x)\frac{h^2}{2}\right]\hfill \\ & =f^{\prime }(x)\mathbb{E}({\widehat{S}}_h^x-x)\hfill \\ & +\frac{f^{″}(x)}{2}[\mathbb{E}{({\widehat{S}}_h^x-x)}^2-(1+\gamma (\gamma -1/2)x^{2(\gamma -1)}ah)x^{2\gamma }ah]\hfill \\ & +\frac{f^{‴}(x)}{6}[\mathbb{E}{({\widehat{S}}_h^x-x)}^3-3\gamma x^{4\gamma -1}{(ah)}^2]\hfill \\ \hfill & +\frac{f^{(4)}(x)}{4!}[\mathbb{E}{({\widehat{S}}_h^x-x)}^4-3x^{4\gamma }{(ah)}^2]\hfill \\ & +\frac{f^{(5)}(x)}{5!}\mathbb{E}{({\widehat{S}}_h^x-x)}^5+r_2(x,h),x\ge 0,h>0,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill |r_2(x,h)|=\frac{1}{5!}\left|\mathbb{E}{\int }_x^{{\widehat{S}}_h^x}{f}^{(6)}(s){({\widehat{S}}_h^x-s)}^5\mathrm{d}s\right|\le \frac{1}{6!}\mathbb{E}\left[\underset{0\le s\le {\widehat{S}}_h^x}{max}\left|f^{(6)}(s)\right|{({\widehat{S}}_h^x-x)}^6\right].\end{array}$$

For brevity, we denote $z:=ah={\sigma }^{2}h$. By the above expression of the remainder $R_2^{h}f(x)$, the discretization scheme ${\widehat{S}}_h^x$ is a potential second-order approximation of the stochastic part (5) if

$$\begin{array}{cc}\hfill \mathbb{E}({\widehat{S}}_h^x-x)& =O(h^3),x\ge 0,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \mathbb{E}{({\widehat{S}}_h^x-x)}^2& =(1+\gamma (\gamma -1/2)x^{2(\gamma -1)}z)x^{2\gamma }z+O(h^3),x\ge 0,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \mathbb{E}{({\widehat{S}}_h^x-x)}^3& =3\gamma x^{4\gamma -1}{z}^2+O(h^3),x\ge 0,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \mathbb{E}{({\widehat{S}}_h^x-x)}^4& =3x^{4\gamma }{z}^2+O(h^3),x\ge 0,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill |\mathbb{E}{({\widehat{S}}_h^x-x)}^5|& =O(h^3),x\ge 0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \mathbb{E}[\underset{0\le s\le {\widehat{S}}_h^x}{max}& |f^{(6)}(s)|{({\widehat{S}}_h^x-x)}^6]=\mathcal{O}(h^3).\hfill \end{array}$$

(12)

Initially, for constructing our approximations, instead of (12), we will require a slightly weaker condition

$$\mathbb{E}{({\widehat{S}}_h^x-x)}^6=O(h^3).$$

(13)

Later, we will see that, actually, all our approximations satisfy the required stronger condition (12).

We easily convert conditions (7)–(11) and (13) for the central moments of ${\widehat{S}}_h^x$ into conditions for the noncentral moments:

$$\mathbb{E}{({\widehat{S}}_h^x)}^i={\widehat{m}}_i+O(h^3),i=1,2,\dots ,6,$$

(14)

where the “moments” ${\widehat{m}}_i={\widehat{m}}_i(x,h)$, $x\ge 0,h>0$, $i=1,2,\dots ,6$, are defined as

$$\begin{array}{cc}\hfill {\widehat{m}}_1=& x,\hfill \\ \hfill {\widehat{m}}_2=& \gamma \left(\gamma -\frac{1}{2}\right)x^{4\gamma -2}{z}^2+x^{2\gamma }z+x^2,\hfill \\ \hfill {\widehat{m}}_3=& \frac{3}{2}\gamma (1+2\gamma )x^{4\gamma -1}{z}^2+3x^{1+2\gamma }z+x^3,\hfill \\ \hfill {\widehat{m}}_4=& 6x^{2+2\gamma }z+3(1+\gamma )(1+2\gamma )x^{4\gamma }{z}^2+x^4,\hfill \\ \hfill {\widehat{m}}_5=& 5(3+2\gamma )(1+\gamma )x^{1+4\gamma }{z}^2+10x^{3+2\gamma }z+x^5,\hfill \\ \hfill {\widehat{m}}_6=& \frac{15}{2}(2+\gamma )(3+2\gamma )x^{2+4\gamma }{z}^2+15x^{4+2\gamma }z+x^6.\hfill \end{array}$$

(15)

4. A Strongly Potential Second-Order Approximation of the CIR Equation

In this section, we construct a strongly potential second-order approximation for the CIR Equation ($\gamma =1/2$) using a three-valued random variable at each generation step without switching to another scheme in a neighborhood of zero. The “moments” (15) in conditions (14) for the central moments $\mathbb{E}{({\widehat{S}}_h^x)}^i$ in this case become as follows (recall that $z:=ah={\sigma }^{2}h$):

$$\begin{array}{cc}\hfill {\widehat{m}}_1& =x,\hfill \\ \hfill {\widehat{m}}_2& =x^2+xz,\hfill \\ \hfill {\widehat{m}}_3& =x^3+3x^{2}z+\frac{3}{2}x{z}^2,\hfill \\ \hfill {\widehat{m}}_4& =x^4+6x^{3}z+9x^2{z}^2,\hfill \\ \hfill {\widehat{m}}_5& =x^5+10x^{4}z+30x^3{z}^2,\hfill \\ \hfill {\widehat{m}}_6& =x^6+15x^{5}z+75x^4{z}^2.\hfill \end{array}$$

(16)

We therefore look for approximations ${\widehat{S}}_h^x$ taking three positive values $x_1,x_2,$ and $x_3$ with probabilities $p_1,p_2,$ and $p_3$ such that

$$\mathbb{E}{({\widehat{S}}_h^x)}^i={\widehat{m}}_i+O(h^3),i=1,2,\dots ,6,$$

(17)

where $x\ge 0,h>0$, together with obvious requirement

$$p_1+p_2+p_3=m_0:=1.$$

(18)

Denote $m_p=m_p(h,x):=\mathbb{E}{(S_h^x)}^p$, $p\in \mathbb{N}$. We have (see [8], Appendix)

$$\begin{array}{cc}\hfill m_1& ={\widehat{m}}_1=x,\hfill \\ \hfill m_2& ={\widehat{m}}_2=x^2+xz,\hfill \\ \hfill m_3& ={\widehat{m}}_3=x^3+3x^{2}z+\frac{3x{z}^2}{2}.\hfill \end{array}$$

Solving the system

$$x_1^i{p}_1+x_2^i{p}_2+x_3^i{p}_3=m_i,i=1,2,3,$$

with respect to unknowns $x_1$, $x_2$, and $x_3$, we get:

$$\begin{array}{cc}\hfill p_1& =\frac{m_1{x}_2{x}_3-m_2(x_2+x_3)+m_3}{x_1(x_3-x_1)(x_2-x_1)},\hfill \\ \hfill p_2& =\frac{m_2(x_1+x_3)-m_1{x}_1{x}_3-m_3}{x_2(x_2-x_1)(x_3-x_2)},\hfill \\ \hfill p_3& =\frac{m_1{x}_1{x}_2-m_2(x_1+x_2)+m_3}{x_3(x_3-x_2)(x_3-x_1)}.\hfill \end{array}$$

(19)

We can get analogous expressions from the last three equations of system (17) (with $m_4,m_5,m_6$ instead of $m_1,m_2,m_3$). However, trying to directly solve the obtained six equations with respect to all unknowns $x_1,x_2,x_3$, $p_1,p_2,p_3$ gave no satisfactory results. In view of the form of approximations presented by Alfonsi [5] and Mackevičius [7] for the CIR equation and of our first-order approximations for the CKLS equations [8], after a number of experiments, we arrived at the following conclusions:

• the values of the discretization scheme ${\widehat{S}}_h^x$ may be chosen of the form

  $$\begin{array}{c}\hfill x_{1,3}=x+A_{1}z\mp \sqrt{(Bx+Cz)z},x_2=x+A_{2}z,\end{array}$$

  (20)

  with parameters $A_1,A_2,B,C>0$;
• Instead of the exact matching of moments $\mathbb{E}{({\widehat{S}}_h^x)}^i=m_i$ for $i=4,5,6$, it is more convenient to require $\mathbb{E}{({\widehat{S}}_h^x)}^i={\widehat{m}}_i$, $i=4,5,6$.

Solving systems (17)–(19) with $x_1,x_2,x_3$ of the form (20), together with ensuring the nonnegativity of the solution $\{x_1,x_2,x_3,p_1,p_2,p_3\}$, still is a rather technical and long task, even with the help of MAPLE. Note that the right-hand sides $O(h^3)$ in conditions (17) give us certain flexibility in finding relatively simple expressions of solutions.

This way we get a family of second-order discretization schemes ${\widehat{S}}_h^x$ depending on the parameter $A\in [3/4,3/2]$:

$$\begin{array}{c}\hfill x_{1,3}=x+(A+\frac{3}{4})z\mp \sqrt{\left(3x+{(A+\frac{3}{4})}^{2}z\right)z},x_2=x+Az,\end{array}$$

(21)

with probabilities $p_1,p_2$, and $p_3$ given by (19). The interval of possible values of the parameter A is conditioned by the necessary nonnegativity of the solution $\{x_1,x_2,x_3,p_1,p_2,p_3\}$. In particular, the value $A=(3+\sqrt{3})/4\approx 1.183$ ensures the exact matching of the fourth moment, $\mathbb{E}{({\widehat{S}}_h^x)}^4=m_4$, in addition to the exact matching of the first three moments.

Theorem 2.

Let ${\widehat{X}}_t^x$ be the discretization scheme defined by composition (6), where ${\widehat{S}}_h^x$ takes the values $x_1$, $x_2$, and $x_3$ defined in (21) with probabilities $p_1$, $p_2$, and $p_3$ defined in (19) $({\widehat{S}}_h^0=0)$. Then ${\widehat{X}}_t^x$ is a strongly potential second-order discretization scheme for the CIR equation.

Proof. 

Let us first check that

$$x_1=x+(A+\frac{3}{4})z-\sqrt{(3x+{(A+\frac{3}{4})}^{2}z)z}\ge 0$$

for all $x\ge 0$ and $z>0$. This is equivalent to

$${(A+\frac{3}{4})}^2{z}^2+2(A+\frac{3}{4})xz+x^2\ge {(A+\frac{3}{4})}^2{z}^2+3xz,$$

which in turn is equivalent to

$$(4A-3)xz+2x^2\ge 0.$$

This implies that $x_1\ge 0$ for all $x,z\ge 0$, provided that $A\ge 3/4$. Obviously, $x_2,x_3\ge x_1\ge 0$.

Now let us check the nonnegativity of $p_1$, $p_2$, and $p_3$. For $p_1$, we have

$$\begin{array}{cc}\hfill p_1& =\frac{m_1{x}_2{x}_3-m_2(x_2+x_3)+m_3}{x_1(x_3-x_1)(x_2-x_1)}\hfill \\ & =\frac{8xz((4A^2-5A+3)z+4x-(1-A)\sqrt{({(4A+3)}^{2}z+48x)z})}{((4A+3)z+4x-\sqrt{({(4A+3)}^{2}z+48x)z})\sqrt{({(4A+3)}^{2}z+48x)z}}\hfill \\ & \times \frac{1}{(\sqrt{({(4A+3)}^{2}z+48x)z}-3z)},\hfill \end{array}$$

where $x\ge 0,z>0$. We have already checked the nonnegativity of

$$4x+(4A+3)z-\sqrt{(48x+{(4A+3)}^{2}z)z}=4x_1.$$

The positivity of $\sqrt{{(4A+3)}^{2}z+48x)z}-3z$ is obvious, and $4A^2-5A+3>0$ for all $A\in \mathbb{R}$. Thus, clearly, $p_1\ge 0$ if $A\ge 1$. Now let $A<1$. Then $p_1\ge 0$ if and only if

$${((4A^2-5A+3)z+4x)}^2\ge {(1-A)}^2({(4A+3)}^{2}z+48x)z$$

or, equivalently,

$$-A(4A-3)(2A-3)z^2-2(2A-1)(A-3)xz+4x^2\ge 0,$$

which clearly holds for all $x\ge 0$ and $z>0$ if $A\in [3/4,3/2]$. Thus, $p_1\ge 0$ for $x\ge 0$ and $z>0$ if $A\in [3/4,3/2]$. For $p_2$, we obviously have

$$\begin{array}{cc}\hfill p_2& =\frac{m_2(x_1+x_3)-m_1{x}_1{x}_3-m_3}{x_2(x_2-x_1)(x_3-x_2)}\hfill \\ & =\frac{32xz(Az+x)}{(-3z+\sqrt{({(4A+3)}^{2}z+48x)z})(Az+x)(3z+\sqrt{({(4A+3)}^{2}z+48x)z})}\hfill \\ & =\frac{32xz}{16A^2{z}^2+24A{z}^2+48xz}=\frac{4x}{2A^{2}z+3Az+6x}\ge 0\hfill \end{array}$$

for $x\ge 0,z>0$. Finally, for $p_3$, we have

$$\begin{array}{cc}\hfill p_3& =\frac{m_1{x}_1{x}_2-m_2(x_1+x_2)+m_3}{x_3(x_3-x_2)(x_3-x_1)}\hfill \\ & =\frac{8xz((4A^2-5A+3)z+4x-(A-1)\sqrt{({(4A+3)}^{2}z+48x)z})}{((4A+3)z+4x+\sqrt{({(4A+3)}^{2}z+48x)z})\sqrt{({(4A+3)}^{2}z+48x)z}}\hfill \\ & \times \frac{1}{(\sqrt{({(4A+3)}^{2}z+48x)z}+3z)}\hfill \end{array}$$

for $x\ge 0$ and $z>0$. The numerator is obviously positive, and the nonnegativity of the denominator follows similarly to that of $p_1$.

Let us check that, indeed, the central moments of ${\widehat{S}}_h^x$ satisfy conditions (7)–(12) (with $\gamma =1/2$). The first three are obvious, since the moments of the random variable ${\widehat{S}}_h^x$ exactly match the three first moments of $S_h^x$, so they also match the first three central moments:

$$\begin{array}{c}\hfill \mathbb{E}({\widehat{S}}_h^x-x)=\mathbb{E}(S_h^x-x)=0,\mathbb{E}{({\widehat{S}}_h^x-x)}^2=\mathbb{E}{(S_h^x-x)}^2=xz,\end{array}$$

$$\begin{array}{c}\hfill \mathbb{E}{({\widehat{S}}_h^x-x)}^3=\mathbb{E}{(S_h^x-x)}^3=3x{z}^2/2.\end{array}$$

Conditions (10), (11), and (13) are satisfied, since, respectively,

$$\begin{array}{c}\hfill \mathbb{E}{({\widehat{S}}_h^x-x)}^4=(-2A^2+3A+9/4)x{z}^3+3x^2{z}^2=3x^2{z}^2+O(h^3),\end{array}$$

$$\begin{array}{cc}\hfill |\mathbb{E}{({\widehat{S}}_h^x-x)}^5|& =|(-6A^3+3A^2+9A+27/8)x{z}^4+(6A+9)x^2{z}^3|=O(h^3),\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathbb{E}{({\widehat{S}}_h^x-x)}^6& =(-14A^4-3A^3+(45/2)A^2+(81/4)A+81/16)x{z}^5\hfill \\ & +(6A^2+36A+81/4)x^2{z}^4+9x^3{z}^3=O(h^3)\hfill \end{array}$$

for $A\in [3/4,3/2]$.

Finally, by the last relation and the expression of the maximal value $x_3$ of ${\widehat{S}}_h^x$, condition (12) is satisfied for every $f\in C_{\mathrm{pol}}^{\infty }(\mathbb{D})$ (suppose $|f^{(6)}(x)|\le C_6(1+x^{k_6})$):

$$\begin{array}{cc}\hfill \mathbb{E}& \left[\underset{0\le s\le {\widehat{S}}_h^x}{max}\left|f^{(6)}(s)\right|{({\widehat{S}}_h^x-x)}^6\right]\le \underset{0\le s\le x_3}{max}\left|f^{(6)}(s)\right|\mathbb{E}{({\widehat{S}}_h^x-x)}^6\hfill \\ & \le C_6(1+x_3^{k_6})\mathbb{E}{({\widehat{S}}_h^x-x)}^6\le C(1+x^{k_6+1})\mathbb{E}{({\widehat{S}}_h^x-x)}^6=\mathcal{O}(h^3).\hfill \end{array}$$

It remains to check that the discretization scheme ${\widehat{S}}_h^x$ has uniformly bounded moments, that is, that there exists $h_0>0$ such that

$$\begin{array}{c}\hfill \underset{0<h\le h_0}{sup}\underset{t\in {\Delta }^h}{sup}\mathbb{E}(|\widehat{S}(x,t){|}^p)<+\infty ,p\in \mathbb{N},x\ge 0.\end{array}$$

By elementary but tedious calculations, we arrive at the following expression for the moments:

$$\begin{array}{cc}\hfill \mathbb{E}{({\widehat{S}}_h^x)}^p& =x^p+\frac{p(p-1)}{2}{x}^{p-1}z+\frac{p{\left(p-1\right)}^2\left(p-2\right)}{8}{x}^{p-2}{z}^2+\dots \hfill \\ \hfill & \le x^p+C(1+x^p)h=x^p(1+Ch)+Ch,x\ge 0,h\le h_0=\frac{1}{{\sigma }^2},\hfill \end{array}$$

where the constant $C>0$ depends on p and $\sigma$, from which the boundedness of the moments of the approximation follows in a standard way (see [5] [Prop. 1.5]). □

Remark 3.

(Third-order approximation for the stochastic part of the CIR equation) By a similar procedure, we can obtain a strongly potential third-order weak approximation of the stochastic part (5) of the CIR Equation (1) ($\gamma =1/2$). Although composition (6) then theoretically gives only second-order approximation, numerical simulations show that, practically, it gives a slightly better accuracy of approximation than with second-order approximation of the stochastic part.

Let $m_i=m_i(x,h)=\mathbb{E}{(S_h^x)}^p$, $i=1,2,3,4$. We look at a discretization scheme ${\widehat{S}}_h^x$ taking four values $x_1,x_2,x_3,x_4$ with probabilities $p_1,p_2,p_3,p_4$ such that

$$\begin{array}{cc}\hfill x_1^i{p}_1+x_2^i{p}_2+x_3^i{p}_3+x_4^i{p}_4& =m_i,i=1,2,3,4,\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill 1-1x_1^i{p}_1+x_2^i{p}_2+x_3^i{p}_3+x_4^i{p}_4& =m_i+O(h^3),i=5,6,7,8.\hfill \end{array}$$

(23)

Its solution with respect to $x_1$, $x_2$, $x_3$, and $x_4$ is as follows:

$$\begin{array}{cc}\hfill p_1& =-\frac{m_1{x}_2{x}_3{x}_4-m_2(x_2{x}_3+x_2{x}_4+x_3{x}_4)+m_3(x_2+x_3+x_4)-m_4}{x_1\left(x_1-x_4\right)\left(x_1-x_3\right)\left(x_1-x_2\right)},\hfill \\ \hfill p_2& =\frac{m_1{x}_1{x}_3{x}_4-m_2(x_1{x}_3+x_1{x}_4+x_3{x}_4)+m_3(x_1+x_3+x_4)-m_4}{\left(x_1-x_2\right)x_2\left(x_2-x_4\right)\left(x_2-x_3\right)},\hfill \\ \hfill p_3& =-\frac{m_1{x}_1{x}_2{x}_4-m_2(x_1{x}_2+x_1{x}_4+x_2{x}_4)+m_3(x_1+x_2+x_4)-m_4}{\left(x_2-x_3\right)\left(x_1-x_3\right)x_3\left(x_3-x_4\right)},\hfill \\ \hfill p_4& =\frac{m_1{x}_1{x}_2{x}_3-m_2(x_1{x}_2+x_1{x}_3+x_2{x}_3)+m_3(x_1+x_2+x_3)-m_4}{x_4\left(x_3-x_4\right)\left(x_2-x_4\right)\left(x_1-x_4\right)}.\hfill \end{array}$$

(24)

Again, after a number of experiments, we chose to look for a solution of (22) and (23), together with ${\sum }_i{p}_i=1$ and $p_i\ge 0$, in the form

$$\begin{array}{cc}\hfill x_{1,3}=x+& A_{1}z\mp \sqrt{(B_{1}x+C_{1}z)z}\ge 0,\hfill \\ \hfill x_{2,4}=x+& A_{2}z\mp \sqrt{(B_{2}x+C_{2}z)z}\ge 0,\hfill \end{array}$$

with parameters $A_1,A_2,B_1,B_2,C_1,C_2>0$ and probabilities $p_1$, $p_2$, $p_3$, $p_4$ defined in (24). The main difficulty was obtaining a nonnegative solution $\{x_1,x_2,x_3,x_4,p_1$, $p_2$, $p_3$, $p_4\}$.

The final result is a strongly potential third-order weak approximation ${\widehat{S}}_h^x$ of the stochastic part (5) of the CIR equation taking the four values

$$\begin{array}{cc}\hfill x_{1,2}=& x+\frac{3}{2}z\mp \sqrt{\left((3-\sqrt{6})x+\frac{3}{4}z\right)z},\hfill \\ \hfill x_{3,4}=& x+\left(\frac{3}{2}+\frac{1}{2}\sqrt{6}\right)z\mp \sqrt{\left((3+\sqrt{6})x+\left(\frac{15}{4}+\frac{3}{2}\sqrt{6}\right)z\right)z},\hfill \end{array}$$

(25)

with the corresponding probabilities $p_i$, $i=1,2,3,4,$ given by (24).

5. A Strongly Potential Second-Order Approximation of the CKLS Equations

In this section, we apply to the CKLS equations the method of constructing second-order approximations used in the previous section in the CIR case. As an example, we present strongly potential second-order approximations in the cases $\gamma =3/4$ and $\gamma =5/6$, where the results look relatively simple.

Let $\gamma =3/4$ in the CKLS Equation (1). Then for the stochastic part $\mathrm{d}{S}_t^x=\sigma {(S_t^x)}^{3/4}\mathrm{d}{B}_t$, $S_0^x=x\ge 0$, we have (see [8], Appendix)

$$\begin{array}{cc}\hfill m_1& =x,\hfill \\ \hfill m_2& =x^2+x^{3/2}z+\frac{3}{16}x{z}^2,\hfill \\ \hfill m_3& =x^3+3x^{5/2}z+\frac{45}{16}{x}^2{z}^2+\frac{15}{16}{x}^{3/2}{z}^3+\frac{45}{512}x{z}^4.\hfill \end{array}$$

In [8], we have constructed a strongly potential first-order two-valued approximation of the stochastic part with

$$\begin{array}{c}\hfill x_{1,2}=\frac{m_2}{m_1}\mp \sqrt{\frac{m_2(m_2-m_1^2)}{m_1^2}}.\end{array}$$

(26)

In particular, for $\gamma =3/4$,

$$\begin{array}{cc}\hfill x_{1,2}& =x+x^{1/2}z+\frac{3}{16}{z}^2\mp \sqrt{\left(x^{3/2}+\frac{19}{16}xz+\frac{3}{8}{x}^{1/2}{z}^2+\frac{9}{256}{z}^3\right)z}.\hfill \end{array}$$

This motivated us to look for the second-order approximations with values of the following form:

$$\begin{array}{cc}\hfill x_{1,3}=x+A_1{x}^{1/2}z+& A_2{z}^2\mp \sqrt{\left(B_1{x}^{3/2}+B_{2}xz+B_3{x}^{1/2}{z}^2+B_4{z}^3\right)z},\hfill \\ \hfill x_2=x+C_1{x}^{1/2}z+& C_2{z}^2,A_1,A_2,B_1,B_2,B_3,B_4,C_1,C_2>0,\hfill \end{array}$$

with probabilities (19). Using the same method as in the CIR case, after tedious and rather complex calculations, we arrived at the scheme with values

$$\begin{array}{cc}\hfill x_{1,3}& =x+\frac{5}{2}{x}^{1/2}z+\frac{15}{64}{z}^2\hfill \\ & \mp \sqrt{\left(3x^{3/2}+\frac{103}{16}xz+\frac{75}{64}{x}^{1/2}{z}^2+\frac{225}{4096}{z}^3\right)z},\hfill \\ \hfill x_2& =x+\frac{11}{8}{x}^{1/2}z+\frac{15}{64}{z}^2,\hfill \end{array}$$

(27)

and probabilities $p_1$, $p_2$, and $p_3$ defined in (19). Similarly, in the case $\gamma =5/6$, we have

$$\begin{array}{cc}\hfill m_1& =x,\hfill \\ \hfill m_2& =x^2+x^{5/3}z+\frac{5}{18}{x}^{4/3}{z}^2+\frac{5}{243}x{z}^3,\hfill \\ \hfill m_3& =x^3+3x^{8/3}z+\frac{10}{3}{x}^{7/3}{z}^2+\frac{140}{81}{x}^2{z}^3+\frac{35}{81}{x}^{5/3}{z}^4+\frac{35}{729}{x}^{4/3}{z}^5+\frac{35}{19683}x{z}^6.\hfill \end{array}$$

The corresponding approximation takes the values

$$\begin{array}{cc}\hfill x_{1,3}& =x+\frac{3}{2}{x}^{2/3}z+\frac{485}{816}{x}^{1/3}{z}^2+\frac{1681}{22032}{z}^3\hfill \\ \hfill & \mp ((3x^{5/3}+\frac{2077}{612}z{x}^{4/3}+\frac{1162907}{1997568}{x}^{2/3}{z}^3\hfill \\ & +\frac{815285}{8989056}{x}^{1/3}{z}^4+\frac{2825761}{485409024}{z}^5+\frac{125695}{66096}{z}^{2}x)z{)}^{1/2},\hfill \\ \hfill x_2& =x+\frac{1}{4}{x}^{2/3}z+\frac{5}{72}{x}^{1/3}{z}^2+\frac{1}{72}{z}^3,\hfill \end{array}$$

(28)

with probabilities $p_1$, $p_2$, and $p_3$ defined in (19).

In summary, we have the following:

Theorem 3.

Let ${\widehat{X}}_t^x$ be the discretization scheme defined by composition (6), where ${\widehat{S}}_h^x$ takes the values $x_1$, $x_2$, and $x_3$ defined in (27) in the case $\gamma =3/4$ or in (28) in the case $\gamma =5/6$ with probabilities $p_1$, $p_2$, and $p_3$ defined in (19) $({\widehat{S}}_h^0=0)$. Then ${\widehat{X}}_t^x$ is a strongly potential second-order discretization scheme for the CKLS equation with $\gamma =3/4$ or $\gamma =5/6$, respectively.

6. Simulation Examples

We indicate a particular $\gamma$ of the stochastic part (5) by the left subscript $\gamma$ as in ${}_{\gamma }{S}_t^x$.

We first give a short algorithm for calculating ${\widehat{X}}_{(i+1)h}$ given ${\widehat{X}}_{ih}=x$ at each simulation step i:

• Substitute $x:=D(x,h/2).$
• Draw a uniform random number U in the interval $[0,1]$.
• Generate a random variable $\widehat{S}$ taking the values $x_1$, $x_2$, and $x_3$ defined by (21), (27), or (28) (for ${}_{1/2}{\widehat{S}}_h^x$, ${}_{3/4}{\widehat{S}}_h^x$, or ${}_{5/6}{\widehat{S}}_h^x$, respectively) with probabilities $p_1$, $p_2$ and $p_3$ defined in (19):
  if $U<p_1$, then $\widehat{S}:=x_1$; otherwise, if $U<p_1+p_2$, then $\widehat{S}:=x_2$; otherwise, $\widehat{S}:=x_3$. If $x=0$, then $\widehat{S}:=0$.
• Calculate (see (6))

  $$\begin{array}{c}\hfill {\widehat{X}}_{(i+1)h}=D\left(\widehat{S},h/2\right).\end{array}$$

In the case of a strongly potential third-order approximation of ${}_{1/2}{\widehat{S}}_h^x$, step (3) should be replaced by

(3’)

Generate a random variable $\widehat{S}$ taking the values $x_1$, $x_2$, $x_3$, and $x_4$ defined by (25) with probabilities $p_1$, $p_2$, $p_3$, and $p_4$ defined in (24):

if $U<p_1$, then $\widehat{S}:=x_1$; otherwise, if $U<p_1+p_2$, then $\widehat{S}:=x_2$; otherwise, if $U<p_1+p_2+p_3$, then $\widehat{S}:=x_3$; otherwise, $\widehat{S}:=x_4$. If $x=0$, then $\widehat{S}:=0$.

Using our discretization schemes, we simulate the solutions of the CLKS Equation (1) or its stochastic part (5) for $\gamma =1/2$, $3/4$, and $5/6$ with test functions $f(x)=x^3$, $x^4$, $x^5$, and ${\mathrm{e}}^{-x}$. Such a choice of f is motivated by having explicit formulas for the expectations $\mathbb{E}f(S_t^x)$ (see Appendix A) and, in the case $\gamma =1/2$,

$$\mathbb{E}{\mathrm{e}}^{-X_t^x}={\left(\frac{\beta }{1/2{\sigma }^2\left(1-{\mathrm{e}}^{-\beta t}\right)+\beta }\right)}^{2\frac{\theta }{{\sigma }^2}}{\mathrm{e}}^{-\frac{x\beta {\mathrm{e}}^{-\beta t}}{1/2{\sigma }^2\left(1-{\mathrm{e}}^{-\beta t}\right)+\beta }}$$

(see, e.g., [11] [Prop. 6.2.4]). We also simulate the solution of the CLKS Equation (1) for $\gamma =1/2$ (i.e., the CIR equation) with discretization scheme defined in (24) and (25) and test function $f(x)={\mathrm{e}}^{-x}$.

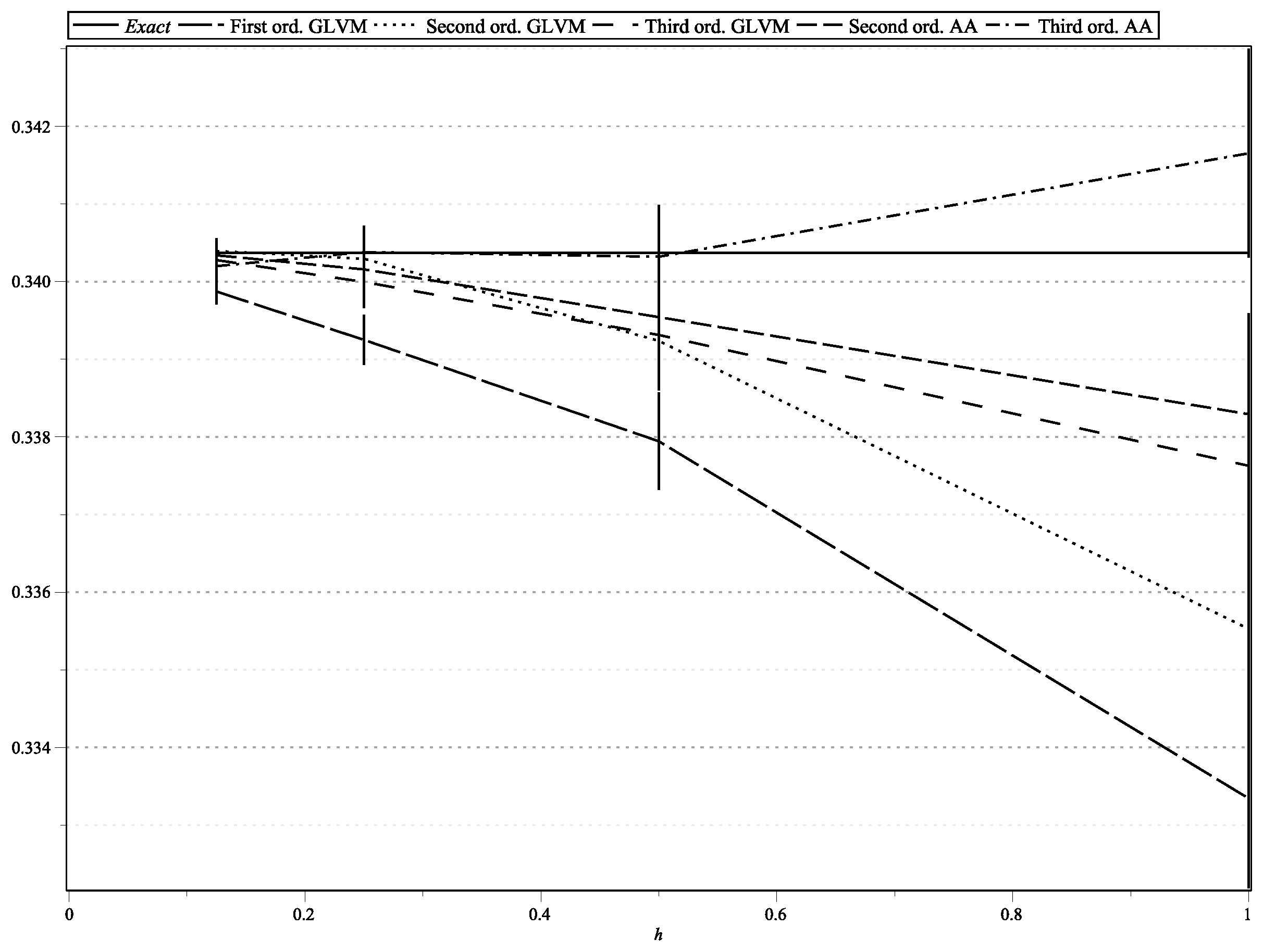
Below, we present the results by a number of figures, where the exact and approximate expectations are given as functions of the approximation step size h. For the reader’s convenience, we give a list of graphs in the figures:

• Figure 1 and Figure 2: $\mathbb{E}{e}^{-{(}_{1/2}{X}_1^x)}$ and $\mathbb{E}{e}^{-{(}_{1/2}{\widehat{X}}_1^x)}$ with the same parameters as in Alfonsi [5];
• Figure 3 and Figure 4: $\mathbb{E}{{(}_{3/4}{S}_1^x)}^3$ and $\mathbb{E}{{(}_{3/4}{\widehat{S}}_1^x)}^3$;
• Figure 5 and Figure 6: $\mathbb{E}{{(}_{3/4}{S}_1^x)}^4$ and $\mathbb{E}{{(}_{3/4}{\widehat{S}}_1^x)}^4$;
• Figure 7 and Figure 8: $\mathbb{E}{{(}_{3/4}{S}_1^x)}^5$ and $\mathbb{E}{{(}_{3/4}{\widehat{S}}_1^x)}^5$;
• Figure 9 and Figure 10: $\mathbb{E}{{(}_{5/6}{S}_1^x)}^3$ and $\mathbb{E}{{(}_{5/6}{\widehat{S}}_1^x)}^3$;
• Figure 11 and Figure 12: $\mathbb{E}{{(}_{5/6}{S}_1^x)}^4$ and $\mathbb{E}{{(}_{5/6}{\widehat{S}}_1^x)}^4$;
• Figure 13 and Figure 14: $\mathbb{E}{{(}_{5/6}{S}_1^x)}^5$ and $\mathbb{E}{{(}_{5/6}{\widehat{S}}_1^x)}^5$;
• Figure 15 and Figure 16: $\mathbb{E}{e}^{-{(}_{3/4}{\widehat{X}}_1^x)}$;
• Figure 17 and Figure 18: $\mathbb{E}{e}^{-{(}_{5/6}{\widehat{X}}_1^x)}$.

Figure 1, Figure 15, and Figure 17 represent the values of $\mathbb{E}{\mathrm{e}}^{-X_1^x}$ with “low” volatility ($\sigma =0.8$, $\theta =0.5$, $\beta =0.5$, $x_0=1.5$). Figure 2, and Figure 16 and Figure 18 represent the values of $\mathbb{E}{\mathrm{e}}^{-X_1^x}$ with “high” volatility ($\sigma =2.0$, $\theta =0.04$, $\beta =0.1$, $x_0=0.3$). Figure 3, Figure 5, Figure 7, Figure 9, Figure 11, and Figure 13 represent values of $\mathbb{E}f(S_1^x)$ with “low” volatility ($\sigma =0.8$, $x_0=1.5$). Figure 4, Figure 6, Figure 8, Figure 10, Figure 12, and Figure 14 represent the values of $\mathbb{E}f(S_1^x)$ with “high” volatility ($\sigma =1.5$, $x_0=0.3$). In all the graphs, the error bars show 95% confidence intervals. To shorten the bars, for approximation time-step sizes $h=1/2^i$, $i=0,1,2,3,4,5$, we have generated $N=90,000·4^i$ samples of approximations.

In the legends of figures, we use the following notation.

• “First ord. GLVM”: the modified first-order scheme for CIR [8] [Rem. 4] (for comparison with higher-order schemes);
• “Second ord. GLVM”: our second-order scheme for CIR (Thm. 2);
• “Third ord. GLVM”: the second-order composition (6) with our third-order scheme ${}_{1/2}{\widehat{S}}_h^x$ taking the values $x_1$, $x_2$, $x_3$, and $x_4$ defined in (25) with probabilities $p_1$, $p_2$, $p_3$, and $p_4$ defined in (24)’
• “First ord.”: our first-order scheme for CKLS [8] [Thm. 2];
• “Second ord.”: our second-order schemes for CKLS (Thm. 3);
• “Second ord. AA”: the second-order scheme of Alfonsi for CIR [5] [Thm. 2.8];
• “Third ord. AA”: the third-order scheme of Alfonsi for CIR [5] [Thm. 3.7].

7. Conclusions

We have constructed second-order weak split-step approximations of the Chan–Karolyi–Longstaff–Sanders (CKLS) and constant elasticity of variance (CEV) processes. The approximations use generation of a three−valued random variable at each discretization step. To illustrate the accuracy of constructed approximations, we performed several simulations with different parameters and test functions. Our method can be applied to constructing second-order weak approximations for other stochastic differential equations. It would be interesting to construct third-order weak approximations for the CKLS equations, as we did for the CIR equation.