Modified Inertial Forward–Backward Algorithm in Banach Spaces and Its Application
Abstract
1. Introduction
- (1)
- (2)
- Can we extend corresponding results in [12] from one strongly monotone operator to a finite family of strongly accretive operators?
- (3)
- Can we extend the corresponding results in [12] from one cocoercive operator to a finite family of inverse strongly accretive operators?
- (4)
- Can the restrictions imposed on the parameters in [12] be relaxed?
| Algorithm 1: The hybrid forward–backward algorithm. |
 |
2. Preliminaries
- (1)
- Uniformly smooth if as ;
- (2)
- q-Uniformly smooth if there exists a fixed constant such that , where .
- (1)
- Nonexpansive if
- (2)
- r-Contractive if there exists such that
- (3)
- η-Strongly accretive if for all there exists and such that
- (4)
- μ-Inverse-strongly accretive if for all there exists and such that
- (1)
- Accretive if for any there exists such that for all and
- (2)
- m-Accretive if T is accretive and for every (equivalently, for some) where I is the identity mapping.
- (i)
- Q is sunny and nonexpansive;
- (ii)
- ;
- (iii)
- ;
- (iv)
- .
- (1)
- Given and
- (2)
- Given there exists a continuous, strictly increasing and convex function with such that for all
- (i)
- ;
- (ii)
- ;
- (iii)
- .
3. Main Results
- (A1)
- E is a uniformly convex and q-uniformly smooth Banach space, and A is m-accretive;
- (A2)
- is -inverse-strongly accretive with constants for each , and ;
- (A3)
- is -Lipschitzian and -strongly accretive with constants for each , and ;
- (A4)
- and .
- (i)
- ;
- (ii)
- ;
- (iii)
- ;
- (iv)
- , .
| Algorithm 2: The modified hybrid forward–backward algorithm. |
 |
- The results in this paper extend corresponding results in [12] from one strongly monotone operator to a finite family of strongly accretive operators.
- The results in this paper extend corresponding results in [12] from one cocoercive operator to a finite family of inverse-strongly accretive operators.
- We omit the condition , which is very necessary in Theorem 1 of Liu et al. [12].
- The proof of our Theorem 1 is very different from the proof of Theorem 1 of Liu et al. [12].
4. Application to Constrained Convex Minimization Problems
| Algorithm 3: The modified hybrid forward–backward algorithm. |
 |
- (i)
- ;
- (ii)
- ;
- (iii)
- ;
- (iv)
- .
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martinet, B. Regularisation d’inéquations variationelles par approximations successives. Rev. Fr. Informat. Rech. Oper. 1970, 4, 154–158. [Google Scholar]
- Martinet, B. Détermination approchée d’un point fixe d’une application pseudo-contractante. Cas L’Application Prox’ C.R. Acad. Sci Paris Sér. A Math. 1972, 274, 163–165. [Google Scholar]
- Rockafellar, R.T. Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 1976, 14, 877–898. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Augmented Lagrangians and applications of the proximal point algorithm in convex programming. Math. Oper. Res. 1976, 1, 97–116. [Google Scholar] [CrossRef]
- Bruck, R.E.; Reich, S. Nonexpansive projections and resolvents of accretive operators in Banach spaces. Houst. J. Math. 1977, 3, 459–470. [Google Scholar]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: New York, NY, USA, 2011. [Google Scholar]
- Cholamjiak, P. A generalized forward-backward splitting method for solving quasi inclusion problems in Banach spaces. Numer. Algor. 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Combettes, P.L.; Wajs, V.R. Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 2005, 4, 1168–1200. [Google Scholar] [CrossRef]
- López, G.; Martín-Márquez, V.; Wang, F.H.; Xu, H.K. Forward-Backward splitting methods for accretive operators in Banach spaces. Abstr. Appl. Anal. 2012, 2012, 109236. [Google Scholar] [CrossRef]
- Dadashi, V.; Postolache, M. Forward-backward splitting algorithm for fixed point problems and zeros of the sum of monotone operators. Arab. J. Math. 2020, 9, 89–99. [Google Scholar] [CrossRef]
- Tseng, P. A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 2000, 38, 431–446. [Google Scholar] [CrossRef]
- Liu, L.; Qin, X.; Yao, J.C. A hybrid forward-backward algorithm and its optimization application. Mathematics 2020, 8, 447. [Google Scholar] [CrossRef]
- Alvarez, F.; Attouch, H. An inertial proximal method for monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Polyak, B.T. Introduction to Optimization; Optimization Software: New York, NY, USA, 1987. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iterarive metheods. Zh. Vychisl. Mat. Mat. Fiz. 1964, 4, 1–17. [Google Scholar]
- Lorenz, D.A.; Pock, T. An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 2015, 51, 311–325. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. A weak-to-strong convergence principle for Fejér-monotone methods in Hilbert spaces. Math. Oper. Res. 2001, 26, 248–264. [Google Scholar] [CrossRef]
- Yao, Y.; Cho, Y.J.; Liou, Y.C. Algorithms of common solutions for variational inclusions, mixed equilibrium problems and fixed point problems. Eur. J. Oper. Res. 2011, 212, 242–250. [Google Scholar] [CrossRef]
- Thong, D.V.; Cholamjiak, P. Strong convergence of a forward-backward splitting method with a new step size for solving monotone inclusions. Comput. Appl. Math. 2019, 38, 1–16. [Google Scholar] [CrossRef]
- Yao, Z.; Wu, Y.K.; Wen, C.F. Strong convergence analysis of iterative algorithms for solving variational inclusions and fixed-point problems of pseudocontractive operators. J. Math. 2021, 2021, 1–7. [Google Scholar] [CrossRef]
- Tan, B.; Qin, X.; Yao, J.C. Strong convergence of self-adaptive inertial algorithms for solving split variational inclusion problems with applications. J. Sci. Comput. 2021, 87, 1–34. [Google Scholar] [CrossRef]
- Reich, S. Asymptotic behavior of contractions in Banach spaces. J. Math. Anal. Appl. 1973, 44, 57–70. [Google Scholar] [CrossRef]
- Song, Y.L.; Ceng, L.C. A general iteration scheme for variational inequality problem and common fixed point problems of nonexpansive mappings in q-uniformly smooth Banach spaces. J. Glob. Optim. 2013, 57, 1327–1348. [Google Scholar] [CrossRef]
- Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Pongsakorn, S.; Poom, K. Iterative methods for variational inequality problems and fixed point problems of a countable family of strict pseudo-contractions in a q-uniformly smooth Banach space. Fixed Point Theory Appl. 2012, 2012. [Google Scholar] [CrossRef]
- Song, Y.L.; Ceng, L.C. Convergence theorems for accretive operators with nonlinear mappings in Banach spaces. Abstr. Appl. Anal. 2014, 12, 1–12. [Google Scholar] [CrossRef]
- Xu, H.K. Iterative algorithm for nonlinear operators. J. Lond. Math. Soc. 2002, 2, 1–17. [Google Scholar] [CrossRef]
- Mitrinović, D.S. Analytic Inequalities; Springer: New York, NY, USA, 1970. [Google Scholar]
- Maingé, P.E. The viscosity approximation process for quasi-nonexpansive mappings in Hilbert spaces. Comput. Math. Appl. 2010, 59, 74–79. [Google Scholar] [CrossRef]
- Song, Y.L.; Ceng, L.C. Strong convergence of a general iterative algorithm for a finite family of accretive operators in Banach spaces. Fixed Point Theory Appl. 2015, 2015, 90. [Google Scholar] [CrossRef]
- Xu, H.K. Viscosity approximation methods for nonexpansive mappings. J. Math. Anal. Appl. 2004, 298, 279–291. [Google Scholar] [CrossRef]
- Meng, S.; Xu, H.K. Remarks on the gradient-projection algorithm. J. Nonlinear Anal. Optim. 2010, 1, 35–43. [Google Scholar]
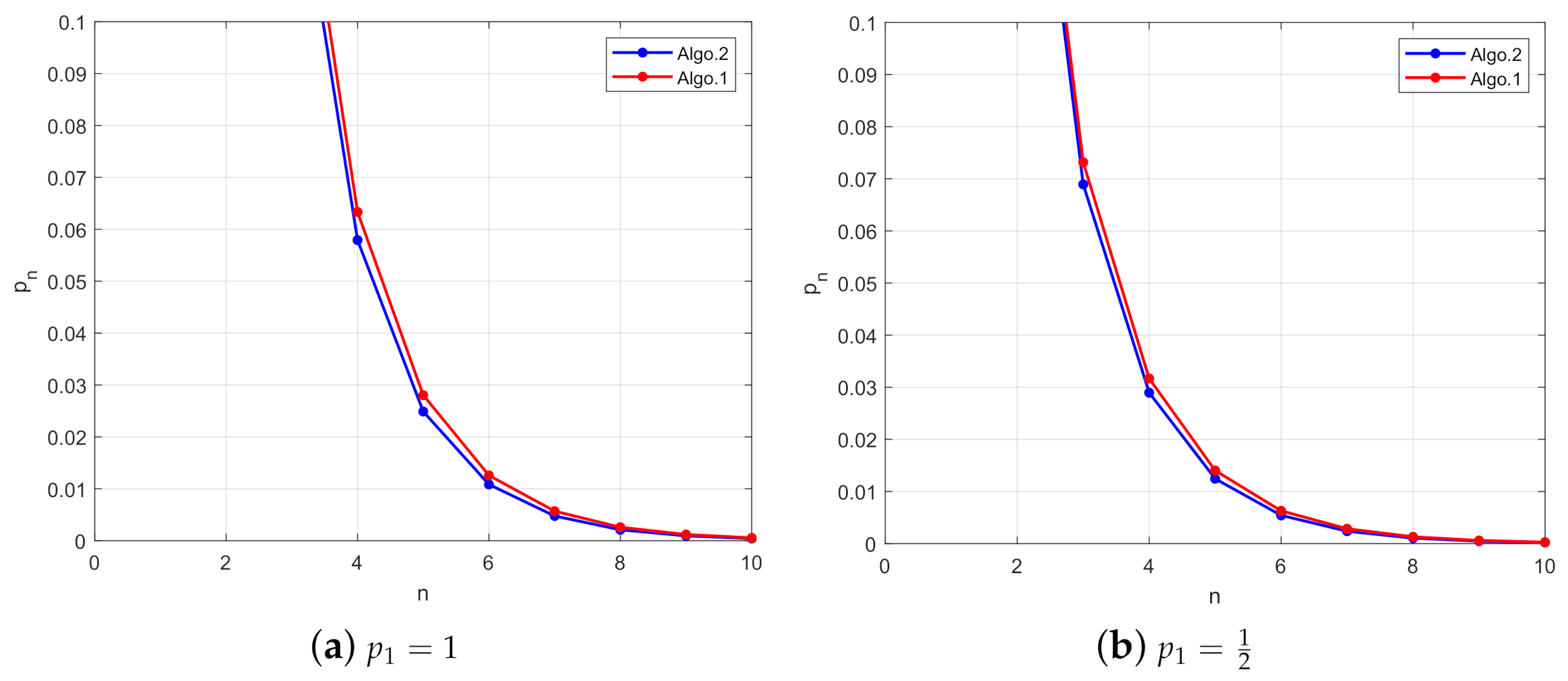
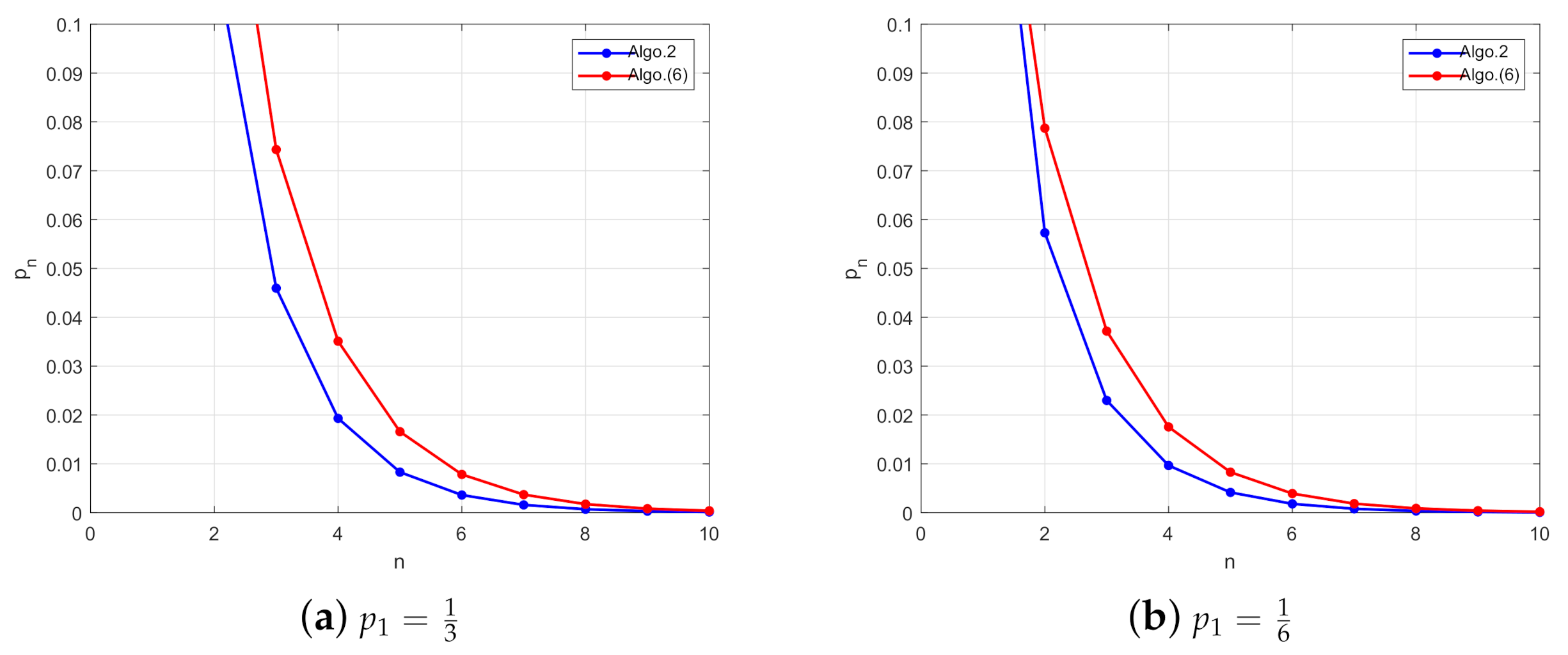
| Iter | ||||
|---|---|---|---|---|
| Algo. 2 | Algo. 1 | Algo. 2 | Algo. 1 | |
| n | ||||
| 1 | 1.000000000000 | 1.000000000000 | 0.500000000000 | 0.500000000000 |
| 2 | 0.343750000000 | 0.354166666667 | 0.171875000000 | 0.177083333333 |
| 3 | 0.137858072917 | 0.146339699074 | 0.068929036458 | 0.073169849537 |
| 4 | 0.057919537580 | 0.063346119738 | 0.028959768790 | 0.031673059869 |
| 5 | 0.024887301304 | 0.028043855092 | 0.012443650652 | 0.014021927546 |
| 6 | 0.010836345776 | 0.012580784993 | 0.005418172888 | 0.006290392496 |
| 7 | 0.004759714377 | 0.005693387653 | 0.002379857189 | 0.002846693827 |
| 8 | 0.002103623765 | 0.002592524735 | 0.001051811882 | 0.001296262367 |
| 9 | 0.000934030864 | 0.001185990048 | 0.000467015432 | 0.000592995024 |
| 10 | 0.000416205883 | 0.000544493888 | 0.000208102941 | 0.000272246944 |
| Iter | ||||
|---|---|---|---|---|
| Algo. 2 | Algo. (6) | Algo. 2 | Algo. (6) | |
| n | ||||
| 1 | 0.333333333333 | 0.333333333333 | 0.166666666667 | 0.166666666667 |
| 2 | 0.114583333333 | 0.157407407407 | 0.057291666667 | 0.078703703704 |
| 3 | 0.045952690972 | 0.074331275720 | 0.022976345486 | 0.037165637860 |
| 4 | 0.019306512527 | 0.035100880201 | 0.009653256263 | 0.017550440101 |
| 5 | 0.008295767101 | 0.016575415651 | 0.004147883551 | 0.008287707825 |
| 6 | 0.003612115259 | 0.007827279613 | 0.001806057629 | 0.003913639806 |
| 7 | 0.001586571459 | 0.003696215373 | 0.000793285730 | 0.001848107686 |
| 8 | 0.000701207922 | 0.001745435037 | 0.000350603961 | 0.000872717519 |
| 9 | 0.000311343621 | 0.000824233212 | 0.000155671811 | 0.000412116606 |
| 10 | 0.000138735294 | 0.000389221239 | 0.000069367647 | 0.000194610619 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Postolache, M. Modified Inertial Forward–Backward Algorithm in Banach Spaces and Its Application. Mathematics 2021, 9, 1365. https://doi.org/10.3390/math9121365
Song Y, Postolache M. Modified Inertial Forward–Backward Algorithm in Banach Spaces and Its Application. Mathematics. 2021; 9(12):1365. https://doi.org/10.3390/math9121365
Chicago/Turabian StyleSong, Yanlai, and Mihai Postolache. 2021. "Modified Inertial Forward–Backward Algorithm in Banach Spaces and Its Application" Mathematics 9, no. 12: 1365. https://doi.org/10.3390/math9121365
APA StyleSong, Y., & Postolache, M. (2021). Modified Inertial Forward–Backward Algorithm in Banach Spaces and Its Application. Mathematics, 9(12), 1365. https://doi.org/10.3390/math9121365







